58 Table 4-3: Percentage error in the estimation of the second order RC parameters with the addition of noise. The security, operational reliability along with ensuring optimal charging of any battery energy storage system (BESS), are the main objectives and the key features of the battery management system (BMS).
Overview
Battery cell protection techniques have been developed by recent research [6] [7]; to ensure that the battery does not encroach on the Safe Operating Area (SOA), leading to longer battery life. The time-varying nature of any battery's characteristics, which include the battery state of charge (SOC), along with impedance parameters, are the main challenges in monitoring battery conditions.
Research Motivation
Thesis Objectives
Thesis Contributions
Thesis Breakdown
Background
LITHIUM-ION BATTERY
Lithium-ion batteries are considered the most famous kind of batteries when it comes to laptops. There are several types of lithium-ion batteries in commercial use, such as lithium-cobalt oxide (LCO), lithium-ion iron phosphate (LFP), lithium-ion nickel manganese cobalt oxide (NMC), lithium nickel cobalt aluminum oxide (NCA) and lithium titanite (LTO).
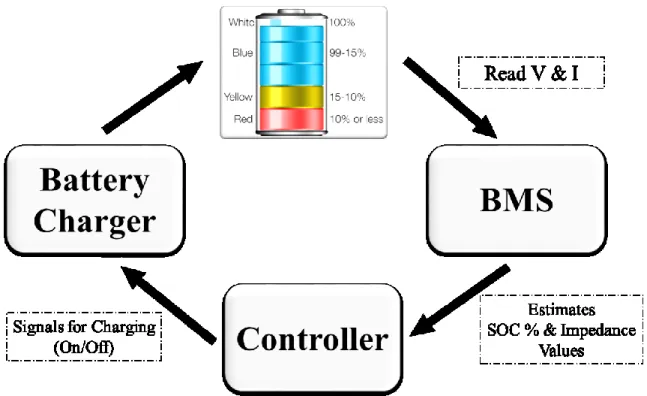
BATTERY MANAGEMENT SYSTEMS (BMS)
It should ensure that the energy of the battery is optimized to power the product. A feature of the BMS is tracking the state of charge (SOC) of the battery.
LITERATURE REVIEW
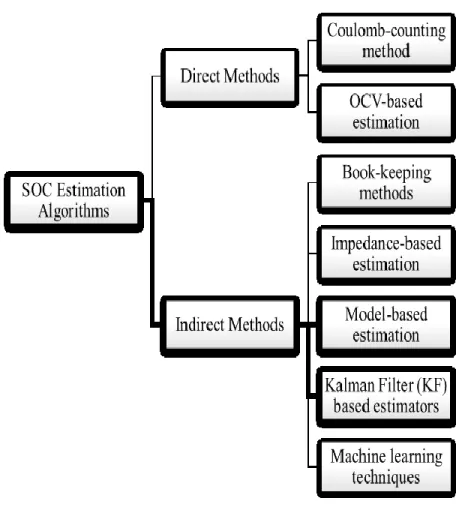
SOC Estimation Algorithms
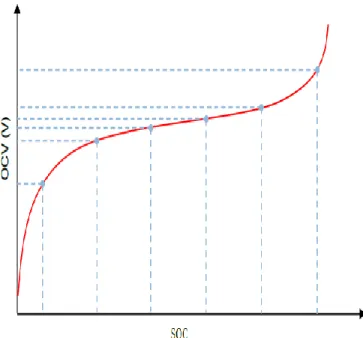
Battery SOC estimation can be done by relating SOC to battery OCV as shown in Figure 2-2. Similar to the OCV method, battery life affects the parameters of the estimation algorithm.
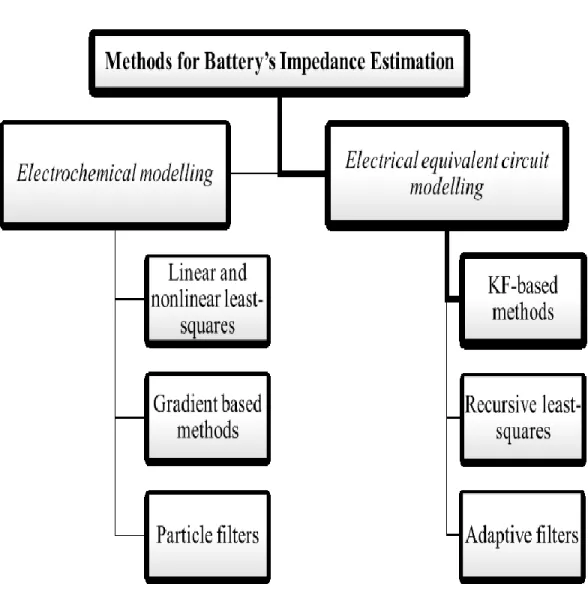
Battery Impedance Characterization Methods
However, and due to the fact that these methods require diverse and huge datasets, a considerable amount of overfitting, and probably require a lot of computational power, they have found that they are usually not applicable to web applications of battery management systems, whose main goal is to to be planned in low-cost controllers. Furthermore, these techniques are difficult to adapt to production variations and battery aging; and this is due to the open-loop nature of these methods. Electrical equivalent circuit models have been useful in many online algorithms for battery condition and parameter estimation.
For example, the authors take a collaborative EKF approach to real-time battery identification, where system unknowns are stacked into a single EKF for simultaneous estimation of model states and parameters. The disadvantage of collaborative EKF for online applications is the increased number of large matrix operations (e.g. matrix inversions) due to the high dimension of the augmented state model.
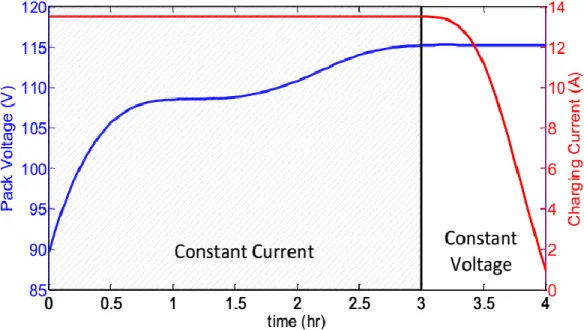
Charging Methods
The charging time of a battery is one of the most important issues in the large deployment of EVs. Pulse charging and negative pulse charging are also good charging strategies for fast charging of an EV battery [22]. A new pulse charging method, which is the variable voltage pulse charging strategy, was proposed in [25].
This method uses a very short discharge pulse during rest during pulse charging to depolarize the battery and remove any gas bubbles formed on the electrode during pulse charging. Negative pulse charging is said to improve the overall charging process and extend battery life.
Model Selection
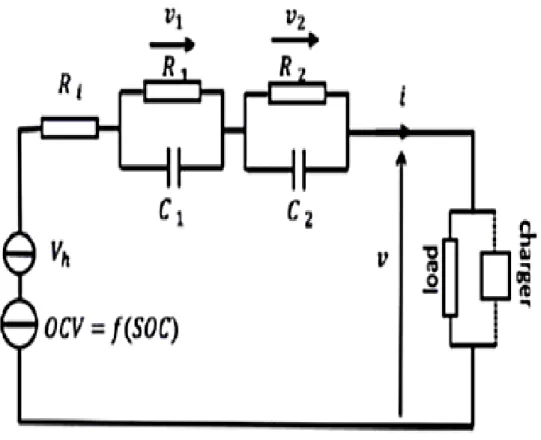
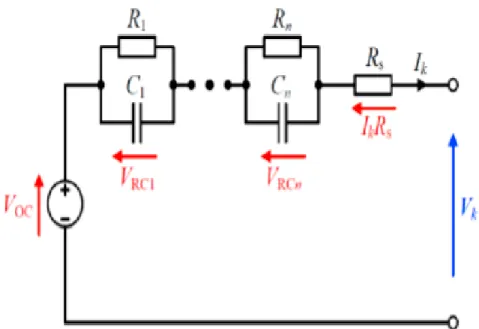
To achieve accurate modeling and state estimation, two key challenges need to be addressed, namely the hysteresis effect and the long relaxation process. In this thesis, we use a second-order electrical circuit model coupled with the hysteresis effect as shown in Figure 3-2, where OCV is the battery open-circuit voltage, and v and i are the battery terminal voltage and current, respectively. . R1C1 is used to capture the short-term relaxation dynamics of the battery, while R2C2 is used to capture the long-term relaxation process.
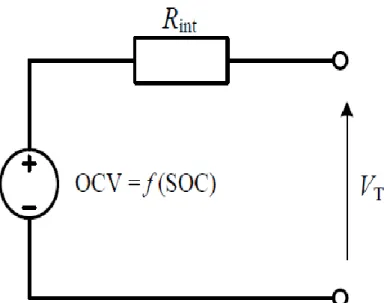
Battery OCV is the voltage across the battery terminals when the battery's internal balance is reached with no load. The battery's OCV depends on the battery's SOC, temperature and previous charge/discharge history, which is called the hysteresis effect and is captured by Vh.
Double-EKF System Identification
Underlying Theory
Due to the temporal variability of the model parameters, it is imperative that the actual cell input/output data (e.g., voltage, current, etc.) convey constant information about the parameters to be estimated. It should be noted that the algorithm is initialized assuming that the model states are known beforehand and the parameters are available. Note that for the parameter time update equation, the new parameter estimate 𝜃̂0− is equal to the previous estimate 𝜃̂𝑘−1+ with an increase in its uncertainty due to the presence of white process noise 𝐫𝑘.
It is noted that for the weight filter's measurement update equations, the total differential 𝐇k𝜃 of the model output equation ℎ(∙,∙,∙) with respect to parameters 𝛉𝑘 is required. 𝐋𝑥k−1 is weakly related to the parameter estimates 𝛉𝑘, so it can be safely neglected in (3-9) to improve the computational efficiency of the weight filter.
Estimation of EKF Noise Statistics
This allows the model parameters with slow transients to be assumed constant over the 100 second period. Note that the error covariance matrices 𝑷𝑥̃,0+ and 𝑷𝜃̃,0+ are set to a large value at the initialization time step 𝑘=0 in order to account for any uncertainty in the initial conditions of the filters.
Double-EKF Performance Under Incorrect Initial Conditions
Formulation of State-Space Equations
Considering the single RC branch, the transient voltage drop across 𝑉RC across the resistor 𝑅 and capacitor 𝐶 with respect to input current 𝐼 can be realized. This chapter highlights the result of applying the proposed methods and discusses its effectiveness in improving the state of charge and the overall charging performance. A set of case studies is considered to verify the robustness of the proposed controllers under different scenarios.
The results confirm the effectiveness of the proposed approaches for a large measure of the SOC estimation, hence the overall charging scheme.
Validate the Proposed Model
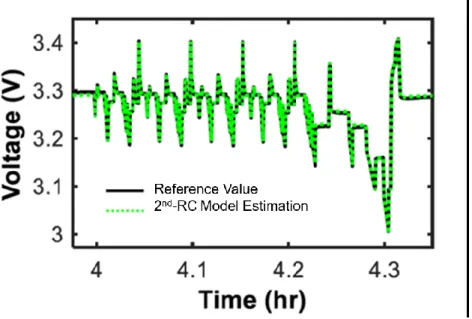
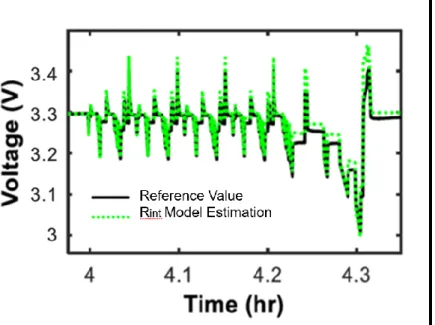
However, in general and for more accurate results in the rest of the research, the RC model showed a very good estimate for the long period of the procedure. Although telescoped and due to the robustness of the DEKF, the output results show a good estimate for both models, as shown in Figure 4-3. It can be observed that while the proposed RC model took almost 5 minutes to start tracking the benchmark, the Rint model took almost 3 times as long to start tracking around 14 minutes from scan initialization.
For estimation accuracy, and as predicted, the second-order RC had shown its accuracy with a maximum percentage error of only about 6%. In contrast, that maximum error value in the Rint model had reached almost double this number at about 13%.
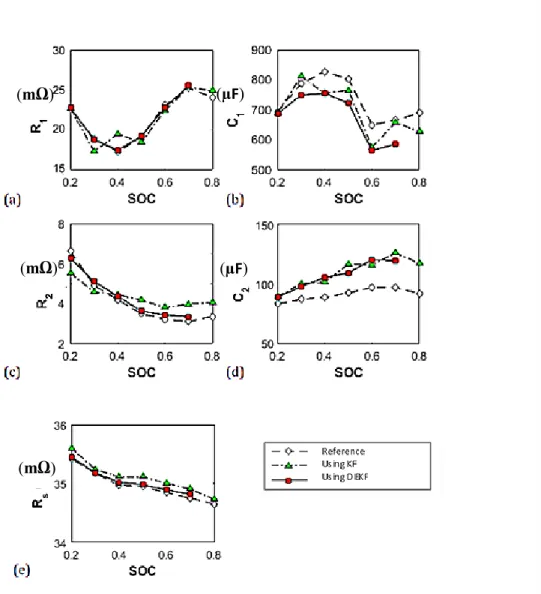
Model Parameter Identification
While Table 4-2 presents the total percentage error for all components using KF and DEKF. And as expected, the largest error in the estimated resistances than before was in R2, with 4.76%, and this is for DEKF, while for the same parameter in KF, the error percentage reached almost twice that of DKEF, with almost 7.5%. The best estimate was a record value of Rs with less than 0.5%, and this high accuracy for this parameter may be due to the fact that its estimation equations are not as complex as the other parameters.
Furthermore, the highest overall error percentage was recorded at C2, which may be related to the nature of the capacitors when using a mathematical representation of the system. The results for all parameters are shown in figure 4-5, while the overall error percentage for the second case are shown in table 4-3.
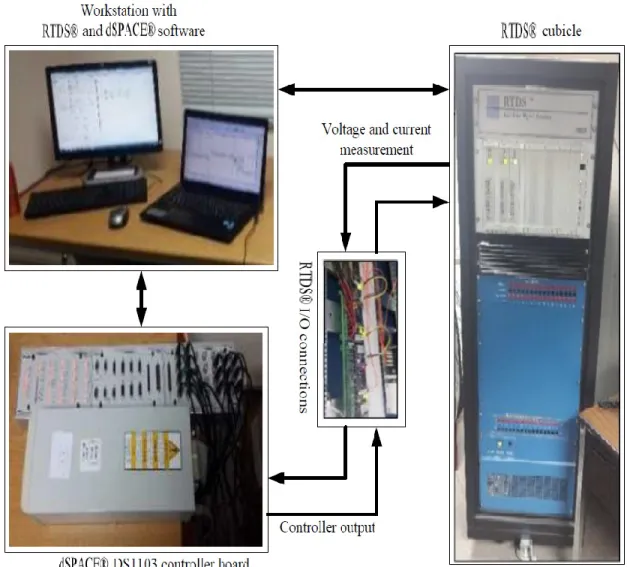
Real Time Digital Simulator (RTDS)
In this section, the two main case studies were implemented, namely the SOC estimation process, and the main purpose of the BMS, namely the charging procedure, is also presented here. It proves that the robustness of the DEKF method had led to accelerated trajectory and value estimation in both the simulation and RTDS from the start within minutes. It can be noted that after a reasonable time and after almost 80% of the SOC, the RTDS values deviate slightly from the simulation values.
This feature may have occurred due to the fact that the system has now moved from the flat loading region of 20-80% to the exponential part from 80%, and that was predicted and it was clearly shown in the RTDS results because it is almost as identical is like real life, and it was done in real time, while that incident was not clearly shown in the perfect environment of the simulation. As expected, the RTDS results showed a small discrepancy, but overall this could be neglected as the simulation and RTDS results generally followed the same pattern over the period of the experiment.
Conclusion
Starting with the validation of the selected model, throughout the assessment of the state of charge (SOC) and ending with the charging procedure, this work has shown a comprehensive study regarding the improvement of battery management systems.
Future Work
Johnso, “A battery state-of-charge indicator for electric wheelchairs,” in IEEE Transactions on Industrial Electronics, vol. Danzer, "A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles", Journal of Power Sources, vol. 34;State-of-Charge and State-of-Health Lithium-Ion Battery's Diagnosis According to Surface Temperature Variation," in IEEE Transactions on Industrial Electronics, vol.
Mi, “State-of-charge estimation of lithium-ion batteries in electric drive vehicles using extended Kalman filtering,” in IEEE Transactions on Vehicular Technology, vol. Ting Goh, “Lithium-ion battery state-of-charge estimation using a square-root unscented spherical Kalman filter (Sqrt-UKFST) in a nanosatellite,” in IEEE Transactions on Power Electronics, vol.