This thesis is submitted in partial fulfillment of the requirements for the degree of Master of Science in Mathematics. I further declare that there is no potential conflict of interest in relation to the research, data collection, authorship, presentation and/or publication of this thesis. Financial modeling by Stochastic Differential Equations SDEs with regime switching was used to move from one economic state to another.
The purpose of this thesis is to address the pricing of European options under a regime switching model where volatility is added. Regime switching models are more realistic as they include the effect of an external event on underlying asset prices. This study proposes a new SDE for underlying financial asset prices under regime switching with a high volatility model.
During my mathematics studies in the Master's program proposed by the University of the United Arab Emirates, I was promoted, validated and encouraged by many people, without whom the completion of the study would not have been possible. I express my deepest gratitude to my supervisor, Professor Youssef El Khatib, for his invaluable support, patience and understanding, with which I was able to overcome all the difficulties in my research. To Adam Diene, Head of the Mathematical Sciences Department, and to all my professors in the department for their support.
My sincere thanks also go to Professor Stéphane Goutte of the University of Paris-Saclay, Paris, France, examiner and Professor Qasem Al-Mdallal for being part of the examination committee.
Introduction and Financial Derivatives
- Introduction
- Financial Derivatives
- Main Types of Financial Derivatives
- Options
- Why Do We Use Options?
- Pricing Options
- Lower and Upper Bounds for the Price of the Option
- Parity Call-Put
One of the most important parameters in stochastic modeling is the so-called volatility, which estimates the rate at which a quantity tends to change. On the other hand, the regime switching model of [4] deals with the impact of external events that can change the price of the underlying asset and thus the value of the option. We then investigate a solution for the SDE and discuss the European option pricing solution.
Solve the stochastic differential equation (SDE) of the underlying asset price of the proposed model. Compare the option price of a regime-switching high-volatility model with the option price of a regime-switching model. Use numerical methods to simulate a continuous time Markov chain process with two states and underlying asset prices.
After introducing the model, the solution for the SDE of the underlying asset price is examined. Transactions in financial derivatives should be treated as separate transactions rather than as integral parts of the value of the underlying transactions to which they may be linked. An underlying asset is an asset that affects the performance or value of a derivative security.
Options contracts are mainly influenced by the primary parameters that are actually the price drivers of an option. Knowing the fair value estimate of an option is important for traders as it helps them adjust their portfolios. Asian Option: An Asian option is a type of option where the profit depends on the average price of the underlying asset over a certain period of time as opposed to standard (American and European) options where the profit depends on the price of the underlying asset.
After the advent of the pioneer Black-Scholes Formula [1] in 1973, options began to be traded in the financial markets. The main assumption of the Black-Scholes model concerns the evolution of the share price. Given a call option built on a stock with prices determined by equation (1.1), then is a lower bound on the price of the option.
Preliminaries from Stochastic Calculus
- Some Tools from Probability
- Stochastic Process
- Stochastic Integration
- One Dimensional Ito Formula
- Stochastic Differential Equations
- Some Applications of Ito’s Formula
- Geometric Brownian Motion
- Cox Ingerson Ross Model (CIR)
- Ornstein-Uhlenbeck Process
A stochastic process is a parameterized collection of random variables (Xt)t∈T, defined on the probability space (Ω,F,P) and takes values in R. One of the most important stochastic processes is the Brownian motion, also known as the Wiener process. If0≤s≤t≤u≤v (ie two intervals [s,t]and[u,v] do not overlap), then Bt−Bs and Bv−Bu are independent random variables.
Let(Ft) be a filtration on(Ω,F,P). A stochastic process(Xt) is Ft-adapted if ∀t≥0Xt is Ft-martingale. If the condition (iii) of the previous definition is replaced by E(Mt/Fs)≥Ms, ∀ 0≤s≤t, then(Mt) is called submartingale. If the condition (iii) of the previous definition is replaced by E(Mt/Fs)≤Ms, ∀ 0≤s≤t, then(Mt) is called supermartingale.
A stochastic process (Xt)t≥0 is called an Ft-predictable process when t >0,X is measurable with respect to the σ-algebra generated by {Xs,s
Taking expectations from both sides and using the independence of the Brownian motion steps, we get this. 6] For every elementary function f(n)Ft-adjusted: the integral. 1-dimensional Ito process) Assume that B is a Brownian motion at (Ω,F,P). An Itô process (or stochastic integral) is any stochastic process Xtof the form. first 1-dimensional Ito formula) Let (Ω,F,P) be a complete probability space, (Bt)t∈R+ be a one-dimensional Brownian motion and f :R →R such that f is continuously differentiable twice.
One of the important notations for the stochastic integral defined over a Brownian motion is that it follows the normal distribution. Now if we use the property of independent increments for Brownian motion, the second moment is given by . The Itô formula is often used to find the solution of the SDEs and to price the financial derivative products.
It is used as a method to predict interest rates and is based on a stochastic differential equation. It is a type of "one factor model" (short rate model), as it describes interest rate movements as driven by only one source of market risk.
Continuous Time Markov Chain
Markov Chains in Continuous Time
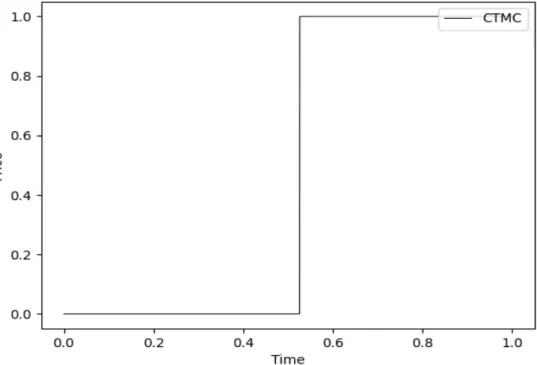
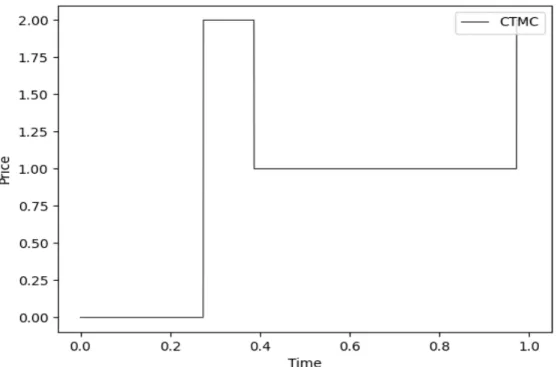
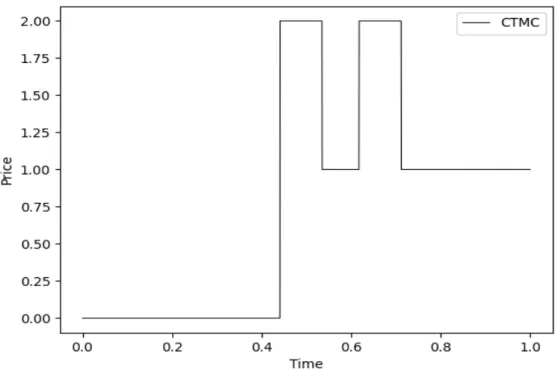
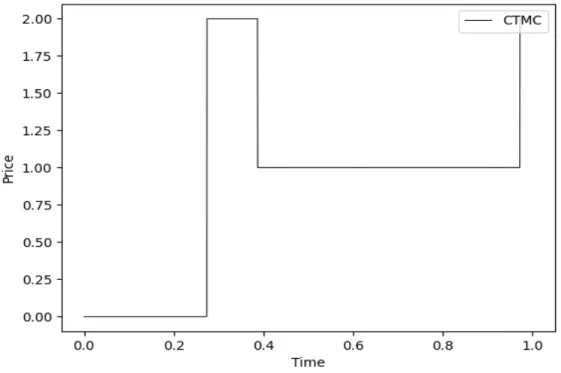
Two States CTMC
Simulation of Continuous-Time Markov Chain with Two States
- Python Code
- Illustrations
High Volatile Regime Switching Market
- The Research Questions
- Answers
- Modeling the Underlying Asset Prices
- Black and Scholes Model
- Our Alternative Model
- Option Pricing
- Solution of the SDE in the High Volatile Model
- On the Valuation of the Premium
- Numerical Simulations
- Asset Prices
- Option Price
- Python Code
- Illustrations
This is due to the relationship between the future and present value of money and the payoff (ST−K)+. Volatilityσ is a measure of uncertainty, which can generally be deterministic or constant, but when the model is stochastic, it is called a "stochastic volatility model". The above model can be seen as a generalization of the Black-Scholes model, as it allows volatility to be stochastic.
In this paper we examine a model which includes features of the crisis model (4.1) and the regime change model (4.2-4.3). Additionally, a continuous Markov chain process models the external events that affect stock prices. It is assumed that the values of σ,α, and rare are all affected by the values of CTMCXt.
In our work, we will assume that the market economy is subject to only two states. In this section, we study the SDE solution in our model, then we study the option pricing problem in our regime switching model. Solving the price of the underlying asset is important to obtain a solution for the option premium.
Now the variation of the constant method by searching for a solution of (4.5) in the form St=Ytζt, with Y0=S0=x, is used. In this subsection, we discuss the value of the option in the regime-changing highly volatile model as presented in (4.5). The proposition below provides a relation between the premium of the regime switching with constant volatility and the premium in our model.
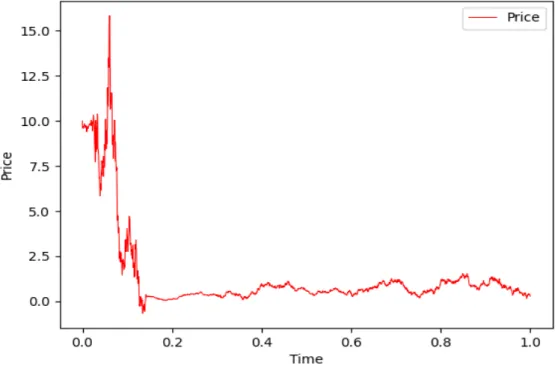
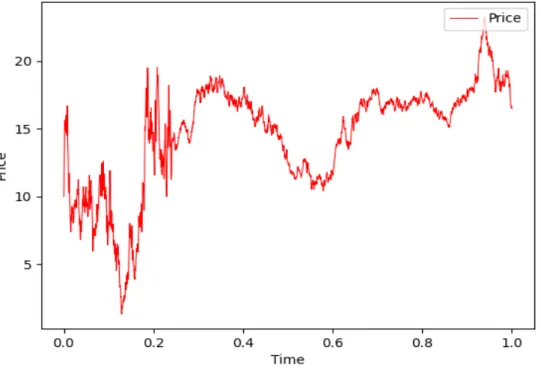
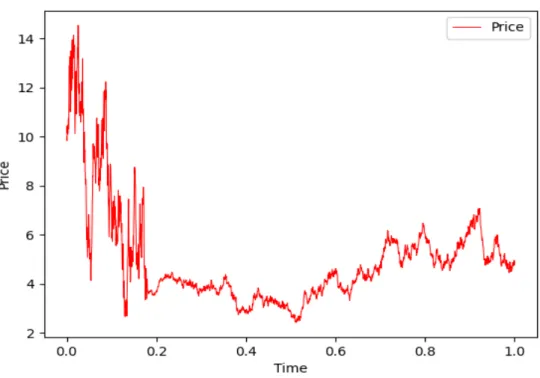
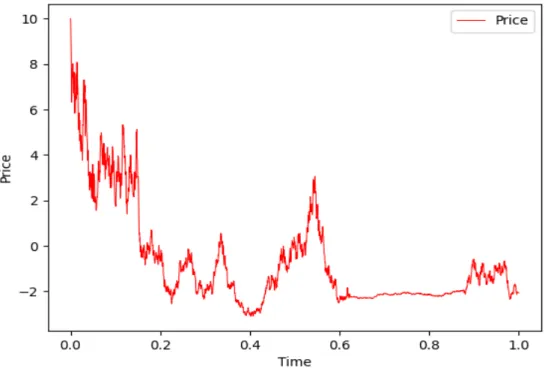
The main focus of the thesis is to study the pricing of a European option under a highly volatile regime switching model. Simulating underlying asset price trajectories is essential in pricing the option itself. The algorithm to simulate equation (4.11) is to simulate Brownian motion and CTMCXt over a continuous time period independently, then generate a path of the underlying price of the asset.
From now on, we will omit the use of the symbol ˜ for the discretized version of a given SDE. This subsection is intended to simulate the European call option premium given by (4.10), where the price of the underlying asset is governed by the SDE (4.5).
Conclusion
Heston, "A closed-form solution for options with stochastic volatility with applications to bond and currency options," The Review of Financial Studies, vol. Yin, "Option pricing in a regime-switching model using the fixed Fourier transform," International Journal of Stochastic Analysis , vol. Liu, “The threshold for a stochastic susceptible-infectious epidemic model during regime change,” Nonlinear Analysis: Hybrid Systems , vol.