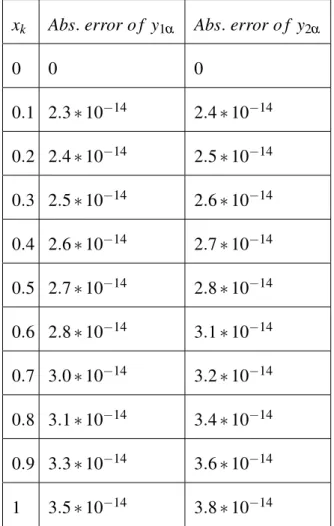
The thesis is submitted as a partial fulfillment of the conditions for obtaining the title of Master of Mathematics. I further declare that there is no potential conflict of interest in relation to the research, data collection, authorship, presentation and/or publication of this dissertation. In the diploma thesis, we will investigate the numerical solution of the fuzzy initial value problem based on the reproduction kernel method.
Problems of this type are either difficult to solve or impossible, in some cases, as they will produce a complicated optimized problem. To overcome this challenge, the reproduction of kernel method will be adapted to solve these types of problems. Theoretical and numerical results will be presented to demonstrate the effectiveness of the proposed method.
It is my pleasure to express my deep thanks and gratitude to my mentor Professor Muhammed I Syam for his constant support in my thesis, for his patience, motivation and vast knowledge. His guidance supports me throughout the research and writing of this thesis.
Fuzzy Logic
Introduction
10] proposed the Simplified Reproduction Kernel Method (SRKM) and the Least Squares Method (LSM) for solving nonlinear singular boundary value problems. The reproduction kernel method was first introduced in the 1907 work of Stanisław Zaremba, who questioned the boundary value problems for harmonic and biharmonic functions. Several researchers study the reproduction kernel method, so Kashkari and Syam [17] used RKM to solve the Fredholm integral-differential equation.
18] developed a kernel-reproducing method for solving Fredholm integro-differential equations with weak singular kernels in the Hilbert kernel-reproducing space. Akgül [20] applied the reproductive kernel method to fractional differential equations with non-local and non-singular kernels. Moradi and Javadi [27] presented a semi-analytical technique for the numerical solution of nonlinear oscillators under the effect of damping using the Hilbert reproductive kernel space method.
30] implemented a relatively recent analytical technique called the Iterative Reproducing Kernel Method (IRKM) to obtain a computational solution to a fuzzy two-point boundary value problem based on the generalized concept of differentiability. To achieve this goal, the reproduction kernel method will be used for initial value problems.
Preliminaries
Fuzzy Numbers
So the top semi-continuous onℜ. Then for λ ∈ℜ and α ∈[0,1] the arithmetic operations in fuzzy numbers are defined by α−cut as. Then the metric dF onFℜ is defined by . Fℜ,dF) is a complete metric space with the following properties for all u,v,w,z∈Fℜ,λ ∈ℜ.
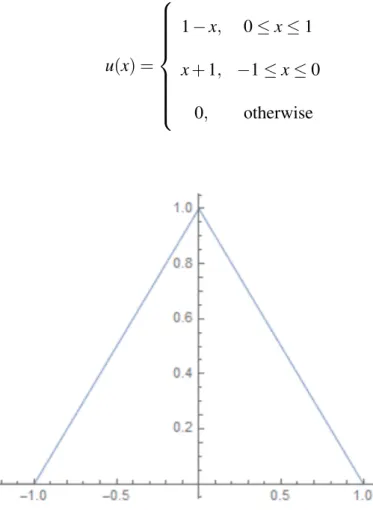
Differentiation of Fuzzy Functions
Let Bbe a subset ofℜ. A fuzzy function F :B→Fℜ H- is said to be differentiable at x0 ∈B if and only if there exists a fuzzy number D f(x0) such that the following limits (with respect to metricdF) exist and. In this case D f(x0) is called Hukuhara derivative of f atx0. If f is H-differentiable at eachx∈B, then f is H-differentiable on B. Remark: It is clear that theorem 2.1.1 gives the necessary condition to the H-differentiations, but not a sufficient condition.
Let x0,x0+h∈B. A fuzzy function f :B→FR is said to be begH-differentiable prix0 if and only if there exists a fuzzy number fgH0 (x0) such that the following limit exists (with respect to the metric dF). If f is gH-differentiable atx∈B, then f is gH-differentiable f over B. Example 2.2.6. a) Let f :ℜ→Fℜ be a fuzzy function defined by.
Fuzzy Initial Value Problems
Direct Method for Solving Fuzzy Boundary Value Problems
If the same technique were to be used to solve the nonlinear case, it will result in a complex optimization problem that cannot be solved explicitly in most cases.
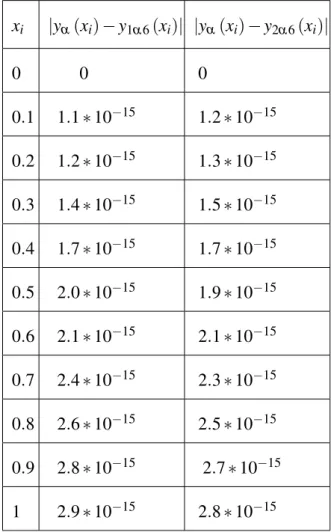
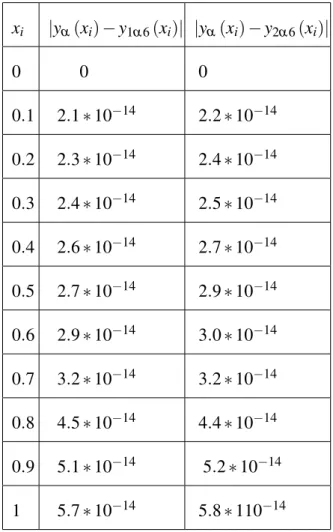
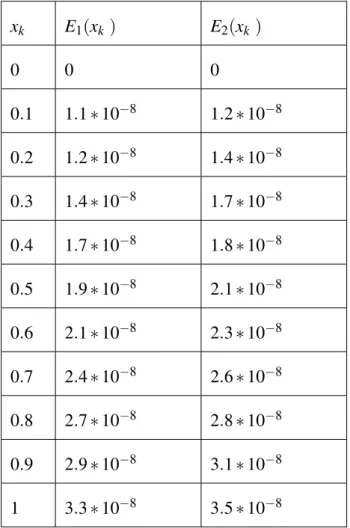
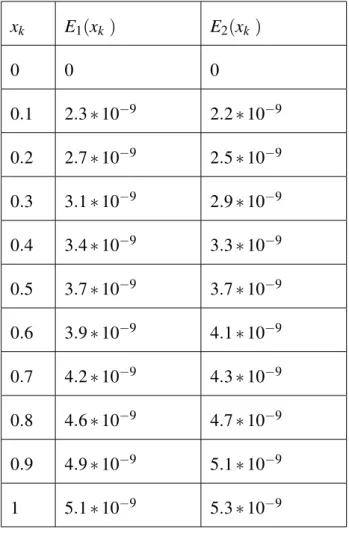
Reproducing Kernel Method for Solving Initial Value Problems
Reproducing Kernel Spaces
The Hilbert space W21[0,1] is a reproducing kernel and its reproducing kernel function Ry(x) can be defined by. The Hilbert space W22[0,1] is a reproducing kernel space and its reproducing kernel function Ry(x) can be defined by. The Hilbert space W23[0,1] is a reproducing kernel space and its reproducing kernel function Ry(x) can be defined by.
The Hilbert space W24[0,1] is a reproducing kernel space and the reproducing kernel function Ry(x) can be defined by.
Structure of the Solution
First Order Fuzzy Initial Value Problem
Linear First Order Fuzzy Initial Value Problem
Nonlinear Fuzzy Initial Value Problem
Second Order Fuzzy Initial Value Problem
Linear Second Order Fuzzy Initial Value Problem
Nonlinear Second Order Fuzzy Initial Value Problem
Conclusion
Fuzzy Laplace transform based on the Henstock integral and its applications in discontinuous fuzzy systems. Fuzzy Sets and Systems 358.1- 28. Mixed Fuzzy Boundary Control Design for Nonlinearly Coupled Systems of ODE and Boundary Distorted Uncertain Beam, IEEE Transactions on Fuzzy Systems. New Numerical Approach to Solving Fuzzy Limit Problems. Annals of Pure and Applied Mathematics.
A numerical scheme based on data non-discretization for boundary value problems of differential equations in fractional order. Revist a de la Real Acadmic de Cincias Exact as, Fsicas y Naturales. A fast and accurate calculation technique for an efficient numerical solution of nonlinear singular boundary value problems. Comparison between numerical solutions of fuzzy initial value problems via interactive and standard arithmetic, International Fuzzy Ssystems Association World Congress, 704-715.
Optimization of one-step block method for solving fuzzy second-order initial value problems.Complexity, 2021. Reproduction of the kernel method for solving Fredholm integral differential equations with weak singularity, Journal of Computational and Applied Mathematics. Numerical solutions of first-order, two-point BVP systems based on the reproducing kernel algorithm.Calcolo.
Reproduction kernel Hilbert space method based on reproduction of kernel functions for studying boundary layer flow of a non-Newtonian fluid from Powell-Eyring. Journal of Taibah University for Science. An efficient meshless reproductive kernel method for buckling analysis of cylindrical shells with and without cutouts.Computational Machines. Simplified Reproducing Kernel Method and Order of Convergence for Linear Volterra Integral Equations with Variable Coefficients.
A modified kernel reproduction method for singularly perturbed boundary value problems with delay. Applied mathematical modeling. A new kernel reproduction method for variable order fractional boundary value problems for functional differential equations. A combined method of kernel reproduction and Taylor series for dealing with nonlinear Volterra integro-differential equations with.