At the same time, the problems provide examples of the application of the theory to the real world. This choice is similar to that made in the 3rd edition of the above book by Jackson.
Overlapping Charged Spheres
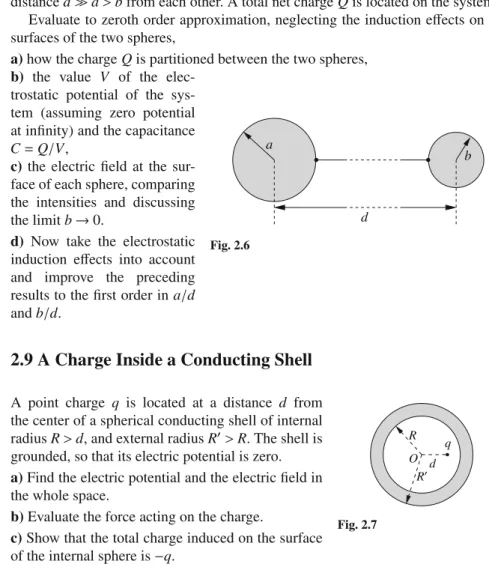
The multipole expansion allows us to obtain simple expressions for the leading terms of the potential and field generated by a charge distribution at a distance much larger than its expansion. 4 1 Basic principles of Electrostatics a) in the "inner" region, where the two spheres overlap, .. b) in the "outer" region, i.e. outside both spheres, which discusses the limit of small displacementsδR.
Charged Sphere with Internal Spherical Cavity
Energy of a Charged Sphere
Plasma Oscillations
Mie Oscillations
Coulomb explosions
Show that the equation of motion of the layer is 1.16) c) Find the initial position of the particles that acquire the maximum kinetic energy during the expansion of the cloud and determine the value of this maximum energy. Compare the total kinetic energy with the potential energy initially stored in the electrostatic field. e) Show that the particle density remains spatially uniform during expansion.
Plane and Cylindrical Coulomb Explosions
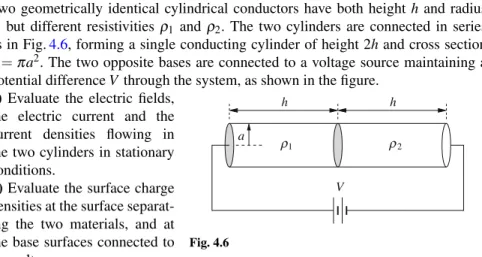
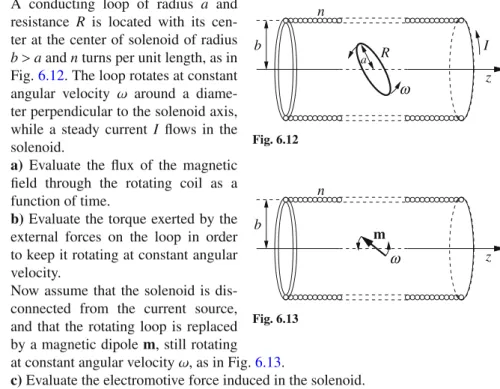
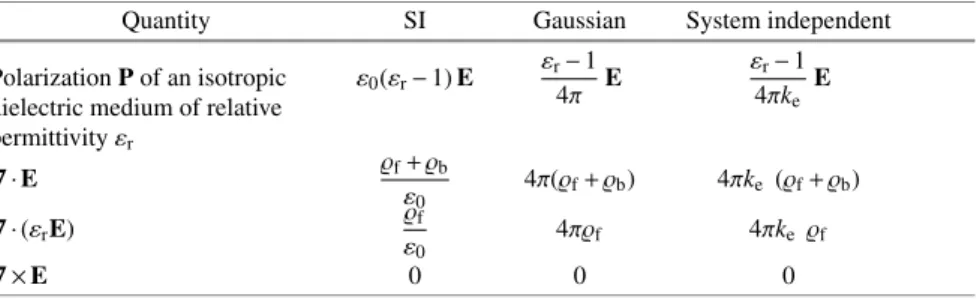
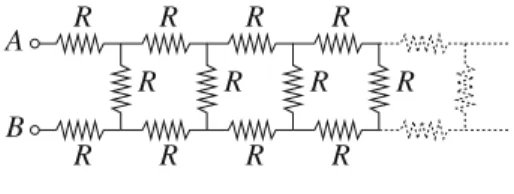
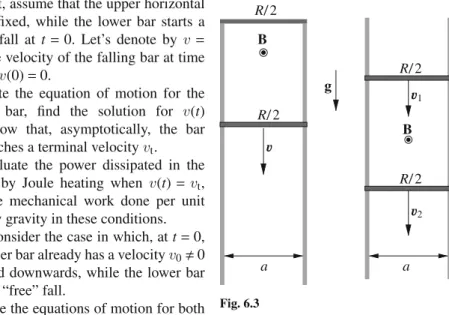
6 1 Fundamentals of electrostatics a) Evaluate the electrostatic potential energy of a charge located at a distance Collision of two Charged Spheres Oscillations in a Positively Charged Conducting Interaction between a Point Charge and an Electric The solution of Poisson's equation is unique if one of the following boundary conditions is true. Modified Neumann boundary condition (also called Robin boundary condition): conditions where boundaries are specified as conductors of known charges. Metal Sphere in an External Field Electrostatic Energy with Image Charges 10 2 Electrostatics of Conductors . b) Now assume that you have a non-conducting surface with the same surface charge distribution as in point a). Find the electric field throughout space. c) A non-conducting sphere surface with a radius has the same charge distribution as the conductive sphere of problem 2.4. A Point Charge in Front of a Conducting Sphere Dipoles and Spheres We expect the induction effects to be important if the radius of the spheres is not negligibly small relative to tor. a Q Q. For simplicity, assume that the spheres are identical and have the same charge Q, as in the figure. b) Evaluate the lowest order correction for the force between the spheres with respect to Coulomb's law (2.3). 12 2 Electrostatics of Conductors and that the force between two charge distributions, each of spherical symmetry, is equal to the force between two point charges. For the sake of clarity, assume that the spheres are identical and have the same charge Q as in the figure. b) Evaluate the lowest order correction to the force between the spheres with respect to Coulomb's law (2.3). b) A conducting sphere of radius is placed in a uniform electric field E0; c) a dipolep0 is located at the center of a conducting spherical shell of radius b. d)Find the solution to the problem c)using the method of tolls. Electrically Connected Spheres A Charge Inside a Conducting Shell A Charged Wire in Front of a Cylindrical Conductor 14 2 Electrostatics of Conductors . radiusR, with center of curvature inO. A point chargeq is located at a distancea >R from O, the line segment from O to q forms an angle θ with the axis of symmetry of the problem. b) An infinite conductor has a hemispherical cavity of radius R. Again, the segment of Otoq forms an angle θ with the axis of symmetry of the problem. The Force Between the Plates of a Capacitor Electrostatic Pressure on a Conducting Sphere When x is such that the interaction energy Uint(x) is no longer negligible with respect to U0 but is still greater than 2R, the total potential energy Upot(x) of the system is. An Arti fi cial Dielectric A point charge q is located in vacuum at a distance from the medium as shown in Fig.3.1. a) Find the electric potential and electric field in the whole space using the method of image charges. An Electrically Polarized Sphere Dielectric Sphere in an External Field Refraction of the Electric Field at a Dielectric Contact Force between a Conducting Slab and a A Conducting Sphere between two Dielectrics Measuring the Dielectric Constant of a Liquid A Conducting Cylinder in a Dielectric Liquid A Dielectric Slab in Contact with a Charged Conductor For such materials, equation (4.3) gives the effect per volume unit that is given off in the material as a consequence of the friction term. But the meaning of the symbols used in the formulas throughout the book should be clear from the context. The Tolman-Stewart Experiment Charge Relaxation in a Conducting Sphere A Coaxial Resistor Electrical Resistance between two Submerged Electrical Resistance between two Submerged Effects of non-uniform resistivity Charge Decay in a Lossy Spherical Capacitor An ionization discharge is started in the gaseous layer at t=0 and the gas instantly becomes conductive. Under these conditions, find the electric field in the capacitor and the free charge density at the surface between the two layers. This is possible because the electric field of the dipole at the perimeter of the junction is An In fi nite Resistor Ladder Let's evaluate the field of image charges in the center of the shell:. Pinch Effect in a Cylindrical Wire We have vacuum in half space 1, while half space 2 is filled by a medium of magnetic permittivity μr. A magnetic dipole, parallel to the y-axis, is in vacuum at position x=−d.. a) the magnetic fieldBin all space, b) the force acting on the magnetic dipole. Magnetic Levitation Uniformly Magnetized Cylinder The electric field everywhere in space is the sum of the fields generated by the two spheres. Cylindrical Conductor with an Off-Center Cavity A conducting cylinder of radius and height rotates around its axis with a constant angular velocity ω in a uniform magnetic field B0, parallel to the axis of the cylinder. h. Assume that the cylinder rotates under stationary conditions. b) the electric field inside the cylinder and the volume and surface charge density;. Rotating Cylindrical Capacitor Thus, for fixed path, the line integral of is Equal to the time derivative of the flux of the time-varying field Bthrough a surface bounded by the contour. For a system of two electric circuits, the magnetic flux through each circuit can be written as a function of the currents flowing in each circuit. 44 6 Magnetic induction and time-varying fields where the terms containing the (self) inductance coefficients are the contribution to the flux generated by the circuit itself, and the terms containing the mutual inductance coefficientsM21=M12 give the flux generated by one circuit over the other. 6.5). a) Find the current flowing in the coil. b) Find the power P dissipated by the coil due to Joule heating and the corresponding frictional force on the coil. A Circuit with “ Free-Falling ” Parts The Tethered Satellite Eddy Currents in a Solenoid Feynman ’ s “ Paradox ” Induced Electric Currents in the Ocean A Magnetized Sphere as Unipolar Motor Induction Heating A Magnetized Cylinder as DC Generator The two brush contacts of point b) are now connected to the ends of the electromagnetic coil, so that the rotating disk provides a current that circulates in turns. The circular current is therefore the result of the rotation of the disk and the presence of the magnetic field B, which the current itself creates by circulating in the solenoid (self-sustaining dynamo). This is the basic model for a self-sustaining spinning dynamo, such as the mechanism for generating the Earth's magnetic field [3]. In fact, only one half of the electric field is due to the charge on the other plate. Skin Effect and Eddy Inductance in an Ohmic Wire Magnetic Pressure and Pinch effect for a Surface A current source supplies a constant current to a solenoid of radius, length ha, so that boundary effects are negligible, and windings per unit length. a) Estimate directly the magnetic pressure on the surface of the solenoid, calculating the magnetic force in the coil. A Homopolar Motor Coupled RLC Oscillators (1) Coupled RLC Oscillators (2) Coupled RLC Oscillators (3) The LC Ladder Network The CL Ladder Network Non-Dispersive Transmission Line An “ Alternate ” LC Ladder Network Resonances in an LC Ladder Network Find the steady-state solution of the equations of motion and calculate the power dissipated by friction as a function of ω. Cyclotron Resonances (2) The second wavepacket can be considered an "attempt" to build a Gaussian wavepacket from its spectral components, but with some errors in the relative phases of the components themselves. Find the width of the wave packet and discuss its shape to demonstrate the deviations from the Gaussian profile. As a reasonable approximation, keep only the factors up to second order in (k−k0)2, for example using Poynting Vector(s) in an Ohmic Wire Poynting Vector(s) in a Capacitor 68 8 Maxwell equations and conservation laws b) Check the law of energy conservation (Poynting's theorem), for a closed inner cylindrical surface, coaxial to the solenoid. c) Now verify Poynting's theorem for an external, coaxial cylindrical surface (remember that B=0 outside an infinite solenoid). Poynting Vector in a Capacitor with Moving Plates 68 8 Maxwell equations and conservation laws b) Check the law of energy conservation (Poynting's theorem), for a closed inner cylindrical surface, coaxial to the solenoid. A Gaussian Beam 70 8 Maxwell's Equations and Conservation Laws a) Write the intensityI=I(r), defined as the “energy flow along z”, i.e., I(r)=Sz= S·ˆzku is the Poynting vector. b) Show that, in addition to the transverse components of the fields, there must also exist the longitudinal components (Ez, Bz) and give their expression. c) Evaluate the SxandSy component of S and discuss the result. d) Show that the angular momentum density (8.12) of the beam can be written as z=z(r)=− r. 70 8 Maxwell Equations and Conservation Laws a)Write the intensityI=I(r), defined as the "energy flow along z", i.e. I(r)=Sz= S·ˆweightSis the Poynting vector. b) Show that, in addition to the transverse components of the fields, longitudinal components (Ez,Bz) must also exist, and give their expression. c) Evaluate the Six and His components of S, and discuss the result. d) Show that the density of angular momentum (8.12) of the beam can be written as z=z(r)=− r. as a function of the total power of the beamkW=∞. where g=E×B/4π is the electromagnetic momentum density. 8.18) to check the conservation of total angular momentum for the system (thereby solving the "paradox" as outlined in Problem 6.6). Relationship of four-current and four-potential to densities and potentials in three-dimensional space. The Fields of a Current-Carrying Wire The Fields of a Plane Capacitor The Fields of a Solenoid The Four-Potential of a Plane Wave S-2.13 Electrostatic pressure on a conducting sphere . a) The surface charge is σ=Q/S, where S =4πa2 is the surface of the sphere. Re fl ection from a Moving Mirror Oblique Incidence on a Moving Mirror Pulse Modi fi cation by a Moving Mirror A plane monochromatic wave of frequency ωi, amplitude Ei and wave vector ki=xˆωi/c, linearly polarized along the y axis, strikes the mirror. a) Show that in the laboratory frameS both the total (i.e. incident+reflected) fields E and Bare are discontinuous at the specular surface lying on the plane x=x(t), where dx/dt=v. b) EM fields can be derived from the vector potential A(x,t). Show that the boundary conditions for EM fields on a specular surface are equivalent to the condition Use the equation Prad=−dU/dt, where U is the electron's total energy, to show that the electron actually spirals toward the "center" of its orbit. Show that spiral motion can be obtained by adding a frictional force ffr proportional to the electron velocity. Evaluate the time constant τ of the energy loss, assuming τω − L1, and provide a numerical estimate. c) The spiral motion cannot occur if we consider the Lorentz force fL=−(e/c)v×B as the only force acting on the electron. Neglect in the following quantities of the order (η/ω0)2 or higher. c) Describe the movement of the electron and determine, a posteriori, the value of η that represents the radiation damping. Radiation Emitted by Orbiting Charges In the following, ignore quantities of order (η/ω0)2 or higher. c) Describe the motion of the electron and a posteriori determine the value of η that reproduces the radiation damping. c) Explain how, based on knowing the mass, radius, rotation period T and time derivative dT/dto of the pulsar, you can estimate the magnetic field on the surface of the pulsar. A Bent Dipole Antenna A Receiving Circular Antenna The sum of the image charges, which is equal to the total induced charge on the spherical surface, is zero. A uniformly charged segment with endpoints at (0,φ,−c) and (0,φ,c), and linear charge densityλ=Q/(2c), generates a constant electric potential ϕ(a,b) on the surface of the ellipsoid. Polarization Effects on Thomson Scattering Scattering and Interference Optical Beats Generating a “ Lighthouse Effect ” Prad(t) dt, (10.9) where is the period of the electron motion and Prad(t) is the instantaneous radiated power, which is given by the Larmor formula. Compare the result with that obtained using the simple classical model of an electron subject to a frictional force. Wave Propagation in a Conductor at High and Low Energy Densities in a Free Electron Gas The problem is solved if we can find values such that the electric potential ϕ is zero everywhere on the surface of the sphere. Transmission and Re fl ection by a Thin Conducting Anti-re fl ection Coating Birefringence and Waveplates Magnetic Birefringence and Faraday Effect Lightning excites transverse EM signals which propagate in the ionosphere, mainly in the direction parallel to the Earth's magnetic field lines. a) Show that, in a frequency interval to be determined, and depending on the polarization of the wave, the dispersion relation for such signals has the form Assuming that the pulse is "short" (in a sense to be clarified a posteriori), estimate the length of the pulse after propagation at a distance L104 km. Wave Propagation in a “ Pair ” Plasma Show that ε1 and ε2 must have opposite signs to get q1,2>0, i.e. vanishing fields for |x| → ∞. f) Find from the results of the points a) and e) the dispersion relation ω=ω(k) as a function of ε1 and ε2, showing that wave propagation requires ε1+ε2<0. g) If medium 1 is vacuum (ε1=1), how should medium 2 and the wave frequency be chosen to satisfy the condition found at point f). Mie Resonance and a “ Plasmonic Metamaterial ” The Coaxial Cable Calculate the electric and magnetic fields on the plane of symmetry between the two wires, and evaluate their magnitude on the ground. TEM and TM Modes in an “ Open ” Waveguide Square and Triangular Waveguides Waveguide Modes as an Interference Effect Further, we assume that the wave is the superposition of two plane waves with wave vectorsk1≡(kx,ky,0)≡ k(sinθ,cosθ,0), andk2≡(kx,−ky,0)≡k(sinθ,− cosθ,0), where θ is the angle of incidence shown in the figure. 12.6). a) Find the relation between kandω and the range of θ for which the wave propagates without loss of energy through the boundary surfaces aty=±a/2. b) The amplitude reflection coefficient=Er/Ei is the ratio of the complex amplitude of the reflected wave to the amplitude of the incident wave, on the surface that separates two media. Wave Propagation in a Filled Waveguide We choose L=2πR⊕, and, to somehow reproduce spherical geometry, we impose periodic boundary conditions on the lateral surface of the parallelepiped, namely. Discuss whether the approximation of the surface of the oceans as a perfect conductor is reasonable at the frequency of the Schumann resonances. Electrically and Magnetically Polarized Cylinders The electric field outside the sphereEout will be given by the sum of E0 and the field of a dipole. located in the center of the of the sphere. The polarization charge densities on the surfaces of the two dielectrics in contact with the sphere are respectively. We assume that during the discharge i) the slowly varying current approximation applies, ii) the surface charge density on the plates remains uniform, iii) we can neglect the effects of the external circuit and the resistance of the plates, iv) other boundary effects are negligible. We use a cylindrical coordinate system (r,φ,z) with the capacitor axis aszaxis, and the origin at the center of the capacitor. a) Calculate the current I =I(z,t) flowing on the plates, and the magnetic fieldB=φˆBφ(r,z,t) inside the capacitor, for|z| (h/2). 106 13 Additional problems c) time-dependent surface current density K=zˆK0e−iωtcoskx, discussion about which values of ω (for fixed k) the fields expand. d) In examplec), calculate the temporal and spatial average power dissipated per unit area on the plane oni=0. Energy and Momentum Flow Close to a Perfect Discuss the result in relation to the findings of point c). a) Find the total force on the mirror and the direction of its acceleration if I1>I2. Now assume that the two waves have equal intensity, I1=I2=I, and that the mirror moves with velocity v=xˆv. b) Evaluate the force on the mirror, in the system where the mirror is at rest. c) Discuss the movement of the mirror under the influence of the force found at point b), at the limitvc. Radiation Pressure on a Thin Foil Discuss the dependence of the emitted spectrum on ω, and the angular distribution of the emitted radiation at the boundaries ωωcandωωc, where ωc=eB0/me is the electron cyclotron frequency in the presence of B0. Undulator Radiation Electromagnetic Torque on a Conducting Sphere This type of motion is known as Mie oscillation (or surface plasmon of the sphere). b) The electrostatic energy of the system is given by the integral Ues=. According to Gauss's law, the total charge induced on the conductor is equal to the sum of the image charges. The Fizeau Effect Lorentz Transformations for Longitudinal Waves In problem (11.3), we showed that the phase speed of this wave vϕ=ωL/kL is undefined and can have arbitrary values. E(r,z,t)=E(r)eikz−iωt, B(r,z,t)=B(r)eikz−iωt, (13.15) with E·zˆ=0 and B·ˆz=0. Estimate the dispersion relation between the frequency ω and the wave vector k. c) Show that the fields and their sources are independent of time in the reference system S , which moves with the phase velocity ˆzvϕ=z(ˆ ω/k) relative to the laboratory frame S, where the wire is at rest. A Waveguide with a Moving End We want to study the propagation of such a "relativistic" wave in a medium with free electrons (ions are considered at rest). a) Show that it is self-consistent to assume that electron motion occurs in the xyplane. Then solve the equations of motion under steady conditions and verify the robustness of the a posteriori assumption. b) Show that the Lorentz factor is independent of time and give its expression. c) Calculate the refractive index for a medium with a density of free electrons. The relativistically correct equation of motion of an electron in the presence of an intense wave is First, assume that at att=0, the zcomponent of the electron momentum is zero, pz=0. An Optomechanical Cavity Radiation Pressure on an Absorbing Medium Scattering from a Perfectly Conducting Sphere Radiation and Scattering from a Linear Molecule Radiation Drag ForceElectric Field of a Charged Hemispherical Surface
Fields Generated by Surface Charge Densities
Coulomb ’ s Experiment
A Solution Looking for a Problem
Hemispherical Conducting Surfaces
Conducting Prolate Ellipsoid
Charge in Front of a Dielectric Half-Space
A Transversally Polarized Cylinder
Dielectric-Barrier Discharge
Charge Distribution in a Long Cylindrical Conductor
The Rowland Experiment
A Magnetic Dipole in Front of a Magnetic
Charged Particle in Crossed Electric and Magnetic
Conducting Cylinder in a Magnetic Field
Magnetized Spheres
A Square Wave Generator
A Coil Moving in an Inhomogeneous Magnetic Field
The Faraday Disk and a Self-Sustained Dynamo
Mutual Induction between Circular Loops
Mutual Induction between a Solenoid and a Loop
Magnetic Pressure on a Solenoid
Cyclotron Resonances (1)
A Quasi-Gaussian Wave Packet
A Wave Packet along a Weakly Dispersive Line
Poynting ’ s Theorem in a Solenoid
Radiation Pressure on a Perfect Mirror
Intensity and Angular Momentum of a Light Beam
Feynman ’ s Paradox solved
Magnetic Monopoles
The Force on a Magnetic Monopole
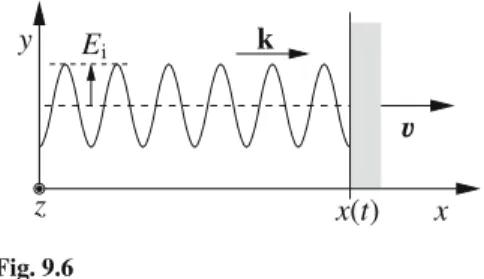
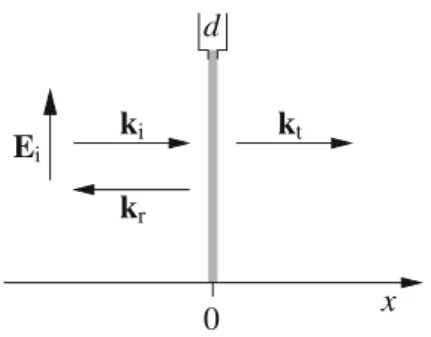
Boundary Conditions on a Moving Mirror
Cyclotron Radiation
Atomic Collapse
Radiative Damping of the Elastically Bound Electron
Spin-Down Rate and Magnetic Field of a Pulsar
Polarization of Scattered Radiation
Radiation Friction Force
Longitudinal Waves
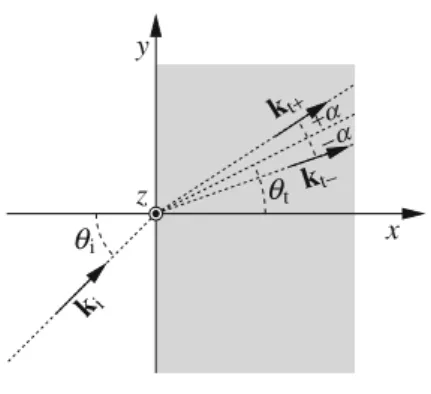
Whistler Waves
Surface Waves
Electric Power Transmission Line
Propagation in an Optical Fiber
Schumann Resonances
Oscillations of a Triatomic Molecule

Discharge of a Cylindrical Capacitor
Fields Generated by Spatially Periodic Surface
Laser Cooling of a Mirror
Thomson Scattering in the Presence of a Magnetic
Surface Waves in a Thin Foil
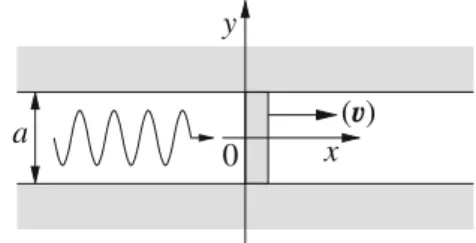
Lorentz Transformations for a Transmission Cable
A “ Relativistically ” Strong Electromagnetic Wave
Electric Current in a Solenoid

![Fig. 4.1The experiment of Tolman and Stewart [1] was](https://thumb-ap.123doks.com/thumbv2/1libvncom/9119110.0/43.659.387.546.705.886/fig-the-experiment-tolman-stewart.webp)