A case study of Lake Harvest Company, Kariba, Zimbabwe. Submitted by DHUBE IAN in partial fulfillment of the requirements for the Master of Business Administration. The expression to be optimized and the inequalities are assumed to be linear functions of the variables.
Introduction
Background of the Study
The introduction of linear programming models as an aid to production planning represents an interesting global modeling challenge. Since 1994, 70% of salmon farming companies in Norway have been liquidated (Kontali, 2014) because they felt that they had failed to exploit the significant potential arising from the use of operational research in fish production planning.
Problem Statement
Aim of the study
Objectives
Research Questions
Scope of the study/Delimitation of study
Significance of the study
Furthermore, the findings from the research will help the company identify other products that can increase its profit margins at minimal cost. Finally, this research was relevant to the researcher as it was part of the Master of Business and Administration (MBA) course requirement that the researcher was undertaking.
Chapter summery
The previous chapter highlighted the background of the study, identified the problem, its importance and the scope of the study. The present study will review studies involving the fish processing sector viz. the production planning process models for the fish biomass until it reaches the consumer.
Background of Linear Models
Randhawa and Bjarnason (1995) conducted a study on integration fisheries and fish processing with the intention of developing a simulation model and an LP optimization model that would do a dual role of optimizing net income and assisting in production planning. The role of the simulation model was to generate data for the LP model, which makes decisions about labor requirements, inventory levels, and production levels.
Fish processing value chain
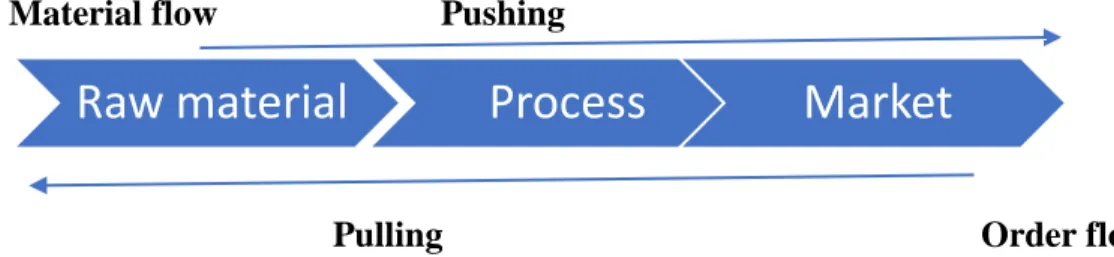
Raw material
One of the main uncertainties is whether fish as raw material will be available for processing. The fishermen themselves are not sure of the quality of the fish they catch, therefore after each load the fish are sorted according to the different sizes and types expected in each load for expedited processing. How the raw materials are handled is an important predictor of the price the fish product will fetch in the market.
It should be noted that some unnecessary procedures such as unnecessary transportation, proper handling including: gutting, bleeding, cooling and important others that can reduce the quality of the final product should be reduced to a greater extent.
Processing
The fishing industry operates in an environment surrounded by uncertainty on a daily basis due to the sensitivity of fish to climate conditions. Fishermen are like hunters and gatherers looking for wild fish in the sea (Jensen, 2009), where the amount of fish to be caught is relative parasites or other undesirable traits (Margeirsson, 2008). The planning of fish production is mainly influenced by the supply of fish, the characteristics of the raw materials and the age of the fish upon arrival at the processing plant.
In addition, processing plant capacity is also a key determinant in influencing the product mix to be produced.
Market
In addition, the pressure on what needs to be processed is influenced by market forces, where some contracts are made in advance and some orders are required at short notice, especially for fresh products.
Linear Models
Overview of Theory
This section presents an overview of important terms and concepts that may contribute to the understanding of the models that will be used to develop the linear model for planning fish production processes at Lake Harvest. A brief introduction to stochastic programming and stochastic modeling and the relevant theory of forecasting and how it can be used in connection with scenario generation is presented.
Representing uncertainty
Introduction to stochastic programming
The decision maker can generate many scenarios based on the individual's knowledge to come up with the best solution to the problem. In scholastic programming, the model is structured in such a way that when decisions are made, emphasis is placed on information available to the decision maker. They represent the ultimate solution to solve any problem and hence the need to identify the decision variables first arises.
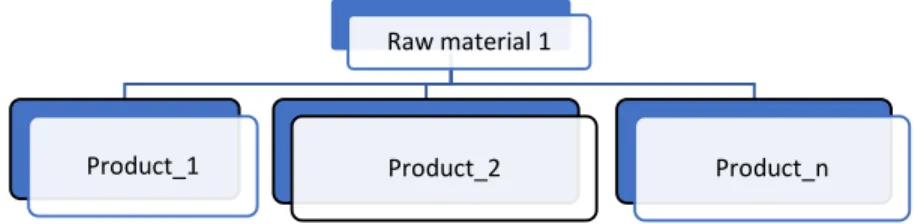
The decision variables determine how much raw material should be allocated to each product combination.
Models of Production Planning Process .1 Mathematical model
Forecasting (Autoregressive models)
- Autoregressive integrated moving average (ARIMA) models
Autoregressive integrated moving average (ARIMA) models on the other hand aim to describe autocorrelations in data (Hyndman and Athanasopoulos, 2015). The stationary process can be represented either in an autoregressive form or in a moving average form. The ARIMA model, the equation in the equation below, consists of the autoregressive representation, a differential part, and the moving average representation.
This is called an ARIMA (p,d,q) model, where p is the order of the autoregressive part, d is the degree of first difference involved and q is the order of the moving average part.
Case studies
Iceland industries
The case study was carried out based on input conditions that were tested and determined by production managers of the company. Our case study is based on the input conditions tested with the production managers of the company under study. An analysis of the results of the model using sensitivity report revealed that two of the machine constraints, the FleXicut and the Gyro Freezer, were tight along with the raw material constraint.
Limitations on machine capacity because labor costs are not taken into account when calculating net profit contribution.
Salmon Industry
- Production and inventory planning
- Sales allocation
- Spot transactions
- Long term contract transactions
- Decisions
- Logistics
There are several ways for a salmon producer to communicate with customers in the global market. While salmon producers can be viewed as price takers in the short term, the salmon producer must decide what volumes to sell and when. In addition, the salmon producer must decide how much fresh HOG salmon he wants to buy on the spot market at any given time.
The producer must decide which part of the total production should be contracted.
Chapter Summary
The mode(s) of transport chosen must bring the product to market in time before it is broken down. There will therefore be a trade-off between the transport costs and the speed with which the product must be delivered, which depends on how quickly the product spoils. Therefore, air freight may be required to get the product to its destination quickly enough, even if it is the more expensive option.
The chapter presents the research approach adopted, design and formulation of the Linear Programming model used to model the maximization of profit contribution for the Lake Harvest.
Research method
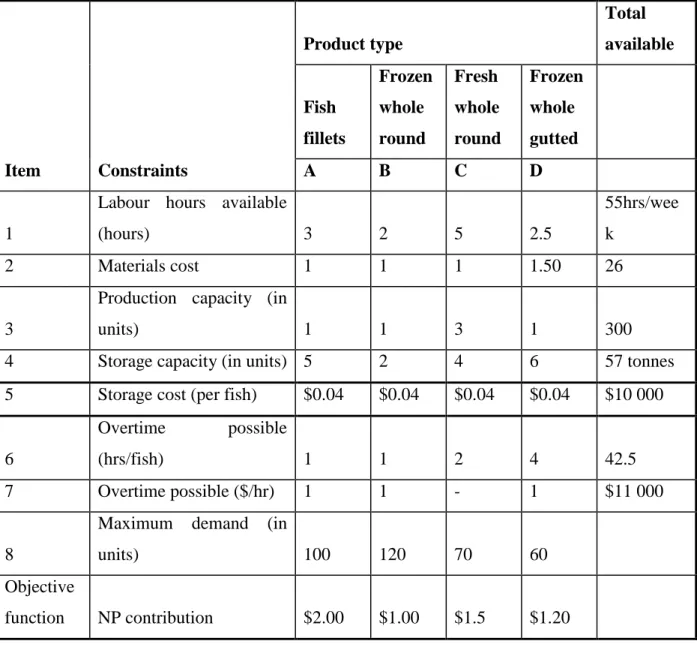
An explanation of the variables based on the constraints on the fish processing planning is also provided.
Research approach
The generated view is then tested against research observations with the aim of confirming or refuting the hypothesis (Snieder and Larner, 2009). The deductive approach is particularly appropriate for the present study given that the focus is on applying the LP model to optimize resource allocation in a product mix. Various studies have proven positive results from the use of the LP model in optimizing the use of scarce resources.
Based on the preliminary findings of the study, the study attempted to apply the same LP model to the case of Lake Harvest in the fisheries process planning procedures.
Research Design
The main objective of the study was to establish optimization of resource allocation in a product mix which increases the net profit contribution at Lake Harvest. This involved an in-depth study of the scenario to obtain rich data from specific cases using methods of probing such as interviews (Krishnaswamy 2006). The objectives of the study are centered around questions about what factors prevented the company from achieving desirable profit targets.
Thus, the research carried out a complete study of this social unit, covering all aspects with an understanding of the complex factors operating in the studied area.
Study setting
Data Collection
Data Analysis
Linear programming model
If a maximum occurs in the feasible region, it must be a vertex of the feasible region. This was performed to reduce the size of the LP problem by eliminating redundant constraints and variables. The computational complexity of the LP solver depends on the number of constraints and variables in the LP problem.
Also, the pre-solving step was performed to assess any infeasibility and unconstrained conditions of the LP problem.
Ethical considerations
These were eliminated before sending the problem to the LP solver, LINGO, in this case to reduce the size of the problem. The concomitant reduction in the size of the LP problem resulted in a decrease in the time it took for the LP solver to solve the problem. When it was determined that there was no infeasibility and limitlessness of the problem, the LP resolution process continued.
However, it was recognized that despite the robustness of the procedure, no pre-solution technique can guarantee the detection of all infeasible and unbounded problems.
Chapter Summary
Introduction
Data Collection and Analysis
Formulation of LP Model
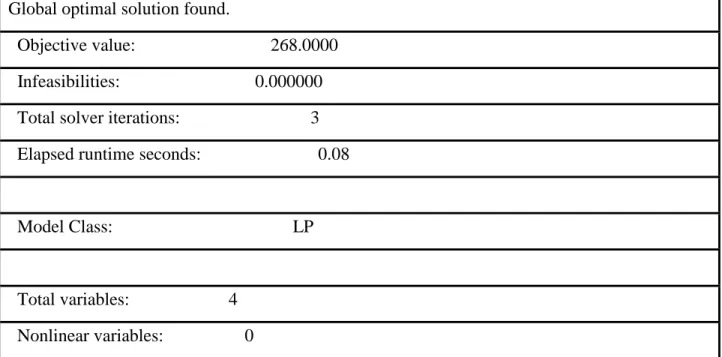
Result of the Maximization Model
The results suggest that a change in labor hours will result in an associated improvement in the objective value of 1.00 units. An increase in working hours at the standard rate may result in an improvement in the objective value. A change in storage costs will result in an associated improvement in objective value of 1.67 units.
A change in the overtime cost will result in an associated improvement in the objective value of 1.67 units.
Model 2 – Optimisation without working overtime with production capacity available
A change in material quantity will cause a corresponding improvement in the objective value by 1.00 units. Increasing the amount of material available is likely to result in an improvement in the objective value. A change in production capacity will cause a corresponding improvement in the objective value by 6.00 units.
It is essential that production capacity is improved so that an objective value also increases.
Comparison of the two models
Chapter four summery
Introduction
Conclusion and Recommendation
It is even more imperative that the production capabilities are improved in order to increase the objective value as well. This may require purchasing additional equipment or replacing outdated equipment with modern state-of-the-art equipment with improved production capacity to maximize profits.
Chapter five summery
Decision making in the cod industry based on value chain data logging and analysis. In Proceedings of the 4th International Workshop on Cold Chain Management, University of Bonn, Bonn.