sigma11-052. 459KB Jun 04 2011 12:10:53 AM
Teks penuh
Gambar
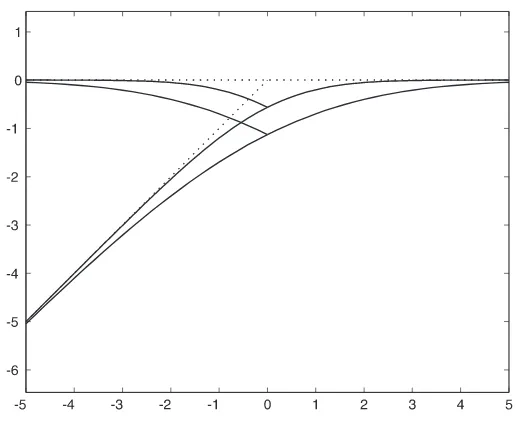
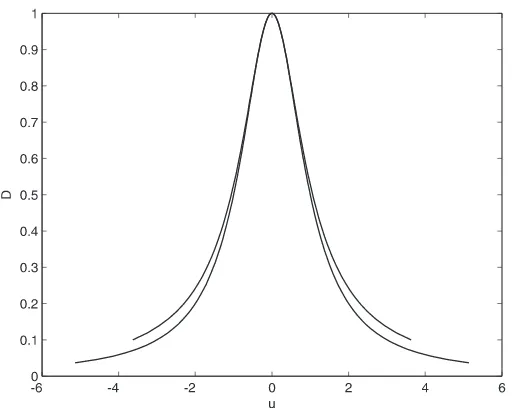
![Figure 4. Filled curve: exact solution withy τ −τ0 = −0.02, K = 5π. Dashed lines: approximate bounds = ±K[τ0 − τ] + (ln 2)/K.](https://thumb-ap.123doks.com/thumbv2/123dok/914277.900827/10.612.189.443.55.257/figure-filled-exact-solution-withy-dashed-approximate-bounds.webp)
Garis besar
Dokumen terkait
The algebraic approach to the solution of the model is presented in Section 3 , in this section the stationary states are expressed through the state vectors of the model and the
Then we can calculate the correlation functions of arbitrary element of density matrix using these algebraic relations, although the calculation become complicated... Unknowns are
It was found in [ 7 ] that the correlation functions of the eight-vertex model can be obtained by using the free field realization of the vertex operators in the eight-vertex SOS
The first is to give an orbital description of the decomposition of τ into irreducibles, in the case when G is a connected, simply connected one-parameter metabelian nilpotent
Consequently, all torsion-free linear connections are projectively equivalent, and the quest for a natural projectively invariant quantization amounts to the quest for a
In the problems we consider, which are also those problems considered previously in the work of Sakai [ 14 ], Murata [ 17 ] and Yamada [ 31 ], the characteristic data defines a
The St¨ackel transform is applied to the geodesic motion on Euclidean space, through the harmonic oscillator and Kepler–Coloumb potentials, in order to obtain ma-
Corollary 4.4 of the present paper (specialised to the case J = 2) establishes strong uniqueness and existence of associated reflected diffusions (with drift and diffusion