vol17_pp139-153. 183KB Jun 04 2011 12:05:59 AM
Teks penuh
Gambar
Garis besar
Dokumen terkait
by studying the Perron vector of G , it is shown that type-I-a graphs and type-I-b (resp. type-II-a).. graphs with some specified properties are not λ 1
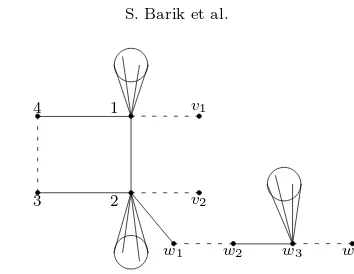
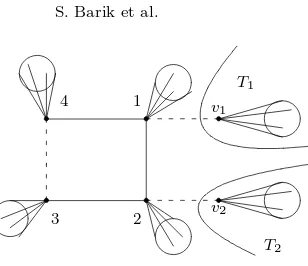
If there are two vertices on the 3-cycle which are adjacent to pendant vertices, then by considering Perron components, we nd that Case A holds, with the 3-cycle as the unique
It was provedfor triangle free graphs in [11], for graphs which contain no odd cycle on 5 or more vertices in [10], for all graphs on 5 vertices which are not the complete graph
Horn [8] gave an example of an exceptional matrix (see Section 3 of this paper). Note that A is not necessarily copositive in this definition, although A being copositive is our
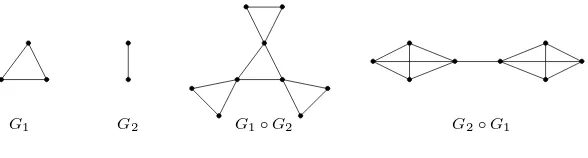
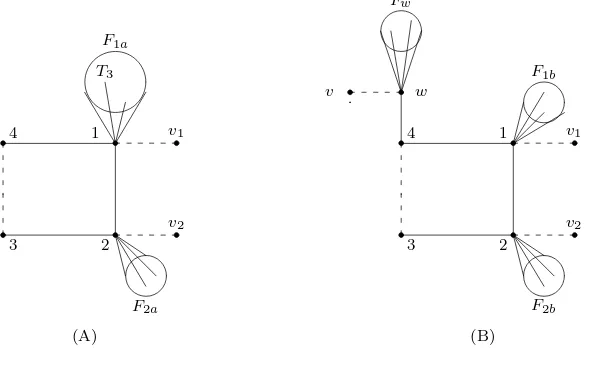
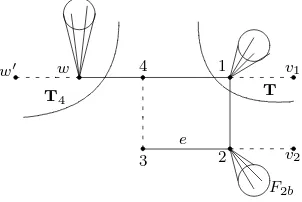
Theorem 1.2. Proof of Theorem 1.1. We will use the following auxiliary results in the proof.. Let SvwT denote the graph obtained from disjoint graphs S, T by adding an edge joining
Young subgroups, Spherical functions, Finite symmetric spaces, Ramanujan graphs, Symmetric groups, Representations, Characters, Spectral graph theory, Gelfand pair.. AMS
Moreover, in any minimum rank problem whatsoever, we need not concern ourselves with any graphs in which two degree two vertices are adjacent, or a degree two vertex is adjacent to
In this paper, by investigating the Perron vector of G, we show that type-I-a graphs are not λ 1 -extremal graphs, and type-I-b (resp. type-II-a) graphs with some.. specified