Wahiduzzaman, Mohammad Abdur Raihan at the Department of Electronics and Telecommunication Engineering (ETE), Daffodil International University, has been accepted as satisfactory in partial fulfillment of the requirements for the Bachelor of Electronics and Telecommunication Engineering degree and approved in terms of style and content . . Tasnuva Ali, Assistant Professor, Department of Electronics and Telecommunication Engineering (ETE), Daffodil International University, Dhaka. This thesis is wholeheartedly dedicated to our dearest guardians, who were our source of motivation and gave us strength when we thought of surrender, who consistently provide their ethical, spiritual, feeling and financial support.
Tasnuva Ali, Assistant Professor at the Department of Electronics and Telecommunications Engineering (ETE) Daffodil International University, Dhaka, who looks set to become our Research Manager due to her endless patience and sound advice, constant encouragement, constant and playful supervision, constructive criticism and invaluable advice, studying bad concepts and correcting them at all stages made it possible to complete this study. We would also like to thank the staff of the ETE department of Daffodil International University. The linear cryptanalysis is widely known as one of the most important tools for designing S-Box security.
The composite design of S Box is based on affine transformation (AT), where various affine matrices and constants are used to improve the security of the design. Therefore, this research is focused on using different affine constants to find the affine transformation and linear cryptanalysis of different S Boxes to study linear ciphertext attacks.
Analysis of Linear cryptanalysis for lightweight AES block cipher
INTRODUCTION
- OVERVIEW
- AIMS AND OBJECTIVE
- MOTIVATION
- ABOUT RESEARCH
- RELATED WORS AND CONTRIBUTIONS
- SELECTION OF LIGHTWEIGHT CRYPTOGRAPHY
- Conventional cryptography: Servers and Desktops; Tablets and smartphones
- Lightweight cryptography: Embedded Systems; RFID and Sensor Networks
- HARDWARE IMPLEMENTATION
- SOFTWARE IMPLEMENTATION
- SELECTION OF AES (ADVANCED ENCRYPTION STANDARD)
- ENCRYPTION WITH AES
- S-BOX (SUBSTITUTION BOX)
- LOOK-UP TABLE
- AFFINE TRANSFORMATION
- LINEAR CRYPTANALYSIS
This research is provided with the help of AES lightweight cryptographic algorithm for linear cryptanalysis. Therefore, the objective of the research is to work with variable constants with a 4 by 4 affine matrix to check the effect of linear cryptanalysis for these different constants and S-Box values. In the second chapter, a review of the discovery and history of types of cryptography, lightweight cryptography, linear cryptanalysis, Advanced Encryption Standard (AES), Substitution Box (S-Box), Lookup Table (LUT) will be discussed. and Affine Transformation. (AT). Chapter 3 will provide the methodology, while Chapter 4 will analyze the data and finally calculate Linear and S-Box Cryptanalysis.
We test the security capacity of the S-box according to a theoretical cryptanalysis system, which is an obvious linear attack. Substitution-Box (S-BOX) will be the most important block of the Advanced Encryption Standard (AES) algorithm that absorbs 75 percent of the overall power through encryption. The improvement of the S-box works using composite field arithmetic operations is based on a different technique.
Although the S-box implementation in each area is significantly smaller than the LUT-based implementation and it is light. These binary equations are structured to balance the inputs and outputs of the various parts of the cipher.

MATERIALS AND METHODOLOGY
METHODOLOGY
KINDS OF CRYPTANALYSIS
- DIFFERENTIAL CRYPTANALYSIS
- LINEAR CRYPTANALYSIS
34;common" in that there were not many studies of a single cipher; attacks work equally well on several different groups of ciphers. Any flaws exploited were not so inherent in the ciphers: the detailed study of the ciphers was not that prompted the attacks Although several cryptanalytic techniques could be focused on an in-depth study of a cipher, we want to concentrate on a few different groups of these ciphers.
In this chapter, we are beginning to discuss a very important class of modern cryptographic algorithm techniques—linear cryptanalysis[22].
THE BLOCK DIAGRAM OF LINEAR CRYPTANALYSIS CALCULATION AND EXPLANATION
STEPS
- LINEAR CRYPTANALYSIS CALCULATION
- AFFINE TRANSFORMATION
- SELECTION OF 2D AFFINE MATRIX
- THE INPUT OF LINEAR CRYPTOGRAPHIC ALGORITHUM
- CONSTANT FOR LINEAR CRYPTOGRAPHIC ALGORITHUM
- LINEAR APPROXIMATION CALCULATION
- MATUSI’S ALGORITHUMS
- MATUSI’S ALGORITHUM 1
- MATUSI’S ALGORITHUM 2
- PILING-UP LEMMA
- PILING –UP LEMMA (MATUSI)
- LINEAR EXPRESSION FOR S-BOXES
- LINEAR ESTIMATION OF A FEW ROUNDS
- EXTRACTING FINAL ROUND KEY BITS
- FINDING LINEAR EXPRESSIONS
- MATSUI OPERATION OF LINEAR EXPESSION
Matsui's pilling up lemma is one of the algorithms that will be implemented. An affine transformation is a transformation that does not want perfect correlation (everything centered on one point lies first on the transformation stage) and ratio (eg, the middle of a line segment remains on the middle of the conversion stage). An affine transformation is often referred to as an affinity, which is an explanation of revolution, interpretation, expansion, and shear.
One of the most significant keystones protecting the equilibrium line with three focused S-boxes in the separation ratio would be a non-linear, inverse conversion from the affine conversion to the security implications at the AES level. After all calculations of iterations, the similarity number is found, which is proved by the conditions of the truth table. If the probability of the events is different from 1/2, you can conclude that this is a bias.
These last three steps are present because we believe that our estimates and probabilities mean that if P is less than 1/2 then we can conclude that the classification of the key is incorrect and if P is greater than 1/2 then the equation is generally valid. Calculate the main bit of each candidate set. That instance number is a T-value for the truth of the text pair with simple numbers of the linear equation. So if the number of N pairs measures T(N/2) (absolute difference value) - for each candidate (N/2) and several key candidates gives you the best optimal form of the result.
Additionally, we need to test all possible values of the input-output value pairs, of which there are 23 (since we now have 3 input bits and the output is entirely determined by these). Additionally, it may be noted that the quantity of any row or any column should be +8 or even -8. the S-box expression is given below. iv) From equations (i) and (ii) following the Pilling Up-lemma. v) From equations (iii) and (iv) following the Pilling Up-lemma. Here the universal key is fixed to 0 or 1 depending on the cipher key.
For low parts of the input and output, we can organize the entire linear cryptanalysis consisting of the construction of various linear expressions. We will use 𝑃𝑖 to denote the ith bit of the plaintext, 𝐾𝑟, to denote the ith bit of the round key, 𝐾𝑟. When we have a linear approximation, the previous round for each particular digit using a large enough case bias, it can try to exploit it to recover some parts of the last round's key parts from the finished key mix.[ 25] .
Here, we are choosing the most effective linear term, B, by induction, constructed from a large doubt and taking care of the ideal term for each particular chip. The input bits leading to the output bits must be possibly p2 (ie, the probability of the linear expression I2 = O2 = 0).

RESULT AND CALCULATION
- LAT CALCULATION
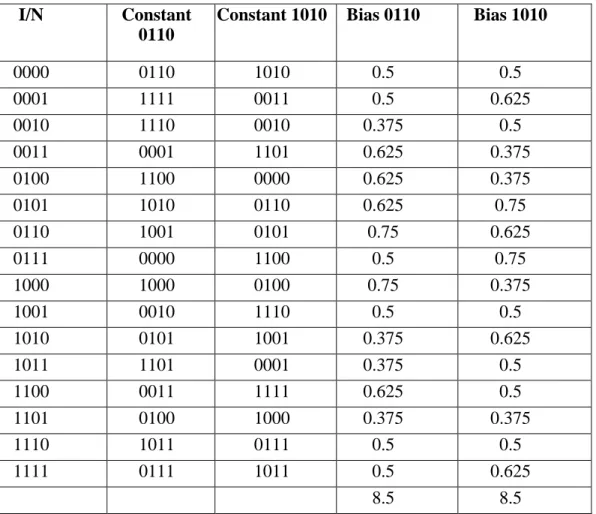
- THE KEY DIFFERENCE OF PARTICULAR VALUE FOR VARIABLES 0110 AND 1010
- PROPOSED S-BOX
- ANALYSIS AND DISCUSSION
From the LAT table we find that value is -2 for the probability of that particular value. The bias discrepancy between the input parameter and the probability can be seen in the table above. The values of plaintext and ciphertext, where the position of the given value has the predecessor of the straight line, which is given by the bits running in the spherical function.
In the final round, it should be remembered that the total counting factor of the S-Box is 65536, where the output random number acts as the counting number according to the input of each round table. Here the first counter number for the given S-box should be taken randomly for the two constants. Most of the time, this counter number depends on the bit size of the S box.
Given the values derived from the table in the query, it can be shown that the S-box counter number for the same input is different. The bias of the linear attack for each input is found against the count number given in the table above, where we have found a relative plaintext/ciphertext for each input continuously in each round. On the other hand, 256 key variations of the same constant are included in each round table.
In a linear distance calculation, the difference between the values given on the graph indicates that all constants for the subject were separated under the linear attack. Ciphertext is primarily a complex S-box source for an additional amount of ciphertext and plaintext collections. Since there is no clear understanding of the given target subkey, we rechecked this efficient algorithm with a possible 256 keys.
If the correct subkey is used for more than half the state, it is fixed on a relatively constant basis (subkey to bias) on the S-box. After verifying both the general text and the ciphertext collection, we use the subkey for the most individual check-in 1/2. The test results of the linear attacks are 1/32, which represents the fraction 0.03125, which is the same for the two compatible properties 1010 and 0110.
Another major bias occurs when the erroneous objective semi-sub key's assessment is not accurately proportional to the opposite of the key with a linear expression. This research paper mainly focuses on the effect of the different constant values of linear cryptanalysis of S-box.

CONCLUSION
CONCLUSION
Future Work
Seo, “Highly efficient implementation of block ciphers in graphics processing units for massively large data,” Appl. Ghosh, "A review of existing 4-bit crypto-box cryptanalysis techniques and two new techniques with 4-bit boolean functions for cryptanalysis of 4-bit crypto-S boxes*", Adv.