My sense of gratitude to all my respected teachers of the Department of Mathematics, KUET for their kind help and valuable suggestions. Finally, I express my deepest gratitude to my parents for whom I can see the beautiful sights and sounds of the world. Numerical solutions are obtained for the velocity and temperature fields as well as the concentration distribution for different values of the physical parameters that enter the problem.

Literature Review
Agrawal et al. (1980) consider steady laminar free convection flow with mass transfer of an electrically conductive fluid along a plane wall with periodic suction. Uwanta (2012) studied the effects of chemical reaction and radiation on heat and mass transfer flux past a semi-infinite vertical porous plate with constant mass flux and dissipation. 2012) presented a theoretical study on the effect of radiation on uniform heat and mass transfer in free convection over an isothermal expansion plate in the presence of a uniform magnetic field with the effect of viscous dissipation. In another paper, Ibrahim examines a detailed numerical study of the combined effects of radiation and mass transfer on a uniform MHD two-dimensional Marangoni convection flow over a flat surface in the presence of Joule heating and viscous dissipation under the influence of suction and injection. (2013).
When heat and mass transfer occur simultaneously in a moving fluid and interact with each other, a cross-diffusion effect occurs, the mass transfer caused by a temperature gradient is called the Soret effect, while the heat transfer caused by the concentration effect is called the Dufour effect. Many researchers have studied the Soret and Dufour effects; for example, Kafousiasis and Williaims (1995) studied Soret and Dufour effects on mixed free forced convection and boundary layer flow for mass transfer with temperature-dependent viscosity. 2008) analyzed MHD fluid flow over a vertical plate with Dufour and Soret effects. Later, Usman and Uwanta (2013) addressed the effect of thermal conductivity on the MHD heat and mass transfer flow past an infinite vertical plate with Soret and Dufour effects.
More recently, Uwatana and Usman (2014) investigated the combined Soret and Dufour effects on the free convective heat and mass transfer on an unsteady boundary layer flow over a vertical channel in the presence of viscous dissipation, using the Crank-Nicolson implicit finite difference scheme. and constant suction.
Some Available Information on MHD
- Magnetohydrodynamics (MHD)
- MHD Boundary Layer Phenomena
- Mass Transfer
- MHD and Heat Transfer
- Mixed Convection
- Heat and Mass Transfer
These waves are produced by disturbances which propagate simultaneously in the conducting fluid and the magnetic field. The number of component equations is reduced to those in the flow direction, and pressure changes across the boundary layer are negligible. Also, the number of viscous terms is reduced to the dominant term, and the heat conduction in the flow direction is negligible.
Variations in the transverse magnetic field component and pressure across the boundary layer are negligible. In many of these processes, the interest lies in determining the total energy transfer, although in processes such as drying, the interest lies primarily in the total mass transfer for moisture removal. But it was precisely in the field of aerodynamic heating that the greatest interest was awakened.
In many of these processes, the interest lies in determining the total energy transfer, although in processes such as drying, the interest lies primarily in the total mass transfer for moisture removal.
Useful Dimensionless Parameters Prandtl Number Pr
The fundamental problem of heat and mass transfer is governed by the combined buoyant effects arising from the simultaneous diffusion of thermal energy and of chemicals. Therefore, the continuity, momentum, energy and concentration equations are only coupled to the buoyancy terms, if the other effects, such as the Soret and Dufour effects, are neglected. This is obtained from the ratio of the magnetic force to the inertial force and is defined as.
It is the ratio of viscous diffusivity to chemical molecular diffusivity and is defined as, Dm. Eckert number phenomena are the result of the distribution created by the shear stress in the fluid at the wall. In other words, it is the kinetic energy of the flow relative to the enthalpy change.
A dimensionless number used in the study of thermodiffusion, equal to the increase in enthalpy of a unit mass during isothermal mass transfer divided by the enthalpy of a unit mass of mixture.
Basic Governing Equations
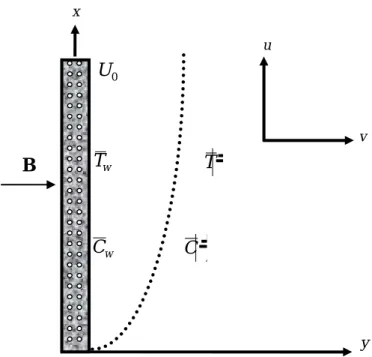
A strong uniform magnetic field B=0,B0,0 is imposed along the y-axis and the magnetic Reynolds number of the flux is assumed to be small enough that the induced magnetic field is negligible compared to the applied magnetic field. In the three-dimensional Cartesian coordinate system, the momentum equation (2.6) becomes, with the help of equations. In the three-dimensional Cartesian coordinate system, the concentration equation (2.16) becomes with the help of Eqs.
Where cp is the specific heat at constant pressure, c is the concentration sensitivity and K(T)K011TT , K is the thermal conductivity of the ambient fluid.0. In the three-dimensional Cartesian coordinate system, the energy equation (2.21) becomes with the help of Eqs. In the three-dimensional Cartesian coordinate system, the continuity equation (2.3), the momentum equations, the concentration equation (2.20), and the energy equation (2.25) are as follows.
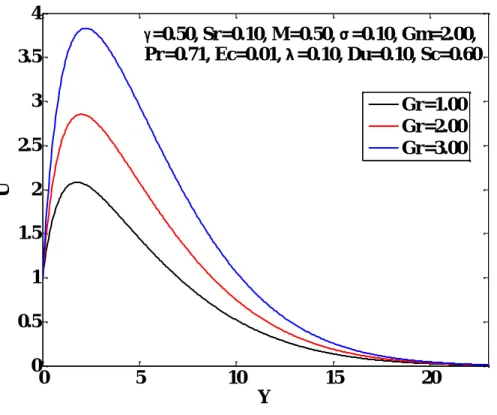
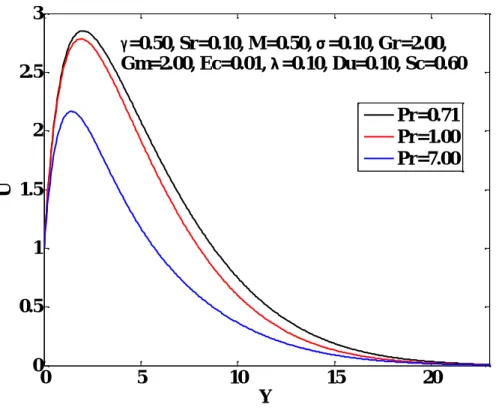
After that, the plate moves with a constant velocity U in its plane and 0 at the time t 0 the temperature of the plate and the concentration rise to. Fluid velocity increases with increasing Grashof number, modified Grashof number, Dufour number, Soret number, Eckert number and variable thermal conductivity parameter. The opposite effects are observed when the Prandtl number, Schmidt number, magnetic parameter, porous medium permeability and suction parameter increase.
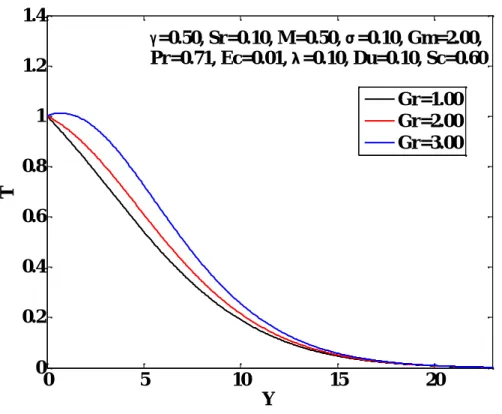
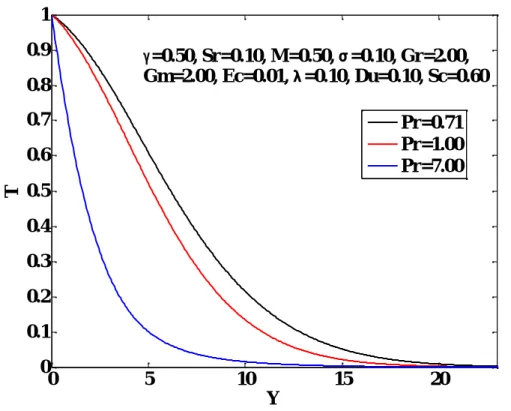
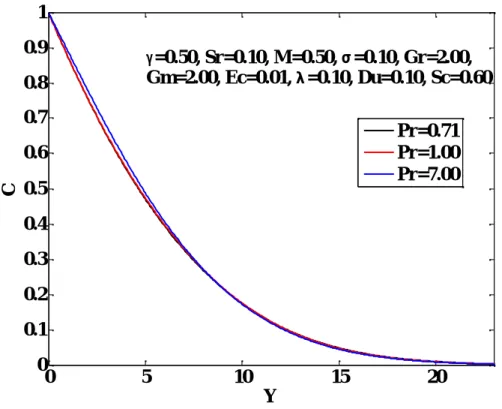
Fluid temperature increases with increasing Grashof number, Modified Grashof number, Dufour number, Soret number, Eckert number and variable thermal conductivity parameter. The opposite effects are seen with increasing Prandtl number, magnetic parameter, porous medium permeability and absorption parameter. There is no significant effect of the observed parameters on the concentration distributions, except the Schmidt number, the Soret number and the absorption parameter.
Here, concentration profiles decrease with increasing both Sc and , but it decreased rapidly with increasing suction parameter. It On the other hand, concentration profiles show increasing behavior with the increase of Soret number, Sr.
Finite Difference Method
Many physical phenomena in applied science and engineering when formulated in mathematical models fall into a category of systems known as nonlinear coupled differential equations. A system of nonlinear partial differential equations associated with boundary conditions is very difficult to solve analytically. The governing equations of our problem contain a system of partial differential equations which are transformed by the usual transformation into a non-dimensional system of nonlinear partial differential equations coupled with boundary conditions.
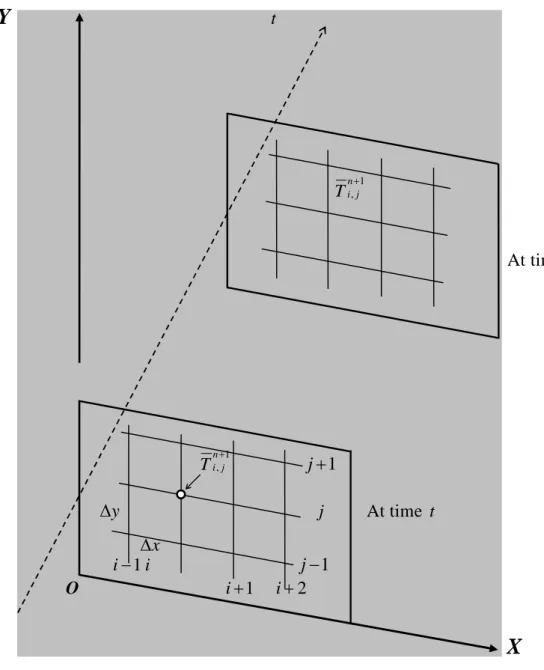
The solution of our problem will therefore be accomplished by the advanced numerical method, the Finite Difference numerical method was used to solve our obtained non-similar coupled partial differential equations. Let the mesh spacing in x and y directions be denoted by x and y also the time step by t. The expressions for mixed derivatives can be obtained by differentiating with respect to each variable in turn.
If we proceed in a similar manner, the central difference approximation turns out to be the third derivative. Finite difference solution of MHD mixed convective flow through an impulsively initiated permeable vertical plate with diffusion thermo and thermal diffusion effects.
Mathematical Model of the Flow
Here, x, y are the Cartesian coordinate system; u and v are the velocity components along and perpendicular to the plate, is the kinematic viscosity, is the fluid viscosity and k1 is the permeability of the porous medium, g is the acceleration due to gravity, T is the coefficient of thermal expansion. , C and the concentration expansion coefficient, is the density, Dis is the mass diffusion coefficient, kt is the thermal diffusion ratio and T is the average liquid temperature, m cpis the specific heat at constant pressure, c is the concentration sensitivity and K(T)K01 1TT (Usman and Uwanta (2013)), K is the thermal conductivity of the ambient fluid.0.
Mathematical Formulation
Numerical Solution
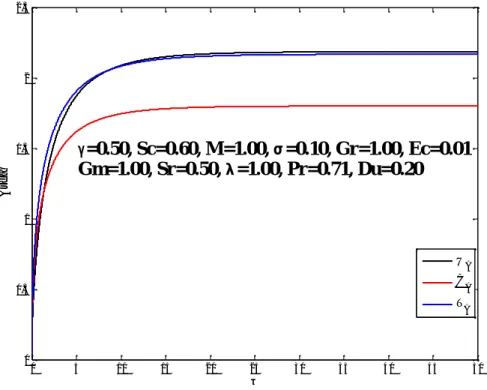
T-distributions at all internal nodes can be calculated by successive applications of the above finite difference equations.
Results and Discussion
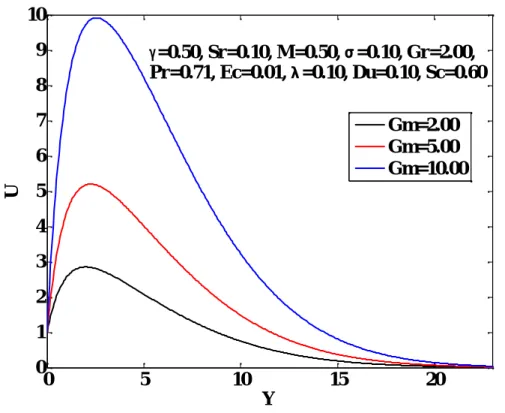
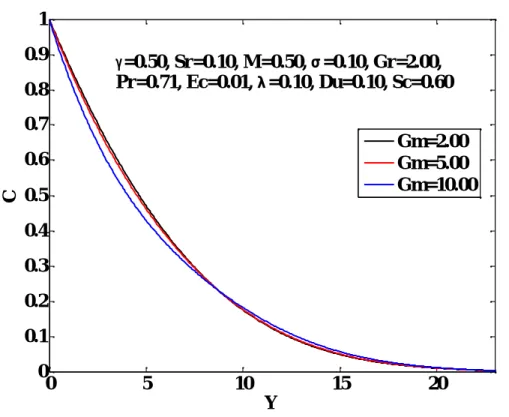
The effects of the modified Grashof number Gm on the velocity, temperature and concentration distributions are shown in Figures 4.6-4.8. There is no significant effect of Pr on the concentration distributions as shown. The influence of the Dufour Du number on the velocity, temperature and concentration distributions is shown in Figs.
The effect of the Schmidt number Sc on the velocity, temperature and concentration distributions are shown in the figures. It is observed that the velocity, temperature and concentration profiles are decreasing with increasing Sc. The influence of the Soret Sr number on the velocity, temperature distributions, and concentration distributions are discussed in Figs.
The effect of magnetic parameter M on the velocity, temperature and concentration distributions is shown in Figures 4.21 –4.23. It is clearly seen from Figure 4.21 that the effects of increasing the magnetic field strength on the thickness of the momentum boundary layer lead to a decrease in the velocity width. This is because a strong magnetic field results in a large damping effect on speed by creating a medicinal force that opposes the field movement.
The influence of the permeability of the porous medium γ on the distribution of velocity, temperature and concentration is shown in Figures 4.24–4.26. The influence of the suction parameter on the distribution of velocity, temperature and concentration is described in Figs. The effect of the Eckert number Ec on velocity, temperature and concentration is shown in Figs.
The influence of variable thermal conductivity, on the velocity, temperature and concentration distributions is described in Figures.