ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b] (STUDI KASUS : FUNGSI POLINOM DAN FUNGSI RASIONAL)

ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b]

(STUDI KASUS : FUNGSI POLINOM DAN FUNGSI RASIONAL)

Oleh: IDA SAFITRI

0817031028

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

ABSTRACT

ANALYSIS OF APPROXIMATION ERROR OF FUNCTIONS BY MINIMUM NORM METHOD IN HILBERT SPACE C[a, b] (STUDI KASUS : FUNGSI POLINOM DAN FUNGSI RASIONAL)

By IDA SAFITRI

Usually, approximation of functions used in numerical analysis. Two main reasons for application of approximation of functions are : to give efective approximation of functions, and to simplified complex function. Given a function f , with some or all point are given, we wish to get approximation of spesific function f that can be easier to be analyzed.. For example, we wish to compute

dx e x



1 

0 2

. Then we approximate its integran by polynomials with n degree (for

large n). Optimization problems, espesially good aprroximation of function that can’t get the best solution (for large errors) in real space , it can be solved by mathematics system simplier, by carryng out the problem to abstract space or vector space, espesially in Hilbert space C[a,b]. The problem known as minimum norm problem in Hilbert Space C[a,b]. By minimum norm method we have minimum approximation errors.

ABSTRAK

ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b]

(STUDI KASUS : FUNGSI POLINOM DAN FUNGSI RASIONAL)

Oleh IDA SAFITRI

Aproksimasi fungsi dalam proses komputasi sering digunakan hampir di semua bidang analisis numerik. Dua alasan utama penggunaan aproksimasi fungsi adalah untuk memberikan fungsi pendekatan yang efektif dan mendekati suatu fungsi yang rumit dengan fungsi yang lebih sederhana. Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapa nilai di titik-titik tertentu saja, kita ingin memperoleh hampiran (aproksimasi) untuk f yang mempunyai bentuk tertentu (misalnya supaya lebih mudah dianalisis) dengan kesalahan yang dapat kita kontrol. Misalnya kita hendak menghitung



ex dx

1

0 2

, kita hampiri integrannya

dengan polinom (suku banyak) berderajat n (dengan n cukup besar). Masalah optimisasi khususnya aproksmasi fungsi terbaik yang tidak medapatkan solusi terbaik (ralat yang besar) dalam ruang fisis atau yang dikenal sebagai ruang real , dapat dipecahkan dengan sistem matematis yang sederhana, dengan membawa masalah aproksimasi tersebut ke ruang abstrak (berisi aksioma-aksioma) atau ruang vekor, khususnya pada ruang Hilbert C[a,b]. Masalah tersebut dikenal sebagai masalah minimum norm dalam ruang Hilbert C[a,b]. Dengan menggunakan konsep minimum norm akan diperoleh kesalahan optimal (galat) yang minimum.

ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b]

(STUDI KASUS : FUNGSI POLINOM DAN FUNGSI RASIONAL)

Oleh Ida Safitri 0817031028

Skripsi

Sebagai Salah Satu Syarat Untuk Mencapai Gelar SARJANA SAINS

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

Judul Skripsi : ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b] (STUDI KASUS : FUNGSI POLINOM DAN

FUNGSI RASIONAL) Nama Mahasiswa : Ida Safitri

Nomor Pokok Mahasiswa : 0817031028 Program Studi : Matematika S1 Jurusan : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

MENYETUJUI 1. Komisi Pembimbing

Amanto, S.Si., M.Si. Agus Sutrisno, S.Si., M.Si. NIP. 19730314 200012 1 002 NIP. 19700831 199903 1 002

2. Mengetahui Ketua Jurusan Matematika

MENGESAHKAN

1. Tim Penguji

Ketua : Amanto, S.Si., M.Si. ………

Sekretaris : Agus Sutrisno, S.Si., M.Si. ………

Penguji

Bukan Pembimbing : Dr. Muslim Ansori, S.Si., M.Si. ………

2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Prof. Suharso, Ph.D.

NIP 19690530 199512 1 001

RIWAYAT HIDUP

Penulis dilahirkan di Bandar Lampung pada tanggal 29 Maret 1991 dan merupakan anak kedua dari dua bersaudara, dari pasangan Bapak Syayuti dan Ibu Mai Muri, serta kakak kandung penulis bernama Adi Yanto, S.Hi.(alm).

Penulis mengawali pendidikan Taman Kanak-kanak di TK Al-Hikmah pada tahun 1995-1996, Sekolah Dasar di SD Negeri 1 Way Halim Permai pada tahun 1996-2002, kemudian pendidikan menengah di SMP Negeri 12 Bandar Lampung pada tahun 2002-2005, dan pendidikan lanjutan di SMA Negeri 9 Bandar Lampung pada tahun 2005-2008.

MOTTO:

Sesungguhnya di balik setiap kesulitan ada kemudahan

(Al-Insyirah:6)

Orang hebat tidak dihasilkan melalui kemudahan,

kesenangan, dan kenyamanan. Mereka dibentuk melalui

kesukaran, tantangan dan air mata.

Jadilah dirimu sendiri, maka kamu akan mengetahui

siapa yang benar-benar peduli terhadap mu

SANWANCANA

Alhamdulillahi robbil ’alamin, puji dan syukur penulis panjatkan kehadirat Allah

SWT yang telah melimpahkan rahmat dan hidayah serta nikmat yang tiada hentinya kepada penulis dan tak lupa shalawat serta salam yang selalu tercurah kepada junjungan kita nabi besar Muhammad SAW yang telah menjadi suri tauladan yang baik bagi kita sehingga dapat terselesaikannya Skripsi yang berjudul “Analisis Aproksimasi Fungsi Dengan Metode Minimum Norm Pada Ruang Hilbert C[a, b] (Studi Kasus : Fungsi Polinom Dan Fungsi Rasional)”.

Dalam penyusunan skripsi ini banyak pihak yang telah membantu, baik dalam memberikan bimbingan maupun saran sehingga skripsi ini dapat terselesaikan tepat waktu. Untuk itu penulis mengucapkan terima kasih kepada :

1. Bapak Amanto, S.Si., M.Si., selaku dosen pembimbing utama yang selalu membimbing penulis dalam penyelesaian skripsi dan selaku pembimbing akademik yang selalu membimbing penulis semasa kuliah sampai sekarang. 2. Bapak Agus Sutrisno, S.Si., M.Si., selaku dosen pembimbing kedua yang

selalu membimbing, memberikan saran kritik bagi penulis selama penyelesaian skripsi.

x

4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D, selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.

5. Bapak Prof. Suharso, Ph.D., selaku Dekan FMIPA Universitas Lampung. 6. Dosen, staf dan karyawan Jurusan Matematika FMIPA Universitas Lampung

yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.

7. Mama, Papa dan Uan Adi(alm) tercinta yang selalu memberi dorongan dan motivasi agar dapat terselesaikannya skripsi ini.

8. Shan Dirgantara Putra yang selalu menemani serta memberikan dukungan dan semangat kepada penulis.

9. Sahabat penulis Wiwid, Aci, Selvi, Wiwik, Mia, Ivip, Septi, Andre, Noven, Edo, Yayat, Rendi, Edi, Fajri, Diyah, Marlina, Nurul, teman-teman Exotic (Matematika 08), dan adek-adek matematika angkatan 2009 dan 2010, serta akma, ka gayoh, chandra, dll terimakasih atas saran, dukungan dan semangat kebersamaannya.

10.Seluruh pihak yang telah membantu penulis yang tidak dapat disebutkan satu persatu, atas peran dan dukungannya dalam menyusun skripsi ini.

Penulis menyadari bahwa skripsi ini masih banyak jauh dari kesempurnaan, akan tetapi semoga skripsi ini dapat berguna dan memberikan manfaat bagi kita semua. Amiin.

Bandar Lampung, 10 Januari 2013 Penulis,

PERSEMBAHAN

Karya kecil ini ku persembahkan untuk Mama dan Papa

tercinta yang selalu mengiringi langkah ku dengan

ketulusan doa dan kasih sayang yang tiada hentinya. Dan untuk alm. Kakak ku, Uan Adi Yanto, S.Hi yang selalu

menjadi motivasi. Serta untuk Shan Dirgantara Putra yang

selalu menemani dan memberikan semangat tersendiri.

1

I. PENDAHULUAN

1.1 Latar Belakang dan Masalah

Dalam dunia aplikasi, sering berhadapan dengan fungsi, di mana fungsi itu mungkin diperoleh dari data numerik dengan interpolasi ataupun regresi. Sering kali fungsi yang diperoleh dengan cara demikian mungkin bukan fungsi yang kita inginkan, tetapi diinginkan fungsi lain. Sehingga fungsi lain yang diperoleh tersebut harus mendekati fungsi yang semula. Cara mencari fungsi tersebut adalah dengan optimisasi. Optimisasi adalah suatu proses memaksimumkan atau meminimumkan suatu fungsi objektif yang memenuhi kendala tertentu. Suatu masalah optimisasi yang tidak mendapatkan solusi terbaik dalam ruang fisis atau ruang real, dapat dipecahkan dengan suatu sistem matematis, yaitu dengan membawa masalah tersebut ke ruang abstrak (berisi aksioma-aksioma) atau ruang vektor (Kreyzig, 1978).

2 masalah tersebut, diantaranya adalah penyelesaian masalah minimum norm pada ruang Hilber L2[a,b] (Amanto dkk, 2003). Selanjutnya penelitian yang sama juga dilakukan pada ruang Hilbert yang lain, yaitu ruang Hilbert C[a,b] (Joko Waluyo, 2003). Dalam hal ini konsep yang digunakan adalah minimum norm pada ruang Hilbert C[a,b]. Fungsi yang akan dicari aproksimasinya adalah fungsi-fungsi kontinu bernilai real yang terdefinisi pada [a,b] . Pada penelitian tersebut baru sampai pada tahap mencari solusinya, belum pada tahap evaluasi atau analisis hasil terkait dengan galat yang dihasilkannya.

Metode optimisasi dengan metode ruang vektor pada dasarnya adalah mencari vektor dengan norma minimum atau meminimumkan norma suatu vektor (Luenberger, 1969). Untuk membahas aproksimasi fungsi digunakan Teorema Proyeksi [Adkinson (2001) & Luenberger (2001)]. Dalam pemecahan masalah ini, langkah penting yang harus dilakukan adalah pemilihan basis yang bebas linear yang membangun ruang fungsi yang akan diaproksimasi dan penentuan kesalahan optimal atau ralat optimal dari aproksimasi yang diambil. Basis ini tidak tunggal. Pemilihan basis yang berbeda akan menghasilkan aproksimasi fungsi yang sama dan juga kesalahan optimal yang sama pula.

1.2 Tujuan Penelitian

3 1.3 Manfaat Penelitian

Manfaat penelitian ini adalah :

1. Memberikan konsep analisa terhadap analisis galat atas pemilihan basis yang dilakukan pada aproksimasi fungsi dengan metode minimum norm pada ruang Hilbert C[a,b] sehingga akan diperoleh aproksimasi fungsi terbaik dengan galat (kesalahan) yang paling kecil.

2. Memberikan kontribusi bagi peneliti tentang metode minimum norm pada ruang hilbert C[a,b].

3. Dapat memberikan sumbangan pemikiran dan menambah wawasan mengenai metode minimum norm pada ruang hilbert C[a,b].

1.4 Batasan Masalah

4 II. LANDASAN TEORI

Pada bab II ini, akan dibahas pengertian-pengertian (definisi) dan teorema-teorema yang medukung untuk pembahasan pada bab IV. Pengertian (definisi) dan teorema tersebut dituliskan sebagai berikut.

2.1. Teorema Proyeksi

Teorema proyeksi merupakan prinsip dasar dalam penyelesaian masalah optimisasi. Sebelum ke Teorema proyeksi, terlebih dahulu akan diperkenalkan konsep ortogonalitas.

Definisi 2.1.1 (Luenberger, 1969)

Dalam suatu ruang pre-Hilbert X, vektor x,y  X dikatakan ortogonal jika <x, y>= 0,

dinotasikan dengan x  y. Suatu vektor x dikatakan ortogonal dengan himpunan S,

dinotasikan x  S jika x  s untuk setiap s  S.

5 Lemma 2.1.1

Misalkan X suatu ruang Hilbert dan x, y  X. Jika x  y, maka xy 2  x2  y 2

Bukti :

y y x y y x x x y x y x y

x 2   ,   ,  ,  ,  ,

= x 2 00 y 2 = x2  y 2. 

Selanjutnya akan dibahas suatu masalah optimisasi yang berhubungan dengan

Teorema proyeksi. Misalkan X suatu ruang Pre-Hilbert, diberikan suatu vektor x X

dan M ruang bagian dari X, maka akan ditentukan vektor m M yang terdekat ke x,

yaitu vektor yang meminimalkan xm .

Jika x berada di M maka penyelesaiannya trivial, yaitu vektor x sendiri. Secara umum ada empat pernyataan penting dalam penyelesaian masalah tersebut yaitu :

1. Adakah vektor m  M yang meminimalkan xm ?

2. Apakah penyelesaiannya tunggal ?

6 Pernyataan nomor 1, 2 dan 3 akan dijawab dengan Teorema proyeksi. Ada dua versi Teorema proyeksi, satu versi pada ruang Pre-Hilbert dan satu versi yang lain pada ruang Hilbert dengan hipotesis dan kesimpulan yang lebih kuat.

Teorema 2.1.2 (Teorema Proyeksi di Ruang pre-Hilbert)

Misalkan X suatu ruang Pre-Hilbert, M suatu ruang bagian dari X dan x sebarang

vektor di X. Jika ada vektor m₀M , sedemikian hingga xm_o  xm,mM,

maka m0 tunggal. Syarat perlu dan cukup m₀M , suatu vektor minimal tunggal di

M adalah vektor selisih x–m0 ortogonal terhadap M.

Bukti :

Akan di tunjukkan jika m0 adalah vektor minimal, maka x–m0 ortogonal terhadap M. Andaikan kondisi sebalinya, terdapat m M yang tidak ortogonal terhadap x – m0.

Tanpa mengurangi keumuman bukti, dimisalkan m 1 dan <x – m0 , m> =0.

7 sebarang mM, berdasarkan Teorema Phytagorea :

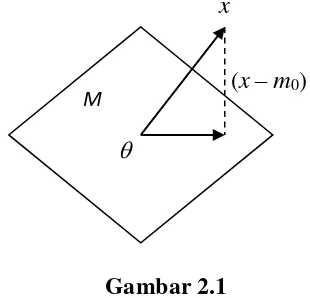
8 Dalam dimensi tiga, teorema proyeksi ini dapat dinyatakan sebagai berikut :

Ruang bagian M adalah bidang yang melalui titik asal dan x di ruang dimensi tiga X. Jika ada vektor minimal m0 M maka m0 tunggal dan vektor selisih x – m0 tegak lurus terhadap bidang M, seperti digambarkan dalam gambar dibawah ini :

x

(x–m0)

Gambar 2.1

Teorema di atas belum menjamin keberadaan vektor minimal, tetapi jika ada vektor minimal m0 , maka m0 tunggal dan vektor selisih x – m0 ortogonal terhadap ruang bagian M. Dengan hipotesis yang lebih kuat didapatkan kesimpulan yang lebih kuat, yaitu terjaminnya keberadaan vektor minimal. Hal ini dinyatakan dalam teorema berikut.

Teorema 2.1.3 (Teorema Proyeksi Klasik)

Misalkan H ruang Hilbert dan M ruang bagian tertutup dari H, maka untuk sebarang

vektor xH, terdapat tunggal vektor m₀M sedemikian hingga

M

9 tunggal adalah vektor selisih x–m0 ortogonal terhadap ruang bagian M.

Bukti :

Ketunggalan dan ortogonalitasnya telah dibuktikan pada Teorema 3.3.2, sehingga tinggal membuktikan keberadaan vektor minimal. Jika xM dan m0 = x maka bukti Menurut hukum jajaran genjang (parallelogram),

2

dengan menyusun kembali persamaan di atas didapatkan :

2

Karena M ruang bagian linier sehingga dari definisi ,

2 j i m m

x  

10 2

2 2

2

4 2

2     



 i j i

j m m x x m

m

karena



 2



2 x

mi , i

Maka



m_jm_i 2



0 , i, j .

Dengan demikian {mi} adalah barisan Cauchy dan karena M ruang bagian tertutup

dari ruang lengkap, maka barisan {mi} mempunyai limit m₀ di dalam M.

Dengan kekontinuan norm maka xm₀ . 

Jadi dalam penulisan ini, Teorema proyeksi klasik menjamin keberadaan dan

ketunggalan penyelesaian optimal serta kondisi yang harus dipenuhi agar keberadaan vector minimal ada penyelesaian optimalnya, penyelesaian optimalnya sendiri belum dapat ditentukan.

Selanjutnya Teorema proyeksi di atas akan ditetapkan untuk membangun sifat

struktural tambahan dari suatu ruang Hilbert, antara lain adalah dalam sebarang ruang bagian tertutup dari ruang Hilbert, sebarang vektor dapat ditulis sebagai jumlahan dua vektor, satu vektor di ruang bagian tertutup dan vektor yang lain ortogonal

11 \Definisi 2.1.2 (Luenberger, 1969)

Misalkan S suatu himpunan bagian dari ruang Pre-Hilbert. Himpunan semua vektor

yang ortogonal terhadap S disebut komplemen ortogonal dari S dan dinotasikan

dengan S.

Teorema 2.1.4

Misalkan S dan T himpunan bagian dari ruang Hilbert dan S, T berturut-turut menyatakan komplemen ortogonal dari S dan T maka :

1. S adalah ruang bagian tertutup

2. S  S

3. Jika ST maka T S

4. S= S

Bukti :

1. Himpunan S merupakan ruang bagian. Ruang S tertutup karena jika

{xn} suatu barisan konvergen dari S, katakan xn  x ; Kekontinuan perkalian dalam menyatakan 0 = <xn, s>  <x, s> untuk semua s S, sehingga x 

S . 

2. Diambil x S. Hal ini berarti x  y untuk semua y S. Sehingga

diperoleh y  z. Untuk setiap z S termasuk z = x.

12 3. Ambil x T. Oleh karena itu maka y  x untuk semua y T.

Karena S  T , maka x  z untuk setiap z  S. Dengan kata lain x S.

4. (S) = S

Harus dibuktikan :

(a) (S)  S

(b) S (S)

Bukti :

(a) Dari Teorema 3.3.4 (bagian 3).

Jika S  S, maka (S)  S. 

(b ) Dari Teorema 3.3.4 (bagian 1)

Karena S  S, maka S (S). 

Definisi 2.1.3 (Luenberger, 1969)

Ruang vektor X dikatakan jumlahan langsung dari ruang bagian M dan N, jika setiap

vektor x  X dapat ditulis secara tunggal, dalam bentuk x = m + n dengan m M dan

13 Teorema 2.1.5

Jika M ruang bagian linear tertutup dari suatu ruang Hilbert H maka H = M  M

dan M = M

Bukti :

Misalkan x H. Karena M ruang bagian tertutup, maka menurut Teorema proyeksi

ada vektor tunggal m0 M sedemikian hingga xm₀  xm untuk semua

m M dan n0 = x – m0 M.

Dengan demikian x = m0 + n0 , dengan m0 M dan n0 M. Jadi x merupakan

jumlahan dari m0  M dan n0  M. Untuk membuktikan ketunggalannya, misalkan

x = m1 + n1, dengan m1  M dan n1  M maka :

0 = (m1 + n1) – (m0 + n0) = m1 – m0 + n1 – n0 , tetapi m 1 – m0 dan n1 – n0 ortogonal, sehingga menurut teorema phytagorean 02  m₁m₀ 2  n₁n₀ 2.

Hal ini menyatakan m0 = m1 dan n0 = n1. Jadi untuk setiap vektor di H dapat

dinyatakan dengan tunggal sebagai jumlahan dari suatu vektor di M dan suatu vektor

di M. Dengan kata lain H = M  M.

Untuk membuktikan M = M tinggal menunjuKkan M M. Karena 

M

14 Diambil x  M dan akan ditunjukkan x  M. Menurut bagian teorema ini,

x = m1+ n1 dengan m1  M dan n1  M, karena x  M dan m  M.

Maka x – m  M, yaitu n1 M. Tetapi n1 M, sehingga n1 n1 yang

menyatakan n1 = 0, sehingga x - m  M dan M M. Terbukti M = M. 

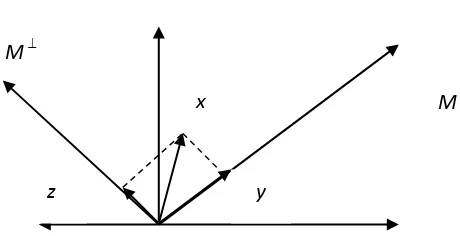
Dalam dimensi dua bagian pertama teorema di atas dapat dinyatakan sebagai berikut. Jika H suatu bidang dan m suatu garis lurus yang melalui titik asal maka untuk setiap x  H dapat dinyatakan dengan tunggal sebagai x = y + z, dengan y  M dan

zM. Hal ini dapat digambarkan sebagai berikut.

Gambar 2.2

Gambar diatas, jika M ruang bagian tetutup dari H maka H = M  M.

M M

x

15 Misalkan M ruang bagian tertutup dari suatu ruang Hilbert H dan vektor x di H.

Vektor m0  M dengan x – m0 M disebut proyeksi ortogonal x pada M.

Jadi sampai disini keberadaan dan ketunggalan penyelesaian optimal masalah optimisasi sudah terjawab, namun penyelesaian optimalnya sendiri belum ditentukan. Ada dua cara untuk menentukan penyelesaian optimal, yaitu dengan menyelesaikan persamaan normal dan dengan prosedur ortogonalisasi Gram-Schmidt bersama deret Fourier. Pada penelitian ini akan dibicarakan dengan menyelesaikan persamaan normal dan matriks Gram.

Definisi 2.1.4 (Luenberger, 1969)

Misalkan y1,y2,...,yn basis dari M. Diberikan sebarang vektor x  H dan akan

dicari vektor m0 di M yang terdekat ke x. Jika vektor m0 dinyatakan dalam suku-suku

dalam vektor yi sebagai :

mo =



 n i

i iy 1



Maka masalah tersebut ekuivalen dengan menemukan skalar _i, i =1, 2, ..., n yang

meminimalkan x₁y₁₂y₂ ..._ny_n .

Menurut Teorema proyeksi, vektor minimal tunggal m0 adalah proyeksi ortogonal x

16

Persamaan dalam koefisien isebanyak n kali ini dikenal sebagai persamaan

normal untuk masalah minimalisasi.

17 disebut matriks Gram dari y1, y2, y3, ..., yn. Matriks ini adalah tranpose dari

matriks koefisien normal.

Teorema 2.1.6

Determinan Gram g = g(y1, y2,…., yn)  0 jika dan hanya jika y1, y2,…., yn bebas linear.

Bukti :

Pernyataan tersebut ekuivalen dengan pernyataan vektor–vektor y1, y2,…., yn bergantung linear jika dan hanya jika g = g(y1, y2,….,yn)= 0.

Misalkan yi bergantung linier, berarti terdapat i yang tidak sama dengan nol

sedemikian sehingga





 . Karena barisan-barisan pada determinan Gram

bergantung pada yi, maka determinannya nol.

Misalkan g = g(y1, y2,…., yn) = 0. Maka ada kebergantungan linier di antara barisan-barisannya sehingga terdapat konstanta I yang tidak semuanya nol sedemikian

18 Walaupun persamaan normal tidak memiliki penyelesaian tunggal jika yi bergantung linier, tetapi selalu ada paling sedikit satu penyelesaian. Jika g = 0 maka selalu dihasilkan penyelesaian yang tidak tunggal, bukan penyelesaian yang tidak konsisten.

Teorema berikut menyatakan jarak minimum suatu vektor ke ruang bagian dapat dicari dengan determinan matriks Gram.

Menurut teorema proyeksi, x -

x ortogonal terhadap M, sehingga secara khusus

19

persamaan ini bersama persamaan normal memberikan n + 1 persamaan linier dalam

n + 1 variabel ₁,₂,...,_n,2. Dengan aturan Cramer didapatkan

2.2. Modifikasi Teorema Proyeksi

Teorema 2.2.1

20 Bukti :

Bagian pertama teorema ini menyatakan jika M ruang bagian tertutup maka terdapat

dengan tunggal x0  V sedemikian hingga x y V y min 0

Dibentuk dua pernyataan :

1. Terdapat m0  M sedemikian hingga x m x m M

m 

 

 min 0

2. Terdapat x0  V sedemikian hingga x y V y min 0

Pernyataan 1, sudah terbukti pada Teorema proyeksi, sehingga jika dapat ditunjukkan kedua pernyataan di atas ekuivalen maka teorema di atas terbukti.

Misalkan pernyataan 1 terpenuhi, maka akan ditunjukkan pernyataan 2 dipenuhi. Didefinisikan x0 = x – m0=x + (-m0). Karena –m  M, maka x0  V. Diambil y  V, maka y = x + (-m) untuk semua –m  M.

Dengan demikian x x m x m y

V y V

y    



 ₀ min min

0 .

21 Diambil mM maka y = x - mV .

Dan xm₀  x x m x m y

V y V

y    



 ₀ min min

0 .

Menurut Teorema proyeksi ada vektor minimal tunggal m0M dan vektor selisih

x – m0 ortogonal terhadap M. Diambil x0 = x – m0V sehingga xo ortogonal terhadap

M.

V = x + M

x0

M x

0

Gambar 2.3

Ada dua jenis variasi linear yang membawa ke masalah berdimensi berhingga. Yang pertama adalah variasi linear berdimensi n yang terdiri dari vektor - vektor berbentuk

x +



 n i

i ix a 1

dengan {x1, …, xn} himpunan bebas linear di H dan x vektor tertentu di

22 Jenis yang kedua adalah variasi linear yang terdiri dari semua vektor x di ruang

Hilbert H yang memenuhi :

<x, y1> = c1

<x, y2> = c2



<x, yn> = cn

dengan y1, y2, ..., yn adalah vektor - vektor bebas linear di H dan c1, c2, ……, cn tertentu.

Jika M adalah ruang bagian yang dibangun oleh y1, y2, ..., yn maka variasi linearnya

adalah ruang bagian M jika ci = 0. Untuk ci  0 variasi linear yang dihasilkan

merupakan translasi dari M. Variasi linear yang berbentuk seperti ini disebut

codimension n. 

Teorema 2.2.2

Misalkan H ruang Hilbert dan {y1,…..,yn }vektor-vektor bebas linear di H. Di antara semua vektor x  N yang memenuhi :

<x1, y1> = c1

23 

<x1, yn> = cn.

Misalkan xo mempunyai norm minimum, maka :

xo =



 n i

i iy 1

 dengan koefisien _i memenuhi persamaan :

<y1, y1> ₁+ <y2, y1> ₂ + …….+ <yn, y1> n = c1

<y1, y2> ₁+ <y2, y2> ₂ + …….+ <yn, y2> n = c2

    

<y1, yn> ₁+ <y2, yn> ₂ + …….+ <yn, yn> n = cn

Bukti :

Misalkan M ruang bagian berdimensi n yang dibangun oleh vektor-vektor yi. Variasi linear yang didefinisikan dengan kendala masalah minimalisasi adalah translasi dari

bagian M. Karena M tertutup, keberadaan dan ketunggalan penyelesaian optimal dijamin oleh teorema proyeksi, sehingga penyelesaiaan optimal xo ortogonal terhadap



M atau xoM. Karena M tertutup maka M = M. Jadi x0 M atau

x0=



 n i

i iy 1

 . Koefisien i dipilih sedemikian sehingga x0 memenuhi n kendala. Hal

24 III. METODOLOGI PENELITIAN

3.1 Tempat dan Waktu Penelitian

Penelitian ini dilakukan di Fakultas Matematika dan Ilmu Pengetahuan Alam, pada jurusan Matematika, Universitas Lampung yang dimulai pada semester Ganjil tahun ajaran 2012/2013.

3.2 Metode Penelitian

Penelitian ini menggunakan metode yang bersifat studi pustaka, yaitu dengan mempelajari, menganalisis masalah dengan definisi-definisi, dan definisi tersebut menjadi acuan berfikir untuk mengemukakan teori yang sesuai dengan masalah yang bersangkutan, dan kemudian membuat kesimpulan. Sumber literatur yang digunakan yaitu dari Perpustakaan Universitas Lampung, dan sumber-sumber lain yang berhubungan dengan masalah dalam penelitian ini.

Langkah-langkah dalam penelitian ini adalah sebagai berikut :

1. Membawa masalah aproksimasi fungsi ke ruang Hilbert C[a,b] dengan cara terlebih dahulu menentukan produk skalar terhadap ruang Hilbert C[a,b] yang sesuai untuk digunakan

25 3. Mencari penyelesaian optimal (aproksimasi fungsi terbaik) dengan

persamaan normal

4. Menentukan kesalahan optimal dari pengambialan basis yang berbeda-beda pada langkah (2) dan melakukan analisis serta evaluasi terhadap galat dan fungsi yang dihasilkan

5. Melakukan langkah (1) s.d. (4) untuk kasus fungsi yang lain

39 V. KESIMPULAN

Masalah optimisasi khususnya aproksimasi fungsi terbaik yang tidak medapatkan solusi terbaik (ralat yang besar) dalam ruang fisis atau yang dikenal sebagai ruang real , dapat dipecahkan dengan sistem matematis yang sederhana, dengan masalah aproksimasi tersebut ke ruang abstrak (berisi aksioma-aksioma) atau ruang vekor, khususnya pada ruang Hilbert C[a,b]. Masalah tersebut dikenal sebagai masalah minimum norm dalam ruang Hilbert C[a,b]. Dengan menggunakan konsep minimum norm akan diperoleh kesalahan optimal (galat) yang minimum.