ANALISIS SENSITIVITAS PERSOALAN TRANSPORTASI
DENGAN ALGORITMA
STEPPING STONE
PADA KASUS OPTIMISASI
SKRIPSI
CAHAYA MANURUNG
050803045
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
2010
2
ANALISIS SENSITIVITAS PERSOALAN TRANSPORTASI DENGAN ALGORITMA STEPPING STONE
PADA KASUS OPTIMISASI
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains.
CAHAYA MANURUNG 050803045
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : ANALISIS SENSITIFITAS PERSOALAN
TRANSPORTASI DENGAN ALGORITMA
STEPPING STONE PADA KASUS OPTIMISASI
Kategori : SKRIPSI
Nama : CAHAYA MANURUNG
Nomor Induk Mahasiswa : 050803045
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAM ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, Maret 2010 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs Henry Rani Sitepu M.Si Prof. Dr. Herman Mawengkang NIP 195303031983031002 NIP 194611281974031001
Diketahui/ Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Dr. Saib Suwilo, M.Si NIP 196401091988031004
iii
PERNYATAAN
ANALISIS SENSITIVITAS PERSOALAN TRANSPORTASI DENGAN ALGORITMA STEPPING STONE
PADA KASUS OPTIMISASI
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebut sumbernya.
Medan, Maret 2010
PENGHARGAAN
Puji dan syukur kepada Yesus Kristus yang memberikan berkat, hikmah, pengetahuan, serta kekuatan kepada penulis sehingga penulis dapat menyelesaikan skripsi ini dengan baik.
Terimakasih kepada semua pihak yang telah bersedia membantu penulis dalam proses pembuatan skripsi ini, dari awal hingga akhir.
1. Kepada komisi pembimbing, Prof. Dr. Herman Mawengkang, Drs. Henry Rani Sitepu M.Si atas bimbingan dan pengajaran yang diberikan kepada penulis dalam proses penulisan skripsi ini. Kepada komisi pembanding, Drs. Ramli Barus M.Si dan Drs. Haluddin Panjaitan yang telah memberikan kritik dan saran yang membangun sehingga menyempurnakan skripsi ini.
2. Kepada Ketua Departemen Matematika, Dr. Saib Suwilo, M.Sc dan semua staf Departemen yang telah banyak membantu penulis dalam kelancaran skripsi ini.
3. Terkhusus kepada kedua orang tua penulis yang sangat luar biasa, Bapak B. Manurung dan M. Siahaan, trimakasih atas bantuan doa, dana dan kepercayaan yang telah diberikan kepada penulis.
4. Kepada adek-adekku, Cici, Febri, Rani, Yoseva yang tercinta, terimakasih buat semua bantuan, dukungan semangat dan doanya.
Skripsi ini masih memiliki banyak kekurangan, oleh karena itu penulis mengharapkan saran dan kritik yang membangun dari semua pihak. Semoga skripsi ini dapat membantu para pembaca untuk mencari biaya minimum dalam permasalahan transportasi.
Medan, Maret 2010 Penulis
Cahaya Manurung
v
ABSTRAK
SENSITIVITY ANALYSIS OF TRANSPORTATION PROBLEM WITH STEPPING STONE ALGORITM
ON OPTIMITATION CASE
ABSTRACT
Transportation problem is a uniquely class in linear programming which used to solving some optimitation problems. The aim in transportation problem is to allocate the commodity on a source and than all of the necessity loaded to the destination (demand located). But the main purpose of transportation problem is to achieve the total cost which out by minimum cost. Stepping Stone algoritm is a technique which used to make a decision from some decision which related with minimum cost in a transportation problem. Post optimality analysis (well know as post optimality or analysis after optimality or sensitivity analysis in unknown situation) is a effar to study the one or some or all of the parameters models if the influence of data to toward the optimality solution.
vii
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel viii
Daftar Gambar ix
Bab 1 Pendahuluan 1
1.1 Perumusan Masalah 2
1.2 Pembatasan Masalah 3
1.3 Tinjauan Pustaka 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 5
1.6 Metode Penelitian 5
Bab 2 Landasan Teori 6
2.1 Permasalahan Transportasi 6
2.1.1 Sejarah Permasalahan Transportasi 6
2.1.2 Persoalan Transportasi 6
2.1.3 Keseimbangan Transportasi 7
2.1.4 Model Umum Permasalahan Transportasi 8
2.1.4.1 Asumsi Dasar 8
2.1.4.2 Model Transportasi 9
2.1.5 Metode Pemecahan 13
2.2 Matriks 16
2.2.1 Invers Matriks 17
2.3 Algoritma Arsham Khan 17
2.4 Analisis Sensitivitas 20
2.4.1 Analisis Sensitivitas Pada Persoalan Transportasi 22
Bab 3 Pembahasan 26
3.1 Perhitungan Solusi Optimal 26
3.2 Analisis Sensitivitas 38
Bab 4 Kesimpulan Dan Saran 40
4.1 Kesimpulan 40
4.2 Saran 40
DAFTAR TABEL
Halaman
Tabel Persoalan Transportasi 12
Tabel Kapasitas Pabrik 25
Tabel Kebutuhan 25
Tabel Biaya Pengangkutan Dari Pabrik Ke Gudang 25
Tabel Biaya Dalam Transportasi 26
Tabel Iterasi 1 Stepping Stone 26
Tabel Iterasi 2 Stepping Stone 27
Tabel Iterasi 3 Stepping Stone 28
Tabel Iterasi 4 Stepping Stone 28
Tabel Iterasi 5 Stepping Stone 29
Tabel Iterasi 6 Stepping Stone 29
Tabel 7. Matriks Tereduksi Baris 30
Tabel 8. Matriks Tereduksi Kolom 31
Tabel 9 Arsham Kahn 36
Tabel 10 Arsham Kahn 36
Tabel 11 Arsham Kahn 37
Tabel 12 Arsham Kahn 37
Tabel 13 Arsham Kahn 38
Tabel 14 Arsham Kahn 38
Tabel 15 Arsham Kahn 39
Tabel 16 Arsham Kahn 39
ix
DAFTAR GAMBAR
Halaman
Gambar 2.1 Diagram model transportasi 10
ABSTRAK
Persoalan transportasi merupakan golongan tersendiri dalam persoalan program linier yang dapat digunakan untuk menyelesaikan beberapa persoalan optimisasi. Sasaran dalam persoalan transportasi ini adalah mengalokasikan barang yang ada pada sumber sedemikian rupa sehingga terpenuhi semua kebutuhan pada tujuan (lokasi permintaan). Namun tujuan utama dari persoalan transportasi ini ialah untuk mencapai jumlah biaya yang dikeluarkan yang serendah-rendahnya (minimum). Algoritma Stepping Stone adalah suatu teknik matematis yang digunakan untuk membuat suatu keputusan dari serangkaian keputusan yang berkaitan dengan pencarian biaya minimum dalam permasalahan transportasi. Analisis postoptimal (disebut juga analisis pasca optimal atau analisis setelah optimal, atau analisis kepekaan dalam suasana ketidaktahuan) merupakan suatu usaha untuk mempelajari nilai-nilai dari peubah-peubah pengambilan keputusan dalam suatu model matematika jika satu atau beberapa atau semua parameter model tersebut berubah atau menjelaskan pengaruh perubahan data terhadap penyelesaian optimal yang sudah ada.
vi
SENSITIVITY ANALYSIS OF TRANSPORTATION PROBLEM WITH STEPPING STONE ALGORITM
ON OPTIMITATION CASE
ABSTRACT
PENDAHULUAN
Persoalan transportasi yang sering muncul dalam kehidupan sehari-hari, merupakan golongan tersendiri dalam persoalan program linier. Maka metode tranportasi ini juga dapat digunakan untuk menyelesaikan beberapa persoalan optimisasi. Persoalan transportasi berkenan dengan pemilihan rute (jalur) pengangkutan yang mengakibatkan biaya total dari pengangkutan itu minimum.
Metode transportasi adalah metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama ke tempat-tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa, karena terdapat perbedaan biaya-biaya alokasi dari satu sumber ke suatu tempat tujuan juga berbeda-beda.
Kasus transportasi timbul ketika seseorang mencoba menentukan cara pengiriman (distribusi) suatu jenis barang (item) dari beberapa sumber (lokasi penawaran) ke beberapa tujuan (lokasi permintaan) yang dapat meminimumkan biaya. Sasaran dalam persoalan transportasi ini adalah mengalokasikan barang yang ada pada sumber sedemikian rupa hingga terpenuhi semua kebutuhan pada tujuan (lokasi permintaan). Namun tujuan utama dari persoalan transportasi ini ialah untuk mencapai jumlah biaya yang dikeluarkan yang serendah-rendahnya (minimum).
Seorang analis jarang dapat menentukan parameter model Program Linier seperti (m, n, Cj, aij, bi) dengan pasti karena nilai parameter ini adalah fungsi dari beberapa uncontrolable variable. Sementara itu solusi optimal model program linier didasarkan pada parameter tersebut.
Akibatnya penulis perlu mengamati pengaruh perubahan parameter tersebut terhadap solusi optimal. Analisis perubahan parameter dan pengaruhnya terhadap
2
solusi disebut Post Optimality Analisis. Istilah post optimality menunjukkan bahwa analisa ini terjadi setelah diperoleh solusi optimal, dengan mengasumsikan seperangkat nilai parameter yang digunakan dalam model, atau analisis postoptimal (disebut juga analisis pasca optimal atau analisis setelah optimal, atau analisis kepekaan dalam suasana ketidaktahuan) merupakan suatu usaha untuk mempelajari nilai-nilai dari peubah-peubah pengambilan keputusan dalam suatu model matematika jika satu atau beberapa atau semua parameter model tersebut berubah atau menjelaskan pengaruh perubahan data terhadap penyelesaian optimal yang sudah ada.
Perubahan atau variasi dalam suatu persoalan Program Linier yang biasanya dipelajari melalui post optimality analysis dapat dipisahkan ke dalam tiga kelompok umum, yaitu :
1. Analisa yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan optimalitasnya, ini dinamakan analisa sensitivitas. Jika suatu perubahan kecil dalam parameter menyebabkan perubahan drastis dalam solusi, dikatakan bahwa solusi adalah sangat sensitif terhadap nilai parameter itu. Sebaliknya, jika perubahan parameter tidak mempunyai pengaruh besar terhadap solusi dikatakan solusi relatif insensitif terhadap nilai parameter tersebut.
2. Analisa yang berkaitan dengan perubahan struktural. Masalah ini muncul bila persoalan program linier dirumuskan kembali dengan menambahkan atau menghilangkan kendala dan atau variabel untuk menunjukkan operasi model alternatif. Perubahan struktural ini dapat dimasukkan dalam analisa sensitivitas.
1.1. Perumusan Masalah
Berdasarkan latar belakang yang tertulis dalam pendahuluan diatas, yang menjadi pokok permasalahan adalah bagaimana melakukan analisis sensitivitas pada permasalahan transportasi.
1.2. Pembatasan Masalah
Sesuai dengan disiplin ilmu yang dimiliki penulis, maka pada tulisan ini masalah akan dibatasi pada tahap sejauh mana penyelesaian optimal semula adalah sensitif terhadap berbagai parameter model untuk pencapaian tujuan yang optimal pada masalah transportasi yaitu pada nilai fungsi objektifnya.
1.3. Tinjauan Pustaka
Sebagai referensi literatur yang mendukung penelitian ini, penulis menggunakan beberapa buku dan jurnal antara lain:
(Pangestu Subgyo, Marwan Asri, Hani Handoko, 2000; 71-88). Setelah ditemukan penyelesaian yang optimal dari permasalahan program linier, kadang-kadang dirasa perlu untuk menelaah lebih jauh kemungkinan-kemungkinan yang terjadi sebagai akibat terjadinya perubahan pada koefisien-koefisien di dalam model pada saat tabel optimal telah diselesaikan. Seseorang dapat saja menghitung kembali dari awal namun membutuhkan waktu yang cukup lama. Maka untuk menghindari hal tersebut lalu lazim dipakai suatu cara yang dinamakan analisis sensitivitas.
(B. D Nasendi, 1985; 131-142). Model transportasi merupakan salah satu bentuk khusus dari program linier yang dikembangkan untuk memecahkan masalah-masalah yang berhubungan dengan transpotasi (pengangkutan) dan distribusi produk atau sumber daya dari sumber ke berbagai tujuan.
4
(Taha, 1996). Dalam masalah transportasi pendistribusian berbagai komoditi dari berbagai berbagai kelompok pusat penerima yang disebut tujuan sedemikian rupa sehingga meminimalisasi biaya distribusi total. Apabila Z merupakan biaya distribusi total dan Xij (i=1,2,...,m; j=1,2,...,n) adalah jumlah unit yang harus didistribusikan dari
sumber i ke tujuan j maka dapat diformulasikan sebagai beriku: Meminimumkan: Z=
m
i n
j
ij ijX
C
1 1
Batasan:
Xij ai;i1,2,...,m
Xij bj;j 1,2,...n Xij 0(P Siagian, 1986;154-193). Sasaran pada masalah transportasi ini adalah mengalokasikan barang barang yang ada pada sumber (lokasi penawaran) sedemikian rupa hingga terpenuhi semua kebutuhan pada tujuan (lokasi permintaan). Dianggap bahwa jumlah barang yang tersedia sama di sumber i sama dengan jumlah barang yang dibutuhkan pada tujuan j maka diformulasikan sbb:
n
j j m
i
i b
a
1 1
(Agustini dan Rahmadi, 2004;100-133). Pada masalah tranportasi, biasanya jumlah barang yang disalurkan dari setiap lokasi permintaan bervariasi. Atas dasar kennyataan bahwa rute pengiriman yang berbeda akan menghasilkan biaya kirim yang berbeda, maka tujuan pemecahan kasus ini adalah menentukan berapa unit barang yang arus dikirim dari setiap sumber ke setiap tujuan sehingga permintaan dari setiap tujuan terpenuhi dan total biaya kirim minimum.
1.4. Tujuan Penelitian
Adapun tujuan penelitian ini terkait dengan pokok permasalahan yang telah diuraikan diatas adalah sebagai berikut:
2. Membantu para pengambil keputusan dalam mengambil keputusan yang optimal dengan kendala-kendala:
a. Setiap permintaan terpenuhi.
b. Sumber tidak mungkin mengirim komoditas lebih besar dari kapasitasnya.
1.5. Manfaat Penelitian
Adapun manfaat yang diharapkan dari penelitian ini adalah:
1. Memberikan dasar pengetahuan bagaimana meng-implementasikan teori transportasi dalam kehidupan sehari-hari yang dapat meringankan biaya.
2. Sebagai penerapan ilmu pengetahuan yang dimiliki, khususnya terapan teori transportasi.
1.6. Metode Penelitian
Metode penelitian yang akan digunakan adalah penelitian secara literatur. Prosedur yang dilakukan adalah:
1. Pengumpula Data.
Penulis mengumpulkan data dari referensi buku dan berbagai jurnal dari internet. 2. Menyelesaikan permasalahan transportasi dengan menggunakan algoritma
Stepping Stone
3. Mencari analisis sensitivitas dari hasil dari algoritma Stepping Stone dengan algoritma Arsham kahn.
4. Penyusunan Rangkuman. 5. Penarikan Kesimpulan.
BAB 2
LANDASAN TEORI
2.1 Permasalahan Transportasi
2.1.1 Sejarah Permasalahan Transportasi
Masalah transportasi ini sebenarnya telah lama dipelajari dan dikembangkan sebelum lahir model program linear. Pada tahun 1939, L.V Kantorovitch mempelajari beberapa permasalahan yang berhubungan dengan model transportasi. Kemudian, pada tahun 1941, F.L. Hitchcock merumuskan model matematika dari persoalan transportasi yang kini dianggap sebagai model matematika dari persoalan transportasi yang kini dianggap sebagai model baku, sehingga sering disebut juga sebagai model Hitchcock. Ada lagi seseorang yang bernama T.C. Koopmans pada tahun 1947 banyak mempelajari hal-hal yang berhubungan dengan program transportasi (PT) atau model transportasi (MT).
2.1.2 Persoalan Transportasi
Situasi dunia yang semakin dinamis menyebabkan waktu pengambilan keputusan menjadi sangat penting. Di saat yang sama, parameter pengambilan keputusan tidak tersedia atau tersedia tetapi tidak lengkap dan jelas. Ketidakjelasan parameter pengambilan keputusan yang diambil tetap optimal. Optimasi adalah salah satu alat bantu seorang manajer dalam pengambilan keputusan.
Ciri-ciri khusus persoalan transportasi adalah :
1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.
2. Kuantitas komoditas atau barang yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan, besarnya tertentu.
3. Komoditas yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai dengan permintaan atau kapasitas sumber.
4. Ongkos pengangkutan komoditas dari suatu sumber ke suatu tujuan, besarnya tertentu.
Data yang dibutuhkan dalam metode transportasi adalah:
1. Level supply pada setiap daerah sumber dan level permintaan pada setiap daerah tujuan untuk kasus pendistribusian barang; jumlah produksi dan jumlah permintaan.
2. Biaya transportasi per unit komoditas dari setiap daerah sumber menuju berbagai daerah tujuan pada kasus pendistribusian; biaya produksi.
Model transportasi merupakan salah satu bentuk khusus atau variasi dari program linier yang di kembangkan khusus untuk memecahkan masalah-masalah yang berhubungan dengan transportasi (pengangkutan) dan disribusi produk atau sumber daya dari berbagai sumber (pusat pengadaan, atau titik supply) ke berbagai tujuan (titik permintaan atau pusat pemakaian) yang lebih efisien dalam hal perhitungan.
Dilihat dari model matematika persolan program linier terdapat tipe/ ciri/ karakteristik khusus pada permasalahan transportasi, yaitu:
1). Semua fungsi kendala bertanda „=‟ 2). Semua nilai aij bernilai 1 atau 0.
2.1.3 Keseimbangan transportasi
Suatu model transportasi dikatakan seimbang apabila total supply (sumber) sama dengan total demand (tujuan). Dengan kata lain:
8
Dalam persoalan transportasi yang sebenarnya, batasan ini tidak selalu terpenuhi atau dengan kata lain jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah demand. Jika hal ini yang terjadi, maka model persoalan disebut sebagai model yang tidak seimbang. Batasan di atas dikemukakan hanya karena itu menjadi dasar dalam pengembangan teknik transportasi. Namun, setiap persoalan transportasi dapat dibuat seimbang dengan memasukkan kolom dummy atau baris dummy.
Jika demand melebihi supply maka dibuat suatu sumber dummy yang akan men-supply kekurangan tersebut yaitu sebanyak
Sebaliknya, jika jumlah supply melebihi jumlah demand, maka dibuat suatu tujuan dummy untuk menyerap kelebihan tersebut yaitu sebanyak
Ongkos transportasi per unit (cij) dari sumber dummy ke seluruh tujuan adalah nol. Hal ini dapat dipahami karena pada kenyataan dari sumber dummy tidak terjadi pengiriman.
2.1.4 Model Umum Permasalahan Transportasi
2.1.4.1 Asumsi Dasar
Asumsi dasar dari model ini adalah bahwa biaya transportasi di sebuah rute tertentu adalah proposional secara langsung dengan jumlah unit yang dikirimkan. Defenisi unit transportasi akan bervariasi bergantung pada jenis barang yang di kirimkan.
Model umum suatu persoalan transportasi dilandasi pada asumsi-asumsi berikut:
1. Bahwa suatu produk yang ingin diangkat tersedia dalam jumlah yang tetap dan diketahui.
2. Bahwa produk tersebut akan dikirim melalui jaringan transpotasi yang ada dengan memakai cara pengakutan tertentu dari pusat-pusat permintaan.
3. Bahwa jumlah permintaan di pusat permintaan pun diketahui dalam jumlah tertentu dan tetap.
4. Bahwa ongkos angkutan per-unit produk yang diangkut pun diketahui, sehingga tujuan kita untuk meminimumkan biaya total angkutan dapat tercapai.
Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber.
2.1.4.2 Model transportasi
Sebuah model transportasi dari sebuah jaringan dengan m sumber dan n tujuan. Sebuah sumber atau tujuan diwakili dengan sebuah node. Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang tersebut. Jumlah penawaran di sumber i adalah ai dan permintaan di tujuan j adalah bj. Biaya unit
transportasi antara sumber i dan tujuan j adalah cij. Anggaplah Xij mewakili jumlah barang yang dikirimkan dari sumber i ke tujuan j; maka model program linier yang mewakili masalah transprotasi ini secara umum adalah sebagai berikut:
Model transportasi berusaha menentukan sebuah rencana transportasi sebuah barang dari sejumlah sumber ke sejumlah tujuan.
10
i =1
j =1
j = 2
i =2
j = 3
i =m
j = n Data dalam model mencakup:
1. Tingkat penawaran di setiap sumber dan jumlah permintaan di setiap tujuan. 2. Biaya transportasi per unit barang dari setiap sumber ke setiap tujuan.
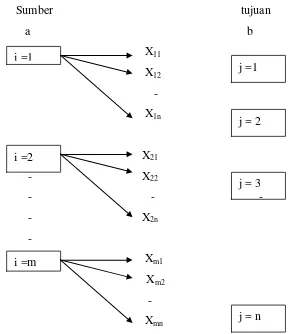
Secara diagramatik, model transportasi dapat digambarkan sebagai berikut: Misalkan ada m buah sumber dan n buah tujuan.
Sumber tujuan
a b
X11
X12
-
X1n
X21
- X22
- - -
- X2n
-
Xm1
Xm2
- Xmn
Gambar 2.1 Diagram Model Transportasi
a. Masing-masing sumber mempunyai kapasitas ai , ݅ = 1, 2, 3, . . . ,݉.
b. Masing-masing tujuan membutuhkan komoditas sebanyak bj, ݆ = 1, 2, 3, . . . ,݊. c. Jumlah satuan (unit) yang dikirimkan dari sumber i ke tujuan j adalah sebanyak
xij.
Dengan demikian, maka formulasi program liniernya adalah sebagai berikut: Minimum; Z =
m
i n
j ij ijx
c
1 1
Batasan:
Xij ai;i1,2,...,m
Xij bj; j1,2,...nXij 0 untuk seluruh i dan j.
Gambar di bawah ini memperlihatkan sebuah model dari sebuah jaringan dengan 3 sumber dan 3 tujuan. Sebuah sumber atau tujuan diwakili dengan sebuah node. Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang tersebut. Jumlah penawaran di sumber i adalah ai dan permintaan di tujuan j adalah bj. Biaya unit transportasi antara sumber i dan tujuan j adalah cij.
Sebagai ilustrasi, jika ada 3 buah sumber dan 3 tujuan (m = 3, n = 3)
M 1
M 2
M 3
N 1
N 2
N 3
SUMBER TUJUAN
X 11
X 12 X 13
X 23
X 22 X21
X 33 X 32 X 31
Gambar 2.2 Representasi Jaringan Model Transportasi
12
formulasi Minimumkan:
Z = c11x11 + c11x11 + c12 x12 + c13x13 + c21x21 + c22x22 + c23x23 + c31x31 + c32x32 + c33x33
Berdasarkan pembatas: x11 + x12 + x13 = a1 x21 + x22 + x23 = a2 x31 + x32 + x33 = a3 x11 + x21 + x31 = b1 x12 + x22 + x32 = b2 x13 + x23 + x33 = b3
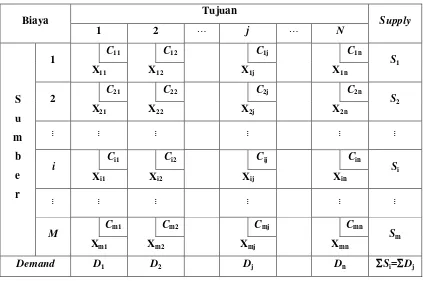
Tabel 2.1 Persoalan Transportasi
Biaya Tujuan Supply
1 2 ڮ j ڮ N
S
u
m
b
e
r
1 C11 C12 C1j C1n S1
X11 X12 X1j X1n
2 C21 C22 C2j C2n S2
X21 X22 X2j X2n
ڭ ڭ ڭ ڭ ڭ ڭ
i Ci1 Ci2 Cij Cin Si
Xi1 Xi2 Xij Xin
ڭ ڭ ڭ ڭ ڭ ڭ
M Cm1 Cm2 Cmj Cmn Sm
Xm1 Xm2 Xmj Xmn
Demand D1 D2 Dj Dn Si=Dj
2.1.5 Metode Pemecahan
1. Menentukan Solusi Fisibel Basis Awal.
2. Manentukan entering variabel dari variabel-variabel nonbasis. Bila semua variabel sudah memenuhi kondisi optimal, STOP. Bila beum lanjutkan ke langkah 3.
3. Tentukan leaving variabel diantara variabel-variabel basis yang ada, kemudian hitung solusi yang ada. Kembali ke langkah 2.
Untuk menentukan solusi basis awal terdapat 3 metode yang dapat digunakan adalah:
1. Metode pojok kiri atas pojok kanan bawah/ metode pojok barat laut/ nort west corner.
Mulai dari pojok kiri atas, alokasi sebesar x11 = min (s1, d1). Artinya bila d1< s1 maka x11= d1; jika d1> s1 maka x11 = s1, selanjutnya yang mendapat giliran untuk dialokasikan adalah x12 sebesar min (s1– d1, d2); kalau x11 = s1 (atau d1 > s1), maka selanjutnya yang mendapat giliran untuk dialokasikan adalah x21 sebesar (d1 – s1, s2) dan seterusnya.
2. Metode ongkos (baris/ kolom) terkecil (least cost).
Prinsip cara ini adalah pemberian prioritas pengelokasian pada tempat yang mempunyai satuan ongkos terkecil.
a. Pendistribusian dimulai dari biaya terkecil dan, apabila terdapat biaya terkecil lebih dari satu, maka dipilih salah satu.
b. Setiap pendistribusian dipilih nilai sebanyak mungkin tanpa mengabaikan jumlah sumber/tujuan.
3. Metode pendekatan vogel (vogel’s approximation method’s/ VAM).
Cara ini merupakan cara yang terbaik dibandingkan dengan cara di atas. Langkah-langkah penerjaan metode diatas adalah:
a. Menghitung opportunity cost yang didasarkan pada dua biaya terkecil pada setiap baris dan kolom dan mengurangkan keduanya, hasil perhitungannya disebut dengan penalty cost.
b. Memilih nilai penalty cost terbesar di antara baris dan kolom.
14
c. Memilih biaya terkecil dari nilai penalty cost terbesar dan mendistribusikan sejumlah nilai. Baris/ kolom penalti yang sudah terpilih diabaikan untuk langkah selanjutnya.
d. Menyesuaikan jumlah permintaan dan penawaran untuk menunjukkan alokasi yang sudah dilakukan. Menghilangkan semua baris dan kolom dimana penawaran dan permintaan telah dihabiskan.
e. Apabila jumlah penawaran dan permintaan belum sesuai, maka ulangi langkah pertama sampai terisi semua.
Untuk mencari solusi optimal terdapat 2 metode yang dapat digunakan yaitu: 1. Metode batu loncatan (Stepping Stone).
Untuk menentukan entering dan leaving variable ini, terlebih dahulu harus dibuat suatu loop tertutup bagi setiap variabel nonbasis loop tersebut berawal dan berakhir pada variabel nonbasis tadi. Dimana tiap sudut loop haruslah merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.
Langkah-langkah penyelesaiannya adalah sebagai berikut :
1. Apakah jumlah variabel basis sama dengan n+m-1 ? Jika kurang dari m+n-1 maka akan terjadi kemerosotan (degeneracy). STOP. Tetapi jika sama maka dapat dihitung Zij –Cij untuk sel-sel yang bukan basis, dengan cara sebagai berikut :
a. Dibuat loop tertutup bagi setiap variabel non basis dimana loop tersebut berawal dan berakhir pada variabel non basis, dan setiap titik sudut loop tersebut harus merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.
b. Dihitung Zij-Cij = jumlahan para Cij pada loop dengan koefisien (+1) dan (-1)bergantian dengan koefisien variabel non basis (-1).
3. Menentukan variabel yang keluar dari basis, caranya: a. Dibuat loop yang memuat Xst.
b. Diadakan pengamatan para Cij dalam loop yang mempunyai koefisien (+1).
c. Variabel Xab yang keluar basis bila dan hanya bila Xab minimum dari langkah 3.
4. Menentukan harga variabel basis (yang berada di dalam loop yang baru/penyesuaian untuk variabel basis yang baru). Xst = Xab = Xpq sedangkan untuk variabel-variabel basis yang lain yang juga berada dalam loop. Xab(baru) = Xab + Xpq (untuk a+b = ganjil) Xab(baru) = Xab – Xpq (untuk a+b = genap).
5. Untuk variabel-variabel basis yang lain di luar loop harganya tetap. Hitung kembali nilai Zij-Cij untuk variable non basis seperti pada langkah 1.
6. Diperoleh tabel optimal jika semua Zij-Cij >0.
7. Jika masih ada nilai Zij-Cij > 0, maka dapat ditentukan kembali Entering Variable dan Leaving Variable seperti pada langkah yang ke-2.
2. Metode faktor pengali (multiplier)/ Metode MODI (Modified Distribution). Metode MODI merupakan variasi dari model Stepping Stone yang didasarkan pada rumusan dual. Perbedaannya dengan metode Stepping Stone adalah pada metode ini tidak harus menentukan semua jalur tertutup variabel non basis, kecuali pada saat akan melakukan perpindahan pengisian tabel. Dengan demikian MODI merupakan cara yang efisien untuk menghitung variabel non basis. Dalam metode MODI terdapat persamaan sebagai berikut :
mi + nj = Cij
16
Di mana : mi = Nilai setiap sel baris
nj = Nilai setiap kolom
Cij = Biaya transportasi per unit
Adapun langkah-langkah dalam metode MODI adalah :
1) Mentukan nilai mi untuk setiap baris dan nilai-nilai nj untuk setiap kolom
dengan menggunakan hubungan Cij = mi + nj untuk semua variabel basis
sebagai entering variabel.
4) Mengalokasikan sejumlah nilai ke entering variabel Xij sesuai dengan
proses Stepping Stone dan mengulangi langkah pertama.
2.2 Matriks
Matriks adalah sekumpulan himpunan objek (bilangan riil atau kompleks, variabel– variabel) yang disusun secara persegi panjang (yang terdiri dari baris dan kolom) yang biasanya dibatasi dengan kurung siku atau biasa. Bilangan-bilangan dalam susunan tersebut dinamakan entri dalam matriks atau disebut juga elemen atau unsur. Jika sebuah matriks memiliki m baris dan n kolom maka matriks tersebut berukuran (ordo) m x n. Matriks dikatakan bujur sangkar (square matrix) jika m = n. Dan skalar– skalarnya berada di baris ke-i dan kolom ke-j yang disebut (ij) matriks entri.
2.2.1 Invers Matriks
Matrik A memiliki invers jika matrik A non-singular (determinan 0 dan rank r = n) ,
A-1 matrik adalah invers dari matrik A. Jika matrik A tidak memiliki invers, maka matrik A disebut singular. Bila matrik A dikalikan dengan matrik A-1 maka akan menghasilkan matrik identitas I, yaitu suatu matrik yang elemen-elemen diagonalnya bernilai 1.
adj A A
) det(
1
1
A
Biasanya untuk matriks berukuran besar yang sering digunakan adalah IA=A-1I
2.3 Algoritma Arsham kahn
Sebelum menguraikan langkah-langkah penyelesaian dengan algoritma ini, terlebih dahulu diperkenalkan notasi-notasi yang akan dipergunakan.
PT : persoalan transportasi PL : program linear
SS : stepping-stone
GJP : Gauss-Jourdan Pivotting VB : variabel basis
HVB : himpunan variabel basis FE : fisibelitas
BP : baris pivot (baris yang ditentukan untuk variabel masuk) KP : kolom pivot (kolom yang berhubungan dengan variabel masuk) EP : elemen pivot
BT : baris terbuka (sebuah baris yang belum diisi variabel basis ; diberi label [?]
[?] : label untuk baris yang belum diisi variabel basis (baris terbuka) NSK : nilai sebelah kanan
K/B : rasio kolom, yakni NSK/KP
18
Algoritma ini dimulai dengan persiapan dan diikuti oleh dua tahapan. Tahap pertama merupakan iterasi VB untuk membangun HVB yang mungkin fisibel atau tidak. Tahap kedua merupakan iterasi FE untuk membangun solusi yang fisibel dan optimum. Kedua tahapan ini menggunakan transformasi GJP. Akan tetapi berbeda dalam metode memilih EP. Iterasi VB menggunakan kriteria simpleks, yang dimodifikasi hanya untuk memilih baris terbuka yang belum diisi VB. Strategi ini membawa kepada tercapainya titik optimal, dan terkadang menyebabkan ketidakfisibelan. Iterasi FE, jika dibutuhkan, membawa kembali solusi kepada fisibelitas dengan menggunakan kriteria dual simpleks untuk memilih EP.
Jelas, dalam suatu persoalan transportasi yang setimbang, satu dari (m+n) konstrain adalah berlebih. Dari pada mengeliminasi konstrain secara sebarang, maka pada algoritma ini dieliminasi konstrain yang akan lebih banyak memberikan pengurangan jumlah iterasi pada tahap pertama.
Adapun dalam tahapan-tahapan ini masing-masing dapat dikelompokkan berdasarkan operasi yang menambah keefisienan dalam pengerjaannya. Langkah 0.1 dan 0.2 mengeliminasi konstrain yang akan lebih banyak mengurangi jumlah iterasi. Kelompok kedua terdiri dari tiga operasi: 1.2c, 2.2a dan 2.2d, yang bersama-sama secara progresif mengurangi ukuran tabel.
Iterasi 0 (Persiapan)
0.0 – Formulasi matriks-biaya PT
0.1 – Reduksi baris-kolom (atau reduksi kolom-baris) Dari setiap baris kurangkan terhadap biaya terkecil.
Akumulasi pengaruh dari setiap reduksi baris menjadi biaya awal. Demikian, dari setiap kolom kurangkan terhadap biaya terkecil. Akumulasi pengaruh dari setiap reduksi kolom menjadi biaya awal. 0.2 – Eliminasi konstrain berlebih
Periksa baris atau kolom yang memiliki nilai nol terbanyak Eliminasi konstrain tersebut.
Gunakan sebuah baris untuk setiap konstrain dan sebuah kolom untuk setiap variabel.
Jangan menambahkan variabel artificial 0.4– Tentukan HVB
Untuk setiap kolom yang merupakan vektor satuan, beri label baris dengan nama variabel pada kolom tersebut.
Beri label baris yang lain dengan tanda tanya (?). 0.5– Hapus kolom VB.
Iterasi 1 (Tahap VB)
1.0 – Uji terminasi iterasi HVB
Jika terdapat label (?) atau terdapat baris terbuka, maka lanjutkan iterasi VB. Jika tidak HVB telah lengkap; mulai tahap FE (langkah 2.0).
1.1 – Pilih VB dari EP
KP : Pilih nilai Cij terkecil dan tetapkan sebagai bakal kolom.
BP : Pilih baris terbuka sebagai bakal baris.
EP : Pilih bakal baris dan kolom dengan K/B non-negatif terkecil.
Jika tidak ada K/B non-negatif, pilih K/B yang bernilai absolut terkecil. Jika elemen pivotnya bernilai nol, maka pilih Cij terbaik selanjutnya.
1.2 – Penambahan HVB (a) Lakukan GJP.
(b) Ubah label baris (?) dengan nama variabel. (c) Pindahkan KP dari tabel.
Lanjutkan iterasi HVB (kembali ke 1.0)
Iterasi 2 (Tahap FE)
2.0 – Uji terminasi iterasi FE
Jika NSK non-negatif, maka tabel sudah optimal. Interpretasikan hasilnya. Jika terdapat NSK negatif maka lanjutkan iterasi FE (langkah 2.1).
2.1 – Pilih FE dari EP
BP : Baris dengan NSK paling negatif .
KP : Kolom dengan sebuah elemen negatif pada BP. Pilih kolom dengan Cij terkecil.
20
2.2 – Transformasi FE
(a) Simpan KP di luar tabel. (b) Lakukan PGJ biasa.
(c) Tukarkan label KP dan BP.
(d) Ganti KP baru dengan KP lama yang disimpan dalam (a). Lanjutkan iterasi FE (kembali ke 2.0)
Bagian Akhir Algoritma, tahap pertama dari algoritma ini dapat digolongkan sebagai pencarian himpunan variabel basis yang menuju kepada titik optimal. Tahap kedua, jika diperlukan, membawa kembali kepada fisibelitas.
2.4 Analisis Sensitivitas
Analisa perubahan parameter dan pengaruhnya terhadap solusi Program Linier disebut Post Optimality Analisis. Istilah post optimality menunjukkan bahwa analisa ini terjadi setelah diperoleh solusi optimal, dengan mengasumsikan seperangkat nilai parameter yang digunakan dalam model, atau analisis postoptimal (disebut juga analisis pasca optimal atau analisis setelah optimal, atau analisis kepekaan dalam suasana ketidaktahuan) merupakan suatu usaha untuk mempelajari nilai-nilai dari peubah-peubah pengambilan keputusan dalam suatu model matematika jika satu atau beberapa atau semua parameter model tersebut berubah atau menjelaskan pengaruh perubahan data terhadap penyelesaian optimal yang sudah ada.
Dapat diketahui bahwa dunia nyata yang diabstraksikan dan disimplifikasikan ke dalam model program linier, tidak sederhana seperti rumusan Program Linier sederhana tersebut. Oleh karena itu dalam dunia pengelolaan dan kehidupan dunia nyata, selalu dihadapkan pada pertanyaan-pertanyaan keragu-raguaan seperti “apa yang akan terjadi, jika” ini dan itu berubah?
memang ”paling mungkin“ dan ”paling mendekati”, atau “perkiraan yang paling tepat”. Uji kepekaan hasil dan pasca optimal yang dapat memberikan jawaban terhadap persoalan-persoalan tersebut diatas.
Perubahan atau variasi dalam suatu persoalan program linier yang biasanya dipelajari melalui post optimality analysis dapat dipisahkan ke dalam tiga kelompok umum, yaitu :
1. Analisa yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan optimalitasnya, ini dinamakan Analisa Sensitivitas. Jika suatu perubahan kecil dalam parameter menyebabkan perubahan drastis dalam solusi, dikatakan bahwa solusi adalah sangat sensitif terhadap nilai parameter itu. Sebaliknya, jika perubahan parameter tidak mempunyai pengaruh besar terhadap solusi dikatakan solusi relatif insensitif terhadap nilai parameter tersebut.
2. Analisa yang berkaitan dengan perubahan struktural. Masalah ini muncul bila persoalan program linier dirumuskan kembali dengan menambahkan atau menghilangkan kendala dan atau variabel untuk menunjukkan operasi model alternatif. Perubahan struktural ini dapat dimasukkan dalam analisa sensitivitas. 3. Analisa yang berkaitan dengan perubahan kontinu parameter untuk menentukan
urutan solusi dasar yang menjadi optimal. Diketahui model matematika persoalan program linier adalah sebagai berikut: Menentukan nilai dari X1, X2,
X3, ..., Xn sedemikian rupa sehingga :
Z = C1X1 + C2X2+ .... + CjXj+ .... + CnXn =
n
j
j jX
C
1
(Optimal)
Yang kemudian disebut sebagai fungsi tujuan (objective function) dengan pembatasan (funsi kendala/syarat ikatan) :
a11 X1 + a12 X2 +...+ a1n Xn ataub1,
a21 X1 + a22 X2 +...+ a2n Xn ataub2,
am1 X1 + am2 X2 +....+ amn Xn ataubm, atau aij Xj atau bi untuk i = 1,2,3, … , m.
22
dan X1 0, X2 0... Xn 0atau Xj 0, dimana j = 1, 2, 3,...., n (syarat non-negatif).
Berdasarkan model matematika persoalan program linier di atas analisis sensitivitas dapat dikelompokkan berdasarkan perubahan-perubahan parameter:
1. Perubahan koefisien fungsi tujuan (Cj),
2. Perubahan koefisien teknologi (aij) (koefisien inpu-output),
3. Perubahan fungsi objektif (bi),
4. Adanya tambahan fungsi kendala baru (perubahan nilai m)
5. Adanya tambahan perubahan (variabel) pengambilan keputusan (Xj).
2.4.1 Analisis Sensitivitas Pada Persoalan Transportasi
Analisis sensitivitas pada persoalan program linear dilakukan setelah diperoleh solusi optimal karena adanya perubahan koefisien fungsi objektif. Berdasarkan perubahan tersebut maka diperiksa dampak perubahannya terhadap solusi optimal dan nilai optimal. Uji terhadap perubahan solusi optimal dan nilai optimal tersebut disebut analisis sensitivitas.
Solusi optimal adalah sebagai berikut:
* 1 * 1
,
x b Z Cb
dimana C adalah vektor koefisien dari fungsi objektif yang koefisiennya berhubungan dengan indeks variabel basis, x* adalah solusi optimal basis dan Z* adalah nilai optimal.
juga memenuhi persamaan keseimbangan model transportasi (
Si
Dj ). Untuk menguji dan mengukur nilai ini, digunakan konsep diferensial lengkap.Definisi :
Untuk fungsi y f x( ), didefinisikan:
(a) dx, disebut diferensial x, dengan hubungan dx x. (b) dy, disebut diferensial y, dengan dy f x dx( ) .
Dari definisi, diferensial peubah bebas adalah sama dengan pertambahan peubah tersebut, tetapi diferensial peubah yang bergantung tidak sama dengan pertambahan peubah tersebut.
Untuk fungsi 2 variabel bebas x dan y z, = f(x, y), didefinisikan dx x dan dy y. Bila x berubah sedangkan y tetap, z merupakan fungsi dari x saja dan diferensial parsial z terhadap x didefinisikan sebagai x x( , ) x
z d z f x y d dx
x
.
Dengan cara yang sama, diferensial parsial zterhadap y didefinisikan sebagai ( , )
y y y
z d z f x y d dy
y
. Diferensial total dz didefinisikan sebagai jumlah diferensial parsialnya, yaitu,
z z
dz dx dy
x y
(1)
Untuk fungsi wF x y z( , , , ..., )t , diferensial total dwdidefinisikan sebagai: ...
w w w w
dw dx dy dz dt
x y z t
(2)
Andaikan bahwa, diantara nilai sebelah kanan k parameter diubah. Selanjutnya, berdasarkan sifat keseimbangan persoalan transportasi,
si djdanj j
d d
dan si si harus dipenuhi. Maka berdasarkan konsep diferensial total,
diperoleh persamaan berikut :
24
* * *
*
1 2
1 2
...
i i i
i
B B B
B m
m
x x x
dx d d d
b b b b b b (3)
Dengan memperhatikan konsep umum perubahan dalam kasus diferensial lengkap, dapat dianggap bahwa db1 b1, sehingga diperoleh * *
i i
B B
dx x . Dengan
menggantikan
* *
,
i
B i k k
dx y
db dalam persamaan (3) dan juga dengan memperhatikan
perubahan dalam k parameter nilai sebelah kanan, persamaan berikut diperoleh:
* * * *
,1 1 ,2 2 ... ,
i
B i i i k k
x y y y
PEMBAHASAN
Suatu perusahaan mempunyai 4 pabrik A, B, C, D. Perusahaan tersebut mengalami masalah alokasi hasil produksinya dari pabrik-pabrik tersebut ke gudang-gudang penjualan di S, T, U, V, W. Kapasitas pabrik, kebutuhan gudang dan biaya pengangkutan dari pabrik ke tiap gudang dapat dilihat pada tabel dibawah ini.
Tabel 3.1 Kapasitas Pabrik
Pabrik Kapasitas produksi (ton) A
Tabel 3.2 Kebutuhan
Gudang Kebutuhan (ton)
S
Tabel 3.3 Biaya Pengangkutan Dari Pabrik Ke Gudang
Dari Biaya kegudang (dalam puluhan ribu)
S T U V W Dari persoalan diatas, diformulasikan ke dalam bentuk transportasi.
26
Tabel 3.4 Biaya Dalam Transportasi
D1 D2 D3 D4 D5 Supply
3.1 Penghitungan Solusi optimal
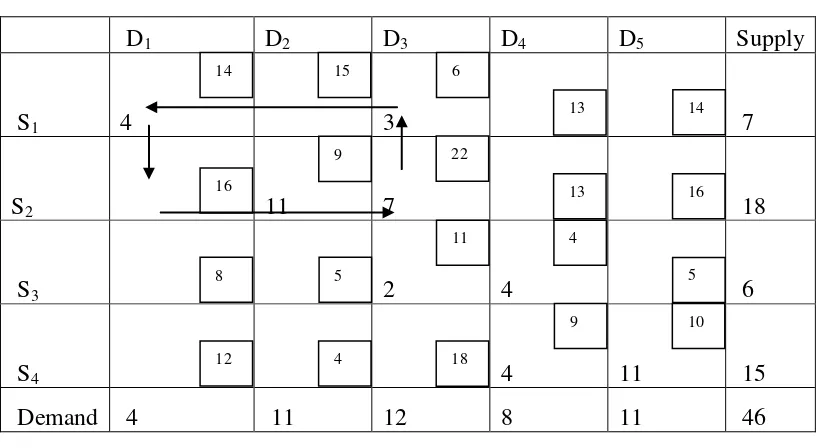
Sebagai langkah awal akan dicari solusi optimal dengan menggunakan algoritma Metode Sudut Barat Laut (North West Corner). Solusi awal menggunakan metode sudut barat laut ditentukan dengan mengisi sel kosong yang masih dapat diisi dan terletak paling kiri atas (sudut barat laut). Jumlah yang dialokasikan pada sel kosong tersebut (xij) tidak boleh melebihi jumlah supply pada sumber i dan jumlah permintaan pada tujuan j.
Sel basis adalah sel 11, 12, 22, 23, 33, 34, 44, 45 sel non basis adalah 13, 14, 15, 21, 24, 25, 31, 32, 35, 41, 42, 43.
Untuk setiap sel non basis:
X13 = c13-c12 + c22– c32 = 6-15+9-22 = -22 terdapat pada sel X13 dan pada sel X13 terjadi perubahan.
28
terjadi perubahan pada X24
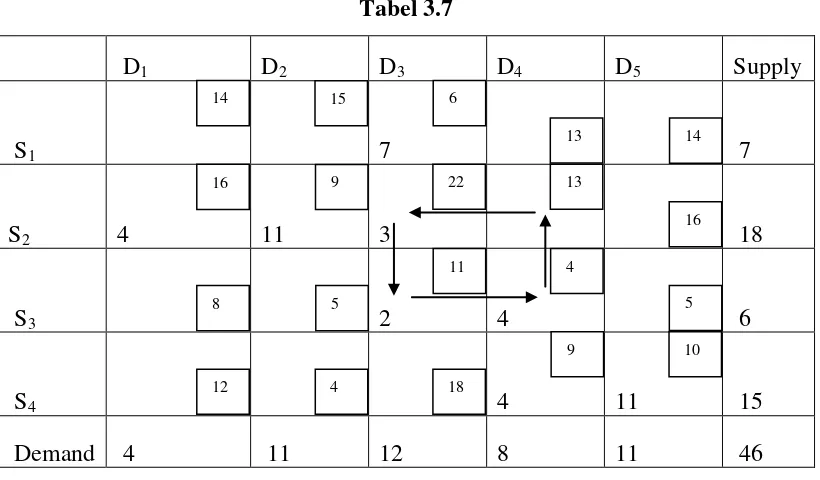
Tabel 3.8
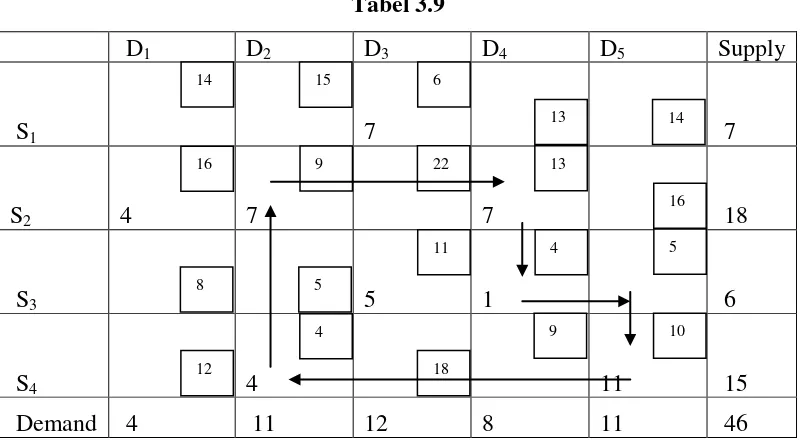
Tabel 3.9
Terjadi perubahan pada X35
Tabel 3.10
Karena tidak terdapat lagi yang negatif maka solusi optimal telah ditemukan. Nilai optimal adalah
30
Arsham-Kahn berikut. Iterasi 0 (Persiapan)
0.0- Formulasi matriks biaya PT
Formulasi matriks biaya telah dinyatakan pada tabel 6 diatas karena persoalan transportasi sudah setimbang.
0.1- Reduksi baris-kolom (reduksi kolom baris). Reduksi baris yaitu dengan mengurangi masing-masing baris dengan biaya terkecil dari baris tersebut, yakni untuk baris 1, 2, 3, dan 4 secara berturut dikurangi dengan 6, 9, 4 dan 4. Berdasarkan tabel baris tereduksi kemudian dilakukan reduksi kolom yaitu dengan mengurangkan masing-masing kolom dengan biaya terkecil dari kolom tersebut, yakni secara berturut untuk kolom 1 sampai 5 dengan 4, 0, 0, 0, 1. Matriks baris tereduksi diberikan oleh tabel 7 dan 8 berikut.
Tabel 3.11 Matriks Tereduksi Baris
T1 T2 T3 T4 T5
Persediaa n
A1
7
A2
18
A3
6
A4
15
Kebutuhan 4 11 12 8 11 46
8
14 0
8
9
0 7 8
4 1
7
1 0
6 5
13
7
0
Tabel 3.12 Matriks tereduksi kolom
0.2– Eliminasi konstrain berlebih
Baris ketiga (Supply 3) memiliki nilai nol terbanyak, maka konstrain Supply 3 akan dieliminasi
0.3– Formulasi tabel simpleks
Pada Tabel 9 ditunjukkan tabel awal sementara yang masih mengandung baris supply 3.
0.4- Menentukan HVB
Pada tabel 10 diperoleh lima variabel sebagai himpunan variabel basis awal dan tiga baris terbuka
0.5- Hapus kolom HVB
Ditunjukkan oleh tabel 10
Iterasi 1 (Tahap VB) 1.0- Uji terminasi HVB
Terdapat label (?) atau terdapat baris terbuka, lanjutkan iterasi HVB pada langkah 1.1
1.1- Memilih VB dari EP
KP: Pilih Cij terkecil, kolom x13, x22, x42 merupakan bakal kolom.
BP: Baris 1, 2 dan 3 merupakan baris terbuka.
32
EP: Bakal EP tak nol diberi tanda [ ] dan ( ) pada tabel 10. Tanda [ ] yakni variabel x13 memiliki K/B non- negatif terkecil.
1.2- Penambahan HVB (a) Lakukan GJP
(b) Ubah label baris (?) dengan variabel x13
(c) Hapus KP dari tabel, diperoleh hasil pada tabel 11. Akhiri iterasi HVB (kembali ke langkah 1.0)
1.0- Uji terminasi iterasi HVB
Terdapat label (?) (terdapat baris terbuka), lanjutkan iterasi VB ke langkah 1.1 Proses ini berlanjut hingga tidak ada lagi baris terbuka, hasil ditunjukkan pada tabel 13. Kemudian dilanjutkan ke tahap feasibelitas.
Iterasi 2 (Tahap FE)
2.0- Uji terminasi iterasi FE
NSK memiliki elemen negatif, lanjutkan iterasi FE (langkah 2.1) 2.1- Pilih FE dari EP
BP: Pilih baris dengan NSK terkecil. Baris x32 memiliki NSK terkecil.
KP: Perhatikan hanya kolom dengan elemen negatif. Pilih kolom dengan Cij
terkecil yakni kolom x21
EP: Elemen pivot diberi tanda [ ] pada tabel 13. 2.2- Transformasi FE
(a) Simpan KP (kolom x21) di luar tabel
(b) Lakukan GJP biasa
(c) Tukar label KP (x21) dan BP (x32)
(d) Ganti KP baru dengan KP lama yang disimpan pada (a) Hasil ditunjukkan pada tabel 14.
Akhiri iterasi FE (kembali ke langkah 2.0) 2.0- Uji terminasi iterasi FE
NSK memiliki elemen negatif, lanjutkan iterasi FE (langkah 2.1) 2.1- Pilih FE dari EP
BP: Pilih baris dengan NSK terkecil. Baris x31 memiliki NSK terkecil.
EP: Elemen pivot diberi tanda [ ] pada tabel 14. 2.2- Transformasi FE
(a) Simpan KP ( kolom x24) di luar tabel
(b) Lakukan GJP biasa
(c) Tukar label KP (x24) dan BP (x31)
(d) Ganti KP baru dengan KP lama yang disimpan pada (a) Hasil ditunjukkan pada tabel 15.
Akhiri iterasi FE (kembali ke langkah 2.0) 2.0- Uji terminasi iterasi FE
NSK memiliki elemen negatif, lanjutkan iterasi FE (langkah 2.1)
Proses ini berulang hingga lima iterasi dan tidak terdapat lagi NSK bernilai negatif dan diperoleh hasil optimal pada tabel 16.
Diperoleh matriks basis B yang berukuran mxn-1, yaitu matriks koefisien pembatas khusus untuk variabel basis. Kolom ke-j dari matriks ini merupakan kolom untuk variabel basis ke-j. Pada persoalan ini, karena veriabel basisnya adalah :
Dengan menggunakan algoritma Arsham Khan diatas diperoleh matriks basis invers B-Idibawah ini diperoleh bahwa
1
S
S2 S4 D1 D2 D3 D4 D5
34 Dimana terjadi perubahan pada beberapa supply dan demand sebagai berikut:
,
Diperoleh solusi optimal yang baru adalah:
= (7+3, 6-4, 5+4, 4+2, 8+0, 5-3, 10-6, 1+5) = (10, 2, 9, 6, 8, 2, 4, 6)
dan nilai optimal yang baru adalah:
Z* = (10x6) + (2x9) + (5x9) + (16x6) + (13x8) + (11x2) + (10x4) + (5x6) = 60 + 18 + 45 + 96 + 104 + 22 + 40 + 30
= 4.060.000,-
Diperoleh bahwa, perubahan pada supply dan demand diatas mengurangi biaya transportasi sebesar
Z Z Z* 4.440.000 4.060.000 Rp380.000,
Tabel 9
VB VBN NSK
X11 X12 X13 X14 X15 X21 X22 X23 X24 X25 X31 X32 X33 X34 X35 X41 X42 X43 X44 X45
? 1 1 1 1 1 7 + s1
? 1 1 1 1 1 18 + s2
? 1 1 1 1 1 6 + s3
? 1 1 1 1 1 15 + s4
? 1 1 1 1 4 +d1
? 1 1 1 1 11 + d2
? 1 1 1 1 12 + d3
? 1 1 1 1 8 + d4
? 1 1 1 1 11 + d5
Cost 4 9 0 7 7 3 0 13 4 6 0 1 7 0 0 4 0 14 5 5
Tabel 10
VB VBN NSK
X11 X12 X13 X14 X15 X21 X22 X23 X24 X25 X41 X42 X43 X44 X45
? 1 1 [1] 1 1 7 + s1
? 1 (1) 1 1 1 18 + s2
? 1 (1) 1 1 1 15 + s4
X31 1 1 1 4 +d1
X32 1 1 1 11 + d2
X33 1 1 1 12 + d3
X34 1 1 1 8 + d4
X35 1 1 1 11 + d5
VB VBN NSK X11 X12 X14 X15 X21 X22 X23 X24 X25 X41 X42 X43 X44 X45
X13 1 1 1 1 7 + s1
? 1 (1) 1 1 1 18 + s2
? 1 [1] 1 1 1 15 + s4
X31 1 1 1 4 +d1
X32 1 1 1 11 + d2
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X34 1 1 1 8 + d4
X35 1 1 1 11 + d5
Cost 11 15 14 14 3 0 13 4 6 4 0 14 5 5
Tabel 12
VB VBN NSK
X11 X12 X14 X15 X21 X22 X23 X24 X25 X41 X43 X44 X45
X13 1 1 1 1 7 + s1
? 1 [1] 1 1 1 18 + s2
X42 1 1 1 1 15 + s4
X31 1 1 1 4 +d1
X32 1 1 -1 -1 -1 -1 -4 - s4+ d2
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X34 1 1 1 8 + d4
X35 1 1 1 11 + d5
Cost 11 15 14 14 3 0 13 4 6 5 8 6 6
Tabel 13
VB VBN NSK
X11 X12 X14 X15 X21 X23 X24 X25 X41 X43 X44 X45
X13 1 1 1 1 7 + s1
X22 1 1 1 1 18 + s2
X42 1 1 1 1 15 + s4
X31 1 1 1 4 +d1
X32 1 [-1] -1 -1 -1 -1 -1 -1 -1 -22 - s4- s2+ d2
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X34 1 1 1 8 + d4
X35 1 1 1 11 + d5
Cost 11 15 14 14 4 14 5 7 5 8 6 6
Tabel 14
VB VBN NSK
X11 X12 X14 X15 X32 X23 X24 X25 X41 X43 X44 X45
X13 1 1 1 1 7 + s1
X22 1 1 0 0 0 -1 -1 -1 -1 -4 - s4+ d2
X42 1 1 1 1 15 + s4
X31 1 1 1 -1 [-1] -1 0 -1 -1 -1 -18+d1 - s4- s2+ d2
X21 -1 -1 1 1 1 1 1 1 1 22 + s4+ s2- d2
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X34 1 1 1 8 + d4
X35 1 1 1 11 + d5
VB VBN NSK X11 X12 X14 X15 X32 X23 X31 X25 X41 X43 X44 X45
X13 1 1 1 1 7 + s1
X22 1 1 0 0 0 -1 -1 -1 -1 -4 -s4+ d2
X42 1 1 1 1 15 + s4
X24 -1 -1 -1 1 -1 -1 0 1 1 1 18-d1 + s4+ s2- d2
X21 1 0 0 0 1 0 1 0 0 0 4+ d1
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X34 1 1 1 1 -1 1 -1 0 -1 0 [-1] -10+d1-s4- s2+d2+d4
X35 1 1 1 11 + d5
Cost 12 20 14 14 5 2 1 10 1 3 1 1
Tabel 16
VB VBN NSK
X11 X12 X14 X15 X32 X23 X31 X25 X41 X43 X44 X34
X13 1 1 1 1 7 + s1
X22 -1 0 -1 0 1 -1 1 -1 0 -1 -1 6-d1+s2-d4
X42 1 1 1 1 -1 1 -1 1 0 1 1 5 +d1- s2+d2+d4
X24 0 0 1 0 0 0 0 0 0 1 1 8+d4
X21 1 0 0 0 1 0 1 0 0 0 4+ d1
X33 -1 -1 -1 -1 1 1 5 - s1 + d3
X45 -1 -1 -1 -1 1 -1 1 0 1 0 -1 10-d1+s4+ s2-d2-d4
X35 1 1 1 1 1 -1 1 0 0 -1 0 1 1+ d5+d1-s4- s2+d2+d4
Cost 13 21 15 14 6 1 2 1 1 2 1 1
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari pembahasan yang telah dilakukan, maka dapat ditarik kesimpulan sebagai berikut:
Pada permasalahan transportasi, nilai akhir yang telah didapat dengan menggunakan algoritma stepping stone belum tentu nilai minimum yang diakibatkan adanya perubahan pada fungsi objektif pada permasalahan transportasi.
4.2 Saran
DAFTAR PUSTAKA
Agustini, H.D.Y.M dan Rahmadi Endra Yus. 2004. Reset Operacional Konsep-konsep Dasar. PT. Rineka Cipta. Jakarta.
Doustdargholi. S, Derakhshan Asl. A dan Abasgholipour. V. 2009. Sensitivity Analysis of Righthand-Side Parameter in Transportation Problem. Iran
Hillier, Frederick. 2005. Introduction to Operation Research. New York: McGraw-Hill Education.
Liu, C.L. 1995. Dasar-Dasar Matematika Diskret. Jakarta : PT. Gramedia.
Mulyono, Sri. 2004. Riset Operasi. Jakarta: Fakultas Ekonomi Universitas Indonesia.
Nasendi, B.D. 1985. Program Linear Dan Variasinya. Jakarta: PT. Gramedia. Siagian, P. 2006. Penelitian Operasional. Penerbit Universitas Indonesia. Jakarta. Subagyo. P, Asri. M dan Handoko. H.T. 2000. Dasar-dasar Operations Research.
BPFE-Yogyakarta. Yogyakarta.
Supranto, Johannes. 1988. Riset Operasi Untuk Pengambilan Keputusan. Jakarta : Universitas Indonesia.
Taha, Hamdy. 1996. Riset Operasi. Jakarta: Binarupa Aksara.
Zulfikarijah Fien. 2004. Operational Research. Bayumedia Publishing. Malang, Jawa Timur.