PENJADWALAN ONLINE DENGAN ZONA
TERLARANG
TESIS
Oleh
SRI MAWARNI
117021001/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
PENJADWALAN ONLINE DENGAN ZONA
TERLARANG
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
SRI MAWARNI 117021001/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
Judul Tesis : PENJADWALAN ONLINE DENGAN ZONA TERLARANG
Nama Mahasiswa : Sri Mawarni
Nomor Pokok : 117021001
Program Studi : Matematika
Menyetujui, Komisi Pembimbing
(Prof. Dr. Opim Salim, M.Sc) (Prof. Dr. Saib Suwilo, M.Sc)
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)
Telah diuji pada
Tanggal 3 Juni 2013
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Opim Salim, M.Sc
Anggota : 1. Prof. Dr. Saib Suwilo, M.Sc 2. Dr. Yulita Moliq, M.Sc
PERNYATAAN
PENJADWALAN ONLINE DENGAN ZONA TERLARANG
TESIS
Dengan ini saya menyatakan bahwa dalam tesis ini tidak terdapat karya yang pernah diajukan untuk memperoleh gelar magister di suatu perguruan tinggi dan sepanjang pengetahuan juga tidak terdapat karya atau pendapat yang pernah di-tulis atau diterbitkan oleh orang lain, kecuali secara terdi-tulis diacu dalam naskah ini dan disebutkan dalam daftar pustaka.
Medan, Juni 2013 Penulis,
ABSTRAK
Penjadwalan on-line dapat dilihat sebagai penjadwalan dengan informasi yang belum lengkap, yakni waktu proses (run times) pada saat pekerjaan tiba belum diketahui, atau pada titik-titik (waktu) tertentu keputusan dibuat tanpa menge-tahui kejadian lengkap, atau tergantung bagaimana cara informasi baru dike-tahui. Dalam konteks manufaktur dan komputasi berbagai kemungkinan adanya periode tertentu dalam setiap interval waktu, di mana pengolahan dapat terus berlangsung tetapi tidak dapat dimulai. Misalkan n pekerjaan dijadwalkan oleh
J1,· · · , Jn, dan misalkanpiwaktu proses padaJi. Untuk selanjutnya asumsikanpi
≤1,∀i. Waktu dipartisi kedalam himpunan intervalI={I1, I2,· · · , Is}denganI1
= [0, 1],I2 = [1, 2], · · ·, Is = [s1, s]. SetiapIj memuat sebuah koresponden zona terlarang Fj ⊆Ij ∀j, dimana F1 = (1
2 , 1], F2 = ( 3
2, 2], · · · , Fs = (s 1
2, s]. Interval Ij\Fj disebut daerah yang diizinkan. Zona terlarang merepresentasikan interval waktu dimana suatu pekerjaan tidak dapat dimulai tetapi dapat diproses. Dalam tesis ini penulis memeriksa masalah penjadwalan online dengan adanya zona ter-larang dan menyelidiki adaptasi algoritma online bin packing yaitu first fit, next fit dan em harmonic untuk persoalan penjadwalan online dengan zona terlarang pada interval waktu I dan zona terlarang F tersebut.
ABSTRACT
Online scheduling can be seen as scheduling with incomplate information, namely processing time are unknown, at certain points (times) decision have to be made without knowing the complate instance or depending on the way how new infor-mation becomes known. In various manufacturing and computing contexts there may be a certain period in each time interval, during which processing may con-tinue but may not be initiated. Suppose the n jobs to be scheduled by J1,· · · , Jn. Let pi be the processing time of Ji. Furthermore, we shall assume from now on that pi ≤1,∀i. Partition time into a set of abutting intervals I = {I1, I2,· · · , Is} with I1 = [0, 1], I2 = [1, 2], · · · , Is = [s1, s]. Each Ij includes a corresponding forbidden zones Fj ⊆ Ij∀j, dimana F1 = (1
2 , 1], F2 = (32, 2], · · · , Fs = (s12, s].
We call the intervals Ij\Fj allowed zones. Forbidden zones represent time inter-vals during which a job cannot be started, but can be processed. In this thesis, the author examine the problems of online scheduling in the presence of such forbid-den zones and investigate adaptation of the online bin packing algorithm there is first fit, next fit and harmonics algorithm for problems of online scheduling with forbidden zones at time interval of I and the forbidden zone of F.
KATA PENGANTAR
Puji syukur kepada Allah SWT yang selalu memberikan rahmat dan hi-dayat yang luar biasa sehingga penulis dapat menyelesaikan tesis dengan judul: PENJADWALAN ONLINE DENGAN ZONA TERLARANG. Penulis menyampaikan terima kasih yang sebesar-besarnya kepada :
Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara.
Bapak Dr. Sutarman, M.Sc, Dekan Fakultas Matematika dan Ilmu Penge-tahuan Alam Universitas Sumatera Utara, yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Magister Matematika di FMIPA Uni-versitas Sumatera Utara.
Bapak Prof. Dr. Herman Mawengkang, Ketua Program Studi Magister Matematika FMIPA Universitas Sumatera Utara, sekaligus pembanding-II yang telah memberi kritik dan saran dalam penyempurnaan tesis ini.
Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Sekretaris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara, sekaligus pembimbing-II yang telah memberikan bimbingan, arahan dan ilmu pengetahuan dalam menye-lesaikan tesis ini.
Bapak Prof. Dr. Opim Salim S, M.Sc, Pembimbing-I yang telah memberikan arahan dan bimbingan dalam penyelesaian dan penyempurnaan tesis ini.
Ibu Dr. Yulita Molliq, M.Sc, Pembanding-I yang memberikan saran dan kritik dalam penyempurnaan tesis ini.
Bapak / Ibu Dosen Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan ilmunya selama masa perkuliahan.
Ucapan terimakasih juga penulis sampaikan kepada Ibunda tercinta,Halifahdan Suami, Sunarto, serta anak-anak, Ibar dan Fauzan yang telah memberikan kasih sayang dan dukungan baik moril maupun materiil selama penulis dalam pendidikan dan penyelesaian tesis ini.
Rekan-rekan mahasiswa Program Studi Magister Matematika FMIPA Universitas Sumatera Utara khususnya angkatan reguler tahun 2011, dan semua pihak yang tidak dapat penulis sebutkan satu persatu pada tesis ini. Semoga Tuhan Yang Maha Kuasa membalas segala kebaikan dan bantuan yang telah diberikan.
Medan, Juni 2013 Penulis,
RIWAYAT HIDUP
Sri Mawarni, dilahirkan di Selatpanjang pada tanggal 17 Desember 1979, merupakan anak kesembilan dari sebelas bersaudara dari Bapak Abdul Wahid dan Ibu Halifah. Penulis menyelesaikan pendidikan Sekolah Dasar (SD) di SD Negeri 005 Selatpanjang pada tahun 1991, Sekolah Lanjutan Tingkat Pertama (SLTP) di SLTP Negeri 1 Selatpanjang pada tahun 1994, dan Sekolah Menengah Atas (SMA) di SMA Negeri 2 Selatpanjang pada tahun 1997.
DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR TABEL ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 4
1.4 Manfaat Penelitian 4
1.5 Metode Penelitian 4
BAB 2 KAJIAN LITERATUR TENTANG BIN PACKING 5
BAB 3 BIN PACKING DAN PERSOALAN ZONA TERLARANG 11
3.1 Bin Packing 11
3.2 Persoalan Zona Terlarang 17
BAB 4 RASIO KOMPETITIF PENJADWALAN ONLINE DENGAN ZONA
TERLARANG JIKA INTERVAL WAKTU DIPERKECIL 20
4.2 Algoritma Online Untuk Persoalan Zona Terlarang 23
BAB 5 KESIMPULAN DAN RISET LANJUTAN 32
5.1 Kesimpulan 32
5.2 Riset Lanjutan 32
DAFTAR TABEL
Nomor Judul Halaman
2.1 Ringkasan heuristik untuk bin packing problem 7
ABSTRAK
Penjadwalan on-line dapat dilihat sebagai penjadwalan dengan informasi yang belum lengkap, yakni waktu proses (run times) pada saat pekerjaan tiba belum diketahui, atau pada titik-titik (waktu) tertentu keputusan dibuat tanpa menge-tahui kejadian lengkap, atau tergantung bagaimana cara informasi baru dike-tahui. Dalam konteks manufaktur dan komputasi berbagai kemungkinan adanya periode tertentu dalam setiap interval waktu, di mana pengolahan dapat terus berlangsung tetapi tidak dapat dimulai. Misalkan n pekerjaan dijadwalkan oleh
J1,· · · , Jn, dan misalkanpiwaktu proses padaJi. Untuk selanjutnya asumsikanpi
≤1,∀i. Waktu dipartisi kedalam himpunan intervalI={I1, I2,· · · , Is}denganI1
= [0, 1],I2 = [1, 2], · · ·, Is = [s1, s]. SetiapIj memuat sebuah koresponden zona terlarang Fj ⊆Ij ∀j, dimana F1 = (1
2 , 1], F2 = ( 3
2, 2], · · · , Fs = (s 1
2, s]. Interval Ij\Fj disebut daerah yang diizinkan. Zona terlarang merepresentasikan interval waktu dimana suatu pekerjaan tidak dapat dimulai tetapi dapat diproses. Dalam tesis ini penulis memeriksa masalah penjadwalan online dengan adanya zona ter-larang dan menyelidiki adaptasi algoritma online bin packing yaitu first fit, next fit dan em harmonic untuk persoalan penjadwalan online dengan zona terlarang pada interval waktu I dan zona terlarang F tersebut.
ABSTRACT
Online scheduling can be seen as scheduling with incomplate information, namely processing time are unknown, at certain points (times) decision have to be made without knowing the complate instance or depending on the way how new infor-mation becomes known. In various manufacturing and computing contexts there may be a certain period in each time interval, during which processing may con-tinue but may not be initiated. Suppose the n jobs to be scheduled by J1,· · · , Jn. Let pi be the processing time of Ji. Furthermore, we shall assume from now on that pi ≤1,∀i. Partition time into a set of abutting intervals I = {I1, I2,· · · , Is} with I1 = [0, 1], I2 = [1, 2], · · · , Is = [s1, s]. Each Ij includes a corresponding forbidden zones Fj ⊆ Ij∀j, dimana F1 = (1
2 , 1], F2 = (32, 2], · · · , Fs = (s12, s].
We call the intervals Ij\Fj allowed zones. Forbidden zones represent time inter-vals during which a job cannot be started, but can be processed. In this thesis, the author examine the problems of online scheduling in the presence of such forbid-den zones and investigate adaptation of the online bin packing algorithm there is first fit, next fit and harmonics algorithm for problems of online scheduling with forbidden zones at time interval of I and the forbidden zone of F.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Penjadwalan diperlukan ketika beberapa pekerjaan harus diproses pada suatu mesin tertentu yang tidak bisa memproses lebih dari satu pekerjaan pada saat yang sama. Penjadwalan yang baik akan memaksimumkan efektivitas peman-faatan setiap sumber daya yang ada.
Penjadwalan adalah kegiatan pengalokasian sumber-sumber atau mesin-me-sin yang ada untuk menjalankan sekumpulan tugas dalam jangka waktu tertentu. Masalah penjadwalan muncul karena adanya keterbatasan waktu, tenaga kerja, jumlah mesin, sifat dan syarat pekerjaan yang akan dilaksanakan. Secara umum ada dua permasalahan utama yang akan diselesaikan melalui penjadwalan yaitu penentuan pengalokasian mesin yang akan digunakan untuk menyelesaikan proses produksi dan penentuan pengurutan waktu pemakaian mesin tersebut, sehingga dalam merencanakan penjadwalan perlu memiliki aturan dan mempertimbangan pendekatan yang digunakan (Barker dan Kenneth, 1974).
Aproksimasi on-line telah menjadi semakin penting dalam bidang penjad-walan, karena dalam merencanakan penjadwalan pengambil keputusan sering mengalami masalah di mana hanya sebagian informasi yang diberikan tetapi dibu-tuhkan solusi yang cepat dan tepat. Penjadwalan on-line dapat dilihat seba-gai penjadwalan dengan informasi yang belum lengkap, yakni waktu proses (run times) pada saat pekerjaan tiba belum diketahui, atau pada titik-titik (waktu) ter-tentu keputusan dibuat tanpa mengetahui kejadian lengkap, atau tergantung ba-gaimana cara informasi baru diketahui. Penjadwalan online membatasi pengam-bil keputusan untuk menjadwalkan pekerjaan berdasarkan informasi yang tersedia saat ini (Khammuang et al., 2007).
penge-2
tahuan tentang masa akan datang. Kurangnya pengetahuan tentang masa akan datang menghalangi scheduler dari menjamin jadwal yang optimal. Dengan demi-kian banyak penelitian telah difokuskan pada menemukan algoritma penjadwalan yang menjamin jadwal yang dalam beberapa cara tidak terlalu jauh dari optimal (Prush et al., 2004).
Penjadwalan dengan waktu mulai, yang dilengkapi zona terlarang, muncul dari persoalan bahwa aktivitas tertentu tidak diizinkan untuk dimulai dalam in-terval waktu tertentu, atau secara umum, dalam beberapa persoalan penjadwalan pengolahan dapat terus berlangsung tetapi tidak dapat dimulai selama interval tertentu (Khammuang et al., 2007). Dalam penelitiannya waktu proses pada pekerjaan yang dijadwalkan diasumsikan tidak lebih dari satu dengan zona ter-larang F ⊂ I, dimana I adalah himpunan interval waktu.
Khammuang et al. (2007) juga mengungkapkan terdapat hubungan antara persoalan zona terlarang dengan solusi optimal dari bin packing. Coffman et al. (1997) menyatakan bahwa bin packing juga telah menjadi dasar teori signifikan se-bagai pembuktian awal bagi banyak pendekatan klasik untuk menganalisis kiner-ja pendekatan algoritma termasuk menentukan kinerkiner-ja rasio worst-case (saat ini disebut rasio kompetitif), mengidentifikasi batas bawah pada kinerja online dan menganalisis perilakunya.
Coffman, et al. (1997) mendefinisikan persoalan bin packing satu dimensi sebagai berikut. Misal diberikan urutan L(a1, a2, . . ., an) item, masing-masing dengan ukurans(ai)∈(0, 1] dan pack menjadi sebuah jumlah minimum pada unit berkapasitas bin (yaitu partisi menjadi sebuah jumlah minimum m dari subset
B1, B2, . . .,Bm sehingga P
ai∈Bjs(ai)≤ 1 , 1≤j ≤ m, persoalan ini merupakan NP-hard.
disu-3
sun berdasarkan sistem permasalahan di dunia nyata dan memenuhi sejumlah batasan-batasan yang ada.
Mengingat masalah penjadwalan yang telah dijelaskan, tugas desainer al-goritma adalah untuk menemukan alal-goritma penjadwalan yang berkinerja baik untuk sebarang input. Melakukan dengan baik biasanya diukur dengan meng-gunakan analisis kompetitif, yaitu membandingkan algoritma dengan sebaik mung-kin (bahkan jika hal ini tidak dapat dicapai dalam praktek) salah satunya adalah menentukan rasio kompetitif batas bawah pada algoritma on-line (Feitelson dan Mu’alem, 2005).
Penelitian berkaitan penjadwalan pada zona terlarang telah dilakukan oleh Kammuang et al. (2007), untuk persoalan zona terlarang waktu dipartisi kedalam interval I = {I1, I2, . . . , Is} dengan I1 = [0, 2], I2 = [2, 4] ,. . . ,Is = [2s-2, 2s]. SetiapIjmemuat sebuah koresponden zona terlarangFj ⊂Ij ,∀j dimanaF = 12I.
Dalam tesis ini dibahas penjadwalan on-line dengan zona terlarang, dalam hal ini zona terlarang merupakan interval waktu pada proses pekerjaan yang dijad-walkan dan dengan mempertimbangkan interval waktu dan zona terlarang yang diperkecil.
1.2 Perumusan Masalah
Dari latar belakang yang dikemukakan, penentuan interval waktu dan zona ter-larang menjadi dasar dari persoalan penjadwalan online dengan zona terter-larang. Permasalahannya adalah menganalisa apakah dengan memperkecil interval waktu dan zona terlarang akan mempengaruhi rasio kompetitif dari algoritma online un-tuk persoalan zona terlarang yang telah dikemukakan Khammuang et al. (2007). Adapun interval waktu dan zona terlarang yang dimaksud adalah I ={I1,I2,. . .,
Is} dengan I1 = [0, 1], I2 = [1, 2] ,. . ., Is = [s-1, s] Setiap Ij memuat sebuah koresponden zona terlarang Fj ⊆Ij ,∀ j dimanaF1 = (1
2, 1], F2 = ( 3
2, 2] ,. . ., Fs
4
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini untuk mengetahui pengaruh interval waktu dan zona terlarang yang diperkecil terhadap rasio kompetitif dari algoritma yang digunakan pada persoalan penjadwalan online dengan zona terlarang.
1.4 Manfaat Penelitian
Penelitian ini bermanfaat dalam penentuan pengaruh interval waktu dan zona terlarang yang dimodifikasi terhadap kinerja dari algoritma untuk persoalan zona terlarang yang telah ditentukan rasio kompetitifnya.
1.5 Metode Penelitian
Metode penelitian ini bersifat studi kepustakaan (literatur) dengan melakukan kajian terhadap beberapa jurnal atau buku pada kepustakaan yang terlampir. Untuk menganalisa rasio kompetitif dari algoritma yang digunakan pada persoalan zona terlarang dilakukan dengan
1. Menganalisa rasio kompetitif batas bawah jika interval waktu dan zona ter-larang diperkecil.
2. Menganalisa algortima untuk persoalan zona terlarang jika interval waktu dan zona terlarangnya diperkecil.
Dalam menganalisa rasio kompetitif batas bawah dilakukan dengan meng-analisa proposisi yang menyatakan hubungan antara solusi optimal dari bin packing dengan persoalan zona terlarang, jika interval waktu dan zona terlarang diperke-cil.
BAB 2
KAJIAN LITERATUR TENTANG BIN PACKING
Pada bab ini akan dibahas kajian literatur tentang bin packing, karena algoritma yang akan digunakan untuk persoalan zona terlarang nantinya merupakan adap-tasi dari algoritma online bin packing.
Dalam persoalan bin packing, misalkan N = { 1, 2,. . ., n} himpunan item dan L = {s1, s2,. . ., sn} himpunan ukuran item sj, dimana 0 < sj ≤ 1, ∀j
∈N. Tujuannya adalah untuk meminimalkan jumlah bin yang digunakan untuk packing item di N ke sebuah bin sehingga total ukuran item dalam bin tidak melebihi kapasitas bin. Asumsikan bin mempunyai kapasitas sama dengan satu. Persoalan bin packing adalah persoalanNP-Complete(Garey dan Johnson, 1979).
Berikut ini ditinjau beberapa heuristik untuk persoalan bin packing atau Bin Packing Problem (BPP). Algoritma online diterapkan setelah item tiba dan item yang tidak dapat dikemas ulang. Yao (1980) menunjukkan bahwa tidak ada algoritma online memiliki rasio asimtotik worst case lebih baik dari 3
2. Yao
juga mengusulkan algoritma online yang disebut First Fit Disempurnakan yang memilikiO(nlogn) waktu dengan rasio asimtotik worst case tidak lebih besar dari
5
3. Liang (1980) menyajikan batas bawah untuk online packing sebesar 1,53635.
Algoritma online untuk bin packing yang ada adalah Next Fit (NF), Harmonic Fit (HF), First Fit (FF), dan Best Fit (BF).
6
1. Harmonic Fit (HF): Gambosi et al. (1990) memodifikasi algoritma Harmo-nic dari online untuk semi-online dengan memungkinkan item yang dikemas untuk dikemas ulang tidak lebih dari sekali. Gambosi mengusulkan dua jenis HF sebagai berikut: i) empat partisi HF di mana dibuktikan bahwa rasio worst case asimtotik yang sama dengan 3
2 dan memerlukan operasi O(n), dan ii) enam-partisi HF di mana dibuktikan bahwa rasio worst case asimtotik yang sama dengan 54 dan memerlukan operasi O(n logn).
2. Algoritma MMP: Ivkovic dan Lloyd (1998) mengusulkan MMP dan mem-buktikan bahwa rasio asimtotik worst case sama dengan 54. Kompleksitas MMP adalah O(logn) dengan penyisipan atau penghapusan item. MMP lebih kompleks daripada algoritma dari Gambosi et.al. (1990).
Algoritma Offline, memiliki asumsi yang berbeda dari pada algoritma online, offline diterapkan setelah item terakhir tiba dan memungkinkan item yang akan diurutkan sebelum pengemasan(packing). Hal ini menghasilkan kinerja worst case lebih baik dibandingkan dengan algoritma online atau semi-online seperti yang dibahas oleh Coffman et al. (1997). Algoritma offline yang ada saat iniNext Fit Decreasing (NFD), First Fit Decreasing (FFD) dan Best Fit Decreasing (BFD). Tabel 2.1 merangkum heuristik dan rasio worst case asymptoticnya untuk masalah bin packing.
Selanjutnya ditinjau algoritmaFirst Fit Decreasing. Pertama, Johnson et al. (1974) menunjukkan bahwa rasio kinerja worst case asimtotik untukFirst Fit(FF) danBest Fit(BF) tidak lebih dari 101, dan tidak lebih dari 119 baik untukFirst Fit Decreasing(FFD) atauBest Fit Decreasing(BFD). Johnson membuktikan bahwa FFD(L) ≤ 119 OPT(L) + 4, ∀ L, dimana L adalah daftar item di BPP, OPT(L) adalah jumlah minimum yang diperlukan bin untuk daftarL, dan FFD(L) adalah jumlah bin yang digunakan oleh heuristik FFD. Untuk menunjukkan kinerja worst case heuristik ini digunakan fungsi pembobotan. Fungsi bobot tergantung pada ukuran item dan lokasi pengepakan.
7
B2F (Best two Fit) yang masing-masing sama dengan 11 9 dan
5
4. Friesen dan
Langston mengusulkan algoritma kompleks, yang menggabungkan algoritma FFD dan B2F keduanya di daerah dimana algoritma tersebut lebih unggul. Kemudian, dibuktikan dengan fungsi pembobotan bahwa kinerja worst case adalah tidak lebih dari 6
5 dan memperpendek panjang bukti dengan mengurangi ukuran dari item
terakhir untuk interval (1 6, 1).
Yue (1991) mengusulkan bukti sederhana dan memberikan batas dengan FFD(L) ≤ 119 OPT(L) + 1, ∀ L. Buktinya didasarkan pada fungsi pembobotan dan contoh konter minimal. Yue menunjukkan bahwa contoh konter tidak ada untuk teoremanya. Selain itu, yue juga mengurangi jumlah interval ukuran item terakhir dengan tiga.
Penelitian yang disebutkan di atas terfokus pada unit-kapasitas masalah bin packing. Di sisi lain, bin packing variabel-size umumnya lebih banyak. Rinciannya dibahas dalam Chu dan La (2001) dan Seiden et al. (2003).
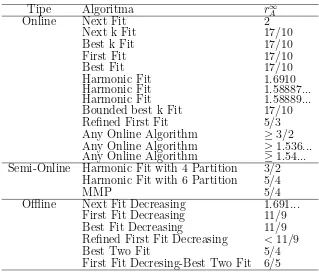
Tabel 2.1 Ringkasan heuristik untuk bin packing problem
Tipe Algoritma r∞
Bounded best k Fit 17/10
Refined First Fit 5/3
Any Online Algorithm ≥3/2 Any Online Algorithm ≥1.536...
Any Online Algorithm ≥1.54...
Semi-Online Harmonic Fit with 4 Partition 3/2 Harmonic Fit with 6 Partition 5/4
MMP 5/4
Offline Next Fit Decreasing 1.691... First Fit Decreasing 11/9
Best Fit Decreasing 11/9
Refined First Fit Decreasing <11/9
Best Two Fit 5/4
8
Beberapa peneliti tertarik dalam studi empiris seperti dibahas dalam Falke-nauer (1996) dan Gent (1998), yang menunjukkan hasil empiris memecahkan BPP oleh algoritma genetika dan metode pencarian lengkap. Selain itu, BPP Dua Di-mensi dibahas dalam Berkey dan Wang (1987), sedangkan Martello et al. (2000) dan Lim dan Ying (2001) mempelajari BPP Tiga-Dimensi.
Aplikasi dari BPP dapat ditemukan dalam berbagai masalah sebagai berikut: i) Masalah Penjadwalan seperti yang dibahas dalam Coffman et al. (1997); ii) Vehicle routing dan masalah penjadwalan seperti dibahas dalam Federgruen dan Ryzin (1997); iii) Masalah vehicle routing seperti dibahas dalam Anily dan Bramel (1999), dan iv) Masalah inventory-routing sebagaimana dibahas dalam Chan et al. (1998a).
Anily et al. (1994) dan Coffman dan Leuker (1991) menyatakan bahwa BPP adalah setara dengan Vehicle Routing Problem (VRP) sebagai berikut: Mi-salkan L = (s1, s2, . . ., sn) menjadi daftar n bilangan real di mana 0 < si ≤ 1 adalah ukuran item i. Item dialokasikan di satu unit kapasitas bin sehingga dapat meminimalkan total biaya semua bin. Biaya bin adalah fungsi dari jumlah item yang dialokasikan dengan monoton increasing dan sifat konkavitas. Dalam VRP, jumlah kendaraan yang digunakan adalah setara dengan jumlah bin yang digunakan.
9
gudang yang ditetapkan pelanggan. Permintaan diasumsikan identik dan sama untuk setiap pelanggan. Oleh karena itu, permintaan dapat dibagi berdasarkan kendaraan.
Bramel et al. (1992) menemukan bahwa heuristik BPP seperti Next-Fit, First-Fit, Best-Fit,First-Fit Decreasing,Best-Fit Decreasing,Next-Fit Increasing danNext-Fit Decreasingmemiliki rasio kinerja worst-case kurang dari dua. Anali-sis average-case VRP dilakukan dengan memecahkan masalah bin packing sehing-ga kapasitas kendaraan sama densehing-gan satu dan permintaan untuk setiap pelangsehing-gan kurang dari satu. Ada sebuah solusi dari VRP berkapasitas sesuai dengan BPP untuk setiap rute. Bienstock et al. (1993) menunjukkan bahwa algoritma untuk VRP dengan permintaan unsplit mirip dengan Next Fit untuk BPP yang bukan asimtotik optimal.
Rhee (1987) dan Coffman dan Leuker (1991), membahas kinerja probabilis-tik bin packing heurisprobabilis-tik. Loulou (1984) mempelajari perilaku probabilisprobabilis-tik dari bin packing optimal.
Bramel dan Simchi-Levi (2001) menunjukkan bahwa di BPP, RFFD tidak lebih dari 32 , sementara Johnson et al. (1974) menunjukkan bahwa R∞
F F D = 119 .
Chan et al. (1998b) menunjukkan bahwa solusi optimal untuk BPP adalah tidak lebih dari 43 nilai solusi optimal yang diperoleh dari pemecahan program linier relaksasi perumusan set-partisi.
Beberapa peneliti telah mengimplementasikan model bin packing dan me-ngembangkannya seperti Parra dan Burtseva (2009), yang mengimplementasikan model bin packing untuk material election dalam membaca pergantian peren-canaan produksi, dan mengusulkankan heuristik algoritma offline untuk menemu-kan jumlah, jenis dan urutan packing kontainer, set fragmen digabung dengan kontainer dan bin, dimana kapasitas bin tidak mempengaruhi algoritma.
ide-10
ide algoritma bin packing klasik (Best Fit) dan pendekatan model mixed integer quadratic programming. Algoritma RCMS dirancang untuk jadwal tugas berat sambil memaksimalkan jumlah tugas ringan yang dapat memenuhi deadline.
Sementara Regin dan Rezgui (2011) mengembangkan model bin packing de-ngan menyajikan model Constraint Programing (CP) dan mengenalkan kendala pertubing model tertentu dan beberapa aturan : 1). Membatasi penugasan bebe-rapa item untuk bebebebe-rapa bin. 2). Bebebebe-rapa item harus cocok dengan bin yang sama dari beberapa bin yang lain. 3). Beberapa item tidak dapat masuk kedalam bin yang sama dari bin yang lain.
Selanjutnya juga ditinjau literatur terkait persoalan online bin packing dan algoritmanya. Seiden (2002) telah mengembangkan metode uniform analisis goritma online bin packing berdasarkan harmonic. Seiden mengembangkan al-goritma baru pada sebuah kasus dari super harmonic yaitu alal-goritma harmo-nic++ dan memiliki asimptotik performa rasio paling besar 1.58889, yang diang-gap memiliki kinerja terbaik dari setiap algoritma online bin packing hingga saat ini.
BAB 3
BIN PACKING DAN PERSOALAN ZONA TERLARANG
3.1 Bin Packing
Dalam persoalan bin packing, diberikan obyek sebanyak n item dengan- ukuran
p1, p2, . . . , pn, yang harus ditempatkan pada bin (tempat penyimpanan) dengan kapasitas L. Setiap bagian memiliki ukuran tetap pada (0, 1]. Setiap item i
membutuhkan unitli dari kapasitas bin. Tujuan bin packing adalah menentukan jumlah bin yang dibutuhkan untuk menampung seluruh onyekn, tidak boleh ada satu obyek yang ditempatkan sebagian di dalam suatu bin dan sebagian lain di dalam bin yang lainnya. Tujuannya adalah untuk meminimalkan jumlah bin yang digunakan.
Khammuang, et al. (2007) mendefinisikan model persoalan bin packing sebagai berikut. Misal diberikan n item dengan ukuran p1, . . . , pn. Asumsikan
pi ≤1∀j,xij = 1 jika item idialokasikan ke binj dan xij = 0 untuk sebaliknya. Juga misalkan zj = 1 jika bin j digunakan dan zj = 0 untuk yang lainnya. Maka persoalan bin packing adalah :
min
n
X
j=1
zj (3.1.1)
kendala
n
X
j=1
xij = 1,∀i (3.1.2)
xij ≤zj,∀i, j (3.1.3)
n
X
i=1
pixij ≤1,∀j (3.1.4)
xij, zj ∈ {0,1}. (3.1.5)
Ken-12
dala (3.1.3) menunjukkan bahwa item dapat ditugaskan ke bin hanya jika bin di-gunakan. Kendala (3.1.4) merupakan kendala ukuran, yaitu bahwa jumlah ukuran item dialokasikan ke unit-ukuran bin tidak dapat melebihi satu.
Dalam versi on-line masalah ini, masing-masing item harus ditugaskan pada gilirannya, tanpa mengetahui tentang item berikutnya. Karena pada umumnya tidak mungkin menghasilkan solusi terbaik saat perhitungan terjadi pada versi online, dengan mempertimbangkan pendekatan algoritma. Pada dasarnya, yang diinginkan adalah mencari sebuah algoritma yang menghasilkan biaya minimum, apa pun inputnya. Faktor ini dikenal sebagai kinerja rasio asimtotik.
Algoritma untuk Persoalan Bin Packing
Algoritma online diterapkan segera setelah item tiba dan Item yang tidak dapat dikemas ulang. Algoritma online yang ada adalah sebagai berikut:
1. Next Fit (NF): NF menguji apakah item j dipacking dalam bin k, dengan memeriksa apakah tidak ada ruang yang tersisa di bink untuk ukuran item
j. Jika demikian, pack itemj dalam bin kdan tinggalkan bin yang terbuka. Jika tidak, tutup bin k, dan buka bin baru yang memuat j sebagai item pertama. NF akan membuka hanya satu bin pada suatu waktu. Strategi Next Fit
(a) Buka bin dan tempatkan objek (item) ke dalam urutannya yang muncul dalam daftar.
(b) Jika item dalam daftar tersebut tidak bisa masuk ke bin terbuka, tutup bin ini secara permanen.
(c) Buka bin yang baru dan terus packing item yang tersisa didaftar.
13
Strategi Harmonic Fit
(a) Item jenis idipack di bin i untuk i= 1,. . ., k-1
(b) Item jenis k dipack menggunakan Next Fit : menggunakan satu bin sampai item berikutnya
(c) Jika tidak sesuai, kemudian buka bin baru
3. First Fit(FF): FF menguji apakah itemjdipacking ke binkdengan memerik-sa apakah tidak ada ruang yang tersimemerik-sa di bin k untuk j. Jika demikian, packing itemj dalam bin yang diindeks terendah. Jika tidak, buka bin baru dan packingj sebagai item pertama. FF memungkinkan beberapa bin yang akan dibuka secara bersamaan. Strategi First Fit
(a) Tempatkan item berikutnya dalam daftar ke bin pertama yang belum terisi penuh di mana item akan sesuai.
(b) Tutup bin yang terisi penuh
(c) Jika sebuah item tidak masuk ke setiap bin yang sedang terbuka, buka bin baru.
4. Best Fit(BF): BF menguji apakah itemj dipaket ke bin dengan memeriksa apakah ada ruang yang tersisa di bink untuk sj. Jika demikian, pack item
j dalam bin dengan konten tertinggi yang memiliki properti ini, ikatan yang dipecah dalam mendukung indeks terendah. Jika tidak, buka bin baru dan paket j sebagai item pertama. StrategiBest Fit
(a) Seleksi semua bin yang terbuka, tempatkan item pada bin yang paling sesuai (akan penuh setelah item ditempatkkan)
(b) Jika tidak ada bin terbuka yang cukup besar (untuk memuat item), buka bin baru.
Pendekatan approksimasi sederhana untuk masalah bin packing adalah al-goritma Next-Fit (NF). Item pertama ditugaskan untuk bin 1. Item 2,. . . , N
14
saat ini. Kompleksitas waktu dari algoritma ini adalah O(n). Untuk setiap keja-dianI pada bin packing Problem (BPP), nilai solusi NF(I) yang disediakan oleh algoritma memenuhi batas
NF(I)≤2z(I).
di mana z(I) menunjukkan nilai solusi optimal. Selain itu, ada kasus yang rasio
N F(I)
z(I) adalah dekat dengan 2, yaitu kinerja rasio worst-case NF adalah r(NF) =
2. Bahwa, untuk masalah minimisasi, untuk kinerja rasio worst-case algoritmaA
didefinisikan sebagai jumlah bilangan riil terkecilr(A) sehingga
A(I)
z(I) ≤r(A),untuk semua I.
dimana A(I) menyatakan nilai solusi optimal dariA.
Sebuah algoritma yang lebih baik, first-fit (FF), menganggap item yang sesuai dengan indeks increasing dan menugaskan setiap item ke indeks terendah bin yang diinisialisasi ke dalam yang sesuai, ketika item saat ini tidak bisa masuk ke setiap bin yang diinisialisasi, diberikan pada bin yang baru . Telah dibuktikan oleh Johnson et al. (1974) bahwa
F F(I)≤ 17
10z(I) + 2. (3.1.6)
untuk semua kejadianI pada BPP, dan bahwa terdapat kejadian I, dengan sem-barang z(I) yang besar, dimana
F F(I)≤ 17
10z(I)−8. (3.1.7)
karena istilah konstan dalam (3.1.6), serta dalam hasil analog untuk algoritma lain, kinerja rasio worst-case tidak dapat memberikan informasi yang lengkap me-ngenai perilaku worst-case. Untuk pendekatan algoritma A, didefinisikan sebagai jumlah minimum bilangan riil r∞(A) sehingga, untuk beberapa bilangan bulat
positif k,
A(I)
z(I) ≤r
∞
A,untuk semua I memenuhi z(I)≥k.
15
Algoritma berikutnya, best-fit, diperoleh dari FF dengan menetapkan item saat ini ke bin layak (jika ada) yang memiliki kapasitas residu terkecil (memu-tuskan hubungan yang mendukung bin diindeks terendah). Johnson, et.al, (1974) telah membuktikan bahwa BF memenuhi batas worst-case yang sama seperti FF, maka r∞(BF) = 17
10.
Sekarang asumsikan bahwa item diurutkan sehingga
w1 ≤w2≤ · · · ≤wn.
dan kemudian NF atau FF, atau BF diterapkan. Dari algoritma yang dihasilkan, kompleksitas waktuO(nlogn), masing-masing disebutNext-Fit Decreasing(NFD), First-Fit Decreasing (FFD) dan Best-Fit Decreasing (BFD). Analisis worst-case tersebut pada NFD telah dilakukan oleh Baker dan Coffman (1981), bahwa FFD dan BFD oleh Johson, et al. (1974) dari hasil sebelumnya oleh Johson (1974) yang membuktikan bahwa
F F D(I)≤ 11
9 z(I) + 4.
untuk semua kejadianI. Hasilnya dirangkum dalam tabel 3.1, diambil dari Coff-man et al. (1997), dalam tiga kolom terakhir yang diberikan, untuk α = 12, 13,
1
4, nilair
∞
a pada asimtotik kinerja rasio worst-case dari algoritma bila diterapkan
pada kejadian memenuhi min1≤i≤npi =αc.
Tabel 3.1 Kinerja rasio asimptotik worst-case pada algoritma bin packing Algoritma Kompleksitas Waktu r∞ r∞
16
Batas Bawah
Mengingat L prosedur batas bawah untuk masalah minimisasi, misalkan
L(I) dan z(I) masing-masing menyatakan, nilai yang dihasilkan olehL dan nilai solusi optimal kejadian I. Kinerja rasio worst-case L selanjutnya didefinisikan sebagai bilangan real terbesar ρ(L) sehingga
L(I)
Z(I) ≥ρ(L),untuk semua I.
Untuk model pada persoalan bin packing, relaksasi kontinu C(BPP) dari persoalan yang diberikan oleh (3.1.1) - (3.1.3) dan
0≤yi ≤1, i∈N,
sehingga batas bawah untuk BPP adalah
L1 =
17
3.2 Persoalan Zona Terlarang
Abdekhodaee dan Ernst, (2004a), yang mempelajari versi off-line mendefinisi kan persoalan zona terlarang sebagai berikut.
Misalkann pekerjaan dijadwalkan olehJ1, . . . , Jn. misalkanpi waktu proses pada Ji. Untuk selanjutnya asumsikan pi ≤ 1 ≤ i. Partisi waktu kedalam him-punan interval I =I1, I2,· · ·, Is dengan I1 = [0, 2], I2 = [2, 4]. Is = [2s−2, 2s]. SetiapIj memuat sebuah koresponden zona terlarang Fj ⊆ Ij∀j, dimana F1 = (1, 2],F2 = (3, 4],. . .,Fs = (2s−1, 2s]. IntervalIj\Fj disebut daerah yang diizinkan. Zona terlarang merupakan interval waktu selama sebuah pekerjaan tidak dapat dimulai, tetapi dapat diproses.
Selanjutnya, jika pekerjaan selesai sebelum akhir sebuah zona terlarang, akan dirilis pada awal interval berikutnya. Dengan demikian, waktu terbaru pekerjaan dapat dimulai dalamIj adalah t = j 12.
Tujuannya adalah untuk mengurutkan pekerjaan supaya jumlah interval yang digunakan minimal. (Jika zona terlarang terakhir memuat pekerjaan, maka ini setara dengan meminimalkan waktu penyelesaian maksimum atau makespan).
Penelitian Abdekhodaee dan Ernst (2004a) juga menunjukkan bahwa, kepu-tusan pada versi off-line dimana semua interval mempunyai panjang yang sama (kIik = I,∀i) dan semua zona terlarang adalah sama (kFik = F,∀i), adalah NP-complete dalam arti yang lemah. Abdekhodaee dan Ernst (2004b) secara em-piris menunjukkan hasil bahwa list penjadwalan dan dengan heuristik sederhana lainnya hasil terbaik ketika F/I adalah mendekati 0 atau 1, dan sebagian besar kasus-kasus sulit terjadi ketika F/I dekat dengan 0,5.
Khammuang et al. (2007) menentukan model untuk persoalan zona ter-larang dengan memodifikasi model pada persoalan bin packing, yaitu
Misalkan xij = 1 jika pekerjaan i dimulai dan berakhir dalam Ij\Fj dan
18
dalam Ij dan berakhir di ¯Fj dan yij = 0 untuk sebaliknya. Kemudian masalah zona terlarang dapat dirumuskan sebagai berikut:
min
Kendala (3.2.4) memastikan bahwa paling banyak satu pekerjaan dapat diproses di zona terlarang.
Definisi 3.1 (algoritma c-kompetitif)
Sebuah algoritma minimisasi on-lineAdikatakanc-kompetitif jikaA(I)/OP T(I)≤
c untuk semua kondisi pekerjaan i, dimana A(I) dan OP T(I) masing-masing adalah nilai-nilai fungsi tujuan untuk algoritmaA dan solusi optimalnya. (Kham-muang et al., 2007).
Definisi 3.2 (asymptotic performance ratio) Asymptotic performance ratioR∞
A(α)didefinisikan sebagai berikut. Misalkanpmax
= α,0< α≤1 maka R∞
A(α) = inf{r ≥1 : untuk suatu N >0, A(I)/OP T(I)≤ r, untuk semua I dengan OP T(I) > N}. Kasus kusus, jika α = 1/m untuk beberapa m bilangan bulat positif. (Khammuang et al., 2007).
19
nilai (biaya atau keuntungan) dari solusi yang diperoleh saat menjalankan ALG pada σ. Secara khusus, misalkan OPT merupakan algoritma offline yang optimal dan misalkan OPT(σ) merupakan nilai solusi terbaik untuk input, maka definisi rasio kompetitif dinyatakan sebagai berikut
Definisi 3.3 (Rasio kompetitif)
Misalkan ALG adalah algoritma online yang ditetapkan untuk masalah optimasi. Jika masalah yang dikaji adalah masalah minimisasi, maka rasio kompetitif ALG adalah
R(ALG) = lim
N→∞ σ:OP Tsup(σ)≥N
ALG(σ)
OP T(σ)
!
.
atau
SR(ALG) = sup
σ
ALG(σ)
OP T(σ).
Jika masalah yang dikaji adalah masalah maksimisasi, maka rasio kompetitif ALG adalah
SR(ALG) = lim
N→∞ σ:OP Tsup(σ)≥N
OP T(σ)
ALG(σ)
!
.
atau
SR(ALG) = sup
σ
OP T(σ)
BAB 4
RASIO KOMPETITIF PENJADWALAN ONLINE DENGAN ZONA TERLARANG JIKA INTERVAL WAKTU DIPERKECIL
Pada bab ini akan disajikan analisa rasio kompetitif dari algoritma zona terlarang yang dikemukakan Khammuang et al., (2007), jika interval waktu dan zona ter-larangnya diperkecil. Persoalan zona terlarang yang akan dianalisa dalam hal ini adalah sebagai berikut
Misalkannpekerjaan dijadwalkan olehJ1, . . . , Jn. Misalkanpi waktu proses pada Ji. Untuk selanjutnya asumsikan pi ≤ 1 ∀i. Partisi waktu kedalam him-punan interval I ={I1, I2, . . . , Is} dengan I1 = [0, 1],I2 = [1,2], . . . , Is = [s−1,
s]. Setiap Ij memuat sebuah koresponden zona terlarang Fj ⊆ Ij , ∀j dimana
F1 = (1
2, 1], F2 = ( 3
2,2], . . . , Fs = (s -1
2 , s]. Interval Ij\Fj di sebut daerah yang
diizinkan.
4.1 Analisa Rasio Kompetitive Batas Bawah.
Atur urutan waktu pekerjaan yang non-increasing dan notasikan list baru dengan
J1, J2, . . . , Jn. Misalkanpi adalah waktu proses padaJi. makap1 ≤p2 ≤. . .≤pn. Berikut ini hubungan antara solusi optimal dari bin packing dengan persoalan zona terlarang.
Proposisi 4.1 (Kammuang et al., 2007). Misalkan solusi optimal persoalan bin packing untuk n-i pekerjaan terkecil adalah i bin. Maka penjadwalan optimal untuk persoalan zona terlarang adalah i interval.
Bukti. Pertama akan ditunjukkan intervali memadai untuk persoalan zona ter-larang. Gunakan solusi optimal bin packing untuk menenpatkan J′
i+1. . . Jn pada
zona yang diizinkan. Tambahkan sisaipekerjaan terpanjangJ′
1. . . Jnpadaizona
sele-21
diperoleh solusi untuk masalah bin packing untukn−ipekerjaan terpendek yang membutuhkan lebih sedikit dariiinterval, hal ini suatu kontradiksi, jadiiinterval adalah penjadwalan optimal untuk persoalan zona terlarang.
Proposisi 4.1. juga berlaku Jika interval waktu diperkecil, karena pada setiap interval waktu Ii memuat satu zona yang diizinkan dan satu zona terlarang.
Beberapa bukti batas bawah untuk on-line bin packing mengandalkan pada pekerjaan dengan waktu proses yang sangat kecil. Proposisi berikut ini meng-gunakan argumen yang diadaptasi dari bukti hasil penelitian, bahwa tidak ada algoritma on-line untuk bin packing lebih baik dari 43-kompetitif (Liang, 1980).
Proposisi 4.2 (Kammuang et al., 2007). Tidak ada algoritma online untuk per-soalan zona terlarang lebih baik dari 97-kompetitif.
Bukti. Asumsikan algoritma A adalah c-competitive. Pertimbangkan untuk urutan pada n pekerjaan panjang masing-masing 12 - ε, dengan syarat bahwa
ε < 1
6, dan n habis dibagi 3, A memerlukan paling banyak a ≤ cn/3 interval,
karena solusi optimal membutuhkan n/3 interval. Misalkan kemudian pekerja-an dengpekerja-an ppekerja-anjpekerja-ang 12 + ε dinyatakan dengan 2n. Andaikan A menggunakan interval tambahan b untuk pekerjaan ini. Setiap interval b dapat menampung paling banyak dua dari pekerjaan baru, sedangkan masing-masing interval per-tama bisa menampung hingga tiga dari n pekerjaan awal. Dengan demikian, 3a+ 2b ≥ 3n, juga a+b ≤ cn karena solusi optimal membutuhkan n interval, dengan demikian(3−2c)n ≤a ≤cn/3. jadi c≥ 9
7.
Algoritma Zona Terlarang
22
1. Jika pi < 1/m abaikan zona terlarang dan tempatkan pekerjaan di zona yang di izinkan tepat ke B yang sesuai. Jika tidak,
2. Jika pi ≥ 1/m tempatkan pekerjaan pada zona diizinkan pertama yang tersedia. Jika hal ini tidak mungkin terjadi dalam zona terlarang pertama yang tersedia. Jika itu tidak mungkin,
3. Buat interval baru dan tempatkan pekerjaan pada interval baru di zona yang diizinkan.
Untuk interval waktu yang diperkecil, algoritma zona terlarang dapat digu-nakan, namun perlu disyaratkan bahwa m ≥2, m bilangan bulat positip, karena interval waktu untuk i = 1 adalah I1 = [0, 1] dan F1 = (22 , 1]. Sehingga lemma berikut juga berlaku untuk m ≥2.
Lemma 4.1.1 Jika algoritma bin packing tidak pernah mengizinkan jeda pada 1 m
dalam sebuah bin maka R∞
B(m1) + ( 1 m)≤R
∞
B′(m1) = m+1m−1.
Bukti. Pertimbangkan kejadian worst-case untuk B. Tidak ada pekerjaan da-pat lebih besar dari 1
m. Ganti setiap pekerjaan berukuran 1
m, dengan pekerjaan
berukuran 1
m-ε. Dengan demikianB tidak akan menempatkan setiap pekerjaan
di zona terlarang.
Misalkan untuk hal ini, solusi optimal untuk persoalan bin packing meng-gunakan n∗ bins dan juga B menggunakan n ≥(R∞
B −ε)n∗ bin. Tambahkan n∗
pekerjaan berukuran m1-ε. KarenaB tidak dapat menjadwalkan pekerjaan dalam zona terlarang, pekerjaan harus ditempatkan pada zona diizinkan yang meng-akibatkan peningkatan pada interval (n∗/m). Namun, berdasarkan solusi optimal
23
Artinya, tidak ada peningkatan jumlah interval. Dengan demikian diperoleh
B′
Di sisi lain, pada worst, B akan meninggalkan semua zona terlarang yang kosong. Celah/gap di setiap zona yang diizinkan, kecuali mungkin yang terakhir, harus kurang dari 1
m. Jadi semua zona yang diizinkan, kecuali mungkin yang terakhir,
dalam solusi B berada pada sedikitnya 1− 1
m penuh. Di sisi lain, dalam solusi
optimal setiap zona terlarang adalah paling banyak m1 penuh.
4.2 Algoritma Online Untuk Persoalan Zona Terlarang
Algoritma List Scheduling (LS)
1. Setiap kali pekerjaan tiba, urutkan pekerjaan berikutnya pada daftar di posisi pertama yang mungkin.
2. Jika pekerjaan sebelumnya telah selesai pada akhir dari zona yang diizinkan saat ini, jadwal pekerjaan berikutnya segera setelah itu.
3. Jika tidak, mulai pekerjaan berikutnya pada awal zona tersedia berikutnya.
4. Jika pekerjaan sebelumnya selesai pada titik akhir zona yang diizinkan mulai pekerjaan berikutnya pada awal berbatasan dengan zona terlarang.
Proposisi 4.3 R∞
LS(m1) = 1 + ( 1 m).
24
pekerjaan dengan panjangε. LS membutuhkan ninterval, sedangkan solusi opti-mal hanya membutuhkan m+1nm interval, untuk ε yang cukup kecil. Di sisi lain, untuk LS, masing-masing zona yang diizinkan kecuali mungkin yang terakhir, adalah penuh. Jadi,LS adalah worst (1 + 1
m)- kompetitif.
Algoritma Half Next Fit (HNF)
Half Next Fitmerupakan algoritma yang diadaptasi dari algoritmaNext Fit(NF) untuk persoalan bin packing, bekerja sebagai berikut. HNF selalu menganggap hanya satu zona yang diizinkan aktif.
1. Setiap kali pekerjaan tiba, jika ukuran pekerjaan yang tiba lebih kecil dari celah (gap) di zona yang diizinkan aktif, tempatkan pekerjaan ke zona ter-sebut. Jika tidak,
2. Jika ukuran pekerjaan lebih besar atau sama dengan12 tempatkan pekerjaan ke zona terlarang pertama yang tersedia.
3. Jika tidak ada zona terlarang tersedia, tutup interval saat ini, buka interval baru dan tempatkan pekerjaan dalam interval zona yang diizinkan tersebut.
4. Jika ukuran pekerjaan kurang dari 12 tutup zona yang diizinkan yang aktif saat ini dan buka yang baru dan tempatkan pekerjaan di zona tersebut.
Berdasarkan Lemma 4.3, dapat diketahui bahwa rasio kompetitif paling sedikit adalah 2,5 karena R∞
N F12 = 2 (Coffman et al, 1997). Namun, proposisi
berikut menunjukkan bahwa, pada kenyataannya, asimtotik kinerja rasio HNF adalah 3.
Proposisi 4.4 R∞
N F = 3.
Bukti. Pertama akan ditunjukkan bahwa R∞
HN F ≥ 3. Misalkan pekerjaan
ber-ukuran 1
25
lebih kecil dari 1
2, HNF tidak dapat menempatkan pekerjaan di zona terlarang.
HNF akan menempatkan pekerjaan berukuran 12−εdan pekerjaan berukuran 3ε
dalam zona yang diizinkan. Gap di zona yang diizinkan adalah lebih kecil dari
1
2 −ε. Oleh karena itu zona yang diizinkan saat ini aktif kemudian ditutup dan
pekerjaan berikutnya ditempatkan di zona yang diizinkan baru yang aktif. HNF akan membutuhkan n zona yang diizinkan dalam hal ini. Sedangkan pada solusi optimal, 3 pekerjaan berukuran 12 −ε dapat dijadwalkan dalam interval (yaitu, pada zona yang diizinkan dan zona terlarang). Untuk n pekerjaan berukuran
1
2 −ε, dibutuhkan n
3 interval. Juga untuk n pekerjaan berukuran 3ε, dan untuk ε cukup kecil solusi optimal akan menempatkan pekerjaan tersebut dalam satu zona yang diizinkan. Oleh karena itu
HNF =n
sekarang akan ditunjukkan RHN F ≤ 3. Misalkan s(ai) adalah jumlah waktu pengolahan pada pekerjaan dalam zona yang diizinkan ke-idans(fi) adalah waktu proses pada pekerjaan dalam zona terlarang ke-i. Berdasarkan definisi dariHNF
bahwa s(aj) > 0 ⇒ s(ai) +s(fi) ≥ 12,∀i < j. Jadi jika HNF(I) = n maka diperoleh setidaknyan−1 kelompok pekerjaan masing- masing berukuran paling sedikit 12 . Jelas bahwa,OP T(I)≥ n−1
Bukti. Buktinya dari lemma 4.1.1 dan fakta bahwa R∞
HN F(m1) = m m−1
26
Proposisi 4.6 R∞
HN F(12) = 3.
Bukti. Berdasarkan proposisi 4.5 diperoleh R∞
HN F(12) ≤ (2
2 + 2)/2(2−1) = 3.
Dalam pembuktian proposisi 4.4 tidak ada pekerjaan berukuran lebih dari 1 2. Jadi R∞
HN F(12)≥3.
Algoritma Half First Fit (HFF)
Heuristik algoritma Half First FIT (HFF) memanfaatkan algoritma First Fit (FF) untuk persoalan bin packing. Prosedur nya adalah sebagai berikut.
1. Setiap pekerjaan tiba, jika ukuran pekerjaan lebih kecil atau sama dengan celah (gap) di salah satu zona yang diizinkan yang ada, jadwalkan pekerjaan ke dalam gap yang pertama. Jika tidak,
2. Jika ukuran pekerjaan lebih besar atau sama dengan1
2 tempatkan pekerjaan
ke zona terlarang pertama yang tersedia.
3. Jika tidak ada zona terlarang tersedia buka interval baru dan tempatkan pekerjaan di zona yang diizinkan pada interval tersebut.
4. Jika ukuran pekerjaan kurang dari 1
2 buka zona yang diizinkan baru dan
tempatkan pekerjaan di zona baru.
Yang menjadi motivasi untuk algoritma ini adalah mencoba untuk menempatkan pekerjaan terpanjang di zona terlarang.
Proposisi 4.7 52 ≤R∞
HF F ≤ 2710.
Bukti. Pertama akan ditunjukkan 52 ≤ R∞
HF F. Berdasarkan hasil dari Johnson,
et al (1974), RHF F∞(0.4) = 3
2. Oleh karena itu, untuk sebarang δ > 0, terdapat i untuk persoalan bin packing, dengan semua item berukuran lebih kecil dari 12, sedemikian rupa sehingga OP TF F(I)(I) ≥ 32 − δ. Misalkan OP T(I) menggunakan n
27
dengan menganggap bin ini sebagai zona yang diizinkan dalam persoalan zona terlarang, hasilnya masih berlaku karena semua zona terlarang kosong. Sekarang buat keadaan baru, I sebagai berikut. Sebuah pekerjaan berukuran ε tersebut disajikan diikuti oleh pekerjaan ukuran 1− ε. Pengaturan ini diulang n kali menghasilkan 2n pekerjaan yang akan dijadwalkan. Kemudian satu set pekerjaan diI disajikan. HF F akan membutuhkann interval untuk 2n pekerjaan pertama dan (32 −δ)n interval untuk pekerjaan dari I. Di sisi lain, solusi optimal akan hanya memanfaatkan n+ 1 interval karena n pekerjaan berukuran 1−δ dapat dimasukkan ke dalam zona terlarang dan satu interval untuk pekerjaan berukuran
ε sudah memenuhi. Jadi 52 ≤R∞
HF F.
Sekarang akan ditunjukkan bahwaR∞
HF F ≤ 2710, dengan sedikit mengadaptasi
bukti dari Johnson et al (1974) yang menunjukkan R∞
HF F = 1.7. Pertimbangkan
i=1w(ai) adalah koresponden fungsi pembobotan. Juga definisikan W(I) =
Pi
j=1w(aij), dimanaaij, j = 1, . . . , t adalah pekerjaan dijadwalkan ke interval I.
Dengan menggunakan dua hasil oleh johnson et al. (1974), untuk persoalan bin packing :
1. Untuk sebarang bin B, W(B)≤ 1710 dan karenanya W(L)≤ 1710OP T(L).
2. Jika F F menggunakan k bin B1, . . . , Bk maka Pk
j=1w(Bj) ≥ k − 2 dan
dengan demikianF F(L)≤W(L) + 2.
28
dengan menganggap zona yang diizinkan sebagai bin B diperoleh W(B) ≤ 17 10.
Setiap pekerjaan di zona terlarang memiliki bobot tidak lebih besar dari satu. Jadi, untuk setiap intervalI, diperolehW(I)≤ 2710. Jadi,W(B)≤ 1710OP T(L).
Perhatikan sebuah jadwal S diperoleh dengan menggunakan HF F. Buat jadwal baru S′
dengan membuang semua pekerjaan yang dijadwalkan ke zona terlarang di S. Perhatikan bahwa jika dengan mempertimbangkan hanya zona diizinkan, S′ yang menggunakan s, dikatakan, zona yang diizinkan (maka
in-terval) dapat dianggap sebuah himpunan dari s bin, B, paket dari F F. Karena
W(B)≥s−2 dengan demikianW(S′
)≥s−2. Jadi,HF F(S) =s≤W(S′
)+2≤
W(S) + 2≤ 17
10OP T(S) + 2, sehingga membuktikan hasilnya.
Algoritma Half HarmonicM (HHM)
Lee dan Lee (1985) mengusulkanMHarmonic, adanya perbaikan padaF F, yang menjagaM bin terbuka pada satu waktu, dan menggunakan urutan berikut, k1 = 1 dan ki + 1 = ki(ki + 1) untuk i ≥ 1, yang sebelumnya diusulkan oleh Liang (1980), Lee menunjukkan bahwa R∞
HF F adalah monoton turun dengan M dan
limM→∞R∞HM =
P∞
i=1 1
ki = 1.6910.
Algoritma ini membagi interval satuan (0, 1] menjadi M subinterval Ij = (j+11 ,1j], 1 ≤ j < M dan IM = (0,M1 ]. Versi yang sesuai untuk persoalan zona terlarang, HHM selalu menganggap M zona yang diizinkan pada suatu waktu. Suatu pekerjaan disebut Ij-pekerjaan jika ukurannya berada pada interval Ij. Sebuah zona yang diizinkan disebut zona yang diizinkan Ij jika zona tersebut hanya ditugaskan untuk proses Ij pekerjaan. Pada satu waktu, terdapat M zona yang diizinkan tersedia, satu untuk setiap Ij, 1≤j ≤M.
Prosedur algoritma HHM adalah sebagai berikut :
29
2. Jika ukuran pekerjaan lebih besar dari 1
2 tempatkan pekerjaan di zona
ter-larang pertama yang tersedia.
3. Jika tidak ada zona terlarang yang tersedia buka interval baru dan buat menjadi zona yang diizinkan tipe I1 dan tempatkan pekerjaan di interval zona yang diizinkan tersebut.
4. Jika ukuran dari pekerjaan kurang atau sama dengan 1
2 buka Ij zona yang
diizinkan baru, untuk 2≤j ≤M yang sesuai dan tempatkan pekerjaan di zona baru yang diizinkan.
Berikut ini, disajikan beberapa lemma, dan menggunakan argumen yang dinyatakan oleh Lee dan Lee (1985), yaitulimM→∞R∞HHM = 1.9231177.
Untuk memudahkan analisis, akan dilihat pekerjaan dengan ukuran lebih besar atau tidak lebih besar dari 12 sebagai pekerjaan besar atau kecil.
Lemma 4.2.1 . Misalkan sebarang kejadianJ pada pekerjaan dinyatakan dalam urutan khusus. Misalkan J′ himpunan yang sama dari pekerjaan pada urutan
yang sama kecuali bahwa pekerjaan besar yang sekarang disajikan terlebih dahulu. Maka HHM(J′)≥HHM(J).
Bukti. zona yang diizinkan I2, . . . , IM untuk kedua J dan J′ adalah identik.
Banyaknya interval I1 untuk J kurang dari atau sama dengan J′ karena dalam
beberapa zona terlarang J dalam I2, . . . , IM mungkin tak-kosong, sedangkan un-tuk J′ semuaI2, . . . , IM zona terlarang adalah kosong.
Lemma 4.2.2 Untuk setiap persoalan zona terlarang, dengan solusi optimal yang terdiri dari n interval, terdapat sebuah solusi optimal yang terdiri dari n pekerjaan besar di zona terlarang.
30
Lemma 4.2.3 limM→∞R∞HHM ≥u∞ = 1.923117753.
Bukti. Untuk membuktikan klaim tersebut, dengan memanfaatkan urutan {l}. Misalkan M = li+1 dimana i → ∞ dan n adalah kelipatan dari li (maka, habis dibagi 2). Pertimbangkan hal-hal berikut Input dalam pekerjaan yang terdiri dari
n pekerjaan berukuran a dimana a ∈I1 dan n pekerjaan berukuran l 1
j+1+ε untuk
setiap j, dimana 2 ≤ j ≤ i. Perhatikan bahwa pekerjaan disajikan ke penjad-walan yang urutannya non-increasing yaitu, n pekerjaan berukuran adisajikan pertama diikuti oleh n pekerjaan berukuran l1
2+1 dan seterusnya. Untuk
keja-dian ini, HHM akan menggunakan ln lj
m
zona yang diizinkan untuk n pekerjaan berukuran 1
lj+1+ε di mana 2 ≤ j ≤ i, karena, untuk pekerjaan ini, HHM akan
meninggalkan semua yang berhubungan dengan zona terlarang yang kosong. Jadi
HHM akan membutuhkanlln j
m
interval untuk n pekerjaan berukuran l 1
j+1+ε.
Se-lain itu, HHMmembutuhkan n2 zona yang diizinkan dan n2 zona terlarang untuk
n pekerjaan berukuran a. Dengan demikian diperoleh
HHM(L) = n
karena, dari asumsi, lln j
m
= ln j.
31
BAB 5
KESIMPULAN DAN RISET LANJUTAN
5.1 Kesimpulan
Dalam tesis ini telah dibahas persoalan penjadwalan online dengan zona ter-larang dengan interval waktu dan zona terter-larang diperkecil. Terdapat hubungan antara persoalan zona terlarang dengan persoalan bin packing. Pada persoalan ini telah diusulkan empat algoritma online yaitu algoritma List Scheduling (LS), Half Next Fit(HNF),Half First Fit(HFF) danHalf Harmonic M(HHM) yang di-adaptasi dari algoritma untuk persoalan online bin packing. Juga telah dianalisa bahwa asymtotic performence ratio algoritma tersebut tidak berubah jika interval waktu dan zona terlarangnya diperkecil, dalam hal ini interval waktuI diperkecil dengan membagi dua interval waktu sebelumnya sedangkan untuk interval zona terlarangnya adalah 1
2I, namun untuk persoalan ini perlu disyaratkan nilaimpada
algoritma zona terlarang,m ≥2. Adapun asymtotic performence ratio algoritma tersebut masing-masing adalah: untuk algoritma LS, R∞
LS (m1)= 1+( 1
m), dengan m ≥ 2, m bilangan bulat positif, untuk algoritma HNF, R∞
HN F (12) = 3, untuk
algoritma HFF, 52 ≤R∞
HF F ≤ 2710 dan untuk algoritma HHM,R
∞
HHM ≥1.9231177.
5.2 Riset Lanjutan
DAFTAR PUSTAKA
Abdekhodaee A dan Ernst AT (2004a). Scheduling Jobs with Forbidden Zones. Technical report, Commonwealth Scientific and Industrial Research Organi-sation, Australia.
Abdekhodaee A dan Ernst AT (2004b). Scheduling jobs with forbidden zones in the context of coal supply chain. In: Van Wassenhove N et al (eds).Proceeding of European Operations Management Association 2004 Operations Management as a Change Agent. INSEAD, Fontainebleau, pp 669676.
Anily S dan Bramel J (1999). Quantitative models for supply chain management. In S. Tayur,R. Ganeshan, and M. Magazine, editors,Vehicle Routing and the Supply Chain, pages 147-196. Kluwer Academic Publishers, Massachusetts. Anily S, Bramel J, dan Simchi-Levi D (1994). Worst-case analysis of heuristics for
the bin packing problem with general cost structures. Operations Research, 42:287-298.
Baker dan Kenneth R. (1974). Introduction to Sequencing and Scheduling. New York: John Wiley & Sons, Inc.
Baker B dan Coffman, E G. Jr. (1981). A tight Asymptotic Bound for Next-Fit-Decreasing Bin-Packing. SIAM J Alg. Disc. Math 2, 147-152.
Bein D, Bein W, dan Venigella S (2012). Cloud Storage and Online Bin Packing. Intelligent Distributed Computing V Studies in Computational Inteligence volume 382, 2012, pp 63-68.
Berkey J dan Wang P (1987). Two-dimensional Finite bin-packing algorithms. Journal of Operation Research Society, 38:423-429.
Bienstock D, Bramel J, dan Simchi-Levi D (1993). A probabilistic analysis of tour partitioning heuristics for the capacitated vehicle routing problem with un-split demands. Math O. R., 18:786-802.
Bramel J dan Simchi-Levi D (2001). The Logic of Logistics: Therory, Algorithms, and Applications for Logistics Management. Springer.
Bramel J,. Shor Jr, dan. Simchi-Levi D (1992). Probabilistic analysis of the capa-citated vehicle routing problem with unsplit demands. Operations Research, 40:1095-1106.
Chan L. M. A, Federgruen A, dan Simchi-Levi D (1998a). Probabilistic analyses and practical algorithms for inventory-routing models. Operations Research, 46:96-106.
34
Chu C dan La R (2001). Variable-sized bin packing: Tight absolute worst-case per-formance ratios for four approximation algorithms. SIAM Journal on Com-puting, 30:2069-2083.
Coffman Jr EG, Garey MR dan Johnson DS (1997). Approximation algorithms for bin packing: a survey. In: Hochbaum DS (ed).Approximation Algorithms for NP-hard Problem. PWS publishing company, Boston, pp 4693.
Coffman Jr. E. dan Lueker G. (1991). Bin packing heuristics. InProbabilistic Analy-sis of Packing and Partitioning Algorithms, pages 121-154. Wiley & Sons. Epstein L,. Favrholdt M L, dan. Kohrt J S (2012). Comparing online algorithm
for bin packing. Journnal of Scheduling, volume 15 issue 1, pp 13-21
Falkenauer E (1996). A hybrid grouping genetic algorithm for bin packing.Journal of Heuristics, 2:5-30.
Federgruen A dan Ryzin G (1997). Probabilistic analysis of a generalized bin packing problem with applications to vehicle routing and scheduling problems. Operations Research, 45:596-609.
Feitelson D. G dan Mualem A. W (2005). On the Definition of On-Line in Job Scheduling Problems. ACM SIGACT News. Vol. 36, No.1
Friesen D dan Langston M (1991). Analysis of a compound bin packing algorithm. SIAM Journal Discrete Mathematics, 4:61-79.
Gambosi G, Postiglione A, dan Talamo M (1990). New algorithm for online bin packing problem a survey in r. petreschi et al. editor. Algorithms and Com-plexity : Proceedings of the First Italian Conference, Rome, Italy, 1-2 October 1990, 1:44-59.
Garey M dan Johnson D (1979). Computers And Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, New York. Gent I (1998). Heuristic solution of open bin packing problems.Journal of
Heuris-tics, 3:299-304.
Ivkovic Z dan Lloyd E (1998). Fully dynamic algorithms for bin packing: Being (mostly) myopic helps. SIAM Journal on Computing, 28:574-611.
Johnson D, Demers A, Ullman J, Garey M, dan Graham R (1974). Worst-case performance bounds for simple one-dimensional packing algorithms. SIAM Journal on Computing, 3:299-325.
Khammuang A, Abdekhodaee A dan Wirth A. (2007). On-line Scheduling With Forbidden Zones. Journal of the Operational Research Society 58 : 8090. Lee CC and Lee DT (1985). A simple on-line bin-packing algorithm.J Assoc
Com-put Mach 32: 562572.
35
Lim A dan Ying W (2001). A new method for the three dimensional container packing problem. In IJCAI, pages 342-350.
Liu C dan Baskiyar S (2008). Scheduling Mixed Tasks with Deadlines in Grids Using Bin Packing. Parallel and Distributed Systems. ICPADS 14th IEEE International Conference
Loulou R (1984). Probabilistic behavior of optimal bin packing.Operation Research Letter, 3:129-135.
Martello S, Pisinger D, dan Vigo D (2000). The three-dimensional bin packing problem.Operations Research, 48:256-267.
Parra R. R dan Burtseva L (2009). Bin Packing Model Implementation for Material Election in Read Switches Production Planning. Proceedings of the World Congress on Engineering and Computer Science Vol II.
Pruhs K, Sgall J dan Torng E (2004). Online scheduling. In: Leung J (ed). Hand-book of Scheduling: Algorithms, Models, and Performance Analysis. CRC Press, Boca Raton, pp 15-115-41.
Regin J.C dan Rezgui M (2011). Discussion about Constraint Programming Bin Packing Models. AI for Data Center Management and Cloud Computing: Papers from AAAI Workshop.
Rhee W (1987). Martingale inequalities and NP-complete problems.Math. Opera-tion Research, 12:177-181.
Seiden S. S (2002). On the Online Bin Packing Problem.Journal of the ACM, Vol. 49, No. 5, pp. 640671.
Seiden. S, Stee R., dan Epstein L (2003). New bounds for variable-sized online bin packing.SIAM Journal on Computing, 32:455-469.
Yao A (1980). New algorithm for bin-packing.Journal of ACM, 27:207-227.