PENYELESAIAN MODEL MANGSA PEMANGSA TIGA
SPESIES DENGAN METODE HOMOTOPI
YULI RAHMAWATI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Model Mangsa Pemangsa Tiga Spesies dengan Metode Homotopi adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
YULI RAHMAWATI. Penyelesaian Model Mangsa Pemangsa Tiga Spesies dengan Metode Homotopi. Dibimbing oleh JAHARUDDIN dan SISWANDI.
Dalam karya ilmiah ini, digunakan metode homotopi untuk menyelesaikan masalah taklinear dari model mangsa pemangsa tiga spesies dengan adanya mangsa, pemangsa, dan pesaing yang didasarkan pada Paparao et al. (2013). Dalam metode ini, didefinisikan fungsi homotopi dengan penambahan beberapa parameter, salah satunya parameter yang digunakan untuk menentukan selang kekonvergenan. Penyelesaian dari masalah tersebut dituliskan dalam bentuk deret hingga order kelima. Hasil yang diperoleh dengan metode homotopi selanjutnya dibandingkan dengan penyelesaian secara numerik. Nilai merupakan nilai dengan galat yang paling kecil.
Kata kunci: mangsa, pemangsa, pesaing, parameter , dan metode homotopi.
ABSTRACT
YULI RAHMAWATI. Solution of Three Species Predator Prey Models by Homotopy Method. Supervised by JAHARUDDIN and SISWANDI.
In this manuscript, a homotopy method was used to solve nonlinear problem of three species predator prey model with a prey, a predator, and a competitor which is based on Paparao et al. (2013). In this method, a homotopy function is defined by adding of several parameters, one of them is parameter which is used to determine the interval of convergence. Solution of the problem is written in the form of series up to fifth order. The results obtained using the homotopy method were compared with the numerical solution. It is found that of is the value with the smallest error.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PENYELESAIAN MODEL MANGSA PEMANGSA TIGA
SPESIES DENGAN METODE HOMOTOPI
YULI RAHMAWATI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Penyelesaian Model Mangsa Pemangsa Tiga Spesies dengan Metode Homotopi
Nama : Yuli Rahmawati
NIM : G54100071
Disetujui oleh
Dr Jaharuddin, MS Pembimbing I
Drs Siswandi, MSi Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Topik yang dipilih dalam penulisan karya ilmiah ini adalah penggunaan metode homotopi untuk kasus model mangsa pemangsa tiga spesies, dengan judul Penyelesaian Model Mangsa Pemangsa Tiga Spesies dengan Metode Homotopi.
Penyusunan karya ilmiah ini tidak lepas dari bantuan berbagai pihak. Oleh karena itu penulis mengucapkan terima kasih kepada semua pihak yang telah membantu dalam proses penyusunan karya ilmiah ini antara lain:
1. Effendi Abdul Kohar (Ayah) dan Linda Buchori (Ibu) selaku orangtua, Elva Gustini (kakak), Imam Riski Abdullah (adik) atas semua do’a, dukungan, semangat, pengorbanan, nasihat, perhatian, dan kasih sayang sehingga penulis dapat menyelesaikan karya ilmiah ini.
2. Dr Jaharuddin, MS selaku dosen pembimbing pertama dan Drs Siswandi, MSi selaku dosen pembimbing kedua atas semua ilmu, motivasi, dan bantuannya selama penulisan karya ilmiah ini.
3. Drs Ali Kusnanto, MSi selaku dosen penguji atas saran dan kritik untuk perbaikan karya ilmiah ini.
4. Seluruh dosen Departemen Matematika yang telah memberikan ilmu kepada penulis.
5. Seluruh staf Departemen Matematika yang telah membantu dalam menyelesaikan karya ilmiah ini.
6. Keluarga besar paguyuban Bidik Misi atas dukungan dan bantuan selama penulis kuliah di IPB.
7. Sahabat terbaik Sabrina, Siwi, Sekar, dan Devi atas motivasi dan semangat yang selalu diberikan kepada penulis.
8. Teman-teman Math 47: Bilyan, Leny, Mira, Novia, Vina, dan semuanya. 9. Kakak-kakak Math 46: kak Dita, kak Windi, kak Risa atas ilmu, nasihat,
motivasi, dan bantuan selama penulis kuliah di Departemen Matematika. 10.Serta teman-teman di Asrama Putri Dramaga.
Penulis menyadari bahwa karya ilmiah ini memiliki kekurangan sehingga perlu saran dan kritik. Semoga karya ilmiah ini dapat bermanfaat dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Karya Ilmiah 2
TINJAUAN PUSTAKA 2
Model Persamaan Mangsa Pemangsa Tiga Spesies 2
Metode Homotopi 3
HASIL DAN PEMBAHASAN 8
Analisis Metode 8
Aplikasi Metode 12
SIMPULAN 17
Simpulan 17
DAFTAR PUSTAKA 18
LAMPIRAN 19
DAFTAR TABEL
1 Galat metode homotopi orde ke sepuluh masalah nilai awal (12) 8
2 Nilai parameter-parameter dari persamaan (1) 13
3 Galat metode homotopi orde ke lima dari persamaan (1) 15
DAFTAR GAMBAR
1 Kurva dari penyelesaian masalah nilai awal (12) dengan metode
homotopi orde ke sepuluh 7
2 Kurva dari penyelesaian persamaan (1) dengan metode homotopi orde
ke sepuluh 14
3 Penyelesaian persamaan (1) dengan metode numerik 16
DAFTAR LAMPIRAN
1 Penurunan persamaan (10) 19
2 Penurunan persamaan (32) 22
PENDAHULUAN
Latar Belakang
Semua makhluk hidup bergantung pada makhluk hidup lain. Di samping itu, setiap individu berinteraksi dengan individu lain dalam satu spesies maupun antarspesies atau individu dalam satu populasi maupun antarpopulasi. Adanya interaksi menyebabkan hubungan makan dan dimakan yang terjadi pada spesies tertentu, sehingga timbul persaingan di antara spesies tersebut.
Persaingan adalah interaksi antara dua spesies atau lebih yang berusaha untuk mendapatkan sumber daya yang sama seperti mangsa. Dalam hal ini, interaksi antara pemangsa dan pesaing mengakibatkan persaingan dalam memperebutkan sumber daya sejenis seperti mangsa yang keberadaannya terbatas, sehingga terjadi persaingan interspesifik (antara dua atau lebih spesies) ataupun intraspesifik (antara anggota spesies yang sama). Contoh persaingan antara populasi kambing (pemangsa) dan populasi sapi (pesaing) di padang rumput (mangsa) dan populasi harimau (pemangsa) dengan populasi singa (pesaing) memperebutkan rusa (mangsa). Berkebalikan dengan itu, sumber daya seperti oksigen jarang mengalami kelangkaan, sehingga jarang terjadi persaingan memperebutkan oksigen.
Di lingkungan yang sama, interaksi antara pemangsa dan pesaing yang terlibat secara langsung dalam kompetisi, dapat bersaing untuk mendapatkan mangsa. Jika salah satu dari mereka mampu bersaing dalam mendapatkan mangsa, maka spesies tersebut akan bertahan hidup, sedangkan yang tidak dapat bersaing dalam mendapatkan mangsa, spesies tersebut akan punah (Campbell et al. 2008). Hal ini mengakibatkan interaksi tiga spesies dengan adanya populasi pesaing (competitor) dapat memengaruhi populasi mangsa (prey) dan populasi pemangsa (predator). Dengan demikian interaksi ini dapat diilustrasikan dalam model yang disebut model mangsa pemangsa tiga spesies. Model persamaan untuk menjelaskan interaksi tersebut dibentuk dalam persamaan diferensial taklinear. Sistem persamaan diferensial ini seringkali sulit diselesaikan secara analitik.
Pada karya ilmiah ini, akan digunakan metode homotopi untuk menyelesaikan permasalahan mangsa pemangsa tiga spesies yang didasarkan pada (Paparao et al. 2013). Sebelum menyelesaikan masalah mangsa pemangsa tiga spesies, metode homotopi telah banyak digunakan peneliti untuk menyelesaikan masalah taklinear dalam bidang sains dan teknologi. Diantaranya, (Jaharuddin 2014) menggunakan metode homotopi untuk menyelesaikan masalah infeksi virus pada populasi spesies tunggal di lingkungan yang kotor, serta (Biazar dan Dezhpasand 2011) menggunakan metode homotopi untuk menyelesaikan masalah mangsa pemangsa secara analitik.
2
mangsa pemangsa tiga spesies dengan menggunakan metode homotopi dimisalkan dalam bentuk deret. Hasil-hasil yang diperoleh dengan metode homotopi akan dibandingkan dengan hampiran penyelesaian secara numerik.
Tujuan Karya Ilmiah
Berdasarkan latar belakang di atas, maka tujuan penelitian ini adalah
a. Menggunakan metode homotopi untuk menyelesaikan masalah mangsa pemangsa tiga spesies dan membandingkan penyelesaian metode tersebut dengan hampiran penyelesaian numerik.
b. Menggambarkan grafik hampiran penyelesaian numerik dari model mangsa pemangsa tiga spesies, kemudian memberikan tafsiran terhadap grafik tersebut.
TINJAUAN PUSTAKA
Pada bagian ini akan dibahas teori-teori yang digunakan dalam menyusun karya ilmiah ini. Teori-teori tersebut meliputi kajian model mangsa pemangsa tiga spesies dengan mangsa (prey), pemangsa (predator), dan pesaing (competitor) serta konsep dasar metode homotopi.
Model Persamaan Mangsa Pemangsa Tiga Spesies
Model mangsa pemangsa tiga spesies merupakan model mangsa pemangsa dengan adanya pesaing yang dikelompokkan menjadi tiga populasi di antaranya, populasi mangsa , populasi pemangsa ( , dan populasi pesaing ( . Pada kasus ini, populasi mangsa, pemangsa, dan pesaing merupakan populasi hewan mamalia yang hidup di lingkungan yang sama. Selain itu, diasumsikan populasi pesaing mengalami penurunan yang disebabkan interaksi dengan mangsa.
Berikut model mangsa pemangsa tiga spesies dalam bentuk persamaan diferensial taklinear yang didasarkan pada (Paparao et al. 2013).
(1)
dan
3 dihambat dengan koefisien interaksi antarspesies mangsa ( , koefisien interaksi antara mangsa dan pemangsa ( ), serta koefisien interaksi antara mangsa dan pesaing ( . Di samping itu, banyaknya populasi pemangsa ( ) dipengaruhi oleh laju pertumbuhan pemangsa secara alami dalam ekor per satuan waktu ( ) yang didukung karena adanya koefisien keberhasilan pemangsa dalam memangsa ( ), tetapi dihambat oleh koefisien interaksi antarspesies pemangsa ( ) dan koefisien interaksi antara pemangsa dan pesaing ( ). Selanjutnya, banyaknya populasi pesaing ( ) dipengaruhi pula oleh laju pertumbuhan pesaing secara alami dalam ekor per satuan waktu ( ) yang dihambat dengan koefisien interaksi antara pesaing dan mangsa ( ), koefisien interaksi antara pesaing dan pemangsa ( ), serta koefisien interaksi antarspesies pesaing ( ).
Metode Homotopi
Berikut ini diberikan ilustrasi konsep dasar metode homotopi didasarkan pada (Liao 2004). Misalkan diberikan persamaan diferensial taklinear
[ ] (2) dengan operator taklinear dan fungsi yang akan ditentukan dan bergantung pada .
Misalkan merupakan pendekatan awal dari penyelesaian persamaan (2). Selanjutnya, didefinisikan pula suatu operator linear yang memenuhi
[ ] bila (3) Selanjutnya, fungsi homotopi pada persamaan (4) dibuat menjadi sama dengan nol yaitu:
,
4
sehingga diperoleh penyelesaian metode homotopi sebagai berikut:
∑
5
( )
[ ] [ ], (14)
( )
[ ] [ ], dengan dan merupakan parameter bantu taknol.
Selanjutnya, misalkan fungsi dan adalah penyelesaian Dari persamaan (16), saat diperoleh persamaan sebagai berikut:
[ ] dan [ ] sehingga berdasarkan persamaan (3) diperoleh
dan . (17) Ketika , berdasarkan persamaan (16) diperoleh persamaan berikut:
[ ] dan [ ] , sehingga berdasarkan persamaan (2) diperoleh
dan . (18) Selanjutnya, konsep deret Taylor untuk fungsi dan terhadap parameter yang bernilai dari sampai 1 dapat diuraikan menjadi
∑ saat sehingga diperoleh penyelesaian metode homotopi sebagai berikut:
∑
6
7
, ,…,
sehingga hampiran penyelesaian masalah nilai awal (12) dengan menggunakan metode homotopi adalah
, dan
.
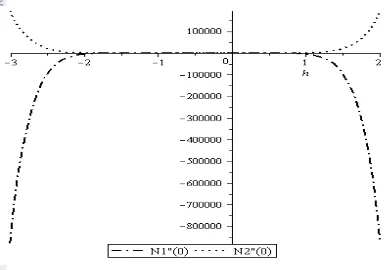
Hampiran penyelesaian dengan metode homotopi dari masalah nilai awal (12) mengandung parameter bantu . Menurut (Jaharuddin 2014) dengan menggunakan kurva , dapat ditentukan selang nilai yang sesuai untuk parameter bantu . Berdasarkan plot dari Gambar 1, dapat ditentukan selang untuk nilai yang sesuai, yakni ketika ruas-ruas garis melintang sejajar di sumbu horizontal. Gambar 1 menggambarkan kurva untuk dan . Dari Gambar 1, jelas bahwa nilai dapat dipilih pada selang sampai 1 untuk mendapatkan suatu penyelasaian dengan selang kekonvergenan yang lebih luas.
Gambar 1 Kurva dari penyelesaian masalah nilai awal (12) dengan metode
homotopi orde ke sepuluh
8
Tabel 1 Galat metode homotopi orde ke sepuluh masalah nilai awal (12)
| | | |
0 0 0 0 0 0 0
0.1 3.87 x 10-6 2.67 x 10-5 3.90 x 10-4 4.35 x 10-6 5.44 x 10-5 2.60 x 10-3
0.2 1.75 x 10-5 7.82 x 10-4 1.10 x 10-2 1.44 x 10-5 3.87 x 10-5 1.21 x 10-2
0.3 6.35 x 10-5 4.40 x 10-3 7.91 x 10-2 5.17 x 10-5 1.34 x 10-3 9.96 x 10-3
0.4 1.71 x 10-4 1.42 x 10-2 2.78 x 10-1 1.57 x 10-4 6.95 x 10-3 5.41 x 10-2
0.5 3.60 x 10-4 3.41 x 10-2 7.05 x 10-1 3.90 x 10-4 2.12 x 10-2 2.64 x 10-1
0.6 6.29 x 10-4 6.81 x 10-2 1.47 x 100 8.22 x 10-4 5.03 x 10-2 7.39 x 10-1
0.7 9.32 x 10-4 1.19 x 10-1 2.67 x 100 1.53 x 10-3 1.01 x 10-1 1.63 x 100
0.8 1.16 x 10-3 1.88 x 10-1 4.41 x 100 2.58 x 10-3 1.83 x 10-1 3.11 x 100
0.9 1.12 x 10-3 2.74 x 10-1 6.74 x 100 4.01 x 10-3 3.03 x 10-1 5.38 x 100
1.0 4.89 x 10-4 3.70 x 10-1 9.67 x 100 5.83 x 10-3 4.70 x 10-1 8.66 x 100
Berdasarkan Tabel 1, rata-rata galat yang dihasilkan oleh saat
sebesar 4.5 x 10-4, 9.76 x 10-2 saat , dan 2.37 x 100 ketika . Di samping itu rata-rata galat yang diperoleh ketika , , dan
berturut-turut adalah 1.4 x 10-3, 1.03 x 10-1, dan 1.80 x 100. Hal ini memperlihatkan bahwa parameter bantu lebih bagus dibandingkan dengan dan , karena hampiran penyelesaian dengan metode homotopi yang dihasilkan mendekati hampiran penyelesaian dengan metode numerik. Dengan menggunakan nilai parameter bantu , penyelesaian dengan metode homotopi pada masalah nilai awal (12) menghampiri penyelesaian numeriknya. Oleh sebab itu, galat yang sangat kecil menunjukkan bahwa metode homotopi dapat menyelesaikan sistem persamaan diferensial dengan nilai awal yang diberikan.
HASIL DAN PEMBAHASAN
Pada bagian ini akan dibahas penggunaan metode homotopi untuk menyelesaikan model mangsa pemangsa tiga spesies. Hasil penyelesaian tersebut akan dibandingkan dengan penyelesaian secara numerik.
Analisis Metode
9
Didefinisikan suatu fungsi homotopi , , dan sebagai berikut:
10 konvergen pada sehingga penyelesaiannya sebagai berikut:
∑
Hasil ini menunjukkan adanya hubungan antara penyelesaian eksak dari masalah nilai awal (1) dan pendekatan awal , , serta ,
, untuk yang akan ditentukan.
Bentuk , , dan ditentukan sebagai berikut. Jika persamaan (25) diturunkan terhadap hingga kali, kemudian dievaluasi pada
dan dibagi , maka diperoleh persamaan orde ke- sebagai berikut:
11
Jika persamaan (22) disubstitusikan ke persamaan (31), maka diperoleh bentuk , , dan sebagai berikut:
Penurunan persamaan (32) diberikan pada lampiran 2, sedangkan fungsi diberikan pada persamaan (11).
Misalkan penyelesaian pendekatan awal , , dan dengan , , dan merupakan suatu konstanta bernilai positif. Jika persamaan (32) disubstitusikan ke persamaan (30) dengan
[ ], [ ], dan [ ] pada persamaan (21), dengan kedua ruas pada persamaan (30) diintegralkan terhadap , serta memilih parameter bantu
, dan fungsi bantu , maka untuk
12
[ ∫
∫ ∫ ∫ ]
(33) [ ∫
∫ ∫ ∫ ]
dan [ ∫
∫ ∫ ∫ ] dengan
∑
∑
dan
∑
untuk setiap 1, 2, dan 3.
Jadi, hampiran penyelesaian masalah nilai awal (1) dengan metode homotopi hingga orde ke lima dinyatakan dalam persamaan sebagai berikut:
,
, dan
.
Aplikasi Metode
13 Tabel 2 Nilai parameter-parameter dari persamaan (1)
Parameter Keterangan Nilai
Laju pertumbuhan mangsa secara alami (ekor per satuan
waktu)
1.00
Laju pertumbuhan pemangsa secara alami (ekor per satuan
waktu)
1.00
Laju pertumbuhan pesaing secara alami (ekor per satuan
waktu)
0.667
Koefisien interaksi antarspesies mangsa 0.02
Koefisien interaksi antara mangsa dengan pemangsa 0.01
Koefisien interaksi antara mangsa dengan pesaing 0.01
Koefisien keberhasilan pemangsa dalam memangsa 0.01
Koefisien interaksi antarspesies pemangsa 0.02
Koefisien interaksi antara pemangsa dengan pesaing 0.01
Koefisien interaksi antara pesaing dengan mangsa 0.01
Koefisien interaksi antara pesaing dengan pemangsa 0.02
Koefisien interaksi antarspesies pesaing 0.02
Banyaknya populasi mangsa, pemangsa, dan pesaing saat yang diperoleh dari (Biazar dan Dezhpasand 2011) berturut-turut adalah 20, 15, dan 10 dalam satuan ratus ekor. Data tersebut dapat ditulis dengan notasi sebagai berikut:
14
Jadi, berdasarkan metode homotopi diperoleh hampiran penyelesaian model mangsa pemangsa tiga spesies sampai orde ke lima sebagai berikut:
,
, dan
.
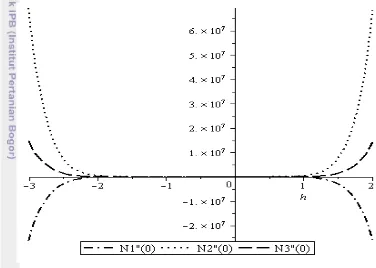
Karena parameter bantu masih terdapat di penyelesaian metode homotopi dari masalah mangsa pemangsa tiga spesies, maka berdasarkan Gambar 2 selang nilai untuk parameter bantu ditentukan dari ruas-ruas garis turunan kedua hampiran penyelesaian metode homotopi orde ke sepuluh untuk ,
, dan saat . Ruas-ruas garis tersebut melintang sejajar di sumbu horizontal. Sehingga, nilai untuk parameter bantu dapat dipilih pada selang sampai 1.
Gambar 2 Kurva dari penyelesaian persamaan (1) dengan metode homotopi orde ke sepuluh
15 Tabel 3 Galat metode homotopi orde ke lima dari persamaan (1)
| | | | | |
0 0 0 0 0 0 0
0.1 6.90 x 10-3 5.20 x 10-3 1.28 x 10-2 2.29 x 10-2 6.25 x 10-4 1.29 x 10-2
0.2 1.33 x 10-2 1.28 x 10-2 2.57 x 10-2 3.80 x 10-2 1.64 x 10-3 4.15 x 10-2
0.3 1.94 x 10-2 1.06 x 10-1 3.70 x 10-2 4.15 x 10-2 2.67 x 10-3 6.64 x 10-2
0.4 2.55 x 10-2 3.26 x 10-1 4.54 x 10-2 3.07 x 10-1 3.23 x 10-3 6.32 x 10-2
0.5 3.16 x 10-2 7.26 x 10-1 4.95 x 10-2 8.54 x 10-1 2.74 x 10-3 3.76 x 10-3
0.6 3.78 x 10-2 1.35 x 100 4.84 x 10-2 1.77 x 10-0 6.08 x 10-4 1.44 x 10-1
0.7 4.41 x 10-2 2.26 x 100 4.23 x 10-2 3.14 x 100 3.73 x 10-3 4.15 x 10-1
0.8 5.03 x 10-2 3.48 x 100 3.22 x 10-2 5.05 x 100 1.07 x 10-2 8.48 x 10-1
0.9 5.57 x 10-2 5.06 x 100 2.10 x 10-2 7.56 x 100 2.07 x 10-2 1.48 x 100
1.0 5.93 x 10-2 7.03 x 100 1.36 x 10-2 10.71 x 100 3.37 x 10-2 2.35 x 100
Berdasarkan Tabel 3, rata-rata galat yang dihasilkan dengan menggunakan metode homotopi untuk populasi mangsa, pemangsa, dan pesaing masing-masing saat sebesar 3.13 X 10-2, 2.98 X 10-2, dan 7.32 X 10-3, serta saat sebesar 1.85 X 100, 2.68 X 100,dan 4.93 X 10-1.
Tabel 3 memperlihatkan bahwa metode homotopi memiliki penyelesaian yang menghampiri penyelesaian numeriknya. Selisih galat yang dihasilkan oleh metode homotopi pada beberapa selang cukup kecil. Galat yang dihasilkan oleh metode homotopi ketika lebih kecil dibandingkan dengan , serta lebih kecil di antara selang nilai lainnya. Hal tersebut dapat dilihat pada lampiran 3. Oleh sebab itu, nilai parameter bantu yang dipilih dalam karya ilmiah ini adalah . Dengan nilai galat yang kecil, hal ini berarti metode homotopi dapat digunakan untuk menyelesaikan masalah mangsa pemangsa tiga spesies.
16
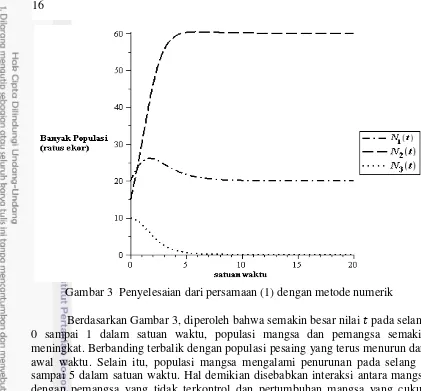
Gambar 3 Penyelesaian dari persamaan (1) dengan metode numerik
Berdasarkan Gambar 3, diperoleh bahwa semakin besar nilai pada selang 0 sampai 1 dalam satuan waktu, populasi mangsa dan pemangsa semakin meningkat. Berbanding terbalik dengan populasi pesaing yang terus menurun dari awal waktu. Selain itu, populasi mangsa mengalami penurunan pada selang 1 sampai 5 dalam satuan waktu. Hal demikian disebabkan interaksi antara mangsa dengan pemangsa yang tidak terkontrol dan pertumbuhan mangsa yang cukup lambat.
17
SIMPULAN
Simpulan
Model mangsa pemangsa tiga spesies dengan adanya pesaing ( ) bagi mangsa ( ) dan pemangsa ( ) merupakan model yang membentuk persamaan diferensial taklinear. Dalam penelitian ini, metode homotopi digunakan untuk menyelesaikan masalah mangsa pemangsa tiga spesies.
Metode homotopi adalah suatu metode pendekatan analitik untuk menyelesaikan masalah linear maupun taklinear. Berdasarkan nilai parameter bantu dan nilai awal yang diberikan, metode homotopi memiliki penyelesaian yang menghampiri penyelesaian numeriknya. Pada fungsi homotopi, parameter bantu ditentukan berdasarkan himpitan grafik turunan kedua dari penyelesaian metode homotopi hingga orde ke sepuluh saat , hal ini bertujuan agar fungsi homotopi menuju suatu titik penyelesaian. Oleh sebab itu, penulis memilih
untuk menyelesaikan permasalahan dalam karya ilmiah ini. Selisih galat yang dihasilkan antara penyelesaian metode homotopi orde ke lima, dan penyelesaian metode numerik saat pada beberapa selang waktu cukup kecil. Berbanding terbalik dengan selisih galat yang dihasilkan antara penyelesaian metode homotopi orde ke lima, dan penyelesaian metode numerik saat yang cukup besar. Berdasarkan penelitian tersebut, penulis memilih nilai parameter bantu untuk mengontrol titik penyelesaian dari masalah mangsa pemangsa tiga spesies.
18
DAFTAR PUSTAKA
Biazar J, Dezhpasand S E. 2011. HAM for Solution of the Prey and Predator Problem. International Journal of Nonlinear Science. 11(1):68-73.
Campbell N A, Reece J B, Urry L A, Cain M L, Wasserman S A, Minorsky P V, Jackson R B. 2008. Biologi. Edisi Kedelapan. Jilid 3. Wulandari D T, penerjemah. Hardani W, Adhika P, editor. Jakarta: Penerbit Erlangga. Terjemahan dari: Biology. Eighth Edition.
Jaharuddin. 2014. A Single Species Population Model in Polluted Environment Solved by Homotopy Analysis Method. Applied Mathematical Sciences. 8(20):951-961.
Liao, S.J. 2004. Beyond Perturbation: Introduction to the Homotopy Analysis Method. Boca Raton, New York.
Paparao A.V, Lakshmi N.K, Shahnaz B. 2013. Computation of Three Species Ecological Model By Homotopy Analysis Method. International Journal of Advanced Research in Computer Science and Software Engineering. 2(6):333-339.
19 Lampiran 1 Penurunan persamaan (10)
Tinjau persamaan deformasi order nol sebagai berikut:
[ ] [ ]
atau
[ ] [ ] [ ]
Selanjutnya, persamaan tersebut diturunkan terhadap hingga kali. Turunan pertama
{ [ ] [ ]} { [ ]}
{ [ ]} { [ ]} { [ ]}
{ [ ]} [ ] { [ ]}
[ ] { [ ]}
[ ] [ ] [ ]
[ ] [ ]
[ ] [ ] [ ]
[ ] [ ]
sehingga diperoleh
[ ] [ ] [ ]
[ ] [ ]
Turunan ke-dua
{ [
] [ ] [
]}
{ [ ]
20
{ [
]} { [ ]} { [
]}
{ [ ]} {
[ ] }
[ ] [ [ ] ] [ [ ] ] [ ]
[ ] [ ] [ ]
sehingga diperoleh
[ ] [ [ ] ] [ ]
[ ] [ ]
Turunan ke-tiga
{ [
] [
[ ]
] [
]}
{
[ ]
} {
[ ] }
[ ] [ ] [ ] [ ]
[ ] [ ] [ ]
sehingga diperoleh
[ ] [ ] [ ]
[ ] [ ]
Dengan langkah yang sama, turunan ke pada saat adalah
[ ] [ ] [ ]
21 Jika kedua ruas dari persamaan di atas dibagi dengan pada saat adalah
[
]| [
]|
[ [ ] ]|
[ ]|
[ ]|
[ [ ] ]|
[ ]|
[ [ ] ]|
atau
[ ] ⃗⃗ dengan
⃗⃗
( ⃗⃗ )
[ ]
|
22
Lampiran 2 Penurunan persamaan (32)
Lihat persamaan (10) yang telah diperluas berikut:
[ ] ( ⃗⃗ ⃗⃗ ⃗⃗ )
[ ] ( ⃗⃗ ⃗⃗ ⃗⃗ )
[ ] ( ⃗⃗ ⃗⃗ ⃗⃗ ) dengan
( ⃗⃗ ⃗⃗ ⃗⃗ )
[ ]
|
( ⃗⃗ ⃗⃗ ⃗⃗ )
[ ]
|
( ⃗⃗ ⃗⃗ ⃗⃗ )
[ ]
|
dan
{
Diberikan operator taklinear sebagai berikut:
[ ] [ ]
[ ] [ ]
[ ] [ ]
Untuk
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[ ]
23 ( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[ ]
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[ ]
Untuk
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
24
Untuk
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
[ ]
( ⃗⃗ ⃗⃗ ⃗⃗ ) [ ]|
[
[ ] ]|
[ ]
25
( ⃗⃗ ⃗⃗ ⃗⃗ )
∑
∑
∑
( ⃗⃗ ⃗⃗ ⃗⃗ )
∑
∑
∑
( ⃗⃗ ⃗⃗ ⃗⃗ )
∑
∑
∑
26
Lampiran 3 Tabel selisih antara penyelesaian metode homotopi dan metode numerik dari masalah mangsa pemangsa tiga spesies
Untuk
| | | | | |
0 0 0 0
0.1 2.088 x 10-2 3.957 x 10-2 1.975 x 10-3
0.2 3.922 x 10-2 8.256 x 10-2 5.727 x 10-3
0.3 5.430 x 10-2 1.276 x 10-1 1.099 x 10-2
0.4 6.556 x 10-2 1.729 x 10-1 1.739 x 10-2
0.5 7.264 x 10-2 2.164 x 10-1 2.437 x 10-2
0.6 7.538 x 10-2 2.558 x 10-1 3.129 x 10-2
0.7 7.383 x 10-2 2.887 x 10-1 3.745 x 10-2
0.8 6.818 x 10-2 3.126 x 10-1 4.208 x 10-2
0.9 5.881 x 10-2 3.258 x 10-1 4.447 x 10-2
1 4.615 x 10-2 3.266 x 10-1 4.397 x 10-2
Rata-rata: 5.227 x 10-2 1.953 x 10-1
2.361 x 10-2
Untuk
| | | | | |
0 0 0 0
0.1 5.779 x 10-4 8.770 x 10-4 8.080 x 10-4
0.2 7.610 x 10-3 6.998 x 10-3 1.294 x 10-3
0.3 2.983 x 10-2 3.905 x 10-2 2.182 x 10-3
0.4 7.586 x 10-2 1.108 x 10-1 1.413 x 10-2
0.5 1.537 x 10-1 2.371 x 10-1 3.977 x 10-2
0.6 2.707 x 10-1 4.301 x 10-1 8.483 x 10-2
0.7 4.327 x 10-1 6.989 x 10-1 1.553 x 10-1
0.8 6.437 x 10-1 1.047 x 10-0 2.574 x 10-1
0.9 9.059 x 10-1 1.474 x 10-0 3.972 x 10-1
1 1.218 x 100 1.971 x 100 5.803 x 10-1
Rata-rata: 3.399 x 10-1 5.470 x 10-1
27
RIWAYAT HIDUP
Penulis dilahirkan di Bekasi pada tanggal 3 Juli 1992 sebagai anak kedua dari tiga bersaudara, anak dari pasangan Effendi Abdul Kohar dan Linda Buchori. Tahun 2007 penulis lulus dari Sekolah Menengah Pertama di SMP Negeri 4 Bekasi. Pada tahun 2010 penulis lulus dari SMA Negeri 4 Bekasi dan pada tahun yang sama penulis lulus masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI).