Analisis model makroskopis dan mikroskopis dari transaksi arbitrase triangular di pasar valuta asing Tunai

TRANSAKSI ARBITRASE

TRIANGULAR

DI PASAR VALUTA ASING TUNAI

SRI MULYATI

G54103021

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

DI PASAR VALUTA ASING TUNAI

SRI MULYATI

G54103021

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

SRI MULYATI. Analysis of Macroscopic and Microscopic Model of Triangular Arbitrage Transaction in the Spot Foreign Exchange Market. Supervised by ENDAR HASAFAH NUGRAHANI and DONNY CITRA LESMANA.

The triangular arbitrage transaction is a financial activity that takes advantage of three exchange rates among three different currencies. A triangular arbitrage opportunity in the spot foreign exchange market is indicated by value of rate product which is larger than one or non-negative value of logarithm rate product.

This paper discusses triangular arbitrage transaction which involves the IDR-JPY rates, the JPY-USD rates and the IDR-USD rates. The triangular arbitrage transaction can be modeled as interaction among three exchange rates. The models are macroscopic and microscopic model. The macroscopic model describes the fluctuation of the data in the real market. In this model, time evolution of the logarithm from each rate and the logarithm rate product depend on independent fluctuation on each rate and interaction function from the logarithm rate product. The microscopic model describes the dynamics of each dealer in the spot foreign exchange market.

SRI MULYATI. Analisis Model Makroskopis dan Mikroskopis dari Transaksi Arbitrase

Triangular di Pasar Valuta Asing Tunai. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan DONNY CITRA LESMANA.

Transaksi arbitrase triangular adalah kegiatan finansial yang mengambil keuntungan dari tiga kurs di antara tiga mata uang yang berbeda. Kesempatan dari transaksi arbitrase triangular di pasar valuta asing tunai ditandai dengan nilai dari hasil kurs yang lebih besar dari satu atau nilai dari logaritma hasil kurs yang tak negatif

Pada tulisan ini dibahas mengenai transaksi arbitrase triangular yang melibatkan kurs IDR/JPY, kurs JPY/USD dan kurs IDR/USD. Transaksi arbitrase triangular yang terjadi dapat dimodelkan dalam suatu model interaksi antara tiga kurs tersebut. Model yang dibahas ada dua macam, yaitu model makroskopis dan model mikroskopis. Model makroskopis menggambarkan fluktuasi dari data di pasar real. Pada model ini, perubahan logaritma dari tiap kurs dan logaritma hasil kurs bergantung pada kebebasan fluktuasi tiap kurs dan fungsi interaksi dari logaritma hasil kurs. Model mikroskopis menggambarkan dinamika dari tiap dealer dalam transaksinya di pasar valuta asing.

TRANSAKSI ARBITRASE

TRIANGULAR

DI PASAR VALUTA ASING TUNAI

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

SRI MULYATI

G54103021

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Nama :

Sri

Mulyati

NRP :

G54103021

Menyetujui:

Pembimbing I,

Dr. Ir. Endar H. Nugrahani, M.S.

NIP. 131842411

Pembimbing II,

Donny Citra Lesmana, M.Fin.Math

NIP. 132311927

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, M.S.

NIP. 131473999

Tiada sanjungan dan pujian yang berhak diucapkan selain hanya kepada Allah SWT, Dzat Yang Maha Segalanya yang telah melimpahkan rahmat dan ridho-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Shalawat dan salam senantiasa tercurahkan kepada teladan kebaikan kita, junjungan Nabi Muhammad SAW, keluarganya, para sahabatnya, dan umat pengikutnya hingga akhir jaman.

Selama proses penulisan karya ilmiah ini, penulis banyak menerima bantuan, baik secara moril maupun materil. Oleh karena itu, pada kesempatan ini penulis ingin mengucapkan terima kasih kepada:

1. Ibu Dr.Ir. Endar H. Nugrahani, M.S. selaku Pembimbing I, yang telah banyak meluangkan waktu, pikiran, masukan dan arahan selama proses pengerjaan karya ilmiah ini.

2. Bapak Donny Citra Lesmana, M.Fin.Math. selaku Pembimbing II, atas bimbingannya selama ini dan saran yang telah diberikan.

3. Bapak Drs. Effendi Syahril, Grad.Dipl., atas kesediaannya menjadi penguji serta saran dan masukkan yang telah diberikan.

4. Kedua orang tua saya, mamah dan bapak, atas dukungan, doa, semangat, dan kasih sayang yang dicurahkan setiap waktu tanpa henti-hentinya.

5. Kakakku, Yani dan kedua adikku Suci dan Dian serta kedua keponakanku Fahri dan Anggi, atas segala doa, dukungan dan semangatnya.

6. Keluarga besar Alm. Bapak Apandi, atas doa dan dukungannya selama ini.

7. Seluruh dosen Departemen Matematika IPB, atas ilmu yang telah diberikan selama masa perkuliahan. Serta kepada seluruh pegawai Departemen Matematika, terima kasih atas bantuan yang telah diberikan.

8. Sahabat-sahabatku, Marlin, Elis, Ulfa, Nchie, Mayang, Ayu, Yuda dan Dwi, atas persahabatan, dukungan, semangat dan doa yang telah kalian berikan selama ini.

9. Tia, Sita dan Eli , atas kesediaannya menjadi pembahas pada saat seminar.

10. Temen-temen Matematika ’40: Vina (atas semangatnya), Septi (atas semangat dan dukungannya), Aam, Lili, Manto, Mayang, Mita, Mufti, Mukafi, Elis, Ica, Yuda, Azis, Prima, Ari, Nchie, Mika, Lili, Abdillah, Yudi, Jayadin, Rusli, Sawa, Berri, Marlin, Rama, Dwi, Indah, Anton, Dimas, Walidah, Ali, Rachmat, Metha, Ulfa, Aci, Herni, Afni, Agatha, Febrian, Tiwi, Yusuf, Nisa, Ifni, Demi, dan Putra. Terima kasih atas persahabatan dan kebersamaan selama ini.

11. Mba-mbaku, mba Nana, mba Sulis dan mba Denok, atas doa dan semangat yang terus-menerus.

12. Sahabat asramaku, A3 lorong 8, 376-378, Srini, Ica, Cici, Ulis, Yuli, Susu, Jowie, mba Arum, Shanti dan Uci, atas persahabatan dan kekeluargaan yang selama ini terjalin.

13. Wisma ayu crew yang tidak bisa disebutkan satu per satu, atas dukungan, semangat, doa, dan kebersamaannya selama ini.

14. Ukhuwah crew yang tidak bisa disebutkan satu per satu, atas dukungan, semangat, doa, dan kebersamaannya.

15. Seluruh Mahasiswa Matematika, kakak kelas dan adik kelas yang telah membantu dan memberikan semangat serta doanya.

16. Serta kepada semua pihak yang telah banyak membantu selama proses penyelesaian tugas akhir ini.

Penulis menyadari masih ada kekurangan dalam karya ilmiah ini. Oleh karena itu, kritik dan saran dari berbagai pihak akan sangat membantu menyempurnakan tulisan ini. Akhir kata, penulis berharap semoga karya ilmiah ini dapat memberikan manfaat bagi kita semua.

Bogor, Oktober 2007

bersaudara. Ayah bernama Pardi dan Ibu bernama Enung Nafisah.

Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1997 di SD Negeri Mustokoredjo Yogyakarta, Sekolah Lanjutan Tingkat Pertama Negeri 2 Ciawi Bogor tahun 2000, Sekolah Menengah Umum Negeri 1 Ciawi Bogor tahun 2003, dan berhasil menjadi mahasiswi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Masuk IPB).

DAFTAR ISI

Halaman

Daftar Isi... ………. vii

Daftar Gambar…...………. viii

Daftar Lampiran ……… viii

I. PENDAHULUAN ... 1

Latar Belakang ... 1

Tujuan... 1

Metode dan Sistematika Penulisan ... 1

II. LANDASAN TEORI ... 2

Definisi Matematis... 2

Definisi Keuangan ... 3

III. PEMBAHASAN ... 8

Model Makroskopis dari Arbitrase Triangular... 8

Keberadaan Kesempatan Arbitrase Triangular... 8

Model Makroskopis ... 10

Persamaan Dasar Waktu Perubahan Logaritma Hasil Kurs ... 10

Penduga Parameter... 11

Model Mikroskopis dari Transaksi Arbitrase Triangular... 12

Model Sato dan Takayasu... 12

Interaksi Dua Sistem dari Model Sato dan Takayasu... 14

Hubungan Kekuatan Interaksi dari Model Makroskopis dan Mikroskopis... 17

IV.SIMPULAN ... 19

V. DAFTAR PUSTAKA ... 20

DAFTAR GAMBAR

Halaman

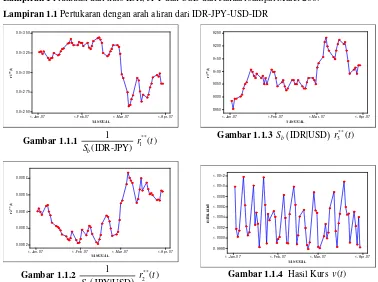
Gambar 1.a Hasil kurs arah transaksi IDR-JPY-USD-IDR ... 9

Gambar 1.b Hasil kurs arah transaksi IDR-USD-JPY-IDR ... 9

Gambar 2.a Logaritma hasil kurs arah transaksi IDR-JPY-USD-IDR ... 10

Gambar 2.b Logaritma hasil kurs arah transaksi IDR-USD-JPY-IDR ... 10

Gambar 3.a Persamaan waktu perubahan dari logaritma hasil kurs IDR-JPY-USD-IDR ... 12

Gambar 3.b Persamaan waktu perubahan dari logaritma hasil kurs IDR-USD-JPY-IDR ... 12

Gambar 4.a Kesempatan arbitrase di pasar X... 15

Gambar 4.b Kesempatan arbitrase di pasar Y ... 15

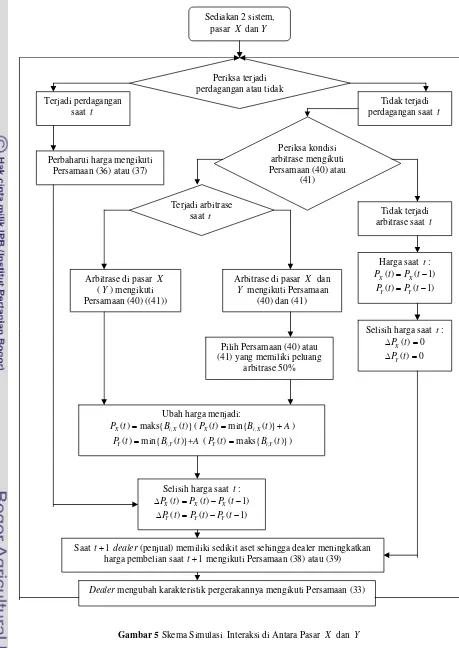
Gambar 5 Skema simulasi interaksi di antara pasar X dan Y ... 18

DAFTAR LAMPIRAN

Halaman Lampiran 1.1 Pertukaran arah aliran IDR-JPY-USD-IDR... 21

Lampiran 1.2 Pertukaran arah aliran IDR-USD-JPY-IDR... 21

Lampiran 2 Aliran kurs dari IDR-USD-JPY-IDR Januari-Maret 2007... 22

Lampiran 2.1 Nilai kurs IDR/JPY Januari-Maret 2007 ... 24

Lampiran 2.2 Nilai kurs JPY/USD Januari-Maret 2007 ... 25

Lampiran 2.3 Nilai kurs IDR/USD Januari-Maret 2007 ... 26

Lampiran 3 Aliran kurs dari IDR-JPY-USD-IDR Januari-Maret 2007... 27

Lampiran 3.1 Nilai kurs IDR/USD Januari-Maret 2007 ... 29

Lampiran 3.2 Nilai kurs USD/JPY Januari-Maret 2007 ... 30

Lampiran 3.3 Nilai kurs JPY/IDR Januari-Maret 2007 ... 31

Lampiran 4.1 Persamaan waktu perubahan logaritma hasil kurs IDR-JPY-USD-IDR... 32

Lampiran 4.2 Persamaan waktu perubahan logaritma hasil kurs IDR-USD-JPY-IDR... 36

Lampiran 5.1 Sebaran dari transaksi arbitrase di pasar X ... 40

I. PENDAHULUAN

1.1 Latar Belakang

Pertukaran valuta asing adalah kegiatan memperdagangkan mata uang dari negara-negara yang berbeda. Istilah valuta asing juga mengacu pada pemilikan mata uang asing di samping jual-beli antar mata uang. Mata uang-mata uang tersebut mengambil bentuk sebagai uang di dalam suatu negara. Uang adalah persediaan aset yang bisa dengan segera digunakan untuk melakukan transaksi. Transaksi antar negara melibatkan berbagai macam mata uang. Uang masing-masing negara memiliki harga yang diukur oleh uang negara-negara lain. Hal inilah yang disebut nilai tukar. Nilai tukar atau kurs adalah satu jenis harga atau nilai uang suatu negara. Jenis lainnya adalah daya beli harga atau nilai uang atas barang dan jasa pada suatu waktu. Jenis ketiga dari harga atau nilai uang adalah biaya penggunaan dan akses terhadapnya untuk periode waktu tertentu. Harga ini adalah tingkat bunga yang dibayarkan peminjam untuk pemakaian uang. Selanjutnya, pengertian nilai tukar yang lebih umum adalah harga mata uang asing (Abdullah. B, 1995). Dalam karya ilmiah ini, lebih lanjut istilah kurs akan dipakai untuk menyatakan nilai tukar.

Transaksi antar pedagang valuta asing umumnya mengacu pada perdagangan antar bank. Perdagangan antarbank tentunya bukan untuk orang-orang kecil atau biasa. Biasanya perdagangan dilakukan oleh pengusaha atau individu yang bergerak dalam bidang ekspor-impor. Kegiatan ekspor-impor sangat berhubungan erat dengan pertukaran valuta asing, sehingga jutaan dollar dapat dipertukarkan dalam setiap menitnya. Hal ini memungkinkan para pedagang mendapatkan keuntungan atau kerugian yang besar dalam waktu singkat.

Dalam karya ilmiah ini, akan dibahas transaksi arbitrase triangular atau arbitrase 3-poin. Transaksi arbitrase triangular adalah kegiatan finansial yang mengambil keuntungan dari tiga nilai tukar asing di antara tiga mata uang yang berbeda. Transaksi ini bisa terjadi karena di pasar valuta asing memungkinkan para pedagangnya untuk mendapat keuntungan yang besar dalam waktu singkat. Keuntungan yang diperoleh dari transaksi ini dinamakan keuntungan

arbitrase karena memanfaatkan selisih harga yang mungkin terjadi.

Transaksi arbitrase triangular terjadi karena fluktuasi kurs di pasar valuta asing. Fluktuasi sangat erat hubungannya dengan proses stokastik sehingga melibatkan model stokastik yang menggambarkan waktu perubahan dari nilai terhadap suatu interaksi.

Model yang akan dibahas dalam karya ilmiah ini adalah model makroskopis dan model mikroskopis. Model makroskopis menggambarkan fluktuasi dari data, sedangkan model mikroskopis menggambarkan dinamika dari pedagang dalam pasar valuta asing.

1.2 Tujuan

Tujuan dari penulisan karya ilmiah ini adalah sebagai berikut:

1. Menunjukkan keberadaan dari kesempatan arbitrase triangular di pasar valuta asing.

2. Mengonstruksi model makroskopis dan mikroskopis bagi transaksi arbitrase triangular di pasar valuta asing.

3. Menentukan hubungan antara kekuatan interaksi dari model makroskopis dengan parameter dari model mikroskopis.

II. LANDASAN TEORI

Dalam bab ini akan dibahas teori-teori yang berkaitan dengan pembahasan selanjutnya. Teori yang terkait ada dua macam, yaitu teori matematis dan teori keuangan. Berikut definisi yang digunakan dalam pembahasan selanjutnya.

2.1 Ruang Contoh, Kejadian dan Peluang

Definisi 2.1.1 (Percobaan Acak)

Suatu percobaan yang dapat diulang dalam kondisi yang sama yang hasilnya tidak dapat diprediksi secara tepat tetapi semua kemungkinan hasil yang muncul dapat diketahui disebut percobaan acak.

[Hogg dan Craig, 1995]

Definisi 2.1.2 (Ruang Contoh dan Kejadian)

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan

Ω

. Suatu kejadian A

adalah himpunan bagian dari

Ω

.

[Grimett dan Stirzaker, 1992]

Definisi 2.1.3 (Medan-σ)

Medan-σ adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian dari

Ω

yang memenuhi kondisi berikut: 1.φ ∈ ℑ,

2. Jika A A1, 2,...∈ ℑ maka 1 t t A ∞ = ∈ ℑ

∪

,

3. Jika A∈ ℑ maka c

A ∈ ℑ.

[Grimett dan Stirzaker, 1992]

Definisi 2.1.4 (Ukuran Peluang)

Misalkan ℑ adalah medan-σ dari ruang contoh

Ω

. Suatu ukuran peluang P pada

(

Ω ℑ,

)

adalah suatu fungsi P:ℑ →

[ ]

0,1 yang memenuhi syarat berikut:

1. P(φ)=0,P(Ω)=1,

2. Jika A A1, 2,...∈ ℑ adalah himpunan yang

saling lepas yaitu A_i∩A_j =φ untuk setiap pasangan i≠ j, maka

∑

∞ = ∞ = = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ 1 1 ) ( i i i

i P A

A

P

∪

Pasangan

(

Ω ℑ, ,P

)

disebut ruang peluang. [Grimett dan Stirzaker, 1992]

2.2 Peubah Acak dan Fungsi Sebaran Definisi 2.2.1 (Peubah Acak)

Misalkan ℑ adalah medan-σ dari ruang contoh

Ω

. Suatu peubah acak (random variable) adalah suatu fungsi X:Ω → dengan sifat bahwa untuk setiap x∈R,

{

ω∈ Ω; ( )X ω ≤x

}

∈ ℑ.

[Grimett dan Stirzaker, 1992]

Definisi 2.2.2 (Fungsi Sebaran)

Misalkan

(

Ω ℑ, ,P

)

adalah ruang peluang. Fungsi sebaran (distribution function) dari suatu peubah acak X adalah fungsi

: [0,1] X

F R→ yang diberikan oleh

( ) ( )

X

F x =P X≤x .

[Grimett dan Stirzaker, 1992]

Definisi 2.2.3 (Peubah Acak Diskret)

Peubah acak X dikatakan diskret jika nilainya hanya berada pada himpunan bagian yang terhitung dari R.

[Grimett dan Stirzaker, 1992]

Definisi 2.2.4 (Fungsi Masa Peluang) Misalkan

(

Ω ℑ, ,P

)

adalah ruang peluang. Fungsi masa peluang (probability mass function) dari suatu peubah acak diskret X

adalah fungsi p:R→[0,1] yang diberikan oleh pX( )x =P X( =x).

[Grimett dan Stirzaker, 1992]

Definisi 2.2.5 (Peubah Acak Kontinu) Peubah acak X dikatakan kontinu jika fungsi sebarannya dapat diekspresikan sebagai

( ) ( ) , x

X x

F x f u du x

−∞

=

∫

∈_R

untuk suatu fungsi f :R→

[

0,∞

)

yang dapat diintegralkan. Fungsi f_X disebut fungsi kerapatan peluang (probability density function) bagi X.

[Grimett dan Stirzaker, 1992]

Definisi 2.2.6 (Sebaran Normal)

Peubah acak X dikatakan menyebar normal dengan nilai harapan μ dan ragam σ2 jika fungsi kerapatan peluangnya adalah:

untuk −∞<x<∞.

[Hogg dan Craig, 1995]

Definisi 2.2.7 (Sebaran Normal Baku) Peubah acak X dikatakan menyebar normal baku jika fungsi sebarannya adalah:

(

)

2

2

( ) ( ) x

t

X

F t P X t t e− dx

−∞

= ≤ = Φ =

∫

atau jika fungsi kerapatan peluangnya adalah:

2 2 2 1 ) ( t e

t = −

Φ

π

[Hogg dan Craig, 1995]

2.3 Proses Stokastik

Definisi 2.3.1 (Ruang State / Keadaan) Misalkan S merupakan himpunan nilai dari barisan peubah acak, maka S disebut ruang

state atau keadaan.

[Grimett dan Stirzaker, 1992]

Definisi 2.3.2 (Proses Stokastik)

Proses stokastik X=

{

Xk:k∈

}

yang terdefinisi pada ruang peluang

(

Ω ℑ, ,P

)

adalah suatu himpunan dari peubah acak yang memetakan ruang contoh

Ω

ke ruang state

S.

[Ross, 1996]

Definisi 2.3.3 (Proses Stokastik Waktu Diskret dan Kontinu)

Suatu proses stokastik X disebut proses stokastik dengan waktu diskret (discrete time stochastic process) jika gugus indeks adalah gugus tercacah (countable set), sedangkan X disebut proses stokastik dengan waktu kontinu (continuous time stochastic process) jika adalah suatu interval.

[Ross, 1996]

Definisi 2.3.4 (Filtrasi)

Misalkan ℑ adalah suatu medan-σ.

{

0, 1,...

}

G= G G merupakan barisan

submedan-σ dari ℑ, G disebut filtrasi jika 1

+

⊆ _k

k G

G untuk semua k∈ .

[Grimett dan Stirzaker, 1992]

Definisi 2.3.5 (Measurable / Terukur) Misalkan X adalah peubah acak yang terdefinisi pada ruang peluang

(

Ω ℑ, ,P

)

. Jika

{

ω∈ Ω; ( )X ω ≤x

}

∈ ℑ, untuk setiap x∈ ,

maka X dikatakan terukur-ℑ.

[Grimett dan Stirzaker, 1992]

Definisi 2.3.6 (Adapted)

Misalkan

(

Ω ℑ, ,P

)

adalah ruang peluang. Barisan peubah acak

{

Xk:k∈

}

dikatakan

adapted terhadap filtrasi ℑ jika Xk

terukur-k

ℑ untuk setiap k.

[Grimett dan Stirzaker, 1992]

Definisi 2.3.7 (Inkremen Bebas)

Suatu proses stokastik dengan waktu kontinu

{

}

X= Xk:k∈ disebut memiliki inkremen bebas (independent increments) jika untuk semua k0<k1<k2< <... kn, peubah acak

1 0, 2 1,..., n n1

k k k k k k

X −X X −X X −X ₋ adalah

bebas (independent).

[Ross, 1996]

Definisi 2.3.8 (Inkremen Stasioner)

Suatu proses stokastik dengan waktu kontinu

{

}

X= Xk:k∈ disebut memiliki inkremen stasioner (stationary increments) jika

k l k

X + −X memiliki sebaran yang sama untuk

semua nilai k.

[Ross, 1996]

Definisi 2.3.9 (Proses Levy)

Misalkan (Xt t)∈ + adalah suatu proses

adapted dengan X0=0 hampir pasti. Jika

t

X :

1. memiliki inkremen bebas; 2. memiliki inkremen stasioner;

3. kontinu dalam peluang sedemikian sehingga P

s s t t

X ⎯⎯⎯_→→X ;

maka Xt adalah suatu proses levy.

[Capasso dan Bakstein, 2004]

Berikut ini teori-teori keuangan yang terkait:

Pasar Valuta Asing

Pasar valuta asing adalah pasar di mana mata uang suatu negara diperjual-belikan menggunakan mata uang negara lain, baik secara langsung maupun tak langsung. Pasar valuta asing merupakan variabel penting makroekonomi karena berdampak nyata pada keadaan ekonomi dan bisnis negara-negara di dunia. Pertukaran di pasar valuta asing diatur oleh pasar OTC (Over-The-Counter). Pertukaran dilakukan oleh berbagai tipe partisipan, seperti arbitragers, hedgers dan

memiliki kepentingan yang berbeda. Selain itu, ada lima kategori partisipan dalam pasar valuta asing, yakni nasabah, bank komersil, institusi keuangan lain, broker dan bank sentral. Sedangkan yang mendominasi perdagangan di pasar valuta asing adalah transaksi pertukaran antar bank.

Berdasarkan waktu penyerahannya pasar valuta asing dibedakan menjadi dua macam yaitu pasar valuta asing tunai (spot foreign exchange market) dan pasar valuta asing dengan penyerahan kemudian (forward exchange market). Pasar valuta asing tunai adalah pasar dengan penyerahan segera sedangkan pasar valuta asing dengan penyerahan kemudian adalah pasar dengan penyerahan 30 hari, 90 hari atau 180 hari kemudian.

[Moosa, 2004]

Exchange Rates (Kurs)

Kurs adalah satu jenis harga atau nilai uang suatu negara. Berdasarkan waktu penyerahannya kurs dibedakan menjadi dua yaitu:

1. Spot Exchange Rates (Kurs Tunai) Kurs tunai merupakan fungsi dari pasar yang menentukan harga komoditas yang diperdagangkan. Kurs tunai adalah nilai yang digunakan untuk melakukan transaksi yang memuat pertukaran dengan segera dari mata uang. Kurs tunai dibedakan menjadi dua, sebagai berikut:

a. Bilateral Spot Exchange Rates (Kurs Tunai Bilateral)

Harga dari satu mata uang terhadap mata uang lain disebut kurs bilateral apabila terdapat dua mata uang terkait dalam transaksinya.

b. Spot Rates Quotations

Spot rates quotations adalah nilai yang digunakan untuk melakukan transaksi pertukaran mata uang yang dinyatakan dalam satu unit mata uang lain (mata uang dasar). Mata uang dasar disebut ‘base currency’

sedangkan mata uang lain yang terkait disebut

‘quoted currency’. Kurs tunai di antara dua mata uang, misalkan x dan y dinyatakan sebagai ( | )S x y artinya sejumlah unit x per unit y, dalam hal ini mata uang y adalah ‘base currency’ dan mata uang x adalah ‘quoted currency’. Nilai dari ( | )S x y yang

meningkat menandakan apresiasi dari y dan depresiasi dari x.

2. Forward Exchange Rates (Kurs Penyerahan Kemudian)

Kurs penyerahan kemudian adalah kurs yang disepakati sekarang untuk penyerahan kemudian.

[Moosa, 2004]

Bid-Ask Rates

Di pasar valuta asing memungkinkan untuk membeli maupun menjual berbagai mata uang untuk mendapatkan keuntungan karena perdagangan bersifat “2 ways quote atau 2 ways rate”, yang berarti bahwa seseorang bisa meraih keuntungan dengan memanfaatkan nilai bid (Sb) ataupun nilai ask (Sa). Selisih di antara nilai bid dan nilai ask dikenal dengan istilah ‘bid-ask spread’ (m=Sa−Sb). Bid-ask spread ditentukan dalam transaksi yang melibatkan penentu harga (dealer) dan penerima harga (customer).

Nilai bid adalah nilai ketika dealer

membeli dan customer menjual. Nilai ini ditentukan oleh interaksi dari kurva permintaan dealer dan kurva penawaran

customer. Sebaliknya, nilai ask ditentukan oleh interaksi dari kurva permintaan customer

dan kurva penawaran dealer. Dalam pasar valuta asing, nilai ask selalu lebih besar dari nilai bid. Secara umum, nilai bid dan ask

untuk dua mata uang, misalkan x dan y

berlaku hubungan berikut: 1 ( | )

( | ) b

a

S y x

S x y

= (1)

dan 1 ( | ) ( | ) a b

S y x

S x y

= . (2)

[Moosa, 2004]

Cross Exchange Rates

Kurs cross adalah kurs di antara dua atau lebih mata uang dengan perantara mata uang lain untuk mendapat kurs baru. Misalkan terdapat tiga mata uang, , , dan x y z, maka berlaku hubungan berikut:

( | ) ( | )

( | )

S x z S x y

S y z

= . (3)

Umumnya z adalah USD atau mata uang domestik karena kurs biasanya dinyatakan dalam USD atau mata uang domestik dengan

Suatu kurs bid-ask cross dapat dihitung dengan asumsi bahwa dua transaksi terjadi. Dengan asumsi tersebut terdapat empat tipe kurs bid-askcross sebagai berikut:

1. Asumsi bahwa customer (B) ingin menukar

x ke dalam y melalui z (cross x→ →z y). Prosedur transaksinya adalah sebagai berikut:

•customer B menjual x ke C dan membeli z dari C pada saat kurs S x za( | )

untuk mendapatkan 1 ( | ) a

S x z unit z. •customer B menjual z ke A dan membeli y dari A pada saat kurs

( | ) b

S y z untuk mendapatkan ( | ) ( | ) b

a

S y z S x z

unit y.

Dari prosedur transaksi di atas dapat

disimpulkan ( | ) ( | ) ( | ) a a

b

S x z S x y

S y z

= menyatakan

kurs cross ask di antara y dan x (kurs pada saat customer B membeli).

Ilustrasi:

A ( | )

y

z

b

S y z

⎯⎯→

←⎯⎯ B ( | )

x

z

a

S x z

⎯⎯→

←⎯⎯ C

2. Asumsi bahwa customer (B) ingin menukar

y ke dalam x melalui z (cross y→ →z x). Prosedur transaksinya adalah sebagai berikut:

• customer B menjual y ke A dan membeli z dari A pada saat kurs

( | ) a

S y z untuk mendapatkan 1 ( | ) a

S y z

unit z.

• customer B menjual z ke C dan membeli x dari C pada saat kurs

( | ) b

S x z untuk mendapatkan ( | ) ( | ) b

a

S x z S y z

unit x.

Dari prosedur transaksi di atas dapat

disimpulkan bahwa ( | ) ( | ) ( | ) b b

a

S x z S x y

S y z =

menyatakan kurs cross bid di antara x dan

y (kurs pada saat customer B menjual). Ilustrasi:

A ( | )

z

y

a

S y z

⎯⎯→

←⎯⎯ B ( | )

z

x

b

S x z

⎯⎯→

←⎯⎯ C

3. Secara langsung dari x→y. Prosedur transaksinya adalah customer B menjual x ke A dan membeli y dari A pada saat S x ya( | )

untuk mendapatkan 1 ( | ) a

S x y unit y.

Ilustrasi:

A ( | )

y

x

a

S x y

⎯⎯→

←⎯⎯ B

4. Secara langsung dari y→x. Prosedur transaksinya adalah customer B menjual y ke A dan membeli x dari A pada saat S x yb( | ) untuk mendapatkan S x yb( | ) unit x. Ilustrasi:

A ( | )

x

y

b

S x y

⎯⎯→

←⎯⎯ B

[Moosa, 2004]

Matriks Kurs Cross

Matriks kurs cross disediakan untuk n

mata uang. Misalkan terdapat n kurs yang dinyatakan dalam quotation tak langsung yang terkait dengan mata uang dasar z, dapat ditulis sebagai S x( 1| ), (z S x2| ),..., (z S xn| )z . Secara umum kurs cross S x( i|xj) mempunyai rumusan sebagai berikut:

( | ) ( | ) ( | ) i i j j

S x z S x x

S x z

= (4)

dan ( | ) ( | ) ( | ) j j i i

S x z S x x

S x z

= . (5)

[Moosa, 2004]

Arbitrase dalam Pasar Tunai Valuta Asing Arbitrase umumnya didefinisikan sebagai pencarian keuntungan dari perbedaan harga sebagai suatu hasil pelanggaran kondisi keseimbangan (no-arbitrage). Proses arbitrase memperbaharui keseimbangan melalui perubahan dalam penawaran dan permintaan komoditas, aset atau mata uang. Dalam pasar valuta asing, arbitrase adalah membeli dan menjual mata uang dengan segera untuk tujuan pencarian keuntungan. Dalam pasar valuta asing tunai terdapat berbagai tipe arbitrase sebagai berikut:

1. Arbitrase 2-poin

yang berbeda dalam dua pasar finansial pada waktu yang bersamaan. Misalkan terdapat dua pasar finansial A dan B, dua mata uang x dan

y dan diasumsikan tidak ada ongkos transaksi serta no-bid-ask spread (tidak ada selisih nilai bid dan ask) maka arbitrase akan terjadi apabila kondisi berikut dilanggar

( | ) ( | )

A B

S x y =S x y . (6) Kondisi di atas menyatakan bahwa kurs di

antara x dan y akan sama baik di A maupun di B. Jika kondisi tersebut tidak terpenuhi (dilanggar) dalam arti bahwa kurs di antara x

dan y berbeda di A untuk nilai tertentu di B, maka satu dari dua mata uang tersebut nilainya akan lebih tinggi di salah satu pasar finansial dan nilainya akan lebih rendah di pasar finansial yang lain. Dalam kasus ini,

dealer akan membeli mata uang di pasar yang nilainya lebih rendah kemudian menjualnya di pasar yang nilainya lebih tinggi. Hal tersebut berdampak pada kenaikan harga di salah satu pasar dan penurunan harga di pasar lain sampai terjadi keseimbangan baru.

2. Arbitrase 3-poin

Arbitrase 3-poin disebut juga dengan arbitrase triangular. Misalkan terdapat tiga mata uang , , dan x y z, dengan asumsi yang sama seperti asumsi yang dipakai dalam arbitrase 2-poin maka arbitrase 3-poin akan terjadi apabila kondisi berikut dilanggar

( | ) ( | )

( | )

S x z S x y

S y z

= . (7)

Dalam kasus ini, tiga mata uang dipersilangkan dalam pasar finansial yang menutup kemungkinan arbitrase 2-poin. Kondisi ini disebut kurs cross yang konsisten dalam arti bahwa jika kita menghitung satu dari tiga mata uang dengan dasar dua mata uang lain maka nilai perhitungan akan identik dengan nilai dari quoted aktualnya. Adapun prosedur dari arbitrase 3-poin adalah sebagai berikut:

1. cek ada tidaknya kondisi yang dilanggar, yang berarti ada tidaknya nilai cross yang konsisten

2. tentukan barisan yang menghasilkan keuntungan.

Misalkan ambil asumsi bahwa kondisi

no-arbitrage dilanggar sedemikian sehingga ( | )

( | )

( | )

S x z S x y

S y z

> , maka selanjutnya dapat

ditentukan barisan yang menguntungkan. Terdapat dua barisan yaitu:

1. x→ → →y z x

ilustrasi:

x

z y

Misalkan dimulai dari 1 unit mata uang x

dengan pergerakan searah jarum jam, maka prosedur transaksinya adalah sebagai berikut:

• menjual x dan membeli y untuk

mendapatkan 1 ( | )

S x y unit y,

• menjual y dan membeli z untuk

mendapatkan 1 ( | ) ( | )

S x y S y z unit z, • menjual z dan membeli x untuk

mendapatkan ( | ) ( | ) ( | )

S x z

S x y S y z unit x.

Kemudian cek nilai berikut:

1 tidak menguntungkan ( | )

1 menguntungkan . ( | ) ( | )

S x z S x y S y z

< ⎧ ⎨> ⎩

2. x→ → →z y x

ilustrasi:

x

z y

Misalkan dimulai dari 1 unit mata uang x

dengan pergerakan berlawanan jarum jam, maka prosedur transaksinya adalah sebagai berikut:

• menjual x dan membeli z untuk

mendapatkan 1 ( | )

S x z unit z,

• menjual z dan membeli y untuk

mendapatkan ( | ) ( | )

S y z

S x z unit y,

• menjual y dan membeli x untuk

mendapatkan ( | ) ( | ) ( | )

S y z S x y

S x z unit x.

Kemudian cek nilai berikut:

1 tidak menguntungkan ( | ) ( | )

1 menguntungkan . ( | )

S y z S x y S x z

< ⎧ ⎨> ⎩

Kemungkinan untuk arbitrase 3-poin dapat diringkas sehingga mengikuti hubungan sebagai berikut:

¾Jika ( | ) ( | ) ( | )

S x z S x y

S y z

= maka pasar

¾Jika ( | ) ( | ) 1 ( | )

S y z S x y

S x z > atau

( | ) ( | )

( | )

S x z S x y

S y z

> maka ada

kesempatan terjadi arbitrase yang mengikuti barisan x→ → →z y x.

¾Jika ( | ) 1

( | ) ( | )

S x z

S x y S y z > atau

( | ) ( | )

( | )

S x z S x y

S y z

< maka ada

kesempatan terjadi arbitrase yang mengikuti barisan x→ → →y z x.

3. Arbitrase n-poin

Arbitrase n-poin adalah arbitrase yang terdiri atas n mata uang dengan n=2, 3,..., tetapi arbitrase 3-poin sudah cukup untuk menetapkan kekonsistenan kurs yang menghapuskan kemungkinan dari arbitrase n

-poin. Dalam kasus arbitrase 3-poin yang memuat tiga mata uang, misalkan , , dan x y z

maka kondisi no-arbitrage dapat ditulis sebagai:

( | ) ( | ) ( | ) 1

S x y S y z S z x = . (7) Jika terdapat empat mata uang, misalkan

1, 2, 3 dan 4

x x x x , maka kita memiliki arbitrase 4-poin, dalam kasus ini no-arbitrage

terpenuhi jika:

1 2 2 3 3 4 4 1

( | ) ( | ) ( | ) ( | ) 1

S x x S x x S x x S x x = . (8) Ketika terdapat n mata uang, kondisi no-arbitrage terpenuhi jika:

1 2 2 3 1 1

( | ) ( | )... ( n | n) ( n| ) 1

S x x S x x S x− x S x x = . (9)

III. PEMBAHASAN

3.1 Model Makroskopis dari Arbitrase

Triangular

Model makroskopis menggunakan data aktual kurs yang diambil dari www.oanda.com

untuk tiga mata uang, yaitu IDR, JPY dan USD, dalam kurun waktu dari Januari sampai Maret 2007 kecuali hari libur. Data-data tersebut akan dianalisis untuk mengetahui apakah dari tiga mata uang tersebut memungkinkan terjadinya kesempatan arbitrase triangular atau arbitrase 3-poin. Lampiran 1 menunjukkan fluktuasi dari masing-masing kurs.

3.1.1 Keberadaan Kesempatan Arbitrase

Triangular

Arbitrase triangular adalah kegiatan finansial yang ingin mengambil keuntungan dari tiga kurs di pasar dunia. Prosedur transaksinya adalah sebagai berikut: pedagang menukar 1 unit mata uang pertama (misalkan

x) untuk sejumlah mata uang kedua (misalkan y), menukar sejumlah mata uang kedua ( )y untuk sejumlah mata uang ketiga (misalkan z), dan menukarkan kembali sejumlah mata uang ketiga ( )z dengan mata uang pertama ( )x pada saat t, dengan z

merupakan ‘base currency’ atau mata uang dasar yang menjadi patokan dalam pertukaran. Umumnya USD merupakan ‘base currency’ dalam pertukaran mata uang. Jika pedagang dapat memperoleh keuntungan melalui transaksi tiga kurs maka dalam pasar tersebut terjadi kesempatan arbitrase triangular. Kesempatan arbitrase triangular terjadi dalam waktu yang singkat dan akan segera hilang dikarenakan banyak pedagang lain yang ingin membuat transaksi yang sama. Untuk memenuhi syarat kesempatan arbitrase

triangular didefinisikan syarat berikut:

3

1

( ) i( ) 1 i

t r t

=

=

∏

>

μ (10)

dengan ( )r ti menyatakan kurs transaksi ke-i pada saat t.

Syarat di atas dinamakan sebagai hasil kurs. Jika hasil kurs μ lebih besar dari unit awal mata uang pertama yang digunakan maka pedagang memperoleh keuntungan dan hal ini menandakan terjadinya kesempatan arbitrase triangular di pasar valuta asing. Arbitrase triangular melibatkan tiga kurs mata uang dengan salah satu dari mata

uang tersebut merupakan ‘base currency’ maka pertukarannya memiliki dua kemungkinan aliran kurs, yang salah satunya akan lebih menguntungkan (akibat adanya kesempatan arbitrase). Arah aliran kurs yang pertama berdasarkan transaksi dengan arah

x→ → →y z x dan yang kedua berdasarkan

transaksi yang mempunyai arah

x→ → →z y x.

Untuk transaksi dengan arah

x→ → →y z x, maka tiap kurs dapat

didefinisikan sebagai berikut:

1 2 3 ( ) ( | ) 1 ( ) ( | ) 1

( ) . (11) ( | )

a

b

a

r t S y x

r t

S y z

r t

S z x =

=

=

Sedangkan untuk transaksi dengan arah

x→ → →z y x, maka tiap kurs didefinisikan

sebagai berikut: 1 2 3 1 ( ) ( | ) 1 ( ) ( | )

( ) ( | ). (12) a

a

b

r t

S x z

r t

S z y

r t S x y

=

=

=

Diasumsikan bahwa seorang arbitran dapat bertransaksi dengan segera pada harga bid dan

ask. Oleh karenanya digunakan harga pada waktu yang sama untuk menghitung hasil kurs.

Berdasarkan hubungan antara nilai bid dan

ask pada Persamaan (1) dan (2) maka hasil kurs μ dapat memiliki dua bentuk lain, didefinisikan sebagai berikut:

3

* *

1

( ) i ( ). i

t r t

μ

=

=

∏

(13)

Transaksi dengan arah x→ → →y z x

memiliki nilai *

( ) i

r t sebagai berikut:

* 1 * 2 * 3 1 ( ) ( | ) ( ) ( | )

( ) ( | ) , (14) b

a

b

r t

S x y

r t S z y

r t S x z

=

= =

dan transaksi dengan arah x→ → →z y x

memiliki nilai *

( ) i

* 1 * 2 * 3 ( ) ( | ) ( ) ( | ) 1

( ) . (15) ( | )

b

b

a

r t S z x

r t S y z

r t

S y x = =

=

Transaksi arbitrase μ* memiliki transaksi pertukaran yang berlawanan dengan transaksi arbitrase μ. Maksud berlawanan di sini adalah berbeda dalam pemakaian kurs bid

atau ask.

Bentuk keduanya adalah:

3

** **

1

( ) i ( ) i

t r t

μ

=

=

∏

. (16)

Untuk bentuk kedua, transaksi dengan arah

x→ → →y z x memiliki nilai **

( ) i

r t sebagai berikut: ** 1 ** 2 ** 3 1 ( ) ( | ) 1 ( ) ( | )

( ) ( | ) , (17) b

b

b

r t

S x y

r t

S y z

r t S x z

=

=

=

dan transaksi dengan arah x→ → →z y x

memiliki nilai ri**( )t sebagai berikut:

** 1 ** 2 ** 3 ( ) ( | ) ( ) ( | ) 1

( ) . (18) ( | )

b

b

b

r t S z x

r t S y z

r t

S y x = =

=

Transaksi arbitrase μ**

yang didefinisikan di atas mengambil asumsi bahwa akan lebih menguntungkan jika menggunakan nilai bid

untuk transaksi terakhir karena di awal telah dinyatakan bahwa nilai bid selalu lebih kecil dari pada nilai ask.

Sama halnya dengan transaksi μ dan μ*

,

**

1

μ > unit mata uang pertama yang

dipertukarkan menunjukkan adanya kesempatan arbitrase. Kesempatan itu akan segera hilang karena banyak transaksi lain yang sama sehingga membuat μ**

konvergen ke nilai rata-rata atau keseimbangannya.

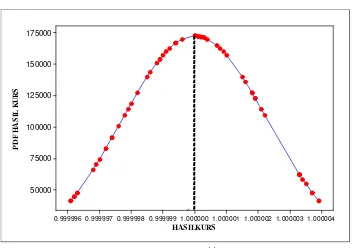
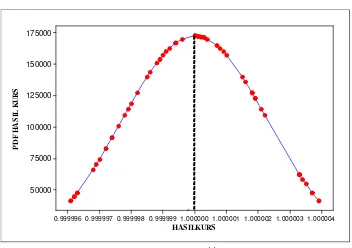
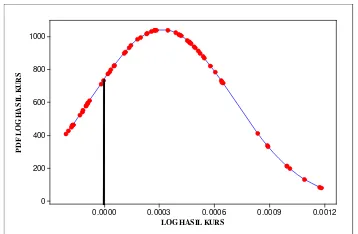
Hasil kurs μ* diasumsikan menyebar normal sehingga diperoleh fungsi kepekatan peluang dari hasil kurs. Hubungan antara hasil kurs dan fungsi kepekatan peluangnya dapat dilihat dalam Gambar 1, dengan daerah di bawah kurva yang lebih besar dari 1 menyatakan terjadinya kesempatan arbitrase.

HASILKURS PD F H A S IL K U R S 1.0012 1.0010 1.0008 1.0006 1.0004 1.0002 1.0000 0.9998 1000 800 600 400 200 0

Gambar 1.a Hasil Kurs **

( )t

μ arah transaksi IDR→JPY→USD→IDR dengan mean 1.000313 dan standar deviasi 0.000382.

HASILKURS PD F H A S IL K U R S 1. 000004 1. 000003 1. 000002 1. 000001 1. 000000 0. 999999 0. 999998 0. 999997 0. 999996 175000 150000 125000 100000 75000 50000

Gambar 1.b Hasil Kurs μ**( )t arah transaksi IDR→USD→JPY→IDR dengan mean 0.9999999 dan standar deviasi 0.0000023.

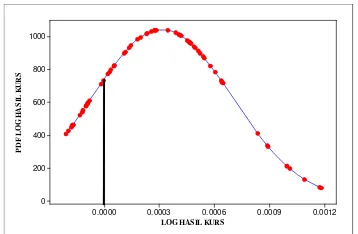
Didefinisikan logaritma hasil kurs ( )v t

sebagai berikut:

3 3

** **

1 1

( ) ln i ( ) ln i ( ) i

i

v t r t r t

= =

=

∏

=

∑

(19)

dengan **

( ) i

r t menyatakan bentuk kedua dari kurs transaksi ke-i pada saat t.Keberadaan dari kesempatan arbitrase triangular dipenuhi apabila logaritma hasil kurs yang didefinisikan di atas memiliki nilai yang tak negatif.

LOG HASIL KURS PD F L OG H A S IL K U R S 0.0012 0.0009 0.0006 0.0003 0.0000 1000 800 600 400 200 0

Gambar 2.a Logaritma Hasil Kurs arah transaksi IDR→JPY→USD→IDR dengan mean 0.000313 dan standar deviasi 0.000382.

LOG HASIL KURS

P D F LO G H A S IL K U R S 0.00 0004 0.00 0003 0.00 0002 0.00 0001 0.00 0000 -0.0 0000 1 -0.0 0000 2 -0.0 0000 3 -0.0 0000 4 175000 150000 125000 100000 75000 50000

Gambar 2.b Logaritma Hasil Kurs arah transaksi IDR→USD→JPY→IDR dengan mean -0.0000001 dan standar deviasi 0.0000023.

Dalam karya ilmiah ini perhitungan untuk hasil kurs dan logaritma hasil kurs yang dipakai adalah bentuk kedua karena dalam tulisan ini lebih memfokuskan pada harga pembelian dealer dari tiap transaksi. Lampiran 2 dan Lampiran 3 menyajikan perhitungan hasil kurs dan logaritma hasil kurs.

3.1.2 Model Makroskopis

Adanya kesempatan arbitrase triangular

dalam pasar mempengaruhi fluktuasi harga. Fluktuasi yang terjadi dapat dikonstruksi dengan suatu model waktu perubahan kurs asing. Model ini menggunakan data untuk menjelaskan fluktuasi yang terjadi secara kuantitatif, bukan sekedar kualitatif. Model ini disebut dengan model makroskopis.

3.1.2.1 Persamaan Dasar Waktu Perubahan Logaritma Hasil Kurs

Didefinisikan persamaan dasar waktu perubahan logaritma dari tiap kurs sebagai berikut:

(

)

** **

lnri (t+ Δ =t) lnri ( )t +f ti( )+g v t( ) (20)

dengan

t

Δ : perubahan waktu yang mengontrol skala waktu dari model; Δ =t 1 karena data yang dipakai adalah data harian, i

f : kebebasan fluktuasi dari transaksi ke-i

yang memenuhi sebaran levy terpotong (truncated levy distribution),

g : fungsi interaksi dari logaritma hasil kurs.

Transaksi arbitrase triangular membuat logaritma hasil kurs v menuju ke rata-rata ε sehingga dapat didefinisikan fungsi interaksi sebagai aproksimasi linear sebagai berikut:

(

)

( )

g v = −k v−ε (21) sehingga 0 jika ( ) 0 jika v g v v ε ε < > ⎧ ⎨> < ⎩ dengan

k : konstanta positif yang menentukan kekuatan interaksi dari logaritma hasil kurs per satuan waktu,

ε : rata-rata dari v.

Persamaan waktu perubahan logaritma dari tiap kurs yang diberikan oleh Persamaan (20) dapat digunakan untuk membentuk persamaan waktu perubahan logaritma hasil kurs, yaitu dengan menjumlahkan Persamaan (20) dan menyubstitusi Persamaan (21) sehingga didapat rumusan sebagai berikut:

(

)

( ) (1 3 ) ( ) ( )

v t+ Δ − = −t ε k v t −ε +F t (22)

dengan

3

1

( ) i( ) i

F t f t

=

=

∑

.

Bukti:

Untuk mendapatkan persamaan dasar waktu perubahan logaritma hasil kurs, dapat diperoleh dengan menjumlahkan persamaan waktu perubahan logaritma dari tiap kurs saat transaksi ke-i sebagai berikut:

3 ** 1

( ) ln i ( )

i

v t t r t t

=

+ Δ =

∑

+ Δ

** ** **

1 2 3

lnr (t t) lnr (t t) lnr (t t)

= + Δ + + Δ + + Δ

(

)

**

1 1

= ln⎡_⎣ r ( )t +f t( )+g v t( ) ⎤_⎦

(

)

**

2 2

+ ln⎡_⎣ r ( )t +f t( )+g v t( ) ⎤_⎦

(

)

**

3 3

+ ln⎡_⎣ r ( )t +f t( )+g v t( ) ⎤_⎦

(

)

3 3

**

1 1

= ln i ( ) i( ) 3 ( )

i i

r t f t g v t

= =

+ +

∑

∑

(

)

(

)

= ( )v t +F t( ) 3+ −k v t( )−ε = ( ) 3 ( ) 3v t − kv t + kε+F t( )

(

)(

)

sehingga terbukti bahwa:

(

)(

)

( ) 1 3 ( ) ( )

v t+ Δ − = −t ε k v t −ε +F t

3.1.2.2 Penduga Parameter

Persamaan (20) bergantung pada parameter fi dan k. Dalam bagian ini akan diduga besarnya masing-masing parameter tersebut. Penduga parameter untuk kekuatan interaksi k berhubungan dengan v, yang dinyatakan sebagai berikut:

(

) ( )

( )

2

2 2

1 3 : ( )

.

k c t

v t t v t

v t − = Δ + Δ − = − ε ε (23)

Dengan menggunakan persamaan di atas, dapat diduga (k Δt) dari data berkala sebagai fungsi dari perubahan waktu Δt, yaitu sebagai berikut:

(

) ( )

( )

2 2 2 1

( ) 1

3

v t t v t k t v t ⎛ _{+ Δ −} ⎞ ⎜ ⎟ Δ = _⎜ − _⎟ ⎜ − ⎟ ⎝ ⎠ ε

ε (24)

dengan

( )

v t+ Δt diperoleh dari data real berkala dengan Δt adalah 1 hari karena data yang digunakan dalam karya ilmiah ini adalah data harian dari kurs.

Dari perhitungan dengan menggunakan Persamaan (24) maka nilai (k Δt) diperoleh yaitu sebesar 0.29 untuk transaksi pertukaran dengan arah IDR→JPY→USD→IDR dan sebesar 0.41 untuk transaksi pertukaran dengan arah IDR→USD→JPY→IDR. Apabila nilai dari selisih logaritma hasil kurs dengan rata-rata logaritma hasil kurs adalah positif maka fungsi interaksi dari logaritma hasil kurs untuk (1)k =0.29 akan lebih kuat dibandingkan dengan (1)k =0.41. Sebaliknya, jika nilai dari selisih logaritma hasil kurs dengan rata-rata logaritma hasil kurs adalah negatif maka fungsi interaksi dari logaritma hasil kurs untuk (1)k =0.29 akan lebih lemah dibandingkan dengan (1)k =0.41.

Kebebasan fluktuasi dari transaksi ke-i

(fi

)

memenuhi sebaran levy terpotong (truncated levy distribution). Sebaran levy

terpotong diperoleh dari suatu sebaran levy

yang menggambarkan distribusi data keuangan yang selalu memiliki variansi yang berhingga (Situngkir & Surya, 2003d). Adapun fungsi karakteristik dari sebaran levy

stabiladalah sebagai berikut:

exp | | 1 ( ) tan ; (0, 2] /{1}

2 ( ) ( ; , , , ) [ ]

2

exp | | 1 ( ) ln | | ; 1 (25)

itX L L

t i sign t i t

t P t E e

t i sign t t i t

⎧ ⎧₋ ⎛ ₋ ⎛ ⎞⎞₊ ⎫ _∈ ⎪ ⎨ ⎜ ⎜_⎝ ⎟_⎠⎟ ⎬ ⎪ ⎩ ⎝ ⎠ ⎭ = = = ⎨ ⎧ ⎛ ⎞ ⎫ ⎪ _{⎨− − + ⎬ =} ⎜ ⎟ ⎪ _{⎩ ⎝ ⎠ ⎭} ⎩ α α πα γ β δ α ϕ α β γ δ γ β δ α π dengan i

β : parameter skewness yang menggambarkan keasimetrikan suatu

sebaran dari transaksi ke-i; β ∈ −

[

1,1

]

dan β =0 menyatakan sebaran simetrik,

α : indeks kestabilan/indeks ekor/tail

eksponen /karakteristik eksponen yang menyatakan nilai di saat ekor dari sebaran meruncing; α ∈

(

0, 2

]

, asumsikan 0.5α = untuk suatu fungsi karakteristik levy (Nolan, 2005),

γ : parameter skala yang menyatakan panjang atau lebar suatu sebaran; γ>0 dan asumsikan 1γ = ,

δ : parameter lokasi yang menyatakan perubahan posisi dari suatu sebaran; asumsikan 0δ = ,

t : parameter yang menyatakan nilai kurs saat transaksi ke-i,

( )

sign t : menyatakan nilai signifikan, dinyatakan sebagai:

( )

1 jika t0 jika t 00 1 jika t 0.

sign t > ⎧ ⎪ =⎨ = ⎪− < ⎩

keseimbangannya sehingga dari suatu sebaran

levy stabil dihasilkan suatu sebaran levy

terpotong (truncated levy distribution). Didefinisikan fungsi karakteristik dari sebaran

levy terpotong dengan l menyatakan

koefisien truncation atau koefisien pemotongan, besarnya mendekati nol karena diharapkan pemotongan dari suatu sebaran

levy sekecil mungkin mendekati sebaran levy

stabil sebagai berikut:

(

)

(

2 2

)

₂

; , , , ( ) exp cos arctan (26)

cos 2

T T

t

P t l t t l l

l ⎧ ⎫ ⎪ ⎛ ⎛ ⎛ ⎞⎞ ⎞⎪ ⎪ ⎪ = = ⎨− _{⎛ ⎞⎜}⎜ + ⎜_⎜ ⎜ ⎟⎟_⎟− ⎟_⎟⎬ ⎝ ⎠ ⎪ _{⎜ ⎟}⎝ ⎝ ⎠ ⎠⎪ ⎪ ⎝ ⎠ ⎪ ⎩ ⎭ α α α γ α γ δ ϕ α πα

Lampiran 4 menyajikan perhitungan k dan

i

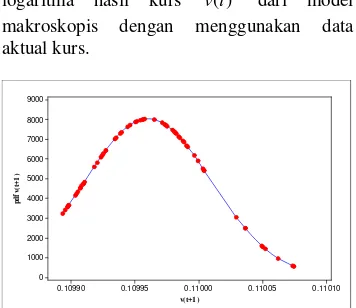
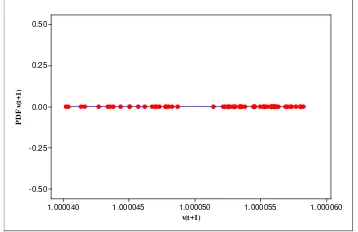
f yang didekati oleh ϕT( )t . Gambar berikut menyatakan persamaan waktu perubahan logaritma hasil kurs ( )v t dari model makroskopis dengan menggunakan data aktual kurs. v(t+1) p d f v (t+ 1 ) 0.11010 0.11005 0.11000 0.10995 0.10990 9000 8000 7000 6000 5000 4000 3000 2000 1000 0

Gambar 3.a Persamaan Waktu Perubahan dari Logaritma Hasil kurs untuk transaksi IDR→JPY→USD→IDR dengan mean

0.10996 dan standar deviasi 0.0000496.

v(t+1) P D F v (t+ 1 ) 1.000060 1.000055 1.000050 1.000045 1.000040 0.50 0.25 0.00 -0.25 -0.50

Gambar 3.b Persamaan Waktu Perubahan dari Logaritma Hasil kurs untuk transaksi IDR→USD→JPY→IDR dengan mean

1.0001 dan standar deviasi 0.00000521.

3.2 Model Mikroskopis dari Arbitrase

Triangular

Dalam karya ilmiah ini akan dibahas lebih lanjut model mikroskopis dari transaksi

arbitrase triangular. Model mikroskopis adalah model yang menggambarkan interaksi di antara dealer dan lebih memfokuskan pada dinamika dari tiap dealer dalam pasar valuta asing. Untuk itu diperkenalkan model Sato

dan Takayasu.

3.2.1 Model Sato dan Takayasu

Asumsi dasar dari model Sato dan

Takayasu adalah dealer ingin membeli mata uang saat harga rendah kemudian menjualnya kembali dengan harga tinggi pada waktu t di pasar valuta asing. Jika dealer membeli mata uang saat harga rendah maka dealer

menetapkan batas harga maksimum pembelian yang dapat dijangkau olehnya. Hal ini berarti bahwa dealer akan membeli mata uang di bawah harga maksimum yang ditetapkannya. Sebaliknya, jika dealer

menjual mata uang saat harga tinggi maka

dealer menetapkan batas harga minimum penjualan yang dapat dia berikan. Hal ini berarti bahwa dealer berusaha untuk menjual mata uang di atas harga minimum yang ditetapkannya. Asumsi di atas menginginkan adanya kesempatan arbitrase dalam transaksi yang terjadi.

Persamaan model ini dengan model makroskopis adalah menginginkan adanya kesempatan arbitrase dalam transaksi perdagangan. Dalam model makroskopis kesempatan arbitrase triangular dipenuhi apabila logaritma hasil kurs tak negatif. Adapun kesempatan arbitrase dalam model

Sato dan Takayasu dipenuhi apabila harga penjualan saat t lebih besar dari harga pembelian saat t.

Dalam model Sato dan Takayasu

didefinisikan komponen-komponen dalam pasar sebagai berikut:

( ) i

B t : harga penawaran dealer pada transaksi ke-i untuk membeli pada waktu t

(nilai bid), ( )

i

S t : harga penawaran dealer pada transaksi ke-i untuk menjual pada waktu t (nilai

ask), ( ) ( )

i i

A=S t −B t : selisih harga jual dan harga beli dealer pada transaksi ke-i saat t. Dalam model ini, jual-beli mata uang dalam model Sato dan Takayasu dilihat dari sudut pandang dealer, sehingga asumsi di atas dapat diperluas yaitu dealer bertujuan untuk minimisasi harga pembeliannya (atau harga penjualan customer). Maksud minimisasi di sini adalah penentuan batas harga maksimum pembelian yang akan menjadi patokan dealer

untuk membeli di bawah harga maksimum yang telah ditetapkan. Di sisi lain bertujuan untuk maksimisasi harga penjualannya (atau harga pembelian customer). Maksud maksimisasi di sini adalah penentuan batas harga minimum penjualan yang akan menjadi patokan dealer untuk menjual di atas harga minimum yang telah ditetapkan. Hal tersebut menyebabkan selisih harga jual dan harga beli

dealer diharapkan positif

(

A=S ti( )−B ti( )>0

)

.

Dengan asumsi di atas, dapat didefinisikan mekanisme pembentukan harga di pasar yang didasarkan pada harga maksimum pembelian dan harga minimum penjualan dealer. Kondisi untuk terjadinya perdagangan diberikan oleh pertidaksamaan berikut:

L t( )=maks

{

B ti( )

}

−min

{

S ti( )

}

≥0 (27) atau

{

}

{

}

( ) maks i( ) min i( )

v t = B t − B t ≥A (28) dengan

{

}

maks B ti( ) : harga pembelian maksimum

dealer saat transaksike-i pada waktu t,

{

}

min S ti( ) : harga penjualan minimum dari

dealer saat transaksi ke-i pada waktu t,

{

}

min B ti( ) : harga pembelian minimum dari

dealer saat transaksi ke-i pada waktu t.

Dalam model makroskopis, transaksi dengan arah x→ → →y z x memiliki

{

}

maks B ti( ) yang sesuai dengan

** 3 ( ) r t

sedangkan min

{

S ti( )

}

sesuai dengan

** 1 ( ) r t . Dalam transaksi tersebut memungkinkan untuk terjadi arbitrase di dalam pasar. Misalkan transaksi dengan arah

x→ → →y z x terjadi di pasar X.

Dalam model makroskopis, transaksi dengan arah x→ → →z y x memiliki

{

}

maks B ti( ) yang sesuai dengan

** 3 ( ) r t

sedangkan min

{

S ti( )

}

sesuai dengan

** 1 ( ) r t . Dalam transaksi tersebut memungkinkan untuk terjadi arbitrase di dalam pasar. Misalkan transaksi dengan arah

x→ → →z y x terjadi di pasar Y.

Harga pasar ( )P t didefinisikan sebagai nilai tengah dari maks

{

B ti( )

}

dan

{

}

min S ti( ) ketika perdagangan terjadi. Harga pasar P t( ) mempertahankan nilai terdahulu ketika tidak terjadi perdagangan. Harga pasar

( )

P t didefinisikan sebagai berikut: maks{ ( )} min{ ( )}

; ( ) 0

( ) 2

( 1) ; ( ) 0 (29)

i i

B t S t

L t P t

P t L t

+

⎧ _≥

⎪ = ⎨

⎪ _{− <}

⎩

atau

maks{ ( )} min{ ( )} ; ( )

( ) 2

( 1) ; ( ) . (30)

i i

B t B t

v t A

P t

P t v t A

+

⎧ _≥

⎪ = ⎨

⎪ _{− <}

⎩

Mekanisme pembentukan harga di atas mempengaruhi karakteristik pergerakan

dealer sehingga algoritma dealer memiliki dua bentuk, yaitu sebagai berikut:

Kasus 1 (Tidak Terjadi Perdagangan) Jika Persamaan (27) atau (28) tidak dipenuhi, yaitu maks

{

B ti( )

}

−min

{

S ti( )

}

<0 atau maks

{

B ti( )

}

−min

{

B ti( )

}

<A maka

harga pembelian pada waktu t+1 dapat didefinisikan sebagai berikut:

( 1) ( ) ( ) ( )

i i i

B t+ =B t +a t + Δc P t (31) dengan

( ) i

a t : karakteristik pergerakan dealer pada transaksi ke-i yaitu menjadi penjual atau pembeli pada waktu t,

( )

P t

Δ : selisih harga pada waktu t dan harga

perdagangan sebelumnya (ΔP t( )=P t( )−P t( −1)),

c : konstanta yang menentukan respon

dealer dari perubahan harga pasar; c>0.

Dealer mengikuti Persamaan (31), sehingga dealer menurunkan harga

{

}

min S ti( ) dengan cara menurunkan harga pembelian

{

B ti( )

}

, di lain pihak dealer lain

Kasus 1

d1 d2

Kasus 2

d1 d2

sampai bisa kembali menjual dan membeli mata uang. Dalam kasus ini, harga hanya mengubah posisi relatif dealer dengan karakteristik pergerakan dealer mempunyai dua bentuk sebagai berikut:

+1 jika sebagai pembeli ( )

-1 jika sebagai penjual . i dealer a t dealer ⎧ = ⎨

⎩ (32)

Catatan:

Bagian c PΔ tidak bergantung pada transaksi ke-i yang dilakukan oleh dealer. Oleh karenanya, c PΔ tidak mengubah posisi relatif dari dealer tapi mengubah keseluruhan posisi

dealer.

Kasus 2 (Terjadi Perdagangan)

Jika Persamaan (27) atau (28) dipenuhi, yaitu maks

{

B ti( )

}

−min

{

S ti( )

}

≥0 atau

{

}

{

}

maks B ti( ) −min B ti( ) ≥A maka harga diperbaharui mengikuti Persamaan (29) atau (30), yaitu sebagai berikut:

{

}

{

}

maks ( ) min ( ) ( )

2

i i

B t S t

P t = +

atau

{

}

{

}

maks ( ) (min ( ) ) ( )

2

i i

B t B t A

P t = + +

dengan karakteristik pergerakan dealer

pada waktu t+1 didefinisikan sebagai berikut:

-1 jika pembeli ( )

( 1) +1 jika penjual

( ) jika tidak sebagai pembeli maupun penjual. (33)

i i

i

dealer a t

a t dealer

a t dealer

⎧₋ ⎧ = ⎨ ⎪ + = ⎨ ⎩ ⎪ ⎩

Berikut merupakan skema dari transaksi model Sato dan Takayasu:

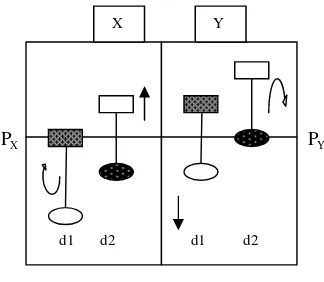
Keterangan:

: menyatakan min

{

S ti( )

}

: menyatakan S ti( ) : menyatakan maks

{

B ti( )

}

: menyatakan B ti( ) di : dealer ke-i; i=1, 2

3.2.2 Interaksi Dua Sistem dari Model Sato

dan Takayasu

Dalam bagian ini, akan dibahas model mikroskopis yang disajikan dalam model Sato

dan Takayasu. Sekumpulan dealer dari model

Sato dan Takayasu membentuk suatu sistem yang dikenal dengan pasar. Dalam model ini, hanya melibatkan dua pasar (misalkan pasar

X dan Y) untuk transaksi triangularnya karena mengambil asumsi bahwa satu dari tiga pasar merupakan pasar ternormalkan.

Mekanisme pembentukan harga di pasar

X dan Y berdasarkan pada harga maksimum pembelian dan harga minimum penjualan

dealer di pasar X atau Y. Kondisi untuk terjadinya suatu perdagangan mengikuti Persamaan (27) dan (28) dalam model Sato

dan Takayasu, yaitu sebagai berikut:

{

,

}

{

,

}

( ) maks i z( ) min i z( ) 0

L t = B t − S t ≥ (34)

atau

{

,

}

{

,

}

( ) maks i z( ) min i z( )

v t = B t − B t ≥A (35) untuk z=X atau Y

dengan

{

,

}

maks Bi z( )t : menyatakan harga pembelian maksimum dari dealer dalam transaksi

ke-i di pasar X atau Y,

{

,

}

min Si z( )t : menyatakan harga penjualan minimum dari dealer dalam transaksi ke-i

di pasar X atau Y,

{

,

}

min Bi z( )t : menyatakan harga pembelian minimum dari dealer dalam transaksi ke-i

di pasar X atau Y.

Harga pasar P tz( ) didefinisikan oleh nilai tengah dari maks

{

Bi z, ( )t

}

dan min

{

Si z, ( )t

}

ketika perdagangan terjadi. Harga pasar P tz( ) mengikuti Persamaan (29) atau (30), yang didefinisikan sebagai berikut:

, ,

maks{ ( )} min{ ( )}

( ) 2

( 1) (36)

i z i z

z

z

B t S t

P t P t + ⎧ ⎪ = ⎨ ⎪ ₋ ⎩ atau , ,

maks{ ( )} (min{ ( )} )

( ) 2

( 1). (37)

i z i z

z

z

B t B t A

P t P t + + ⎧ ⎪ = ⎨ ⎪ ₋ ⎩

Jika Persamaan (34) atau (35) tidak dipenuhi maka harga pembelian pada waktu

1

t+ mengikuti Persamaan (31) yang didefinisikan sebagai berikut:

, ( 1) , ( ) , ( ) ( )

i X i X i X X

dan

, ( 1) , ( ) , ( ) ( )

i Y i Y i Y Y

B t+ =B t +a t + Δc P t . (39) Dalam model ini, harga akan lebih berfluktuasi apabila tercipta transaksi baru di luar transaksi di dalam pasar masing-masing (X dan Y) misalkan transaksi antar X dan Y

sehingga membuat sistem lebih berinteraksi. Adanya harga yang berfluktuasi memungkinkan terjadinya transaksi arbitrase. Transaksi arbitrase bisa terjadi jika kondisi berikut dapat dipenuhi:

, ,

( ) maks{ ( )} (min{ ( )} ) 0

X i X i Y

v t = B t − B t +A ≥

...(40) atau

, ,

( ) maks{ ( )} (min{ ( )} ) 0

Y i Y i X

v t = B t − B t +A ≥

…(41) Kondisi arbitrase vX( )t ≥0 dan v tY( )≥0 berhubungan dengan arbitrase ( )v t ≥0 di pasar aktual.

Dari model Sato dan Takayasu, pasar X

dan Y memiliki maksimum pembelian dan minimum penjualan sehingga memungkinkan adanya kesempatan arbitrase di antara pasar

X dan pasar Y. Kesempatan arbitrase di pasar X atau pasar Y memenuhi Persamaan (40) atau Persamaan (41). Adapun sebaran dari arbitrase di pasar X dan arbitrase di pasar Y yang mengikuti logaritma hasil kurs pada data aktual diberikan sebagai berikut:

1. Transaksi Arbitrase di Pasar X

Transaksi arbitrase di pasar X memuat transaksi dengan arah pertukaran

x→ → →y z x. maks

{

Bi X, ( )t

}

bersesuaian

dengan transaksi pertukaran secara langsung dari z ke x yang diberikan oleh **

3

lnr ( )t . Di pasar Y tidak terdapat transaksi langsung dari

z ke x dalam transaksi pertukaran arah

x→ → →z y x sehingga dibutuhkan

perantara y. min

{

Si Y, ( )t

}

dengan arah

transaksi pertukaran dari z ke x melalui y

diberikan oleh lnr2**( ) lnt + r3**( )t . Lampiran

5.1 menyajikan perhitungan dari kondisi arbitrase di pasar X.

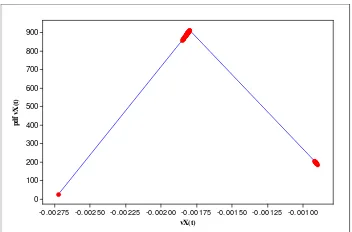
Gambar berikut memperlihatkan kesempatan arbitrase di pasar X. Nilai

( ) 0 X

v t < menyatakan kesempatan arbitrase yang negatif di pasar X artinya diperoleh keuntungan yang negatif dari pertukaran di antara pasar X dan Y sehingga memungkinkan untuk tidak melakukan transaksi pertukaran antar pasar karena transaksi merugikan. vX(t) p d f v X (t) -0.00100 -0.00125 -0.00150 -0.00175 -0.00200 -0.00225 -0.00250 -0.00275 900 800 700 600 500 400 300 200 100 0

Gambar 4.a Kesempatan arbitrase di pasar

X

2. Transaksi Arbitrasedi Pasar Y

Transaksi arbitrase di pasar Y memuat transaksi dengan arah pertukaran

x→ → →z y x. maks

{

Bi Y, ( )t

}

bersesuaian

dengan transaksi pertukaran secara langsung dari y ke x yang diberikan oleh **

3

lnr ( )t . Di pasar X tidak terdapat transaksi langsung dari y ke x dalam transaksi pertukaran arah

x→ → →y z x sehingga dibutuhkan

perantara z. min

{

Si X, ( )t

}

dengan arah

transaksi pertukaran dari y ke x melalui z diberikan oleh ** **

2 3

lnr ( ) lnt + r ( )t . Lampiran 5.2 menyajikan perhitungan dari kondisi arbitrase di pasar Y.

Gambar berikut memperlihatkan adanya kesempatan arbitrase di pasar Y. Nilai

( ) 0 Y

v t ≥ menyatakan kesempatan arbitrase yang tak negatif di pasar Y artinya diperoleh keuntungan dari pertukaran di antara pasar

dan

X Y sehingga memungkinkan untuk melakukan transaksi pertukaran antar pasar karena transaksi menguntungkan.

vY(t) p d f v Y (t) 0.00275 0.00250 0.00225 0.00200 0.00175 0.00150 0.00125 0.00100 600 500 400 300 200 100 0

Gambar 4.b Kesempatan arbitrase di Pasar

d1 d2 d1 d2

d1 d2 d1 d2

Prosedur simulasi dari model mikroskopis adalah sebagai berikut:

1. Sediakan dua sistem dari model Sato

dan Takayasu, misalkan pasar X dan

Y.

2. Periksa Persamaan (34) atau (35) dan perbaharui harga dengan Persamaan (36) atau (37). Jika Persamaan (34) atau (35) dipenuhi, lanjutkan ke langkah 4, dan jika sebaliknya maka lanjutkan ke langkah 3.

3. Periksa kondisi transaksi arbitrase, yaitu Persamaan (40) dan (41). Jika Persamaan (40) dipenuhi, perbaharui harga P tX( ) untuk maks

{

Bi X, ( )t

}

dan

harga ( )P tY untuk min

{

Bi Y, ( )t

}

+A.

Jika Persamaan (41) dipenuhi, perbaharui harga ( )P tX untuk

{

,

}

min Bi X( )t +A dan harga P tY( )

untuk maks

{

Bi Y,