Analisis struktur 2

1 !

Deflected Shape of Structures

!

Method of Consistent Deformations

!

Maxwell’s Theorem of Reciprocal

Displacement

2 -M

P

+M

-M Deflection Diagrams and the Elastic Curve

∆ = 0

θ = 0

fixed support

∆ = 0

roller or rocker

support

P

θ

3 -M

P

∆ = 0

pined support

4 Moment diagram

P

inflection point

inflection point • Fixed-connected joint

5 P

• Pined-connected joint

pined-connected joint

6 P

inflection point

7 -M

+M

x M

P₂

P₁

A B C D

8 x

-M

+M P₁

P₂

9

+

A C B

A C B

P

=

A C B

P

∆´_B

f_{BB x R} B

1 ∆´_B + f_BB R_B = ∆_B = 0

Method of Consistent Deformations

Beam 1 DOF

R_B A_y

10 w

w

=

+

+

= ∆1 ∆₂ ∆´₁

∆´₂

R₁ R₂

×R₂

Compatibility Equations. ∆´₁ + f₁₁R₁ + f₁₂R₂ = ∆₁ = 0

×R₁

f₁₂

f₂₂

0 0 Beam 2 DOF

∆´₂ + f₂₁R₁ + f₂₂R₂ = ∆₂ = 0

1

1 1

4 3

5 2

∆´₁ ∆´₂

f₁₁ f₂₁

+

11 w

P₁ P₂

=

w

P₁ P₂

+

+

+

1

1 f₃₂ f₂₂

1

Compatibility Equations.

θ

´₁ + f₁₁M₁ + f₁₂R₂ + f₁₃R₃ = θ₁ = 0

×R₂

×R₃

=

θ

₁

∆₂ ∆₃ f₃₁

f₃₃ f₂₃

f₁₃

2 4

6 1

5 3

∆´₂

θ

_´

1 ∆´3 Beam 3 DOF

∆´₂ + f₂₁M₁ + f₂₂R₂ + f₂₃R₃ = ∆₂ = 0 ∆´₃ + f₃₁M₁ + f₃₂R₂ + f₃₃R₃ = ∆₃ = 0

×M₁

θ

´₁ ∆´₂ ∆´₃

+

f₁₁ f₁₂ f₁₃ f₂₁ f₂₂ f₂₃ f₃₁ f₃₂ f₃₃

M₁ R₂

R₃

0 0 0

12 If ∆₁ = ∆₂=……= ∆_n = 0 ;

or

[∆´] + [f][R] = 0

[R] = - [f]-1_[∆_´] Compatibility Equation for n span.

∆´₁ + f₁₁R₁ + f₁₂R₂ + f₁₃R₃ = ∆ ₁ ∆´₂ + f₂₁R₁ + f₂₂R₂ + f₂₃R₃ = ∆₂ ∆´_n + f_n1R₁ + f_n2R₂ + f_nnR_n = ∆_n

∆ ´₁ ∆´₂

+

f₁₁ f₁₂ R₁ R₂

=

0 0 ∆´ _n

f₁₃ f₂₁ f₂₂ f₂₃

f _{n 1} f _{n 2} f_{n n R}

n 0

[f_ij] = Flexibility matrix dependent on

Equilibrium Equations

[Q] = [K][D] + [Qf_]

Stiffness matrix

Fixed-end force matrix

Solve for displacement [D];

[D] = [K]-1_{[Q] - [Q}f_]

GJ EA

EI

1 , 1 , 1

ij ij

13

A B

A B

EI

1=i 2=j

M_j = m_j f₁₂ = f_ij

f₁₁ = f_ii

f₂₂ = f_jj M_i = m_i

Maxwell’s Theorem of reciprocal displacements

1

1 f₂₁ = f_ji

∫

=

EI dx M m f_{ij i j}

∫

=

EI dx m m_{i j}

∫

=

EI dx M m f_{ji j i}

∫

=

EI dx m m_{j i}

14 Example 1

Determine the reaction at all supports and the displacement at C.

A

B C

50 kN

15 50 kN

=

∆´_B +

f_BB

1 kN

x R_B A

B C

50 kN

6 m 6 m

SOLUTION

R_B M_A

R_A

0

' + =

∆ _B f_BBR_B ---(1) Compatibility equation :

• Principle of superposition

∆´_B

16 Conjugate beam Conjugate beam 50 kN

∆´_B

Real beam

50 kN 300 kN•m

6 m 6 m

/EI

300 900/EI

6 + (2/3)6 = 10 m

9000/EI • Use conjugate beam in obtaining ∆∆∆∆´_B and f_BB

900/EI

12 /EI

72/EI

(2/3)12 = 8 m

576/EI f_BB

1 kN

Real beam 1 kN

12 kN•m

72/EI

∆´_B = M´_B = -9000/EI ,

f_BB = M´´_B = 576/EI,

17 R_B = +15.63 kN, (same direction as 1 kN)

0 )

576 ( 9000

:− + =

↑

+ R_B

EI EI

50 kN

∆´_B 50 kN

300 kN•m

x R_B = 15.63 kN

=

A

B C

50 kN

15.63 kN 34.37 kN

34.37 kN•m

f_BB

1 kN 1 kN

12 kN•m

18 93.6/EI

-113/EI

6 m 6 m

A B

C

50 kN

Use conjugate beam in obtaining the displacement

113 kN•m

34.4 kN 15.6 kN

EI EI

EI

M'_C = 281(2)− 223(6) = −776

↓ −

= =

∆ ' 776, EI M _C

C

Real Beam

Conjugate Beam M

(kN•m) x (m)

3.28 m 6 m 12 m

93.6

-113

223/(EI)

4 m 2 m

M´_C

V´_{C 223/(EI)}

19 10 kN

A

C

B

4 m

3EI _2EI

2 m 2 m

Example 2

20

+

10 kN

=

1 kN

Compatibility equation:

∆´_B + f_BBR_B = ∆_B = 0

x R_B ∆´_B

f_BB 10 kN

A

C

B

4 m

3EI _2EI

21 Conjugate Beam 10 kN

A

C

B

4 m

3EI _2EI

2 m 2 m

Real Beam

10 kN 40 kN•m

• Use conjugate beam in obtaining ∆´_B

26.66/EI

177.7/EI x (m)

V (kN) 10 10

+

x (m) M

(kN•m) 40

-40/3EI = 13.33/EI

22 Conjugate Beam A

C

B

4 m

3EI _2EI

2 m 2 m

Real Beam 1 kN

4/(2EI)=2EI • Use conjugate beam for f_BB

1 kN 8 kN•m

x (m) V (kN)

--1 -1

x (m) M

(kN•m)

8

4 +

8 3EI =

2.67 EI

4/(3EI)=1.33EI

60.44/EI 12/EI

23

+

10 kN

=

1 kN x R_B ∆´_B

f_BB 10 kN

A

C

B

4 m

3EI _2EI

2 m 2 m

Compatibility. equation:

∆´_B + f_BBR_B = ∆_B = 0

R_B = +2.941 kN, (same direction as 1 kN) 0

) 44 . 60 ( 7 . 177

:− − + =

↑

+ R_B

24 10 kN

A

C

B

4 m

3EI _2EI

2 m 2 m 2.94 kN

7.06 kN 16.48 kN•m

7.06

-2.94 -2.94

+

- x (m)

V (kN)

∆_C

-16.48

11.76

-+ x (m)

M (kN•m)

2.33 m

1.67 m

25 10 kN

A

C

B

4 m

3EI _2EI

2 m 2 m

↓ −

= −

= 3.263(0.555) 6.413(3.222) 18.85,

EI EI

EI

2.941 kN

7.059 kN 16.48 kN•m

∆_C • Use the conjugate beam for find ∆∆∆∆_C

Real beam

↓ −

= × − = =

∆ 18.85 ,

) 5 200 (

85 . 18

' mm

M _C

C 16.48

3EI

11.76 3EI

11.76 2EI 2.335 m

1.665 m

Conjugate beam

6.413 EI

3.263 EI

(1.665)/3=0.555 m

26 Example 3

Draw the quantitative Shear and moment diagram and the qualitative deflected curve for the beam shown below.EI is constant. Neglect the effects of axial load.

A B

4 m 4 m

27

α

_BB

α

_AB

α

_BA

α

_AA

θ

´_B

θ

´_A

θ

´_A

1 kN•m 5 kN/m

1 kN•m

A B

4 m 4 m

5 kN/m SOLUTION

• Principle of superposition

θ

´_B

=

+

α

_AA

α

_BA A

M ×

α

_BB

B M ×

α

_AB

+

Compatibility equations:

θ

_A

θ

_B

A M ×

B M × A

M ×

B M ×

) 1 ( '

0 = + + −−−

= _{A AA A AB B}

A θ f M f M

θ

) 2 ( '

0 = + + −−−

= _{B BA A BB B}

B θ f M f M

28 • Use formula provided in obtaining

θ

´_A,

θ

´_B,

α

_AA,

α

_BA,

α

_BB,

α

_AB

Note: Maxwell’s theorem of reciprocal displacement, α_AB = α_BA 1 kN•m

α

_AA

α

_BA

8 m 1 kN•m

α

_BB

α

_AB 8 m EI EI EI L M_o AA 667 . 2 3 ) 8 ( 1

3 = =

=

α

EI EI EI L M_o BA 333 . 1 6 ) 8 ( 1

6 = =

=

α

EI EI EI L M_o BB 667 . 2 3 ) 8 ( 1

3 = =

=

α

EI EI EI wL B 67 . 46 384 ) 8 )( 5 ( 7 384 7 ' 3 3 = = =

θ

EI EI EI wL A 60 128 ) 8 )( 5 ( 3 128 3 ' 3 3 = = =

θ

4 m 4 m

θ

´_B

θ

´_A

θ

´_A

5 kN/m

θ

´_B

EI EI EI L M_o AB 333 . 1 6 ) 8 ( 1

6 = =

=

29

α

_BB

α

_AB

Real Beam 1 kN•m

α

_BB

α

_AB

8 m

α

_BA

Real Beam 1 kN•m

α

_AA

α

_BA

α

_AA

8 m

Conjugate Beam 4/EI

1/EI

(1/8) (1/8)

2.67/EI 1.33/EI

(1/8) (1/8)

Conjugate Beam

1/EI

4/EI

1.33/EI 2.67/EI

EI V _A

AA

667 . 2 ' = − =

α

EI V _B

BB

667 . 2 ' = =

α

EI V _A

AB

333 . 1 ' = − =

α

EI V _B

BA

333 . 1 ' = =

α

30 1 kN•m 5 kN/m 1 kN•m A B 4 m 4 m 5 kN/m

=

+

+

θ_A θ_B

B M × EI AA 667 . 2 =

α

A M × EI V _B BA 333 . 1 ' = =

α

EI B 67 . 46 ' =

θ

EI A 60 ' =

θ

EI AB 333 . 1 =

α

EI BB 667 . 2 =

α

Solve simultaneous equations, M_A = -18.33 kN•m, + M_B = -8.335 kN•m, + Compatibility equation

+ 60 +₍2.667_{) A} +₍1.333_)MB =₀

EI M

EI EI

+ ) 0

667 . 2 ( ) 333 . 1 ( 67 . 46 = +

+ _A M_B

EI M

31 M_A = -18.33 kN•m,

M_B = -8.335 kN•m,

A B

4 m 4 m

5 kN/m

18.33 kN•m 8.335 kN•m

R_B R_A

R_B = 3.753 kN, R_a = 16.25 kN, + ΣM_A = 0: 18.33−20(2)+ RB(8)−8.355= 0

ΣF_y = 0: +

3.753

0 20 = −

32

A B

4 m 4 m

5 kN/m

18.33 kN•m 8.36 kN•m

3.75 kN 16.25 kN

V diagram

M diagram

Deflected Curve

-3.75 16.25

3.25 m

-18.33

6.67

-8.36 8.08

33 Example 4

Determine the reactions at the supports for the beam shown and draw the quantitative shear and moment diagram and the qualitative deflected curve. EI is constant.

A

C

4 m 4 m

2 kN/m

34 1 kN ) 2 ( 0 ' ' ' ) 1 ( 0 ' ' ' − − − = + + ∆ − − − = + + ∆ C CC B BC C C CB B BB B R f R f R f R f Compatibility equations: • Principle of superposition

A C 4 m 4 m 2 kN/m B 4 m

4 m B

A C 2 kN/m B ' ∆ C ' ∆ A C 4 m

4 m B

BB

f ' f 'CB

1 kN

A 4 m B 4 m C

B R × C R × BC

35 A C A C B A C 2 kN/m 1 kN • Solve equation

A C 4 m 4 m 2 kN/m B 1 kN EI B 64 ' = − ∆ EI C 33 . 149 ' = − ∆ EI

f '_BB = 21.33 f CB _EI 33 . 53 ' =

EI f '_BC = 53.33

EI f '_CC =170.67

) 1 ( 0 33 . 53 33 . 21 64 − − = + +

− _B R_C

EI R EI EI Compatibility equations: ) 2 ( 0 67 . 170 33 . 53 33 . 149 − − = + +

− _B R_C

36 • Diagram

A

C

4 m 4 m

2 kN/m

B

3.71 kN 0.29 kN kN

A_y =8+0.29−3.71= 4.58 m

kN M_A

• =

− +

= 48 . 3

) 4 ( 71 . 3 ) 8 ( 29 . 0 ) 2 ( 8

x (m) V (kN)

4.58

0.29

-3.42

2.29 m

x (m) M (kN•m)

-3.48

1.76

-1.16

x (m) Deflected shape

37 Example 5

Draw the quantitative Shear and moment diagram and the qualitative deflected curve for the beam shown below.

(a) The support at B does not settle (b) The support at B settles 5 mm. Take E = 200 GPa, I = 60(106_{) mm}4_.

16 kN

2 m 2 m 4 m

38 16 kN

2 m 2 m 4 m

A B C

16 kN SOLUTION

• Principle of superposition

∆´_B

1 kN f_BB

B R × ∆´_B

f_BB

B R ×

=

+

∆_B = 5 mm

Compatibility equation : + ∆B =0 = ∆'B+ fBBRB ---(1) : no settlement B

BB B

B =− m = ∆ + f R

39 16 kN

∆´_B Real

beam

A B

C

• Use conjugate beam method in obtaining ∆´_B

2 m 2 m 4 m

12 kN

M´ diagram

16

Conjugate beam

EI 24 EI

24

EI 72

3 4

3 2

2 m 4 m

24

EI 40 EI

56

4 kN

0 ) 4 ( 40 )

3 4 ( 32

'' + − =

−

EI EI

M _B EI 16

EI 32

EI 40 V´´_B

M´´_B

3 4

4 3 2

+ ΣMB = 0:

↓ −

= =

∆' '' 117.33, EI M _B

B

∆´_B Real

40 Real

beam

1 kN

4 m 4 m

A

B

C f_BB

• Use conjugate beam method in obtaining f_BB

0.5 kN 0.5 kN

m´ diagram

-2 Conjugate

beam

EI 2 − EI

4 −

EI 4 −

EI 4 EI

4

v´´_B m´´_B

EI 4 −

EI 4 3

4

4 3 2

0 ) 4 ( 4 ) 3 4 ( 4

'' − + =

−

EI EI

m _B + ΣMB = 0:

↑ =

= '' 10.67, EI m

41 • Substitute ∆´_B and f_BB in Eq. (1)

, 67 . 10 33

. 117 0

; R_B

EI EI + −

= ↑

+ _R

B = 11.0 kN,

xR_B = 11.0 kN

=

16 kN

A B C

11.0 kN

= 6.5 kN R_C = 1.5 kN

R_A

no settlement

↓ −

=

∆' 117.33, EI B

↑ =10.67,

EI f_BB

16 kN

12 kN ∆´B 4 kN 1 kN

+

0.5 kN 0.5 kN

42 • Substitute ∆´_B and f_BB in Eq. (2)

B R EI EI

m 117.33 10.67 005

. 0

; − = − +

↑ +

B R EI

m) 117.33 10.67 005

. 0

(− =− +

R_B = 5.37 kN,

B R 67 . 10 33 . 117 )

60 200 )( 005 . 0

(− × = − +

xR_B = 5.37

=

16 kN

A B C

5.37 kN

= 9.31 kN R_C = 1.32 kN

R_A

with 5 mm settlement

↓ −

=

∆' 117.33, EI B

↑ =10.67,

EI f_BB

16 kN

12 kN ∆´B 4 kN 1 kN

+

0.5 kN 0.5 kN

43 • Quantitative shear and bending diagram and qualitative deflected curve

16 kN

A B C

2 m 2 m 4 m

11 kN

6.5 kN _{1.5 kN}

V diagram

6.5

-9.5

1.5

M diagram

13

-6

+

-Deflected Curve

16 kN

∆_B = 5 mm

A B C

2 m 2 m 4 m

5.37 kN

9.31 kN _{1.32 kN}

V diagram

9.31

-6.69

-1.32

M diagram

18.62

5.24

+

Deflected

Curve _∆

44 Example 6

Calculate supports reactions and draw the bending moment diagrams for (a) D₂ = 0 and (b) D₂ = 2 mm.

4 m 6 m

w 2 kN/m

45

+

2 kN/m

=

Compatibility equation: ∆´₂ + f₂₂R₂ = ∆₂

∆´₂

1 f₂₂

×R₂

4 m 6 m

w 2 kN/m

1 2 3

46

4 m 6 m

w 2 kN/m

1 2 3

12.92 kN

4.83 kN 2.25 kN

Compatibility.equation: -6.2+ 0.48R₂ = -2

R₂ = 8.75 kN

4 m 6 m

w 2 kN/m

1 2 3

For ∆₂ = 2 mm For ∆₂ = 0

Compatibility equation: -6.2+ 0.48R₂ = 0

R₂ = 12.92 kN

x (m) V

(kN)

2.25

-5.75 7.17

-4.83 +

-1.125 m

2.415 m

x (m) V

(kN)

2.375 m

3.25 m -+

+

-4.75 5.5

-3.25

-6.5

x (m) M

(kN•m)

1.27

-7

5.85 +

-+

x (m) M

(kN•m)

5.64

3

10.56

+ +

6.5 kN

47 L

w Basic Beams: Single span

wL/2

- wL/2 V

wL2_/8 M

APPENDIX

wL/2 L/3 L/3 wL/2

1

EI wL 384

48 • Find ∆∆∆∆₁ by Castigliano’s

w

L

L/2 L/2

x₁ x₂

1

2 3

P 2 2 P wL + 2 2 P wL + 2 2 P wL + x₂ w V₂ M₂ 2 2 P wL

+ x1 _V

1 M₁ w

+ ΣΜ = 0;

49 0

∫

∫

+ ∂_∂ ∂ ∂ = ∆ = ∆ 2 / 0 2 2 2 2 / 0 1 1 1 max

1 ( ) ( )

L L EI dx M P M EI dx M P M

∫

∂_∂ = 2 / 0 1 1 1₎ ( 2 L EI dx M P M 2 1 2 1 1 ) 2 2 (

2 x M

P wL wx

M = − + + =

1 1 2 1 2 / 0

1 _{) )}

50 L

L /2 L /2

P 1

P/2 P/2

V

P/2

- P/2 +

-PL/4 M

EI L f

P f EI PL

48 48

3

11 11

3

11 = = → =

δ

51 L = 2l

l = L/2 l = L/2 1

w

1.25 wl

0.375 wl 0.375 wl

0.375 wl

-0.375 wl -0.625 wl

0.625 wl +

-+

-0.070 wl2 _{0.070 wl}2

-0.125 wl2

+ +

-EI

wl 185 4

max = ∆

EI wl 185 4

max = ∆

52 l = L/3 l = L/3 l = L/3

1

w 2

1.1wl 1.1wl

0.4wl 0.4wl

∆_max = wl4 145 EI

V 0.4wl

- 0.4wl - 0.6wl

0.5wl

-0.5wl 0.6wl

+

-+

-+

-0.08 wl2 _{0.08 wl}2

0.025 wl2

-0.1 wl2 -0.1 wl2 +

-

-+ +

1

!

Trusses

!

Vertical Loads on Building Frames

!

Lateral Loads on Building Frames: Portal

Method

!

Lateral Loads on Building Frames: Cantilever

Method Problems

2

P₁ P₂

(a) Trusses

R₁ R₂

a

a

(b)

R₁

a

a

V ₌ R

1 F

1

F

2

F

b

F

a

Method 1 : If the diagonals are intentionally designed to be long and slender, it is reasonable to assume that the panel shear is resisted entirely by the tension diagonal, whereas the compressive diagonal is assumed to be a zero-force member.

3

Example 1

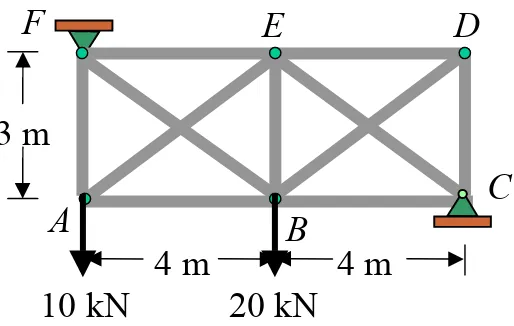
[image:55.842.263.520.257.420.2]

Determine (approximately) the forces in the members of the truss shown in

Figure. The diagonals are to be designed to support both tensile and compressive forces, and therefore each is assumed to carry half the panel shear. The support reactions have been computed.

10 kN 20 kN

4 m 4 m

3 m

A _B C

D E

4

+ ΣMA = 0: FFE(3) - 8.33cos36.87o(3) = 0 F_FE = 6.67 kN (C)

Σ_{Fy = 0:}

+ 20 - 10 - 2Fsin(36.87o) = 0 F = 8.33 kN

F_FB = 8.33 kN (T)

F_AE = 8.33 kN (C)

+ ΣMF = 0: FAB(3) - 8.33cos36.87o(3) = 0 F_AB = 6.67 kN (T)

Σ_{Fy = 0:}

+ FAF - 10 - 8.33sin(36.87o) = 0 F_AF = 15 kN (T)

10 kN 20 kN

4 m 4 m

3 m

A _B C

D E

F

10 kN 20 kN

V _{= 10 kN} F

FE

F AB F

AE= F

F

FB= F

θ

_{= 36.87}o

10 kN 3 m

A F

20 kN

θ

θ

6.67 kN 8.33

F AF

10 kN

θ

5

C D

10 kN

3 m

θ

θ

Σ_{Fy = 0:}

+ 10 - 2Fsin(36.87o_{) = 0}

F = 8.33 kN

F_DB = 8.33 kN (T)

F_EC = 8.33 kN (C)

+ ΣM_C = 0: F_ED(3) - 8.33cos36.87o_{(3) = 0}

F_ED = 6.67 kN (C)

+ ΣMD = 0: FBC(3) - 8.33cos36.87o(3) = 0 F_BC = 6.67 kN (T)

θ

_{= 36.87}o

V _{= 10 kN}

θ

_{= 36.87}o

D

θ

6.67 kN

8.33 kN

F DC

Σ_{Fy = 0:}

+ F_DC - 8.33sin(36.87o_{) = 0}

F_DC = 5 kN (C)

Σ_{Fy = 0:}

+

F_EB = 2(8.33sin36.87o_{) = 10 kN (T)}

E

θ θ 6.67 kN

6.67 kN

8.33 kN 8.33 kN

θ

_{= 36.87}o

F EB

F_ED

F_BC

F = F EC F = F

6

Example 2

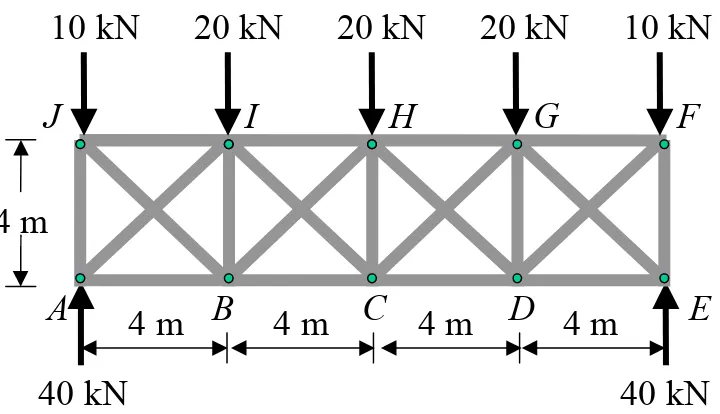
[image:58.842.237.597.213.420.2]

Determine (approximately) the forces in the members of the truss shown in Figure. The diagonals are slender and therefore will not support a compressive force. The support reactions have been computed.

40 kN 40 kN

4 m

A B C

G H

J

D E

F I

10 kN 20 kN 20 kN 20 kN 10 kN

7

F

BH = 0

F_IH

F_BC F_IC

40 kN 4 m

A J

10 kN

45o

V _{= 10 kN}

F

BH = 0

Σ_{Fy = 0:}

+ 40 - 10 - 20 - FICcos 45o = 0 F_IC = 14.14 kN (T) + ΣMA = 0: FJI(4) - 42.43sin 45o(4) = 0

F_JI = 30 kN (C)

+ ΣMJ = 0: FAB(4) = 0

F_AB = 0

0 0

F_JA

40 kN

θ

A

Σ_{Fy = 0:}

+ FJA = 40 kN (C)

F

AI = 0

F_JI

FAB FJB

V _{= 30 kN}

Σ_{Fy = 0:}

+ 40 - 10 - FJBcos 45o = 0 F_JB = 42.43 kN (T)

F

AI = 0

40 kN 4 m

A B

J I

10 kN 20 kN

4 m

8

+ ΣMB = 0:

F_IH(4) - 14.14sin 45o_{(4) + 10(4) - 40(4) = 0}

F_JH = 40 kN (C)

F_BC = 30 kN (T)

+ ΣMI = 0: FBC(4) - 40(4) + 10(4) = 0

F_BH = 0

F_IH

F_BC F_IC

V _{= 10 kN}

40 kN 4 m

A B

J I

10 kN 20 kN

4 m

45o

B 30 kN

0

0 42.3 kN FBI

45o

45o 45o

Σ_{Fy = 0:}

+ FBI = 42.3 sin 45o = 30 kN (T)

Σ_{Fy = 0:}

+

F_BI = 2(14.1442.3 sin 45o_{)= 20 kN (C)}

C 30 kN

30 kN

14.14 kN 14.14 kN FCH

45o

9

Vertical Loads on Building Frames

10

w

A B

L (b)

0.21L 0.21L

point of zero moment

approximate case w

L

(d) assumed points of zero moment

0.1L 0.1L

model w

(e) • Assumptions for Approximate Analysis

0.1L _0.8L 0.1L w

A B

L

Simply supported

(c)

column column

girder w

A B

L (a)

Point of zero moment

11

Example 3

Determine (approximately) the moment at the joints E and C caused by members EF and CD of the building bent in the figure.

B D

F

A C

E

12

1 kN/m

1 kN/m

4.8 m 4.8 kN

0.6 m

0.6 kN 2.4 kN

3 kN 0.6(0.3) + 2.4(0.6) = 1.62 kN•m

0.6 m 0.6 kN

2.4 kN

3 kN

1.62 kN•m

0.1L=0.6 m _{0.6 m} 4.8 m

13

P

h

l (a)

P

h

l (b) Portal Frames and Trusses

• Frames: Pin-Supported

∆ ∆

assumed hinge

h L/2

(c) P

h

L/2

Ph/l

P/2

Ph/l

P/2

P/2 P/2

Ph/l

Ph/2 Ph/2

Ph/2 Ph/2

(d)

14

h/2 • Frames : Fixed-Supported

P

h

l (a)

P/2

Ph/2l P/2

Ph/2l

P

h

l (b)

∆ ∆

assumed hinges

(c)

h/2 L/2

P

h/2

L/2

P/2 P/2

Ph/2l

P/2

Ph/2l

P/2

Ph/2l

Ph/2l

Ph/2l

P/2 P/2

Ph/2l

Ph/4 _Ph/4

Ph/4 Ph/4

Ph/4 Ph/4

(d)

15

• Frames : Partial Fixity

P

(b) P

h

l (a)

h/3 h/3

assumed hinges

θ

θ

• Trusses

P

h

l (a)

P

l (b)

P/2 P/2

h/2

assumed hinges

16

Example 4

Determine by approximate methods the forces acting in the members of the Warren portal shown in the figure.

40 kN

7 m

8 m 2 m

4 m

A B C

4 m 2 m

2 m

D E F

H G

17

40/2 = 20 kN = V

N N

20 kN = V

I 3.5 m

A

V = 20 kN

N N

V = 20 kN

V = 20 kN

N N

20 kN = V

M M

40 kN

3.5 m 2 m

B C

4 m 2 m

2 m

D E F

H G

J K

+ ΣM_J = 0:

N(8) - 40(5.5) = 0

N = 27.5 kN

+ ΣMA = 0:

M - 20(3.5) = 0

18

20 kN

27.5 kN 40 kN

3.5 m 2 m

B C

2 m

D

J

F_CD

F_BD F_BH 45o

+ ΣMB = 0: FCD(2) - 40(2) - 20(3.5) = 0

F_CD = 75 kN (C)

+ ΣMD = 0:FBH(2) + 27.5(2) - 20(5.5) = 0

F_BH = 27.5 kN (T)

Σ_{Fy = 0:}

+ -27.5 + FBDcos 45o = 0 F_BD = 38.9 kN (T)

+ ΣMG = 0: FEF(2) - 20(3.5) = 0

F_EF = 35 kN (T)

+ ΣME = 0:FGH(2) + 27.5(2) - 20(5.5) = 0

F_GH = 27.5 kN (C)

Σ_{Fy = 0:}

+ 27.5 - FEGcos 45o = 0 F_EG = 38.9 kN (C)

3.5 m 2 m

27.5 kN 20 kN = V

2 m

E F

G

K

F_GH F_EG

F_EF

19

Σ_{Fy = 0:}

+ F_DHsin 45o _{- 38.9sin 45}o _{= 0}

F_DH = 38.9 kN (C) D

75 kN

38.9 kN

F_DE

F_DH

x y

45o 45o

75 - 2(38.9 cos 45o_{) - F}

DE = 0

F_DE = 20 kN (C)

Σ_{Fx = 0:}

+

H 27.5 kN 27.5 kN

38.9 kN F_HE

x y

45o 45o

Σ_{Fy = 0:}

+ F_HEsin 45o _{- 38.9sin 45}o _{= 0}

20

= inflection point P

(a)

Lateral Loads on Building Frames: Portal Method

(b)

21

Example 5

Determine by approximate methods the forces acting in the members of the Warren portal shown in the figure.

4 m 4 m 4 m

5 kN

3 m

A B

C D

E

F G

22

5 kN

1.5 m

B D F G

I J K L

M N O

4 m 4 m 4 m

5 kN

3 m

A B

C D

E

F G

H

I J K L

M N O

V 2V 2V V

I_y J_y K_y L_y

Σ_{Fx = 0: 5 - 6V = 0}

23

L y

0.625 kN = 0.625kN

K

y = 0

4.167 kN

0.625 kN

I

y = 0.625kN

2.501kN

0.625kN

J

y = 0

1.5 m A I 0.625 kN 0.833kN 0.625 kN 0.833 kN H L 1.5 m 0.833 kN

0.625 kN 1.25 kN•m

C J 1.5 m 1.666 kN 1.666kN 2.50 kN•m 0.835 kN E K 1.5 m 1.666 kN 1.666kN 2.5 kN•m 0.833 kN

0.625 kN 1.25 kN•m

5 kN

1.5 m

B 2 m

0.833 kN M I 2.501 kN 0.625kN F 1.666 kN 1.5 m 2 m 2 m N O K G 0.833 kN 1.5 m 2 m O L 0.625 kN 0.835 kN 0.625 kN D 1.666 kN

2 m 2 m

1.5 m N

J

24

Example 6

Determine (approximately) the reactions at the base of the columns of the frame shown in Fig. 7-14a. Use the portal method of analysis.

20 kN

30 kN

8 m 8 m

5 m

6 m

G H I

A B C

25

20 kN

30 kN

8 m 8 m

5 m

6 m

G H I

A B C

D E F

S

N

J K L

O P Q

R

26

P_y V

O_y V

P_y 2V

Σ_F

x = 0: 20 - 4V = 0 V = 5 kN +

L_y V´

J_y V´

K_y 2V´

Σ_{Fx = 0: 20 + 30 - 4V´ = 0 V´ = 12.5 kN}

+ 20 kN

2.5 m

G I

20 kN

30 kN 5 m

3 m

G H I

27

O

y = 3.125 20 kN

2.5 m

G 4 m R

5 kN

R

x = 15 kN R

y = 3.125 kN

S

x = 5 kN

S

y = 3.125 kN

P

y = 0 kN

M

x = 22.5 kN M

y = 12.5 kN

J

y = 15.625 kN

N

x = 7.5 kN

N

y = 12.5 kN

K

y = 0 kN

B K

3 m 25 kN

A J

3 m

15.625kN

12.5 kN

B_x = 25 kN

B_x = 0 MB = 75 kN•m

A_x = 12.5 kN

A_x = 15.625 kN MA = 37.5 kN•m

25 kN

2.5 m

N

K P

M

3 m 4 m 4 m

10 kN

22.5 kN

12.5 kN 10 kN

H S

R

15 kN

3.125 kN

2.5 m 4 m

4 m

5 kN 3.125 kN

12.5 kN 30 kN

J O

M 2.5 m

28

Lateral Loads on Building Frames: Cantilever Method

P

beam (a)

building frame (b)

In summary, using the cantilever method, the following assumptions apply to a fixed-supported frame.

1. A hinge is place at the center of each girder, since this is assumed to be point of zero moment.

2. A hinge is placed at the center of each column, since this is assumed to be a point of zero moment.

3. The axial stress in a column is proportional to its distance from the centroid of the cross-sectional areas of the columns at a given floor level. Since stress equals force per area, then in the special case of the columns having equal cross-sectional areas,

29

Example 7

Determine (approximately) the reactions at the base of the columns of the frame shown. The columns are assumed to have equal crossectional areas. Use the cantilever method of analysis.

30 kN

15 kN

6 m C

D

B

E

A F

30

30 kN

15 kN

6 m C

D

B

E

A F

4 m 4 m

x

6 m

3 ) ( 6 ) ( 0 ~

= +

+ =

=

∑

∑

A A

A A

A A x x

G H

I

J

K

31

I

3 m 3 m

H_y H_x

K_y K_x

30 kN C _D

2 m

M

+ ΣMM = 0: -30(2) + 3Hy + 3Ky = 0

The unknowns can be related by proportional triangles, that is

y y

y y

K H

or K

H

= =

3 3

kN K

H_y = _y =10

G_y G_x

L_y L_x

N 30 kN

15 kN

C

D

B

E

4 m _H

I

J

K

3 m 3 m

2 m

+ ΣMN = 0: -30(6) - 15(2) + 3Gy + 3Ly = 0

The unknowns can be related by proportional triangles, that is

y y

y y

L G

or G

G

= =

3 3

kN L

32

10 kN 30 kN

2 m

C 3 m _I

x = 15 kN I

y = 10 kN

H_x = 15 kN

10 kN D I

15 kN

10 kN

2 m 3 m

K_x = 15 kN

35 kN

15 kN 10 kN

15 kN

G H

J 2 m

2 m 3 m Jx = 7.5 kN J

y = 25 kN

G

x = 22.5 kN

35 kN 2 m

L K

J

2 m 3 m

15 kN

7.5 kN

25 kN

10 kN

L

x = 22.5 kN

A G

2 m 35 kN

22.5 kN

A_x = 22.5 kN

A_x = 35 kN MA = 45 kN•m

F_x = 22.5 kN

F_y = 35 kN MF = 45 kN•m F

L

2 m

33

Example 8

Show how to determine (approximately) the reactions at the base of the columns of the frame shown. The columns have the crossectional areas show. Use the cantilever of analysis.

35 kN

45 kN

6 m 6 m

4 m

P Q R

A B C D

L M N O

E F G H

I J K

4 m 8 m

5000mm2

5000mm2

4000 mm2

4000 mm2

6000 mm2

6000 mm2

6000 mm2

34

35 kN

45 kN

6 m 4 m

P Q R

A B C D

L M N O

E F G H

I J K

6 m 4 m 8 m

6 m 4 m 8 m

6000 mm2 5000mm2 _{4000 mm}2 _{6000 mm}2

x

m A

A x

x 8.48

6000 4000

5000 6000

) 18 ( 6000 )

10 ( 4000 )

6 ( 5000 )

0 ( 6000 ~

= +

+ +

+ +

+ =

=

35

35 kN 2 m

P Q R

L_y L_x M_y M_x N_y N_x O_y O_x 1.52 m 2.48 m

8.48 m 9.52 m

+ ΣM_NA = 0: -35(2) + L_y(8.48) + M_y(2.48) + N_y(1.52) + O_y(9.52) = 0 ---(1)

) 2 ( ) ) 10 ( 6000 ( 48 . 8 48 . 2 ) 10 ( 5000 ; 48 . 8 48 . 2 ; 48 . 8 48 .

2 = = −6 = −6 −−−−−

y y

L M

L

M

σ

σ

σ

M L

σ

) 3 ( ) ) 10 ( 6000 ( 48 . 8 52 . 1 ) 10 ( 4000 ; 48 . 8 52 . 1 ; 48 . 8 52 .

1 = = −6 = −6 −−−−−

y y

L N

L

N

σ

σ

σ

N L

σ

) 4 ( ) ) 10 ( 6000 ( 48 . 8 52 . 9 ) 10 ( 6000 ; 48 . 8 52 . 9 ; 48 . 8 52 .

9 = = −6 = −6 −−−−−

y y

L O

L

O

σ

σ

σ

O L

σ

Since any column stress

σ

is proportional to its distance from the neutral axis

36

35 kN

45 kN

3 m

L M N O

I J K

4 m E_y E_x F_y F_x G_y G_x H_y H_x 1.52 m 2.48 m

8.48 m 9.52 m

+ ΣMNA = 0: -45(3) - 35(7) + Ey(8.48) + Fy(2.48) + Gy(1.52) + Hy(9.52) = 0 ---(5)

) 6 ( ) ) 10 ( 6000 ( 48 . 8 48 . 2 ) 10 ( 5000 ; 48 . 8 48 . 2 ; 48 . 8 48 .

2 = = −6 = −6 −−−−−

y y

E F

E

F

σ

σ

σ

F E

σ

) 7 ( ) ) 10 ( 6000 ( 48 . 8 52 . 1 ) 10 ( 4000 ; 48 . 8 52 . 1 ; 48 . 8 52 .

1 = = −6 = −6 −−−−−

y y

E G

E

G

σ

σ

σ

G E

σ

) 8 ( ) ) 10 ( 6000 ( 48 . 8 52 . 9 ) 10 ( 6000 ; 48 . 8 52 . 9 ; 48 . 8 52 .

9 = = −6 = −6 −−−−−

y y

E H

E

H

σ

σ

σ

H E

σ

Since any column stress

σ

_{is proportional to its distance from the neutral axis ;}

37

One can continue to analyze the other segments in sequence, i.e.,

PQM, then MJFI, then FB, and so on. 35 kN

2 m

3.508 kN 3 m

I

x= 114.702 kN I

y= 15.536 kN L

x= 5.262 kN

E

x= 64.44 kN

P

x= 29.738 kN P

y= 3.508 kN

45 kN

3 m

I 2 m

19.044 kN 5.262 kN 3.508 kN

3 m

3 m E

19.044 kN

64.44 kN

A_x = 64.44 kN

1

!

Force Method of Analysis: Beams

!

Maxwell

’

s Theorem of Reciprocal Displacements;

Betti

’

s Law

!

Force Method of Analysis: Frames

!

Force Method of Analysis: Trusses

!

Force Method of Analysis: General

!

Composite Structures

2

+

=

P

A

C

B

+

P

=

P

A

C

B

L

Force Method of Analysis : Beams

• Compatibility of displacement

∆_´

2

1 f₂₂

∆_´

2 + f22R2 = ∆2 = 0

2

R ×

θ

_´1

1 α₁₁

θ

_{´1 +} α

11M1 =

θ

1= 0

R₂ R₁

M₁

1

M × 1 Degree of freedom

2 1

α 11

1

M ×

θ

_´1

f₂₂ ×R₂ ∆_´

2

L P

A

C

B

• Compatibility of slope

2 1

R₂ R₁

3 x R₁

x R₂

A D

+

A D

+

A B C

P

D

A B C

P

D 2 Degree of freedom

1 2

∆_´

2 + f21 R1 + f22 R2 = ∆₂ = 0

∆_{´1 + f}

11 R1 + f12 R2 = ∆

1 = 0

∆_´1 ∆´₂

1 f₁₁

f₂₁

x R₁

f₁₂

f₂₂

x R₂ 1

∆_´1

f₁₁

x R₁

f₁₂

x R₂ ∆_´2

f₂₁

f₂₂

R₁ R_{2 D}

y

4

A B

m₁

m₂ 1

f₁₂ 1

f₂₁ f₁₁

f₂₂

Maxwell’s Theorem of Reciprocal Displacements; Betti’s Law

1 2

A B

∫

∫

=

= •

L L

dx EI

m m dx

EI M m

f₂₁ 2 1 2 1

1

∫

=

L

dx EI

5

A B

1 2

A B

m₂

1

m₁ f₁₂

f₂₂

f₁₁ f21

1

∫

∫

=

= •

L L

dx EI

m m dx

EI M m

f₁₂ 1 2 1 2

1

Maxwell’s Theorem:

ji ij f

f =

12 21 f

f =

∫

=

L

dx EI

m m

f 1 2

12

f₁₂

∫

=

L

dx EI

6

A 1 B

m₂ f₁₂ f₂₂ 1 2 A B 1 m₁ f₂₁ f₁₁

∫

∫

= = • L L dx EI m m dx EI M m

f₁₁ 1 1 1 1

1

∫

∫

= = • L L dx EI m m dx EI M m

f₂₂ 2 2 2 2

1 In general,

∫

= = • L j i ij dx EI m m f f 1

∫

= = • L i j ji ji dx EI m m f f 1

7

A D

P₁

d

21 = f21 P1

d

11 = f11 P1

P₂

d

12 = f12 P2 d22 = f22 P2

A D

8

f

₁₂

f

₂₂

f

₁₁

f

₂₁

∆

´

₁

∆

´

₂

+

+

w

=

Force Method of Analysis: General

∆

´

₁

∆

´

₂

=

∆

1

∆

₂

Compatibility Eq.

∆

´

₁

+

f

₁₁

R

₁

+

f

₁₂

R

₂

=

∆

₁

= 0

General form:

f

₁₁

f

₂₁

f

_n1

f

₁₂

f

₂₂

f

_n2

..

.

f

_1n

f

_2n

f

_nn

R

₁

R

₂

R

_n

..

.

=

-∆

´

₁

∆

´

₂

∆

´

_n

..

.

f

₁₁

f

₁₂

f

₁₂

f

₂₂

R

₁

R

₂

∆

´

₁

∆

´

₂

=

-∆

´

₂

+

f

₂₁

R

₁

+

f

₂₂

R

₂

=

∆

₂

= 0

∆

´

₁

∆

´

₂

x

R

₁

f

₁₁

f

₂₁

1

x

R

₂

f

₁₂

f

₂₂

1

x

R

₁

x

R

₂

x

R

₁

x

R

₂

+

f

11

f

12

f

₁₂

f

₂₂

R

₁

R

₂

0

0

1

9

Example 9-1

Determine the reaction at all supports and the displacement at C.

A C B

50 kN

10

x R_B f_BB

+ 50 kN

=

A

B C

50 kN

6 m 6 m

SOLUTION

x R_B ∆_´B

f_BB R_B

M_A

R_A

∆_´B Use compatibility of displacement for find reaction

0

' + =

∆ _{B fBBRB} ---(1) Compatibility equation :

• Principle of superposition

11

6 m 6 m

A C B

50 kN

θ

_´C

∆_´

C

6

θ

´_C ∆´B

∆_´

B = ∆´C+ (6 m)

θ

´C

EI P EI

P

B

2 ) 6 ( ) 6 ( 3

) 6 ( '

2 3

+ =

∆ = + = 9000,↓

2 ) 6 )( 50 ( ) 6 ( 3

) 6 (

50 3 2

EI EI

EI

↑ =

=

= 576_,

3 ) 12 )( 1 ( 3

3 3

EI EI

EI PL f_BB

• Use formulation for ∆´_B and f_BB

1

A C B

12

6 m 6 m

A C B

50 kN

R_B = 15.63 kN, 0

) 576 ( 9000

:− + =

↑

+ _RB

EI EI

15.63 kN R_A

M_A

Equilibrium equation :

+ ΣMA = 0: MA −50(6)+15.63(12) =0,

Σ_F

y = 0:

+ + RA −50+15.63= 0, Ra = 34.37 kN,

M_A = 112.4 kN, +

↓ =

∆_' 9000_, EI

B

↑ = 576_,

EI f_BB

13

6 m 6 m

A C B

50 kN

15.63 kN

M

(kN•m) x (m)

3.28 6 12

93.78

-112.44 V

(kN) x (m)

112.4 kN•m

34.37 kN

34.37

-15.63 -15.63

14

θ

_´A

f_AA

+

A

B C

=

A

B C

50 kN

A C B

50 kN

6 m 6 m

R_B M_A

R_A

θ

_´A

f_AA

x M_A Or use compatibility of slope to obtain reaction

x M_A

Compatibility equation :

0 '_A+ f_AAM_A =

θ

_A=

θ

---(2)

• Principle of superposition

15

16 ) 12 )( 50 ( 3 16

3 ₌

= PL

M_{A = 112.5 kN•m, +}

• Use the table on the inside front cover for θ´_B and f_BB

A

B C

50 kN

θ

_´A

θ

_´A

A

B C

1 _f

AA

f_AA

0 3

16

2

= +

−

A

M EI L EI

PL + :

0 '_A+ f_AAM_A =

θ

_A=

θ

Substitute the values in equation: EI PL

A

16 '

2

=

θ

EI L f_CC

16

A C B

50 kN

6 m 6 m

M₁ = (12R_B - 300) + (50 - R_B)x₁ M

diagram

x (m) Or use Castigliano least work method

50 - R_B = 12R_B - 300 =

R_B M_A

R_A

x₁ x₂

12R_B - 300 M₂ = R_Bx₂

∫

_∂∂ = = ∆ L B B dx EI M R M 0 ) ( 0

∫

∫

− − + − + = 6 0 2 2 2 6 0 1 1 1

1 ( )

1 ) 50 300 12 )( 12 ( 1

0 x R x dx

EI dx x R x R x

EI B B B

R_B =15.63 kN,

6 0 6 0 3 ) 3 3 50 2 24 2 900 3600 144 ( 0 3 2 3 1 3 1 2 1 2 1 1

1 B B B

B R x R x x R x x x x

R − + − − + +

17

Conjugate Beam

6 m 6 m

A B

C 50 kN

93.6/EI

-112/EI 223/(EI)

Use conjugate beam for find the displacement

M

(kN•m) x (m)

3.28 6 12

93.6

-112 112 kN•m

34.4 kN 15.6 kN

EI EI

EI

M'_C = 281(2)− 223(6) = −776

↓ −

= =

∆ _' 776_, EI M _C

C

Real Beam

4 m 2 m

M´_C

V´_{C 223/(EI)}

281/(EI)

C

18

6 m 6 m

A B

C 50 kN

Use double integration to obtain the displacement

M

(kN•m) x (m)

3.28 6 12

93.6

-112 112 kN•m

34.4 kN 15.6 kN

1 2 2 4 . 34 112 x dx d

E