Fungsi, Limit dan Kekontinuan, Turunan
6. FUNGSI
6.1 Fungsi dan Grafiknya
Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz sejak akhir abad ke-17, namun definisi fungsi yang kita kenal sekarang berakar pada rumusan Leonhard Euler pada 1749, yang disempurnakan kemudian oleh Joseph Fourier pada 1822 dan Lejeune Dirichlet pada 1837.
Sebuah fungsi dari himpunan A ke himpunan B adalah suatu aturan yang mengaitkansetiapx∈Adengan sebuah elementunggal y∈B, ditulis
f :A→B x7→y.
Elemen y yang terkait dengan x disebut peta dari x (di bawah f) dan kita tulis
y = f(x). Bila f(x) mempunyai rumus yang eksplisit, fungsi f sering dinyatakan sebagai persamaan
y=f(x).
Dalam buku ini, kita membatasi pembahasan kita pada fungsi dariA ⊆R ke B ⊆ R, yakni fungsi bernilai real dengan peubah real. Dalam hal ini, kita dapat
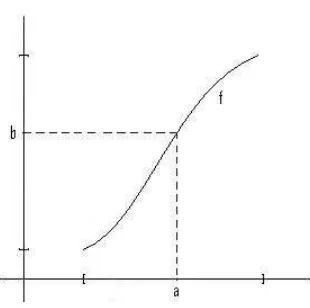
menggambar grafik fungsif :A→B sebagaigrafik persamaan y=f(x) pada sistem koordinat Cartesius (lihat Gambar 6.1). Definisi di atas menjamin bahwa setiap garis vertikal yang memotong A akan memotong grafik tepat pada satu buah titik (tidak mungkin lebih).
Gambar 6.1 Grafik sebuah fungsi
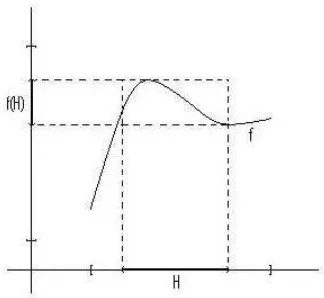
Jikaf terdefinisi padaH, maka kita definisikanpetadariH di bawahf sebagai
f(H) :={f(x) :x∈H}.
Untuk ilustrasi, lihat Gambar 6.2 di bawah ini. Dalam hal H =A, himpunan f(A) disebut sebagaidaerah nilaif. Catat bahwaf(A) tidak harus sama denganB.
Gambar 6.2 Peta dariH di bawahf
Contoh 1. Persamaan y = x2 mendefinisikan sebuah fungsi dariR ke R. Untuk
tiap x ∈ R terdapat tepat sebuah y ∈ R yang memenuhi aturan y = x2. Amati
grafik y =x2 tepat pada sebuah titik. Daerah asal fungsi ini adalah R dan daerah
nilainya adalah [0,∞). Peta dari (−0.5,1], misalnya, adalah [0,1].
Gambar 6.3 Grafik persamaany=x2
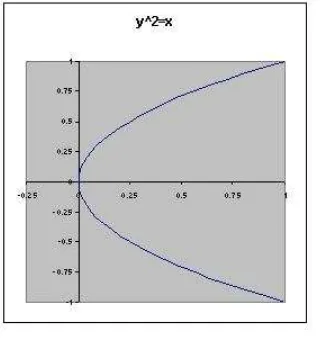
Contoh 2. Persamaany2=xtidak mendefinisikan fungsi dari [0,∞) ke R. Untuk
tiapx >0 terdapat dua buahy∈R, yakniy=±√x, yang memenuhi aturany2=x.
Dalam Gambar 6.4, amati bahwa setiap garis vertikal yang memotong sumbu-xpada
x0>0 akan memotong grafiky2=xpada dua buah titik.
Gambar 6.4 Grafik persamaany2=x
memenuhi aturany2=x. Dalam Gambar 5.5, amati bahwa setiap garis vertikal yang memotong sumbu-xpadax0 ≥0 akan memotong grafiky2 =x, y ≥0, tepat pada
sebuah titik.
Gambar 6.5 Grafik persamaany2=x, y
≥0
Soal Latihan
1. Gambar grafik himpunan semua titik (x, y) sedemikian sehingga
y=
5 jikax≥1 2 jikax <1
Jelaskan mengapa grafik tersebut merupakan grafik sebuah fungsi dari R ke R. Tentukan daerah nilainya. Tentukan pula peta dari [1,2] di bawah fungsi
tersebut.
2. Apakah persamaan x2+y2 = 1 mendefinisikan sebuah fungsi dari [−1,1] ke
[−1,1]? Jelaskan.
3. Apakah persamaanx2+y2= 1, y
≥0, mendefinisikan sebuah fungsi dari [−1,1] ke [0,1]? Jelaskan.
4. Diketahui f terdefinisi pada H dan A, B ⊆ H. Selidiki apakah f(A∪B) =
6.2 Fungsi Polinom dan Fungsi Rasional
Jikaa0, a1, . . . , an ∈R, maka persamaany=a0+a1x+· · ·+anxnmendefinisikan
sebuah fungsi dari R ke R. Sembarang nilai x yang disubstitusikan ke ruas kanan
akan memberi kita sebuah nilaiyyang berkaitan dengannya. Untukn∈N, fungsi ini
dikenal sebagaipolinom berderajat n asalkanan 6= 0. Untuk n= 0,fungsi konstan
y=a0 merupakan polinom berderajat 0.
MisalkanP dan Qadalah fungsi polinom, dan S adalah himpunan semua bi-langanx∈RdenganQ(x)6= 0. Maka, persamaan
y= P(x)
Q(x)
mendefinisikan sebuah fungsi dariS keR. Fungsi ini dikenal sebagai fungsirasional.
Contoh 4. Fungsi yang diberikan oleh persamaan
y=x3−3x2+ 2x
merupakan polinom berderajat 3 (atau ‘polinom kubik’). Grafik fungsi ini dapat dilihat dalam Gambar 6.6. Perhatikan bahwa grafik memotong sumbu-xpada tiga buah titik (yang merupakan akar persamaan kubikx3−3x2+ 2x= 0).
Gambar 6.6 Grafik fungsiy=x3−3x2+ 2x
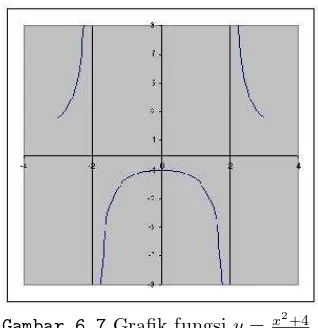
Contoh 5. Fungsi yang diberikan oleh persamaan
y= x
2+ 4
merupakan polinom rasional. Daerah asalnya adalah{x : x6=±2}. Grafiknya dapat dilihat dalam Gambar 6.7.
Gambar 6.7 Grafik fungsiy= x2+4
x2−4
Soal Latihan
1. Tentukan daerah nilai fungsi polinomy= 4x−4x2 dan sketsalah grafiknya.
2. Tentukan daerah asal fungsi rasionaly= 11+−xx dan sketsalah grafiknya.
6.3 Operasi pada Fungsi; Fungsi Invers
Jika H ⊆ R, f, g : H → R, dan λ ∈ R, maka kita definisikan f +g dan λf
sebagai fungsi yang memenuhi aturan
(f +g)(x) :=f(x) +g(x), x∈H; (λf)(x) :=λf(x), x∈H.
Selain itu kita definisikan pulaf g danf /gsebagai (f g)(x) :=f(x)g(x), x∈H; (f /g)(x) :=f(x)/g(x), x∈H, g(x)6= 0.
MisalkanA, B ⊆R, g: A→B, danf : B →R. Maka kita definisikan fungsi komposisif◦g:A→Rsebagai
(f◦g)(x) :=f(g(x)), x∈A.
Perhatikan bahwa untuk tiapx∈A
x7→g(x)7→f(g(x)).
Di sini fungsi g beroperasi terlebih dahulu terhadapx, dan setelah itu fungsif ber-operasi terhadapg(x).
Contoh 6. Misalkanf :R→Rdidefinisikan sebagai
f(x) = x
2−1
x2+ 1, x∈R,
dang:R→Rdidefinisikan sebagai
g(x) =x2.
MisalkanAdanBadalah himpunan danfadalah fungsi dariAkeB. Ini berarti bahwa bahwasetiapanggota a∈Amempunyai sebuah petatunggalb=f(a)∈B. Kita sebutf−1fungsiinversdarif apabilaf−1merupakan fungsi dariBkeAdengan
sifat
x=f−1(y) jika dan hanya jikay=f(x).
Tidak semua fungsi mempunyai fungsi invers. Dari definisi di atas jelas bahwa
f :A→B mempunyai fungsi inversf−1:B
→Ajika dan hanya jika setiapb∈B
merupakan peta dari sebuah anggotatunggala∈A. Fungsi dengan sifat ini disebut sebagai suatukorespondensi1−1 antaraA danB.
Secara geometris, f : A → B merupakan korespondensi 1−1 antara A dan
B jika dan hanya jika setiap garis vertikal yang memotongA juga memotong grafik
f merupakan fungsi, sementara kondisi kedua memastikan bahwa f−1 merupakan fungsi. Lihat Gambar 6.8 di bawah ini.
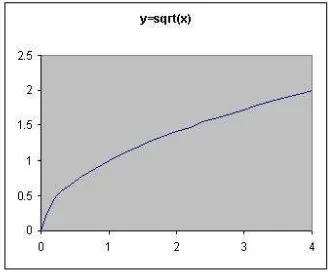
Contoh 7. Fungsi f(x) = √x merupakan korespondensi 1−1 antara [0,∞) dan [0,∞). Fungsi ini mempunyai fungsi invers, yaitu
f−1(x) =x2, x≥0.
Gambar 6.8 Korespondensi 1−1
Soal Latihan
1. Misalkan f : [0,1]→[0,1] didefinisikan sebagai
f(x) =1−x
1 +x, 0≤x≤1,
dang: [0,1]→[0,1] didefinisikan sebagai
g(x) = 4x−4x2, 0≤x≤1.
Tentukan aturan untukf◦g dang◦f. Apakah mereka sama?
2. Untuk fungsi f dan g pada Soal 1, tunjukkan bahwa f−1 ada sedangkan g−1
tidak ada. Tentukan aturan untukf−1.
6.4 Fungsi Terbatas
Misalkanf terdefinisi padaH. Kita katakan bahwaf terbatas di atas padaH
oleh suatu batas atasM apabila untuk tiapx∈H berlaku
f(x)≤M.
Ini setara dengan mengatakan bahwa himpunan
f(H) ={f(x) : x∈H}
terbatas di atas oleh M. Jika f terbatas di atas pada H, maka menurut Sifat Ke-lengkapanf(H) mempunyai supremum. Misalkan
B := sup
x∈H
f(x) = supf(H).
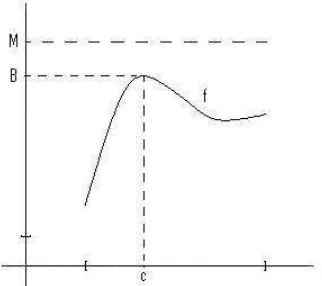
Secara umum, belum tentu terdapatc∈H sehinggaf(c) =B. Jika terdapatc∈H
sehingga f(c) = B, maka B disebut sebagai nilai maksimum f pada H dan nilai maksimum ini ‘tercapai’ dic. Untuk ilustrasi, lihat Gambar 6.9 di bawah ini.
Gambar 6.9 Fungsi terbatas dan nilai maksimumnya
Definisi fungsiterbatas di bawah dan nilai minimum dapat dirumuskan secara serupa. Jika f terbatas di atas dan juga di bawah pada himpunan H, maka f
dikatakan terbatas pada H. Menurut Proposisi 2 pada Bab 1, f terbatas pada H
Contoh 8. Misalkanf : (0,∞)→Rdidefinisikan sebagai f(x) = 1
x, x >0.
Fungsi ini terbatas di bawah pada (0,∞) dan inf
x>0f(x) = 0, namunf tidak mempunyai
nilai minimum. Perhatikan pula bahwa f tidak terbatas di atas pada (0,∞). Contoh 9. Misalkanf : [0,1]→[0,1] didefinisikan oleh
f(x) = 1−x.
Fungsi ini terbatas pada [0,1], mencapai nilai maksimumnya (yaitu 1) di 0, dan juga mencapai nilai minimumnya (yaitu 0) di 1.
Soal Latihan
1. Selidiki apakahf : [0,1]→[0,1] yang didefinisikan sebagai
f(x) =1−x
1 +x, 0≤x≤1,
terbatas serta mencapai nilai maksimum dan minimumnya. 2. Selidiki apakahg: [0,1]→[0,1] yang didefinisikan sebagai
g(x) = 4x−4x2, 0≤x≤1.
terbatas serta mencapai nilai maksimum dan minimumnya. 3. Tunjukkan bahwa f(x) = 1
1+x2 terbatas pada R. Apakah f mencapai nilai
maksimum dan minimumnya?
4. Misalkan f dangterbatas di atas padaH dana∈R. Buktikan bahwa
• sup
7. LIMIT DAN KEKONTINUAN
7.1 Limit Fungsi di Suatu Titik
Diberikan sebuah fungsif yang terdefinisi pada interval (a, b) kecuali mungkin di sebuah titikc∈(a, b), kita tertarik untuk mengamati nilaif(x) untukxdi sekitar
c. Khususnya, kita bertanya: apakah f(x) menuju suatu bilangan tertentu bila x
menujuc? Berikut ini adalah definisi limit sepihak, yaitulimit kiridanlimit kanan, di suatu titik.
Misalkan f terdefinisi pada interval (a, c) dan L ∈R. Kita katakan bahwa f menujuLbilaxmenujuc dari kiri, dan kita tulis
f(x)→L bilax→c−
atau
lim
x→c−f(x) =L,
apabila untuk setiapǫ >0 terdapatδ >0 sedemikian sehingga jikac−δ < x < c, maka |f(x)−L|< ǫ.
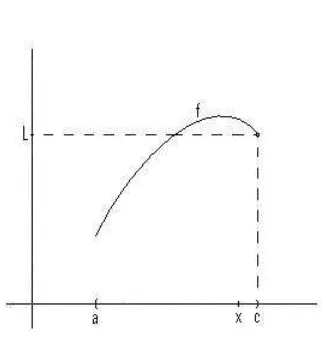
Misalkanf terdefinisi pada interval (c, b) danM ∈R. Kita katakan bahwaf menujuM bilaxmenujucdari kanan, dan kita tulis
f(x)→M bilax→c+
atau
lim
x→c+f(x) =M,
Gambar 7.1 Limit Kirif di c
BilanganL danM disebut sebagailimit kiridanlimit kanan darif di c. Nilai |f(x)−L|(atau|f(x)−M|) menyatakan jarak antaraf(x) danL(atau jarak antara
f(x) danM), yang dapat kita interpretasikan sebagai kesalahan dalam menghampiri nilaiLatauM denganf(x) (atau sebaliknya menghampiri nilaif(x) denganLatau
M). Kesalahan ini dapat dibuat sekecil yang kita kehendaki dengan cara mengambil
xsedekat-dekatnya kecdari kiri atau kanan.
Contoh 1. Misalkanf :R→Radalah fungsi yang didefinisikan sebagai
f(x) =
1−x, x≤1; 2x, x >1.
Maka,
lim
x→1−f(x) = 0 dan limx→1+f(x) = 2.
Perhatikan bahwa nilaif(1) terdefinisi, yaknif(1) = 0.
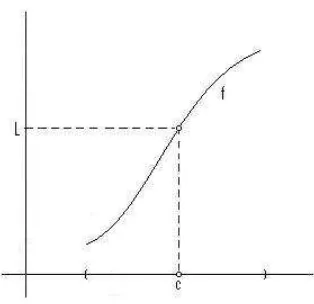
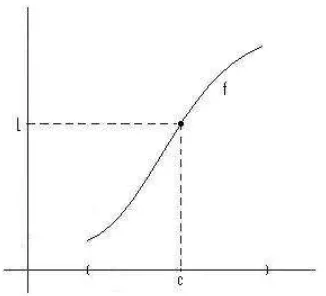
Misalkan f terdefinisi pada interval (a, b) kecuali mungkin di titik c ∈ (a, b), danL∈R. Kita katakan bahwaf menujukeL bilaxmenujuc, dan kita tuliskan
f(x)→L bilax→c
atau
lim
apabila untuk setiapǫ >0 terdapatδ >0 sedemikian sehingga jika 0<|x−c|< δ, maka |f(x)−L|< ǫ.
Dalam hal ini, bilanganL disebut sebagailimit f di c, danf dikatakanmempunyai
limitLdic.
Gambar 7.2 Limitf di c
Perhatikan bahwa kondisi 0<|x−c|< δsetara dengan−δ < x−c < δ, x6=c. Jadi, 0<|x−c|< δjika dan hanya jikaxmemenuhi salah satu dari dua pertaksamaan berikut:
c−δ < x < catauc < x < c+δ.
Sehubungan dengan itu, kita mempunyai proposisi berikut. Proposisi 2. lim
x→cf(x) =Ljika dan hanya jikaxlim→c−f(x) =Ldanxlim→c+f(x) =L.
Menurut Proposisi 2, fungsi pada Contoh 1 tidak mempunyai limit di 1 karena limit kiri dan limit kanannya tidak sama.
Contoh 3. Misalkanf(x) =xx2−−11. Fungsi ini terdefinisi pada (−∞,1) dan juga pada (1,∞). Bila kita tinjau nilaif(x) untukx <1, maka kita dapatkan bahwa
f(x)→2 bilax→1−.
Bila kita amati nilaif(x) untukx >1, maka kita dapatkan bahwa
Jadi, limit kiri darif di csama dengan limit kanannya, yaitu 2. Karena itu lim
x→cf(x) = 2.
(Perhatikan bahwa pada contoh ini,f tidak terdefinisi di 1.) Proposisi 4. (i) lim
1. Misalkann∈N. Buktikan, dengan menggunakan definisi, bahwa lim
x→0+x
1/n= 0.
2. Misalkan f :R→Radalah fungsi yang didefinisikan sebagai
f(x) =
3. Buktikan, dengan menggunakan definisi, bahwa lim
7.2 Kekontinuan di Suatu Titik
Dalam definisi lim
x→cf(x), nilaif dicsama sekali tidak diperhatikan. Kita hanya
tertarik dengan nilaif(x) untukxmenujuc, bukan dengan nilaif dic. Jadi mungkin saja f mempunyai limitL di c sekalipun f tidak terdefinisi di titik c. Dalam hal f
terdefinisi dic, dapat terjadif(c)6=L.
Misalkanf terdefinisi pada (a, b) danc∈(a, b). Kita katakan bahwaf kontinu
di titikc jika dan hanya jika
lim
x→cf(x) =f(c).
Berdasarkan Proposisi 2,f kontinu dicjika dan hanya jika untuk setiapǫ >0 terdapat
δ >0 sedemikian sehingga jika |x−c|< δ, maka |f(x)−f(c)|< ǫ.
Secara intuitif,f kontinu di cberarti grafik fungsif tidak ‘terputus’ di c.
Seperti halnya limit sepihak, kita juga mempunyai definisi kekontinuan sepihak. Jikafterdefinisi pada (a, c] dan lim
x→c−f(x) =f(c), maka kita katakan bahwafkontinu
kiridic. Jikaf terdefinisi pada [c, b) dan lim
x→c+f(x) =f(c), maka kita katakan bahwa
f kontinu kanandi c.
Gambar 7.3 Fungsi Kontinu di Suatu Titik
Contoh 5. (i) Untuk setiapn∈N, fungsif(x) =x1/nkontinu kanan di 0.
Teorema 6. Misalkan f terdefinisi pada (a, b)kecuali mungkin di c∈(a, b). Maka,
lim
x→cf(x) = L jika dan hanya jika, untuk setiap barisan hxni di (a, b) dengan xn 6=
c (n∈N) dan lim
n→∞xn=c, berlakunlim→∞f(xn) =L.
Catatan. Jikaf kontinu di c, makaL=f(c) dan Teorema 6 menyatakan bahwa lim
n→∞f(xn) =f nlim→∞xn
;
yakni, limit dapat ‘bertukar’ dengan f. Hasil serupa berlaku untuk limit kiri dan limit kanan.
Dengan menggunakan Teorema 6, kekontinuanf(x) =px+qdi sebarang titik
c∈Rdapat dibuktikan sebagai berikut. Misalkanhxniadalah sebarang barisan yang
konvergen kec. Maka, menurut Proposisi 5 pada Bab 3,
f(xn) =pxn+q→pc+q=f(c), untukn→ ∞.
Menurut akibat dari Teorema 6,f kontinu dic. Soal Latihan
1. Buktikan Teorema 6.
2. Buktikan bahwa f(x) =√xkontinu di setiapc >0. 3. Buktikan bahwa f(x) =|x|kontinu di setiap titik.
4. Misalkanf(x) =xuntukxrasional danf(x) =−xuntukxirrasional. Buktikan bahwaf kontinu hanya dic= 0.
5. Misalkanf terdefinisi pada (a, b) dan kontinu di suatu titikc∈(a, b). Buktikan jikaf(c)>0, maka terdapatδ >0 sehinggaf(x)>0 untukx∈(c−δ, c+δ). 6. Konstruksi sebuah fungsif :R→Ryang kontinuhanyadi sebuah titik.
7.3 Sifat-sifat Limit dan Kekontinuan
Proposisi 7. Misalkan f dan g terdefinisi pada interval (a, b) kecuali mungkin di c∈(a, b). Misalkan lim
(i) lim
Akibat 9. Fungsi polinom kontinu di setiap titik. Fungsi rasional kontinu di setiap titik dalam daerah asalnya.
Bukti. Menurut Proposisi 4,f(x) =kdan g(x) =xkontinu di sebarang titikc∈R.
Menurut Proposisi 7(ii),h(x) =xi kontinu di sebarang titikc
∈R, untuk tiapi∈N.
Akibatnya, menurut Proposisi 7(i), fungsi polinom
p(x) =anxn+an−1xn−1+· · ·+a1x+a0
kontinu di setiap titik c ∈ R. Untuk membuktikan kekontinuan fungsi rasional di
setiap titik dalam daerah asalnya, kita perlu menggunakan Proposisi 7(iii).
2. Berikan contoh fungsi f dan g dengan lim
x→0f(x) tidak ada, limx→0g(x) ada, dan
lim
x→0f(x)g(x) ada. Apakah ini bertentangan dengan Proposisi 7(ii) atau 7(iii)?
3. Benar atau salah: Jika lim
x→cg(x) =L dan limy→Lf(y) =M, maka limx→cf(g(x)) =
M?
4. Buktikan jika lim
x→cg(x) =Ldanf kontinu diL, maka limx→cf(g(x)) =f(L).
5. Kita katakan bahwa lim
x→c+f(x) = +∞ apabila, untuk setiap M > 0 terdapat
δ >0 sehinggaf(x)> M untukc < x < c+δ. Buktikan bahwa lim
x→0+
1
8. FUNGSI KONTINU PADA INTERVAL
8.1 Kekontinuan pada Interval
Secara geometris,f kontinu di suatu titik berarti bahwa grafiknya tidak terputus di titik tersebut. Serupa dengan itu,f kontinu pada suatu interval apabila grafiknya tidak terputus pada interval tersebut. Secara intuitif,f kontinu pada suatu interval apabila kita dapat menggambar grafik fungsi f pada interval tersebut tanpa harus mengangkat pena dari kertas.
Secara formal, sebuah fungsi f dikatakan kontinu pada suatu interval bukaI
jika dan hanya jikaf kontinu di setiap titik padaI. Fungsif dikatakankontinupada interval tutupI= [a, b] jika dan hanya jikaf kontinu di setiap titikc∈(a, b), kontinu kanan dia, dan kontinu kiri dib. (Lihat Gambar 8.1 dan 8.2.)
Gambar 8.1 Grafik fungsi kontinu pada interval buka
Contoh 1. Misalkanf :R→Rdidefinisikan sebagai f(x) =
x, x≤1;
3
Perhatikan bahwaf kontinu di setiap titik kecuali dic= 1. Namunf kontinu kiri di
c= 1, dan karenanyaf kontinu pada interval [0,1]. Karenaf tidak kontinu kanan di
c= 1, makaf tidak kontinu pada interval [1,2].
Gambar 8.2 Grafik fungsi kontinu pada interval tutup
Proposisi 2. Misalkan f terdefinisi pada suatu interval I. Maka, f kontinu pada I jika dan hanya jika, untuk setiap x∈I dan setiap ǫ >0 terdapat δ >0 sedemikian sehingga
|f(x)−f(y)|< ǫ untuk y∈I dengan|x−y|< δ.
Contoh 3. (i) Fungsi f(x) =px+qkontinu pada sebarang intervalI. (ii) Fungsig(x) =|x|kontinu pada sebarang intervalI.
(iii) Fungsih(x) =√xkontinu pada sebarang intervalI⊆[0,∞).
Soal Latihan
1. Misalkan f : [0,5]→Rdidefinisikan sebagai
f(x) =
2x, 0≤x <1; 1, 1≤x≤5.
Selidiki apakahf kontinu di setiap titik pada interval [0,5]. Selidiki kekontinuan
2. Buktikan bahwa fungsif pada Soal 1 terbatas. Tentukan apakah ia mempunyai nilai maksimum dan nilai minimum.
3. Misalkan K >0 danf :I→Radalah fungsi yang memenuhi
|f(x)−f(y)| ≤K|x−y| untuk setiapx, y∈I. Buktikan bahwaf kontinu padaI.
8.2 Sifat-sifat Fungsi Kontinu pada Interval
Sebagai akibat dari Proposisi 8 dan Teorema 11 yang telah dibahas pada Bab 7, kita mempunyai Proposisi 4 dan Proposisi 6 di bawah ini.
Proposisi 4. Misalkan f dan g kontinu pada suatu interval I dan λ, µ∈R. Maka λf+µg danf g kontinu padaI. Juga, jika g6= 0, maka fg kontinu padaI.
Contoh 5. (i) Setiap fungsi polinom kontinu pada sebarang interval.
(ii) Setiap fungsi rasional kontinu pada sebarang interval dalam daerah asalnya. Se-bagai contoh,f(x) = 1x kontinu pada (0,∞).
(iii) Fungsif(x) =x+√xkontinu pada sebarang intervalI⊆[0,∞), karenaf1(x) =x
danf2(x) =√xkontinu pada sebarang intervalI⊆[0,∞).
Proposisi 6. Misalkan g : I →J kontinu pada interval I dan f : J → R kontinu pada intervalJ. Makaf◦g kontinu pada I.
Contoh 7. (i) Fungsih(x) =|1+x|kontinu pada sebarang interval, karenaf(x) =|x|
dang(x) = 1 +xkontinu pada sebarang interval.
(ii) Fungsih(x) =1+1−√√xx kontinu pada sebarang intervalI⊆[0,∞).
Soal Latihan
1. Jelaskan mengapa fungsi berikut kontinu pada sebarang interval. • f(x) =1+1|x|.
2. Misalkan f kontinu pada suatu interval I dan untuk setiap bilangan rasional
r∈I berlakuf(r) =r2. Buktikan bahwaf(x) =x2untuk setiap x
∈I. 3. Misalkan f : [0,1] → [0,1] adalah fungsi kontraktif, yakni memenuhi
ketak-samaan
|f(x)−f(y)| ≤C|x−y|, x, y∈[0,1],
untuk suatu konstantaC dengan 0< C <1. Konstruksi barisan hxnidengan
x1 ∈I dan xn+1 =f(xn), n∈ N. Buktikan bahwa hxni konvergen ke suatu
L∈[0,1], danL=f(L).
8.3 Lebih jauh tentang Fungsi Kontinu pada Interval
Sebagaimana telah disinggung dalam Bab 2, interval [a, b] yang tertutup dan terbatas merupakan himpunan kompak diR. Sekarang kita akan mempelajari
keis-timewaan yang dimiliki oleh fungsi kontinu pada interval kompak [a, b].
Teorema 8. Misalkan f kontinu pada interval [a, b]. Makaf([a, b]) juga merupakan suatu interval kompak.
Teorema ini merupakan konsekuensi dari beberapa teorema berikut.
Teorema 9. Misalkanf kontinu pada suatu interval I. Maka daerah nilainya, yaitu f(I), juga merupakan suatu interval.
Teorema 10 (Teorema Nilai Antara). Misalkanf kontinu pada suatu intervalI yang memuat a danb. Jika uterletak di antara f(a) danf(b), maka terdapat c di antaraa danbsedemikian sehingga f(c) =u.
Catatan. Teorema 10 setara dengan Teorema 9. Oleh karena itu kita cukup mem-buktikan salah satu di antara mereka.
Bukti Teorema 10. Tanpa mengurangi keumuman, asumsikan a < b dan f(a) < u < f(b). Tinjau himpunan H := {x ∈ [a, b] : f(x) < u}. Jelas bahwa H 6= ∅ karena a ∈ H. KarenaH juga terbatas, maka H mempunyai supremum, sebutlah
Andaikan f(c)< u. Karenaf kontinu di c, maka terdapat δ > 0 sedemikian sehingga f c+δ2
< u(?). Jadi c+δ2 ∈ H. Ini bertentangan dengan fakta bahwa
c = supH. Sekarang andaikan f(c) > u. Sekali lagi, karena f kontinu dic, maka terdapat δ > 0 sedemikian sehinggaf(x) > uuntuk c−δ < x≤ c (?). Jadi tidak ada satu pun anggotaH pada interval (c−δ, c]. Ini juga bertentangan dengan fakta bahwac= supH.
Teorema 11. Misalkan f kontinu pada interval[a, b]. Makaf terbatas pada[a, b]. Bukti. Misalkanf tak terbatas pada [a, b]. Maka terdapat suatu barisanhxnidi [a, b]
sedemikian sehingga
|f(xn)| →+∞untuk n→ ∞. (1)
Karena hxniterbatas, maka menurut Teorema Bolzano - Weierstrass terdapat suatu
sub-barisan hxnki yang konvergen ke suatu titik c ∈ [a, b]. Tetapi f kontinu di c,
sehinggaf(xnk)→f(c) untukk→ ∞. Ini bertentangan dengan (1). Jadi mestilah
f terbatas pada [a, b].
Teorema 12. Misalkan f kontinu pada interval [a, b]. Maka f mencapai nilai mak-simum dan nilai minimum pada [a, b].
Bukti. Dari Teorema 11 kita tahu bahwa f terbatas pada [a, b]. Misalkan v := supf([a, b]). Konstruksi barisan hxni di [a, b] dengan f(xn) → v untuk n → ∞.
Karena hxni terbatas, terdapat sub-barisanhxnkiyang konvergen ke suatu titik c∈
[a, b]. Namun kekontinuan di c mengakibatkan f(xnk)→ f(c) untuk k→ ∞. Jadi
mestilah v = f(c), dan ini berarti bahwa v merupakan nilai maksimum. Serupa dengan itu,f juga mencapai nilai minimumnya.
Contoh 13. Persamaan 10x7
−13x5
−1 = 0 mempunyai sebuah akar c ∈(−1,0). Untuk menunjukkannya, misalkan f(x) = 10x7−13x5−1. Maka, f(−1) = 2 dan
f(0) = −1. Karena f kontinu pada [−1,0] dan 0 terletak di antara f(−1) dan
f(0), maka menurut Teorema Nilai Antara terdapatc∈(−1,0) sedemikian sehingga
f(c) = 0. Bilanganc dalam hal ini merupakan akar persamaan di atas.
Contoh 14. Misalkan f : [a, b]→[a, b] kontinu pada [a, b]. Maka, terdapat c∈[a, b] sedemikian sehingga f(c) = c. [Bilangan c demikian disebut sebagai titik tetap f.] Perhatikan bahwa peta dari [a, b] merupakan himpunan bagian dari [a, b], sehingga
kontinu pada [a, b], maka g juga kontinu pada [a, b]. Namun g(a) = f(a)−a ≥ 0 dang(b) =f(b)−b≤0. Menurut Teorema Nilai Antara, mestilah terdapatc∈[a, b] sedemikian sehinggag(c) = 0. Akibatnyaf(c) =c.
Soal Latihan
1. Lengkapi Bukti Teorema Nilai Antara, khususnya bagian yang diberi tanda tanya (?).
2. Buktikan bahwa setiap polinom berderajat ganjil mempunyai sedikitnya satu akar real.
3. Misalkanf kontinu pada suatu interval kompakI. Misalkan untuk setiapx∈I
terdapaty∈I sedemikian sehingga
|f(y)| ≤ 12|f(x)|.
Buktikan bahwa terdapat suatuc∈Isedemikian sehinggaf(c) = 0.
8.4 Kekontinuan Seragam
Proposisi 2 menyatakan bahwa suatu fungsi f kontinu pada sebuah interval I
jika dan hanya jika untuk setiap x∈I dan setiap ǫ >0 terdapat δ >0 sedemikian sehingga
|f(x)−f(y)|< ǫ
untuky∈Idengan|x−y|< δ. Contoh berikut memperlihatkan bahwa secara umum nilaiδ bergantung padaǫdanx.
Contoh 16. Kita telah mengetahui bahwaf(x) = 1
x kontinu pada (0,1]. Diberikan
Dalam kasus tertentu, nilaiδ hanya bergantung padaǫ, tidak pada x. Hal ini terjadi pada, misalnya, f(x) =px+q, x∈R, dengan p6= 0. Diberikanǫ >0, kita
dapat memilihδ= ǫ
|p| sedemikian sehingga
|f(x)−f(y)|=|p| · |x−y|< ǫ
untuk x, y ∈ R dengan |x−y| < δ. Kekontinuan f(x) = px+q dalam hal ini
merupakan kekontinuan ‘seragam’ padaR.
Fungsif :I→Rdikatakankontinu seragampadaI apabila untuk setiapǫ >0
terdapatδ >0 sedemikian sehingga
|f(x)−f(y)|< ǫ
untuk x, y∈I dengan |x−y|< δ. Perhatikan bahwa dalam definisi di atasxdany
muncul setelahδ, yang mengindikasikan bahwaδ tidak bergantung padax(dany). Teorema 17. Fungsi f :I → Rtidak kontinu seragam pada I jika dan hanya jika
terdapatǫ0>0 dan dua barisanhxnidanhynidiIsedemikian sehingga|xn−yn|< 1n
dan|f(xn)−f(yn)| ≥ǫ0 untuk setiapn∈N.
Teorema berikut menyatakan bahwa kekontinuan pada interval kompak meru-pakan kekontinuan seragam.
Teorema 18. Jikaf kontinu pada [a, b], makaf kontinu seragam pada [a, b].
Bukti. Andaikan f tidak kontinu seragam pada [a, b]. Maka, menurut Teorema 17, terdapatǫ0>0 dan dua barisanhxnidanhynidi [a, b] sedemikian sehingga|xn−yn|<
1
n dan|f(xn)−f(yn)| ≥ǫ0 untuk setiapn∈N. Karenahxniterbatas di [a, b], maka
menurut Teorema Bolzano-Weierstrass terdapat sub-barisan hxnki yang konvergen,
sebutlah kec ∈[a, b]. Karena |xn−yn| < n1 untuk setiap n∈N, maka sub-barisan
hynkiakan konvergen ke c juga. Selanjutnya, karena f kontinu di c, maka hf(xnk)i
danhf(ynk)ikonvergen kef(c). Akibatnya,|f(xnk)−f(ynk)| →0 untukk→ ∞. Ini
Soal Latihan
1. Contoh 16 memperlihatkan bahwa fungsi f(x) = 1
x tampaknya tidak kontinu
seragam pada (0,1]. Buktikan bahwa iamemangtidak kontinu seragam pada (0,1].
2. Selidiki apakahf(x) =x2 kontinu seragam pada [0,
∞). 3. Buktikan jika fungsif :I→Rmemenuhi ketaksamaan
|f(x)−f(y)| ≤K|x−y|, x, y∈I,
9. TURUNAN
9.1 Turunan di Suatu Titik
Diberikan sebuah fungsi, kita seringkali perlu mempelajari bagaimana nilai fungsi itu berubah terhadap peubahnya. Salah satu caranya adalah dengan menghi-tungturunandari fungsi itu.
Misalkanfterdefinisi pada suatu interval terbukaIyang memuat titikc. Maka,
f dikatakanmempunyai turunandi titikc apabila limit
lim
x→c
f(x)−f(c)
x−c
ada, dan dalam hal ini nilai limit tersebut disebut turunan dari f di titik c, yang biasanya dilambangkan denganf′(c) atauDf(c).
Jadi, untuk fungsif yang mempunyai turunan dic, kita mempunyai
f′(c) = lim
x→c
f(x)−f(c)
x−c .
Dengan menggantixdenganc+h, kita peroleh
f′(c) = lim
h→0
f(c+h)−f(c)
h .
Catat bahwa f mempunyai turunan di c jika dan hanya jika terdapat suatu bilanganL=f′(c) sedemikian sehingga
f(c+h)−f(c)−Lh=ǫ(h) dengan ǫ(hh) →0 untukh→0.
singgung tersebut adalahf′(c). Untuk ilustrasi, lihat Gambar 9.1. Persamaan garis singgung pada grafik fungsiy=f(x) di titik (c, f(c)) dalam hal ini adalah
y=f(c) +f′(c)(x−c).
Persamaan ini merupakan hampiran linear untuky=f(x). Jikaxberubah daric ke
c+h, makay akan bertambah kira-kira sebesarhf′(c). Jadi, dengan mengetahuif′, kita mengetahui bagaimanaf berubah (bilaxberubah).
Sebagai catatan, masalah menentukan persamaan garis singgung pada kurva di titik tertentu pertama kali dipelajari oleh Rene Descartes pada 1620-an. Namun, kalkulus diferensial dan integral yang kita kenal sekarang ini ‘ditemukan’ oleh Isaac Newton pada 1665 (namun dipublikasikan pada 1704) dan Gottfried Wilhelm von Leibniz pada 1684.
Gambar 9.1 Grafik fungsif yang mempunyai turunan di titik c
Contoh 1. Misalkanf(x) =x2 dan c= 1. Untuk memeriksa apakahf mempunyai
turunan di 1, kita hitung
lim
x→1
f(x)−f(1)
x−1 = limx→1
x2
−1
x−1 = limx→1(x+ 1) = 2.
Jadif mempunyai turunan di 1, denganf′(1) = 2.
Contoh 2. Misalkanf(x) =|x|danc= 0. Perhatikan bahwa
tidak ada (?). Karena itu,f tidak mempunyai turunan di 0.
Proposisi 3. Misalkanf terdefinisi pada suatu interval terbukaI yang memuat titik c. Jikaf mempunyai turunan dic, maka f kontinu di c.
Bukti. Perhatikan bahwa
f(x)−f(c) = f(x)−f(c)
x−c ·(x−c)→f
′(c)·0 = 0 untukx→c. Jadif(x)→f(c) untukx→c.
Dalam prakteknya, kita sering pula menggunakan kontraposisi dari Proposisi 3 yang menyatakan: jikaf tidak kontinu dic, makaf tidak akan mempunyai turunan di c. Sebagai contoh, fungsif : [0,2]→Ryang didefinisikan sebagai
f(x) =
2x, 0≤x <1; 1, 1≤x≤2,
tidak mungkin mempunyai turunan di 1 karenaf tidak kontinu di titik tersebut. Catatan. Proposisi 3 menyatakan bahwa kekontinuanf dicmerupakan syarat perlu bagi f untuk mempunyai turunan di c. Namun, Contoh 2 memperlihatkan bahwa kekontinuanf dic bukan merupakan syarat cukup untuk mempunyai turunan dic. Soal Latihan
1. Tentukan persamaan garis singgung pada kurvay=x2 di titik (1,1).
2. Tunjukkan bahwaf(x) =x2 mempunyai turunan di setiap titikc
∈R, dengan f′(c) = 2c.
3. Diketahui f(x) =x|x|, x∈R. Selidiki apakahf mempunyai turunan di 0.
4. Berikan sebuah contoh fungsi f yang kontinu di 0 tetapi tidak mempunyai tu-runan di sana, selainf(x) =|x|.
5. Konstruksi sebuah fungsif :R→Ryang mempunyai turunanhanyadi sebuah
6. Buktikan jikaf mempunyai turunan dic, maka
f′(c) = lim
h→0
f(c+h)−f(c−h)
2h .
Berikan sebuah contoh fungsi yang tidak mempunyai turunan di suatu titik namun limit di atas ada.
9.2 Sifat-sifat Dasar Turunan
Teorema 4. Misalkanf dang terdefinisi pada suatu interval terbukaIyang memuat titikc. Misalkanλdanµbilangan real sembarang. Jikaf dangmempunyai turunan di c, maka λf+µg, f g,dan f /gmempunyai turunan dic, dan
Fakta ini dapat dibuktikan secara induktif. Untukn= 1 atau f(x) =x, jelas bahwa
f(x) = xk, maka f′(x) = kxk−1. Maka, untuk n = k+ 1 atau f(x) = xk+1, kita peroleh
f′(x) =D(xk.x) =D(xk).x+xk.D(x) =kxk−1.x+xk= (k+ 1)xk.
Jadi, menurut Prinsip Induksi Matematika, pernyataan benar untuk setiapn∈N.
Teorema 6 (Aturan Rantai). Misalkan g mempunyai turunan di c danf mem-punyai turunan di y=g(c). Maka,f◦g mempunyai turunan dic dan
Namun, bila g konstan (misalnya), maka argumentasi di atas gugur. Untuk meng-atasinya, definisikan
Perhatikan bahwahkontinu di g(c). Mengingatg kontinu di c, maka menurut Teo-rema 10 pada Bab 7,h◦gkontinu di c. Akibatnya
1. Buktikan Teorema 4 bagian (iii).
3. Misalkan n∈N. Buktikan
• jika f(x) =x−n (x= 0), maka6 f′(x) =−nx−n−1.
• jika f(x) =x1/n(x >0), makaf′(x) = 1
nx
1/n−1.
4. Buktikan bahwa untuk bilangan rasionalrsembarang berlaku
D(xr) =rxr−1
asalkanx >0.
5. Misalkan f : R → R mempunyai turunan di x. Buktikan jika f mempunyai
inversf−1:R→Rdanf−1 mempunyai turunan diy=f(x), maka
Df−1(y) = 1
Df(x).
9.3 Turunan Tingkat Tinggi
Jikaf mempunyai turunan di setiap titik dalam suatu interval terbukaI, maka kita katakan f mempunyai turunan padaI. Dalam hal ini turunan dari f, yaituf′, merupakan fungsi yang juga terdefinisi padaI.
Selanjutnya kita dapat mendefinisikan turunan kedua dari f sebagai turunan darif′, yang nilainya dic adalah
f′′(c) = lim
x→c
f′(x)−f′(c)
x−c ,
asalkan limit ini ada. Dapat diperiksa bahwa bilaf mempunyai turunan kedua dic, maka
Setelah menghitung turunan pertama dan kedua dari f, turunan ketiga dan seterusnya dapat didefinisikan secara serupa. Secara umum,f(n)(x) menyatakan
tu-runan ke-n, n∈N, darif.
Bilaf mempunyai turunan ke-npada suatu interval yang memuat titikc, maka
f dapat dihampiri oleh suatu polinom berderajat n−1 dan kesalahannya dapat ditaksir dengan turunan ke-n. Lihat Teorema Taylor pada bab berikutnya.
Soal Latihan
1. Buktikan bilaf mempunyai turunan kedua dic, maka
f(c+h)−f(c)−hf′(c)−h
2
2 f
′′(c) =ǫ(h),
dengan ǫh(h2) →0 untukh→0.
2. Tentukan pada interval mana grafik fungsif(x) =x3 cekung ke atas dan pada
interval mana ia cekung ke bawah.
3. Tentukan rumus umum turunan ke-ndarif(x) = 1
10. TEOREMA NILAI RATA-RATA
10.1 Maksimum dan Minimum Lokal
Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c ∈ (a, b). Kita katakan bahwaf mencapai nilai maksimum lokaldic apabila
f(x)≤f(c)
untuk setiap xdalam suatu interval terbukaI yang memuatc. Titikc dalam hal ini disebut sebagaititik maksimum lokal.
Nilaidantitik minimum lokaldidefinisikan secara analog.
Gambar 10.1f mencapai nilai maksimum lokal dic
Jikaf(c) merupakan nilai maksimumf pada seluruh interval (a, b), maka ten-tunyaf mencapai nilai maksimum lokal di c. Namun sebaliknya belum tentu benar, nilai maksimum lokal belum tentu merupakan nilai maksimumf.
Contoh 1. Misalkanf :R→Radalah fungsi yang didefinsikan sebagai f(x) =
x+ 2, x <−1,
|x|, x≥ −1.
Maka,f mencapai nilai maksimum lokal di−1, namunf(−1) = 1 bukan merupakan nilai maksimum f pada R. Demikian pula f mencapai nilai minimum lokal di 0,
namun f(0) = 0 bukan merupakan nilai minimumf padaR.
Teorema 2. Misalkan f mempunyai turunan pada (a, b) dan c ∈ (a, b). Jika f mencapai nilai maksimum lokal dic. Selanjutnya misalkanx∈(c−δ, c) sembarang. Maka,x−c <0 dan (1) memberikanf(x)−f(c)<0 atauf(x)< f(c). Jadif juga tidak mungkin mencapai nilai minimum lokal dic.
Hal serupa terjadi ketika f′(c) < 0. Jadi, jika f′(c)6= 0, maka f tidak akan mencapai nilai maksimum atau minimum lokal dic.
Catatan. Kebalikan dari Teorema 2 tidak berlaku: jika f′(c) = 0, belum tentu f mencapai nilai maksimum atau minimum lokal dic.
Soal Latihan
2. Berikan sebuah contoh fungsi f yang mempunyai turunan nol di suatu titik tetapif tidak mencapai nilai maksimum atau minimum lokal di titik tersebut.
10.2 Titik Stasioner
Titikc dengan f′(c) = 0 disebuttitik stasioner f. Sebagaimana telah dicatat sebelumnya, tidak semua titik stasioner merupakan titik maksimum atau minimum lokal. Sebagai contoh, jika f(x) = x3, maka f′(x) = 3x2, sehingga 0 merupakan
titik stasioner. Namun, 0 bukan merupakan titik maksimum maupun minimum f. (Titik 0 dalam hal ini merupakan titik infleksi f, yaitu titik terjadinya perubahan kecekungan grafik fungsif.) Situasi yang lebih parah dapat terjadi. Sebagai contoh, fungsif(x) =x2sin1
x untukx6= 0 danf(0) = 0 mempunyai turunanf′(0) = 0 tetapi
0 bukan merupakan titik maksimum atau minimum lokal, ataupun titik infleksi.
Gambar 10.2Grafik fungsif(x) =x3
Teorema 3 (Teorema Rolle). Misalkan f kontinu pada [a, b] dan mempunyai turunan pada(a, b). Jika f(a) =f(b), maka f′(c) = 0 untuk suatuc∈(a, b).
Bukti. Karenaf kontinu pada interval kompak [a, b], maka menurut sifat kekontinuan
f mencapai nilai maksimum M di suatu titik c1 ∈ [a, b] dan juga mencapai nilai
Misalkan c1 dan c2 adalah titik-titik ujung [a, b]. Karena f(a) = f(b), maka
m = M dan dengan demikian f konstan pada [a, b]. Akibatnya f′(c) = 0 untuk setiap c ∈ (a, b). Jika c1 bukan titik ujung [a, b], maka c1 ∈ (a, b) dan f mencapai
nilai maksimum lokal di c1. Menurut Teorema 2,f′(c1) = 0. Hal serupa terjadi bila
c2bukan titik ujung [a, b].
Soal Latihan
1. Diketahui f(x) =x|x|, x∈R. Tunjukkan bahwa 0 merupakan titik stasioner.
Selidiki apakahf mencapai nilai maksimum atau minimum lokal di 0.
2. Beri contoh sebuah fungsi f yang terdefinisi pada [a, b], mempunyai turunan pada (a, b), danf(a) =f(b), namun tidak ada c∈(a, b) denganf′(c) = 0.
10.3 Teorema Nilai Rata-rata dan Teorema Taylor
Sebagai perumuman dari Teorema Rolle, kita mempunyai teorema berikut. Teorema 4 (Teorema Nilai Rata-rata). Misalkanf kontinu pada[a, b]dan mem-punyai turunan pada(a, b). Maka
f′(c) =f(b)−f(a)
b−a
untuk suatu c∈(a, b).
Catatan. Nilai f(b)b−−af(a) disebutnilai rata-rataf pada [a, b]. Nilai ini sama dengan gradien ruas garis singgung yang menghubungkan titik (a, f(a)) dan (b, f(b)). Teo-rema Nilai Rata-rata menyatakan bahwa pada kurva y =f(x) terdapat suatu titik (c, f(c)) dengan gradien garis singgung sama dengan nilai rata-rataf pada [a, b].
Bukti Teorema 4. MisalkanF didefinisikan pada [a, b] sebagai
F(x) =f(x)−hx
denganhkonstanta. MakaF kontinu pada [a, b] dan mempunyai turunan pada (a, b). Kita pilih konstantahsedemikian sehinggaF(a) =F(b), yakni
h= f(b)−f(a)
KarenaF memenuhi hipotesis Teorema Rolle, makaF′(c) = 0 untuk suatuc∈(a, b). Namun
F′(c) =f′(c)−h= 0,
sehingga teorema pun terbukti.
Jika f mempunyai turunan di c, maka persamaan garis singgung pada kurva
y=f(x) di titik (c, f(c)) adalah
y=f(c) + (x−c)f′(c).
Untuk x dekat c, nilai f(c) + (x−c)f′(c) merupakan hampiran yang ’baik’ untuk
f(x). Namun seberapa besar kesalahan dalam penghampiran ini?
Lebih jauh, misalkanf mempunyai turunan ke-(n−1) dic. Maka polinom
P(x) =f(c) + (x−c)f′(c) +(x−c)
c. Namun, sekali lagi, seberapa besar kesalahan dalam penghampiran ini. Teorema Taylor di bawah ini menjawab pertanyaan tersebut.
Teorema 5 (Teorema Taylor). Misalkanf mempunyai turunan ke-npada interval terbukaI yang memuat titikc. Maka, untuk setiapx∈I, berlaku
f(x) =f(c) + (x−c)f′(c) +(x−c)
Proof. Untuktdi antara xdanc, definisikan
Maka, G(x) = G(c) = 0, sehingga menurut Teorema Rolle, terdapat ξ di antarax sedemikian sehinggaf′(c) sama dengan nilai rata-rata tersebut.
2. Misalkan f kontinu pada [a, b] dan mempunyai turunan pada (a, b). Buktikan jikaf′(x) = 0 untuk setiapx∈(a, b), maka f konstan pada [a, b].
3. Misalkan f :R→Rmempunyai turunan di setiap titik danf′(x) =x2 untuk
setiapx∈R. Buktikan bahwaf(x) = 1
3x
3+C, denganCsuatu konstanta.
4. Diketahui f :R→Rmemenuhi ketaksamaan
|f(x)−f(y)| ≤C|x−y|p, x, y
∈R,
untuk suatuC >0 danp >1. Buktikan bahwaf konstan. 5. Buktikan jikaf mempunyai turunan kedua dic, maka
f′′(c) = lim
h→0
f(c+h)−2f(c) +f(c−h)
h2 .
Berikan sebuah contoh fungsi yang tidak mempunyai turunan kedua di suatu titik namun limit di atas ada.
6. Misalkan c ∈ R dan n ∈ N. Buktikan dengan menggunakan Teorema Taylor
11. FUNGSI MONOTON (DAN FUNGSI
KONVEKS)
11.1 Definisi dan Limit Fungsi Monoton
Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik
padaH apabila untuk setiapx, y∈H denganx < y berlaku
f(x)≤f(y).
Jika ketaksamaan<berlaku, maka kita katakan bahwaf naik sejatipadaH. Definisi serupa dapat dirumuskan untuk fungsiturundanturun sejatipadaH. Fungsi naik atau turun disebut fungsimonoton. Fungsi yang naik dan turun sekaligus padaH mestilah konstan padaH.
Contoh 1. (i) Fungsi f : R→ Ryang didefinisikan sebagai f(x) = x3 merupakan
fungsi naik sejati padaR.
(ii) Fungsi g : (0,∞) → R yang didefinisikan sebagai g(x) = 1
x merupakan fungsi
turun sejati pada (0,∞).
Proposisi 2. Jikaf naik pada[a, b], makaf mencapai nilai minimum diadan nilai maksimum di b.
Bukti. Misalkana < x < b. Maka menurut definisi kita mempunyai
f(a)≤f(x)≤f(b).
Jadif mencapai nilai minimum diadan nilai maksimum di b.
Sekarang kita akan membahas limit fungsi monoton. Untuk itu, kita perke-nalkan notasi
f(c−) = lim
Gambar 11.1(i)Grafik fungsif(x) =x3
Gambar 11.1(ii)Grafik fungsig(x) = 1
x
dan
f(c+) = lim
x→c+f(x),
asalkan kedua limit ini ada.
Contoh 3. Misalkanf :R→Rdidefinisikan sebagai f(x) =
x, x≤1;
3
Maka,f(1−) = 1 =f(1), sedangkanf(1+) = 32.
Teorema 4. (i)Jikaf naik dan terbatas di atas pada(a, b), maka f(b−) = sup
x∈(a,b)
f(x).
(ii)Jikaf naik dan terbatas di bawah pada(a, b), maka f(a+) = inf
x∈(a,b)f(x).
Bukti. (i) MisalkanM = sup
x∈(a,b)
f(x). Diberikanǫ >0 sembarang, kita harus mencari suatu δ > 0 sedemikian sehingga jika b−δ < x < b, maka |f(x)−M| < ǫ atau
M −ǫ < f(x)< M+ǫ.
Ketaksamaanf(x)< M +ǫselalu terpenuhi karenaM merupakan batas atas untuk f pada (a, b). Selanjutnya, karenaM −ǫbukan merupakan batas atas untuk
f pada (a, b), maka terdapat suatu y ∈ (a, b) sedemikian sehingga M −ǫ < f(y). Namunf naik pada (a, b), sehingga untuk setiapxyang memenuhiy < x < bberlaku
M−ǫ < f(y)≤f(x).
Jadi, pilihlahδ=b−y. (ii) Serupa dengan (i).
Akibat 5. Misalkan f naik pada(a, b). Jikac∈(a, b), maka f(c−)danf(c+)ada, dan
f(x)≤f(c−)≤f(c)≤f(c+)≤f(y)
untuk a < x < c < y < b.
Soal Latihan
1. Buktikan Teorema 4 bagian (ii). Mulai dengan memisalkan m= inf
x∈(a,b)f(x).
2. Buktikan jikaf turun dan terbatas di bawah pada (a, b), maka
f(b−) = inf
Gambar 11.2Kasus f(c−)< f(c)< f(c+)
3. Buktikan jikaf dang naik (sejati) padaH, makaf+gnaik (sejati) padaH. 4. Diketahui f(x) > 0 untuk setiap x ∈ H, dan g := 1f. Buktikan jika f naik
(sejati) padaH, makag turun (sejati) padaH.
5. Diketahui f naik sejati pada A. Buktikan bahwaf merupakan korespondensi 1-1 antaraAdanB :=f(A), sehinggaf−1ada. Buktikan bahwaf−1naik sejati
padaB.
11.2 Fungsi Monoton yang Mempunyai Turunan
Pada bagian ini kita akan membahas bagaimana kita dapat menyelidiki kemono-tonan suatu fungsi melalui turunannya, bila fungsi tersebut mempunyai turunan. Persisnya, kita mempunyai teorema berikut.
Teorema 6. Misalkan f kontinu pada[a, b] dan mempunyai turunan pada(a, b).
(i)Jikaf′(x)≥0untuk tiapx∈(a, b), makaf naik pada [a, b]. Jikaf′(x)>0 untuk
tiapx∈(a, b), makaf naik sejati pada[a, b].
(ii) Jika f′(x) ≤0 untuk tiap x∈ (a, b), makaf turun pada [a, b]. Jika f′(x) <0
Bukti. (i) Misalkan x dan y bilangan sembarang di [a, b] dengan x < y. Maka f
memenuhi hipotesis Teorema Nilai Rata-rata pada [x, y] dan karenanya
f′(c) =f(y)−f(x)
y−x
untuk suatu c ∈ (x, y). Jika f′(t) ≥ 0 untuk tiap t ∈ (a, b), maka f′(c) ≥ 0 dan karenanyaf(x)≤f(y). Jadi f naik pada [a, b].
Jikaf′(t)>0 untuk tiapt∈(a, b), makaf′(c)>0 dan karenanyaf(x)< f(y). Jadif naik sejati pada [a, b].
(ii) Serupa dengan (i).
Contoh 7. Misalkanf :R→Rdidefinisikan sebagaif(x) =x(1−x). Turunannya
adalah
f′(x) = 1−2x.
Jadi f′(x)≥0 untuk x≤ 1
2 dan f′(x) ≤0 untuk x≥ 1
2. Dengan demikianf naik
pada (−∞,12] dan turun pada [12,∞).
Soal Latihan
1. Misalkan n ∈ N. Buktikan bahwa fungsi f : [0,∞) → R yang didefinisikan
sebagai
f(x) = (x+ 1)1/n−x1/n
merupakan fungsi turun pada [0,∞).
2. Misalkan f mempunyai turunan dan naik pada suatu interval terbukaI. Buk-tikan bahwa f′(x) ≥ 0 untuk tiap x ∈ I. Jika f naik sejati pada I, apakah dapat disimpulkan bahwaf′(x)>0 untuk tiapx∈I? Jelaskan.
11.3 Invers Fungsi Monoton
Menurut Soal 11.1 No. 5, fungsifyang naik sejati padaAmendefinisikan suatu korespondensi 1-1 antaraAdanB:=f(A). Dalam hal inif akan mempunyai invers
Dalam kasus di manaf kontinu dan daerah asalf merupakan interval, sebutlah
I, maka daerah nilainya juga merupakan suatu interval, sebutlahJ =f(I) (Teorema 10 pada Bab 8). Lebih jauh, kita mempunyai teorema berikut.
Teorema 8. Misalkan f :I→J denganI interval dan J =f(I). Jika f naik sejati dan kontinu pada I, maka f−1:J
→I kontinu pada J.
Bukti. Andaikanf−1tidak kontinu di suatu titikd∈J. Asumsikan bahwadbukan
titik ujungJ. Maka, mengingatf−1 naik sejati pada J, f−1(d
−) danf−1(d+) ada,
danf−1(d−)< f−1(d+). Sekarang misalkanc∈I sedemikian sehingga
f−1(d−)< c < f−1(d+) danc6=f−1(d).
Karena ituf(c) tidak terdefinisi (buatlah ilustrasinya!), dan ini bertentangan dengan hipotesis bahwaf terdefinisi padaI.
Teorema 9. MisalkanI danJ interval,I◦danJ◦interval terbuka yang mempunyai
titik ujung sama dengan titik ujung I dan J. Misalkan f : I → J kontinu dan J =f(I). Jikaf mempunyai turunan padaI◦danf′(x)>0untuk tiapx∈I◦, maka
f−1 :J →I ada dan kontinu pada J. Lebih jauh,f−1 mempunyai turunan pada J◦ dan
(f−1)′(y) = 1
f′(x)
untuk tiap y∈J◦ danx=f−1(y).
Catatan. Bukti Teorema 9 dapat dilihat di [2].
Soal Latihan
1. Misalkan f :R→Rdidefinisikan sebagaif(x) = 1 +x+x3. Tunjukkan bahwa f mempunyai invers dan hitunglah nilai (f−1)′(−1).
2. Berikan sebuah contoh fungsi f :A→Ryang naik sejati dan kontinu padaA,
tetapi f−1 tidak kontinu pada B = f(A). (Petunjuk. Himpunan A tentunya
11.4 Fungsi Konveks*
Misalkan I ⊆R suatu interval. Fungsi f : I → Rdikatakan konvekspada I
apabila untuk setiapt∈[0,1] danx1, x2∈I berlaku
f((1−t)x1+tx2)≤(1−t)f(x1) +tf(x2).
Catat bahwa untukx1< x−2, titik (1−t)x1+tx2 bergerak darix1 kex2 ketikat
bergerak dari 0 ke 1. Jadi jikaf konveks padaIdanx1, x2∈I, maka ruas garis yang
menghubungkan titik (x1, f(x1)) dan (x2, f(x2)) berada di atas grafik fungsif (lihat
Gambar 11.3).
Gambar 11.3Grafik fungsi konveks
Sebuah fungsi konveks tidak harus mempunyai turunan di setiap titik. Sebagai contoh, f(x) = |x| merupakan fungsi konveks pada R tetapi tidak mempunyai
tu-runan di 0. Namun, dapat ditunjukkan jikaf konveks pada interval terbukaI, maka
f mempunyai ‘turunan kiri’ dan ‘turunan kanan’ di setiap titik dalam I. Sebagai akibatnya, setiap fungsi konveks pada interval terbuka merupakan fungsi kontinu.
Teorema berikut memperlihatkan kaitan antara fungsi konveks dan turunan keduanya, bila fungsi tersebut mempunyai turunan kedua. Istilah konveks dalam hal ini setara dengan istilah ‘cekung ke atas’ yang telah kita bahas pada Bab 9.
Bukti. Misalkanf konveks padaI. Untuk tiapc∈I, kita mempunyai
Berdasarkan Teorema Taylor, terdapatξ1 di antarax0 danx1 sedemikian sehingga
f(x1) =f(x0) + (x1−x0)f′(x0) +
(x1−x0)2
2 f
′′(ξ
1)
dan juga terdapatξ2 di antarax0dan x2 sedemikian sehingga
2. Buktikanf konveks pada intervalIjika dan hanya jika untuk setiapx1, x2, x3∈
Idenganx1< x2< x3berlaku
f(x2)−f(x1)
x2−x1 ≤
f(x3)−f(x1)
x3−x1 .
Berikan interpretasi geometrisnya beserta ilustrasinya. 3. Buktikan jikaf konveks pada interval terbukaI, maka
lim
h→0−
f(c+h)−f(c)
h dan hlim→0+
f(c+h)−f(c)
h
ada untuk setiapc∈I, dan sebagai akibatnyaf kontinu padaI.
4. Misalkan f mempunyai turunan pada interval terbuka I. Buktikan f konveks jika dan hanya jikaf′ naik padaI.
5. Misalkan I interval terbuka, f : I → Rnaik sejati, konveks, dan mempunyai
turunan pada I. Misalkan c ∈ I sedemikian sehingga f(c) = 0. Konstruksi barisanhxnidengan x1> cdan
xn+1=xn− f(xn)
f′(xn), n= 1,2,3, . . . .
Buktikan bahwa xn → c untuk n → ∞. (Metode penghampiran ‘akar’ f ini
dikenal sebagai Metode Newton-Raphson. Untuk f(x) = x2