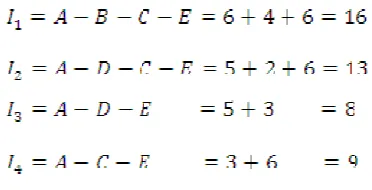ALGORITMA SEMUT UNTUK MENCARI JALUR TERPENDEK
YAAYU
060803040
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
ALGORITMA SEMUT UNTUK MENCARI JALUR TERPENDEK
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
YAAYU
060803040
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : ALGORITMA SEMUT UNTUK MENCARI JALUR
TERPENDEK
Kategori : SKRIPSI
Nama : YAAYU
Nomor Induk Mahasiswa : 060803040
Program Studi : SARJANA (S!) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Dituliskan di
Medan, 27 Juni 2012
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Elly Rosmaini, M.Si Drs. James P. Marbun, M.Kom NIP. 19600520 198503 2 002 NIP. 19580611 198603 1 002
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
ALGORITMA SEMUT UNTUK MENCARI JALUR TERPENDEK
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, 27 Juni 2012
PENGHARGAAN
Dengan segala kerendahan hati penulis memanjatkan puji dan syukur kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpahan karunia-Nya kertas kajian ini mampu diselesaikan dalam yang telah ditetapkan.
ABSTRAK
ANT ALGORITHM FOR FIND THE SHORTEST PATH
ABSTRACT
DAFTAR ISI
1.2 Perumusan Masalah 3
1.3 Pembatasan Masalah 3
1.4 Tinjauan Pustaka 4
1.5 Tujuan Penelitian 7
1.6 Kontribusi Penelitian 7
1.7 Metode Penelitian 7
Bab 2 Landasan Teori 8
2.1 Teori Dasar Graf 8
2.1.1 Graf Berbobot (Weighted Graph) 11
2.1.2 Representasi Graf 11
2.2 Optimisasi 14
2.2.1 Pengertian Optimisasi 14
2.2.2 Pengertian Nilai Optimasi 14
2.2.3 Macam-Macam Permasalahan Optimisasi 14
2.2.4 Penyelesaian Masalah Optimisasi 15
2.3 Jalur Terpendek (Shortest Path) 16
2.3.1 Penerapan Algoritma Semut 16
2.3.2 Contoh Kasus 16
Bab 3 Pembahasan 18
3.1 Algoritma Semut 18
3.2 Cara Kerja Semut Mencari Jalur Terpendek 19 3.3 Analisis Algoritma Semut Untuk Mencari Nilai Optimal
Menggunakan Graf 21
3.4 Penyelesaian Masalah dengan Algoritma Semut 24
Bab 4 Kesimpulan dan Saran 39
4.1 Kesimpulan 39
4.2 Saran 39
DAFTAR TABEL
Halaman
Tabel 3.1 Jarak Antarkota dij 25
Tabel 3.2 Visibilitas Antarkota
ij
d
1 =
η 25
Tabel 3.3 Probabilitas Kota untuk Dikunjungi Siklus Ke-1 Kasus 1 26 Tabel 3.4 Panjang Jalur Semut Siklus Ke-1 Kasus 1 26 Tabel 3.5 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-2 Kasus 1 27
Tabel 3.6 Probabilitas Kota untuk Dikunjungi Siklus Ke-2 Kasus 1
dengan τij Telah Diperbaharui 27
Tabel 3.7 Panjang Jalur Semut Siklus Ke-2 Kasus 1 27 Tabel 3.8 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-3 Kasus 1 28
Tabel 3.9 Probabilitas Kota untuk Dikunjungi Siklus Ke-3 Kasus 1
dengan τijTelah Diperbaharui 28
Tabel 3.10 Panjang Jalur Semut Siklus Ke-3 Kasus 1 28 Tabel 3.11 Probabilitas Kota untuk Dikunjungi Siklus Ke-1 Kasus 2 29 Tabel 3.12 Panjang Jalur Semui Siklus Ke-1 Kasus 2 29 Tabel 3.13 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-2 Kasus 2 30
Tabel 3.14 Probabilitas Kota untuk Dikunjungi Siklus Ke-2 Kasus 2
dengan τijTelah Diperbaharui 30
Tabel 3.15 Panjang Jalur Semut Siklus Ke-2 Kasus 2 30 Tabel 3.16 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-3 Kasus 2 31
Tabel 3.17 Probabilitas Kota untuk Dikunjungi Siklus Ke-3 Kasus 2
dengan τijTelah Diperbaharui 31
Tabel 3.18 Panjang Jalur Semut Siklus Ke-3 Kasus 2 31 Tabel 3.19 Probabilitas Kota untuk Dikunjungi Siklus Ke-1 Kasus 3 32 Tabel 3.20 Panjang Jalur Semui Siklus Ke-1 Kasus 3 32 Tabel 3.21 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-2 Kasus 3 33
Tabel 3.22 Probabilitas Kota untuk Dikunjungi Siklus Ke-2 Kasus 3
dengan τijTelah Diperbaharui 33
Tabel 3.23 Panjang Jalur Semut Siklus Ke-2 Kasus 3 33 Tabel 3.24 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-3 Kasus 3 34
Tabel 3.25 Probabilitas Kota untuk Dikunjungi Siklus Ke-3 Kasus 3
dengan τijTelah Diperbaharui 34
Tabel 3.27 Probabilitas Kota untuk Dikunjungi Siklus Ke-1 Kasus 4 35 Tabel 3.28 Panjang Jalur Semui Siklus Ke-1 Kasus 4 35 Tabel 3.29 Perubahan Harga Intensitas Jejak Kaki Semut
τ
ijAntarkota Siklus Ke-2 Kasus 4 36
Tabel 3.30 Probabilitas Kota untuk Dikunjungi Siklus Ke-2 Kasus 4
dengan τijTelah Diperbaharui 36
Tabel 3.31 Panjang Jalur Semut Siklus Ke-2 Kasus 4 36 Tabel 3.32 Perubahan Harga Intensitas Jejak Kaki Semut τij
Antarkota Siklus Ke-3 Kasus 4 37
Tabel 3.33 Probabilitas Kota untuk Dikunjungi Siklus Ke-3 Kasus 4
dengan τijTelah Diperbaharui 37
DAFTAR GAMBAR
Halaman
Gambar 2.1 Graf G(4,5) 8
Gambar 2.2 Graf Berarah 9
Gambar 2.3 Graf Tak-berarah 10
Gambar 2.4 Graf Terhubung 10
Gambar 2.5 Graf Tak-terhubung 10
Gambar 2.6 Graf Berbobot 11
Gambar 2.7 Dua Buah Graf dengan Matriks ketetanggaannya
Masing-Masing 12
Gambar 2.8 Graf dengan Matriks Bersisian 13
Gambar 2.9 Graf dengan Daftar ketetanggaan 13
Gambar 2.10 Graf Berarah dan Berbobot 17
Gambar 3.1 Jalur Awal Semut Menuju Tempat Makanan 19 Gambar 3.2 Jalur Optimal Semut Menuju Tempat Makanan 20 Gambar 3.3 Jalur Awal Semut Menuju Tempat Makanan 21
Gambar 3.4 Jalur Semut Menuju Sarang 22
Gambar 3.5 Jalur Semut Menuju Makanan pada Iterasi Ke-1 22 Gambar 3.6 Jalur Semut Menuju Sarang pada Iterasi Ke-2 23 Gambar 3.7 Jalur Optimal Semut Untuk Menuju Tempat Makanan 23
ABSTRAK
ANT ALGORITHM FOR FIND THE SHORTEST PATH
ABSTRACT
BAB 1
PENDAHULUAN
1.1Latar Belakang
Masalah untuk mencari jalur terpendek di dalam graf merupakan salah satu masalah optimisasi. Graf yang digunakan dalam pencarian jalur terpendek adalah graf yang setiap sisinya memiliki suatu nilai atau bobot atau yang lebih dikenal dengan graf berbobot (weighted graph).
Bobot yang ada pada setiap sisinya dapat menyatakan jarak antarkota, waktu pengiriman pesan, ongkos pembangunan, waktu tempuh antarkota dan lain sebagainya. Namun kata “terpendek“ dalam masalah ini tidak selalu diartikan secara fisik sebagai panjang minimum, sebab kata “terpendek” berbeda-beda maknanya, tergantung pada jenis masalah yang akan diselesaikan sehingga secara umum “terpendek“ berarti meminimisasi bobot pada suatu jalur di dalam graf. Asumsi yang digunakan adalah bahwa semua bobot bernilai positif. Persoalan jalur terpendek ini memiliki tujuan untuk menemukan jalur terpendek namun bukan untuk sebuah sirkuit Hamilton yang terdapat pada Traveling Salesman Problem (TSP) melainkan jalur terpendek dari sebuah simpul ke simpul lainnya.
Secara umum, pencarian jalur terpendek dapat dibagi menjadi dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional ini lebih mudah dipahami daripada metode heuristik. Akan tetapi metode heuristik seperti Simulated
Annealing, Algoritma Semut, Algoritma Genetika, Tabu Search, dan lain sebagainya
Algoritma semut diadopsi dari perilaku koloni semut dalam mencari makanan yang diperkenalkan oleh Marco Dorigo tahun 1990 untuk mencari jalur terpendek pada graf, digunakan untuk menyelesaikan masalah optimisasi kombinatorial dengan perhitungan waktu yang lebih singkat terutama pada masalah dasar graf (Dorigo dan St tzle, 2004).
Secara alamiah koloni semut mampu menemukan jalur terpendek dalam perjalanan dari sarang ke tempat-tempat sumber makanan. Koloni semut dapat menemukan jalur terpendek antara sarang dan sumber makanan berdasarkan jejak kaki pada jalur yang telah dilalui. Semakin banyak semut yang melalui suatu jalur, maka akan semakin jelas bekas jejak kakinya. Hal ini akan menyebabkan jalur yang dilalui semut dalam jumlah sedikit, semakin lama akan semakin berkurang kepadatan semut yang melewatinya, atau bahkan akan tidak dilewati sama sekali. Sebaliknya, jalur yang dilalui semut dalam jumlah banyak, semakin lama akan semakin bertambah kepadatan semut yang melewatinya, atau bahkan semua semut akan melalui jalur tersebut.
Pada algoritma semut setiap semut ditempatkan di semua titik graf (dalam hal ini titik–titik yang dikunjungi) yang kemudian akan bergerak mengunjungi seluruh titik. Setiap semut akan membuat jalur masing-masing sampai ke tempat tujuan yanng telah ditentukan. Jika sudah mencapai keadaan ini, maka semut telah menyelesaikan sebuah siklus (tour). Solusi akhir adalah menemukan jalur terpendek yang dihasilkan oleh pencarian semut-semut tersebut.
Dalam kehidupan sehari-hari algoritma semut telah banyak digunakan dalam berbagai bidang untuk persoalan seperti:
1. Traveling Salesman Problem (TSP)
2. Quadratic Assignment Problem (QAP)
3. Job-shop Scheduling Problem (JSP)
4. Vehicle Routing Problem (VRP)
5. Pengaturan jalur kendaraan
6. Pewarnaan graf Implementasi pada jaringan komunikasi
Dalam hal ini salah satu algoritma optimisasi yang akan digunakan adalah algoritma semut yang merupakan suatu algoritma optimisasi yang cara kerjanya mengadopsi kehidupan perilaku kelompok semut dalam mencari makanan dengan beberapa kriterianya termasuk yang berhubungan dengan nilai optimum dari masalah yang juga sering dihadapi oleh kelompok semut dalam mencari sumber makanannya. Dengan membuat suatu asumsi permasalahan yang dihadapi oleh kelompok semut, maka akan ditemukan suatu solusi efektif yang berhubungan dengan permasalahan dalam kehidupan manusia untuk mencari jalur terpendek.
.
1.2Perumusan Masalah
Permasalahan yang akan dibahas dalam penelitian ini adalah bagaimana pengaruh nilai parameter α dan β terhadap nilai probabilitas kota untuk dikunjungi dan
pengaruh nilai parameter
ρ
terhadap nilai τij pada pencarian jalur terpendek denganmenggunakan algoritma semut.
1.3Pembatasan Masalah
Dari latar belakang dan rumusan masalah yang telah dijelaskan, pencarian jalur terpendek dibatasi pada salah satu jenis algoritma yang digunakan dalam metode heuristik, yaitu Algoritma Semut. Batasan masalah yang diperlukan dalam penelitian ini yaitu:
1. Masukan yang diperlukan berupa model representasi graf yang terdiri dari jumlah simpul (vertex) dan label simpulnya.
2. Jenis graf yang dipakai adalah graf berarah (direct graph).
3. Bobot antarsimpul yang digunakan hanyalah bobot jarak dan mengabaikan bobot lainnya.
4. Laporan yang dihasilkan hanyalah berupa solusi antarsimpul dan jarak. 5. Program alat bantu untuk perhitungan yang digunakan dibangun dengan
1.4Tinjauan Pustaka
Maharani (2009), menyatakan bahwa algoritma semut ini diinspirasi oleh tingkah laku koloni semut, bagaimana kemampuan individu dengan yang sederhana dapat menemukan jalur terpendek (sarang semut dengan sumber makanan) jika bersama dalam suatu koloni.
St tzle (2005), menyatakan bahwa Algoritma Semut adalah berbasis populasi, teknik pencarian umum untuk solusi dari masalah kombinatorial yang sulit yang terinspirasi oleh peletakkan jejak feromon perilaku koloni semut.
G nay (2007), menyatakan Algoritma Semut adalah suatu metaheuristik untuk optimasi kombinatorial yang terinspirasi dari perilaku semut mencari makanan yang pertama kali diusulkan oleh Marco Dorigo pada tahun 1992.
Mutakhiroh et al (2007), menyatakan bahwa koloni semut yang sudah terdistribusi ke sejumlah atau setiap kota, akan mulai melakukan perjalanan dari kota pertama masing-masing sebagai kota asal dan salah satu kota-kota lainnya sebagai kota tujuan. Kemudian dari kota kedua masing-masing, koloni semut akan melanjutkan perjalanan dengan memilih salah satu dari kota-kota yang tidak terdapat pada tabuk sebagai kota tujuan selanjutnya. Perjalanan koloni semut berlangsung terus
menerus sampai semua kota satu per satu dikunjungi atau telah menempati tabuk. Jika s menyatakan indeks urutan kunjungan, kota asal dinyatakan sebagai tabuk(s) dan
kota-kota lainnya dinyatakan sebagai {N-tabuk}, maka untuk menentukan kota tujuan
digunakan persamaan probabilitas kota untuk dikunjungi sebagai berikut:
[ ] [ ]
= Intensitas jejak semut antarkota dan perubahannya
Q = Tetapan siklus semut
= Tetapan pengendali intensitas jejak semut = Tetapan pengendali visibilitas
m = Banyak semut
= Tetapan penguapan jejak semut
= Visibilitas antarkota
Jumlah siklus maksimum (Ncmax) bersifat tetap selama algoritma dijalankan, sedangkan akan selalu diperbaharui nilainya pada setiap siklus algoritma mulai
dari siklus pertama (NC=1) sampai tercapai jumlah siklus maksimum (NC=Ncmax) atau sampai terjadi konvergensi. Setelah inisialisasi dilakukan, kemudian m semut
ditempatkan pada kota pertama tertentu secara acak.
Perhitungan panjang jalur setiap semut dilakukan setelah satu siklus
diselesaikan oleh semua semut. Perhitungan ini dilakukan berdasarkan tabuk
masing-masing dengan persamaan sebagai berikut:
−
diketahui maka dapat dihitung berdasarkan persamaan:
2
Setelah setiap semut dihitung maka akan didapat nilai minimal panjang jalur
setiap siklus atau LminNC dan nilai minimal panjang jalur secara keseluruhan atau Lmin.
kemungkinan terjadinya perubahan nilai intensitas jejak kaki semut antarkota.
dengan adalah perubahan nilai intensitas jejak kaki semut antarkota setiap semut yang dihitung berdasarkan persamaan:
lainnya kemungkinan berubah karena adanya penguapan dan perbedaan jumlah semut yang melewati. Untuk siklus selanjutnya, semut yang akan melewati jalur tersebut nilai intensitasnya telah berubah. Nilai intensitas jejak kaki semut antarkota untuk siklus selanjutnya dihitung dengan persamaan:
ij ij ij ρ τ τ τ =(1− ). +∆
Pengembalian nilai perubahan intensitas jejak kaki semut antarkota. Untuk siklus selanjutnya perubahan nilai intensitas jejak semut antarkota perlu diatur kembali agar memiliki nilai sama dengan nol. Tabu list perlu dikosongkan untuk diisi lagi dengan urutan kota yang baru pada siklus selanjutnya, jika jumlah siklus maksimum belum tercapai atau belum terjadi konvergensi maka algoritma diulang lagi dengan nilai parameter intensitas jejak kaki semut antarkota yang sudah diperbaharui.
1.5Tujuan Penelitian
1.6Kontribusi Penelitian
Penelitian ini diharapkan dapat digunakan sebagai bahan referensi dalam penyelesaian dan perhitungan jalur terpendek dalam suatu aplikasi perangkat lunak yang lebih mudah digunakan oleh pihak lainnya.
1.7Metode Penelitian
Dalam melancarkan penelitian ini metode yang digunakan adalah dengan studi literatur berdasarkan rujukan pustaka dan pengembangan sistem, yaitu:
1. Menjelaskan pengertian dasar graf dan pengertian jalur terpendek.
2. Memberikan penjelasan penyelesaian dengan contoh kasus yang sederhana. 3. Membuat intruksi untuk menjalankan suatu fungsi pada perangkat keras
BAB 2
LANDASAN TEORI
2.1 Teori Dasar Graf
Graf G didefinisikan sebagai pasangan himpunan (V,E), ditulis dengan notasi
G=(V,E), yang dalam hal ini V adalah himpunan tidak-kosong dari simpul-simpul
(vertices atau simpul) dan E adalah himpunan sisi (edges atau arcs) yang
menghubungkan sepasang simpul (Munir, 2005).
Definisi graf G(V,E) menyatakan bahwa simpul V tidak boleh kosong sedangkan sisi E boleh kosong karena tidak ada sisi yang tanpa simpul yang disebut graf trivial.
Simpul pada graf dapat menyatakan objek sembarang seperti kota, atom-atom suatu zat, komponen alat elektronik, nama suatu objek dan sebagainya yang dinomori dengan huruf, bilangan asli atau gabungan dari keduanya. Sedangkan sisi dapat menunjukkan hubungan sembarang seperti ikatan atom, sambungan telepon, jalur penerbangan, jalan raya dan sebagainya yang menghubung antarsimpul pada graf dinyatakan dengan pasangan (u,v) atau dinyatakan dengan Jika e adalah sisi yang menghubungkan simpul u dengan simpul v maka e=(u,v).
A e1 B
e2 e3 e4
C e5 D
G(4,5) adalah graf dengan himpunan simpul V dan himpunan sisi E adalah:
V = { A, B, C, D }
E = { (A, B), (A, C), (A, D), (B, D), (C, D) }
= { }
Berdasarkan ada tidaknya gelang atau sisi ganda pada sautu graf, maka graf dapat digolongkon menjadi dua jenis:
1. Graf sederhana (simple graph) adalah graf yang tidak mengandung gelang (loop) maupun sisi ganda.
2. Graf tak-sederhana (unsimple-graph) adalah graf yang mengandung gelang (loop) maupun sisi ganda.
Berdasarkan orientasi arah pada sisi,maka secara umum graf dibedakan atas 2 jenis:
1. Graf berarah (directed graph atau digraph) adalah graf yang sisinya mempunyai orientasi arah dengan urutan pasangan simpul yang terhubung oleh sisi-sisinya diperhatikan maka (u,v) (v,u) adalah sisi yang berbeda.
Pada graf berarah, gelang (loop) diperbolehkan tetapi sisi ganda tidak diperbolehkan.
A
B C
D
Gambar 2.2 Graf berarah
A B
C D
Gambar 2.3 Graf tak-berarah
Graf tak-berarah G disebut graf terhubung (connected graph) jika untuk setiap pasang simpul u dan v pada himpunan V terdapat jalur atau sisi ei (yang juga harus
berarti ada jalur atau sisi ei) pada himpunan E. Jika tidak, maka G disebut graf
tak-berhubung (disconnected graph).
A C E
B D F
Gambar 2.4 Graf terhubung
A F
C D E H
B G
Gambar 2.5 Graf tak-terhubung
2.1.1 Graf Berbobot (Weighted Graph)
Graf berbobot adalah graf yang setiap sisinya diberi sebuah nilai atau bobot (Munir, 2005).
Bobot pada setiap sisi graf dapat berbeda-beda bergantung pada masalah yang dimodelkan. Bobot dapat menyatakan jarak antara dua buah kota, biaya perjalanan antara dua buah kota, waktu tempuh antara dua buah kota, waktu tempuh pesan antara simpul komunikasi dengan simpul komunikasi lainnya (dalam jaringan komputer), ongkos produksi dan sebagainya. Graf berbobot juga sering dikaitkan dengan istilah graf berlebel yang definisinya lebih luas lagi. Label tidak hanya diberikan pada sisi tapi juga pada simpul yang berupa bilangan non negatif.
P 9 Q 6 7 12 T 6 R 9 S
Gambar 2.6 Graf berbobot
2.1.2 Representasi Graf
Ada beberapa representasi yang mungkin untuk graf yang sering digunakan, yaitu:
1. Matriks ketetangaan (adjacency matrix)
Misalkan G = (V,E) adalah graf dengan n simpul, . Matriks
ketetanggaan G adalah matriks bujursangkar yang berukuran n x n. Bila matriks tersebut dinamakan , maka jika simpul i dan j
bertetanggaan, sebaliknya jika simpul i dan j tidak bertetanggaan
dinyatakan 1 jika simpul i dan j bertetanggaan dan 0 untuk yang
lainnya (Kenneth, 2003).
1 2
3 4
1 2
3 4
Gambar 2.7 Dua buah graf dengan matriks ketetanggaannya masing-masing
2 Matriks Bersisian (incidency matrix)
Misalkan G=(V,E) graf dengan n simpul dan m buah sisi. Matriks bersisian G
adalah matriks bujursangkar yang berukuran n x m. Baris menunjukkan label simpul, sedangkan kolom menunjukkan label sisinya. Bila matriks tersebut dinamakan , maka jika simpul i bersisian dengan sisi j,
1 3 5
2 4 6
Gambar 2.8 Graf dengan matriks bersisian
3 Daftar ketetanggaan (adjacency list)
Representasi dengan daftar ketetanggaan dapat disajikan dengan membuat tabel simpul dan tetangga simpulnya (Amir Hamzah, 2011, hal: 40). Representasi dengan daftar ketetanggaan digunakan untuk mengatasi masalah pada graf yang matriksnya bersifat jarang yaitu mengandung banyak elemen nol, sedangkan elemen yang bukan nol sedikit.
Simpul Simpul Tetangga
A B C D E
C, B, D A A, D, E A, C, E C, D
B A C
D E
2.2 Optimisasi
2.2.1 Pengertian Optimisasi
Optimisasi adalah suatu proses untuk mencapai hasil yang ideal atau optimal (nilai efektif yang dapat dicapai). Dalam disiplin matematika optimisasi merujuk pada studi permasalahan yang mencoba untuk mancari nilai minimal atau maksimal dari suatu fungsi nyata. Untuk dapat mencari nilai optimal baik minimal atau maksimal tersebut, secara sistematis dilakukan pemilihan nilai variabel integer atau nyata yang akan memberikan solusi optimal (Wardy, 2007).
2.2.2 Pengertian Nilai Optimal
Nilai optimal adalah nilai yang didapat melalui suatu proses dan dianggap menjadi suatu solusi jawaban yang paling baik dari semua solusi yang ada (Wardy, 2007).
Nilai optimal dapat dicari dengan dua cara, yaitu:
1. Cara konvensional, yaitu mencoba semua kemungkinan yang ada dengan mencatat nilai yang didapat. Cara ini kurang efektif karena optimasi akan berjalan sangat lambat.
2. Cara kedua adalah dengan menggunakan rumus sehingga nilai optimal dapat diperkirakan dengan cepat dan tepat.
2.2.3 Macam-Macam Permasalan Optimisasi
1. Menentukan jalur terpendek dari suatu tempat ke tempat yang lain. 2. Mengatur jalur kendaraan umum agar semua lokasi dapat dijangkau.
3. Mengatur routing jaringan kabel telpon agar biaya pemasangan kabel tidak terlalu besar dan penggunaannya tidak boros.
4. Menentukan jumlah pekerja seminimal mungkin untuk melakukan suatu proses produksi agar biaya pengeluaran biaya pekerja diminimalkan dan hasil produksi tetap maksimal.
Selain beberapa contoh di atas, masih banyak persoalan lainnya yang terdapat dalam berbagai bidang.
2.2.4 Penyelesaian Masalah Optimisasi
Secara umum penyelesaian masalah pencarian jalur terpendek dapat dilakukan dengan dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional diterapkan dengan cara perhitungan matematis seperti biasa, sedangkan metode heuristik diterapkan dengan sistem pendekatan (Mutakhiroh et al, 2007).
Metode konvensional berupa metode yang menggunakan perhitungan matematis biasa. Ada beberapa metode konvensional yang biasa digunakan untuk melakukan pencarian jalur terpendek, diantaranya algoritma Djikstra, algoritma Floyd-Warshall, dan algoritma Bellman-Ford (Mutakhiroh et al, 2007).
2.3 Jalur Terpendek (Shortest Path)
2.3.1 Penerapan Algoritma Semut
Algoritma semut telah digunakan dalam kehidupan sehari-hari untuk menghasilkan penyelesaian yang mendekati optimal. Aplikasi algoritma semut dalam kehidupan sehari-hari mencakup beberapa persoalan, yaitu:
1. Quadratic Assignment Problem (QAP), yaitu menugaskan sejumlah n
resources untuk ditempatkan pada sejumlah m lokasi dengan meminimalisasi biaya penugasan (assignment).
2. Job-shop Scheduling Problem (JSP) juga salah satu contoh aplikasi Ant Colony
Optimization, yaitu untuk mencari jalur sejumlah n pekerjaan menggunakan
sejumlah m mesin demikian sehingga seluruh pekerjaan diselesaikan dalam waktu yang seminimal mungkin.
3. Vehicle Routing Problem (VRP) adalah masalah optimisasi penentuan jalur
dengan keterbatasan kapasitas kendaraan yang bertujuan meminimumkan total jarak yang ditempuh kendaraan dengan mengatur urutan-urutan yang harus dikunjungi serta kapan kembalinya kendaraan untuk mengisi kapasitasnya lagi.
4. Traveling Salesman Problem (TSP), yaitu untuk mencari jalur terpendek dalam
sebuah graph yang menggunakan jalur Hamilton.
2.3.2 Contoh Kasus
Permasalahan mencari jalur terpendek di dalam graf merupakan permasalahan optimisasi yang dapat dimodelkan dengan graf berbobot (weighted graph). Graf berbobot adalah suatu graf dengan masing-masing sisi diberi bobot dengan nilai suatu bilangan tertentu. Gambar 2.10 merupakan suatu graf ABCDEF yang berarah dan berbobot.
A 5 F 5 4 3 2 6 C 2 D 3
4 6 B 8 E
Gambar 2.10 Graf berarah dan berbobot
Gambar 2.10 di atas, misalkan dari kota A ingin menuju kota E. Untuk menuju kota E, dapat dipilih beberapa jalur yang tersedia yaitu:
BAB 3
PEMBAHASAN
3.1 Algoritma Semut
Algoritma semut diadopsi dari perilaku semut yang dikenal sebagai sistem semut (Dorigo et al, 1996). Koloni semut merupakan algoritma yang bersifat heuristik untuk menyelesaikan masalah optimasi. Algoritma ini terinspirasi oleh lingkungan koloni semut pada saat mencari makanan. Semut mampu menemukan jalur terpendek dari suatu sumber makanan menuju sarangnya, tanpa harus melihatnya secara langsung. Semut mempunyai penyelesaian yang unik dan sangat maju, yaitu menggunakan jejak
feromon pada suatu jalur untuk berkomunikasi dan membangun solusi, semakin
banyak jejak feromon ditinggalkan maka jalur tersebut akan diikuti oleh semut lain.
Feromon adalah zat kimia yang berasal dari kelenjar endokrin yang digunakan
oleh makhluk hidup untuk mengenali sesama jenis individu lain, kelompok dan untuk membantu proses reproduksi. Feromon menyebar keluar tubuh dan hanya dapat mempengaruhi dan dikenali oleh individu lain yang sejenis.
Proses peninggalan feromon ini dikenal dengan stigmery, yaitu sebuah proses memodifikasi lingkungan yang tidak hanya bertujuan untuk mengingat jalan pulang ke sarang, tetapi juga memungkinkan para semut berkomunikasi dengan koloninya.
3.2 Cara Kerja Semut Mencari Jalur Optimal
Secara alamiah semut mampu menemukan jalur terpendek dalam perjalanan dari sarang ke tempat-tempat sumber makanan. Koloni semut dapat menemukan jalur terpendek antara sarang dan sumber makanan berdasarkan jejak kaki pada jalur yang dilaluinya. Semakin banyak semut yang melalui jalur tersebut maka akan semakin jelas jejak kakinya. Hal ini akan menyebabkan jalur yang dilalui semut dalam jumlah sedikit, semakin lama akan semakin berkurang kepadatan semut yang melewatinya, atau bahkan akan tidak dilalui sama sekali. Sebaliknya jalur yang akan dilalui semut dalam jumlah banyak, semakin lama semakin bertambah kepadatan semut yang melewatinya, atau bahkan semua semut akan melalui jalur tersebut.
Agar semut mendapatkan jalur optimal, diperlukan beberapa proses:
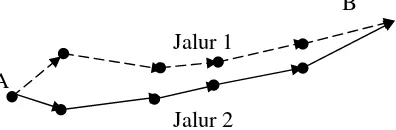
1. Pada awalnya semut berkeliling secara acak hingga menemukan makanan. Lihat gambar di bawah ini:
B Jalur 1 A
Jalur 2
Gambar 3.1 Jalur awal semut menuju tempat makanan
Keterangan:
A : Tempat awal koloni semut (sarang) B : Tujuan koloni semut (makanan) Jalur 1: Jalur yang ditempuh oleh semut 1 Jalur 2: Jalur yang ditempuh oleh semut 2
2. Ketika menemukan makanan mereka kembali ke koloninya sambil memberikan tanda dengan jejak feromon.
4. Kembali dan menguatkannya jika pada akhirnya mereka pun menemukan makanan.
5. Seekor semut yang tidak sengaja menemukan jalur optimal akan menempuh jalur ini lebih cepat dan melakukan round-trip lebih sering yang dengan sendirinya meninggalkan feromon lebih banyak dari jalur-jalur yang lambat ditempuh.
6. Feromon yang berkonsentrasi tinggi pada akhirnya akan menarik
semut-semut lain untuk berpindah jalur menuju jalur yang optimal sedangkan jalur lainnya akan ditinggalkan.
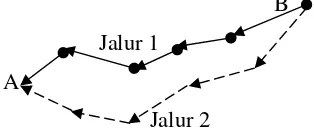
7. Pada akhirnya semua semut yang tadinya menempuh jalur yang berbeda-beda akan beralih kesebuah jalur tunggal yang ternyata paling optimal dari sarang menuju ketempat makanan. Lihat gambar di bawah ini:
B
A
Gambar 3.2 Jalur optimal semut menuju tempat makanan
Ketarangan:
A : Tempat awal koloni semut (sarang) B : Tujuan koloni semut (makanan)
3.3 Analisis Algoritma Semut untuk Mencari Nilai Optimal Menggunakan
Graf
Algoritma semut menggunakan sistem multi agen, yang berarti mengerahkan seluruh koloni semut yang masing-masingnya bergerak sebagai agen tunggal. Setiap semut menyimpan daftar tabu yang memuat simpul-simpul yang sudah pernah dilalui, dimana ia tidak diijinkan untuk melalui simpul-simpulyang sama dua kali dalam satu kali perjalanan.
Sebuah koloni semut diciptakan dan setiap semut ditempatkan pada masing-masing simpul secara merata untuk menjamin bahwa tiap simpul memiliki peluang untuk menjadi titik awal dari jalur optimal yang dicari. Setiap semut selanjutnya harus melakukan perjalanan mengunjungi semua simpul-simpul pada graf tersebut.
Berikut ini adalah tahapan-tahapan algoritma semut menggunakan graf, yaitu:
1. Dari sarang semut berkeliling secara acak mencari makanan sambil mencatat jarak antara simpul yang ia lalui.
2. Ketika sampai ke makanan, total jarak dari tiap simpul yang ia tempuh dijumlahkan untuk mendapatkan jarak dari sarang ke makanan.
B Jalur 1
A
Jalur 2
Gambar 3.3 Jalur awal semut menuju tempat makanan
Keterangan:
3. Ketika kembali ke sarang, sejumlah konsentrasi feromon ditambahkan pada jalur tersebut yang telah ditempuh berdasarkan total jarak jalur tersebut. Makin kecil total jarak (makin optimal) maka makin banyak kadar feromon
yang dibubuhkan pada masing-masing busur pada jalur tersebut. B
Jalur 1 A
Jalur 2
Gambar 3.4 Jalur semut menuju sarang
Keterangan: A : Sarang semut
B : Tempat ditemukannya makanan
Jalur 1: Jalur yang ditempuh oleh semut 1 dengan pemberian kadar feromon
yang tinggi
Jalur 2: Jalur yang ditempuh oleh semut 2 dengan pemberian kadar feromon
yang rendah
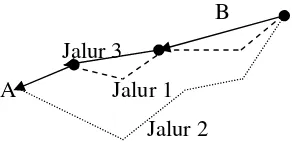
4. Untuk melalui busur mana yang harus dilalui berikutnya, digunakan sebuah rumus yang pada intinya menerapkan suatu fungsi heuristik untuk menghitung intensitas feromon yang ditinggalkan pada suatu busur.
B Jalur 3
A Jalur 1 Jalur 2
Gambar 3.5 Jalur semut menuju makanan pada iterasi ke-1
Keterangan: A : Sarang semut
B : Tempat ditemukannya makanan
Jalur 2 : Jalur yang tidak ditempuh oleh semut karena kadar feromon yang rendah
Jalur 3 : Jalur yang ditemukan oleh semut 2
5. Pada iterasi berikutnya, busur-busur yang mengandung feromon lebih tinggi ini akan cenderung dipilih sebagai busur yang harus ditempuh berikutnya berdasarkan rumus pemilihan busur. Akibatnya, lama-kelamaan akan terlihat jalur optimal pada graf yaitu jalur yang dibentuk oleh busur-busur dengan kadar feromon yag tinggi yang pada akhirnya akan dipilih oleh semua multi agen semut.
B Jalur 3
A Jalur 1 Jalur 2
Gambar 3.6 Jalur semut menuju sarang pada iterasi ke-2
Keterangan: A : Sarang semut
B : Tempat ditemukannya makanan
Jalur 1: Jalur yang ditempuh oleh semut 2 dengan pemberian kadar feromon
yang rendah
Jalur 2: Jalur yang tidak ditempuh
Jalur 3: Jalur yang ditempuh oleh semut 2 dengan pemberian kadar feromon
yang tinggi
Jalur 3 B Jalur 2 A
Jalur 2
Keterangan: A : Sarang semut
B : Tempat ditemukannya makanan
Jalur 1 : Jalur yang tidak ditempuh karena kadar feromon yang rendah Jalur 2 : Jalur yang tidak ditempuh karena kadar feromon yang sangat rendah Jalur 3 : Jalur optimal yang ditempuh oleh semut karena kadar feromon yang tinggi
3.4 Penyelasaian Masalah dengan Algoritma Semut
Setiap semut akan berperan sebagai agen yang mampu melakukan tugas sederhana untuk melakukan solusi dengan kriteria:
1. Semut akan berpindah dari kota i ke kota j, pada interval antara t dan (t+1). Kota j dipilih berdasarkan probabilitas terhadap jarak antarkota dan juga jumlah jejak yang ada pada sisi yang menghubungkan antara i dan j.
2. Semut akan berpindah dari kota asal ke kota yang lain yang belum pernah dikunjunginya atau kota yang memungkinkan jaraknya maka akan sering untuk dikunjungi dan pada akhirnya semut tersebut akan sampai pada kota tujuan.
3. Jika jalur suatu jalur memiliki jarak paling pendek maka jumlah semut yang ada akan memilih jalur tersebut, sehingga semua semut akan berada pada jalur yang terpendek.
A
D
B
E C
Gambar 3.8 Contoh kasus
Tabel 3.1 Jarak antarkota dij
A B C D E
A 0 5 7 3 0
B 5 0 4 0 0
C 7 4 0 0 5
D 3 0 0 0 4
E 0 0 5 4 0
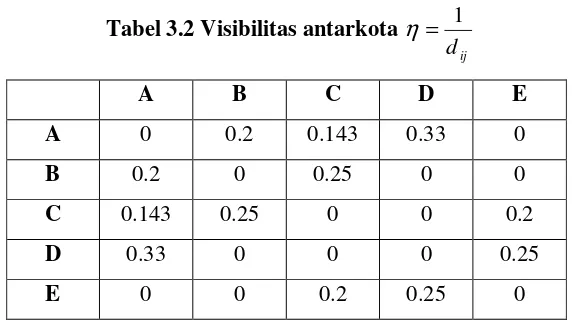
Dari jarak kota yang telah diketahui dapat dihitung visibilitas antarkota
ij
d
1
=
η
sebagai berikut:Tabel 3.2 Visibilitas antarkota ij
d
1
=
η
A B C D E
A 0 0.2 0.143 0.33 0
B 0.2 0 0.25 0 0
C 0.143 0.25 0 0 0.2
D 0.33 0 0 0 0.25
Kasus 1:
Parameter-parameter yang digunakan adalah sebagai berikut:
E
Dari intensitas jejak semut τij yang telah ditetapkan dan perhitungan visibilitas
antarkota
Tabel 3.3 Probabilitas kota untuk dikunjungi siklus ke-1 kasus 1
A B C D E
Sehingga didapat panjang jalur semut pada siklus ke-1 sebagai berikut:
Tabel 3.4 Panjang jalur semut siklus ke-1 kasus 1
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – B – C – E 14
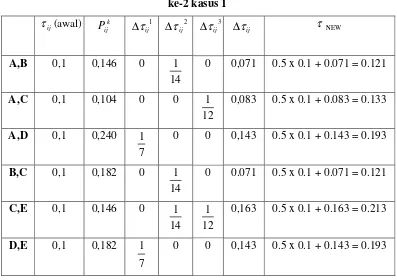
Dari perjalan semut pada siklus ke-1 maka akan terjadi perubahan harga intensitas jejak kaki semut τij antarkota untuk siklus selanjutnya sebagai berikut:
Tabel 3.5 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-2 kasus 1
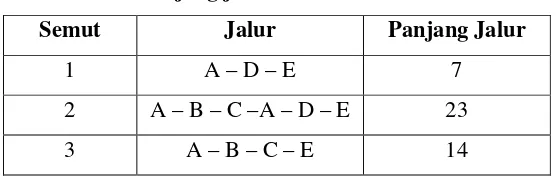
Tabel 3.7 Panjang jalur semut siklus ke-2 kasus 1
Semut Jalur Panjang Jalur
1 A – C – E 12
2 A – D – E 7
3 A – B – C – A – D - E 23
Tabel 3.8 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-3 kasus 1
Tabel 3.10 Panjang jalur semut siklus ke-3 kasus 1
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – C – E 12
3 A – D – E 7
Dari ke-3 siklus yang telah dilakukan akan diperoleh jalur terpendek dari kota asal A ke kota tujuan E yaitu A – D – E dengan panjang jalur 7. Karena siklus yang diinginkan hanya 3 siklus maka langkah selanjutnya tidak dikerjakan lagi karena sudah terjadi konvergensi.
Kasus 2:
Parameter-parameter yang digunakan adalah sebagai berikut:
E
Tabel 3.11 Probabilitas kota untuk dikunjungi siklus ke-1 kasus 2
Tabel 3.12 Panjang jalur semut siklus ke-1 kasus 2
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – B – C –A – D – E 23
3 A – B – C – E 14
Tabel 3.13 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-2 kasus 2
Tabel 3.14 Probabilitas kota untuk dikunjungi siklus ke-2 kasus 2 dengan
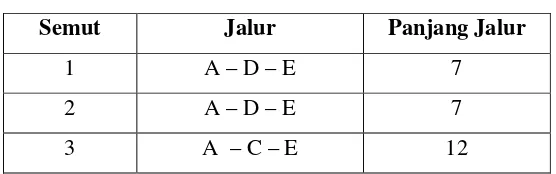
Tabel 3.15 Panjang jalur semut siklus ke-2 kasus 2
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – D – E 7
3 A – C – E 12
Tabel 3.16 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-3 kasus 2
Tabel 3.17 Probabilitas kota untuk dikunjungi siklus ke-3 kasus 2 dengan
Tabel 3.18 Panjang jalur semut siklus ke-3 kasus 2
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – D – E 7
3 A – D – E 7
Dari ke-3 siklus yang telah dilakukan akan diperoleh jalur terpendek dari kota asal A ke kota tujuan E yaitu A – D – E dengan panjang jalur 7. Karena siklus yang diinginkan hanya 3 siklus maka langkah selanjutnya tidak dikerjakan lagi karena sudah terjadi konvergensi.
Kasus 3:
Parameter-parameter yang digunakan adalah sebagai berikut:
E
Tabel 3.19 Probabilitas kota untuk dikunjungi siklus ke-1 kasus 3
Tabel 3.20 Panjang jalur semut siklus ke-1 kasus 3
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – B – C – E 14
3 A – C – E 12
Tabel 3.21 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-2 kasus 3
Tabel 3.22 Probabilitas kota untuk dikunjungi siklus ke-2 kasus 3 dengan
Tabel 3.23 Panjang jalur semut siklus ke-2 kasus 3
Semut Jalur Panjang Jalur
1 A – C – E 12
2 A – D – E 7
3 A – B – C – A – D - E 23
Tabel 3.24 Perubahan harga intensitas jejak kaki semut τij antarkota siklus ke-3 kasus 3
Tabel 3.25 Probabilitas kota untuk dikunjungi siklus ke-3 kasus 3 dengan
Tabel 3.26 Panjang jalur semut siklus ke-3 kasus 3
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – C – E 12
3 A – D – E 7
Kasus 4:
Parameter-parameter yang digunakan adalah sebagai berikut:
E
Tabel 3.27 Probabilitas kota untuk dikunjungi siklus ke-1 kasus 4
A B C D E
Tabel 3.28 Panjang jalur semut siklus ke-1 kasus 4
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – B – C – E 14
Tabel 3.29 Perubahan harga intensitas jejak kaki semut τij antarkota
Tabel 3.30 Probabilitas kota untuk dikunjungi siklus ke-2 kasus 4 dengan
ij
Tabel 3.31 Panjang jalur semut siklus ke-2 kasus 4
Semut Jalur Panjang Jalur
1 A – C – E 12
2 A – D – E 7
Tabel 3.32 Perubahan harga intensitas jejak kaki semut τij antarkota
Tabel 3.33 Probabilitas kota untuk dikunjungi siklus ke-3 kasus 4 dengan
ij
Tabel 3.34 Panjang jalur semut siklus ke-3 kasus 4
Semut Jalur Panjang Jalur
1 A – D – E 7
2 A – C – E 12
Semut akan memilih jalur yang memiliki kadar feromon yang besar. Itu berarti jalur yang jarang dilalui, kadar feromon akan berkurang sehingga semut-semut tidak akan memilih jalur tersebut.
Nilai paramater dan mempengaruhi nilai Pijk , dimana Pijk merupakan
probabilitas dari kota i ke kota j. Semakin besar nilai parameter keduanya, semakin besar pula probabilitas dari kota yang sekarang ke kota berikutnya. Ini berarti nilai
paramater dan berbanding lurus dengan nilai Pijk .
Nilai parameter akan mempengaruhi nilai τij, dimana τij merupakan
intensitas jejak kaki semut. Intensitas jejak kaki semut setiap kota berbeda-beda. Setiap iterasi yang dilakukan menyebabkan perubahan pada intensitas jejak kaki semut tersebut. Jadi setiap iterasi diadakan perubahan nilai intensitas jejak kaki semut.
Semakin besar nilai akan memperkecil nilai τij, sedangkan semakin kecil nilai
akan memperbesar nilai τij. Ini berarti nilai berbanding terbalik dengan nilai τij.
Semakin besar nilai , maka intensitas jejak kaki semut τij menjadi lebih kecil
sedangkan semakin kecil nilai , maka intensitas jejak kaki semut τij menjadi lebih
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari penelitian tentang pencarian jalur terpendek menggunakan algoritma semut, dapat diambil kesimpulan sebagai berikut:
1. Algoritma semut merupakan alternatif lain yang digunakan dalam permasalahan optimisasi.
2. Algoritma semut dapat digunakan untuk melakukan pencarian jalur terpendek berdasarkan jarak yang ditempuh.
3. Hasil yang diperoleh dari metode heuristik lebih variatif dan lebih cepat. 4. Pemanfaatan teknologi informasi pada pencarian jalur terpendek
menghasilkan suatu hasil atau keluaran yang akurat dan tepat, untuk pilihan perjalanan seseorang dengan mempertimbangkan beberapa parameter yang lain.
4.2 Saran
DAFTAR PUSTAKA
Dorigo, Marco. dan Thomas St tzle. 2004. Ant Colony Optimization. Slides Large: hal. 1-53.
G nay, Akin. 2007. Ant Colony Optimization. Slides Large: hal. 1-15.
Hamzah, Amir. 2011. Matematika Diskrit. Yogyakarta: Fakultas Teknologi Industri Institut Sains dan Teknologi Akprind.
Maharani, Warih. 2009. Analisis algoritma hybrid ant colony optimization (aco) dan local search untuk optimasi pemotongan bahan baku. SNATI2009 1907-5022: hal. E63-E68.
Munir, Rinaldi. 2005. Matematika Diskrit. Edisi ketiga. Bandung: Informatika.
Mutakhiroh, I’ing., Fajar Saptono, Nur Hasanah, dan Romi Wiryadinata. 2007. Pemanfaatan metode heuristik dalam pencarian jalur terpendek dengan algoritma semut dan algoritma genetika. SNATI2009 1907-5022: B33-B39.
Mutakhiroh, I’ing., Indrato, dan Taufiq Hidayat. 2007. Pencarian jalur terpendek menggunakan algoritma semut. SNATI2009 1907-5022: hal. B81-B85.
Rosen, K.H. 2003. Discrete Mathematics and Its Applications. Fifth edition. New York: McGraw-Hill.
St tzle, Thomas. 2005. Ant Colony Optimization An Introduction. Slides Large: hal. 1-46.
Wardy, Ibnu Sina. 2007. Penggunaan graf dalam algoritma semut untuk melakukan optimisasi. Jurnal Program Studi Teknik Informatika ITB: hal. 1-10.
Wibisono, Samuel. 2008. Matematika Diskrit. Edisi kedua. Jakarta: Graha Ilmu.
LAMPIRAN : LISTING PROGRAM
float alpha, beta, rho, tho, x, pk[100][100], v[100][100], p[100][100]; int jarak[100][100], solusi1[100], solusi2[100], tabu[100][100], solusi[100];
mulai:
system("cls");
printf("\n\n---\n");
printf("PROGRAM KOMPUTASI JALUR TERPENDEK DENGAN ALGORITMA SEMUT\n");
printf("---\n\n");
srand(time(0));
//Inisial parameter algoritma semut
printf("Tentukan banyak titik = "); scanf("%d", &titik); printf("Tentukan titik awal = "); scanf("%d", &awal); printf("Tentukan titik tujuan = "); scanf("%d", &akhir); printf("Tentukan banyak siklus = "); scanf("%d", &Q); printf("Tentukan besar intensitas = "); scanf("%f", &tho); printf("Tentukan besar alpha = "); scanf("%f", &alpha); printf("Tentukan besar beta = "); scanf("%f", &beta); printf("Tentukan banyak semut = "); scanf("%d", &semut);
//Input jarak antar titik
//---
printf("\n\nPROSES ITERASI ALGORITMA SEMUT\n"); printf("---\n");