Kajian Terhadap Algoritma Semut (sudi Kasus : Penyelesaian Travelling Salesperson Problem)

(1)

KAJIAN TERHADAP ALGORIMA SEMUT (STUDI KASUS:

PENYELESAIAN TRAVELLING SALESPERSON PROBLEM)

SKRIPSI

ZUHROH

051411029

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

PERSETUJUAN

Judul : KAJIAN TERHADAP ALGORITMA SEMUT

(STUDI KASUS: PENYELESAIAN TRAVELING SALESPERSON PROBLEM)

Kategori : SKRIPSI

Nama : ZUHROH

Nomor Induk Mahasiswa : 051411029

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MTEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, April 2008

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Drs. Bambang Irawan, M.Sc

Diketahui / Disetujui Oleh

(3)

PERNYATAAN

KAJIAN TERHADAP ALGORITMA SEMUT

(STUDI KASUS: TRAVELING SALESPERSON PROBLEM)

SKRIPSI

Saya mengaku bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, April 2008

(4)

PENGHARGAAN

Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpahan rahmat dan karunia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan.

(5)

ABSTRAK

(6)

STUDY OF ANT ALGORITHM (CASE STUDY: TRAVELING SALESPERSON PROBLEM SOLUTION)

ABSTRACT

(7)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel viii

Daftar Gambar ix

BAB 1 PENDAHULUAN 1

Latar Belakang 1

Perumusan Masalah 4

Tinjauan Pustaka 4

Tujuan Penelitian 5

Manfaat Penelitian 5

Metode Penelitian 6

BAB 2 LANDASAN TEORI 7

2.1. Teori Graf 7

2.2.1. Definisi Graf 7

2.2.2. Graf Hamilton 8

2.2.3. Representasi Graf pada Komputer 9 2.2. Traveling Salesperson Problem 10 2.3. Sejarah Singkat Traveling Salesperson Problem 11

2.4. Algoritma semut 12

2.4.1. Sejarah Algoritma Semut 12

2.4.2. Prinsip Perilaku Semut 12

2.5. Algoritma Semut pada Traveling Salesperson Problem 18

BAB 3 PEMBAHASAN 23

3.1. Analisis Algoritma 23

3.2. Implementasi TSP dengan Algoritma Semut 24 3.3. Perancangan Program Penyelesaian TSP dengan Algoritma Semut 36 3.3.1. Perancangan Flowchart 36 3.3.2. Kebutuhan Perangkat Keras 38 3.3.3. Perancangan Perangkat Lunak 38 3.4. Coding untuk Algoritma Semut 41

3.5. Hasil Analisis 44

3.5.1 Analisis Berdasarkan Regresi 45

BAB 4 KESIMPULAN dan SARAN 46

DAFTAR PUSTAKA 47

(8)

DAFTAR TABEL

Halaman

Tabel 2.1 Daftar History dari TSP 11

Tabel 3.1 Koordinat Kota 27

Tabel 3.2 Jarak antar Kota 28

Tabel 3.3 Visibilitas antar Kota 28

(9)

DAFTAR GAMBAR

Halaman

Gambar 2.1 Graf dengan Empat Verteks dan Tujuh Edge 7

Gambar 2.2 Graf Berarah 8

Gambar 2.3 Penggambaran Graf Hamilton 8 Gambar 2.4 Lintasan Awal Semut Menuju Tempat Makanan 14 Gambar 2.5 Lintasan Optimal Semut Menuju Tempat Makanan 14 Gambar 2.6 Lintasan Semut Menuju Sarang 16 Gambar 2.7 Lintasan Semut Menuju Makanan pada Iterasi ke-2 16 Gambar 2.8 Lintasan Semut Menuju Sarang pada Iterasi ke-2 17 Gambar 2.9 Lintasan Optimal Semut Menuju Tempat Makanan 18 Gambar 3.1 Graf dengan Empat Vertex dan Enam Edge 27 Gambar 3.2 Flowchart dari Algoritma Semut untuk Penyelesaian TSP 37 Gambar 3.3 Tampilan Halaman Utama 39

Gambar 3.4 Data Graf dengan 10 Kota 39

Gambar 3.5 Tampilan Hasil Komput asi 40

Gambar 3.6 Tampilan Halaman Hasil 41

(10)

ABSTRAK

(11)

STUDY OF ANT ALGORITHM (CASE STUDY: TRAVELING SALESPERSON PROBLEM SOLUTION)

ABSTRACT

(12)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Traveling Salesperson Problem selanjutnya dalam tulisan ini disingkat menjadi TSP, digambarkan sebagai seorang penjual yang harus melewati sejumlah kota selama perjalanannya, dengan jarak tempuh yang minimum dan kembali ke kota asal keberangkatannya, di mana jarak antarkota diketahui dan terhubung ke kota lain tepat atau hanya satu jalan dengan catatan jalur yang dilalui adalah sama.

Persoalan TSP ini dimodelkan sebagai graf lengkap dengan n buah vertex. Bobot pada setiap setiap sisi menyatakan jarak antara dua buah kota yang bertetangga. Dengan menetapkan sejumlah n kota, TSP dapat didefinisikan sebagai permasalahan dalam mencari jalur terpendek dengan melakukan tour tertutup (yang dimulai dari suatu kota dan kembali ke kota tersebut) di mana setiap kota yang ada hanya dikunjungi sekali.

Dalam persoalan TSP yang digambarkan dengan penjual yang harus menemukan tour terpendek dengan melewati beberapa kota hanya sekali dan kembali lagi ke kota asal keberangkatannya, dengan memodelkan kota sebagai simpul (vertex) dan jalan sebagai sisi (edge) digambarkan persoalan tersebut adalah persoalan graf dengan menemukan sirkuit Hamilton dengan bobot minimum.

(13)

Algoritma Brute Forceuntuk persoalan TSP:

1. Enumerasikan (list) semua sirkuit Hamilton dari graf lengkap dengan n buah simpul.

2. Hitung (evaluasi) bobot setiap sirkuit Hamilton yang ditemukan pada langkah pertama.

3. Pilih sirkuit Hamilton yang mempunyai bobot terkecil.

Untuk n buah simpul semua rute perjalanan yang mungkin dibangkitkan dengan permutasi dari n – 1 buah simpul. Permutasi dari n – 1 buah simpul adalah (n – 1)!. Jika persoalan TSP diselesaikan dengan metode Brute force, maka harus dienumerasi sebanyak (n – 1)!/2 buah sirkuit Hamilton, menghitung setiap bobotnya, dan memilih sirkuit Hamilton dengan bobot terkecil. Untuk ukuran masukan yang besar, algoritma Brute force menjadi sangat tidak mangkus. Pada persoalan TSP misalnya, untuk jumlah simpul n = 20 akan terdapat (19!)/2 = 6 × 1016

1. Mulai dari sembarang kota.

sirkuit Hamilton yang harus dievaluasi satu per satu.

Sedangkan penyelesaian TSP dengan algoritma Greedy adalah sebagai berikut:

2. Evaluasi semua biaya tetangga.

3. Ambil tetangga dengan biaya terkecil dan diulang pada langkah ke dua hingga kota telah terlewati semua.

(14)

algoritma ini tidak selalu benar. Tetapi ketika algoritma Greedy bekerja, lebih mudah untuk diterapkan dan cukup cepat untuk dilaksanakan.

Dalam algoritma Semut (Ant Algorithm) penyelesaian masalah TSP dengan cara menemukan jalur terbaik melalui grafik. perjalanan semut menuju makanan, terdapat suatu mekanisme untuk mencari lintasan optimal yang akan dilalui semut. Pada awalnya, semut berkeliling secara acak, hingga menemukan makanan. Ketika menemukan makanan mereka kembali ke koloninya sambil memberikan tanda dengan jejak feromon. Setiap semut memiliki feromon, yaitu jejak yang mengidentifikasi sesamanya. Semut lain yang menemukan jalur tersebut tidak akan berjalan dengan acak lagi, melainkan akan mengikuti jejak tersebut dan jika pada akhirnya menemukan makanan kembali menguatkan jejaknya dengan feromon. Seekor semut yang secara tidak sengaja menemukan jalur optimal akan menempuh jalur ini lebih cepat dari rekan-rekannya, melakukan round-trip lebih sering dan dengan sendirinya meninggalkan feromon lebih banyak dari jalur-jalur yang lebih lambat ditempuh. Feromon yang berkonsentrasi tinggi pada akhirnya akan menarik semut-semut lain untuk berpindah jalur, menuju jalur paling optimal, sedangkan jalur lainnya akan ditinggalkan. Pada akhirnya semua semut yang tadinya menempuh jalur yang berbeda-beda akan beralih ke sebuah jalur tunggal yang ternyata paling optimal dari sarang menuju ke tempat makanan.

(15)

1.2 Perumusan Masalah

Perumusan masalah yang akan diteliti dalam tulisan ini adalah bagaimana algoritma Semut menghasilkan penyelesaian yang optimal pada kasus Traveling Salesperson Problem.

1.3 Tinjauan Pustaka

Marco Dorigo dan Luca Gambardella dalam jurnalnya yang berjudul Ant Colonies for The Traveling Salesman Problem, menjelaskan bahwa semut riil mampu untuk menemukan jalur paling pendek dari suatu sumber makanan ke sarang tanpa menggunakan isyarat visual. Juga mereka mampu untuk beradaptasi pada perubahan lingkungan, misalnya menemukan suatu jalur baru yang paling pendek sekali ketika yang lama tidak lagi mungkin dilalui karena suatu rintangan. Semut menyimpan feromon dalam jumlah tertentu saat berjalan, dan masing-masing semut secara probabilistik mengikut i arah yang memiliki banyak feromon. Dasar perilaku dari semut riil ini dapat digunakan untuk menjelaskan bagaimana mereka dapat menemukan jalur yang paling pendek dan menyambung kembali suatu jalan yang terputus setelah mendapat rintangan yang tak terduga. Faktanya, ketika mendapat rintangan, hanya semut yang berada di depan rintangan yang tidak bisa melanjutkan mengikuti jejak feromon dan oleh karena itu mereka harus memilih antara memutar atau meninggalkan.

Marco dorigo dan Gianni Di Caro dalam jurnal yang berjudul Ant Algorithms for Discrete Optimization, menjelaskan bahwa aplikasi dari algoritma Semut telah digunakan pada percobaan Traveling Salesperson Problem. Ide mengapa mengunakan TSP adalah karena TSP merupakan salah satu permasalahan NP-hard pada optimisasi kombinatorik, yang dipilih dari permasalahan menemukan jalur terpendek menggunakan metafora koloni semut.

(16)

Semut adalah meniru perilaku ‘semut tiruan’ berjalan seputar grafik yang menunjukkan persoalan yang harus bisa diselesaikan. Ada banyak sekali penerapan algoritma Semut dalam berbagai persoalan kehidupan sehari-hari. Persoalan tersebut adalah Traveling Salesman Problem (TSP), Quadratic Assignment Problem (QAP), Job-shop Scheduling Problem (JSP), dan sejumlah aplikasi lain mencakup pengaturan jalur kendaraan, pewarnaan graf dan network routing.

Situs Wikipedia menjelaskan bahwa algoritma Semut telah digunakan untuk menghasilkan penyelesaian yang mendekati optimal pada masalah salesman yang melakukan perjalanan. Algoritma Semut lebih menguntungkan daripada pendekatan

penguatan tiruan (simulated annealing) da

berubah secara dinamis; algoritma Semut dapat berjalan secara kontinyu dan menyesuaikan dengan perubahan secar(real time).

1.4 Tujuan Penelitian

Penelitian ini secara umum bertujuan untuk mengkaji tentang Algoritma Semut dan menerapkannya untuk menyelesaikan Traveling Salesperson Problem sehingga diperoleh perjalanan yang optimal dan mengimplementasikan ke dalam bahasa pemrograman.

1.5 Manfaat Penelitian

(17)

1.6 Metode Penelitian

Dalam penyusunan tulisan ini, penulis menggunakan tahapan sebagai berikut:

1. Mendefinisikan istilah-istilah dalam algoritma dengan istilah pada teori graf.

2. Menyajikan persolan TSP dalam bentuk graf.

3. Menerapkan algoritma Semut untuk penyelesaian kasus Traveling Salesperson Problem.

(18)

BAB 2

LANDASAN TEORI

2.1 Teori Graf

2.2.1 Definisi Graf

Graf didefinisikan dengan G = (V, E), di mana V adalah himpunan tidak kosong dari vertex-vertex = {v1, v2, v3,...} dan E himpunan sisi (edges atau arcs) yang menghubungkan sepasang vertex {e1, e2, e3, ...}. Vertex dalam graf pada tulisan ini merupakan kota dan edge atau sisi merupakan rute atau jalan yang menghubungkan antar kota.

B

D

C A

Gambar 2.1 Graf dengan Empat Vertex dan Tujuh Edge

Keterangan Gambar:

G adalah graf dengan:

V = { a, b, c, d }

(19)

Berdasarkan orientasi arah pada sisi, secara umum graf dapat dibedakan atas dua jenis:

1. Graf tak-berarah (undirected graph) Graf yang sisinya tidak mempunyai orientasi arah disebut graf tak-berarah.

2. Graf berarah (directed graph atau digraph) Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf berarah.

B

D

C A

Gambar 2.2 Graf Berarah

2.2.2 Graf Hamilton

Graf Hamilton adalah graf yang memiliki sirkuit Hamilton, sedangkan graf yang hanya memiliki lintasan Hamilton disebut graf semi-Hamilton. Lintasan Hamilton ialah lintasan yang melalui tiap vertex di dalam graf tepat satu kali. Sedangkan sirkuit Hamilton ialah sirkuit yang melalui tiap vertex di dalam graf tepat satu kali, kecuali vertex asal sekaligus vertex akhir yang dilalui dua kali.

Teorema 2.1. Setiap graf lengkap adalah graf Hamilton.

Gambar 2.3 Penggambaran Graf Hamilton

a _b

c d

a

c

b

d

a b

c

d

(20)

Keterangan gambar:

(a) graf yang memiliki lintasan Hamilton (misal:c, b, a, d) (b) graf yang memiliki sirkuit Hamilton (a, b, c, d, a)

(c) graf yang tidak memiliki lintasan maupu n sirkuit Hamilton

2.2.3 Representasi Graf Pada Komputer

Untuk mengimplementasikan suatu algoritma graf dalam bahasa pemrograman komputer, dibutuhkan suatu cara untuk menterjemahkan bentuk graf ke dalam bentuk lain yang dikenal oleh komputer, sebab komputer tidak dapat mengenal graf dalam bentuk gambar graf biasa. Matriks dapat digunakan untuk menyatakan suatu graf, jika graf dinyatakan sebagai matriks maka perhitungan-perhitungan yang diperlukan dapat dilakukan dengan mudah. Representasi graf pada komputer dapat dilakukan dengan beberapa cara, yaitu:

1. Matriks Adjacency

Matriks adjacency didefinisikan sebagai berikut , misalkan A matriks berordo

nxn (n baris dan n kolom). Jika antara dua vertex terhubung (adjacent) maka elemen matriks bernilai 1, dan sebaliknya jika tidak terhubung bernilai 0. Matriks adjacency dari graf Gambar 2.2 adalah:

A =             0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0

(21)

2. Matriks Incidency

Matriks incidence atau matriks bersisian adalah matriks yang merepresentasikan hubungan antara vertex dan edge. Misalkan B adalah matriks dengan m baris untuk setiap vertex dan n kolom untuk setiap edge. Jika vertex terhubung dengan edge, maka elemen matriks bernilai 1. Sebaliknya, jika vertex tidak terhubung dengan edge maka elemen matriks bernilai 0. Matriks bersisian dari graf Gambar 2.2 adalah:

B =             1 1 1 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1

Seperti halnya matriks kedekatan untuk matriks berbobot, untuk matriks bersisian elemen dari matriks juga merupakan bobot dari setiap edge dari graf.

2.2 Traveling Salesperson Problem

Traveling Salesperson Problem (TSP) adalah masalah menemukan perjalanan (tour) terpendek pada n buah kota dan setiap kota saling berhubungan satu sama lain. Seorang sales memulai perjalanannya dari satu kota, melalui setiap kota lainnya hanya sekali dan kembali lagi ke kota asal keberangkatan.

Jarak antara setiap kota satu sama lain diketahui dan ingin meminimalkan ongkos yang harus dikeluarkannya untuk perjalanannya tersebut.

(22)

2.3 Sejarah Singkat Traveling Salesperson Problem

Permasalahan TSP dalam ilmu matematika dilakukan pada tahun 1800 oleh ahli matematika Irlandia William Rowan Hamilton dan ahli matematika Inggris Thomas Penyngton Kirkman, dengan membuat permainan untuk menyelesaikan perjalanan melalui 20 titik dengan menggunakan koneksi yang sudah ditetapkan. Permainan yang disebut game Icosian tersebut tak lain adalah menemukan siklus Hamilton di atas suatu bidang dengan mengunjungi tiap-tiap sisinya (edge) sekali dan akhirnya kembali ke sisi awal, suatu permainan yang jelas seperti rumus TSP.

TSP kemudian dipelajari oleh ahli matematika Karl Menger di Vienna, Harvard sert dan menuliskan bentuk umumnya. Karena pertumbuhan algoritma yang semakin meningkat dari tahun ke tahun, mulai tahun 1950 penyelesaian TSP dipecahkan dengan komputer. Tahun 1954 pertumbuhan penting dari TSP diteliti oleh para peneliti yaitu: Dantzig, Fulkerson dan Jhonson yang terus mengembangkan metode baru untuk menyelesaikan permasalahan TSP.

Tabel 2.1 Daftar History dari TSP

Tahun Tim Periset Ukuran

1954 G. Dantzig, R. Fulkerson, dan S. Johnson 49 kota 1971 M. Held dan R.M. Karp 64 kota 1975 P.M. Camerini, L. Fratta, dan F. Maffioli 67 kota

1977 M. Grötschel 120 kota

1980 H. Crowder dan M.W. Padberg 318 kota 1987 M. Padberg dan G. Rinaldi 532 kota 1987 M. Grötschel dan O. Holldan 666 kota 1987 M. Padberg dan G. Rinaldi 2.392 kota 1994 D. Applegate, R. Bixby, V. Chvátal, dan

W. Cook 7.397 kota

1998 D. Applegate, R. Bixby, V. Chvátal, dan

W. Cook 13.509 kota

2001 D. Applegate, R. Bixby, V. Chvátal, dan

(23)

TSP juga merupakan percobaan pertama dalam aplikasi algoritma Semut pada tahun 1991, dengan mengadaptasi perilaku kehidupan semut dalam menemukan jalur terpendek. Didefinisikan V adalah vertex sebagai kota dan E adalah edge atau sisi yang terhubung secara penuh pada V. Permasalahannya adalah menemuka n sirkuit Hamilton dalam sebuah graf G = (V, E).

2.4 Algoritma Semut

2.4.1Sejarah Algoritma Semut

Seiring berkembangnya pemikiran, ditemukan sejumlah algoritma dalam AI

(Artifical Intelligence) yang mendapat inspirasi dari alam. Algoritma tersebut di

antaranya adalah: cara kerja otak yang luar biasa mengilhami neural network,

genetic algorithm belajar dari proses evolusi, dan dari semut menyelesaikan

masalah optimisasi.

Pada tahun 1996, dunia AI diperkenalkan dengan algoritma Semut oleh Moyson dan Manderick dan secara meluas dikembangkan oleh Marco Dorigo, merupakan teknik probabilistik untuk menyelesaikan masalah komputasi dengan menemukan jalur terbaik melalui grafik. Sebagai sebuah simulasi yang menggunakan metafora alami semut untuk menyelesaikan problem ruang fisik. Algoritma ini terinspirasi oleh perilaku semut dalam menemukan jalur dari sarangnya menuju makanan.

2.4.2 Prinsip Perilaku Semut

(24)

Semut juga mampu mengindera lingkungannya yang kompleks untuk mencari makanan dan kemudian kembali ke sarangnya dengan meninggalkan zat feromon pada jalur-jalur yang mereka lalui. Feromon adalah zat kimia yang berasal dari kelenjar endokrin dan digunakan oleh makhluk hidup untuk mengenali sesama jenis, individu lain, kelompok, dan untuk membantu proses reproduksi. feromon menyebar ke luar tubuh dan hanya dapat mempengaruhi dan dikenali oleh individu lain yang sejenis (satu spesies).

Proses peninggalan feromon ini dikenal sebagai stigmergy, yaitu sebuah proses memodifikasi lingkungan yang tidak hanya bertujuan untuk mengingat jalan pulang ke sarang, tetapi juga memungkinkan para semut berkomunikasi dengan sesamanya. Seiring waktu, bagaimanapun juga jejak feromon akan menguap dan akan mengurangi kekuatan daya tariknya. Lebih lama seekor semut pulang pergi melalui jalur tersebut, lebih lama jugalah feromon menguap.

Agar semut mendapatkan jalur optimal dalam perjalanannya, diperlukan beberapa proses:

1. Pada awalnya, semut berkeliling secara acak, hingga menemukan makanan.

2. Ketika menemukan makanan mereka kembali ke sarangnya sambil memberikan tanda dengan jejak feromon.

3. Jika semut-semut lain menemukan jalur tersebut, maka mereka tidak akan

bepergian dengan acak lagi, melainkan akan mengikuti jejak tersebut.

(25)

5. Seekor semut yang secara tidak sengaja menemukan jalur optimal akan menempuh jalur ini lebih cepat dari rekan-rekannya, melakukan round-trip

lebih sering, dan dengan sendirinya meninggalkan feromon lebih banyak dari jalur-jalur yang lebih lambat ditempuh.

6. Feromon yang berkonsentrasi tinggi pada akhirnya akan menarik semut-semut lain untuk berpindah jalur, menuju jalur paling optimal, sedangkan jalur lainnya akan ditingga lkan.

7. Pada akhirnya semua semut yang tadinya menempuh jalur yang berbeda-beda akan beralih ke sebuah jalur tunggal yang ternyata paling optimal dari sarang menuju ke tempat makanan.

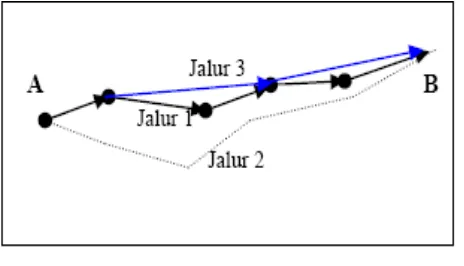
Gambar 2.4 Lintasan Awal Semut Menuju Tempat Makanan

Keterangan Gambar:

A: Tempat awal semut (sarang) B: Tujuan semut (makanan)

 : Lintasan yang ditempuh oleh semut 1 → : Lintasan yang ditempuh oleh semut 2

(26)

Keterangan Gambar:

A: Tempat awal semut(sarang) B: Tujuan semut (makanan)

Jalur Optimal: Jalur yang dilewati semut setelah beberapa iterasi.

Perilaku semut itu telah menginspirasikan sebuah metodologi baru dalam mencari solusi terhadap suatu permasalahan kombinatorial dengan cara bertukar informasi melalui feromon yang diletakkan pada edge-edge sebuah graf. Telah diamati bahwa pada saat berjalan semut meninggalkan sejumlah feromon pada jalur yang dilaluinya untuk menandai jalur tersebut, sehingga semut lain yang mengikut i jalur tersebut dapat mengidentifikasi feromon yang diletakkan semut sebelumnya, memutuskan untuk mengikutinya dan menguatkan jalur tersebut dengan feromon miliknya. Perilaku inilah yang menjelaskan bagaimana semut mampu menemukan jalur terpendek. Bentuk komunikasi yang diperantarai feromon ini di sebut stigmergy.

Berikut adalah tahapan-tahapan algoritma Semut dalam graf:

1. Dari sarang, semut berkeliling secara acak mencari makanan sambil mencatat jarak antara vertexyang ia lalui.

2. Ketika sampai ke makanan, Total jarak dari tiap vertex yang ia tempuh dijumlahkan untuk mendapatkan jarak dari sarang ke makanan.

(27)

Gambar 2.6 Lintasan Semut Menuju Sarang

Keterangan Gambar: A: Sarang semut

B: Tempat ditemukannya makanan

: Jalur yang ditempuh oleh semut 1 dengan pemberian kadar

feromon yang tinggi.

→ : Jalur yang ditempuh oleh semut 2 dengan pemberian kadar

feromon yang rendah.

4. Untuk memilih edge mana yang harus dilalui berikutnya, digunakan sebuah rumus yang pada intinya menerapkan suatu fungsi heuristik untuk menghitung intensitas feromon yang ditinggalkan pada suatu busur.

Gambar 2.7 Lintasan Semut Menuju Makanan pada Iterasi ke-2

(28)

→: Jalur 1 adalah yang ditempuh oleh semut 1 karena kadar

....: Jalur yang tidak ditempuh oleh semut karena kadar feromon yang rendah.

 : Jalur yang ditemukan oleh semut 2

5. Pada iterasi berikutnya, edge-edge yang mengandung feromon lebih tinggi ini akan cenderung dipilih sebagai edge yang harus ditempuh berikutnya berdasarkan rumus pemilihan edge. Akibatnya, lama-kelamaan akan terlihat jalur optimal pada graf, yaitu jalur yang dibentuk oleh edge dengan kadar feromon yang tinggi, yang pada akhirnya akan dipilih oleh semua semut.

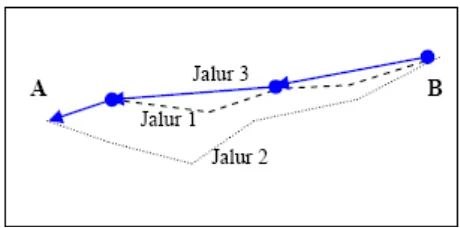
Gambar 2.8 Lintasan Semut Menuju Sarang pada Iterasi ke-2

----: Jalur 1 jalur yang ditempuh oleh semut 2 dengan pemberian kadar feromon yang rendah.

...: Jalur 2, jalur yang tidak ditempuh.

 : Jalur 3 adalah yang ditempuh oleh semut 2 dengan pemberian

(29)

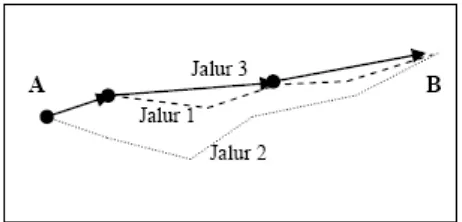
Gambar 2.9 Lintasan Optimal Semut Menuju Tempat Makanan

----: Jalur 1 yaitu jalur yang tidak ditempuh karena kadar feromon yang rendah.

...: Jalur 2, jalur yang tidak ditempuh karena kadar feromon yang sangat rendah.

→: Jalur 3, jalur optimal yang ditempuh oleh semut karena kadar

Oleh karena itu sistem ini dinamai dengan algoritma Semut. Semut yang digunakan dalam sistem ini berbeda dengan hewan semut yang asli, antara lain semut disini memiliki memori yang dalam tulisan ini dinamakan daftar semut dan semut akan berada pada lingkungan yang waktunya adalah diskrit.

2.5 Algoritma Semut Pada Traveling Salesperson Problem

TSP direpresentasikan dengan menggunakan sebuah graf di mana graf tersebut merupakan graf yang lengkap, artinya semua vertexnya terhubung satu sama lain. Jadi, jika terdapat n buah vertex maka graf tersebut memiliki (n! / ((n-2)! 2!))

(30)

simetris, artinya jarak antara kota i ke kota j sama dengan jarak antara kota j

ke kota i ( δ( (i,j)=δ( (j,i)). Algoritmanya sebagai berikut: Input : Matriks D untuk jarak

Inisialisasi Parameter pada Algoritma: α, β, Q, p, τ0

m = n {Jumlah semut sama dengan jumlah kota} begin

for i=1:n // untuk setiap edge// for j=1:n

if i = j

η(i,j) =1/D(i,j) //Visibility//

τ(i,j) = τ0

( )

[

] [ ]

( )

[

] [ ]











∑

=

∈ ∉ ∈ ik ik J t ij ij ij ij ik J j jika t t j j if k ij

t

P

β α β α η τ η τ . . , 0 , //feromon// else τ(i,j) = 0

end end end

for k =1 : m

<Menempatkan semut secara acak untuk memilih kota> end

<Pilih Rute terpendek T dan hitung panjangnya L> Loop

For t = 1 : tmax //tmax = nomor iterasi// For k = 1:m // untuk setiap semut://

< Membangun rute menurut aturan:

>

(31)

< Update T dan L > End

For i = 1 : n

For j = 1 : n //untuk setiap edge// < Update feromon trail menurut aturan:

∑

= ∆ + − = + m k k ij ij

ij t p t t

1 , ( ) ) ( ) 1 ( ) 1 ( τ τ τ > End End End

Output: Rute Terpendek

Algoritma ini mengasumsikan suatu graf terhubung, antara lain semut boleh memilih vertex mereka sendiri. Masing-Masing semut mulai dari suatu kota yang berbeda, semut memilih kota yang belum dikunjungi. Pilihan didasarkan pada suatu fungsi heuristik (alur paling pendek) dan alur yang memiliki jumlah feromon terbesar.

Sekali edge dipilih, semut menurunkan feromon. Jumlah feromon dibagi dengan jarak. Ini memberikan banyak feromon ke alur paling pendek. Feromon yang lama kemudian menguap dan setiap rute pada sisi yang feromonnya telah bekurang menjadi lebih kecil.

(32)

atau memiliki tingkat feromon yang tinggi. Setiap semut memiliki sebuah memori, dinamai daftar semut, yang berisi semua kota yang telah dikunjunginya pada setiap tour. Daftar semut ini mencegah semut untuk mengunjungi kota-kota yang sebelumnya telah dikunjungi selama tour tersebut berlangsung, yang membuat solusinya menjadi mungkin.

Setelah semua semut menyelesaikan tour mereka dan daftar semut menjadi penuh, sebuah aturan pembaruan feromon dilaksanakan pada setiap semut. Penguapan feromon pada semua edge dilakukan, dan kemudian setiap semut menghitung panjang tour yang telah mereka lakukan lalu menaruh sejumlah feromonpada edge-edge yang merupakan bagian dari tour mereka yang sebanding dengan kualitas dari solusi yang mereka hasilkan. Semakin pendek sebuah tour yang dihasilkan oleh seekor semut, jumlah feromon yang diletakkan pada edge-edge yang dilaluinya pun semakin besar, dengan demikian edge-edge yang merupakan bagian dari tour-tour yang pendek adalah edge-edge yang menerima jumlah feromon yang lebih besar. Hal ini menyebabkan edge yang diberi feromon lebih banyak akan lebih diminati/dipertimbangkan pada tour-tour selanjutnya, dan sebaliknya edge-edge yang tidak diberi feromon menjadi kurang diminati. Dan juga, jalur terpendek yang ditemukan oleh semut disimpan dan semua daftar semut dikosongkan kembali.

Aturan pemilihan kota berikut nya yang digunakan oleh algoritma Semut yang ditunjukkan oleh persamaan (1), merupakan probabilitas dari semut k pada kota i yang memilih untuk menuju ke kota j.

( )

[

] [ ]

( )

[

] [ ]











∑

=

∈ ∉ ∈ ik ik J t ij ij ij ij ik J j jika t t j j jika k ij

t

P

β α β α η τ η τ . . , 0 ,

α ≥ 0 dan β ≥ 0 adalah parameter yang menjelaskan bobot dari feromon

(33)

dipilih, dan ketika β=0, berarti hanya memperhitungkan feromon yang

menandakan bahwa semua semut memilih satu rute suboptimal.

τ adalah feromon, η=1/ δ adalah visibility (invers dari jarak δ(i,j)), Jik

T

adalah kumpulan kota yang akan dikunjungi oleh semut k yang sedang berada pada kota i (untuk membuat solusinya menjadi mungkin), dan β adalah sebuah parameter yang mengontrol bobot (weight) relatif dari feromon terhadap jarak (β>0). Pada persamaan (1) feromon pada edge (i,j) dikalikan dengan nilai visibility η(i,j), untuk memilih edge yang lebih pendek dan memiliki jumlah feromonyang lebih besar.

Dalam algoritma Semut, aturan pembaruan feromon diimplementasikan sebagai berikut: Setelah semua semut membuat tour mereka, feromon yang ada pada semua edge diperbarui menurut persamaan:

k(t) adalah rute semut k pada iterasi t, Lk(t) adalah panjang dari rute Tk

[ ]

0,1 ∈

p

(t),

dan Q > 0 adalah parameter yang ditentukan.

Penguapan feromon dilakukan untuk mencegah stagnasi yaitu situasi di mana semut berakhir dengan melakukan tour yang sama. Jika koefisien

penguapan ditandai dengan , maka bentuk aturan pembaharuan feromon

adalah:

∑

=

∆

+

−

=

+

m k k ij ij

ij

t

p

t

1 ,

(

)

(

)

1

(

)

1

(

τ

m adalah jumlah semut dan nilai feromon pada edge adalah sama dengan bilangan kecil positif τ0

( )

) ( ) , ( , 0 ), ( ) , ( , t T j i jika t T j i jika t L Q k k k ∉ ∈     = ∆τij,k(t)

.

(34)

BAB 3

PEMBAHASAN

3.1 Analisis Algoritma

Algoritma Semut untuk mencari jalur terpendek dari sebuah graf pada tulisan ini menggunakan semut sebagai agen, yang setiap semut memiliki tournya masing-masing mulai dari kota awal dan kembali ke kota tersebut dengan mengunjungi masing-masing kota yang ada hanya sekali, untuk mendapatkan hasil terbaik.

(35)

menjadi tour terbaik. Namun pencarian jalur terpendek akan terus berjalan sampai mencapai siklus maksimum yang diinput kan oleh user. Semakin besar angka yang di inputkan pada input kota dan parameter, hasil pencarian dari algoritma ini semakin beragam. Dari analisa terhadap algoritma Semut ini, beberapa hal yang penting adalah:

1. Dalam pemilihan kota berdasarkan persamaan probabilitas diperlukan nilai

parameter q0 yang merupakan sebuah bilangan acak dimana 0≤ q 0≥ 1.

2. Setiap semut harus memiliki daftar semut untuk menyimpan hasil tournya masing-masing. Daftar semut berisi kumpulan edge dan vertex yang merupakan bagian dari tour setiap semut. Nilai dari masing-masing daftar semut akan dikosongkan kembali setiap kali semut akan memulai tournya.

3. Proses perbaikan jejak feromon dipengaruhi oleh dua parameter yaitu ρ suatu

koefisien yang bernilai antara 0 sampai 1 dan ∆τ didapat dari hasil perkalian antara panjang tour dengan jumlah vertex yang ada pada graf tersebut.

3.2 Implementasi TSP dengan Algoritma Semut

Diberikan sejumlah kota dan jarak antar kota. Tentukan sirkuit terpendek yang harus dilalui oleh seorang pedagang, bila pedagang itu berangkat dari sebuah kota asal dan menyinggahi setiap kota tepat satu kali dan kembali lagi ke kota asal keberangkatan. Permasalahan melewati setiap kota tepat satu kali dan kembali ke kota asal adalah meliputi pencarian lintasan terpendek pada sebuah graf Hamilton. Apabila contoh kasus tersebut diubah menjadi persoalan pada graf, maka dapat dilihat bahwa kasus tersebut adalah bagaimana menentukan sirkuit Hamilton yang memiliki bobot minimum pada graf tersebut.

(36)

Langkah 1:

a. Inisialisasi harga parameter-parameter algoritma adalah:

1. Intensitas jejak feromon antar kota dan perubahannya (τij)

2. Banyak kota (n) termasuk koordinat (x,y) atau jarak antar kota (dij)

3. Tetapan siklus-semut (Q)

4. Tetapan pengendali intensitas jejak semut (α), nilai α≥ 0

5. Tetapan pengendali visibilitas (β), nilai β≥ 0

6. Visibilitas antar kota = 1/dij (ηij)

7. Banyak semut (m)

8. Tetapan penguapan jejak feromon (ρ), nilai ρ harus > 0 dan < 1 untuk mencegah jejak feromone yang tak terhingga.

9. Jumlah siklus maksimum (NCmax) bersifat tetap selama algoritma dijalankan, sedangkan τij akan selalu diperbaharui harganya pada setiap

siklus algoritma mulai dari siklus pertama (NC=1) sampai tercapai jumlah siklus maksimum (NC=NCmax).

b. Inisialisasi kota pertama setiap semut.

Setelah inisialisasi τij dilakukan, kemudian m semut ditempatkan pada kota

(37)

Langkah 2:

Pengisian kota pertama ke dalam daftar semut. Hasil inisialisasi kota pertama setiap semut dalam langkah 1 harus diisikan sebagai elemen pertama daftar semut (DS). Hasil dari langkah ini adalah terisinya elemen pertama daftar semut setiap semut dengan indeks kota tertentu, yang berarti bahwa setiap DS(1) bisa berisi indeks kota antara 1 sampai n sebagaimana hasil inisialisasi pada langkah 1.

Langkah 3:

Penyusunan rute kunjungan setiap semut ke setiap kota. Semut yang sudah terdistribusi ke sejumlah atau setiap kota, akan mulai melakukan perjalanan dari kota pertama masing-masing sebagai kota asal dan salah satu kota-kota lainnya sebagai kota tujuan. Kemudian dari kota ke dua masing-masing, semut akan melanjutkan perjalanan dengan memilih salah satu dari kota-kota yang tidak terdapat pada DS sebagai kota tujuan selanjutnya. Perjalanan semut berlangsung terus menerus sampai semua kota satu persatu dikunjungi atau telah menempati DS. Jika s menyatakan indeks urutan kunjungan, kota asal dinyatakan sebagai DS(s) dan kota-kota lainnya dinyatakan sebagai {N-DS}, maka untuk menentukan kota tujuan digunakan persamaan probabilitas kota untuk dikunjungi.

Langkah 4:

Perhitungan panjang rute tertutup (length closed tour) atau Lk setiap semut dilakukan setelah satu siklus diselesaikan oleh semua semut. Perhitungan ini dilakukan berdasarkan daftar semut masing-masing. setelah Lk setiap semut dihitung, akan didapat harga minimal panjang rute tertutup setiap siklus. Kemudian akan dihitung perbaikan jejak feromon atau perubahan harga feromon antar kota. Persamaan perubahan ini adalah:

∑

=

∆ =

∆ m

k k ij ij

1 τ τ

dengan ∆τ_ijk adalah perubahan feromon antar kota setiap semut yang dihitung

berdasarkan persamaan:

(38)

k ij

τ

∆ =

Lk

Q _{, untuk (i,j) ∈ kota dalam daftar semut.}

k ij

τ

∆ = 0, untuk (i,j) lainnya.

Langkah 5:

Perhitungan jejak feromon antar kota untuk siklus selanjutnya. Harga jejak feromon pada semua lintasan antar kota ada kemungkinan berubah sebab adanya perbedaan jumlah semut dan penguapan feromon. Selanjutnya harga feromon dihitung dengan persamaan:

ij ij

ij ρτ τ

τ = . +∆

Langkah 6:

Pengosongan daftar semut, dan ulangi Langkah 2 jika diperlukan. Pengosongan daftar semut dilakukan untuk melakukan pengisian urutan kota yang baru pada siklus selanjutnya, jika jumlah maksimum belum tercapai.

[image:38.595.270.385.446.536.2]

Berikut contoh penyelesaian TSP dengan Algoritma Semut: Diketahui sebuah graf:

Gambar 3.1 Graf dengan Empat Vertex dan Enam Edge

Dengan input kota berupa koordinat lokasi:

Tabel 3.1 Koordinat Kota Kota ke- X Y

1 10 0

2 30 0

3 15 20

4 25 20

(

) (

)

1 ₂

4 3

(3.2)

(3.3)

(39)

[image:39.595.212.426.106.201.2]

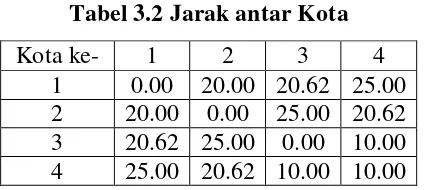
Tabel 3.2 Jarak antar Kota Kota ke- 1 2 3 4

1 0.00 20.00 20.62 25.00 2 20.00 0.00 25.00 20.62 3 20.62 25.00 0.00 10.00 4 25.00 20.62 10.00 10.00

Parameter–parameter yang digunakan adalah: Alfa (α) = 1.00

Beta (β) = 1.00 Rho (ρ) = 0.50

τij awal = 0.01

Maksimum siklus (NCmax) = 2 Tetapan siklus semut (Q) = 1 Banyak semut (m) = 4

Dari jarak kota yang telah diketahui dapat dihitung visibilitas antar kota (ηij) = 1/dij

Kota ke-

: Tabel 3.3 Visibilitas Antar Kota

1 2 3 4

1 0 0.05 0.049 0.04 2 0.05 0 0.04 0.049 3 0.049 0.04 0 0.1 4 0.04 0.049 0.1 0

Siklus ke-1:

Isi daftar semut awal: 1 2 3 4

Untuk t =1

Jumlah semut tiap kota: Kota 1 = 1

Kota 2 = 1 Kota 3 = 1 Kota 4 = 1

(40)

- Probabilitas dari kota 1 ke setiap kota berikutnya dapat dihitung dengan persamaan

( )

t

=

P

ij,k

( )

[ ]

( )

[ ]

( )

∑

∈jik

t ij ij ij ij t t t t β α β α η τ η τ

untuk Σ[τij]α.[ηij]β

- Probabilitas Komulatif = 0.000 0.360 0.712 1.000

= (0.01*0) + (0.01*0.05) + (0.01*0.049) + (0.01*0.04) = 0.00139 dengan demikian dapat dihitung probabilitas dari kota 1 menuju setiap kota = Kota 1 = 0.00

Kota 2 = (0.01)1.00 . (0.05)1.00/ 0.00139 = 0.360 Kota 3 = (0.01)1.00 . (0.049)1.00/ 0.00139 = 0.353 Kota 4 = (0.01)1.00 . (0.04)1.00/ 0.00139 = 0.288

- Bilangan Random = 0.706 - Kota dipilih = 3

- Daftar semut = 1 3

Setelah hasil perhitungan probabilitas semut menuju kota yang akan dipilih berikutnya, kemudian dicari probabilitas kumulatifnya (qk), dimana q1 = pi1, sedangkan qk = qk-1 + pij, untuk k = 2, 3, …, N. Kemudian bangkitkan bilangan

random (r) antara 0 sampai 1. Kota ke-k akan terpilih jika r > qk-1 dan r ≥ qk

( )

t

=

P

ij,k

.

Semut ke – 2: - Daftar semut = 2

- Probabilitas dari kota 2 ke kota berikutnya dapat dihitung dengan persamaan

( )

[ ]

( )

[ ]

( )

∑

∈jik

untuk Σ[τij]α.[ηij]β = (0.01*0.05) + (0.01*0) +(0.01*0.04) + (0.01*0.049) = 0.0139

Dengan demikian dapat dihitung probabilitas dari kota 2 menuju kota = Kota 1 = (0.01)1.00 . (0.05)1.00/ 0.0139 = 0.360

Kota 2 = 0.00

(41)

- Kota dipilih = 3 - Daftar semut = 2 3 Semut ke – 3:

- Daftar semut = 3

- Probabilitas dari kota 3 ke kota berikutnya dapat dihitung dengan persamaan

( )

t

=

P

ij,k

( )

[ ]

( )

[ ]

( )

∑

∈jik

( )

t

=

P

_ij_,_k

= (0.01*0.049) + (0.01*0.04) +(0.01*0) + (0.01*0.1) = 0.00189 Dengan demikian dapat dihitung probabilitas dari kota 3 menuju kota =

Kota 1 = (0.01)1.00 . (0.049)1.00/ 0.00189 = 0.259 Kota 2 = (0.01)1.00 . (0.04)1.00/ 0.00189 = 0.212 Kota 3 = 0.00

Kota 4 = (0,01)1.00 . (0.01)1.00/ 0.00189 = 0.529 - Probabilitas Komulatif = 0.259 0.471 0.471 1.000 - Bilangan Random = 0.580

- Kota dipilih = 4 - Daftar semut = 3 4

Semut ke – 4: - Daftar semut = 4

- Probabilitas dari kota 4 ke setiap kota berikutnya dapat dihitung dengan persamaan

( )

[ ]

( )

[ ]

( )

∑

∈jik

- Probabilitas Komulatif = 0.212 0.471 1.000 1.000

= (0.01*0.04) + (0.01*0.049) + (0.01*0.1) + (0.01*0) = 0.00189 Dengan demikian dapat dihitung probabilitas dari kota 4 menuju kota =

Kota 1 = (0.01)1.00 . (0.04)1.00/ 0.00189 = 0.212 Kota 2 = (0.01)1.00 . (0.049)1.00/ 0.00189 = 0.259 Kota 3 = (0.01)1.00 . (0.01)1.00/ 0.00189 = 0.0529 Kota 4 = 0.00

(42)

- Daftar semut = 4 2

Untuk t =2

Jumlah semut tiap kota = 0 1 2 1

Semut ke-1

Probabilitas = 0.000 0.286 0.000 0.714 Probabilitas kumulatif = 0.000 0.286 0.286 1.000 Bilangan Random = 0.302

Kota dipilih = 4 Daftar semut = 1 3 4

Semut ke-2

Semut ke-3

Semut ke-4

(43)

Semut ke-1

Kota dipilih = 2

Daftar semut = 1 3 4 2

Semut ke-2

Kota dipilih = 1

Semut ke-3

Kota dipilih = 2

Semut ke-4

Kota dipilih = 1

Panjang Jalur Setiap Semut 1 = 71.232

(44)

3 = 80 4 = 91.232

Jalur Terpendek = 71.232

Perbaikan Jejak:

0.0100 0.0106 0.0107 0.0100 0.0100 0.0100 0.0109 0.0100 0.0105 0.0100 0.0100 0.0139 0.0110 0.0112 0.0100 0.0100

Siklus ke -2

Isi Daftar Semut Awal Daftar semut [1,1]=1 Daftar semut [2,1]=2 Daftar semut [3,1]=3 Daftar semut [4,1]=4

Untuk t =1

Semut ke-1

Kota dipilih = 4 Daftar semut = 1 4

Semut ke-2

(45)

Semut ke-4

Untuk t =2

Semut ke-1

Semut ke-2

Semut ke-3

(46)

Bilangan Random = 0.950 Kota dipilih = 4

Daftar semut = 3 2 4

Semut ke-4

Kota dipilih = 1

Daftar semut = 4 3 1

Untuk t =3

Semut ke-1

Kota dipilih = 2

Semut ke-2

Kota dipilih = 3

Semut ke-3

(47)

Daftar semut = 3 2 4 1 Semut ke-4

Kota dipilih = 2

Panjang Jalur Setiap Semut 1 = 80

2 = 91.232 3 = 91.232 4 = 71.232

Jalur Terpendek = 71.232

Perbaikan Jejak:

0.0100 0.0120 0.0119 0.0105 0.0100 0.0100 0.0119 0.0111 0.0118 0.0109 0.0100 0.0178 0.0129 0.0124 0.0127 0.0100

Perhitungan akan dilanjutkan hingga semut menyelesaikan perjalanannya mengunjungi tiap-tiap kota. Hal ini akan berulang hingga sesuai dengan jumlah siklus maksimum yang ditentukan. Kemudian dihasilkan jarak terpendek dari semut dari masing-masing siklus.

3.3 Perancangan Program Penyelesaian TSP dengan Algortima Semut

3.3.1 Perancangan Flowchart

(48)

ya

Berhenti

Perbarui intensitas jejak feromon Konvergen

siklus = siklus maksimum

semut = banyak semut

Mulai

Bangkitkan Random Inisialisasi Parameter

Siklus = 1

Semut = 1

Hitung Probabilitas semut ke-2/n

Hitung Jarak Kota tujuan

dicapai tidak

Semut = Semut +1

Siklus=Siklus +1 ya

ya

tidak

[image:48.595.105.453.80.741.2]

(49)

3.3.2 Kebutuhan Perangkat Keras

Perangkat keras yang digunakan dalam menyelesaikan aplikasi algoritma Semut untuk penyelesaian kasus TSP pada tulisan ini adalah:

1. Intel Celeron 1.5Ghz 2. Memori 256 MB 3. Hardisk 40 GB

4. OS Windows XP Profesional SP 2

3.3.3 Perancangan Perangkat Lunak

Implementasi dari algoritma semut untuk penyelesaian TSP pada tulisan ini diaplikasikan dalam bahasa pemrograman Visual Basic 6.0, aplikasi dari algoritma Semut ini dibatasi hanya pada pencarian jalur terpendek dari data graf yang di input oleh penggun a. Tampilannya terdiri dari beberapa form yang memiliki fungsi masing-masing yang tampil sesuai dengan urutan yang telah diprogram.

1. Halaman Utama

(50)

[image:50.595.110.524.84.399.2] [image:50.595.106.524.442.731.2]

(51)

2. Halaman Komputasi

Halaman komputasi digunakan untuk melihat hasil komputasi dari program aplikasi pencarian jalur terpendek. data input adalah jumlah kota, koordinat kota, parameter algoritma termasuk siklus maksimum, alfa, beta, Q, Rho dan Tij. Program akan

[image:51.595.103.526.250.556.2]

menampilkan gambar graf dan perhitungan jarak. Berikut tampilan dari halaman komputasi.

Gambar 3.5 Tampilan Hasil Komputasi

3. Halaman Hasil

(52)

[image:52.595.113.518.82.399.2]

Gambar 3.6 Tampilan Halaman Hasil

Coding untuk Algoritma Semut

Berikut adalah coding untuk penyelesaian TSP dengan Algoritma Semut yang ditulis dengan Microsoft Visual Basic 6.0.

1. Inisialisasi Input Parameter:

Ncmax = CInt(Flex.TextMatrix(1, 1)) alpa = CDbl(Flex.TextMatrix(2, 1)) Beta = CDbl(Flex.TextMatrix(3, 1)) rho = CDbl(Flex.TextMatrix(5, 1)) Tij = CDbl(Flex.TextMatrix(6, 1))

2. Inisialisasi Input Koordinat

(53)

Else

angka = CInt(Flex.TextMatrix(x, y)) End If

Kordinat(x, y) = angka

Next Next

HitungJarak

3. Inisialisasi Daftar semut

' isi daftar semut awal cetak ""

cetak "Isi Daftar semut Awal " l = 0

l = l + 1 For k = 1 To N Tabu(k, l) = k Next

4. Probabilitas Semut ke Setiap Kota

totP = 0

For u = 1 To N 'cari totP

If Not CariDaftarSemut(j, u, T) Then

totP = totP + Tho(DaftarSemut(j, T), u) ^ alpa * visib(DaftarSemut(j, T), u) ^ Beta

End If Next u 'bagikan kt = "" kt2 = "" ReDim p(N) ReDim q(N) For u = 1 To N

If CariDaftarSemut(j, u, T) = False Then p(u) = (Tho(Tabu(j, T), u) ^ alpa * visib

(DaftarSemut(j, T), u) ^ Beta) / totP Else

p(u) = 0 End If

kt = kt & Format(p(u), "#,##0.000") & " " Next

5. Probabilitas Kumulatif

For u = 1 To N If u = 1 Then q(u) = p(u) Else

(54)

kt2 = kt2 & Format(q(u), "#,##0.000") & " " Next

6. Panjang Jalur Setiap Semut

Public Function HitungLk(ByVal s As Integer) As Double Dim pk As Double

For a = 1 To UBound(DaftarSemut) - 1

pk = pk + jarak (DaftarSemut (s, a), DaftarSemut s, a + 1))

pk = pk + jarak(DaftarSemut(s, a), (DaftarSemut(s, 1)))

HitungLk = pk End Function

7. Penentuan Jalur Terpendek

JlrTerpendek(Nc) = 1.79769313486232E+307 temp = 0

For k = 1 To N

temp = HitungLk(k) PanjangJalur(k) = temp cetak k & " = " & temp

If temp < JlrTerpendek(Nc) Then JlrTerpendek(Nc) = temp End If

For k = 1 To N

PanjangJalur(k) = HitungLk(k) For s = 1 To N - 1

Dtho(DaftarSemut(k, s), DaftarSemut(k, s + 1)) = _ Dtho(DaftarSemut(k, s), DaftarSemut(k, s + 1))+ visib(DaftarSemut(k, s),

DaftarSemut(k, s + 1)) / PanjangJalur(k)

visib(DaftarSemut(k, N), DaftarSemut(k, 1))/PanjangJalur(k)

For k = 1 To N

(55)

Hasil Analisis

[image:55.595.209.426.271.408.2]

Setelah algoritma Semut diimplementasikan dalam bahasa pemrograman, kemudian diuji dengan masukan beberapa jumlah kota untuk mendapatkan jalur terpendek. Dari pengujian yang dilakukan dapat dilihat perbandingan waktu pada proses komputasi dengan masukan kota yang berbeda. Pengujian dilakukan pada spesifikasi komputer yang penulis gunakan, hasil waktu proses algoritma tidak selalu sama pada jenis komputer yang berbeda.

Tabel 3.4. Perhitungan Waktu antar Kota

Jumlah Kota Waktu Proses (Detik)

5 0.625

10 14.688 15 97.188 20 376.094 25 1147.516

[image:55.595.179.453.493.731.2]

Hasil pengukuran terhadap waktu proses dari algoritma Semut ini ditunjukkan pada grafik berikut:

(56)

3.5.1 Analisis Berdasarkan Regresi

Regresi adalah bagian ilmu statistik yang mempelajari data berpasangan yang terdiri atas satu variabel takbebas dan minimal satu variabel bebas. Ada dua jenis persamaan regresi, yaitu regresi linier dan regresi non linier. Persamaan regresi linier adalah persamaan matematik yang memungkinkan peramalan nilai suatu peubah takbebas (dependent variable) dari nilai peubah bebas (independent variable).

(57)

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Berdasarkan hasil penelitian mengenai algoritma Semut dalam penyelesaian kasus

TSP dapat disimpulkan bahwa untuk data kota yang lebih besar dari 25 waktu proses

algoritma lebih besar dari 19 menit dan waktu proses algoritma Semut untuk jumlah

kota yang digambarkan secara grafik berdasarkan analisis regresi adalah fungsi non

linier model eksponensial.

4.2. Saran

Penulis menyarankan untuk pengembangan penelitian selanjutnya dengan data

verteks yang lebih besar dan menggunakan algoritma Semut yang berkembang saat

ini seperti Ant Colony System (ACS), ACS-3-Opt dan Ant-Q untuk menyelesaikan

persoalan TSP yang lebih kompleks dan menggunakan bahasa pemrograman yang

(58)

DAFTAR PUSTAKA

Dorigo, Marco dan Gambardella L.M, 1996. “Ant Colonies for the Traveling Salesman Problem”. Elsevier Biosystem Journal 43: hal. 73-81.

Dorigo, Marco dan Di Caro, Gianni. 1999. Ant Algorithm for Discrete Optimization. Belgia: MIT Press.

Refianti, R dan Mutiara A. B. "Solusi Optimal Travelling Salesman Problem dengan Ant Colony System (ACS)". Universitas Gunadarma

Shtovba, S. D, 2004. " Ant Algorithm: Theory and Applications". Programming and Computer Software, Volume 31, No.4: hal. 168-169.

Sri Kusumadewi dan Hari Purnomo. 2005. Penyelesaian Masalah Optimisasi dengan

Teknik-teknik Heuristik. Yogyakarta:Graha Ilmu.

Wardy, Ibnu Sina, 2006. “Penggunaan Graf dalam Algoritma Semut untuk Melakukan Optimisasi". Institut Teknologi Bandung.

Wikipedia. 2007. “Ant Colony Optimization–Wikipedia, the free encyclopedia”.

(59)

Regression

Va riab les Ent ere d/Re mo vedb

Jumlah

Kotaa . Enter

Model 1 Variables Entered Variables Removed Method

All reques ted variables ent ered. a.

Dependent Variable: logwp b.

Model Summar y

.976a .953 .938 .32041

Model 1

R R Square

Adjusted R Square

Std. Error of the Estimate

Predictors: (Constant), Jumlah Kota a.

ANOV Ab

6.298 1 6.298 61.347 .004a

.308 3 .103

6.606 4 Regres sion Residual Total Model 1 Sum of

Squares df Mean S quare F Sig.

Predic tors: (Constant), Jumlah K ota a.

Dependent Variable: logwp b.

Co effi cien tsa

-.664 .336 -1. 975 .143

.159 .020 .976 7.832 .004

(Const ant) Jumlah Kota Model

1

B St d. E rror Unstandardized

Coeffic ient s

Beta St andardiz ed

Coeffic ient s

t Sig.

Dependent Variable: logwp a.

De scri ptiv e St atist ics

1.7171 1.28512 5

15.00 7.906 5

logwp Jumlah Kot a

(60)

Co rre latio ns

1.000 .976

.976 1.000

. .002

.002 .

5 5

logwp Jumlah Kota logwp Jumlah Kota logwp Jumlah Kota Pearson Correlation

Sig. (1-tailed)

N

logwp Jumlah Kota

Co llin eari ty Diag nost icsa

1.905 1.000 .05 .05

.095 4.467 .95 .95

Dimension 1

2 Model 1

Eigenvalue

Condit ion

Index (Const ant) Jumlah Kota Variance P roportions

Dependent Variable: logwp a.

Residuals Statisticsa

.1299 3.3043 1.7171 1.25481 5

-.33400 .27051 .00000 .27749 5

-1.265 1.265 .000 1.000 5

-1.042 .844 .000 .866 5

Predicted Value Residual

Std. Predicted Value Std. Residual

Minimum Maximum Mean Std. Deviation N