Estimasi Heteroskedastis Tak Linear Model Deret Waktu

ESTIMASI HETEROSKEDASTIS TAK LINEAR

MODEL DERET WAKTU

TESIS

Oleh

SINDAK SITUMORANG 097021069/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

ESTIMASI HETERODKEDASTIS TAK LINIEAR

MODEL DERET WAKTU

T E S I S

Diajukan Sebagai Salah Satu Syarat

untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

SINDAK SITUMORANG 097021069/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

Judul Tesis : ESTIMASI HETERODKEDASTIS TAK LINIEAR MODEL DERET WAKTU

Nama Mahasiswa : Sindak Situmorang Nomor Pokok : 097021069

Program Studi : Matematika

Menyetujui, Komisi Pembimbing

(Dr. Sutarman, M.Sc) (Prof. Dr. Herman Mawengkang)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

Telah diuji pada

Tanggal : 14 Juni 2011

PANITIA PENGUJI TESIS

Ketua : Dr. Sutarman, M.Sc

ABSTRAK

Penaksiran parameter dalam model time series heteroskedastik yang diteliti. Eksi-sistensi kuadrat-terkecil bersyarat dan estimator likelihood bersyarat dibuktiikan. Konsistensi dan normalitas asymptotiknya dipastikan. Estimator densitas dengan kernel dan derivatifnya didefenisikan dan ditunjukkan konsisten keseragamannya. Percobaan simulasi yang dilaksanakan menunjukkan bahwa estimator berkinerja dengan baik untuk ukuran sampel besar.

ABSTRACT

Parameter estimation in a class of heteroscedastic time series models is investiga-ted. The existence of conditional least-squares and conditional likelihood estimators is proved. Thei consistency and their asymptotic normality are established. Ker-nel estimators of the noises density and its derivatives are defined and shown to be uniformly consistent. A simulation experiment conducted shows that the estimators perform well for large sample size.

KATA PENGANTAR

Dengan rendah hati penulis ucapkan segala puji dan syukur kehadirat Tuhan Yang Maha Esa atas berkat dan rahmatNya sehingga penulis dapat menyelesaikan studi Program Magister Matematika pada FMIPA USU. Tesis ini merupakan salah satu syarat penyelesaian studi para Program Studi Magister Matematika FMI-PA USU. Pada kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada :

Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H. M.Sc. (CTM), Sp.A (K)selaku Rektor Universitas Sumatera Utara yang memberi kesempatan kepada penulis untuk menempub pendidikan di Universitas Sumatera Utara.

Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, yang juga menjadi pembimbing tesis ini.

Prof. Dr. Herman Mawengkang selaku Ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara, yang juga menjadi pembimbing tesis ini.

Bapak Dr. Saib Suwilo, M.Sc selaku Sekretaris Program Studi Magister Ma-tematika FMIPA USU.

Bapak Prof. Dr. Opim Salim S, M.Sc dan Bapak Drs. Marihat Situ-morang, M.Kom., selaku Penguji tesis ini.

Bapak/Ibu Dosen Program Studi Magister Matematika FMIPA USU ; Bapak Prof. Dr. Drs. Iryanto, M.Si., Prof. Dr. Tulus, M.Si., Drs. Marwan Harahap, M.Eng., Drs. Open Darnius, M.Sc., Drs. Sawaluddin, M.IT., Drs. Arriswoyo, M.Si, dan Ibu Dra. Mardiningsih, M.Si., yang telah membekali ilmu pengetahuan kepada penulis selama perkuliahan hingga se-lesai.

Gubernur Sumatera Utara, yang telah member bantuan beasiswa pendidikan kepada penulis melalui BAPEDASU.

Bedagai dan jajarannya yang telah memberi ijin untuk mengikuti perkuliahan Pro-gram Pasca Sarjana Magister Matematika Universitas Sumatera Utara.

Bapak Kepala Sekolah SMA Negeri 1 Tanjung Beringin Drs. Manga-ra Sagala atas arahan dan petunjuknya serta memberikan ijin untuk mengikuti perkuliahan Program Pasca Sarjana Universitas Sumatera Utara.

Rekan-rekan Guru SMA Negeri 1 Tanjung Beringin yang telah memberi dorongan dan semangat yang mendalam selama mengikuti perkuliaahan.

Ibu Misiani, S.Si selaku Staf Administrasi Program Studi Magister Matemati-ka FMIPA USU yang telah memberiMatemati-kan pelayanan administrasi selama mengikuti pendidikan.

Ucapan terima kasih yang tak terhingga penulis ucapkan kepada istri tercinta Nur-mida Sihaloho dan juga putriku yang tersayang Dian Lasmarito br Situ-morang yang selalu memberi dukungan dan semangat serta mendoakan penulis selama mengikuti perkuliahan di program studi Magister Matematika pada Seko-lah Pascasarjana Universitas Sumatera Utara.

Secara khusus penulis menyampaikan terima kasih dan saying yang mendalam kepada ibunda tersayangD br Sinagasemasa hidupnya yang senantiasa memberi dukungan dan Doa kepada penulis dalam menyelesaikan perkuliahaan ini.

Tak lupa rekan-rekanMahasiswa program studi Magister Matematika FMI-PA USU tahun 2009 Tohom Paha Mei Banjarnahor, Atur Hamonangan, Sopar Siregar Bistok Purba, M.Nur Edi,atas kerjasama dan hubungan yang baik selama perkuliahaan, Semoga persahabatan yang kita jalin abadi, dan terus menyemangati panggilan kita sebagai pendidik yang profesional.

Akhir kata penulis ucapkan, kiranya kekurangan yang ada pada penulisan tesis ini dapat disempurnakan bagi pihak yang memerlukan karena penulis sebagai manusia yan tidak sempurna memiliki keterbatasan dalam menyelesaikan tesis ini.

Medan, 14 Juni 2011 Penulis,

RIWAYAT HIDUP

DAFTAR ISI

Halaman

ABSTRAK i

ABSTRACT ii

KATA PENGANTAR iii

RIWAYAT HIDUP v

DAFTAR ISI vi

DAFTAR TABEL viii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Rumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

1.5 Metode Penelitian 4

BAB 2 TINJAUAN PUSTAKA 5

2.1 Heteroskedastis 5

2.2 Asumsi Umum 8

BAB 3 TINJAUAN PUSTAKA 10

3.2 Konsep Dasar pada Analisis Model Deret Waktu 11

BAB 4 PEMBAHASAN ESTIMASI KUADRAT TERKECIL BERSYARAT, ESTIMASI LIKELIHOOD BERSYARAT DAN ESTIMASI

DENSI-TAS DENGAN KERNEL DAN DERIVATIFNYA 13

4.1 Estimasi Kuadrat Terkecil Bersyarat 13

4.2 Estimasi Likehood Bersyarat 18

4.3 Estimasi Densitas dengan Kernel 22

4.4 Studi Simulasi 26

BAB 5 KESIMPULAN 32

DAFTAR TABEL

Nomor Judul Halaman

4.1 Estimator kuadrat terkecil bersyarat untuk parameter dari model (i) dengan Gaussian (2 kolom ditengah) dan fungsi Laplace (dua

kolom terakhir) dan ukuran sampel n = 50 27

4.2 Estimator kuadrat terkecil bersyarat untuk parameter dari model ARCH (1) pada model (ii) (ρ0 = ρ1 = 0) dan fungsi Gaussian, untuk sampel berukuran n= 100, n = 200, dann = 400 27

4.3 Estimator likelihood maximum bersyarat untuk parameter model ARCH (1) pada model (ii) (ρ0 = ρ1 = 0) dan fungsi Gaussian, untuk sampel berukuran n= 100, n = 200, dann = 400 28

4.4 Estimator Kuadrat terkecil bersyarat untuk parameter dari model iii dengan ρ1 = 0 dan fungsi Gaussian, untuk sampel berukuran

DAFTAR GAMBAR

Nomor Judul Halaman

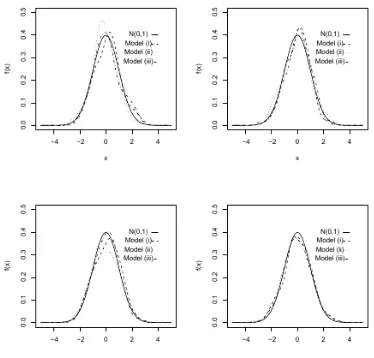
4.1 Estimasi fungsi densitas pada model (i), (ii), dan (iii) untuk n =

100,200,400,600 29

ABSTRAK

Penaksiran parameter dalam model time series heteroskedastik yang diteliti. Eksi-sistensi kuadrat-terkecil bersyarat dan estimator likelihood bersyarat dibuktiikan. Konsistensi dan normalitas asymptotiknya dipastikan. Estimator densitas dengan kernel dan derivatifnya didefenisikan dan ditunjukkan konsisten keseragamannya. Percobaan simulasi yang dilaksanakan menunjukkan bahwa estimator berkinerja dengan baik untuk ukuran sampel besar.

ABSTRACT

Parameter estimation in a class of heteroscedastic time series models is investiga-ted. The existence of conditional least-squares and conditional likelihood estimators is proved. Thei consistency and their asymptotic normality are established. Ker-nel estimators of the noises density and its derivatives are defined and shown to be uniformly consistent. A simulation experiment conducted shows that the estimators perform well for large sample size.

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Pemodelan statistik parametik merupakan salah satu model statistik yang berkembang dengan pesat seiring dengan perkembangan komputasi. Teknik pera-malan pemodelan sangat beragam, dikembangkan dari berbagai disiplin ilmu dan untuk berbagai maksud. Setiap teknik yang akan dipilih memiliki sifat tertentu, tingkat kesulitan dan biaya tersendiri yang harus dipertimbangkan. Dan pemo-delan ini digunakan untuk menjelaskan hubungan tak linier antar variabel dan beberapa prosedur pengujian untuk mendeteksi adanya keterkaitan tak linier.

Model deret waktu merupakan salah satu contoh model non linier yang mem-punyai bentuk fungsional yang fleksibel dan mengandung beberapa parameter yang tidak dapat diinterpretasikan seperti pada model parametrik. Pada saat ini banyak penelitian dilakukan secara luas dengan motivasi adanya kemungkinan untuk meng-gunakan model deret waktu sebagai suatu alat untuk menyelesaikan berbagai ma-salah terapan.

Model deret waktu dalam beberapa studi empirik seringkali terdiri atas penga-matan dari beberapa variabel sebagai contoh, sering kali dalam kehidupan sehari-hari dijumpai data yang tidak hanya mengandung keterkaitan dengan kejadian pada waktu-waktu sebelumnya,tetapi juga mempunyai keterkaitan dengan lokasi atau tempat yang lain.

Dalam suatu estimasi model seharusnya konstan sehingga variansnya sama (homogen) tetapi seringkali justru berubah-ubah, hal ini biasa terjadi pada data cross section. Estimasi diartikan menaksir ciri-ciri tertentu dari populas (parame-ter) dengan nilai sampel.

dike-2

tahui akan diestimasi berdasarkan statistik sampel yang diambil dari populasi yang bersangkutan.

Estimasi nilai parameter memiliki dua cara yaitu estimasi titik dan estimasi selang. Estimasi titik adalah estimasi dengan menyebut satu nilai sedangkan esti-masi selang adalah estiesti-masi dengan menyebut daerah pembatasan dimana diten-tukan batas minimum dan maksimum suatu estimator

Nachrowi dan Usman(2006) menjelaskan bahwa data cross section sering memunculkan varians error yang heteroskedastis. Analogi sederhana pada kejadian heteroskedastis dapat dilihat pada model hubungan antara harga dengan permin-taan (demand). Berdasarkan hipotesis jika harga meningkat, maka perminpermin-taan akan turun, demikian juga sebaliknya. Pada kejadian adanya indikasi masalah heteroskedastis adalah jika harga meningkat maka permintaan akan konstan. Ji-ka keragaman residual/error tidak bersifat konstan.data dapat diJi-kataJi-kan bersifat heteroskedastis. Kondisi heteroskedastis memperlihatkan bahwa semakin besar ni-lai variabel bebas semakin jauh koordinat tersebut dari garis regresi. Beberapa asumsi dalam model regresi yang terkait dengan heteroskedastis antara lain adalah residual (e) memiliki nilai rata-rata nol, keragaman yang konstan, dan residual pada model tidak saling berhubungan. Adanya heteroskedastis menyebabkan esti-masi (perkiraan) parameter menjadi tidak efisien baik dalam sampel kecil maupun sampel besar sehingga estimasi varians akan bias.

Bagaimana cara mendeteksi dan mengatasi adanya heteroskedastis akan diba-has pada bab berikutnya. Heteroskedastis dipandang bukan sebagai suatu masa-lah tetapi justru memanfaatkan kondisi tersebut untuk membuat model. Bahkan dengan memanfaatkan heteroskedastis dalam residu dengan tepat maka akan diper-oleh varians yang lebih efisien. Model ini dikenal dengan model ARCH dan GARCH.

3

Dalam penelitian ini akan digunakan model deret waktu dalam mengestimasi parameter yang heteroskedastis tak linier, dengan mengingat eksistensi kuadrat-terkecil bersyarat (estimasi conditional least-Squares) dan estimator likelihood bersyarat (estimasi conditional Likelihood),kemudian. Konsistensi dan normali-tas asymptotiknya dipastikan serta Estimator densinormali-tas dengan kernel didefenisikan dan ditunjukkan konsisten keseragamannya.

1.2 Rumusan Masalah

Berdasarkan latar belakang diatas, permasalahan yang akan dikaji dalam penelitian ini adalah : Bagaimana cara menentukan nilai-nilai parameter dalam mengestimasi data yang heteroskedastis tak linier dengan menggunakan model deret waktu.

1.3 Tujuan Penelitian

Adapun tujuan penelitian ini adalah :

1. Mempelajari cara mengkontruksi data yang hetereskedastis tak linier

2. Menentukan estimator untuk parameter-parameter yang ada pada model deret waktu dengan menggunakan metode estimasi heteroskedastis tak li-nier

1.4 Manfaat Penelitian

Penelitian ini diharapkan dapat memberikan manfaat antara lain :

4

2. Secara umum diharapkan dapat memberikan sumbangan pengetahuan dan gambaran tentang estimasi heteroskedastis tak linier model deret waktu.

1.5 Metode Penelitian

Metedologi penelitian yang dilakukan adalah bersifat literatur dengan mengum-pulkan informasi dari berbagai referensi buku, jurnal dan hasil-hasil penelitian yang berhubungan dengan judul.

Adapun langkah-langkah yang ditempuh adalah sebagai berikut :

a. Menjelaskan tentang Heteroskedastis

b. Menjelaskan Model Deret Waktu

c. Menjelaskan estimasi Kuadrat terkecil bersyarat.

d. Menjelaskan estimasi likelihood bersyarat

BAB 2

TINJAUAN PUSTAKA

2.1 Heteroskedastis

Masalah serius lainnya yang mungkin kita hadapi dalam analisis regresi ada-lah heteroskedastis.Ini timbul pada saat bahwa varians dari faktor konstan untuk semua nilai dari variabel bebas yang tidak terpenuhi.

Heteroskedastis adalah keadaan dimana faktor gangguan tidak memiliki va-rian yang sama. Heteroskedastis merupakan suatu fenomena dimana estimator regresi bias, namun tidak efisien,sebagai contoh yang berhubungan dengan penge-luaran dari keluarga yang berpendapatan rendah biasanya lebih kecil dibandingkan dari keluarga yang berpendapatan tinggi karena kebanyakan pengeluaran keluarga yang berpendapatan rendah biasanya merupakan barang kebutuhan pokok,dengan kemungkinan yang terbatas untuk kehendak lainnya.Maka jika data tentang penge-luaran keluarga digunakan sebagai variabel penjelas,analisis regresi akan cenderung memiliki masalah heteroskedastis. Gangguan heteroskedastis ini membawa kita pada hasil uji statistik yang tidak tepat serta interval keyakinan untuk estimasi parameter yang kurang tepat pula.

Uji heteroskedastis bertujuan untuk menguji apakah dalam model regresi terjadi ketidaksamaan varian dari residual satu pengamatan ke pengamatan lain. Jika varian residual satu pengamatan ke pengamatan lain tetap, maka disebut homoskedastis, dan jika berbeda disebut heteroskedastis. Keadaan heteroskedastis tersebut dapat terjadi karena beberapa sebab, antara lain:

1. Data dari satu variabel atau lebih mengandung nilai dengan jarak (range) yang lebar antara data paling kecil dengan data paling besar.

6

3. Dalam data sendiri terdapat heteroskedastis.

Model heteroskedastis yang memperhitungkan perubahan tersebut dapat mem-buat penggunaan dan estimasi data menjadi lebih efisien.

Beberapa asumsi/ contoh dalam model regresi yang terkait dengan heteros-kedastis antara lain, misalnya:

1. Kesalahan orang yang baru belajar mengetik. Semakin dia berlatih, kesala-han yang dilakukan semakin sedikit.

2. Meningkatnya pendapatan, maka tabungan secara rata-rata juga meningkat. Artinya keluarga yang berpendapatan tinggi secara rata-rata menabung lebih banyak daripada keluarga berpendapatan rendah,tetapi variabilitas dalam tabungannya juga besar.

Konsekuensi heteroskedastis adalah:

1. Koefisien tetap tidak bias namun nilai koefisien berfluktuasi tajam jika model diperbaharui dengan menambah data atau sampel yang berbeda.

2. Estimasi menjadi tidak akurat.

Makridakis et.al (1992), mengatakan ada beberapa cara untuk mendeteksi ada atau tidaknya heteroskedastis, yaitu metode informal dan metode formal. Metode informal biasanya dilakukan dengan melihat grafik dari nilai prediksi variabel inde-penden dengan residualnya. Variabel dinyatakan tidak terjadi heteroskedastis jika terdapat pola yang jelas dan titik-titik menyebar disekitar angka nol pada sumbu

y, dan metode formal untuk mendeteksi keberadaan heteroskedastis antara lain dengan : Uji Park, Uji Glijser, Uji White dan uji Goldfold-Quandt.

permasala-7

kali mempunyai varians error yang tidak konstan. Sekalipun keberadaan heteros-kedastis masih memberikan pendugaan yang tidak bias dan konsisten, pendugaan tersebut sudah tidak efisien yaitu varians dari estimator tidak minimum. Akibat-nya pada uji t, interval kepercayaan dan berbagai ukuran lainnya menjadi tidak tepat. Salah satu cara untuk mengakomodasi heteroskedastis adalah dengan mela-kukan pemodelan varians yang dapat melamela-kukan estimasi dengan tepat. Ini berarti penyimpangan antara varians aktual dengan varians ramalan tidak jauh berbeda.

Berbagai model parametrik telah banyak dibuktikan pada dekade terakhir ini, untuk lebih jelas lihat, Brockwell dan Davis (1996), Shumway dan Stofler (2001) dan Tong (1990). Estimasi parameter untuk model linier telah banyak dikaji, sementara untuk model tak linier masih sedikit karena kompleksitasnya/ kerumitannya.

Penelitian pada umunya dilakukan untuk kasus tertentu saja,misalnya :Esti-masi parameter model ARCH (Autoregresive Conditional Heteroscedasticity) dan GARCH (Generalized Autoregresive Conditional Heteroscedasticity) yang masing-masing diperkenalkan oleh Engle (1982) dan Bollerslev (1986). Bahwa dalam model ARCH (Q), perubahan varians dipengaruhi oleh sejumlah Q data acak sebelum-nya. Model GARCH merupakan penyempurnaan dari model ARCH, yaitu sebuah konsep tentang ketidakkonstanan varians dari data acak, dan perubahan varians ini dipengaruhi oleh data acak sebelumnya yang tersusun dalam urutan waktu. Mo-del GARCH cukup baik untuk memoMo-delkan data yang berubah variansnya, namun tidak untuk data yang benar-benar acak.

8

Pendekatan stokastik pada analisis estimasi heteroskedastis tak linier model deret waktu dilakukan dengan menggunakan model-model statistik untuk menje-laskan perilaku dinamis, dari suatu model deret waktu. Hal ini mengasumsikan bahwa suatu deret waktu dibangkitkan dari suatu mekanisme atau model stokastik yang didefenisikan dengan suatu persamaan :

Xi =m(ρ;Zi−1) + σ(θ;Zi−1)ε i, i∈ Z (2.1.1)

Dimana (Xi)i∈ adalah titik stasioner dan titik ergodik; (Zi =Xi, . . . , Xi−q+1;

Xi−q)i∈Z adalah barisan dimensi−q dengan q bilangan bulat positif tak hingga ; (_∈i)i∈Z adalah variabel acak dengan variansi satu sedemikian sehingga∈i indepen-den pada σ(Zj, j < i); parameter vektor kolomnya Ψ = (ρ, θ)′ merupakan anggota dari Ψ = ΘxΘ˜ _⊂RI_xRJ _{untuk I, J bilangan bulat positif dan fungsi m (ρ;z) dan}

σ(θ;z) mempunyai bentuk yang diketahui.

2.2 Asumsi Umum

Transpose dari suatu vektor atau matriks fungsi dari H(x) dinotasikan de-nganH(x).

Misalkan r adalah fungsi riil untuk I atau j diberikan untuk fungsi F(α;z) yang terdefenisi pada himpunan tak kosong dan fungsiRr_×Rq _{dan fungsiK(Ψ;z) yang} terdefenisi pada himpunan bagian tak kosong dariRI _×RJ _×Rq_{, maka didapat :}

9

Selanjutnya diasumsikan bahwa vektor parameter Ψ0= (ρ0,Θ0) dari (2.1) sedemi-kian sehingga ρ0 ∈ int(Θ) dan Θ0 ∈ int( ˜Θ), di mana int(Θ) dan int( ˜Θ) meno-tasikan masing-masing interior tak-kosong dari Θ dan ˜Θ. andaikan juga bahwa semua variabel acak dalam tulisan ini didefinisikan atas ruang probabilitas yang sama (Ω, W, P), di mana Ω adalah suatu himpunan, W adalah suatu field-σ dari Ω dan P adalah ukuran probabilitas W. Dengan asumsi-asumsi berikut:

(A1) Momen orde empat dari himpunan berhingga εi

(A2) Fungsim(ρ;z) dan σ(Θ;z) terdiferensialkan dua kali secara kontinu masing-masing terhadap ρ _∈ int(Θ) dan terhadap Θ _∈ int( ˜Θ), dan terdapat suatu fungsi positip α(z) sedemikian sehingga E[α4_(Z

BAB 3

TINJAUAN PUSTAKA

3.1 Model Deret Waktu

Secara umum analisis deret waktu menurut Chatfield (2001) mempunyai be-berapa tujuan, yaitu estimasi, pemodelan dan kontrol. Estimasi berkaitan dengan problem, pembentukan model dan metode yang dapat digunakan untuk meng-hasilkan suatu ramalan yang akurat. Pemodelan bertujuan untuk mendapatkan suatu model statistik yang sesuai dalam mempresentasikan perilaku jangka pan-jang suatu deret waktu.

Dalam perkembangan analisis deret waktu telah banyak diketahui berbagai fenomena yang menarik dan sederhana seringkali merupakan fenomena yang tak linier, misalnya hubungan antara kejadian di masa lalu dan saat ini adalah tak linier. Dengan demikian kelompok pemodelan deret waktu yang linier telah banyak dikaji. Sementara untuk model deret waktu tak linier masih sedikit dan saat ini telah menjadi fokus perhatian utama peneliti. Beberapa bentuk model tak linier telah dikembangkan dan diaplikasikan pada beberapa kasus deret waktu, hal ini dapat dilihat pada Tjosthein (1986), Tjosthein (1990), dan Tong (1990).

Data deret waktu adalah data yang disusun berdasarkan urutan waktu atau data yang dikumpulkan dari waktu ke waktu. Waktu yang digunakan dapat berupa minggu, bulan, tahun dan sebagainya. Dengan adanya data berkala maka pola gerakan data atau nilai-nilai variabel dapat diikuti atau diketahui.

Dengan demikian data berkala dapat dijadikan sebagai dasar untuk :

1. Pembuatan keputusan pada saat ini.

2. Estimasi perdagangan dan ekonomi pada masa yang akan dating.

11

Menurut Makridakis, et al (1992), langkah penting dalam memilih suatu metode deret waktu yang tepat adalah dengan mempertimbangkan jenis pola da-tanya. Pola data dapat dibedakan menjadi empat, yaitu :

1. Pola horizontal, terjadi bilamana data berfluktuasi di sekitar nilai rata-rata yang konstan atau stasioner terhadap nilai rat-ratanya.

2. Pola musiman, terjadi bilamana suatu deret data dipengaruhi oleh faktor musiman ( misalnya kuartal tahun tertentu, bulanan, atau hari pada minggu tertentu).

3. Pola siklis, terjadi bilamana datanya dipengaruhi oleh fluktuasi ekonomi jang-ka panjang seperti yang berhubungan dengan siklus bisnis atau ekonomi. 4. Pola tren, terjadi bilamana terdapat kenaikan atau penurunan jangka panjang

dalam data.

3.2 Konsep Dasar pada Analisis Model Deret Waktu

Pada bagian ini akan dijelaskan secara ringkas beberapa konsep dasar pa-da analisis model deret waktu, berkaitan dengan ide pa-dasar pa-dan beberapa konsep definisi yang sering digunakan. Secara lebih lengkap hal ini dapat dilihat pada Brockwell dan Davis (1991).

Model deret waktu adalah suatu deret (barisan) dari pengamatan Yt pada suatu variabelY, yang tiap-tiap pengamatan dicatat pada suatu waktu tertentut_∈ T. Dalam hal iniT adalah himpunan dari waktu dimana pengamatan-pengamatan tersebut dilakukan. Jika T adalah suatu himpunan yang diskrit, maka _{Yt, t ∈

T) adalah suatu model deret waktu yang diskrit _{Yt, t ∈ T} merupakan notasi keseluruhan suatu model deret waktu, dimanaYt adalah pengamatan dari {Yt, t∈

T) pada waktu ke t. Pada kasus model deret waktu yang diskrit, pengamatan biasanya diambil pada interval waktu yang sama. Dalam hal ini axis waktu T

12

Pendekatan statistik pada analisis model deret waktu dilakukan dengan meng-gunakan model-model statistik untuk menjelaskan perilaku dinamis dari model deret waktu. Hal ini mengasumsikan bahwa suatu deret waktu dibangkitkan dari suatu mekanisme atau model yang stokastik, yang biasanya didefenisikan dengan suatu persamaan beda yang stokastik.persamaan beda yang stokastik terdiri dari suatu persamaan dan beberapa kondisi awal. Hasil atau solusi dari model ini ada-lah suatu proses stokastik, yaitu suatu barisan dari variabel random _{Yt} yang didefenisikan pada ruang probabilitas (Ω, F, P). Untukω _∈Ω tertentu,Yt(ω) ada-lah suatu nilai realisasi dari variabel randomYtyang nilai-nilainya diperoleh dalam ruang Euclidean d-dimensiRd

Contoh diberikan suatu model linear AR orde pertama

Yt=φ1Yt−1+εt, t= 1,2, . . . (3.2.1)

danYo adalah suatu variabel random yang mempresentasikan kondisi awal. Dalam hal ini _{εt} adalah suatu barisan yang terdistribusikan secara identik dan inde-penden dari variabel random yang merepresentasikan gangguan atau error atau

disturbance term. Penyelesaian _{Yt} dari persamaan (3.1) adalah suatu proses stokastik

Yt=φt1Y0+ t−1

X

t=0

φt₁εt−1, t= 1,2, . . . (3.2.2)

BAB 4

PEMBAHASAN ESTIMASI KUADRAT TERKECIL BERSYARAT, ESTIMASI LIKELIHOOD BERSYARAT DAN ESTIMASI

DENSITAS DENGAN KERNEL DAN DERIVATIFNYA

4.1 Estimasi Kuadrat Terkecil Bersyarat

Bagian ini akan menjelaskan estimator ψ0 = (ρ0, θ0) dengan menggunakan conditional least-squares. Bahwa fungsi mean conditional dan fungsi varians con-ditional dari (2.1) dapat didefenisikan untuk semuaz _∈Rq _{oleh E(X1|Z0 =z) =}

m(ρ;z) andE_{[X1−m(ρ;Z0)]2|Z0 =z}=σ2(θ;z).]

Dari persamaan ini fungsi terukur terbatasnya γ(z) and λ(z), dimana E[(X1 −

m(ρ;Z0))λ(Z0)] = 0 dan E[(X1−m(ρ;Z0))2−σ2(θ;Z0)γ(Z0)] = 0

Untuk estimasiψ0 diperoleh dengan menentukan gradien nolnya dari varians sam-pel dari barisan variabel randomnya

(Xi₋m(ρ;Zi−1)), i= 1, . . . , ndan ([Xi−m(ρ;Zi−1)]2−σ2(θ;Zi−1)), i= 1, ..., n

Diberikan barisan X−q, . . . , X−1, X0, X1, . . . , Xn, dan dinotasikan dengan Xn = (Xn, . . . , X1, X0, X−1, . . . , X−q) dan barisan fungsi randomnya didefenisikan dengan

:

U n(ρ;Xn) = n

X

i=1

[X_i−m(ρ;Zi−1)]2λ2(Zi−1) (4.1.1)

Sn(ψ;Xn) = n

X

i=1

[X_i−m(ρ;Zi−1)]2−θ2(θ;Zi−1)}γ2(Zi−1) (4.1.2)

Dan matriksnya

Ψ11= 2E

λ2(Z0)σ(θ0;Z0)∂m(ρ0;Z0)∂m(ρ0;Z0)

Ψ22 = 8E

λ2(Z0)σ2(θ0;Z0)∂σ(θ0;Z0)∂σ(θ0;Z0)

Diasumsikan pada positif tertentu. Matriksnya didefenisikan

△11 = 4E

λ4_(Z0)σ2_(θ0;Z0)(Φ−1

11)∂m(ρ0;Z0)∂m(ρ0;Z0)Φ

−1 11

14

Teorema 4.1. Asumsikan bahwa asumsi-asumsi (A1)₋(A3) berlaku dan _△ adalah definit positif, Maka,

(i) Terdapat suatu barisan estimatorψn= (ρn, θ′

n) sedemikian sehinggaψn_−→a.s ψ0, dan untuk setiapc >0, terdapat suatu kejadianS1denganP(S1)<1−ε, dan suatu bilangan nonnegatifn1 sedemikian sehingga padaS1, untukn > n1

a. ∂U n(′

ρn;Xn) = 0 dan U n(ρ;Xn) mencapai minimum relatip di ρ=ρn b. Dengan mengasumsikanρntetap,∂θSn((ρn, θn);Xn) = 0 danSn((ρn, θ);Xn)

mencapai minium relatif di θ =θn.

(ii) n1/2_(ψ

n−ψ0) D

−→N(0,_△).

Bukti. Cukup diperiksa hipotesa-hipotesa dari Teorema 3.2.23 Taniguchi dan Kakizawa (2000), yang dibuktikan Klimko dan Nelson (1978) dengan meng-gunakan Teorema Egorov (lihat, misalnya, Taniguchi dan Kakizawa (2000). Dari perhitungan sederhana dapat diperoleh :

∂Un(ρ;Xn) =₋2

15

Untuk setiap vektorp∗

∈int (Θ) mendefenisikan barisan fungsi-fungsi matriks acak

V n(ρ∗

Dengan demikian, dari sudut pandang (A1)₋(A3), tidak sulit dilihat bahwa ter-dapat suatu fungsi bernilai riil positif Vlk dengan ℓk(z) dengan E[?4ℓk(Z0)] < ∞

terletak di antara ρ dan ρ0, di peroleh menurut ketaksamaan di atas bahwa : 1

Selanjutnya, menurut ergoditas, ruas kanan dari ketaksamaan terakhir konvergen a.s. ke E[ℓk(Z0)] <_∞ apabila n mendekati tak berhingga. Maka jelaslah bahwa untuk setiap (l, k)

lim sup 1

nδ |Vn(p∗;Xn)lk|<∞ (4.1.3)

Dari teorema 3.1.3 ( Taniguchi dan Kakizawa, 2000) diperoleh bahwa terdapat suatu barisan estimator-estimator ρn sedemikian sehingga ρn → p0 hampir pasti, apabila n _{→ ∞} dan untuk ε > 0, bisa didapat kejadian E1 dengan P(E1) > 1₋ε dan bilangan bulat non negatif n sedemikian sehingga atas E1, untuk n >

¯

16

dari perhitungan sederhana :

∂θSn((ρn, θ0) ;Xn)

17

Untuk δ > 0 sedemikian sehingga_kθ₋θ0kε < δ, dan untuk θ∗ terletak di antara

θdan θ0, diperoleh dari rumus di atas bahwa : 1

Menurut teorema ergodik, bahwa ruas kanan pertikdasamaan terakhir konvergen keE[olk(Z0)]<∞

Apabila n mendekati tak berhingga Maka jelaslah bahwa untuk setiap (l, k) (3.3) berlaku denganTn(θ∗

;Xn)ℓk. Karena itu dengan mengaplikasikan Teorema 3.2.23. Taniguchi dan Kakizawa 2000), bisa ditentukan barisan estimator-estimator θn sedemikian sehingga θn → θ0 hampir pasti, apabila n → ∞ dan untuk ε > 0, dapat ditentukan suatu kejadian E2 dengan P(E2) < 1−ε dan bilangan bulat non negatif n sedemikian sehingga atas E1 ∩E2, untuk n > nn, ∂θSn(ψn;Xn) = 0 dan Sn((ρn, θ);Xn) mencapai minimum relatip di θ = θn. Adalah mudah untuk memeriksa bahwa untuk semua ε > 0, P(E1 ∩E2) > 1−ε). Dengan demikian, dengan mengambilS1 =E1∩E2 dann1 = max(n, n) menghasilkan bagian pertama dari Teorema 3.1.1. Untuk menyelesaikan bagian kedua dapat dilihat bahwa:

1

dan dengan ekspansi Taylor orde satu fungsi∂U n(ρ;Xn) di sekitarρ0, untuk nilai

n yang lebih besar ditulis:

√

Juga bisa dilihat bahwa 1

Dan ditulis untuk nilain yang lebih besar,

18

Kemudian dengan memasukkan dalam Teorema 1( Ngatchou dan Wandji, 2005) :

wi =εi, Yi =Zi−1, T1(x) =x, T2(x) =x2−1,Π1(z) = 2λ2(z)σ(θ0;z)∂′m(ρ0;z)Θ−111 , dan Π2(z) = 4γ2_(z)σ3_(θ0;z)∂′

σ(θ0;z)Θ−1

11, dihasilkan:

√

n(ψn−ψ0) D

−→N(0,_△)

4.2 Estimasi Likehood Bersyarat

Fungsi dentitas f seperti pada model (2.1.1) berguna untuk penulisan fungsi likelihood dan/ atau fungsi conditional likehood.

Untuk memilih fungsi densitas ini, rumus (2.1.1) terlebih dahulu dicocokkan dengan metode kuadrat terkecil (least-squares). Selanjutnya, berbagai tes bisa di-aplikasikan pada residual dari model yang dicocokkan tersebut untuk membantu menetapkan fungsi densitas f-nya (tidak selalu fungsi GAUSS). Akan tetapi, hal ini akan mempermudah mengestimasi parameter-parameternya, yang secara umum dapat menggunakan metode estimasi pseudo-likehood. Pengkajian estimasi Like-lihood bersyarat atas parameter-parameter tersebut dilakukan bila fungsi densitas f-nya tidak selalu berupa fungsi GAUSS Hal ini juga telah diteliti oleh Berkes dan Horvath (2004) dalam kasus model GARCH. Untuk memudahkan, penelitian ini hanya dilakukan pada model (2.1) dimana hanya untuk fungsi σ(θ, z) yang memenuhi : (B0) untuk semuaσ(θ, z)_∈Rj ×Rq, σ(θ, z)_≥K, untuk K >0

Dengan (B0), log-likelihood dari sampel tertentuXn= (Xn. . . X1, Xn, X0, X11, X−q)

Yang bersyarat terhadap Z0 adalah:

Ln(ψ;Xn) = n

X

i=1

{−log[σ(θ;Zi−1)] + log[f(∈1 (ψ))]} (4.2.6)

Dimanaψ= (p, θ; )_∈ψdan untuk semuai_∈Z,_∈I (ψ) = [Xi −m(p;Zi−1)]/σ(θ;Zi−1) Dalam Ngatchou dan Wandji( 2005) membuat asumsi fungsi densitas f-nya sebagai berikut:

(B1)_→f(x)>0 unttuk x_∈R1 dan terdifrensial dua kali

19

(B3)_→Terdapat suatu fungsi positif V(z) sedemikian sehingga

E[υ4_{(Z0)]<∞, untuk i∈Z dan ψ1, ψ2∈Ψ, a.s.,}

max_{|ξi(ψ1)₋ξi(ψ2)_|,_|ξ?i(ψ1)₋ξ?i(ψ2)_|,_|ζi(ψ1)₋ζi(ψ2)_|

|ζ?i(ψ1)₋ζ?i(ψ2)_|,_|ζi(ψ1)₋ζi(ψ2)_{|} ≤}υ(Zi)_||ψ1₋ψ2_{|| ∈} (B4) Terdapat suatu fungsi positif τ(z), sedemikian sehingga

tE[τ4_{(Z0)]<∞ Untuki∈Z, a.s.}

max_{sup_{| ∈}i (ψ)|,sup| ∈i (ψ)|,sup| ∈i (ψ)|,sup| ∈i (ψ)|,sup| ∈i (ψ)|,} ≤τ(Zi) Asumsi-asumsi di atas setidaknya dapat dipenuhi oleh model Autoregresif linier yaitu model EXPAR, dan TAR dan lebih umum model -ARCH dengan Gaussian

f.

definit negatip. Jika R

φf(x)dx= 0dan

R

xφff(x)dx= 1 ,maka

(i) Terdapat suatu barisan estimatorψn= (ρ′

n, θ′

n)′

20

Bukti Cara membuktikannya sama seperti pada teorema 3.1.1 DefenisikanQn(ψn;ψ0)_{−→ −}D Ln(ψ;Xn). Maka

Dapat dilihat, apabila n mendekati tak hingga: 1

Tampak jelas bahwa matriks ¯P

adalah definit positif. Untuk setiap vektor ψn ∈ int (Ψ), definisikan barisan fungsi-fungsi acak:

τn(ψn:Xn) =∂2Qn(ψn;Xn)−∂2Qn(ψ0;Xn),

dan notasikan τn(ψn :Xn)lk adalah entri ke(−l, k)-nya. Setiap entri ∂2Qn(ψ0;Xn) adalah suatu konstanta dikali penjumlahan atasi= 1, . . . , ndari pergandaan kom-ponen=komponen atau entri-entri dari∂m(θ0;Zi−1), ∂2m(θ0;Zi−1), ∂σ(θ0;Zi−1) dan fungsi-fungsi acak σ(θ0;Zi−1),∈i (ψ0), ξi(ψ0), ξi(ψ0), ξi(ψ0)ξi(ψ0) dan ξi(ψ0), atau

penjumlahan atau selisih dari suku-suku sedemikian. Maka diperoleh :

21

Dari asumsi (A1)₋(A3) dan (B0)₋(B4), dapat disimpulkan dari contoh di atas bahwa untuk setiap (l, k),terdapat suatu fungsi bernilai-riil positif µlk dengan

E[µ4

Kemudian, untuk δ >0 sedemikian sehingga:

kψ₋ψ0k ∈< δ,(nδ)−1|τn(ψ∗;Xn)lk|dibatasi dari kanan olehn−1 n

P

i=1

µlk(Zi−1) yang,

menurut teorema ergodik, adalah konvergen keE[µlk(Z0)]<∞apabilanmendekati tak berhingga. Dengan demikian dapat disimpulkan bahwa untuk semua (l, k), (4.2.1) berlaku dengan τn(ψ∗

, Xn)lk.

Seperti halnya dalam bukti Teorema 4.2.1, terdapat barisan estimator - es-timator ψn = (ρ′n, θ dan maksimum relatip untuk Ln(ψ;Xn), bagian pertama dari hasil ini terbukti. Untuk bagian kedua, harus dibuktikan bahwa n−1/2_{∂Qn(ψ;Xn) konvergen dalam} distribusi ke suatu vektor acak Gaussian dengan mean 0 dan matriks kovariansi . Hasil ini terbukti jika dimasukkan kedalam Teorema 1 Ngatchou dan Wandji (2005) : wi =∈i (ψ), Yi=Zi−1,Φi(z) =∂

−1_{(θ0;z)∂m(ρ0;z) dan Φ1(z) = ∂}−2_{(θ0;z)T1(x) =}

Φf(x), T2(x) = xφf(x)−1.

Kemudian, dengan mengaplikasikan kembali bagian kedua dari Teorema 3.2.23 dari Taniguchi dan Kakizawa (2000) di peroleh bahwa

√

n(ψn−ψ0) D

−→N(0,X−1_ΛX₋₁

)

Akibat 4.2.1. Asumsikan bahwa asumsi-asumsi teorema 4.2.1 berlaku dan bahwa:

22

berlaku. Maka

√

n(ψn−ψ0) D

−→N(0,X−1_{), n}

→ ∞

Karena syarat-syarat integral dalam teorema 4.2.1 dan akibat 4.2.1 dipenuhi untuk fungsi densitas f Gaussian, maka matriks Fisher Konvergen ke P

. Karenanya, batas Cramer - Rio dipenuhi secara asymptotik dan ψn efisien secara asymptotik juga.

4.3 Estimasi Densitas dengan Kernel

Dalam analisis data cenderung diartikan sebagai proses perhitungan dalam penerapan metode statistika, misalnya perhitungan mean, varian, koefisien regre-si ataupun perhitungan jumlah kuadrat dalam analisa varian, sehingga peranan dan kegunaan sebenarnya menjadi sering terlupakan. Proses analisis data pada dasarnya meliputi upaya penelusuran dan pengungkapan informasi yang relevan yang terkandung dalam data seperti penelusuran dan pengungkapan struktur dan pola data, dan penyajian hasilnya dalam bentuk lebih ringkas dan sederhana, se-hingga pada akhirnya mengarah kepada keperluan adanya penjelasan dan penaf-siran. Penelusuran struktur dan bertujuan memeriksa apakah suatu data dapat diwakili oleh suatu model tertentu, sedangkan dalam penelusuran pola data bertu-juan untuk memeriksa apakah distribusi datanya cenderung mengumpul di satu nilai tertentu atau pada beberapa nilai.

23

Dalam analisis deret waktu (time series) distribusi bersyarat sangat bergu-na untuk studi fenomebergu-na tak linear seperti simetri dan struktur multimodalitas dari deret waktu. Dalam model (2.1 ) distribusi bersyarat adalah distribusi den-sitas. Estimasi nonparametrik atas distribusi bersyarat telah dikaji antara lain oleh Hyndman dan Yao (2002) yang menggunakan metode Kernel, dan Fan, et al (1996) yang menggunakan pendekatan polinomial lokal, kemudian Fan dan Yim (2004) yang menggunakan metode pengesahan-silang (a crossvalidation method), juga Hyndman dan Yao (2002) yang menggunakan metode Kernel dan mengem-bangkan test untuk simetri bersyarat dari estimator densitasnya. Sementara Bai dan Ng (2001) juga mengembangkan test untuk simetri bersyarat yang didasarkan pada estimator densitas bersyarat dengan Kernel dan derivatifnya.

Dalam bagian ini diasumsikan bahwa εi mempunyai fungsi densitas kontinu seragam yang tak diketahui f nya, dan didefenisikan estimator kernelnya dan estimator derivatifnya. Kemudian ditunjukkan konsistensi keseragamannya dari estimator-estimator ini. Hasil-hasil dari bagian ini bisa menghasilkan pengem-bangan estimator adaptif untuk Ψ0 atau menghasilkkan konstruksi test kecookan untuk fungsi f. Akan tetapi, masalah ini tidak dikaji di sini.

Untuk semuai _∈Z dan Ψ = (ρ;θ)_∈Ψ didefenisikan fungsi acak

∈i (Ψ) =

Xi−m(ρ, Zi−1)

σ(θ;Zi−1)

(4.3.7) Misalkan Ψn = (ρn, θn) adalah estimator konsisten atas Ψ0 sedemikian sehingga

n1/2_{(Ψn−Ψ0) konvergen dalam distribusi untuk distribusi Gaussian dengan mean} 0 dan matriks varians Γ. Misalkanp adalah suatu bilangan bulat non negatif dan

K adalah suatu fungsi kernel yang bisa dideferensialkan hingga orde p+ 1, dengan modulus kontinuitas wk. Misalkan (hn) adalah barisan bilangan riil sedemikian sehinggan hn → 0 apabila n mendekati tak berhingga. Untuk n = 1,2, . . . , dan untuk semua x_∈R, defenisikan fungsi acaknya.

f_n(p)(ψ , x) = 1

nhp+1n n

X

i=1

K(p)

x_{− ∈}i (ψ)

hn

(4.3.8)

Untuk_∈i (ψ) yang bisa diamati, konvergensi estimator Bhattacharya diatas untuk

24

(H1)K adalah kontinu seragam dengan variasi terbatas (H2)R (H7) Transformasi Fourier dariK tidak identik dengan transformasi Fourier dalam setiap neighborhood dari 0.

Dalam Silverman (1978), asumsi (H1)₋(H5) dipakai untuk konvergensi darifn(ψ0;x) ke f(x), sementara (H1),(H2),(H4),(H5)₋(H7) memungkinkan konvergensi dari

fn(p)(ψ0;x) kef(p)(x), p≥1.

Asumsi-asumsi ini berlaku setidaknya untuk kernel Gaussian

Teorema 4.3.1. Asumsikan (B0) dan(H6)berlaku, dan fungsi K(p+1) _adalah

kon-tinu.

Misalkanr adalah suatu bilangan bulat sedemikian sehingga 0_≤r_≤p. Asumsikan n1/2_hr+2

Bukti : misalkan 0 _≤r_≤p, adalah integer oleh ekspansi Taylor dan, vektor

25

Karena fungsi K(r+1) _{kontinu, maka berdasarkan (H6) fungsi ini terbatas, dan} terdapat konstantaC >0 sedemikian sehingga hampir pasti,

sup

Juga, berdasarkan (B0) dan (A1), dapat ditentukan fungsi positip χ(z) dengan

E(χ4_{(Z0)]<∞sedemikian sehingga untuk semua 1 ≤i≤n,}

sup ψ=(ψ1,ψ2)∈Ψ

k∂′

εi(ψ)kε 6χ(Zi−1)

Dari kedua ketaksamaan ini, diperoleh:

sup

Berdasarkan asumsi diatas, diperoleh bahwa _k√n(ψ0−ψn)kε konvergen dalam distribusi ke_kN(0,Γ)_kε. Menurut teorema ergodik, hampir pasti,

n

X

i=1

χ(Zi−1)→E[χ(Z0)]

Kemudian hasil diperoleh berdasarkan fakta bahwan1/2_hr+2

n → ∞, apabilan → ∞ Akibat 4.3.1. Asumsikan bahwa (B0)berlaku dan fungsi K(p+1) kontinu.

(i) Asumsikan bahwa(H1)−(H4)berlaku dan bahwan1/2h2n → ∞dan(nhn)−1log

26

Catatan 4.3.1. Ambilhn =Cst.n−1/9. Maka, diperoleh n1/2h2n → ∞ dan (nhn)

−1 log(n) _→ 0 apabila n _{→ ∞}, yang memenuhi hipotesa bagian (i) dari akibat di atas. Untuk 1_≤p_≤2, diperoleh n1/2_hp+2

n → ∞, n

−1_h−2p−1

n log(1/hn)→ 0 apabila

n_{→ ∞} dan persyaratan dari bagian (ii) dipenuhi.

4.4 Studi Simulasi

Untuk menguraikan sebagian hasil di atas, penulis mengambil dari percobaan simulasi yang dilakukan dan oleh Ngatchou dan Wandji (2007). Dibatasi pada model yang bisa memperoleh rumus eksplisit dan sederhana untuk estimator. Hal ini untuk menghindari metode numerik

Xi =

ρ0+ρ1exp −κXi2−1

Xi−1+

q

θ0+θ1Xi2−1εi (4.4.10)

Di mana parameter ρ0, ρ1, k > 0, θ1 ≥ 0 pada akhirnya memenuhi beberapa syarat yang menjamin eksistensi, sifat mempunyai invers, sifat stasioner dan er-godisitas dari (Xi)i∈Z. Sebagai contoh misalnya, untuk model (ii) di bawah ini,

(4.4.1) membuat penyelesaian stasioner dan ergodik (Xi)i∈Z untuk 0 ≤θ1 <1.

Fungsi densitas f yang di gunakan adalah Gaussian atau Laplace

Untuk lebih jelasnya lihat studi kasus berikut ini :

(i) ρ0 = 0,0 < ρ1 < 1, K = 0,1 dan θ1 = 0, dengan f adalah Gaussian atau Laplace

(ii) ρ0= 0, ρ1 = 0, K = 0 dan 0 < θ1 <1, dengan F Gaussian

(iii) ρ1= 0, K = 0 dan 0<1θ1 <1, denganf Gaussian.

27

Tabel 4.1 Estimator kuadrat terkecil bersyarat untuk parameter dari model (i) dengan Gaussian (2 kolom ditengah) dan fungsi Laplace (dua kolom terakhir) dan ukuran sampel n = 50

ρ1 θ0 ρ1 θ0 ρ1 θ0

-0.80 0.10 -0.77 0.098 -0.778 0.097 -0.50 0.50 -0.47 0.493 -0.482 0.486 0.20 0.10 0.191 0.098 0.197 0.098 0.80 0.80 0.763 0.795 0.782 0.779 0.90 1.00 0.864 0.998 0.886 0.976

(Ngatchou dan Wandji, 2007)

Tabel 4.2 Estimator kuadrat terkecil bersyarat untuk parameter dari model ARCH (1) pada model (ii) (ρ0 =ρ1 = 0) dan fungsi Gaussian, untuk sampel berukuran n = 100, n = 200, dann = 400

n= 100 200 400

θ0 θ1 θ0 θ1 θ0 θ1 θ0 θ1

0.40 0.30 0.433 0.210 0.428 0.243 0.418 0.264 0.50 0.20 0.525 0.146 0.515 0.169 0.510 0.180 0.30 0.10 0.304 0.075 0.304 0.089 0.300 0.095 0.40 0.40 0.472 0.271 0.451 0.306 0.442 0.329 0.60 0.50 0.610 0.031 0.608 0.036 0.603 0.044

(Ngatchou dan Wandji, 2007)

Untuk penghitungan estimator kuadrat-terkecil, fungsi bobot adalah λ(z) =

γ(z) = 1, yang menghasilkan estimator kuadrat - terkecil. Dalam masing-masing kasus, estimasi dihitung berdasarkan 1.000 sampel dengan panjang n. Untuk mo-del (i), dari perhitungan sederhana, tidak sulit diperiksa bahwa estimator kuadrat terkecil bertepatan dengan estimator likelihood maksimum untuk fungsi Gaussian f. Hasil hasil tentang model ini ditunjukkan dalam Tabel 4.1. Hasil-hasil tersebut menunjukkan bahwa, untuk sampel berukuran n = 50, dan untuk fungsi densitas yang lain dipertimbangkan, estimator kuadrat-terkecil mendekati nilai parameter yang sebenarnya. Perhitungan dengan cara kalkulus menunjukkan bahwa estima-tor ini tak bias. Percobaan untuk model ini juga dilaksanakan untuk n _≥ 100. Dari hasil-hasi yang tidak dipresentasikan di sini, estimasi yang diperoleh lebih akurat.untuk model (ii), hasil-hasil pada umumnya lebih baik untuk estimator likelihood maksimum daripada kuadrat- terkecil, untuk semua sampel berukuran

28

Tabel 4.3 Estimator likelihood maximum bersyarat untuk parameter model ARCH (1) pada model (ii) (ρ0 =ρ1 = 0) dan fungsi Gaussian, untuk sampel berukuran n = 100, n = 200, dann = 400

C 100 200 400

θ0 θ1 θ0 θ1 θ0 θ1 θ0 θ1

0.40 0.30 0.413 0.268 0.407 0.284 0.041 0.297 0.50 0.20 0.508 0.175 0.505 0.188 0.503 0.191 0.30 0.10 0.194 0.105 0.300 0.100 0.299 0.100 0.40 0.40 0.415 0.364 0.406 0.381 0.402 0.393 0.60 0.05 0.583 0.067 0.593 0.055 0.596 0.1015

(Ngatchou dan Wandji, 2007)

Untuk model (iii), hanya estimator kuadrat-terkecil yang dihitung dan ini dilakukan untukn = 100,200,400. Dalam kasus ini dapat diamati bahwa estimasi ρ0 baik sementara θ0 selalu ditaksir terlalu tinggi dan θ1 ditaksir terlalu rendah (lihat tabel 4.4). Estimasi kuadrat-terkecil untuk model (ii) juga seperti ini. Ini mungkin disebabkan dari fakta bahwa estimator kuadrat-terkecil untuk model ini sangat bias. Dari percobaan simulasi yang dilakukan oleh Ngatchou dan Wandji, 2007 tampak bahwa biasnya konvergen lambat ke 0, apabila n semakin besar. Tabel 4.4 Estimator Kuadrat terkecil bersyarat untuk parameter dari model iii

dengan ρ1 = 0 dan fungsi Gaussian, untuk sampel berukuran n = 100, n = 200, dann= 400

n= 100 200 400

ρ0 θ0 θ1 ρ0 θ0 θ1 ρ0 θ0 θ1 ρ0 θ0 θ1

0.20 0.40 0.30 0.189 0.447 0.184 0.196 0.435 0.291 0.198 0.424 0.253 0.30 0.50 0.20 0.292 0.534 0.131 0.292 0.524 0.155 0.295 0.517 0.173 0.50 0.30 0.10 0.491 0.313 0.060 0.494 0.307 0.075 0.494 0.303 0.085 0.60 0.40 0.05 0.582 0.411 0.025 0.591 0.408 0.033 0.594 0.405 0.040 0.40 0.40 0.10 0.390 0.415 0.062 0.389 0.410 0.077 0.399 0.405 0.086

29

(Ngatchou dan Wandji, 2007)

30

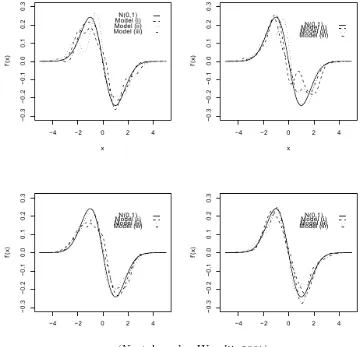
(Ngatchou dan Wandji, 2007)

Gambar 4.2 Estimasi fungsi densitas dari turunan pertama dalam model (i), (ii), dan (iii) untuk n = 100,200,400,600

Untuk estimasi densitas kernel, dibatasi percobaan pada model (i) - (iii) de-ngan fungsi densitas f Gaussian. Residual dihitung dari kecocokan kuadrat-terkecil denganγ(z) =λ(z) = 1. Diambilψn= ¯ψn(lihat Bagian 3 dan 5), kernel Gaussian dengan hn =chh−1/9, dengan menotasikan standar deviasi empiris dengan σn dan kwartil pertama dan ketiga dari (X1, . . . , Xn) dengan Xn,1/4 dan Xn,3/4

cn =

0,9 min_{σn(Xn,3/4 −Xn/1/4)} 1,34

hasil-31

sian dan barisan (hn) jelas-jelas memenuhi asumsi-asumsi dari Teorema 4.3.1. Di-ambilρ1=−0,5, θ1 = 1 untuk (i),θ0 = 0,4, θ1 = 0,1 untuk (ii) danρ0 = 0,6, θ0 = 0,4,

BAB 5 KESIMPULAN

Bahwa untuk mengestimasi fungsi densitasf dapat dilakukan, jika informasi model distribusi X tak diketahui maka f dapat diestimasi dengan menggunakan pendekatan nonparametrik.

Percobaan dilaksanakan untuk n = 100,200,400,600. Estimasi yang diper-oleh untuk fungsi densitas adalah estimasi yang baik (lihat Gambar 1). Estimasi densitas dengan derivatifnya tidak baik untuk n = 100,200, terutama di dekat maksimum. Estimasi tersebut lebih baik untukn= 400,600 (lihat gambar 2). Un-tuk fungsi densitas dengan derivatif pertamanya bias diperiksa pada estimasi dari model (ii) dan (iii) sangat mendekati fungsi sebenarnya. Hal ini disebabkan karena fluktuasi pengambilan sampel atau disebabkan bias estimator kuadrat terkecil dari parameter-parameter model ini.

DAFTAR PUSTAKA

An, H., Chen, M. Das Huang, F. (1997). The Geometric Ergilicity and Existence of Moments for a cless of non linier time series mizuls. Statiss. Probab left. 31, 213-224.

Bai, J. dan Ng.S. (2001). A Consistent test for conditional symmetry in time series models. J. Econometrics, 103, 225 258 MR1838200

Berkes, I. and Horvath, L (2004). The efficiency of the estimators of the parameters in GARCH process. Ann. Statist. 32, 633-655. MR2060172

Bollerslev, T. (1986). Generalized autoregressive conditional heteroscedasticity. J. Econometrics, 31, 307-327. MR085351

Brockwell, P.J and Davis, R.A. (1991). Time Series : Theory and Methods Second edition. Springer Verlag. MR 1093459

Brockwell, P.J and Davis, R.A. (1996). Introduction to Time Series and Forecasting. Springer Verlag. MR 1416563

Chatterjee, S. and Das, S. (2003). Parameter estimation in conditional heterosedas-tic models.Comm Statist, 32, 1135-1153. MR 1983236

Chen, M. and An, H.Z (1998) . A note on the stationarity and the existence of moments of the GARCH models. Statist. Sin, 8, 505-510. MR1624371

Chatfieldh. C. (2001). Time Series Forecasting Chapman dan Hall, London.

Engle, R.F. (1982). Autoregressive conditional heterocedasticity with estimates of the variance of United Kingdom inflation. Economitrica, 50, 987 1007. MR0666121

Fan, J. Yao, Q. and Tong, H (1996). Estimation of conditional densities and sen-sitivity measurs in nonlinear dynamical systems. Biometrika, 83, 189-206. MR1399164

Fan, J. and Yim, T.H. (2004). A Cross validation method for estimating conditional densities. Biometrika, 90. MR2126035

Francg, C. and Zakoian, J.M (2004). Maximum likelihood estimation for pure GARCH and ARMA-GARCH process. Bernoulli, 05-637. MR2076065

Giraitis, L. dan Robinson, P.M (2001), Wittle Estimation of Arch Models. Econo-metry theory. 17. 608 631

Hyndman, R.J and Yao, Q (2002). Nonparametric estimation and symmetry tests for conditional density functions. J. Nonparametr. Stat. 14, 259-278 MR1905751

34

Nachrowi, Nachrowi Djalal, dan Usman Hardius, (2006). Ekonometrika Untuk Ana-lisis Ekonomi dan Keuangan, Jakarta : LPFE UI.

Ngatchou-Wandji, J. (2005). Checking nonlinear heteroscedastic time series models. J. Statist. Plann. Infer, 133, 33 68 MR2162567

Ngatchou Wandji. (2007). Estimation in a class of nonlinear heteroscedastic time series models. Electronic Journal of Statistics, 2, 40 62

Peng, L. and Yao, Q (2003). Least absolute deviations estimation for ARCH and GARCH models. Biometrika, 90, 967 975. MR2024770

Shumway, R.H. and Stoffer, D.S. (2001). Times Series Analysis and Its Applications. Springer. MR228626

Tjostheim, D. (1986). Estimation in nonlinear time series models.Stoch. Proc. Appl. 21, 251 273. MR0833954

Tjostheim, D. (1990). Non-Linear time series and Markov chains. Adv. Appl. Prob. 22, 587 611 MR1066965

Tong, H. (1990). Non-linear Time Series. A Dynamic System Approach. Oxford : Oxford University Press. MR1079320

Weiss, A. (1986). Asymptotic theory for ARCH models: estimation and testing.