GRAF PRIMITIF JARANG DENGAN SCRAMBLING
INDEX 1
SKRIPSI
Oleh
Nadia Vela Walni 100803002
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
GRAF PRIMITIF JARANG DENGAN SCRAMBLING
INDEX 1
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains
Nadia Vela Walni 100803002
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : GRAF PRIMITIF JARANG DENGAN
SCRAMBLING INDEX 1
Kategori : SKRIPSI
Nama : NADIA VELA WALNI
Nomor Induk Mahasiswa : 100803002
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU
PENGETA-HUAN ALAM
Medan, Juni 2014
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Diketahui oleh :
Departemen Matematika FMIPA USU
Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
GRAF PRIMITIF JARANG DENGAN SCRAMBLING INDEX 1
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa
kutipan dan ringkasan penting yang masing-masing disebutkan sumbernya.
Medan, Juni 2014
Nadia Vela Walni
PENGHARGAAN
Segala puji dan syukur bagi Tuhan semesta alam, Allah SWT yang
melimpah-kan rahmat dan ridho-Nya sehingga penulis dapat menyelesaimelimpah-kan skripsi yang berju-dul ”GRAF PRIMITIF JARANG DENGAN SCRAMBLING INDEX 1” ini dengan baik. Shalawat beriring salam kepada Nabi Muhammad SAW beserta
keluarga dan para sahabat.
Dalam menyelesaikan skripsi ini penulis banyak mendapatkan bantuan,
mo-tivasi, do’a dari berbagai pihak. Dan pada kesempatan ini penulis mengucapkan
terima kasih kepada:
1. Bapak Prof. Dr. Tulus, M.Si, dan Ibu Dr. Mardiningsih, M.Si, selaku Ketua
dan Sekretaris Departemen Matematika FMIPA USU Medan.
2. Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Dosen Pembimbing I dan Ibu Dr.
Mardiningsih, M.Si, selaku Dosen Pembimbing II, yang telah banyak
memban-tu penulis dan memberikan dukungan baik berupa nasihat, motivasi maupun ilmu pengetahuan kepada penulis dalam menyelesaikan penelitian ini.
3. Bapak Prof. Dr. Tulus, M.Si, selaku Dosen Pembanding I, dan Bapak Dr. Suwarno Ariswoyo, M.Si, selaku Dosen Pembanding II, yang telah memberikan
nasehat, kritik dan saran yang membangun selama penelitian.
4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakultas
Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara, Medan.
5. Ibunda Syufniarti dan Ayahanda Drs. Raswal serta adinda Ahmad Arfandi
yang sangat sabar membimbing, memotivasi, mend’oakan dan memberikan
du-kungan moril maupun materil selama penulisan skripsi ini.
Matematika 2010 khususnya bidang murni Zati, Fitriana, Ardi, Hamka, Adanan,
Junliade, dan Sri. Serta Septian yang sangat banyak membantu penulis dalam me-nulis skripsi ini.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu
saran dan kritik yang membangun dari pembaca sangat diperlukan. Akhir kata pe-nulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini bermanfaat.
Medan, Juni 2014
ABSTRAK
Sebuah graf terhubung G dikatakan primitif bila terdapat bilangan bulat positif k sehingga untuk setiap pasangan vertex udanv terdapat jalan yang menghubungkan u dan v dengan panjang k. Scrambling index dari sebuah graf primitif G, k(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan vertex u dan v yang berbeda terdapat sebuah vertex w dengan sifat bahwa ada jalan yang menghubungkan u dan w dan jalan yang menghubungkan v dan w dengan panjang k. Pada penelitian ini didiskusikan syarat perlu dan cukup bagi graf primitif dengan scrambling index 1. Selanjutnya diperlihatkan bahwa sebuah graf primitif atas n vertex dengan scrambling index 1 memiliki sedikitnya 3n−3
2 edge bilan adalah ganjil dan memiliki sedikitnya 3n−2
2 edge bila n adalah genap.
ABSTRACT
A connected graphGis primitive there is a positive integerksuch that for every pair of vertices uand v there is a walk of lengthk from vertex u to vertex v. Scrambling index of a primitive graph G, denoted by k(G), is the smallest positive integer k such that for every pair of vertices uand v there is a vertex w such that we can get to w from u and v in G using a walk of length k. This paper discusses necessary and sufficient conditions for primitive graph with scrambling index 1. And than a primitive graph with n ≥ 3 vertices and scrambling index 1, the minimum number of edge is 3n−3
2 if n is odd and 3n−2
2 if n is even.
DAFTAR ISI
Halaman
ABSTRAK . . . i
ABSTRACT . . . ii
DAFTAR ISI . . . iii
DAFTAR GAMBAR . . . v
BAB 1 PENDAHULUAN . . . 1
1.1 Latar Belakang . . . 1
1.2 Perumusan Masalah . . . 4
1.3 Tujuan Penelitian . . . 4
1.4 Manfaat Penelitian . . . 4
BAB 2 GRAF PRIMITIF . . . 5
2.1 Definisi Graf . . . 5
2.2 Matriks Ketetanggan dari Graf . . . 6
2.3 Primitifitas dari Graf Terhubung . . . 7
2.4 Matriks Tak Negatif . . . 10
2.5 Scrambling Index Graf Primitif . . . 11
2.5.1 Scrambling Index Lokal Graf Primitif . . . 11
2.5.2 Scrambling Index Graf Primitif . . . 11
BAB 3 METODOLOGI PENELITIAN . . . 15
BAB 4 HASIL DAN PEMBAHASAN . . . 16
4.2 Graf Primitif Jarang . . . 17
BAB 5 KESIMPULAN DAN SARAN . . . 23
5.1 Kesimpulan . . . 23
5.2 Saran . . . 23
DAFTAR GAMBAR
Nomor Judul Halaman
2.1 Graf dengan 5 vertex dan 6 edge . . . 6
2.2 Graf dengan 6 vertex dan 7 edge . . . 7
2.3 (a) Graf terhubung dan (b) graf tidak terhubung . . . 8
2.4 Contoh graf primitif . . . 9
2.5 Graf dengan 5 vertex dan 6 edge . . . 10
2.6 Graf dengan 5 vertex dan 7 edge . . . 10
4.1 Graf memuat loop yang memiliki scrambling index 1 . . . 17
4.2 Graf dengan k(S3) = 1 . . . 18
4.3 Graf dengan k(S4)6= 1 . . . 18
4.4 Graf dengan k(S4) = 1 . . . 19
4.5 Graf dengan k(S5)6= 1 . . . 19
4.6 Graf 5 vertex dengan scrambling index 1 dan tidak memiliki banyak edge yang minimum . . . 20
4.7 Graf dengan k(S5) = 1 . . . 20
4.8 Graf dengan k(S6) = 1 . . . 21
4.9 Graf dengan dengan scrambling index 1 memuatnganjil vertex dan 3n−3 2 edge yang minimum . . . 21
ABSTRAK
Sebuah graf terhubung G dikatakan primitif bila terdapat bilangan bulat positif k sehingga untuk setiap pasangan vertex udanv terdapat jalan yang menghubungkan u dan v dengan panjang k. Scrambling index dari sebuah graf primitif G, k(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan vertex u dan v yang berbeda terdapat sebuah vertex w dengan sifat bahwa ada jalan yang menghubungkan u dan w dan jalan yang menghubungkan v dan w dengan panjang k. Pada penelitian ini didiskusikan syarat perlu dan cukup bagi graf primitif dengan scrambling index 1. Selanjutnya diperlihatkan bahwa sebuah graf primitif atas n vertex dengan scrambling index 1 memiliki sedikitnya 3n−3
2 edge bilan adalah ganjil dan memiliki sedikitnya 3n−2
2 edge bila n adalah genap.
ABSTRACT
A connected graphGis primitive there is a positive integerksuch that for every pair of vertices uand v there is a walk of lengthk from vertex u to vertex v. Scrambling index of a primitive graph G, denoted by k(G), is the smallest positive integer k such that for every pair of vertices uand v there is a vertex w such that we can get to w from u and v in G using a walk of length k. This paper discusses necessary and sufficient conditions for primitive graph with scrambling index 1. And than a primitive graph with n ≥ 3 vertices and scrambling index 1, the minimum number of edge is 3n−3
2 if n is odd and 3n−2
2 if n is even.
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Studi mengenai scrambling index dari sebuah graf primitif dapat dilakukan dengan pendekatan mengenai scrambling index dari matriks tak negatif A. Matriks tak ne-gatifAadalah sebuah matriks ordenyang setiap entriaij ≥0. MatriksA dikatakan primitif jika terdapat bilangan bulat positif l, Al adalah positif, yaitu semua entri
dari matriks Al bernilai positif.
Persoalan mengenai scrambling index dari sebuah graf primitif G biasanya diselesaikan menggunakan matriks A(G), yakni sebuah matriks tak negatif A yang bersesuaian dengan graf primitif G. Matriks A(G) adalah sebuah matriks orde n dengan entri aij akan bernilai 1 jika terdapat edge darivi kevj pada graf primitifG, dan entriaij akan bernilai 0 jika tidak terdapat edge darivikevj pada graf primitifG.
Scrambling index dari graf primitifGsama dengan scrambling index dari matriks tak negatif A yang bersesuaian dengan graf primitif tersebut. Matriks yang bersesuaian dengan graf primitif G kemudian disebut denganmatriks ketetanggaan.
Scrambling index dari sebuah graf primitifG, dinotasikan dengank(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan dua vertex u dan v yang berbeda terdapat sebuah vertexwdengan sifat terdapat sebuah jalan dariuke w dan sebuah jalan dari v kew dengan panjang k. Untuk dua vertexu dan v yang berbeda, scrambling index lokal dari u dan v adalah bilangan bulat positif ku,v(G)
yang didefinisikan sebagai,
lanjut perhatikan bahwa karena G adalah terhubung, maka untuk setiap bilangan bulat l ≥ku,v(G) dapat ditemukan sebuah vertex w′ sehingga terdapat u↔w′ dan
v ↔w′ dengan panjang l. Hal ini berakibat,
k(G) = max
2
Akelbek dan Kirkland (2009a) mengemukakan tentang batas atas pada scramb-ling index dari digraf primitifD dengann vertex dans girth. Makak(D)≤K(n, s)
Lebih lanjut Akelbek dan Kirkland (2009b) juga mengemukakan tentang ka-rakteristik dari semua digraf primitif sehingga scrambling index sama dengan batas atas pada scrambling index digraf primitif D. Misal D digraf primitif dengan n vertex, s≥2, dan k(D) =K(n, s). Maka,
1. Tidak ada lingkaran dengan panjangp, s < p < n, sehingga gcd(s, p) = 1.
2. D memuat subgraf Ds,n dan gcd(s, n) = 1.
Chen dan Liu (2009) mendiskusikan tentang hubungan antara eksponen dan scramb-ling index dari digraf primitif simetri dengan n ≥ 2. Untuk digraf yang demiki-an maka k(D) = ⌈exp2(D)⌉. Himpunan scrambling index dari kelas Sn(r) adalah
scrambling index dari kelas Hn(l) adalah,
1. Jika 2≤l ≤n− ⌈n−21⌉ maka K∗(n, l) = {1,2,· · · , n−l}.
2. Jika n− ⌈n−1
2 ⌉ ≤l≤n maka K
∗(n, l) ={1,2,· · · ,⌈n−1 2 ⌉}.
3
yang lebih kecil darir, sedangkanHn(l) himpunan digraf primitif simetri orde ndan
mempunyai l loop.
Chen dan Liu juga mendiskusikan tentang karakteristik digraf primitif simetri yang scrambling index sama dengan nilai maksimum dari scrambling index digraf primitif yang demikian. Untuk n, r, m, l, dan hbilangan bulat, maka
Liu dan Huang (2010) mendiskusikan tentang beberapa batas atas baru pada scramb-ling index digraf primitif dengan d loop, yaitu
1. k(D)≤n− ⌈d
2⌉, ndan dbilangan bulat, n ≥2, 1≤d ≤n,D∈Pn(d), dengan Pn(d) merupakan himpunan digraf primitif dengann vertex dan d loop.
2. k(D)≤n−1,D memuat loop.
Lebih lanjut Liu dan Huang mengemukakan beberapa batas atas baru untuk bebe-rapa digraf khusus sebagai berikut:
1. UntukD∈DSn, n ≥2 maka
4
2. UntukD∈M Sn, n≥3 maka
k(D)≤
2n−3, jika n ganjil
2n−4, jika n genap
denganM Sn merupakan himpunan digraf primitif micro-symmetricorde n.
Pada umumnya peneliti terdahulu mengkaji tentang graf-graf dengan scrambling in-dex besar. Dengan demikian, penulis mengkaji tentang graf-graf dengan scrambling index terkecil yakni scrambling index 1.
1.2 Perumusan Masalah
Andaikan G adalah suatu graf primitif jarang atas n vertex dan tanpa loop. Ma-salah penelitian ini adalah menentukan graf mana yang memiliki scrambling index 1.
1.3 Tujuan Penelitian
Penelitian ini bertujuan untuk menentukan syarat perlu dan cukup bagi graf primitif jarang G memiliki scrambling index 1. Kemudian menentukan bentuk umum dari graf primitif dengan scrambling index 1.
1.4 Manfaat Penelitian
BAB 2 GRAF PRIMITIF
Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisigraf,terhubung kuat,primitifitas,graf primitif jarang, danscrambling index.
2.1 Definisi Graf
Pada subbab ini akan diberikan definisi tentang graf serta notasi-notasi yang akan dipergunakan dalam pembahasan selanjutnya.
Secara sederhana, graf dinotasikan denganGmerupakan himpunan tak kosong dari titik-titik selanjutnya disebut vertex yang dihubungkan oleh garis selanjutnya disebut edge dari graf G tersebut. Secara matematika, sebuah graf G terdiri dari dua himpunan, yaitu:
1. Himpunan vertex yang dinotasikan denganV ={v1, v2,· · · , vn}dengani
ada-lah bilangan bulat positif danvi adalah elemen dari himpunanV dann(V)6= 0.
2. Himpunan edge dari grafGyang dinotasikan dengan E merupakan himpunan bagian dari pasangan tak berurut dari elemen-elemen di V.
Jika diberikan notasi e = (v1, v2) adalah sebuah edge dari graf G, maka v1 disebut sebagai vertex awal danv2 sebagai vertex akhir.
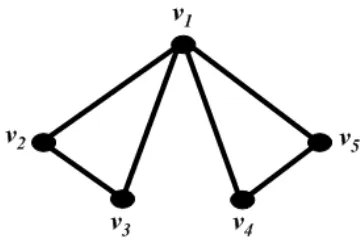
Contoh 2.1 Perhatikan himpunan vertex V = {v1, v2, v3, v4, v5} bersama dengan himpunan bagian pasangan tak berurut E ={{v1, v2},{v1, v3},{v1, v4},{v1, v5},
6
Gambar 2.1 : Graf dengan 5 vertex dan 6 edge
Andaikan G sebuah graf. Misalkan u dan v adalah vertex di G. Sebuah jalan dengan panjang m dari u kev adalah sebuag barisan m edge dalam bentuk
u=v0 ↔v1 ↔ · · · ↔vm−1 ↔vm =v
Dengan m ≥ 0, v0 = u dan vm = v. Jika u = v maka jalan tersebut dikatakan
jalan tertutup dan jika u6= v maka jalan tersebut dikatakan jalan terbuka. Sebuah lintasan adalah sebuah jalan tanpa perulangan vertex kecuali mungkin kedua vertex ujungnya. Jika kedua vertex ujungnya sama maka dinamakan lintasan tertutup atau lebih dikenal dengan sebuah lingkaran. Loop adalah lingkarang yang panjangnya satu. Dengan menggunakan graf pada Contoh 2.1 akan dijelaskan beberapa definisi diatas.
1. Barisan edge v1 ↔ v2 ↔ v3 ↔ v1 ↔ v4 ↔ v5 adalah sebuah jalan yang menghubungkan v1 dengan v5, tetapi bukan sebuah lintasan karena ada peru-langan vertex v1.
2. Barisan edgev3 ↔v1 ↔v4 adalah sebuah lintasan dari v3 ke v4.
3. Barisan edegev1 ↔v2 ↔v3 ↔v1 adalah sebuah lingkaran.
2.2 Matriks Ketetanggan dari Graf
7
Sebuah matriks ketetanggaan dari grafGatasn vertex adalah matriks berorde n,A(G) = [aij] dengan
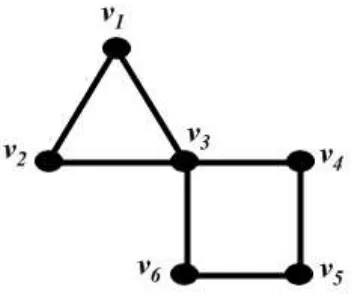
Contoh 2.2 Perhatikan grafG pada gambar di bawah ini.
Gambar 2.2 : Graf dengan 6 vertex dan 7 edge
Matriks ketetanggaan dari graf di atas adalah sebagai berikut.
A(D) =
2.3 Primitifitas dari Graf Terhubung
8
terhubung jika terdapat sebarang satu vertex atau lebih sehingga tidak terdapat jalan dari udan v.
Contoh 2.3 Berikut contoh graf terhubung dan tidak terhubung.
Gambar 2.3 : (a) Graf terhubung dan (b) graf tidak terhubung
Gambar 2.3(a) menunjukan graf terhubung karena terdapat jalan dari setiap pasang-an vertex di G, dan gambar 2.3(b) menunjukan graf yang tidak terhubung karena tidak terdapat jalan yang menghubungkan v5 dengan vertex lainnya.
Berikut diberikan syarat perlu dan cukup agar satu graf terhubung G adalah graf primitif.
Teorema 2.1 Andaikan G adalah suatu graf. Graf G dikatakan primitif jika dan hanya jika terhubung dan mengandung lingkaran ganjil.
9
dan kembali ke vertex u melalui lintasan puv yang sama. Andaikan l(wuu) adalah
panjang jalan dari vertex u keu. Perhatikan bahwa l(wuu) adalah genap. Agar wuu
mempunyai panjang ganjil makawuu hrus melewati satu lingkaran ganjil disebarang
vertex, misalnya vertexx. Jalanwuuyang terdiri dari lintasan pux, lintasanpxx, dan lintasan pxu adalah suatu jalan wuu dengan panjang ganjil. Sehingga untuk setiap
vertex u dan v di Gharuslah mempunyai lingkaran ganjil.
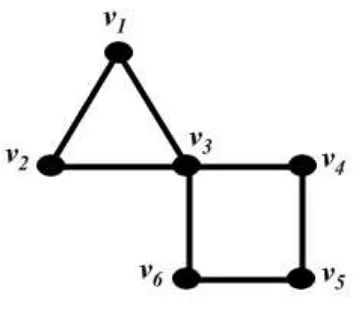
Contoh 2.4 Berikut contoh graf primitif
Gambar 2.4 : Contoh graf primitif
Graf diatas merupakan graf primitif karena memuat lingkaran dengan panjang ganjil yakni lingkaran v1 →v2 →v3 →v1 dengan panjang 3.
10
Contoh 2.5 Berikut contoh graf primitif jarang
Gambar 2.5 : Graf dengan 5 vertex dan 6 edge
Gambar 2.6 : Graf dengan 5 vertex dan 7 edge
Kedua graf diatas merupakan graf dengan 5 vertex dan scrambling index 1. Gambar 2.5 dibentuk dengan 6 edge, sedangkan Gambar 2.6 dibentuk dengan 7 edge sehing-ga graf pada Gambar 2.5 merupakan graf primitif jarang karena dibentuk densehing-gan jumlah edge yang minimum dibandingkan dengan graf pada Gambar 2.6.
2.4 Matriks Tak Negatif
Matriks tak negatifA merupakan sebuah mariks yang setiap entri aij dari A adalah
bilangan bulat tak negatif, sebaliknya jika setiap entri aij dari matriks A adalah
11
2.5 Scrambling Index Graf Primitif
2.5.1 Scrambling Index Lokal Graf Primitif
Untuk u, v ∈ V(G)(u 6= v), scrambling index lokal dari setiap pasangan dua vertex berbeda di G didefinisikan sebagai,
ku,v(G) =min{k :u k
↔w dan v ↔k w untuk semua w∈V(G)}
2.5.2 Scrambling Index Graf Primitif
Scrambling index dari sebuah graf primitifG, dinotasikan dengank(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap pasangan dua vertex u dan v yang berbeda terdapat sebuah vertex w dengan sifat terdapat sebuah jalan dari u ke wdan sebuah jalan dari v kew dengan panjang k,
atau
k(G) = max
u,v∈V(G){ku,v(G)}
12
Contoh 2.6 Perhatikan Contoh 2.2 Menurut definisi, diperoleh scrambling index
lokal dari graf primitif di atas sebagai berikut, kv1,v2(G) =min{2,2,1,2,3,2}= 1
kv1,v3(G) =min{2,1,2,3,4,3}= 1
kv1,v4(G) =min{2,2,1,2,3,2}= 1
kv1,v5(G) =min{3,3,2,3,4,3}= 2
kv1,v6(G) =min{2,2,1,2,3,2}= 1 kv2,v3(G) =min{1,2,2,4,4,3}= 1
kv2,v4(G) =min{2,2,1,2,3,2}= 1
kv2,v5(G) =min{3,3,2,3,4,3}= 2
kv2,v6(G) =min{2,2,1,2,3,2}= 1
kv3,v4(G) =min{2,2,3,4,4,4}= 2
kv3,v5(G) =min{3,3,2,1,2,1}= 1
kv3,v6(G) =min{2,2,3,4,5,4}= 2
kv4,v5(G) =min{3,3,4,5,6,5}= 3
kv4,v6(G) =min{2,2,1,2,1,2}= 1
kv5,v6(G) =min{3,3,4,5,6,5}= 3
Dari definisi diperoleh k(G) = max
u,v∈V(G){ku,v(G)}= 3
Scrambling index dari graf primitifGdapat dicari menggunakan matriks kete-tanggaan A(G). Jika untuk setiap dua baris pada A(G)k terdapat sedikitnya satu
13
Contoh 2.7 Perhatikan Contoh 2.2
1. Untukk = 1, diperoleh
Graf pada Contoh 2.2 tidak memiliki scrambling index 1, karena setidaknya ada dua baris pada matriks A1, yaitu baris pertama dan baris kelima tidak memiliki entri positif pada kolom yang sama.
2. Untukk = 2, diperoleh
Graf pada Contoh 2.2 tidak memiliki scrambling index 2, karena setidaknya ada 2 baris pada matriks A2, yaitu baris keempat dan baris kelima tidak memiliki entri positif pada kolom yang sama.
14
BAB 3
METODOLOGI PENELITIAN
Untuk menentukan scrambling index dari sebuah kelas graf primitif yang tidak me-muat loop, akan dilakukan dalam beberapa langkah pendekatan sebagai berikut:
1. Komputasi Nilai Scrambling Index. Dengan menggunakan program yang di-tulis dalam MATLAB akan diperoleh sebuah bilangan bulat positif terkecil k yang merupakan scrambling index dari suatu graf primitif. Berikut algoritma untuk mencari scrambling index dari graf primitif G dengan n≥3.
(a) Menginput matriks ketetanggaan dari graf primitif G.
(b) Mengecek primitifitas graf primitif.
(c) Jika untuk dua baris pada Ak sedikitnya terdapat satu elemen yang
nilai-nya positif pada kolom yang sama maka k merupakan scrambling index dari graf primitifG.
2. Menentukan syarat perlu dan cukup agar sebuah graf primitif G memiliki scrambling index 1 dan pembuktiannya.
BAB 4
HASIL DAN PEMBAHASAN
Pada bab ini akan diperlihatkan hasil dari penelitian ini, yaitu syarat perlu dan cukup agar sebuah graf primitif memiliki scrambling index 1 dan bentuk umum dari graf primitif dengan scrambling index 1.
4.1 Syarat Perlu dan Cukup
Lemma 4.1AndaikanGadalah sebuah graf primitif dengann ≥3 vertex dan tanpa loop. Scrambling indexk(G) = 1 jika dan hanya jika memenuhi dua kondisi berikut.
1. Setiap vertex dari grafG berada pada sebuah segitiga.
2. Untuk setiap dua vertex u dan v yang terletak pada dua segitiga berbeda, terdapat jalan dengan panjang 2 yang menghubungkan u dan v.
Bukti. Andaikan k(G) = 1, dan misalkan u adalah sebarang vertex di G. Karena G terhubung, maka terdapat sebuah vertex v di G sehingga {u, v} adalah sebuah edge di G. Karenak(G) = 1, terdapat sebuah vertex w sehingga {u, w} dan {v, w}
masing-masing adalah sebuah edge dari graf G. Akibatnya, edge {u, v}, {u, w}dan
{v, w} membentuk sebuah segitiga yang memuatu. Jadi setiap vertex di G terletak pada sebuah segitiga. Andaikan x dan y adalah dua vertex di graf G yang terletak pada sebuah segitiga berbeda. Karena k(G) = 1, maka terdapat sebuah vertex z di G sehingga {x, z} dan {y, z} masing-masing adalah sebuah edge pada graf G. Akibatnya jalan x ↔ z ↔ y adalah sebuah jalan yang menghubungkan x dan y dengan panjang 2.
Sekarang misalkan G adalah primitif dan memenuhi kondisi (1) dan kondisi (2) pada Lemma 4.1. Untuk setiap dua vertex u dan v yang berbeda diperlihatkan bahwaku,v(G) = 1. Jikaudanv terletak pada sebuah segitiga, maka terdapat vertex
w pada segitiga sehingga ada jalan u ↔1 w dan v ↔1 w. Jadi ku,v(G) = 1. Jika u
dan v berada pada dua segitiga yang berbeda, maka kondisi (2) menjamin bahwa terdapat jalan dengan panjang 2 yang menghubungkan u dan v. Hal ini berakibat terdapat vertexwdi graf Gsehingga ada jalanu↔1 wdan v ↔1 w. Jadiku,v(G) = 1.
17
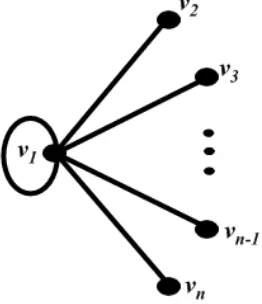
Berikut ini diperlihatkan bahwa syarat graf tanpa loop pada Lemma 4.1 adalah diperlukan. Perhatikan graf Ln atas n vertex dengan himpunan edge {{v1, v1}} ∪
{{v1, vi} :i = 1,2, . . . , n} . Graf Ln adalah sebuah graf primitif dengan scrambling
index 1, tetapi Ln tidak memuat segitiga. SehinggaLn tidak memenuhi kondisi (1) pada Lemma 4.1, seperti yang diperlihatkan pada Gambar 4.1.
Gambar 4.1 : Graf memuat loop yang memiliki scrambling index 1
4.2 Graf Primitif Jarang
Pada bagian ini didiskusikan kelas graf primitif atas n vertex dengan scrambling index 1 dan mempunyai jumlah edge minimum. Untuk bilangan bulat positif n≥3, didefinisikan Sn sebagai sebuah graf primitif atas n vertex dengan k(Sn) = 1 dan
banyak edge minimum.
Teorema 4.1 Andaikan Sn adalah graf primitif atas n ≥ 3 vertex tanpa loop dan
k(Sn) = 1. Minimum banyaknya edge dari Sn adalah 3n−23 bila n adalah ganjil dan
3n−2
2 bila n adalah genap.
Bukti. AndaikanSnadalah graf primitif tanpa loop dengank(Sn) = 1. Dari Lemma
18
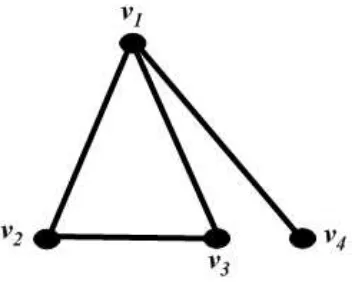
Gambar 4.2 : Graf dengank(S3) = 1
Andaikan ditambahkan sebuah edge yang menggabungkanv4 keS3 padav1 sehingga membentuk S4, seperti yang diperlihatkan pada Gambar 4.3.
Gambar 4.3 : Graf dengank(S4)6= 1
19
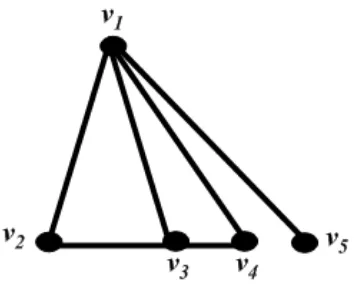
Gambar 4.4 : Graf dengank(S4) = 1
Kemudianv5 ditambahkan padaS4. Jika v5 dan sebuah edge ditambahkan pada S4, maka graf tersebut tidak memiliki scrambling index 1 karena v5 tidak berada pada sebuah segitiga, seperti yang diperlihatkan pada Gambar 4.5.
Gambar 4.5 : Graf dengank(S5)6= 1
20
Gambar 4.6 : Graf 5 vertex dengan scrambling index 1 dan tidak memiliki banyak edge yang minimum
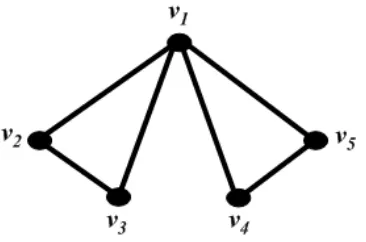
Tetapi Gambar 4.6 tidak memiliki banyak edge yang minimum, makaS5dapat diben-tuk dengan menggabungkan sebuah limtasan v1 ↔v4 ↔v5 ↔v1 pada S3, sehingga diperolehS5 dengan minimum banyaknya edge adalah 6, seperti yang diperlihatkan pada Gambar 4.7.
Gambar 4.7 : Graf dengank(S5) = 1
21
Gambar 4.8 : Graf dengank(S6) = 1
Untuk membentuk S7 dilakukan dengan cara menggabungkan sebuah segitiga pa-da S5, dan S8 dilakukan dengan menggabungkan sebuah segitiga pada S6. Seca-ra umum untuk i ≥ 5, Si dapat dibentuk dengan menggabungkan sebuah
segiti-ga pada Si−2. Minimum banyaknya edge dari Sn jika n ≥ 3 dan n ganjil adalah
3,6,9,12,· · · ,3n−3
2 , dan minimum banyaknya edge dari Sn jika n ≥ 4 dan n genap
adalah 5,8,11,14,· · · ,3n−2
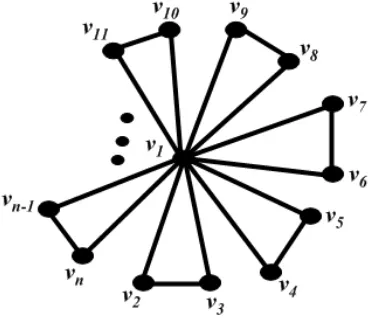
2 . Dari proses tersebut diperoleh graf seperti yang diper-lihatkan pada Gambar 4.9 untuk n ganjil vertex dan Gambar 4.10 untuk n genap vertex.
Gambar 4.9 : Graf dengan dengan scrambling index 1 memuat n ganjil vertex dan 3n−3
22
Gambar 4.10 : Graf dengan dengan scrambling index 1 memuat ngenap vertex dan 3n−2
2 edge yang minimum
Perhatikan graf Sn di atas. Terdapat dua jenis edge pada graf tersebut, yaitu
edge yang insiden dengan v1 dan edge yang tidak insiden dengan v1. Jika salah satu edge dihilangkan pada sebarang graf Sn, maka k(Sn) 6= 1 karena Sn tidak
memenuhi Lemma 4.1(1). Jadi, terbukti bahwa Sn merupakan graf primitif jarang
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Penelitian ini memperlihatkan syarat perlu dan cukup bagi graf primitif dengan scrambling index 1. Andaikan Gadalah suatu graf primitif dengan n≥3 vertex dan tanpa loop. Scrambling index k(G) = 1 jika dan hanya jika memenuhi dua kondisi berikut.
1. Setiap vertex dari grafG berada pada sebuah segitiga.
2. Untuk setiap dua vertex u dan v yang terletak pada dua segitiga berbeda, terdapat jalan dengan panjang 2 yang menghubungkan u dan v.
Selanjutnya diperlihatkan bahwa sebuah graf primitif atas n vertex dengan scramb-ling index 1 memiliki sedikitnya 3n−2 3 bila n adalah ganjil dan 3n−2 2 bila n adalah genap.
5.2 Saran
DAFTAR PUSTAKA
Akelbek, M. and Kirkland, S. 2009. Coefficient of Ergodicity and The Scrambling Index. Linear Algebra Appl. 430:1111-1130.
Akelbek, M. and Kirkland, S. 2009. Primitive Digraphs with The Largest Scrambling Index. Linear Algebra Appl. 430:1099-1110.
Brualdi, R.A. and Ryser, H.J. 1991.Combinatorial Matrix Theory. Cambridge: Cam-bridge University Press.
Chen, S and Liu, B. 2010.The Scrambling Index of Symetric Primitive Matrices.
Linear Algebra Appl. 433:1110-1126.
Fuyi, W., Maoquan, C. and Jianzhong, W. 1999. On Odd Primitive Graphs. Austra-lasian Journal of Combinatorics. 19:11-15.
Liu, B. and Huang, Y. 2010. The Scrambling Index of Primitive Digraphs.Computers and Mathematics with Applications. 60:706-721.
Kim, B.M., Song, B.C. and Hwang, W. 2005. Nonnegative Primitive Matrices with Exponent 2. Linear Algebra Appl. 407:162-168.