UKURAN PEMUSATAN DATA SIRKULAR
CICI SUHAENI
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Pendugaan Selang Kepercayaan Bootstrap bagi Ukuran Pemusatan Data Sirkular adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan tercantum dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Mei 2012
for Circular Data. Under direction of I MADE SUMERTAJAYA and ANIK DJURAIDAH.
The confidence interval is an estimator based on the sampling distribution. When the sampling distribution can not be derived from population distribution, the bootstrap method can be used to estimate it. Three methods used to estimate the bootstrap confidence interval for circular data were equal-tailed arc (ETA), symmetric arc (SYMA), and likelihood-based arc (LBA). In this study, three methods were evaluated through simulation study. The most important criterion to evaluate them were true coverage and interval width. The simulation results indicated in all methods, the interval width shortened when the concentration parameter increased. True coverage approached confidence level when the concentration parameter were one or more. For small concentration parameter, all three methods appeared unstable. Based on the true coverage, SYMA was the best, while in terms the interval width, LBA was the best one. For both criterion could be summarized that ETA is the best result. ETA and SYMA applicated for estimate the period of Dengue Fever outbreaks in Bengkulu. The estimation showed that Dengue Fever outbreaks in 2009 were October through January. In 2010, it were January through March, and in 2011, it were June through September.
RINGKASAN
CICI SUHAENI. Pendugaan Selang Kepercayaan Bootstrap bagi Ukuran Pemusatan Data Sirkular. Dibimbing oleh I MADE SUMERTAJAYA dan ANIK DJURAIDAH.
Data sirkular merupakan salah satu jenis data berarah yang bersifat periodik. Data diukur menggunakan instrumen kompas dan jam. Seperti pada kasus data linier, pada data sirkular juga dapat dijumpai kondisi sulitnya menentukan sebaran penarikan contoh dari sebaran populasi yang tidak diketahui maupun diketahui. Oleh karena itu, pendugaan selang kepercayaan menggunakan resampling bootstrap pada data sirkular menjadi kajian yang menarik dilakukan.
Metode yang telah berkembang untuk pendugaan selang kepercayaan bootstrap pada data sirkular ada tiga, yaitu busur ekor sama (BES), busur simetri (BSIM), dan busur berbasis kemungkinan (BBK). Baik buruknya selang kepercayaan dievaluasi melalui dua kriteria, yaitu lebar selang dan kemampuan selang dalam mencakup parameter sesungguhnya. Selang kepercayaan ini ditentukan oleh keragaman data. Pada data sirkular dengan sebaran von Mises, keragaman data dapat dilihat dari parameter konsentrasi.
Penelitian ini bertujuan untuk mengkaji pengaruh parameter konsentrasi terhadap dugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median pada metode BES, BSIM, dan BBK. Kemudian, menerapkan metode terbaik pada kasus waktu (bulan) kejadian Demam Berdarah Dengue (DBD) di Provinsi Bengkulu.
Data yang digunakan adalah data simulasi dan data riil. Data simulasi diperoleh dari proses pembangkitan melalui sebaran vonMises. Data riil berupa data waktu (bulan) kedatangan pasien DBD di instalasi rawat inap RSUD M Yunus Bengkulu Tahun 2009, 2010, dan 2011. Penelitian dibagi menjadi empat tahap. Tahapan 1 membangkitkan data, Tahapan 2 menentukan selang kepercayaan bootstrap, Tahapan 3 mengevaluasi hasil selang dugaan bootstrap, dan Tahapan 4 implementasi metode terbaik terhadap data riil.
Hasil studi simulasi menunjukkan bahwa pada parameter konsentrasi yang kecil ( , ketiga metode pendugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median menghasilkan cakupan selang yang tidak stabil. Metode yang terbaik untuk selang kepercayaan bagi arah rata-rata adalah BES dan bagi arah median adalah BSIM. Untuk , ketiga metode cenderung memberikan cakupan yang stabil dekat dengan tingkat kepercayaan. Metode yang terbaik adalah BSIM.
adalah Januari sampai Maret, dan tahun 2011 adalah Juni sampai September.
© Hak Cipta milik IPB, tahun 2012 Hak Cipta dilindungi Undang-undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan yang wajar bagi IPB.
CICI SUHAENI
Tesis
Sebagai salah satu syarat untuk memperoleh gelar
Magister Sains pada
Program Studi Statistika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Nama : Cici Suhaeni
NRP : G151100011
Disetujui Komisi Pembimbing
Dr. Ir. I Made Sumertajaya, MSi. Ketua
Dr. Ir. Anik Djuraidah, MS. Anggota
Diketahui,
Ketua Program Studi Statistika
Dr. Ir. Erfiani, MSi.
Dekan Sekolah Pascasarjana
Dr. Ir. Dahrul Syah, MSc. Agr.
PRAKATA
Puji syukur kehadirat Allah SWT atas kemudahan yang diberikan sehingga tesis dengan judul “Pendugaan Selang Kepercayaan Bootstrap bagi Ukuran Pemusatan Data Sirkular” ini dapat diselesaikan dengan baik. Penelitian untuk penulisan tesis ini dilakukan dengan simulasi dan diaplikasikan pada kasus waktu kejadian Demam Berdarah Dengue (DBD) di Provinsi Bengkulu.
Terimakasih penulis ucapkan kepada pihak-pihak yang telah membantu proses penyusunan tesis ini, yaitu :
1. Dr. Ir. I Made Sumertajaya, MSi. dan Dr. Ir. Anik Djuraidah, MS. selaku pembimbing, atas arahan dan bimbingannya selama penulisan tesis ini.
2. Dr. Ir. Hari Wijayanto, MSi. dan Dr. Ir. Aji Hamim Wigena, MSc. yang telah turut memberikan masukan positif pada pelaksanaan ujian tesis.
3. Dr. Ir. Erfiani, MSi. selaku Ketua Program Studi Statistika S2 yang telah turut membantu kelancaran penyelesaian tesis ini.
4. Tanoto Foundation yang telah memberikan beasiswa dan bantuan biaya penelitian sehingga memperlancar semua kegiatan dalam studi dan penyusunan tesis ini.
5. Seluruh keluarga yang turut membantu penulis berupa materi, mendapatkan data, serta memberikan dukungan moral dan doa yang tulus.
6. dr. Syafriadi dari RSUD M Yunus Bengkulu yang telah membantu penulis dalam memperoleh data DBD.
7. Seluruh mahasiswa Program Studi Statistika dan Statistika Terapan baik S2 maupun S3, serta semua yang turut membantu penulis secara fisik, ilmu, maupun dukungan moral dalam penyusunan tesis ini.
Penulis menyadari sepenuhnya bahwa tesis ini masih banyak kekurangan. Masukan-masukan yang membangun sangat penulis harapkan demi perbaikan di masa yang akan datang. Semoga, tesis ini dapat bermanfaat.
Bogor, Mei 2012
Penulis dilahirkan di Sri Bawono (Lampung Tengah) pada tanggal 5 Februari 1983 dari ayah Sudarso dan ibu Sarni. Penulis merupakan putri kelima dari tujuh bersaudara.
DAFTAR ISI
Halaman
DAFTAR TABEL ... xii
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
PENDAHULUAN ... 1
Latar Belakang ... 1
Tujuan Penelitian ... 2
TINJAUAN PUSTAKA ... 3
Penduga Titik dan Selang Kepercayaan ... 3
Data Sirkular ... 4
Ukuran Pemusatan Data Sirkular (Preferred Direction) ... 6
Ukuran Konsentrasi dan Penyebaran ... 7
Sebaran von Mises dan Parameter Konsentrasi ... 8
Metode Bootstrap... 8
Selang Kepercayaan Bootstrap untuk Data Sirkular ... 10
METODOLOGI ... 12
Data ... 12
Metode Analisis ... 13
HASIL DAN PEMBAHASAN ... 17
Selang Kepercayaan Bootstrap bagi arah Rata-rata dan Arah Median ... 17
Selang Kepercayaan Waktu Terjadinya wabah DBD di Provinsi Bengkulu ... 30
SIMPULAN DAN SARAN ... 33
Kesimpulan ... 33
Saran ... 33
DAFTAR PUSTAKA ... 34
DAFTAR GAMBAR
Halaman
1 Hubungan antara koordinat kartesius dan koordinat polar ... 6
2 Selang kepercayaan busur ekor sama, busur simetri, dan busur berbasis kemungkinan ... 11
23 Peringkat dari cakupan selang kepercayaan bagi arah rata-rata... 27
24 Peringkat dari cakupan selang kepercayaan bagi arah median ... 27
25 Peringkat dari lebar selang kepercayaan bagi arah rata-rata ... 28
26 Peringkat dari lebar selang kepercayaan bagi arah median ... 28
27 Peringkat dari keragaman lebar selang kepercayaan bagi arah rata-rata . 29 28 Peringkat dari keragaman lebar selang kepercayaan bagi arah median ... 30
Halaman
1 Pola sebaran data untuk berbagai parameter konsentrasi ... 37
2 Nilai harapan dari arah rata-rata dan arah median 1000 simulasi ... 38
3 Hasil selang kepercayaan bagi arah rata-rata ... 39
4 Hasil selang kepercayaan bagi arah median... 40
5 Konversi bulan ke dalam derajat arah ... 41
6 Interpretasi sudut ke dalam bulan ... 42
7 Progam R untuk konversi sudut ... 41
8 Program R untuk fungsi BES, BSIM, dan BBK bagi arah rata-rata ... 44
9 Program R untuk fungsi BES, BSIM, dan BBK bagi arah median... 46
PENDAHULUAN
Latar Belakang
Statistika adalah ilmu yang mempelajari tentang pendugaan parameter. Selang kepercayaan merupakan penduga parameter yang sangat penting sebagai pelengkap bagi penduga titik. Proses pendugaannya tergantung pada sebaran penarikan contoh yang diturunkan dari sebaran populasi (Moore & McCabe 1998). Pada beberapa kasus, terkadang dijumpai masalah tidak dapat menentukan sebaran penarikan contoh karena sebaran populasi tidak diketahui dan rumitnya menurunkan sebaran penarikan contoh meskipun sebaran populasi diketahui. Masalah tersebut dijumpai baik untuk data linier maupun data sirkular. Untuk mengatasinya, dapat didekati dengan metode bootstrap (Rice 2007).
Metode pendugaan selang kepercayaan bootstrap banyak dikaji oleh para peneliti, diantaranya, Hall (1988a), Hall (1988b), dan Benton & Krishnamoorthy (2002) mengkaji untuk data linier. Pada data sirkular, Fisher & Hall (1989) memperkenalkan metode pendugaan selang kepercayaan bootstrap berdasarkan besaran pivot, yaitu metode busur ekor sama (BES), metode busur simetri (BSIM), dan metode busur berbasis kemungkinan (BBK). Metode ini merupakan pengembangan metode yang diusulkan oleh Ducharme et al. (1985) yaitu hanya menggunakan metode busur simetri.
Hal terpenting yang digunakan untuk mengevaluasi baik buruknya selang kepercayaan adalah lebar selang dan seberapa besar peluang selang tersebut dapat mencakup nilai parameter yang sesungguhnya (Casella & Berger 2002). Lebar selang sangat dipengaruhi oleh keragaman data. Pada data sirkular berdistribusi von Mises (normal sirkular), ukuran keragaman data dapat dilihat dari besarnya parameter konsentrasi ( .
ketiga metode bootstrap dengan menggunakan masih memberikan efek yang kecil terhadap perubahan selang kepercayaan, sehingga disarankan untuk dilakukan studi simulasi yang lebih luas agar diperoleh kesimpulan yang bersifat umum.
Kasus yang akan dikaji dalam penelitian ini adalah kejadian Demam Berdarah Dengue (DBD) di Provinsi Bengkulu. Permasalahan ini menarik untuk dikaji karena DBD merupakan penyakit yang mewabah, terjadi secara nasional, dan dapat menyebabkan kematian. Peubah yang akan dikaji dalam penelitian ini adalah waktu kejadian DBD yang akan diukur melalui waktu (bulan) kedatangan pasien DBD di instalasi rawat inap Rumah Sakit Umum Daerah (RSUD) Bengkulu. Data waktu (bulan) kedatangan pasien DBD ini merupakan data sirkular yang sebaran populasinya masih sulit untuk diidentifikasi, sehingga analisis terhadap data ini dapat didekati dengan metode bootstrap untuk data sirkular.
Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk :
1. Mengkaji pengaruh parameter konsentrasi terhadap dugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median pada metode busur ekor sama, busur simetri, dan busur berbasis kemungkinan.
TINJAUAN PUSTAKA
Penduga Titik dan Selang Kepercayaan
Penduga bagi parameter populasi ada dua jenis, yaitu penduga titik dan penduga selang atau disebut sebagai selang kepercayaan. Penduga titik dari suatu parameter adalah bilangan tunggal yang dapat dianggap sebagai nilai yang paling dekat dengan Penduga titik diperoleh dengan cara memilih statistik yang sesuai dan menghitung nilai statistik tersebut dari data contoh yang diberikan. Statistik yang terpilih disebut sebagai penduga titik dari (Devore 2004).
Statistik adalah suatu fungsi peubah acak yang tidak tergantung pada (Casella & Berger 2001). Standar deviasi dari suatu penduga
(statistik) dinamakan galat baku statistik, yang dinotasikan dengan (Johnson & Bhattacharyya 1992). Jika galat baku dari statistik melibatkan parameter yang tidak diketahui, maka nilai dari galat baku dapat diduga. Dengan mensubstitusikan nilai dugaan parameter ini ke maka dihasilkan dugaan galat baku statistik (Devore 2004). Galat baku dari statistik ini yang dijadikan sebagai dasar dalam menentukan selang kepercayaan.
Selang kepercayaan merupakan penduga parameter yang berupa kisaran nilai. Sebuah selang kepercayaan dengan tingkat kepercayaan sebesar C bagi parameter adalah selang yang dihitung dari data contoh dengan suatu metode tertentu yang memiliki peluang sebesar C untuk menghasilkan selang yang mengandung nilai parameter sesungguhnya (Moore & McCabe 1998). Secara matematis, Casella & Berger (2001) mendefinisikan selang dugaan tertutup bagi parameter yaitu selang tertutup yang ujung bawah dan ujung atasnya masing-masing dan atau untuk
Jika besarnya peluang pencakupan adalah , maka selang ini disebut selang kepercayaan bagi . Misalnya, untuk maka diperoleh selang kepercayaan 95% bagi .
Bentuk umum dari selang kepercayaan adalah (Moore & McCabe 1998) :
Dugaan titik adalah perkiraan untuk parameter yang tidak diketahui. Batas kesalahan (margin of error) menunjukkan seberapa akurat nilai dugaan tersebut dapat dipercaya, berdasarkan variasi dugaan yang diperoleh.
Selanjutnya, Levy & Lemeshow (1999) memaknai selang kepercayaan 95% sebagai berikut : jika kita lakukan pengambilan sampel berukuran dari sebuah populasi yang sama berulangkali, dan untuk setiap sampel dilakukan perhitungan selang kepercayaan, maka 95% dari selang kepercayaan tersebut akan mencakup nilai parameter populasi yang sesungguhnya.
Penentuan selang kepercayaan bagi parameter populasi dapat dilakukan dengan pembalikan statistik uji, menggunakan besaran pivot, pivoting fungsi sebaran kumulatif, dan metode bayes. Baik buruknya selang kepercayaan dugaan yang diperoleh dari berbagai metode tersebut, dapat dievaluasi dengan melihat dua aspek, yaitu lebar selang dan peluang pencakupan. Lebar selang didefinisikan sebagai selisih antara batas atas dan batas bawah selang kepercayaan (Casella & Berger 2001).
Data Sirkular
Data sirkular merupakan salah satu jenis data berarah (directional data). Secara umum, data berarah dibagi menjadi dua, yaitu data berarah dua dimensi dan tiga dimensi. Untuk data berarah dua dimensi disebut data sirkular (circular data) dan untuk tiga dimensi disebut data bola (spherical data) (Jammalamadaka & SenGupta 2001).
5
berupa jam/hari/bulan/tahun) (Mardia & Jupp 2000). Contoh pengamatan yang diukur menggunakan kompas adalah arah angin dan arah migrasi binatang. Sedangkan, contoh pengamatan yang diukur menggunakan jam adalah waktu terjadinya kecelakaan lalu lintas.
Pengamatan sirkular dapat dianggap sebagai titik pada lingkaran dengan satu unit jari-jari, atau satu unit vektor pada garis (Mardia & Jupp 2000). Representasi numerik dari data sirkular adalah sudut yang diukur berdasarkan pemilihan titik awal (starting point) dan arah positif rotasinya yaitu searah atau berlawanan arah dengan jarum jam. Pemilihan titik awal ini bersifat sembarang sehingga besarnya sudut untuk sebuah pengamatan bisa berbeda-beda. Meskipun titik awal dan arah rotasinya bersifat sembarang, analisis statistika sirkular tetap memberikan hasil yang sama. Namun, penentuan titik awal yang bersifat sembarang ini, membuat data sirkular tidak dapat dianalisis menggunakan prosedur analisis statistika untuk data linier karena akan memberikan kesimpulan yang tidak tepat (Jammalamadaka & SenGupta 2001).
Khusus data sirkular bersatuan waktu, harus dikonversikan menjadi data sirkular bersatuan derajat arah. Misalkan, x adalah data hasil pengamatan bersatuan waktu dan adalah nilai maksimumnya. Rumus konversi data sirkular bersatuan waktu menjadi bersatuan derajat arah adalah :
Untuk menganalisis data sirkular ada dua fungsi trigonometri yang digunakan sebagai dasar, yaitu sinus dan cosinus. Kedua fungsi dasar trigonometri ini digunakan untuk membantu menentukan posisi suatu data dan untuk menyelaraskan dua sistem koordinat, yaitu sistem koordinat kartesius (X,Y) dengan titik pusat 0 dan sumbu tegak lurus X dan Y yang melalui pusat, dan sistem koordinat polar (r α) dengan r adalah jarak titik pusat ke keliling lingkaran dan α adalah sudutnya. Misal titik P dengan koordinat polar (r α). Maka koordinat kartesius titik P adalah : , dan . Hal ini diilustrasikan pada Gambar 1.
yaitu vektor yang mempunyai panjang satu, atau r = 1. Setiap arah berhubungan dengan sebuah titik P dalam keliling suatu lingkaran. Kebalikannya, titik ini dalam suatu lingkaran dapat dinyatakan sebagai sudut. Jika titik P terletak dalam keliling lingkaran, perubahan koordinat polar dan koordinat kartesius adalah
(1)
Gambar 1. Hubungan antara koordinat kartesius dan koordinat polar
Ukuran Pemusatan Data Sirkular (Preferred Direction)
Ukuran pemusatan data sirkular yang dikaji dalam penelitian ini adalah arah rata-rata dan arah median. Penjelasannya adalah sebagai berikut.
a. Arah rata-rata (mean direction)
Perhitungan rata-rata yang tepat untuk data sirkular diperoleh dengan memperlakukan data sebagai vektor-vektor unit, kemudian arah rata-rata adalah arah dari vektor resultannya. Misalkan adalah pengamatan-pengamatan sirkular dengan sebagai vektor-vektor unit yang berkaitan. Misalkan dan adalah komponen-komponen kartesius dari . Vektor resultan dari didapatkan dari penjumlahan komponen-komponen vector .
Dengan menggunakan persamaan (1), vektor resultan dari menjadi :
(2)
dan arah rata-rata sirkularnya ( adalah
dengan dan .
Untuk berbagai kemungkinan nilai C dan S, arah rata-rata akan bernilai : 1. jika
7
3. jika
4. jika 5. tidak terdefinisi, jika .
(Fisher 1995; Jammalamadaka & SenGupta 2001; Mardia & Jupp 2000). b. Arah Median (Median Direction)
Arah median contoh diperkenalkan oleh Mardia pada tahun 1972 dan dikenal dengan Mardia median. Untuk sekumpulan sudut atau titik data , arah median didefinisikan sebagai sebuah sudut (atau titik tengah dari dua sudut yang berdekatan jika ukuran contohnya genap) yang memenuhi : (i) setengah dari titik-titik data terletak pada busur dan (ii) mayoritas dari titik-titik data tersebut lebih dekat ke daripada . (iii) Simpangan rata-rata sirkular
dari , yaitu
adalah minimum (Mardia & Jupp 2000; Fisher 1995; Ratanaruamkarn 2009).
Ukuran Konsentrasi dan Penyebaran
Ukuran konsentrasi data dapat dilihat dari panjang rata-rata resultan dan ukuran penyebaran data dapat dilihat dari ragam sirkular. Dari persamaan (2) dapat dihitung panjang dari vektor resultan, yaitu :
; dan panjang rata-rata resultan (mean resultant length), yaitu :
Jika data cenderung mengumpul disekitar rata-ratanya, maka akan bernilai 1. Namun, jika data cenderung menyebar di sekeliling lingkaran maka bernilai 0. Untuk keperluan deskriptif dan inferensia, penggunaan panjang rata-rata resultan lebih baik dari pada ukuran penyebaran data. Namun, untuk tujuan pembandingan dengan data pada garis, terkadang lebih baik menggunakan ragam sirkular sebagai ukuran penyebaran data (Mardia & Jupp 2000), yaitu :
Titik sudut dalam arah yang sama mengindikasikan pemusatan yang besar, nilai R dapat sebesar n. Sebaliknya data yang menyebar merata pada sekeliling lingkaran mengindikasikan tidak adanya pemusatan, R dapat mendekati nilai 0. Artinya, semakin besar ragam sirkular maka semakin besar pula sebaran data dan semakin kecil konsentrasi data terhadap arah rata-ratanya (Jammalamadaka & SenGupta 2001).
Sebaran von Mises dan Parameter Konsentrasi
Sebaran von Mises diperkenalkan oleh von Mises pada Tahun 1918. Parameter pada sebaran ini adalah arah rata-rata ( ) dan parameter konsentrasi ( ). Fungsi kepekatan peluang dari sebaran von Mises adalah :
Parameter konsentrasi menunjukkan seberapa besar data menuju suatu arah tertentu. Parameter konsentrasi dilambangkan dengan . Pendugaan pada sebaran von Mises dilakukan menggunakan metode kemungkinan maksimum. Hasil dugaannya adalah (Fisher 1995) : sebaran data terkonsentrasi pada arah rata-ratanya.
Metode Bootstrap
9
satu alternatif metode untuk menduga sebaran statistik, galat baku statistik, bias, selang kepercayaan, dan beberapa parameter lain selain rata-rata (Efron 1981; Efron & Tibsirani 1993). Efron memberikan dua pendekatan bootstrap, yaitu bootstrap non parametrik dan bootstrap parametrik. Berikut akan dijelaskan bagaimana konsep kedua pendekatan ini dan kapan pendekatan tersebut cocok digunakan.
a. Bootstrap non parametrik
Pada pendekatan bootstrap non parametrik, sebaran peluang populasi tidak diketahui. Metode ini bertujuan untuk memperoleh dugaan parameter dan sebaran populasi. Asumsikan adalah contoh acak dari sebaran peluang populasi F yang tidak diketahui dan adalah parameter yang ingin diduga. Prinsip pembangkitan contoh bootstrap adalah sebagai berikut. Ambil contoh berukuran n secara acak dengan pengembalian dari fungsi sebaran empiris . adalah sebaran diskret yang menentukan peluang untuk stiap pengamatan , untuk . Lakukan sebanyak B kali. Untuk setiap contoh bootstrap dihitung dugaan , sehingga diperoleh gugus data . Sebaran dari B buah dapat digunakan untuk menduga sebaran dari . Nilai rata rata dari B buah adalah penduga bootstrap. Pada umumnya, ukuran B antara 50–200 untuk menduga galat baku , dan paling sedikit 500 untuk menduga selang kepercayaan (Efron & Tibsirani 1993).
b. Bootstrap Parametrik
dapat didekati dengan frekuensi sebaran dari . (Benton & Krishnamoorthy 2002). Efron (1993) memberikan ilustrasi bootstrap parametrik untuk menghitung galat baku dari koefisien korelasi. Bootstrap parametrik cenderung memberikan dugaan yang lebih halus mengenai sebaran dari data dengan ukuran contoh kecil dan untuk parameter yang hanya melibatkan sedikit nilai numerik dari data contoh, misalnya median, nilai minimum, dan nilai maksimum (Otieno 2002).
Selang Kepercayaan Boostrap untuk Data Sirkular
Metode pendugaan selang kepercayaan bootstrap untuk data sirkular pertama kali diusulkan oleh Ducharme (1985) menggunakan metode busur simetri (syimmetric arc). Kemudian, Fisher & Hall (1989) mengembangkannya menjadi tiga metode, yaitu metode busur ekor sama (equal-tailed arc), metode busur simetri (syimmetric arc) dan metode busur berbasis kemungkinan (likelihood based arc).
a. Busur Ekor Sama (Equal-Tailed Arc)
Metode busur ekor sama menggunakan dugaan titik dari ukuran pemusatan (Preferred Direction, PD) sebagai pengamatan tengah. Titik ujung selang kepercayaan didefinisikan sebagai lokasi dimana dari nilai bootstrap terletak antara ujung selang dan PD. Ilustrasi mengenai metode ini dapat dilihat pada Gambar 2a. Metode ini cukup baik untuk mengatasi sebaran miring. Fisher (1995) menyebut metode ini sebagai metode dasar. Prosedur penentuan selang kepercayaan 100% bagi ukuran pemusatan populasi adalah menghitung perbedaan antara ukuran pemusatan dari data asli dan ukuran pemusatan dari contoh bootstrap ke-b, yaitu :
11
, dengan adalah nilai pada posisi ke- dan
adalah nilai pada posisi ke- .
b. Metode Busur Simetri (Symmetric-Arc Method)
Metode busur simetri menggunakan dugaan titik dari ukuran pemusatan sebagai titik tengah interval dan memilih sudut D*, sedemikian rupa sehingga dari nilai-nilai terletak dalam selang. Besar D* di atas dan bawah dugaan titik adalah sama. Ilustrasi untuk metode ini dapat dilihat pada Gambar 2b. Metode ini dirancang untuk menduga selang dengan asumsi sebaran simetri. Fisher (1995) menyebut metode ini sebagai metode sebaran simetris. Prosedur penentuan selang kepercayaan 100% bagi ukuran pemusatan populasi adalah menghitung perbedaan mutlak antara ukuran pemusatan data asli dan contoh bootstrap ke-b, yaitu :
, b = 1, .., B
Kemudian, nilai-nilai diurutkan dari yang terkecil hingga terbesar. Misalkan adalah bilangan bulat yang lebih kecil atau sama dengan dan . Selang kepercayaan 100% untuk ukuran pemusatan populasi adalah .
c. Busur Berbasis Kemungkinan (Likelihood Based Arc)
Metode busur berbasis kemungkinan adalah metode yang paling fleksibel. Melalui metode ini, dimungkinkan untuk menemukan selang sempit yang memenuhi persyaratan dari selang kepercayaan 100%. Caranya adalah dengan memilih busur terpendek yang mengandung dari nilai-nilai . D** adalah lebar selang kepercayaan. Gambaran mengenai metode ini diilustrasikan pada Gambar 2c.
(a) (b) (c)
Data
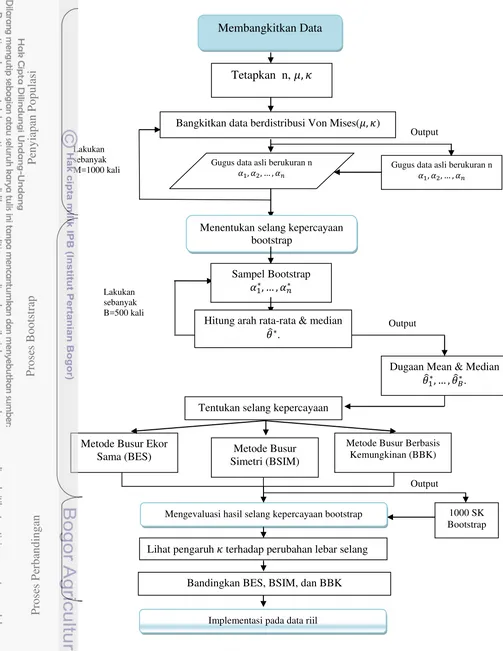
Data yang digunakan dalam penelitian ini ada dua jenis, yaitu data simulasi dan data riil. Data simulasi digunakan untuk melihat pengaruh perubahan parameter konsentrasi ( ) terhadap karakteristik selang kepercayaan. Simulasi dilakukan dengan membangkitkan data berdistribusi von Mises dengan nilai . . . , ukuran contoh N=10, 30, 50, 100, dan arah rata-rata . Untuk melihat konsistensi nilai dugaan, maka pembangkitan data ini akan diulang sebanyak M=1000 kali. Proses pembangkitan dan analisis data dilakukan dengan menggunakan Package CircStat dan Circular dalam R.
Dasar penentuan parameter konsentrasi yang digunakan dalam simulasi adalah dengan mengambil parameter konsentrasi yang mewakili pola keadaan data dari yang sangat menyebar hingga sangat mengumpul. Caranya adalah dengan melihat plot sebaran titik-titik data pada berbagai parameter konsentrasi. Gambar 3 berikut menampilkan ilustrasi pola sebaran titik-titik data di sekeliling lingkaran untuk . dan N=50 yang dianggap cukup menjadi dasar pemilihan parameter konsentrasi dalam simulasi seperti disebutkan di atas. Untuk
yang lain dapat dilihat pada Lampiran 1.
(a) . (b) (c)
Gambar 3. Pola sebaran data dengan = 0.05, 5, dan 50
13
Metode Analisis
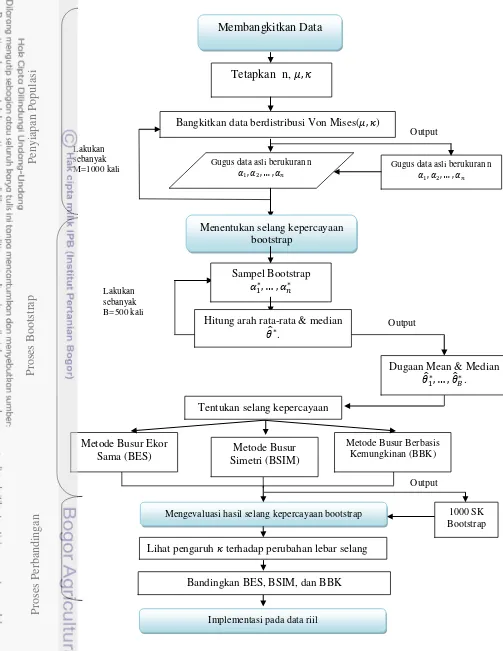
Langkah-langkah analisis data yang dilakukan berkaitan dengan tujuan penelitian terbagi menjadi tiga tahap. Tahap-tahap tersebut, yaitu :
Tahap I : Membangkitkan data.
Langkah-langkah dalam membangkitkan data adalah sebagai berikut : 1. Menetapkan ukuran contoh ( ).
Tahap II : Menentukan selang kepercayaan bootstrap
Dari data yang telah dibangkitkan pada tahap I, selanjutnya dilakukan analisis untuk menduga selang kepercayaan bootstrap bagi arah rata-rata dan arah median. Selang kepercayaan yang akan dibentuk menggunakan α . dan dilakukan pada 1000 contoh dari data simulasi. Adapun langkah-langkah dalam menentukan selang kepercayaannnya adalah sebagai berikut :
1. Pengambilan contoh (sampling)
Pada tahap ini, ambil contoh acak berukuran dari gugus data asli dengan pengembalian. Gugus data hasil sampling tersebut dinotasikan dengan
.
2. Menghitung arah rata-rata dan arah median dugaan
Dari gugus data hasil sampling yang diperoleh pada langkah 1, kemudian dihitung dugaan arah rata-rata dan arah median, selanjutnya dinotasikan dengan .
3. Pengambilan contoh ulang (resampling)
Ulangi langkah 1 dan 2 sebanyak B=500 kali untuk memperoleh dugaan arah rata-rata dan arah median . Dengan demikian, akan diperoleh sebanyak 500 dugaan bagi arah rata-rata dan arah median.
4. Menentukan selang kepercayaan bootstrap.
a. Metode busur ekor sama (BES) Prosedurnya :
1) Menghitung perbedaan ukuran pemusatan (arah rata-rata dan arah median) dari data asli ( dan contoh bootstrap ke-b , dengan rumus :
2) Urutkan nilai-nilai dari yang terkecil sampai yang terbesar.
3) Selang kepercayaan Busur Ekor Sama :
dengan :
= bilangan bulat terbesar
b. Metode busur simetri (BSIM) Prosedurnya :
1) Menghitung perbedaan ukuran pemusatan dari data asli ( dan contoh bootstrap ke-b ( , dengan rumus :
2) Urutkan dari yang terkecil sampai yang terbesar
3) Selang kepercayaan busur simetri adalah :
dengan :
= nilai pada posisi ke-m.
c. Metode busur berbasis kemungkinan (BBK)
15
Tahap III : Mengevaluasi hasil selang dugaan bootstrap
Evaluasi selang kepercayaan didasarkan pada tiga ukuran, yaitu :
a. Cakupan sebenarnya (true coverage), yaitu persentase dari jumlah selang kepercayaan yang dengan benar mencakup arah rata-rata sesungguhnya. Cakupan yang terbaik adalah cakupan yang dekat atau sama dengan cakupan nominal (tingkat kepercayaan).
b. Lebar selang, yang merupakan rata-rata lebar selang dari 1000 simulasi. Selang yang terbaik adalah selang terpendek.
c. Keragaman lebar selang, yang diukur menggunakan ragam sirkular dari 1000 lebar selang hasil simulasi. Semakin kecil nilai dari keragaman lebar selang ini, maka lebar selang yang dihasilkan semakin seragam atau konsisten.
Proses evaluasi ini ada dua tahap, yaitu :
1. Melihat pengaruh perubahan nilai terhadap cakupan dan lebar selang.
2. Membandingkan selang kepercayaan bootstrap dari ketiga metode yang digunakan pada Tahap II.
Prosedur pembandingannya adalah dengan cara memberikan peringkat terhadap ketiga metode pada masing-masing ukuran contoh. Peringkat tertinggi diberi nilai 3, tertinggi kedua diberi nilai 2, dan terendah diberi nilai 1. Kemudian, dihitung rata-rata peringkat dari empat ukuran contoh yang digunakan dalam simulasi ini. Metode yang menempati peringkat tertinggi pada interval tertentu dikatakan metode terbaik.
3. Menarik kesimpulan
Tahap IV : Implementasi terhadap data riil Langkah-langkahnya adalah :
1. Melakukan konversi bulan ke dalam derajat arah. Tabel konversi disajikan pada Lampiran 4.
2. Menentukan selang kepercayaan bootstrap menggunakan metode terbaik yang diperoleh dari Tahap III.
3. Menginterpretasikan batas atas dan batas bawah selang ke dalam bulan. Tabel konversi disajikan pada Lampiran 5.
DAFTAR PUSTAKA
Gambar 4. Diagram alir tahapan penelitian
P
Lihat pengaruh terhadap perubahan lebar selang
HASIL DAN PEMBAHASAN
Sebelum dilakukan pendugaan selang kepercayaan, terlebih dahulu dilihat ketakbiasan dari penduga titik. Caranya adalah dengan menghitung nilai harapan dari arah rata-rata dan arah median 1000 contoh data simulasi. Hasil perhitungan untuk seluruh contoh menunjukkan bahwa nilai harapan dari arah rata-rata dan arah median relatif sama dengan arah rata-rata atau arah median populasi, yaitu (Lampiran 2). Hal ini berarti bahwa, dugaan arah rata-rata dan arah median dari data contoh merupakan penduga tak bias bagi parameter sesungguhnya.
Selang Kepercayaan Bootstrap bagi Arah Rata-rata dan Arah Median
Hasil dugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median secara lengkap disajikan pada Lampiran 3 dan 4. Berikut ini akan dibahas hasil simulasi untuk selang kepercayaan dari metode busur ekor sama, busur simetri, dan busur berbasis kemungkinan, serta evaluasi hasil ketiga metode tersebut.
a. Busur ekor sama (BES)
Cakupan sebenarnya dari selang kepercayaan busur ekor sama bagi arah rata-rata (BES Mean) ditampilkan pada Gambar 5. Gambar tersebut memperlihatkan bahwa untuk semua nilai parameter konsentrasi dan ukuran contoh, cakupan sebenarnya selalu berada di bawah cakupan nominal (tingkat kepercayaan), yaitu 95%. Ukuran contoh kecil (N=10) selalu menghasilkan cakupan selang yang lebih rendah dari yang lain. Pada . , cakupan selang dari semua ukuran contoh terlihat paling rendah dan jauh di bawah tingkat kepercayaan. Cakupan selang BES Mean ini stabil mendekati 95% untuk . Hal ini menunjukkan bahwa, saat datanya menyebar di sekeliling lingkaran, kemampuan selang dalam mencakup arah rata-rata sesungguhnya jauh lebih rendah dari tingkat kepercayaan selang, terlebih lagi jika ukuran contohnya kecil.
kecil juga menghasilkan cakupan yang lebih kecil dari yang lainnya. Hal ini juga mengindikasikan bahwa, data yang menyebar di sekeliling lingkaran akan membuat selang kepercayaan BES Median tidak mampu mencakup arah median sesungguhnya dengan baik.
(a) . s.d (b) s.d Gambar 5. Cakupan selang kepercayaan BES Mean
(a) . s.d (b) s.d Gambar 6. Cakupan selang kepercayaan BES Median
Lebar selang BES Mean akan semakin sempit seiring peningkatan parameter konsentrasi (Gambar 7). Ukuran contoh kecil memberikan lebar selang yang lebih besar dari yang lainnya. Namun, setelah lebar selang dari keempat macam ukuran contoh sudah cenderung sama. Hasil ini menunjukkan bahwa data yang menyebar di sekeliling lingkaran akan membuat selang kepercayaan BES Mean menjadi lebar, dan sebaliknya.
19
selang kepercayaan BES Median akan menjadi lebar saat datanya menyebar di sekeliling lingkaran.
(a) . s.d (b) s.d Gambar 7. Lebar selang kepercayaan BES Mean
(a) . s.d (b) s.d Gambar 8. Lebar selang kepercayaan BES Median
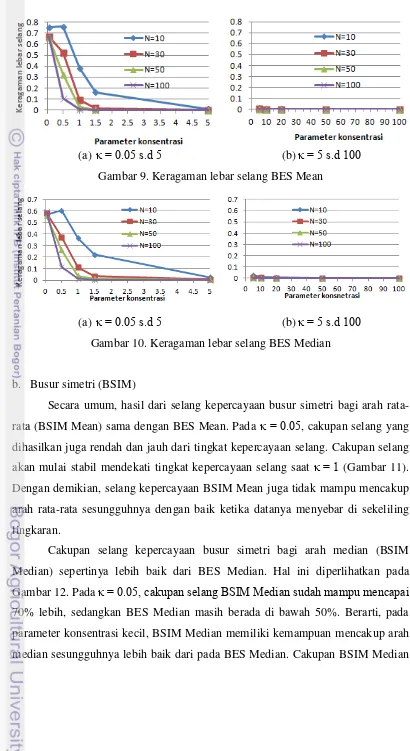
Keragaman lebar selang BES Mean juga akan semakin kecil seiring dengan meningkatnya parameter konsentrasi (Gambar 9). N=10 cenderung memiliki keragaman lebar selang yang lebih besar dari yang lain. Setelah keragaman lebar selang terlihat cenderung sama. Dengan demikian, data yang menyebar akan membuat lebar selang menjadi tidak konsisten. Dengan kata lain, untuk parameter konsentrasi yang kecil, lebar selang BES Mean yang dihasilkan dari 1000 simulasi sangat bervariasi.
(a) . s.d (b) s.d Gambar 9. Keragaman lebar selang BES Mean
(a) . s.d (b) s.d Gambar 10. Keragaman lebar selang BES Median
b. Busur simetri (BSIM)
Secara umum, hasil dari selang kepercayaan busur simetri bagi arah rata-rata (BSIM Mean) sama dengan BES Mean. Pada . , cakupan selang yang dihasilkan juga rendah dan jauh dari tingkat kepercayaan selang. Cakupan selang akan mulai stabil mendekati tingkat kepercayaan selang saat (Gambar 11). Dengan demikian, selang kepercayaan BSIM Mean juga tidak mampu mencakup arah rata-rata sesungguhnya dengan baik ketika datanya menyebar di sekeliling lingkaran.
Cakupan selang kepercayaan busur simetri bagi arah median (BSIM Median) sepertinya lebih baik dari BES Median. Hal ini diperlihatkan pada Gambar 12. Pada . cakupan selang BSIM Median sudah mampu mencapai 70% lebih, sedangkan BES Median masih berada di bawah 50%. Berarti, pada parameter konsentrasi kecil, BSIM Median memiliki kemampuan mencakup arah median sesungguhnya lebih baik dari pada BES Median. Cakupan BSIM Median
21
ini sudah stabil mendekati atau sama dengan % sejak . . Untuk yang lebih besar dijumpai cakupan BES Median dapat mencapai 99%.
(a) . s.d (b) s.d Gambar 11. Cakupan selang BSIM Mean
(a) . s.d (b) s.d Gambar 12. Cakupan selang BSIM Median
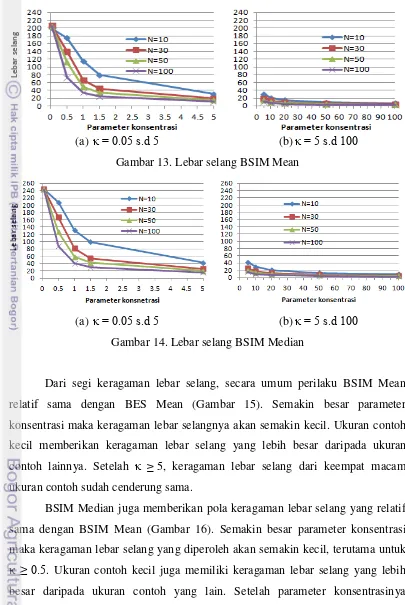
Untuk lebar selang, BSIM Mean juga menunjukkan pola yang sama dengan BES Mean (Gambar 13). Semakin besar parameter konsentrasi maka lebar selang kepercayaan BSIM Mean akan semakin sempit. Ukuran contoh kecil terlihat memberikan lebar selang yang lebih besar dari ukuran contoh lainnya. Lebar selang dari keempat ukuran contoh juga akan mulai sama saat . Hasil ini juga menunjukkan bahwa data yang menyebar akan membuat selang kepercayaan BSIM Mean menjadi lebar.
BES Median dan BSIM Mean, yaitu selang akan semakin lebar ketika datanya menyebar di sekeliling lingkaran.
(a) . s.d (b) s.d Gambar 13. Lebar selang BSIM Mean
(a) . s.d (b) s.d Gambar 14. Lebar selang BSIM Median
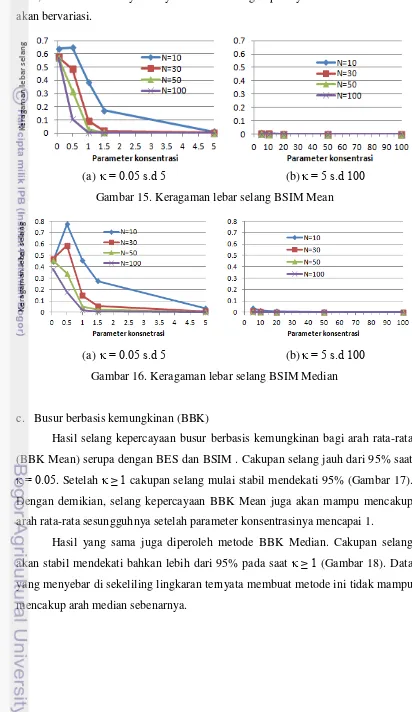
Dari segi keragaman lebar selang, secara umum perilaku BSIM Mean relatif sama dengan BES Mean (Gambar 15). Semakin besar parameter konsentrasi maka keragaman lebar selangnya akan semakin kecil. Ukuran contoh kecil memberikan keragaman lebar selang yang lebih besar daripada ukuran contoh lainnya. Setelah 5, keragaman lebar selang dari keempat macam ukuran contoh sudah cenderung sama.
BSIM Median juga memberikan pola keragaman lebar selang yang relatif sama dengan BSIM Mean (Gambar 16). Semakin besar parameter konsentrasi maka keragaman lebar selang yang diperoleh akan semakin kecil, terutama untuk . . Ukuran contoh kecil juga memiliki keragaman lebar selang yang lebih besar daripada ukuran contoh yang lain. Setelah parameter konsentrasinya mencapai 5, maka keragaman lebar selang dari empat macam ukuran contoh
Le
b
ar
se
lan
g
Le
b
ar
se
lan
23
cenderung sama. Hasil tersebut memberi kesimpulan yang sama dengan metode BES, bahwa saat datanya menyebar maka selang kepercayaan dari 1000 simulasi akan bervariasi.
(a) . s.d (b) s.d Gambar 15. Keragaman lebar selang BSIM Mean
(a) . s.d (b) s.d Gambar 16. Keragaman lebar selang BSIM Median
c. Busur berbasis kemungkinan (BBK)
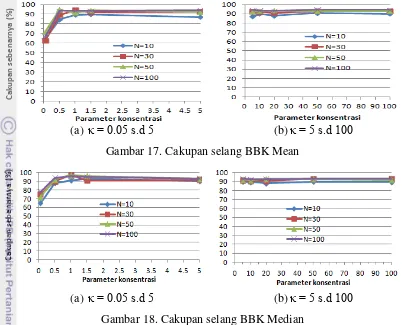
Hasil selang kepercayaan busur berbasis kemungkinan bagi arah rata-rata (BBK Mean) serupa dengan BES dan BSIM . Cakupan selang jauh dari 95% saat . . Setelah cakupan selang mulai stabil mendekati 95% (Gambar 17). Dengan demikian, selang kepercayaan BBK Mean juga akan mampu mencakup arah rata-rata sesungguhnya setelah parameter konsentrasinya mencapai 1.
(a) . s.d (b) s.d Gambar 17. Cakupan selang BBK Mean
(a) . s.d (b) s.d Gambar 18. Cakupan selang BBK Median
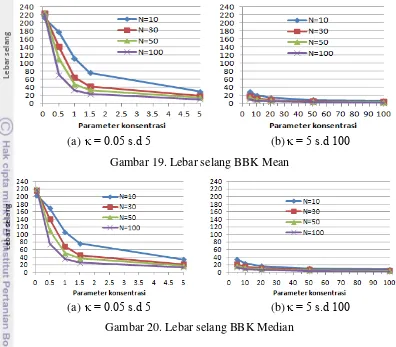
Lebar selang BBK Mean juga akan semakin sempit seiring dengan meningkatnya parameter konsentrasi. N =10 menghasilkan selang yang paling lebar dan N=100 menghasilkan selang yang paling sempit. Pada , keempat ukuran contoh memberikan lebar selang yang cenderung sama (Gambar 19). Hal ini sama dengan selang BES dan BSIM. Sehingga kesimpulan yang sama juga dapat diperoleh metode BBK Mean ini, yaitu selang akan menjadi sempit ketika datanya mengumpul, dan sebaliknya.
25
(a) . s.d (b) s.d Gambar 19. Lebar selang BBK Mean
(a) . s.d (b) s.d Gambar 20. Lebar selang BBK Median
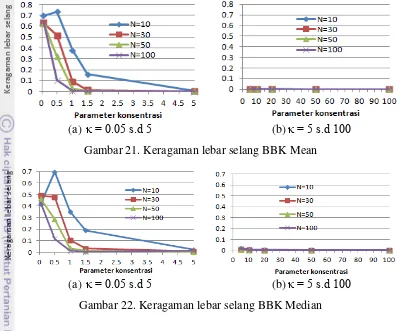
Keragaman lebar selang BBK Mean memiliki perilaku yang sama dengan selang BSIM. Keragaman lebar selang saat 0.05 lebih kecil dari pada saat 0.5. Setelah itu, keragaman akan terus menurun seiring dengan meningkatnya parameter konsentrasi. Pada , keempat macam ukuran contoh sudah memberikan hasil yang cenderung sama (Gambar 21). Hasil ini semakin meyakinkan bahwa data yang menyebar akan membuat selang kepercayaan dari 1000 simulasi menjadi tidak konsisten.
(a) . s.d (b) s.d Gambar 21. Keragaman lebar selang BBK Mean
(a) . s.d (b) s.d Gambar 22. Keragaman lebar selang BBK Median
d. Evaluasi ketiga metode
Dari uraian hasil selang kepercayaan BES, BSIM, dan BBK bagi arah rata-rata dan arah median, secara umum diperoleh kesamaan perilaku selang kepercayaan berdasarkan tiga ukuran. Cakupan selang kepercayaan akan terlihat stabil dan mendekati tingkat kepercayaan 95% saat parameter konsentrasinya lebih dari atau sama dengan 1. Selang kepercayaan dari ketiga metode akan semakin sempit dan sama (konvergen) seiring dengan meningkatnya parameter konsentrasi. Hasil ini sama dengan penelitian Otieno (2002). Kekonvergenan lebar selang dari ketiga metode dijumpai saat parameter konsentrasinya sudah mencapai 20. Artinya, pada data dengan = 20 berapapun ukuran contohnya ketiga metode memberikan lebar yang relatif sama. Keragaman lebar selang memiliki pola yang sama dengan lebar selangnya, yaitu semakin kecil seiring meningkatnya parameter konsentrasi. Ukuran contoh kecil selalu memberikan keragaman lebar selang yang paling besar.
Parameter konsentrasi merupakan ukuran konsentrasi data terhadap arah rata-ratanya (Jammalamadaka & SenGupta 2001; Fisher 1995). Parameter
27
konsentrasi yang kecil menandakan bahwa titik-titik data menyebar di sekeliling lingkaran, dan sebaliknya. Keragaman lebar selang menunjukkan konsistensi lebar selang dari 1000 simulasi. Keragaman yang besar menandakan bahwa lebar selang yang dihasilkan dari 1000 simulasi cenderung beragam atau tidak konsisten, dan sebaliknya. Hasil dugaan selang dari ketiga metode mengindikasikan bahwa, saat datanya menyebar di sekeliling lingkaran selang kepercayaan dari 1000 simulasi akan memiliki lebar yang beragam atau tidak konsisten. Saat datanya mengumpul, berapapun ukuran contohnya lebar selang dari 1000 simulasi akan cenderung seragam atau konsisten.
Hasil perbandingan ketiga metode untuk selang kepercayaan arah rata-rata menunjukkan bahwa pada = 0.05 metode BES memiliki cakupan yang paling baik dan BSIM sama dengan BBK. Pada = 0.5 metode BES sama dengan BSIM memiliki cakupan terbaik. Setelah 1, cakupan selang mulai stabil dan metode BSIM yang memiliki cakupan tertinggi, metode BES tertinggi kedua, dan BBK memiliki cakupan yang paling rendah (Gambar 23). Dengan demikian, saat parameter konsentrasinya kecil maka ketiga metode memberikan cakupan yang tidak stabil.
(a) . s.d (b) s.d Gambar 23. Rata-rata peringkat dari cakupan selang kepercayaan
bagi arah rata-rata
(a) . s.d (b) s.d Gambar 24. Rata-rata peringkat dari cakupan selang kepercayaan
Perbandingan cakupan selang bagi arah median menunjukkan bahwa secara umum metode yang memberikan cakupan terbaik adalah BSIM. Hal ini terlihat dari Gambar 24, bahwa BSIM hanya menempati peringkat kedua saat , selebihnya selalu menempati peringkat tertinggi. Metode terbaik kedua adalah BES karena, setelah 1, metode ini stabil berada pada peringkat kedua dan metode BBK memberikan cakupan yang paling rendah.
(a) . s.d (b) s.d Gambar 25. Rata-rata peringkat dari lebar selang kepercayaan
bagi arah rata-rata
(a) . s.d (b) s.d Gambar 26. Rata-rata peringkat dari lebar selang kepercayaan
bagi arah median
Berdasarkan lebar selang untuk arah rata-rata, pada = 0.05 metode BSIM memberikan selang tersempit dan metode BES memberikan selang terlebar. Pada parameter konsentrasi 0.5, metode BBK paling sempit dan BES paling lebar. Hal tersebut juga mengindikasikan bahwa saat parameter konsentrasinya kecil, lebar selang dari ketiga metode terlihat tidak stabil. Setelah 1, metode BBK stabil memberikan selang tersempit dan BSIM memberikan selang terlebar, sedangkan BES berada ditengah-tengah (Gambar 25).
29
Kemudian, pebandingan keragaman lebar selang bagi arah rata-rata dapat dilihat pada Gambar 27. Gambar tersebut memperlihatkan bahwa pada saat 1, metode BSIM memberikan keragaman lebar selang terkecil, sedangkan BES memberikan keragaman terbesar. Namun, untuk , metode BBK memiliki keragaman terkecil, BSIM memiliki keragaman terbesar, dan BES stabil berada di tengah-tengah. Karena metode BBK memberikan keragaman yang paling kecil untuk 1, maka pada metode tersebut memiliki lebar selang lebih konsisten atau seragam dari yang lainnya. Sehingga, BBK merupakan metode yang terbaik berdasarkan lebar selang karena memiliki lebar tersempit dan keragamaan lebar selang terkecil. Metode terbaik kedua adalah BES dan terakhir adalah BSIM.
(a) . s.d (b) s.d Gambar 27. Rata-rata peringkat dari keragaman lebar selang kepercayaan
bagi arah rata-rata
Perbandingan keragaman lebar selang untuk arah median juga memberikan hasil yang relatif sama dengan arah rata-rata. Pada Gambar 28 tampak bahwa, Ketidakstabilan posisi peringkat dari ketiga metode mengindikasikan bahwa saat parameter konsentrasinya kecil ( < 1), selang kepercayaan yang dihasilkan dari ketiga metode cenderung tidak stabil. Namun, secara umum dapat dikatakan pula bahwa selang kepercayaan bagi arah median yang terbaik dari segi lebar selang adalah metode BBK, karena memberikan selang tersempit dan keragaman lebar selang yang paling kecil. Hal ini sama dengan arah rata-rata.
(a) . s.d (b) s.d Gambar 28. Rata-rata peringkat dari keragaman lebar selang kepercayaan
bagi arah median
Berdasarkan perbandingan-perbandingan sesuai tiga ukuran selang kepercayaan, tidak ada metode yang konsisten selalu menempati peringkat tertinggi, terlebih lagi saat < 1. Oleh karena itu, untuk < 1 penentuan metode terbaik tergantung pada kondisi data dan parameter apa yang akan diduga. Ukuran utama yang dijadikan dasar penentuan kebaikan selang adalah cakupan sebenarnya, karena ini terkait dengan keakuratan dugaan terhadap parameter populasi. Namun, untuk ketiga metode menghasilkan perbedaan angka yang tidak terlalu besar. Sehingga metode terbaik diambil dari metode yang memiliki posisi peringkat konsisten berada di tengah-tengah dari semua ukuran selang. Metode tersebut adalah busur ekor sama.
Selang Kepercayaan Waktu Terjadinya Wabah DBD di Provinsi Bengkulu Gambar 29 merupakan diagram mawar yang menunjukkan gambaran data DBD. Juring yang panjang menghadap sudut tertentu menunjukkan jumlah penderita banyak terdapat pada bulan yang bersesuaian dengan sudut tersebut. Pada tahun 2009 kasus DBD banyak dijumpai pada bulan Januari dan Desember, tahun 2010 pada Januari dan Februari, serta tahun 2011 pada Juni, Juli, dan Desember .
(a) Tahun 2009 (b) Tahun 2010 (c) Tahun 2011 Gambar 29. Diagram mawar data DBD Provinsi Bengkulu
31
Tabel 1. Statistik deskriptif sirkular dan selang kepercayaan data DBD
Ukuran Batas atas selang 51.001o Januari 109.413o Maret 278.801o September Batas bawah
selang 314.119o Oktober 56.436o Januari 225.916o Juli
Arah median 0o Desember 60.047o Februari 240o Agustus
Batas atas selang 59.976o Januari 90.000o Maret 299.966o September Batas bawah
selang 300.024o Oktober 30.093o Januari 180.034o Juni
Parameter
konsentrasi 0.209 - 0.309 - 0.325 -
Ragam sirkular 0.896 - 0.847 - 0.839 -
Pada tahun 2009 terjadi wabah pada bulan Oktober sampai Januari. Tahun 2010 terjadi pada bulan Januari sampai Maret. Sedangkan tahun 2011, terjadi sekitar bulan Juni sampai September. Perbedaan dugaan periode mewabahnya DBD di Provinsi Bengkulu pada tiga tahun terakhir ini dapat disebabkan karena adanya perubahan keadaan mengenai faktor-faktor yang berpengaruh terhadap peningkatan kejadian DBD tersebut pada setiap tahunnya, terutama perubahan iklim.
SIMPULAN DAN SARAN
Simpulan
Pada parameter konsentrasi yang kecil ( , ketiga metode pendugaan selang kepercayaan bootstrap menghasilkan cakupan yang cenderung tidak stabil. Untuk selang kepercayaan bagi arah rata-rata, busur ekor sama memiliki cakupan terbaik, namun bagi arah median, busur simetri yang terbaik. Setelah , ketiga metode memberikan cakupan yang stabil mendekati tingkat kepercayaan. Metode yang terbaik adalah busur simetri.
Lebar selang dari ketiga metode juga tidak stabil pada pada . Untuk selang kepercayaan bagi arah rata rata yang terbaik adalah busur simetri, namun bagi arah median yang terbaik adalah busur ekor sama. Pada 1, ketiga metode memiliki lebar yang stabil. Metode yang terbaik adalah busur berbasis kemungkinan. Secara umum, ketiga metode cenderung memberikan selang yang semakin sempit dan sama (konvergen) seiring dengan meningkatnya parameter konsentrasi. Kekonvergenan lebar selang ini dicapai saat parameter konsentrasinya sekitar 20. Dari segi cakupan dan lebar selang, pada 1 metode terbaik adalah busur ekor sama.
Periode waktu wabah DBD di Provinsi Bengkulu selalu berbeda pada tiga tahun terakhir. Tahun 2009 periodenya adalah Oktober sampai Januari, tahun 2010 adalah Januari sampai Maret, dan tahun 2011 adalah Juni sampai September.
Saran
Amiri S, Rosen DV, Zwanzig. 2008. On the Comparison of Parametric and Nonparametric Boostrap. UUDM report. Sweden : Uppsala University.
Batschelet E. 1981. Circular Statistics in Biology. London : Academic Press. Benton D, Krishnamoorthy K. 2002. Performance of the Parametric Bootstrap
Method in Small Sample Interval Estimates. Adv. & Appl. In Stat, 2 : 269-285
Casella G, Berger RL. 2002. Statistical Inference. California : Duxbury.
Devore JL. 2004. Probability and Statistics for Engenering and the sciences. Sixth edition. Canada : Duxbury.
Ducharme GR, Jhun M, Romano J, dan Truong KN. 1985. Bootstrap Confidence Cones for Directional Data. Biometrika, 72 : 637 – 45.
Efron B. 1979. Another Look at the Jackknife. The Annals of Statistics, 7 : 1 – 26. Efron B, Tibsirani RJ. 1993. An Introduction to The Bootstrap. New York :
Chapman Hall.
Efron B. 1981. Nonparametric Standard Errors and Confidence Intervals. Can. J. Statist, 9 : 589 – 599.
Fisher NI, Hall P. 1989. Bootstrap Confidence Regions for Directional Data. Journal of the American Statistical Association, 84 : 996-1002.
Fisher NI. 1995. Statistical Analysis of Circular Data. Cambridge : Cambridge University Press.
Hall P. 1988a. On Symetric Bootstrap Confidence Intervals. Journal of the Royal Statistical Society. Series B (methodological), 50 : 35 – 45.
Hall P. 1988b. Theoretical Comparison of Bootstrap Confidence Intervals. The Annals of Statistics, 16 : 927 – 953.
Jammalamadaka SR, SenGupta A. 2001. Topics in Circular Statistics. Singapore: World Scientific.
35
Kemenkes. 2010. Demam Berdarah Dengue. Buletin Jendela Epidemiologi, Volume 2. Pusat Data dan Surveilans Epidemiologi Kementrian Kesehatan RI.
Levy PS, Lemeshow S. 1999. Sampling of Populations Methods and Applications. Third Edition. New York : John Wiley & Sons.
Mardia KV, Jupp PE. 2000. Directional Statistics. West Sussex : John Wiley & Sons.
Moore DS, McCabe GP. 1998. Introduction to the Practice of statistics. Third edition. New York : W.H. Freeman and Company.
Otieno BS. 2002. An Alternative Estimate of Preferred Direction for Circular Data. Disertasi. Virginia Polytechnic Institute and State University.
Ratanaruamkarn S. 2009. Central Quasi Median Estimator when the Sample Size is Odd. KKU Science Journal, 37 : 172:183.
37
39
Lampiran 3 Hasil selang kepercayaan bagi arah rata-rata
N Kappa
Cakupan sebenarnya Lebar selang Keragaman selang
Lampiran 4 Hasil selang kepercayaan bagi arah median
N Kappa
Cakupan sebenarnya Lebar selang Keragaman selang
41
Lampiran 5 Konversi bulan ke dalam derajat arah
Bulan Derajat Januari 30 Februari 60
Maret 90
April 120
Mei 150
Juni 180
Juli 210
Lampiran 6 Interpretasi sudut ke dalam bulan
Derajat Bulan
Januari Februari Maret April Mei Juni Juli Agustus September Oktober November
43
Lampiran 7 Progam R untuk konversi sudut
library(CircStats) rangeang<-function(x){
sudut<-ifelse(x< (-pi),x+2*pi,x)
sudut2<-ifelse(sudut>pi,sudut-2*pi,sudut) return(sudut2)
45
Lampiran (lanjutan…)
###BUSUR BERBASIS KEMUNGKINAN## library(CircStats)
BBK<-function(dataasli,alpha,B,p){ databot<-matrix(nrow=B,ncol=p) ratabot<-matrix(nrow=B,ncol=1) set.seed(73)
for(j in 1:B){
databot[j,]<-sample(dataasli,p,replace=T) ratabot[j,]<-circ.mean(databot[j,])
}
rata.sort<-as.matrix(sort(rangeang(ratabot))) lenB<-length(rata.sort)
minang<-matrix(nrow=lenB,ncol=1) for (r in 1:lenB){
minang[r]<-quantile((rata.sort-rata.sort[r])%%(2*pi),1-alpha) }
poslower<-rata.sort[round(minang-min(minang),4)==0] rataasli<-circ.mean(dataasli)
rataasli
rangeang(rataasli)
BB<-rataasli-sort(abs(rangeang(poslower-rataasli)))[1] BA<-BB+min(minang)
lebar<-abs(BA-BB)
47
Lampiran (Lanjutan…)
###BUSUR BERBASIS KEMUNGKINAN### library(CircStats)
library(circular)
MED.LBA.CIR<-function(dataasli,alpha,B,p){ median.asli<-rangeang(medianCircular(dataasli)) databot<-matrix(nrow=B,ncol=p)
median.bot<-matrix(nrow=B,ncol=1) set.seed(73)
for(j in 1:B){
databot[j,]<-sample(dataasli,p,replace=T)
median.bot[j,]<-rangeang(medianCircular(databot[j,])) }
median.sort<-as.matrix(sort(median.bot)) lenB<-length(median.sort)
minang<-matrix(nrow=lenB,ncol=1) for (r in 1:lenB){
minang[r]<-quantile((median.sort-median.sort[r])%%(2*pi),1-alpha) }
poslower<-median.sort[(minang-min(minang))==0]
BB<-median.asli-sort(abs(rangeang((poslower-median.asli))))[1] BA<-BB+min(minang)
lebar<-abs(BA-BB)
ABSTRACT
CICI SUHAENI. Bootstrap Confidence Interval Estimation of Preferred Direction for Circular Data. Under direction of I MADE SUMERTAJAYA and ANIK DJURAIDAH.
The confidence interval is an estimator based on the sampling distribution. When the sampling distribution can not be derived from population distribution, the bootstrap method can be used to estimate it. Three methods used to estimate the bootstrap confidence interval for circular data were equal-tailed arc (ETA), symmetric arc (SYMA), and likelihood-based arc (LBA). In this study, three methods were evaluated through simulation study. The most important criterion to evaluate them were true coverage and interval width. The simulation results indicated in all methods, the interval width shortened when the concentration parameter increased. True coverage approached confidence level when the concentration parameter were one or more. For small concentration parameter, all three methods appeared unstable. Based on the true coverage, SYMA was the best, while in terms the interval width, LBA was the best one. For both criterion could be summarized that ETA is the best result. ETA and SYMA applicated for estimate the period of Dengue Fever outbreaks in Bengkulu. The estimation showed that Dengue Fever outbreaks in 2009 were October through January. In 2010, it were January through March, and in 2011, it were June through September.
Pemusatan Data Sirkular. Dibimbing oleh I MADE SUMERTAJAYA dan ANIK DJURAIDAH.
Data sirkular merupakan salah satu jenis data berarah yang bersifat periodik. Data diukur menggunakan instrumen kompas dan jam. Seperti pada kasus data linier, pada data sirkular juga dapat dijumpai kondisi sulitnya menentukan sebaran penarikan contoh dari sebaran populasi yang tidak diketahui maupun diketahui. Oleh karena itu, pendugaan selang kepercayaan menggunakan resampling bootstrap pada data sirkular menjadi kajian yang menarik dilakukan.
Metode yang telah berkembang untuk pendugaan selang kepercayaan bootstrap pada data sirkular ada tiga, yaitu busur ekor sama (BES), busur simetri (BSIM), dan busur berbasis kemungkinan (BBK). Baik buruknya selang kepercayaan dievaluasi melalui dua kriteria, yaitu lebar selang dan kemampuan selang dalam mencakup parameter sesungguhnya. Selang kepercayaan ini ditentukan oleh keragaman data. Pada data sirkular dengan sebaran von Mises, keragaman data dapat dilihat dari parameter konsentrasi.
Penelitian ini bertujuan untuk mengkaji pengaruh parameter konsentrasi terhadap dugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median pada metode BES, BSIM, dan BBK. Kemudian, menerapkan metode terbaik pada kasus waktu (bulan) kejadian Demam Berdarah Dengue (DBD) di Provinsi Bengkulu.
Data yang digunakan adalah data simulasi dan data riil. Data simulasi diperoleh dari proses pembangkitan melalui sebaran vonMises. Data riil berupa data waktu (bulan) kedatangan pasien DBD di instalasi rawat inap RSUD M Yunus Bengkulu Tahun 2009, 2010, dan 2011. Penelitian dibagi menjadi empat tahap. Tahapan 1 membangkitkan data, Tahapan 2 menentukan selang kepercayaan bootstrap, Tahapan 3 mengevaluasi hasil selang dugaan bootstrap, dan Tahapan 4 implementasi metode terbaik terhadap data riil.
Hasil studi simulasi menunjukkan bahwa pada parameter konsentrasi yang kecil ( , ketiga metode pendugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median menghasilkan cakupan selang yang tidak stabil. Metode yang terbaik untuk selang kepercayaan bagi arah rata-rata adalah BES dan bagi arah median adalah BSIM. Untuk , ketiga metode cenderung memberikan cakupan yang stabil dekat dengan tingkat kepercayaan. Metode yang terbaik adalah BSIM.
Penerapan metode BES dan BSIM terhadap data riil menunjukkan bahwa periode waktu wabah DBD di Provinsi Bengkulu selalu berbeda pada tiga tahun terakhir. Tahun 2009 periodenya adalah Oktober sampai Januari, tahun 2010 adalah Januari sampai Maret, dan tahun 2011 adalah Juni sampai September.
Latar Belakang
Statistika adalah ilmu yang mempelajari tentang pendugaan parameter. Selang kepercayaan merupakan penduga parameter yang sangat penting sebagai pelengkap bagi penduga titik. Proses pendugaannya tergantung pada sebaran penarikan contoh yang diturunkan dari sebaran populasi (Moore & McCabe 1998). Pada beberapa kasus, terkadang dijumpai masalah tidak dapat menentukan sebaran penarikan contoh karena sebaran populasi tidak diketahui dan rumitnya menurunkan sebaran penarikan contoh meskipun sebaran populasi diketahui. Masalah tersebut dijumpai baik untuk data linier maupun data sirkular. Untuk mengatasinya, dapat didekati dengan metode bootstrap (Rice 2007).
Metode pendugaan selang kepercayaan bootstrap banyak dikaji oleh para peneliti, diantaranya, Hall (1988a), Hall (1988b), dan Benton & Krishnamoorthy (2002) mengkaji untuk data linier. Pada data sirkular, Fisher & Hall (1989) memperkenalkan metode pendugaan selang kepercayaan bootstrap berdasarkan besaran pivot, yaitu metode busur ekor sama (BES), metode busur simetri (BSIM), dan metode busur berbasis kemungkinan (BBK). Metode ini merupakan pengembangan metode yang diusulkan oleh Ducharme et al. (1985) yaitu hanya menggunakan metode busur simetri.
Hal terpenting yang digunakan untuk mengevaluasi baik buruknya selang kepercayaan adalah lebar selang dan seberapa besar peluang selang tersebut dapat mencakup nilai parameter yang sesungguhnya (Casella & Berger 2002). Lebar selang sangat dipengaruhi oleh keragaman data. Pada data sirkular berdistribusi von Mises (normal sirkular), ukuran keragaman data dapat dilihat dari besarnya parameter konsentrasi ( .
2
ketiga metode bootstrap dengan menggunakan masih memberikan efek yang kecil terhadap perubahan selang kepercayaan, sehingga disarankan untuk dilakukan studi simulasi yang lebih luas agar diperoleh kesimpulan yang bersifat umum.
Kasus yang akan dikaji dalam penelitian ini adalah kejadian Demam Berdarah Dengue (DBD) di Provinsi Bengkulu. Permasalahan ini menarik untuk dikaji karena DBD merupakan penyakit yang mewabah, terjadi secara nasional, dan dapat menyebabkan kematian. Peubah yang akan dikaji dalam penelitian ini adalah waktu kejadian DBD yang akan diukur melalui waktu (bulan) kedatangan pasien DBD di instalasi rawat inap Rumah Sakit Umum Daerah (RSUD) Bengkulu. Data waktu (bulan) kedatangan pasien DBD ini merupakan data sirkular yang sebaran populasinya masih sulit untuk diidentifikasi, sehingga analisis terhadap data ini dapat didekati dengan metode bootstrap untuk data sirkular.
Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk :
1. Mengkaji pengaruh parameter konsentrasi terhadap dugaan selang kepercayaan bootstrap bagi arah rata-rata dan arah median pada metode busur ekor sama, busur simetri, dan busur berbasis kemungkinan.
Penduga Titik dan Selang Kepercayaan
Penduga bagi parameter populasi ada dua jenis, yaitu penduga titik dan penduga selang atau disebut sebagai selang kepercayaan. Penduga titik dari suatu parameter adalah bilangan tunggal yang dapat dianggap sebagai nilai yang paling dekat dengan Penduga titik diperoleh dengan cara memilih statistik yang sesuai dan menghitung nilai statistik tersebut dari data contoh yang diberikan. Statistik yang terpilih disebut sebagai penduga titik dari (Devore 2004).
Statistik adalah suatu fungsi peubah acak yang tidak tergantung pada (Casella & Berger 2001). Standar deviasi dari suatu penduga
(statistik) dinamakan galat baku statistik, yang dinotasikan dengan (Johnson & Bhattacharyya 1992). Jika galat baku dari statistik melibatkan parameter yang tidak diketahui, maka nilai dari galat baku dapat diduga. Dengan mensubstitusikan nilai dugaan parameter ini ke maka dihasilkan dugaan galat baku statistik (Devore 2004). Galat baku dari statistik ini yang dijadikan sebagai dasar dalam menentukan selang kepercayaan.
Selang kepercayaan merupakan penduga parameter yang berupa kisaran nilai. Sebuah selang kepercayaan dengan tingkat kepercayaan sebesar C bagi parameter adalah selang yang dihitung dari data contoh dengan suatu metode tertentu yang memiliki peluang sebesar C untuk menghasilkan selang yang mengandung nilai parameter sesungguhnya (Moore & McCabe 1998). Secara matematis, Casella & Berger (2001) mendefinisikan selang dugaan tertutup bagi parameter yaitu selang tertutup yang ujung bawah dan ujung atasnya masing-masing dan atau untuk
4
Jika besarnya peluang pencakupan adalah , maka selang ini disebut selang kepercayaan bagi . Misalnya, untuk maka diperoleh selang kepercayaan 95% bagi .
Bentuk umum dari selang kepercayaan adalah (Moore & McCabe 1998) :
Dugaan titik adalah perkiraan untuk parameter yang tidak diketahui. Batas kesalahan (margin of error) menunjukkan seberapa akurat nilai dugaan tersebut dapat dipercaya, berdasarkan variasi dugaan yang diperoleh.
Selanjutnya, Levy & Lemeshow (1999) memaknai selang kepercayaan 95% sebagai berikut : jika kita lakukan pengambilan sampel berukuran dari sebuah populasi yang sama berulangkali, dan untuk setiap sampel dilakukan perhitungan selang kepercayaan, maka 95% dari selang kepercayaan tersebut akan mencakup nilai parameter populasi yang sesungguhnya.
Penentuan selang kepercayaan bagi parameter populasi dapat dilakukan dengan pembalikan statistik uji, menggunakan besaran pivot, pivoting fungsi sebaran kumulatif, dan metode bayes. Baik buruknya selang kepercayaan dugaan yang diperoleh dari berbagai metode tersebut, dapat dievaluasi dengan melihat dua aspek, yaitu lebar selang dan peluang pencakupan. Lebar selang didefinisikan sebagai selisih antara batas atas dan batas bawah selang kepercayaan (Casella & Berger 2001).
Data Sirkular
Data sirkular merupakan salah satu jenis data berarah (directional data). Secara umum, data berarah dibagi menjadi dua, yaitu data berarah dua dimensi dan tiga dimensi. Untuk data berarah dua dimensi disebut data sirkular (circular data) dan untuk tiga dimensi disebut data bola (spherical data) (Jammalamadaka & SenGupta 2001).