Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003). Di bawah bimbingan INDAHWATI dan ANANG KURNIA.
Pendugaan area kecil (small area estimation) sangat dibutuhkan untuk mendapatkan informasi pada suatu area dengan ukuran contoh kecil. Pendugaan langsung yang dilakukan memiliki nilai keragaman yang besar karena ukuran contohnya kecil. Salah satu solusi yang digunakan adalah melakukan pendugaan tidak langsung dengan cara menambahkan peubah-peubah pendukung berupa informasi dari dalam maupun luar area tersebut untuk menduga parameter. Pendugaan tidak langsung pada area kecil dalam penelitian ini diterapkan untuk kasus pendugaan pengeluaran per kapita di Kota Bogor tahun 2003. Salah satu metode yang dapat digunakan dalam kasus tersebut adalah metode empirical Bayes (EB).
(Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003)
ARTA YUNITA
G14103014
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003). Di bawah bimbingan INDAHWATI dan ANANG KURNIA.
Pendugaan area kecil (small area estimation) sangat dibutuhkan untuk mendapatkan informasi pada suatu area dengan ukuran contoh kecil. Pendugaan langsung yang dilakukan memiliki nilai keragaman yang besar karena ukuran contohnya kecil. Salah satu solusi yang digunakan adalah melakukan pendugaan tidak langsung dengan cara menambahkan peubah-peubah pendukung berupa informasi dari dalam maupun luar area tersebut untuk menduga parameter. Pendugaan tidak langsung pada area kecil dalam penelitian ini diterapkan untuk kasus pendugaan pengeluaran per kapita di Kota Bogor tahun 2003. Salah satu metode yang dapat digunakan dalam kasus tersebut adalah metode empirical Bayes (EB).
(Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003)
Arta Yunita
Skripsi
sebagai salah satu syarat memperoleh gelar Sarjana Sains
pada Departemen Statistika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
NRP : G14103014
Menyetujui:
Pembimbing I,
Pembimbing II,
Ir. Indahwati, M.Si
Anang Kurnia, M.Si
NIP.131909223
NIP. 132158749
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Dr. Drh. Hasim, DEA
NIP. 131578806
atas segala rahmat, hidayah serta karunia-Nya sehingga Penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam semoga selalu tercurahkan kepada Rasulullah SAW, keluarga, sahabat, dan umatnya hingga akhir zaman.
Karya ilmiah ini berjudul “Penerapan Metode Empirical Bayes pada Pendugaan Area Kecil (Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003)”. Penelitian ini bertujuan untuk mengkaji metode empirical Bayes pada pendugaan area kecil dan menerapkan metode tersebut untuk menduga pengeluaran per kapita di Kota Bogor tahun 2003.
Terima kasih Penulis ucapkan kepada semua pihak yang telah membantu dalam penyelesaian karya ilmiah ini, terutama kepada:
• Ibu Ir. Indahwati, M.Si dan Bapak Anang Kurnia, M.Si terima kasih atas segala bimbingan, saran, dan kritik sehingga karya ilmiah ini dapat diselesaikan.
• My family: bapak, ibu, adik, serta seluruh keluarga besar yang aku sayangi, terima kasih atas do’a, dukungan, semangat, dan kasih sayang yang selalu diberikan kepada Penulis.
• Seluruh staf pengajar Departemen Statistika FMIPA IPB terima kasih atas pengajaran yang diberikan sehingga penulis dapat menyelesaikan studi dan karya ilmiah ini.
• Seluruh staf pegawai Departemen Statistika FMIPA IPB: Bu Markonah, Bu Sulis, Bu Dedeh, Pak Ian, Pak Sudin, Pak Dur, Pak Herman, Pak Heri, dan Bu Aat yang selalu siap membantu segala keperluan dalam penyelesaian studi dan karya ilmiah ini.
• Myclosed friend Enta, Proe, Dina, Tiwi, dan Cecep terima kasih atas do’a, kebersamaan, dan dukungannya.
• Sahabatku Chichie, Muti, Lala, Mba Dian, Aril, Edo, Rosit, dan Dwi terima kasih untuk semua bantuannya.
• Rekan-rekan Statistika 40 tercinta yang tidak bisa penulis sebutkan satu per satu. Keep contact! • Seluruh kakak kelas dan adik-adik Statistika angkatan 41,42, dan 43.
• Teman-teman GAMAPURI, asrama A1 027 (Wnie, Veni, Anjar dan Wywy) serta teman satu kosan di Citra Islamic 2 dan Pondok Adinda.
• Semua pihak yang telah memberikan dukungan kepada penulis yang tidak dapat disebutkan satu per satu.
Penulis menyadari bahwa banyak kekurangan dalam karya ilmiah ini karena kesempurnaan hanyalah milik Allah SWT. Semoga karya ilmiah ini dapat bermanfaat.
Bogor,
Suhendro dan Ibu Supriyati. Penulis merupakan putri pertama dari dua bersaudara dengan adik bernama Huda Arta Bahri.
Penulis menyelesaikan sekolah dasar di SD Negeri Butuh I pada tahun 1997. Pendidikan selanjutnya ditempuh di SLTP Negeri I Kutoarjo yang diselesaikan pada tahun 2000. Penulis melanjutkan ke SMU Negeri I Purworejo dan lulus tahun 2003. Pada tahun yang sama berhasil masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis memilih jurusan Statistika.
DAFTAR TABEL...viii
DAFTAR LAMPIRAN ...viii
PENDAHULUAN...1
Latar Belakang ...1
Tujuan...1
TINJAUAN PUSTAKA...1
Pengeluaran Per Kapita ...1
Pendugaan Area Kecil ...1
Penduga Sintetik...2
Model Area Kecil ...2
Metode Empirical Bayes...2
Pendekatan Jackknife dalamPendugaan MSE ...3
BAHAN DAN METODE ...3
Bahan...3
Metode...4
HASIL DAN PEMBAHASAN ...4
Eksplorasi Data...4
Pendugaan Langsung...4
Pendugaan Tidak Langsung...5
KESIMPULAN ...7
DAFTAR PUSTAKA ...7
DAFTAR TABEL
Halaman
1. Hasil Pendugaan Beta ...5
2. Pendugaan pengeluaran per kapita (x Rp. 10.000,00) dengan pendugaan langsung dan
pendekatan EB - jackknife beserta nilai RRMSE (%)...5
3. Perbandingan statistik MSE ...6
DAFTAR LAMPIRAN
Halaman
1. Scatterplot, boxplot, dan nilai korelasi peubah-peubah pendukung (xi)...9
2. Pendugaan langsung pengeluaran per kapita (x Rp. 10.000,00) beserta nilai Di...10
PENDAHULUAN
Latar Belakang
Dewasa ini permintaan akan statistik area kecil (small area statistics) semakin meningkat dalam berbagai bidang. Pendugaan area kecil sangat dibutuhkan untuk mendapatkan informasi-informasi pada area kecil, misalnya pada lingkup kabupaten/kota, kecamatan, maupun kelurahan/desa. Informasi tersebut menjadi sangat penting seiring dengan berkembangnya era otonomi daerah di Indonesia karena dapat digunakan sebagai acuan menyusun sistem perencanaan, pemantauan, dan kebijakan daerah lainnya tanpa harus mengeluarkan biaya besar untuk mengumpulkan data sendiri. Metode yang terus dikembangkan untuk menduga statistik area kecil adalah pendugaan area kecil (small area
estimation).
Pendugaan secara langsung (direct
estimation) pada area kecil akan menghasilkan
nilai ragam yang besar jika contoh yang diambil berasal dari data survei yang dirancang untuk skala besar/nasional. Hal ini disebabkan oleh ukuran contoh yang terambil pada area tersebut kecil. Salah satu solusi yang digunakan adalah melakukan pendugaan tidak langsung dengan cara menambahkan peubah-peubah pendukung dalam menduga parameter. Peubah pendukung tersebut berupa informasi dari area lain yang serupa, survei terdahulu pada area yang sama, atau peubah lain yang berhubungan dengan peubah yang ingin diduga.
Evaluasi hasil pendugaan tidak langsung dapat diketahui dengan membandingkan nilai RRMSE (Relative Root Mean Squared Error) pendugaan langsung dengan nilai RRMSE pendugaan tidak langsung. Pendugaan tidak langsung untuk area kecil dalam penelitian ini diterapkan untuk kasus pendugaan pengeluaran per kapita di Kota Bogor tahun 2003. Metode yang digunakan untuk menduga pengeluaran per kapita tersebut adalah metode empirical
Bayes dengan pendekatan jackknife untuk
menghitung MSE.
Tujuan
Tujuan dari penelitian ini adalah:
1.Mengkaji metode empirical Bayes pada pendugaan area kecil.
2.Menerapkan metode empirical Bayes untuk menduga pengeluaran per kapita di Kota Bogor tahun 2003.
TINJAUAN PUSTAKA
Pengeluaran Per Kapita
Pengeluaran per kapita menunjukkan besarnya pengeluaran setiap anggota rumah tangga dalam kurun waktu satu bulan (BPS, 2003). Pengertian rumah tangga yang dimaksud pada definisi di atas yaitu sekelompok orang yang mendiami sebagian atau seluruh bangunan fisik dan biasanya tinggal bersama serta makan dari satu dapur (BPS, 2003). Satu rumah tangga bisa terdiri dari satu, dua, atau lebih kepala keluarga.
Perhitungan pengeluaran per kapita dirumuskan sebagai berikut:
q p y =
dimana;
y = pengeluaran per kapita
p = pengeluaran rumah tangga sebulan q = jumlah anggota rumah tangga
Pendugaan Area Kecil
Pendugaan area kecil saat ini sangat umum digunakan dalam survey sampling, dimana banyak metode analisis data telah dikemukakan dalam beberapa literatur. Area kecil (small area) diartikan sebagai bagian dari wilayah populasi (small domain) baik berdasarkan geografi, ekonomi, sosial budaya, ataupun yang lainnya (Rao, 2003). Suatu daerah disebut
small area jika dalam daerah tersebut jumlah
contoh yang terambil kurang besar untuk mendapatkan nilai pendugaan langsung yang akurat. Nilai pendugaan langsung pada area kecil merupakan penduga tak bias tetapi memiliki ragam yang besar karena diperoleh dari ukuran contoh yang kecil (Ramsini et.al
(2001) dalam Kurnia dan Notodiputro (2006b)).
Metode pendugaan yang dapat digunakan untuk mendapatkan pendugaan area kecil yaitu pendugaan langsung dan pendugaan tidak langsung. Pendugaan tidak langsung (indirect
estimation) dilakukan dengan cara
memanfaatkan informasi peubah lain yang berhubungan dengan parameter yang diamati. Contoh informasi yang dapat digunakan adalah catatan sensus ataupun survei pada area tersebut. Ada beberapa metode pada pendugaan tidak langsung untuk area kecil antara lain EBLUP (Empirical Best Linear Unbiased
Prediction), EB (Empirical Bayes), dan HB
Small area estimation merupakan pendugaan suatu area yang lebih kecil dengan memanfaatkan informasi dari luar area, informasi dari dalam area itu sendiri, dan dari luar survei (Longford, 2005). Pendugaan secara tidak langsung pada small area estimation
mempunyai beberapa keuntungan, yaitu mendapatkan penduga optimal, memperoleh model valid yang berasal dari data contoh, serta dapat menjelaskan berbagai macam model berdasar pada respon alami suatu peubah dan kekomplekan struktur data (Rao, 2003).
Penduga Sintetik
Penduga sintetik merupakan penduga tak bias yang diperoleh dari sebuah survei contoh untuk area yang besar, ketika penduga ini digunakan sebagai penduga untuk sub-area (area yang lebih kecil) dengan mengasumsikan bahwa sub-area tersebut memiliki karakteristik yang sama dengan area besar (Gonzales (1973) dalam Ghosh dan Rao (1994)). Metode ini cocok digunakan untuk semua desain sampling.
Penduga sintetik pada pendugaan area kecil dapat digunakan untuk menduga nilai respon pada sub-area yang tidak disurvei. Penduga sintetik dapat memberikan dugaan dengan memanfaatkan informasi dari area kecil lain yang diasumsikan mirip dengan area kecil yang akan diduga.
Model Area Kecil
Pendugaan area kecil terdiri atas dua jenis model dasar yaitu basic area level model dan
basic unit level model (Rao, 2003).
a. Basic area level (type A) model yaitu model
yang didasarkan pada ketersediaan data pendukung yang hanya ada untuk level area tertentu, misalkan xi = (x1i,…,xpi)T dan
parameter yang akan diduga θi, diasumsikan mempunyai hubungan dengan xi. Data
pendukung tersebut digunakan untuk membangun model: θi = xiT β + bivi ,
i =1,…,m dengan v
(ii) θ
i ~ N(0, σ2v), sebagai
pengaruh acak yang diasumsikan normal. Kesimpulan mengenai θi, dapat diketahui
dengan mengasumsikan bahwa model penduga langsung yi telah tersedia yaitu:
yi = θi + ei , i =1,…,m dengan sampling error ei ~N(0, σ2ei) dan σ2ei diketahui.
Pada akhirnya, kedua model digabungkan dan menghasilkan model gabungan:
yi= xiT β + bivi + ei , i =1,…,m dimana bi
diketahui bernilai positif konstan (diasumsikan bernilai 1).
Model tersebut merupakan bentuk khusus dari model linier campuran (general linear
mixed model) yang terdiri dari pengaruh
tetap (fixed effect) yaitu β dan pengaruh acak
(random effect) yaitu vi (Saei dan Chambers,
2003).
b. Basic unit level (type B) model yaitu suatu
model dimana data-data pendukung yang tersedia bersesuaian secara individu dengan data respon, misal xij = (xij1,...,xijp)T, sehingga
dapat dibuat suatu model regresi tersarang yij = xijTβ + vi + eij; i=1,…,m dan j=1,...,Ni
dengan vi ~N(0, σ2v) dan ei ~N(0, σ2ei).
Penelitian ini menggunakan model basic area
level (type A) karena data pendukungnya hanya
ada untuk level area tertentu yaitu pada level desa.
Metode Empirical Bayes
Metode empirical Bayes (EB) merupakan salah satu pendekatan yang dapat digunakan pada pendugaan area kecil. Hal pertama yang ingin didapatkan pada metode Bayes adalah sebaran posterior untuk parameter yang diamati yang dinotasikan f (θi |yi, β, σ2v), dengan asumsi β dan σ2v diketahui. Sedangkan pada metode
EB, inferensia yang diperoleh berdasar pada dugaan sebaran posterior dari θi dengan memasukkan nilai dugaan β dan σ2v yaitu
f(θi|yi,βˆ,σˆv2).
Model Fay dan Heriot (1979) untuk model
basic area level adalah:
yi= xiTβ+ vi + ei
dimana vi ~N(0, σ2v) dan ei ~N(0, σ2ei), vi dan
ei saling bebas. β dan σ2v tidak diketahui
sedangkan σ2ei diasumsikan diketahui (Kurnia
dan Notodiputro, 2006b).
Misal σ2v dan σ2ei disimbolkan dengan A
dan Di, selanjutnya merupakan penduga
Bayes untuk θ Β
i
θˆ
i, dengan mengikuti model
Bayes:
(i) yi|θi ~N(θi, Di)
i ~ N(xiTβ, A) adalah sebaran prior
untuk θi, i=1,2,...,m.
Model Bayes dijelaskan oleh:
⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = 2 i i i i
i (y )
Di 2 1 exp D 2 1 ) | y ( f θ π
θ dan
⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = 2 ) ( 2 1 exp 2 1 ) ( θ β π θ π T i i i x A A dan
∏
= ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = m 1 i 2 i i i i ii (y )
D 2 1 exp D 2 1 ) A , | , y ( f θ π β θ ⎟ ⎠ ⎞ ⎜ ⎝
⎛− − 2
) ( 2 1 exp 2
1 θ β
π T i i x A A
untuk yi = (y1, y2,...,ym)T dan θi = (θ1,θ2,...,θm)T.
Lihat dua fungsi eksponensial tanpa faktor (-1/2) dari f(yi, θi |β, A),
2 2 ) ( 1 ) (
1 θ θ Tβ i i i i i x A y
D − + −
) ) ( 2 ( 1 ) 2 (
1 2 θ θ2 θ2 θ β Tβ 2
i T i i i i i i i i x x A y y
D − + + − +
= * i i T i i i 2 i i a A x D y 2 A 1 D 1 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β θ * i i T i i i i T i i i i T i i i i 2 i i a A 1 D 1 A x D y A 1 D 1 A x D y A 1 D 1 A x D y 2 A 1 D 1 + ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + × ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = β β β θ θ * i 2 i T i i i i i a A 1 D 1 A x D y A 1 D 1 + ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β
dengan ai* adalah konstanta dan bebas dari θi.
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + Ν −1 1 1 , ~ ) , , | ( A D D A x D Ay A y i i T i i i i i β β θ
(
)
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + + Ν i i T i i i T i D A AD β x y D A Α β x , ~ ) A , , y | (θi i βBerdasarkan formula tersebut diperoleh suatu penduga:
Β
i
θ
ˆ
= E (θi | yi, β, A) = xiTβ+ (1 – BBi)(yi - xi
Tβ
), dengan Bi = Di / (A + Di)
MSE(θˆiΒ )= Var (θi | yi, β, A) = ADi / (A + Di ) Parameter A pada formula diatas dapat diduga dengan metode momen, minimum variance quadratic unbiased estimation
(MIVQUE), maximum likelihood (ML), atau
restricted/residual maximum likelihood
(REML). Sedangkan parameter β dapat diduga dengan metode momen ataupun weighted least
square (WLS).
Jika A dan β diduga, maka akan diperoleh suatu penduga empirical Bayes:
(
)
(
β)
β
θˆ ˆ 1 ˆ T ˆ
i i i i
i = x + −Β y −x
Τ
ΕΒ ,
dengan Βˆi =Di/(Αˆ+Di)
Berdasarkan metode Bayes, diperoleh: MSE(θˆiΕΒ) = Var (θi |yi,βˆ ˆ,Α) =
(
)
i i/Aˆ D
D Aˆ +
Penduga MSE tersebut menjadi bersifat
underestimate karena adanya pendugaan pada
nilai A dan β. Hal tersebut dapat dikoreksi dengan menggunakan pendekatan jackknife
(Jiang, Lahiri, dan Wan, 2002) maupun dengan pendekatan bootstrap (Butar dan Lahiri (2003) dalam Rao (2003)). Penelitian ini menggunakan metode jackknife untuk mengoreksi MSE tersebut.
Pendekatan Jackknife dalam Pendugaan MSE( ΕΒ)
i
θˆ
Pendekatan jackknife merupakan salah satu metode yang sering digunakan dalam survei karena konsepnya yang sederhana (Jiang, Lahiri, dan Wan, 2002). Metode ini diperkenalkan oleh Tukey (1958) dan berkembang menjadi suatu metode yang dapat mengoreksi bias suatu penduga. Prosedur yang dilakukan yaitu dengan menghapus observasi ke-i untuk i = 1,2,...,m dan selanjutnya melakukan pendugaan parameter.
Small area estimation menerapkan metode
jackknife untuk mengoreksi pendugaan MSE
akibat adanya pendugaan β dan A, dengan: MSE( Β) = AD
i
θˆ i / (A + Di ) = g1i(A) dimana A
diduga oleh s2v (Kurnia dan Notodiputro,
2006a). Tahapan-tahapan untuk menghitung MSEJ(θˆiΕΒ) adalah sebagai berikut:
1.Hitung nilai h1i dengan rumus:
( )
∑
[
(
) (
]
= − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = m 1 u 2 v i 1 2 ) u ( v i 1 2 v i 1 i1 g s g s
m 1 m s g h
)
dimana g1i(s2v(-u)) diperoleh dengan
menghapus pengamatan ke-u pada himpunan data g1i(s2v).
2.Hitung nilai h2i dengan rumus:
( ) ( )
[
]
21 ) (
2 ˆ ˆ
1
∑
= ΕΒ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = m u EB i u i i m mh θ θ
dimana ( ) diperoleh dengan menghapus
pengamatan ke-u pada himpunan data .
( ) ΕΒ −u i θˆ ΕΒ i θˆ
3.Hitung nilai MSE: MSEJ(θˆiΕΒ) = h1i + h2i
BAHAN DAN METODE
Bahan
Data yang digunakan dalam penelitian ini adalah data SUSENAS 2003 dengan informasi data berbasis rumah tangga serta PODES 2003 sebagai sumber data peubah pendukung .
Peubah respon yang menjadi perhatian dalam penelitian ini adalah pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor. Peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita yaitu,
x1 = persentase keluarga prasejahtera dan
sejahtera 1
x2 = persentase keluarga pengguna listrik
PLN
x3 = persentase surat miskin yang
Metode
Tahapan-tahapan pada penelitian ini adalah: 1.Memilih peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita berdasarkan eksplorasi data serta penelitian-penelitian sebelumnya.
2.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa secara langsung (direct estimation).
3.Melakukan pendugaan A dan β dengan metode momen.
4.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa dengan metode empirical Bayes (θˆiΕΒ). 5.Menghitung MSEJ( ) dengan konsep
jackknife menggunakan proc IML pada SAS
9.1.
ΕΒ
i
θˆ
6.Membandingkan nilai RRMSE pendugaan langsung dan nilai RRMSEJ( ), dengan
perhitungan RRMSE sebagai berikut: ΕΒ
i
θˆ
( )
( )
100%ˆ ˆ MSE ˆ
RRMSE
i i
i = ×
θ θ θ
Software yang digunakan adalah Minitab
14, Microsoft Excell dan SAS 9.1.
HASIL DAN PEMBAHASAN
Eksplorasi Data
Eksplorasi untuk masing-masing peubah dilakukan dengan menggunakan scatterplot,
boxplot, dan nilai korelasi Pearson yang tersaji
pada Lampiran 1. Scatterplot data menunjukkan bahwa desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga pengguna listrik dan jumlah penduduk yang besar pula. Selain itu, desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga prasejahtera dan sejahtera 1 serta persentase surat miskin yang dikeluarkan desa kecil. Nilai korelasi Pearson yang dihasilkan juga sesuai dengan hasil scatterplot.
Boxplot digunakan untuk mengetahui
ukuran pemusatan data. Boxplot untuk peubah x1, x2, dan x4 menunjukkan bahwa tidak ada
data yang jauh dari kumpulan data, sedangkan pada peubah x3 ada satu data yang agak jauh
dari kumpulan data.
Berdasarkan eksplorasi data yang telah dilakukan, terlihat bahwa hasilnya sesuai dengan logika. Peubah tersebut juga digunakan dalam penelitian sebelumnya pada skripsi
(Dewi, 2006). Berdasar alasan-alasan di atas, peubah x1, x2, x3, dan x4 cukup sesuai
digunakan untuk menggambarkan pengeluaran per kapita rumah tangga pada beberapa desa di Kota Bogor.
Pendugaan Langsung
Hasil yang didapatkan dari pendugaan langsung pengeluaran per kapita yaitu besarnya pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor dan nilai simpangan bakunya. Jumlah desa/kelurahan yang diamati adalah 34 desa/kelurahan yang ada di Kota Bogor.
Nilai ragam sampling error (Di) yang
menjadi perhatian diduga oleh si2/ni yang
merupakan rasio antara ragam di dalam area dengan banyaknya contoh. Nilai Di dapat
dihitung dari hasil pendugaan langsung. Hasil pendugaan langsung dan nilai ragam sampling
error (Di) dapat dilihat pada Lampiran 2.
Pendugaan langsung pengeluaran per kapita rumah tangga pada beberapa kelurahan/desa di Kota Bogor dilakukan berdasarkan data survei dengan objek survei sebanyak 16 rumah tangga untuk masing-masing desa, kecuali untuk desa Sukadamai sebesar 15 rumah tangga. Jumlah tersebut termasuk kecil untuk merepresentasikan seluruh rumah tangga pada masing-masing desa, sehingga memberikan hasil dugaan dengan ragam yang besar.
Penelitian sebelumnya (Dewi, 2006) menggunakan prosedur proc tabulate pada SAS 9.1 untuk menghitung pengeluaran per kapita, menggunakan lima peubah pendukung, dan menggunakan metode REML untuk menduga parameter A dan β. Perbedaan penelitian ini dengan penelitian tersebut adalah perhitungan pengeluaran per kapita menggunakan rumus sebagai berikut:
16 ,..., 2 , 1 j ; q p y
j
j =
=
∑
∑
dimana;
y = pengeluaran per kapita suatu desa
∑
p
j= jumlah pengeluaran seluruh rumah tangga contoh selama sebulan∑
q
j= jumlah seluruh anggota rumah tangga contohPenelitian ini hanya menggunakan empat peubah pendukung, menggunakan metode momen untuk menduga parameter A dan β, dan menambahkan pendugaan pengeluaran per kapita untuk desa-desa di Kota Bogor yang tidak disurvei.
Pendugaan Tidak Langsung Nilai dugaan beta yang diperoleh tidak bertentangan dengan hasil eksplorasi. Tanda positif (+) dan negatif (-) pada dugaan koefisien regresi sama dengan tanda pada nilai korelasi Pearson.
Nilai dugaan ragam pengaruh acak (keragaman antar desa) yang diperoleh dengan metode momen yaitu =100.6987, sedangkan nilai dugaan beta ( ) tersaji pada Tabel 1.
Αˆ
βˆ
Tabel 1. Hasil Pendugaan Beta
xi Beta Ragam Beta Duga
x0 -1.6806 2.57072
x1 -0.3473 5.59824
x2 0.3290 2.04967
x3 -0.2830 40.18948
x4 0.0015 0.00004
Pendugaan tidak langsung pada area kecil dalam penelitian ini menggunakan metode
empirical Bayes dengan pendekatan jackknife.
Software yang digunakan adalah SAS 9.1
dengan prosedur proc IML. Hasil perbandingan pendugaan langsung dan tidak langsung pada pengeluaran per kapita beberapa desa di Kota Bogor tersaji pada Tabel 2.
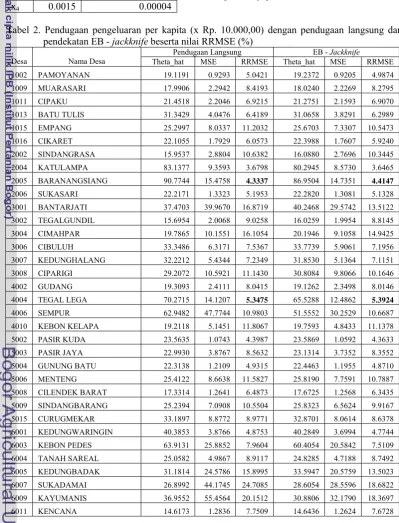
Tabel 2. Pendugaan pengeluaran per kapita (x Rp. 10.000,00) dengan pendugaan langsung dan pendekatan EB - jackknife beserta nilai RRMSE (%)
Pendugaan Langsung EB - Jackknife
Pengeluaran per kapita rumah tangga untuk masing-masing desa dengan pendugaan tidak langsung tidak berbeda jauh nilainya dengan hasil pendugaan langsung. Ada beberapa desa yang mempunyai nilai dugaan pengeluaran per kapita sangat besar dibanding desa yang lain yaitu Katulampa, Baranangsiang, Tegal Lega, Sempur, dan Kebon Pedes. Desa-desa tersebut merupakan desa dengan sumber utama penghasilan penduduknya adalah industri, perdagangan, dan jasa. Sebagian besar penduduknya juga sudah berlangganan telepon, menggunakan bahan bakar gas untuk memasak, dan sumber air untuk minum/memasak bersumber dari PAM/air kemasan dan sumur. Beberapa desa letaknya dekat dengan pusat kota, mempunyai perguruan tinggi/akademi, dan fasilitas pendidikannya cukup memadai. Berdasarkan pada karakteristik-karakteristik tersebut, desa-desa dengan nilai dugaan pengeluaran per kapita yang besar dapat digolongkan sebagai desa yang cukup maju dibandingkan desa-desa yang lain.
Nilai MSE ( ) yang diperoleh dengan pendekatan jackknife sangat beragam dengan jangkauan nilai yang cukup besar. Perbandingan nilai MSE pendugaan langsung dan MSE EB-jackknife terdapat pada Tabel 2.
Boxplot perbandingan nilai MSE dari hasil
pendugaan langsung (MSE_n) dan MSE
EB-jackknife (MSE_j) tersaji pada Gambar 1.
ΕΒ
i
θˆ
D
a
ta
MSE_j MSE_n
60 50 40 30 20 10 0
Boxplot
Gambar 1. Boxplot nilai MSEJ(θˆiΕΒ)
Semua nilai MSE untuk metode empirical
Bayes lebih kecil daripada nilai MSE pada
pendugaan langsung. Bahkan terdapat beberapa desa dengan nilai MSE EB-jackknife jauh lebih kecil dari nilai MSE pendugaan langsung. Beberapa desa masih memiliki nilai MSEJ( ) yang cukup besar, di atas 20, yaitu
desa Bantarjati, Sempur, Kebon Pedes, Kedungbadak, Sukadamai, dan Kayumanis. Hal ini terjadi karena nilai ragam sampling
error (D
ΕΒ
i
θˆ
i) pada desa-desa tersebut juga besar.
Perbandingan beberapa statistik untuk MSE dari hasil pendugaan langsung dan MSE
EB-jackknife terdapat pada Tabel 3.
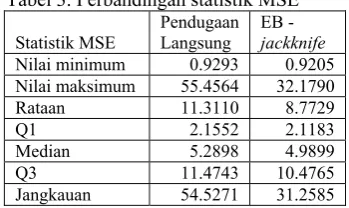
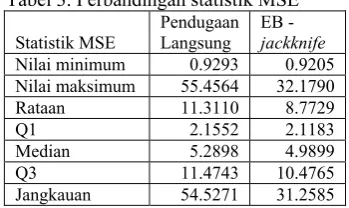
Tabel 3. Perbandingan statistik MSE
Statistik MSE
Pendugaan Langsung
EB -
jackknife
Nilai minimum 0.9293 0.9205 Nilai maksimum 55.4564 32.1790
Rataan 11.3110 8.7729
Q1 2.1552 2.1183
Median 5.2898 4.9899
Q3 11.4743 10.4765
Jangkauan 54.5271 31.2585
Evaluasi hasil pendugaan langsung dan tidak langsung dapat diketahui dengan membandingkan nilai RRMSE keduanya. Nilai RRMSE untuk metode EB-jackknife secara umum lebih kecil daripada nilai RRMSE pada pendugaan langsung, kecuali untuk desa/kelurahan Baranangsiang dan Tegal Lega. Hal ini menunjukkan bahwa pendugaan tidak langsung menggunakan metode EB-jackknife
dapat memperbaiki hasil pendugaan langsung. Hasil tersebut juga memperlihatkan bahwa
small area estimation baik digunakan untuk
pendugaan parameter pada level desa/kelurahan yang memiliki ukuran contoh kecil (15 dan 16 rumah tangga) dengan nilai keragaman antar desa yang besar.
Ada beberapa desa di Kota Bogor yang tidak disurvei pada SUSENAS 2003. Konsep penduga sintetik dapat digunakan untuk menduga pengeluaran per kapita desa-desa yang tidak disurvei tersebut, dengan asumsi perilaku antar desa di Kota Bogor sama (nilai
sama). Nilai harapan dari model small area adalah x
βˆ
iTβ, sehingga pengeluaran per kapita
dihitung dengan rumus:
β
ˆ
x
yˆ
Ti
i
=
Sedangkan rumus pendugaan MSE adalah:
( )
( )
(
pi4
0 p
2 pi T
i
i Var x ˆ x Var ˆ
yˆ
MSE β
∑
β= =
=
)
Hasil pendugaan pengeluaran per kapita untuk desa-desa yang tidak disurvei terdapat pada Lampiran 3.
Kajian lebih lanjut diperlukan untuk penyelesaian pendugaan area kecil dengan berbagai metode terutama dalam penerapannya pada data BPS. Pemilihan peubah pendukung pada pendugaan tidak langsung sangat penting untuk mendapatkan model yang sesuai. Peubah pendukung yang dipilih sebaiknya benar-benar berkaitan dengan peubah respon, sesuai dengan logika yang telah ada dan dapat menggambarkan peubah respon dengan baik.
KESIMPULAN
Jiang, J., Lahiri, P., dan Wan. S. M. 2002. A Unified Jackknife Theory, Annals of Statistics, 30.Pendugaan tidak langsung pada area kecil menggunakan metode empirical Bayes dengan pendekatan jackknife memiliki presisi yang baik dalam menduga pengeluaran per kapita rumah tangga di Kota Bogor. Pendugaan tidak langsung tersebut mampu memperbaiki nilai RRMSE pendugaan langsung meskipun kondisi datanya memiliki ragam sampling
error yang heterogen dan keragaman antar desa
yang besar. Namun demikian, masih ada nilai RRMSE pendugaan tidak langsung yang lebih besar dari nilai RRMSE pendugaan langsung.
Kurnia, A. dan Notodiputro, K.A. 2006a. Penggunaan Metode Jackknife dalam Pendugaan Area Kecil. Makalah disampaikan pada Seminar Nasional Matematika. UNPAD Bandung, 22 April 2006.
Kurnia, A. dan Notodiputro, K.A. 2006b. EB-EBLUP MSE Estimator on Small Area Estimation with Application to BPS Data. Paper presented in International Conference on Mathematical Sciences 1. Bandung 19-21 June 2006.
DAFTAR PUSTAKA
Longford, N. T. 2005. Missing Data and Small Area Estimation : Modern Analytical
Equipment for the Survey Statistician. New
York : Springer Science + Business Media, Inc.
Badan Pusat Statistik. 2003.http://www.bps. go.id/publikasi/2003[ Agustus 15, 2007]
Dewi, L. 2006. Penerapan Metode Empirical Bayes pada Model Small Area Estimation dalam Pendugaan Pengeluaran Per Kapita
di Kota Bogor [skripsi]. Bogor: Fakultas
Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Rao, J. N. K. 2003. Small Area Estimation. New Jersey: John Willey & Sons, Inc.
Saei, A. dan Chambers. 2003. Small Area Estimation : A Review of Methods Based on the application of Mixed Models. S3RI Methodologi Working Paper M03/16. University of Southampton, UK.
Lampiran 1. Scatterplot, boxplot, dan nilai korelasi peubah-peubah pendukung (xi)
p
e
n
g
e
lu
a
ra
n
p
e
r
k
a
p
it
a
60 45 30 15
0 20 40 60 80 100
1000000
800000
600000
400000
200000
20 15 10
5 0
1000000
800000
600000
400000
200000
25000 20000
15000 10000
5000
x1 x2
x3 x4
Scatterplot
60
45
30
15
0
100
80
60
40
20
20
15
10
5
0
25000
20000
15000
10000
5000
x1 x2
x3 x4
Boxplot
Korelasi xi dengan pengeluaran per kapita: rx1 = -0.264
Lampiran 2. Pendugaan langsung pengeluaran per kapita (x Rp. 10.000,00) beserta nilai Di
Desa Nama Desa N Pengeluaran
per kapita StDev Di
1002 PAMOYANAN 16 19.1191 3.8561 0.9293
1009 MUARASARI 16 17.9906 6.0587 2.2942
1011 CIPAKU 16 21.4518 5.9392 2.2046
1013 BATU TULIS 16 31.3429 8.0474 4.0476
1015 EMPANG 16 25.2997 11.3375 8.0337
1016 CIKARET 16 22.1055 5.3560 1.7929
2002 SINDANGRASA 16 15.9537 6.7887 2.8804
2004 KATULAMPA 16 83.1377 12.2372 9.3593
2005 BARANANGSIANG 16 90.7744 15.7357 15.4758
2006 SUKASARI 16 22.2171 4.6170 1.3323
3001 BANTARJATI 16 37.4703 25.2878 39.9670
3002 TEGALGUNDIL 16 15.6954 5.6665 2.0068
3004 CIMAHPAR 16 19.7865 12.7468 10.1551
3006 CIBULUH 16 33.3486 10.0535 6.3171
3007 KEDUNGHALANG 16 32.2212 9.3247 5.4344
3008 CIPARIGI 16 29.2072 13.0182 10.5921
4002 GUDANG 16 19.3093 6.2110 2.4111
4004 TEGAL LEGA 16 70.2715 15.0310 14.1207
4006 SEMPUR 16 62.9482 27.6476 47.7744
4010 KEBON KELAPA 16 19.2118 9.0731 5.1451
5002 PASIR KUDA 16 23.5635 4.1460 1.0743
5003 PASIR JAYA 16 22.9930 7.8757 3.8767
5004 GUNUNG BATU 16 22.3138 4.4016 1.2109
5006 MENTENG 16 25.4122 11.7737 8.6638
5008 CILENDEK BARAT 16 17.3314 4.4973 1.2641 5009 SINDANGBARANG 16 25.2394 10.6514 7.0908
5015 CURUGMEKAR 16 33.1897 11.9179 8.8772
6001 KEDUNGWARINGIN 16 40.3853 7.8757 3.8766 6003 KEBON PEDES 16 63.9131 20.3510 25.8852
6004 TANAH SAREAL 16 25.0582 8.9324 4.9867
6005 KEDUNGBADAK 16 31.1814 19.8307 24.5786
6007 SUKADAMAI 15 26.8992 25.7414 44.1745
6009 KAYUMANIS 16 36.9552 29.7876 55.4564
Lampiran 3. Pendugaan pengeluaran per kapita (x Rp. 10.000,00) untuk desa yang tidak disurvei beserta nilai RRMSE (%)
Nama Desa
Pengeluaran
per Kapita MSE RRMSE
MULYAHARJA 31.9639 2.7144 5.1544
RANGGAMEKAR 33.4561 3.0821 5.2475
GENTENG 22.1764 3.4638 8.3924
BOJONGKERTA 29.0968 2.7861 5.7366
HARJASARI 33.4401 2.5359 4.7621
PAKUAN 19.3847 4.2761 10.6680
LAWANG GINTUNG 27.6699 1.0697 3.7378
BONDONGAN 33.6287 3.3373 5.4323
SINDANG SARI 29.4229 3.2154 6.0944
TAJUR 28.0761 2.5875 5.7293
TANAH BARU 45.8028 3.2873 3.9585
CILUAR 18.3914 1.9703 7.6322
PALEDANG 34.1114 2.3757 4.5185
BABAKAN PASAR 23.0592 2.9059 7.3925
BABAKAN 26.5659 1.6324 4.8093
PABATON 23.3994 1.8963 5.8850
CIBOGOR 25.6134 1.7711 5.1958
PANARAGAN 14.6340 2.6196 11.0599
CIWARINGIN 36.4841 2.1587 4.0271
PASIR MULYA 22.3987 2.1103 6.4856
LOJI 29.8252 3.2767 6.0692
CILENDEK TIMUR 26.6234 3.5175 7.0446
MARGAJAYA 30.3393 2.4968 5.2081
BALUMBANG JAYA 26.0864 2.9556 6.5904
BUBULAK 22.2129 1.5797 5.6582
SEMPLAK 17.5101 4.5532 12.1860
CURUG 29.7435 2.8444 5.6702
KEDUNGJAYA 30.4747 2.8173 5.5078
SUKARESMI 30.8295 3.1219 5.7312
CIBADAK 37.3416 3.2635 4.8378
(Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor Tahun 2003)
ARTA YUNITA
G14103014
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PENDAHULUAN
Latar Belakang
Dewasa ini permintaan akan statistik area kecil (small area statistics) semakin meningkat dalam berbagai bidang. Pendugaan area kecil sangat dibutuhkan untuk mendapatkan informasi-informasi pada area kecil, misalnya pada lingkup kabupaten/kota, kecamatan, maupun kelurahan/desa. Informasi tersebut menjadi sangat penting seiring dengan berkembangnya era otonomi daerah di Indonesia karena dapat digunakan sebagai acuan menyusun sistem perencanaan, pemantauan, dan kebijakan daerah lainnya tanpa harus mengeluarkan biaya besar untuk mengumpulkan data sendiri. Metode yang terus dikembangkan untuk menduga statistik area kecil adalah pendugaan area kecil (small area
estimation).
Pendugaan secara langsung (direct
estimation) pada area kecil akan menghasilkan
nilai ragam yang besar jika contoh yang diambil berasal dari data survei yang dirancang untuk skala besar/nasional. Hal ini disebabkan oleh ukuran contoh yang terambil pada area tersebut kecil. Salah satu solusi yang digunakan adalah melakukan pendugaan tidak langsung dengan cara menambahkan peubah-peubah pendukung dalam menduga parameter. Peubah pendukung tersebut berupa informasi dari area lain yang serupa, survei terdahulu pada area yang sama, atau peubah lain yang berhubungan dengan peubah yang ingin diduga.
Evaluasi hasil pendugaan tidak langsung dapat diketahui dengan membandingkan nilai RRMSE (Relative Root Mean Squared Error) pendugaan langsung dengan nilai RRMSE pendugaan tidak langsung. Pendugaan tidak langsung untuk area kecil dalam penelitian ini diterapkan untuk kasus pendugaan pengeluaran per kapita di Kota Bogor tahun 2003. Metode yang digunakan untuk menduga pengeluaran per kapita tersebut adalah metode empirical
Bayes dengan pendekatan jackknife untuk
menghitung MSE.
Tujuan
Tujuan dari penelitian ini adalah:
1.Mengkaji metode empirical Bayes pada pendugaan area kecil.
2.Menerapkan metode empirical Bayes untuk menduga pengeluaran per kapita di Kota Bogor tahun 2003.
TINJAUAN PUSTAKA
Pengeluaran Per Kapita
Pengeluaran per kapita menunjukkan besarnya pengeluaran setiap anggota rumah tangga dalam kurun waktu satu bulan (BPS, 2003). Pengertian rumah tangga yang dimaksud pada definisi di atas yaitu sekelompok orang yang mendiami sebagian atau seluruh bangunan fisik dan biasanya tinggal bersama serta makan dari satu dapur (BPS, 2003). Satu rumah tangga bisa terdiri dari satu, dua, atau lebih kepala keluarga.
Perhitungan pengeluaran per kapita dirumuskan sebagai berikut:
q p y =
dimana;
y = pengeluaran per kapita
p = pengeluaran rumah tangga sebulan q = jumlah anggota rumah tangga
Pendugaan Area Kecil
Pendugaan area kecil saat ini sangat umum digunakan dalam survey sampling, dimana banyak metode analisis data telah dikemukakan dalam beberapa literatur. Area kecil (small area) diartikan sebagai bagian dari wilayah populasi (small domain) baik berdasarkan geografi, ekonomi, sosial budaya, ataupun yang lainnya (Rao, 2003). Suatu daerah disebut
small area jika dalam daerah tersebut jumlah
contoh yang terambil kurang besar untuk mendapatkan nilai pendugaan langsung yang akurat. Nilai pendugaan langsung pada area kecil merupakan penduga tak bias tetapi memiliki ragam yang besar karena diperoleh dari ukuran contoh yang kecil (Ramsini et.al
(2001) dalam Kurnia dan Notodiputro (2006b)).
Metode pendugaan yang dapat digunakan untuk mendapatkan pendugaan area kecil yaitu pendugaan langsung dan pendugaan tidak langsung. Pendugaan tidak langsung (indirect
estimation) dilakukan dengan cara
memanfaatkan informasi peubah lain yang berhubungan dengan parameter yang diamati. Contoh informasi yang dapat digunakan adalah catatan sensus ataupun survei pada area tersebut. Ada beberapa metode pada pendugaan tidak langsung untuk area kecil antara lain EBLUP (Empirical Best Linear Unbiased
Prediction), EB (Empirical Bayes), dan HB
PENDAHULUAN
Latar Belakang
Dewasa ini permintaan akan statistik area kecil (small area statistics) semakin meningkat dalam berbagai bidang. Pendugaan area kecil sangat dibutuhkan untuk mendapatkan informasi-informasi pada area kecil, misalnya pada lingkup kabupaten/kota, kecamatan, maupun kelurahan/desa. Informasi tersebut menjadi sangat penting seiring dengan berkembangnya era otonomi daerah di Indonesia karena dapat digunakan sebagai acuan menyusun sistem perencanaan, pemantauan, dan kebijakan daerah lainnya tanpa harus mengeluarkan biaya besar untuk mengumpulkan data sendiri. Metode yang terus dikembangkan untuk menduga statistik area kecil adalah pendugaan area kecil (small area
estimation).
Pendugaan secara langsung (direct
estimation) pada area kecil akan menghasilkan
nilai ragam yang besar jika contoh yang diambil berasal dari data survei yang dirancang untuk skala besar/nasional. Hal ini disebabkan oleh ukuran contoh yang terambil pada area tersebut kecil. Salah satu solusi yang digunakan adalah melakukan pendugaan tidak langsung dengan cara menambahkan peubah-peubah pendukung dalam menduga parameter. Peubah pendukung tersebut berupa informasi dari area lain yang serupa, survei terdahulu pada area yang sama, atau peubah lain yang berhubungan dengan peubah yang ingin diduga.
Evaluasi hasil pendugaan tidak langsung dapat diketahui dengan membandingkan nilai RRMSE (Relative Root Mean Squared Error) pendugaan langsung dengan nilai RRMSE pendugaan tidak langsung. Pendugaan tidak langsung untuk area kecil dalam penelitian ini diterapkan untuk kasus pendugaan pengeluaran per kapita di Kota Bogor tahun 2003. Metode yang digunakan untuk menduga pengeluaran per kapita tersebut adalah metode empirical
Bayes dengan pendekatan jackknife untuk
menghitung MSE.
Tujuan
Tujuan dari penelitian ini adalah:
1.Mengkaji metode empirical Bayes pada pendugaan area kecil.
2.Menerapkan metode empirical Bayes untuk menduga pengeluaran per kapita di Kota Bogor tahun 2003.
TINJAUAN PUSTAKA
Pengeluaran Per Kapita
Pengeluaran per kapita menunjukkan besarnya pengeluaran setiap anggota rumah tangga dalam kurun waktu satu bulan (BPS, 2003). Pengertian rumah tangga yang dimaksud pada definisi di atas yaitu sekelompok orang yang mendiami sebagian atau seluruh bangunan fisik dan biasanya tinggal bersama serta makan dari satu dapur (BPS, 2003). Satu rumah tangga bisa terdiri dari satu, dua, atau lebih kepala keluarga.
Perhitungan pengeluaran per kapita dirumuskan sebagai berikut:
q p y =
dimana;
y = pengeluaran per kapita
p = pengeluaran rumah tangga sebulan q = jumlah anggota rumah tangga
Pendugaan Area Kecil
Pendugaan area kecil saat ini sangat umum digunakan dalam survey sampling, dimana banyak metode analisis data telah dikemukakan dalam beberapa literatur. Area kecil (small area) diartikan sebagai bagian dari wilayah populasi (small domain) baik berdasarkan geografi, ekonomi, sosial budaya, ataupun yang lainnya (Rao, 2003). Suatu daerah disebut
small area jika dalam daerah tersebut jumlah
contoh yang terambil kurang besar untuk mendapatkan nilai pendugaan langsung yang akurat. Nilai pendugaan langsung pada area kecil merupakan penduga tak bias tetapi memiliki ragam yang besar karena diperoleh dari ukuran contoh yang kecil (Ramsini et.al
(2001) dalam Kurnia dan Notodiputro (2006b)).
Metode pendugaan yang dapat digunakan untuk mendapatkan pendugaan area kecil yaitu pendugaan langsung dan pendugaan tidak langsung. Pendugaan tidak langsung (indirect
estimation) dilakukan dengan cara
memanfaatkan informasi peubah lain yang berhubungan dengan parameter yang diamati. Contoh informasi yang dapat digunakan adalah catatan sensus ataupun survei pada area tersebut. Ada beberapa metode pada pendugaan tidak langsung untuk area kecil antara lain EBLUP (Empirical Best Linear Unbiased
Prediction), EB (Empirical Bayes), dan HB
(Hierarchical Bayes).
Small area estimation merupakan pendugaan suatu area yang lebih kecil dengan memanfaatkan informasi dari luar area, informasi dari dalam area itu sendiri, dan dari luar survei (Longford, 2005). Pendugaan secara tidak langsung pada small area estimation
mempunyai beberapa keuntungan, yaitu mendapatkan penduga optimal, memperoleh model valid yang berasal dari data contoh, serta dapat menjelaskan berbagai macam model berdasar pada respon alami suatu peubah dan kekomplekan struktur data (Rao, 2003).
Penduga Sintetik
Penduga sintetik merupakan penduga tak bias yang diperoleh dari sebuah survei contoh untuk area yang besar, ketika penduga ini digunakan sebagai penduga untuk sub-area (area yang lebih kecil) dengan mengasumsikan bahwa sub-area tersebut memiliki karakteristik yang sama dengan area besar (Gonzales (1973) dalam Ghosh dan Rao (1994)). Metode ini cocok digunakan untuk semua desain sampling.
Penduga sintetik pada pendugaan area kecil dapat digunakan untuk menduga nilai respon pada sub-area yang tidak disurvei. Penduga sintetik dapat memberikan dugaan dengan memanfaatkan informasi dari area kecil lain yang diasumsikan mirip dengan area kecil yang akan diduga.
Model Area Kecil
Pendugaan area kecil terdiri atas dua jenis model dasar yaitu basic area level model dan
basic unit level model (Rao, 2003).
a. Basic area level (type A) model yaitu model
yang didasarkan pada ketersediaan data pendukung yang hanya ada untuk level area tertentu, misalkan xi = (x1i,…,xpi)T dan
parameter yang akan diduga θi, diasumsikan mempunyai hubungan dengan xi. Data
pendukung tersebut digunakan untuk membangun model: θi = xiT β + bivi ,
i =1,…,m dengan v
(ii) θ
i ~ N(0, σ2v), sebagai
pengaruh acak yang diasumsikan normal. Kesimpulan mengenai θi, dapat diketahui
dengan mengasumsikan bahwa model penduga langsung yi telah tersedia yaitu:
yi = θi + ei , i =1,…,m dengan sampling error ei ~N(0, σ2ei) dan σ2ei diketahui.
Pada akhirnya, kedua model digabungkan dan menghasilkan model gabungan:
yi= xiT β + bivi + ei , i =1,…,m dimana bi
diketahui bernilai positif konstan (diasumsikan bernilai 1).
Model tersebut merupakan bentuk khusus dari model linier campuran (general linear
mixed model) yang terdiri dari pengaruh
tetap (fixed effect) yaitu β dan pengaruh acak
(random effect) yaitu vi (Saei dan Chambers,
2003).
b. Basic unit level (type B) model yaitu suatu
model dimana data-data pendukung yang tersedia bersesuaian secara individu dengan data respon, misal xij = (xij1,...,xijp)T, sehingga
dapat dibuat suatu model regresi tersarang yij = xijTβ + vi + eij; i=1,…,m dan j=1,...,Ni
dengan vi ~N(0, σ2v) dan ei ~N(0, σ2ei).
Penelitian ini menggunakan model basic area
level (type A) karena data pendukungnya hanya
ada untuk level area tertentu yaitu pada level desa.
Metode Empirical Bayes
Metode empirical Bayes (EB) merupakan salah satu pendekatan yang dapat digunakan pada pendugaan area kecil. Hal pertama yang ingin didapatkan pada metode Bayes adalah sebaran posterior untuk parameter yang diamati yang dinotasikan f (θi |yi, β, σ2v), dengan asumsi β dan σ2v diketahui. Sedangkan pada metode
EB, inferensia yang diperoleh berdasar pada dugaan sebaran posterior dari θi dengan memasukkan nilai dugaan β dan σ2v yaitu
f(θi|yi,βˆ,σˆv2).
Model Fay dan Heriot (1979) untuk model
basic area level adalah:
yi= xiTβ+ vi + ei
dimana vi ~N(0, σ2v) dan ei ~N(0, σ2ei), vi dan
ei saling bebas. β dan σ2v tidak diketahui
sedangkan σ2ei diasumsikan diketahui (Kurnia
dan Notodiputro, 2006b).
Misal σ2v dan σ2ei disimbolkan dengan A
dan Di, selanjutnya merupakan penduga
Bayes untuk θ Β
i
θˆ
i, dengan mengikuti model
Bayes:
(i) yi|θi ~N(θi, Di)
i ~ N(xiTβ, A) adalah sebaran prior
untuk θi, i=1,2,...,m.
Model Bayes dijelaskan oleh:
⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = 2 i i i i
i (y )
Di 2 1 exp D 2 1 ) | y ( f θ π
θ dan
⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = 2 ) ( 2 1 exp 2 1 ) ( θ β π θ π T i i i x A A dan
∏
= ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = m 1 i 2 i i i i ii (y )
D 2 1 exp D 2 1 ) A , | , y ( f θ π β θ ⎟ ⎠ ⎞ ⎜ ⎝
⎛− − 2
) ( 2 1 exp 2
1 θ β
π T i i x A A
Lihat dua fungsi eksponensial tanpa faktor (-1/2) dari f(yi, θi |β, A),
2 2 ) ( 1 ) (
1 θ θ Tβ i i i i i x A y
D − + −
) ) ( 2 ( 1 ) 2 (
1 2 θ θ2 θ2 θ β Tβ 2
i T i i i i i i i i x x A y y
D − + + − +
= * i i T i i i 2 i i a A x D y 2 A 1 D 1 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β θ * i i T i i i i T i i i i T i i i i 2 i i a A 1 D 1 A x D y A 1 D 1 A x D y A 1 D 1 A x D y 2 A 1 D 1 + ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + × ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = β β β θ θ * i 2 i T i i i i i a A 1 D 1 A x D y A 1 D 1 + ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β
dengan ai* adalah konstanta dan bebas dari θi.
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + Ν −1 1 1 , ~ ) , , | ( A D D A x D Ay A y i i T i i i i i β β θ
(
)
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + + Ν i i T i i i T i D A AD β x y D A Α β x , ~ ) A , , y | (θi i βBerdasarkan formula tersebut diperoleh suatu penduga:
Β
i
θ
ˆ
= E (θi | yi, β, A) = xiTβ+ (1 – BBi)(yi - xi
Tβ
), dengan Bi = Di / (A + Di)
MSE(θˆiΒ )= Var (θi | yi, β, A) = ADi / (A + Di ) Parameter A pada formula diatas dapat diduga dengan metode momen, minimum variance quadratic unbiased estimation
(MIVQUE), maximum likelihood (ML), atau
restricted/residual maximum likelihood
(REML). Sedangkan parameter β dapat diduga dengan metode momen ataupun weighted least
square (WLS).
Jika A dan β diduga, maka akan diperoleh suatu penduga empirical Bayes:
(
)
(
β)
β
θˆ ˆ 1 ˆ T ˆ
i i i i
i = x + −Β y −x
Τ
ΕΒ ,
dengan Βˆi =Di/(Αˆ+Di)
Berdasarkan metode Bayes, diperoleh: MSE(θˆiΕΒ) = Var (θi |yi,βˆ ˆ,Α) =
(
)
i i/Aˆ D
D Aˆ +
Penduga MSE tersebut menjadi bersifat
underestimate karena adanya pendugaan pada
nilai A dan β. Hal tersebut dapat dikoreksi dengan menggunakan pendekatan jackknife
(Jiang, Lahiri, dan Wan, 2002) maupun dengan pendekatan bootstrap (Butar dan Lahiri (2003) dalam Rao (2003)). Penelitian ini menggunakan metode jackknife untuk mengoreksi MSE tersebut.
Pendekatan Jackknife dalam Pendugaan MSE( ΕΒ)
i
θˆ
Pendekatan jackknife merupakan salah satu metode yang sering digunakan dalam survei karena konsepnya yang sederhana (Jiang, Lahiri, dan Wan, 2002). Metode ini diperkenalkan oleh Tukey (1958) dan berkembang menjadi suatu metode yang dapat mengoreksi bias suatu penduga. Prosedur yang dilakukan yaitu dengan menghapus observasi ke-i untuk i = 1,2,...,m dan selanjutnya melakukan pendugaan parameter.
Small area estimation menerapkan metode
jackknife untuk mengoreksi pendugaan MSE
akibat adanya pendugaan β dan A, dengan: MSE( Β) = AD
i
θˆ i / (A + Di ) = g1i(A) dimana A
diduga oleh s2v (Kurnia dan Notodiputro,
2006a). Tahapan-tahapan untuk menghitung MSEJ(θˆiΕΒ) adalah sebagai berikut:
1.Hitung nilai h1i dengan rumus:
( )
∑
[
(
) (
]
= − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = m 1 u 2 v i 1 2 ) u ( v i 1 2 v i 1 i1 g s g s
m 1 m s g h
)
dimana g1i(s2v(-u)) diperoleh dengan
menghapus pengamatan ke-u pada himpunan data g1i(s2v).
2.Hitung nilai h2i dengan rumus:
( ) ( )
[
]
21 ) (
2 ˆ ˆ
1
∑
= ΕΒ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = m u EB i u i i m mh θ θ
dimana ( ) diperoleh dengan menghapus
pengamatan ke-u pada himpunan data .
( ) ΕΒ −u i θˆ ΕΒ i θˆ
3.Hitung nilai MSE: MSEJ(θˆiΕΒ) = h1i + h2i
BAHAN DAN METODE
Bahan
Data yang digunakan dalam penelitian ini adalah data SUSENAS 2003 dengan informasi data berbasis rumah tangga serta PODES 2003 sebagai sumber data peubah pendukung .
Peubah respon yang menjadi perhatian dalam penelitian ini adalah pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor. Peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita yaitu,
x1 = persentase keluarga prasejahtera dan
sejahtera 1
x2 = persentase keluarga pengguna listrik
PLN
x3 = persentase surat miskin yang
dikeluarkan desa x4 = jumlah penduduk
Lihat dua fungsi eksponensial tanpa faktor (-1/2) dari f(yi, θi |β, A),
2 2 ) ( 1 ) (
1 θ θ Tβ i i i i i x A y
D − + −
) ) ( 2 ( 1 ) 2 (
1 2 θ θ2 θ2 θ β Tβ 2
i T i i i i i i i i x x A y y
D − + + − +
= * i i T i i i 2 i i a A x D y 2 A 1 D 1 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β θ * i i T i i i i T i i i i T i i i i 2 i i a A 1 D 1 A x D y A 1 D 1 A x D y A 1 D 1 A x D y 2 A 1 D 1 + ⎪ ⎪ ⎪ ⎪ ⎭ ⎪ ⎪ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + × ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = β β β θ θ * i 2 i T i i i i i a A 1 D 1 A x D y A 1 D 1 + ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = θ β
dengan ai* adalah konstanta dan bebas dari θi.
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + Ν −1 1 1 , ~ ) , , | ( A D D A x D Ay A y i i T i i i i i β β θ
(
)
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + + Ν i i T i i i T i D A AD β x y D A Α β x , ~ ) A , , y | (θi i βBerdasarkan formula tersebut diperoleh suatu penduga:
Β
i
θ
ˆ
= E (θi | yi, β, A) = xiTβ+ (1 – BBi)(yi - xi
Tβ
), dengan Bi = Di / (A + Di)
MSE(θˆiΒ )= Var (θi | yi, β, A) = ADi / (A + Di ) Parameter A pada formula diatas dapat diduga dengan metode momen, minimum variance quadratic unbiased estimation
(MIVQUE), maximum likelihood (ML), atau
restricted/residual maximum likelihood
(REML). Sedangkan parameter β dapat diduga dengan metode momen ataupun weighted least
square (WLS).
Jika A dan β diduga, maka akan diperoleh suatu penduga empirical Bayes:
(
)
(
β)
β
θˆ ˆ 1 ˆ T ˆ
i i i i
i = x + −Β y −x
Τ
ΕΒ ,
dengan Βˆi =Di/(Αˆ+Di)
Berdasarkan metode Bayes, diperoleh: MSE(θˆiΕΒ) = Var (θi |yi,βˆ ˆ,Α) =
(
)
i i/Aˆ D
D Aˆ +
Penduga MSE tersebut menjadi bersifat
underestimate karena adanya pendugaan pada
nilai A dan β. Hal tersebut dapat dikoreksi dengan menggunakan pendekatan jackknife
(Jiang, Lahiri, dan Wan, 2002) maupun dengan pendekatan bootstrap (Butar dan Lahiri (2003) dalam Rao (2003)). Penelitian ini menggunakan metode jackknife untuk mengoreksi MSE tersebut.
Pendekatan Jackknife dalam Pendugaan MSE( ΕΒ)
i
θˆ
Pendekatan jackknife merupakan salah satu metode yang sering digunakan dalam survei karena konsepnya yang sederhana (Jiang, Lahiri, dan Wan, 2002). Metode ini diperkenalkan oleh Tukey (1958) dan berkembang menjadi suatu metode yang dapat mengoreksi bias suatu penduga. Prosedur yang dilakukan yaitu dengan menghapus observasi ke-i untuk i = 1,2,...,m dan selanjutnya melakukan pendugaan parameter.
Small area estimation menerapkan metode
jackknife untuk mengoreksi pendugaan MSE
akibat adanya pendugaan β dan A, dengan: MSE( Β) = AD
i
θˆ i / (A + Di ) = g1i(A) dimana A
diduga oleh s2v (Kurnia dan Notodiputro,
2006a). Tahapan-tahapan untuk menghitung MSEJ(θˆiΕΒ) adalah sebagai berikut:
1.Hitung nilai h1i dengan rumus:
( )
∑
[
(
) (
]
= − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = m 1 u 2 v i 1 2 ) u ( v i 1 2 v i 1 i1 g s g s
m 1 m s g h
)
dimana g1i(s2v(-u)) diperoleh dengan
menghapus pengamatan ke-u pada himpunan data g1i(s2v).
2.Hitung nilai h2i dengan rumus:
( ) ( )
[
]
21 ) (
2 ˆ ˆ
1
∑
= ΕΒ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = m u EB i u i i m mh θ θ
dimana ( ) diperoleh dengan menghapus
pengamatan ke-u pada himpunan data .
( ) ΕΒ −u i θˆ ΕΒ i θˆ
3.Hitung nilai MSE: MSEJ(θˆiΕΒ) = h1i + h2i
BAHAN DAN METODE
Bahan
Data yang digunakan dalam penelitian ini adalah data SUSENAS 2003 dengan informasi data berbasis rumah tangga serta PODES 2003 sebagai sumber data peubah pendukung .
Peubah respon yang menjadi perhatian dalam penelitian ini adalah pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor. Peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita yaitu,
x1 = persentase keluarga prasejahtera dan
sejahtera 1
x2 = persentase keluarga pengguna listrik
PLN
x3 = persentase surat miskin yang
Metode
Tahapan-tahapan pada penelitian ini adalah: 1.Memilih peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita berdasarkan eksplorasi data serta penelitian-penelitian sebelumnya.
2.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa secara langsung (direct estimation).
3.Melakukan pendugaan A dan β dengan metode momen.
4.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa dengan metode empirical Bayes (θˆiΕΒ). 5.Menghitung MSEJ( ) dengan konsep
jackknife menggunakan proc IML pada SAS
9.1.
ΕΒ
i
θˆ
6.Membandingkan nilai RRMSE pendugaan langsung dan nilai RRMSEJ( ), dengan
perhitungan RRMSE sebagai berikut: ΕΒ
i
θˆ
( )
( )
100%ˆ ˆ MSE ˆ
RRMSE
i i
i = ×
θ θ θ
Software yang digunakan adalah Minitab
14, Microsoft Excell dan SAS 9.1.
HASIL DAN PEMBAHASAN
Eksplorasi Data
Eksplorasi untuk masing-masing peubah dilakukan dengan menggunakan scatterplot,
boxplot, dan nilai korelasi Pearson yang tersaji
pada Lampiran 1. Scatterplot data menunjukkan bahwa desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga pengguna listrik dan jumlah penduduk yang besar pula. Selain itu, desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga prasejahtera dan sejahtera 1 serta persentase surat miskin yang dikeluarkan desa kecil. Nilai korelasi Pearson yang dihasilkan juga sesuai dengan hasil scatterplot.
Boxplot digunakan untuk mengetahui
ukuran pemusatan data. Boxplot untuk peubah x1, x2, dan x4 menunjukkan bahwa tidak ada
data yang jauh dari kumpulan data, sedangkan pada peubah x3 ada satu data yang agak jauh
dari kumpulan data.
Berdasarkan eksplorasi data yang telah dilakukan, terlihat bahwa hasilnya sesuai dengan logika. Peubah tersebut juga digunakan dalam penelitian sebelumnya pada skripsi
(Dewi, 2006). Berdasar alasan-alasan di atas, peubah x1, x2, x3, dan x4 cukup sesuai
digunakan untuk menggambarkan pengeluaran per kapita rumah tangga pada beberapa desa di Kota Bogor.
Pendugaan Langsung
Hasil yang didapatkan dari pendugaan langsung pengeluaran per kapita yaitu besarnya pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor dan nilai simpangan bakunya. Jumlah desa/kelurahan yang diamati adalah 34 desa/kelurahan yang ada di Kota Bogor.
Nilai ragam sampling error (Di) yang
menjadi perhatian diduga oleh si2/ni yang
merupakan rasio antara ragam di dalam area dengan banyaknya contoh. Nilai Di dapat
dihitung dari hasil pendugaan langsung. Hasil pendugaan langsung dan nilai ragam sampling
error (Di) dapat dilihat pada Lampiran 2.
Pendugaan langsung pengeluaran per kapita rumah tangga pada beberapa kelurahan/desa di Kota Bogor dilakukan berdasarkan data survei dengan objek survei sebanyak 16 rumah tangga untuk masing-masing desa, kecuali untuk desa Sukadamai sebesar 15 rumah tangga. Jumlah tersebut termasuk kecil untuk merepresentasikan seluruh rumah tangga pada masing-masing desa, sehingga memberikan hasil dugaan dengan ragam yang besar.
Penelitian sebelumnya (Dewi, 2006) menggunakan prosedur proc tabulate pada SAS 9.1 untuk menghitung pengeluaran per kapita, menggunakan lima peubah pendukung, dan menggunakan metode REML untuk menduga parameter A dan β. Perbedaan penelitian ini dengan penelitian tersebut adalah perhitungan pengeluaran per kapita menggunakan rumus sebagai berikut:
16 ,..., 2 , 1 j ; q p y
j
j =
=
∑
∑
dimana;
y = pengeluaran per kapita suatu desa
∑
p
j= jumlah pengeluaran seluruh rumah tangga contoh selama sebulan∑
q
j= jumlah seluruh anggota rumah tangga contohPenelitian ini hanya menggunakan empat peubah pendukung, menggunakan metode momen untuk menduga parameter A dan β, dan menambahkan pendugaan pengeluaran per kapita untuk desa-desa di Kota Bogor yang tidak disurvei.
Metode
Tahapan-tahapan pada penelitian ini adalah: 1.Memilih peubah pendukung xi yang
diasumsikan mempengaruhi dan menggambarkan pengeluaran per kapita berdasarkan eksplorasi data serta penelitian-penelitian sebelumnya.
2.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa secara langsung (direct estimation).
3.Melakukan pendugaan A dan β dengan metode momen.
4.Menduga pengeluaran per kapita rumah tangga untuk masing-masing kelurahan/ desa dengan metode empirical Bayes (θˆiΕΒ). 5.Menghitung MSEJ( ) dengan konsep
jackknife menggunakan proc IML pada SAS
9.1.
ΕΒ
i
θˆ
6.Membandingkan nilai RRMSE pendugaan langsung dan nilai RRMSEJ( ), dengan
perhitungan RRMSE sebagai berikut: ΕΒ
i
θˆ
( )
( )
100%ˆ ˆ MSE ˆ
RRMSE
i i
i = ×
θ θ θ
Software yang digunakan adalah Minitab
14, Microsoft Excell dan SAS 9.1.
HASIL DAN PEMBAHASAN
Eksplorasi Data
Eksplorasi untuk masing-masing peubah dilakukan dengan menggunakan scatterplot,
boxplot, dan nilai korelasi Pearson yang tersaji
pada Lampiran 1. Scatterplot data menunjukkan bahwa desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga pengguna listrik dan jumlah penduduk yang besar pula. Selain itu, desa dengan pengeluaran per kapita yang besar diindikasikan oleh persentase keluarga prasejahtera dan sejahtera 1 serta persentase surat miskin yang dikeluarkan desa kecil. Nilai korelasi Pearson yang dihasilkan juga sesuai dengan hasil scatterplot.
Boxplot digunakan untuk mengetahui
ukuran pemusatan data. Boxplot untuk peubah x1, x2, dan x4 menunjukkan bahwa tidak ada
data yang jauh dari kumpulan data, sedangkan pada peubah x3 ada satu data yang agak jauh
dari kumpulan data.
Berdasarkan eksplorasi data yang telah dilakukan, terlihat bahwa hasilnya sesuai dengan logika. Peubah tersebut juga digunakan dalam penelitian sebelumnya pada skripsi
(Dewi, 2006). Berdasar alasan-alasan di atas, peubah x1, x2, x3, dan x4 cukup sesuai
digunakan untuk menggambarkan pengeluaran per kapita rumah tangga pada beberapa desa di Kota Bogor.
Pendugaan Langsung
Hasil yang didapatkan dari pendugaan langsung pengeluaran per kapita yaitu besarnya pengeluaran per kapita anggota rumah tangga pada beberapa desa di Kota Bogor dan nilai simpangan bakunya. Jumlah desa/kelurahan yang diamati adalah 34 desa/kelurahan yang ada di Kota Bogor.
Nilai ragam sampling error (Di) yang
menjadi perhatian diduga oleh si2/ni yang
merupakan rasio antara ragam di dalam area dengan banyaknya contoh. Nilai Di dapat
dihitung dari hasil pendugaan langsung. Hasil pendugaan langsung dan nilai ragam sampling
error (Di) dapat dilihat pada Lampiran 2.
Pendugaan langsung pengeluaran per kapita rumah tangga pada beberapa kelurahan/desa di Kota Bogor dilakukan berdasarkan data survei dengan objek survei sebanyak 16 rumah tangga untuk masin