Diskretisasi Model Dinamik Kontinu

(1)

DISKRETISASI MODEL DINAMIK KONTINU

MUHAMMAD ARIF TIRTANA

G54102014

DEPARTEMEN M ATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

MUHAMMAD ARIF TIRTANA. Diskretisasi Model Dinamik Kontinu. Dibimbing oleh NGAKAN KOMANG KUTHA ARDANA dan ALI KUSNANTO.

Diskretisasi diperlukan untuk mendapatkan model dinamik diskret dari model dinamik kontinu. Proses tersebut didapat dengan mentransformasi persamaan diferensial pada model dinamik kontinu menjadi persamaan beda pada model dinamik diskret.

Tulisan ini memperlihatkan bagaimana memperoleh persamaan beda sebagai model diskret dari fungsi eksponensial kontinu dan fungsi logistik kontinu. Berdasarkan pola perilaku model diskret dan model kontinu pada fungsi eksponensial dan fungsi logistik, diperoleh bahwa semua pola perilaku pada model kontinu dimiliki oleh model diskret, tetapi model kontinu tidak memiliki semua pola perilaku pada model diskret.

Tulisan ini juga memperlihatkan proses diskretis asi pada sistem persamaan diferensial menjadi sistem persamaan beda sebagai model diskretnya. Berdasarkan perbandingan pola perilaku model diskret dan model kontinu pada model penyebaran AIDS diperoleh bahwa pola perilaku pada model diskret mengimplementasikan pola perilaku pada model kontinunya.

(3)

MUHAMMAD ARIF TIRTANA. Discretization of Continuous Dynamic Model. Supervised by NGAKAN KOMANG KUTHA ARDANA and ALI KUSNANTO.

Discretization is a process to form a discrete dynamic model from a continuous one. This can be done by transforming differential equations of continuous model into difference equations of discrete model.

This paper shows how to get the difference equations from a continuous exponential and a continuous logistic function. Based on the pattern of the continuous and the discrete model of exponential and logistic function, it is found that all pattern of continuous models are satisfied by discrete models, but continuous models don’t necessarily have all pattern of discrete models.

(4)

DISKRETISASI MODEL DINAMIK KONTINU

Skripsi

Sebagai Salah Satu Syarat Memperoleh Gelar Sarjana Sains

pada Program Studi Matematika

G54102014

(5)

Menyetujui:

Tanggal Lulus :

Pembimbing I,

Ir. N. K. Kutha Ardana, M.Sc.

NIP 131 842 421

Pembimbing II,

Drs. Ali Kusnanto, M.Si.

NIP 131 913 135

Mengetahui

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

(6)

nikmat, jasmani maupun rohani, sehingga penulis dapat menyelesaikan skripsi ini. Shalawat serta salam penulis tuturkan kepada junjungan Nabi besar, Rasulullah Muhammad SAW yang telah memberikan teladan dalam menjalani hidup.

Pada kesempatan ini penulis mengucapkan banyak terima kasih kepada semua pihak yang telah sangat banyak membantu dalam menyelesaikan karya ilmiah ini, antara lain:

• Ibunda tercinta atas kasih dan sayang yang berlimpah. • Ayahanda tercinta atas segala saran, nasihat serta petuahnya. • Adik-adik tersayang: Dewi, Mega, Isan, Iwan, dan Putri.

• Seluruh keluarga besar ku atas segala dukungan moral yang diberikan.

• Bapak N. K. Kutha Ardana dan bapak Ali Kusnanto yang tak pernah jera membimbing dan membantu penulis menyelesaikan karya ilmiah ini.

• Ibu Farida Hanum sebagai dosen penguji.

• Husna, Tari, Diah dan Dian Sastro Wardoyo yang menjadi sinar hidupku. • Seluruh dosen Departemen Matematika atas ilmu yang tak ternilai harganya. • Seluruh staf Departemen Matemat ika atas segala bantuannya.

• Sahabat – sahabat tercinta, Dina, Erita, Avi, Ade, Febi, dan Ardhi. • Saudara senasib sepenanggungan: Irwan, Kabul, dan Fitrah.

• Sahabat – sahabat kosan pink: Deni ”Ben Haim”, Eko ”Taz”, Zainul ”Luni”, Gian ”Golo”, Ridwan ”Aracong”, Mian, dan Toni.

• Sahabat – sahabat kosan kuning di sebelah masjid: Samba, Basyar serta David. • Rekan – rekan Futsal yang telah memberikan kemenangan dan kenangan yang indah. • Teman – teman seperjuangan, Matematika angkatan 39 (t.a 2002) .

• Rekan – rekan Matematika angkatan 37, 38, 40 dan 41.

• Agung “Culai” dan Riki “Ma’el” serta teman – teman dari SMU Patra Nusa. • Teman – teman seperjuangan dari tanah rencong , Nanggroe Aceh Darussalam.

• Cao-Cao, Liu Bei, Sun Quan, Jendral Guan Yu, Zhuge Liang, Ieyasu Tokugawa, Sasaki Kojiro, Miyamoto Musashi, Adolf Hitler, Zengish Khan, Ir. Soekarno dan Albert Einstein, yang menjadi sumber inspirasiku.

• Seluruh pihak yang telah membantu penyelesaian karya ilmiah ini.

Penulis sadar sepenuhnya bahwa banyak sekali kekurangan dalam penyusunan karya ilmiah ini. Harapan penulis adalah bahwa karya ilmiah ini dapat memberikan banyak manfaat bagi penulis maupun pembacanya.

Bogor, September 2008

(7)

adalah putra pertama dari enam bersaudara dari pasangan Bapak Muhammad Nurdin dan Ibu Wirdahanum.

Pada tahun 1996 penulis lulus dari SD Inpres Desa Paya Bedi, Aceh Tamiang. Tiga tahun kemudian, tepatnya pada tahun 1999, penulis lulus dari SMP Negeri 1 Kuala Simpang, Aceh Tamiang. Tahun 2002 penulis lulus dari SMU PLUS PATRA NUSA, Aceh Tamiang, dan diterima untuk melanjutkan kuliah di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA), Institut Pertanian Bogor.

Selama menempa ilmu di bangku perkuliahan, penulis juga menjalani aktivitas lain, yaitu berorganisasi di dalam dan di luar kampus. Di dalam kampus penulis pernah menjabat sebagai staf Departemen Sumber Daya Manusia GUMATIKA (Gugusan Mahasiswa Matematika) 2004-2005 dan 2005-2006, staf Departemen Informasi dan Komunikasi BEM FMIPA 2003-2004, dan menjadi panitia di berbagai kegiatan BEM FMIPA.

(8)

DAFTAR GAMBAR... viii

DAFTAR LAMPIRAN ... viii

I. PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan... 1

1.3 Ruang Lingkup ... 1

II. LANDASAN TEORI 2.1 Persamaan Beda... 1

2.2 Analisis Kestabilan Titik Tetap pada Orde Tiga atau Lebih ... 2

2.3 Metode Rekursif untuk Mencari Solusi Persamaan Beda ... 2

2.4 Model Kermack dan McKendrick ... 3

III. PEMBAHASAN 3.1. Diskretisasi Fungsi Eksponensial ... 3

3.2. Diskretisasi Fungsi Logistik ... 6

3.3. Diskretisasi Sistem Persamaan Differensial ... 9

3.3.1 Model kont inu wabah penyakit AIDS : Model SIA ... 9

3.3.2 Diskretisasi Model Kontinu Penyebaran AIDS ... 10

IV. SIMPULAN dan SARAN 4.1 Simpulan ... 12

4.2 Saran ... 12

DAFTAR PUSTAKA... 12

(9)

1. Perbandingan Grafik F ungsi Eksponensial Kontinu dan Diskret terhadap k ... 4

2. Perbandingan Grafik F ungsi Logistik Kontinu dan Diskret terhadap r ... 7

3. Model Penyebaran AIDS... 9

4. Perbandingan Grafik Model Penyebaran AIDS Kontinu dan Diskret ... 11

DAFTAR LAMPIRAN

Halaman 1. Solusi Persamaan (1.1) ... 14

2. Solusi Persam aan (1.3) ... 14

3. Solusi Persamaan (2.1) ... 15

4. Penurunan persamaan (3.2) dan (3.3) dari persamaan (3.1) ... 17

5. Penurunan persamaan (3.4) dari persamaan (3.1) ... 18

6. Program Mathematica untuk Persamaan (1.1) ... 21

10. Program Mathematica untuk Model Kontinu Penyebaran AIDS (3.1)... 22

(10)

M odel matematik telah banyak digunakan pada bidang fisika dan biologi, terutama dalam masalah dinamik. Pemodelan fenomena alam yang terjadi dalam kehidupan nyata secara matematis dapat mempermudah para peneliti untuk menjelajahi efek dari perubahan–perubahan berbagai parameter yang berpengaruh dengan lebih mudah, cepat dan murah dibandingkan bila hany a bereksperimen, selain tidak murah dan memakan waktu yang cukup lama, kadang hasil yang didapat kan tidak fisibel.

Sebagian besar model matematik yang menggambarkan fenomena–fenomena alam dinyatakan dalam model kontinu. Namun, sebagian besar dari fenomena tersebut hanya berubah pada waktu–waktu tertentu dan tidak setiap saat, sehingga penggambaran secara kontinu terasa kurang tepat. Oleh karena itu diperlukan sebuah model diskret untuk mengimplementasikan fenomena–fenomena alam yang hanya berubah pada waktu–waktu tertentu, seperti proses kelahiran atau kematian, penyebaran atau penyembuhan penyakit, dan sebagainya. Meskipun begitu, terdapat beberapa model matematik yang telah menggambarkan fenomena alam secara diskret. Namun, untuk memperoleh model diskret dari sebuah model matematik yang menggambarkan fenomena alam secara

model kontinu menjadi model diskret. Bagaimanapun juga, pembentuka n sec ara eksplisit pada model matematik dibuat dengan analisis yang detail secara matematis melalui proses-proses yang lebih mudah dimengerti. M odel kontinu telah banyak digunakan dalam pemodelan, namun dalam kehidupan nyata sebagian kasus lebih berupa sistem diskret, sehingga akan lebih tepat bila menggunakan model diskret untuk menggambarkan sebagian fenomena–fenomena alam dalam kehidupan nyata. Dalam tulisan ini diperlihat kan cara memperoleh proses transformasi untuk mendapatkan model diskret yang memadai bagi sebuah sistem kontinu .

1.2 Tujuan

Tujuan dari penulisan karya ilmiah ini adalah mempelajari proses transformasi sebuah model kontinu dinamik menjadi sebuah model diskret.

1.3 Ruang Lingkup

Ruang lingkup penulisan karya ilmiah ini mencakup: (1) melakukan proses transformasi fungsi kontinu menjadi fungsi diskret pada fungsi eksponensial dan fungsi logistik; (2) merekonstruksi jurnal Modelling AIDS Epidemic and Treatment with Difference Equations oleh Tamizhmani et al, 2004.

II LANDASAN TEORI

2.1 Persamaan Beda Definisi 1 (Persamaan Beda)

Persamaan beda adalah suatu persamaan yang menghubungkan anggota–anggota yang berbeda dari barisan bilangan

{

y y y0, 1, 2,...,yn,...

}

yang akan dicari dan ditentukan nilainya.

[Farlow, 1994] Definisi 2 (O rde Persamaan Beda)

Orde persamaan beda adalah perbedaan antara indeks tertinggi dengan indeks terendah yang muncul pada persamaan yang diberikan. Misal kan diberikan persamaan seperti di bawah ini:

(

, 1, 2,...,

)

k n k n k n k

y ₊ =F k y _{+ -} y _{+ -} y

Persamaan di atas adalah sebu ah persamaan beda berorde n jika y_k yang muncul dalam fungsi F di sisi kanan adalah y dengan indeks ter endah di sisi kanan dan indeks tertinggi di sisi kanan adalah n – 1.

Contoh 1:

1 2

n n

y ₊ = y + , persamaan beda orde 1.

2 1

n n n

y ₊ = y ₊ + y , persamaan beda orde 2. dengan n = 0, 1, 2, 3, ...

[Farlow, 1994] Definisi 3 (Persamaan Beda Linear)

(11)

( )

1 1 2 2

1 1

...

k n k n k n

n

n k k k

y a k y a k y

a k y a k y R

+ + - +

--

-+ + +

+ + =

dengan

( )

, 1 , 2 , 3 , . . . , i

a k i= n dan Rk

merupakan fungsi terhadap k. Contoh 2:

(1) y_n₊₁= y_n+ 2

(2) y_n₊₂+ 3y_n₊₁+ y_n = sin(np)

dengan n = 0, 1, 2, 3, ...

[Farlow, 1994] Definisi 4 (Solusi Persamaan Beda)

Solusi persamaan beda adalah fungsi yang merupakan barisan bilangan dari variabel bersangkutan, misalkan x_n atau y_n, yang memenuhi persamaan beda yang diberikan untuk setiap n, dengan n = 0, 1, 2, ...

[Farlow, 1994] Definisi 5 (Sistem Persamaan Beda Linear (SPBL))

Misalkan sebuah persamaan beda linear orde satu dinyatakan sebagai berikut:

1 n n 0 ...(1) n

y ₊ + x y =

Misalkan terdapat fungsi n

g di luar persamaan (1) tetapi sangat mempengaruhi persamaan (1), dengan

n

g merupakan sebuah persamaan beda linear, misalkan:

1 n 0

n

x ₊ + a x = , dengan a adalah konstanta. Hubungan kedua persamaan tersebut dapat dituliskan sebagai berikut:

1 n n 0, 1 n 0 ...(2)

n n

y ₊ + x y = x ₊ + a x =

dengan (n = 0, 1, 2, ...).

Persamaan (2) disebut Sistem P ersamaan Beda Linear (SPBL).

[Farlow, 1994] Definisi 6 (Solusi Sistem Persamaan Beda Linear )

Solusi s istem p ersamaan beda linear adalah fungsi yang merupakan barisan bilangan dari setiap variabel bersangkutan, misalkan x_n dan y_n, yang memenuhi sistem persamaan beda linear yang diberikan untuk setiap n, dengan n = 0, 1, 2, ...

[Farlow, 1994] Definisi 7 (Titik Tetap)

Misal kan diberikan sistem persamaan beda sebagai berikut:

(

1, 2,...,

)

k n k n k n k

y ₊ = f y _{+ -} y _{+ -} y

dengan y_n merupakan sebuah nilai anggota barisan bilangan dari persamaan di atas, dengan n = 0, 1, 2, ...

Titik tetap y diperoleh dari nilai yang memenuhi hubungan berikut:

1 1 ...

n n n y

y y y

+ = = - = =

[Kaplan, 1995] 2.2 Analisis Kestabilan Titik Tetap pada Orde Tiga atau Lebih pada Persamaan Beda

Diberikan sistem persamaan beda sebagai berikut:

(

)

(

)

(

)

1 1 1 ₂ 1 , ,..., , ,..., , ,...,

...

n n n

n _n n n

x

z

f x y z

y f x y z

f x y z

+ + + = = =

Dapat diperoleh matriks Jacobi sebagai berikut:

1 1 1

2 2 2

n n n

f f f

x y z

f f f

x y z

f f f

x y z

J

¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶ ¶

é

ù

ê

ú

ê

ú

ê

ú

ê

ú

ê

ú

ê

ú

= ê

ú

ê

ú

ê

ú

ê

ú

ê

ú

ê

ú

ê

ú

ë

û

L

M

M O

M

L

sehingga diperoleh persamaan polinomial nilai eigen (l) dari persamaan karakterist ik

0 J- lI = , yaitu:

1

1 1

( ) n n ... _n _n

Pl =l + al - + + a_- l + a

Agar titik tetap stabil, dip enuhi:

1. P(1)=1+a₁+ a₂+ ...+a_n_-₁+ a_n >0 2.

(

1

)

n

( )

1

(

1

) ( )

n

[

1n ₁

(

1

)

n 1

P- - a -

-- = - +

( ) 1 1

... an- - an

]

0

+ +

+

>

[Kaplan, 1995] 2.3 Metode Rekursif untuk Mencari Solusi

Persamaan Beda

Misalkan diketahui sebuah persamaan beda berorde 1 sebagai berikut:

1 0

n n k

(12)

Misalkan diketahui persamaan beda orde 2 sebagai berikut: y_n₊₂+ y_n₊₁+y_n+ k=0 Untuk mendapatkan nilai y_n₊₂ maka harus diketahui nilai dari y_n₊₁ dan y_n.

Misalkan diketahui persamaan beda orde 3 sebagai berikut:

3 2 1 0

n n n n k

y ₊ + y ₊ + y ₊ + y + = Untuk mendapatkan nilai y_n₊₃ maka harus diketahui nilai dariy_n₊₂, y_n₊₁ dan y_n. Misalkan diketahui persamaan beda orde m, sebagai berikut:

1 ... 1 0

n m n m n n k

y₊ + y _{+ -} + + y ₊ + y + =

Untuk mendapatkan nilai y_n₊_m maka harus diketahui nilai dari y_{n m}_{+ -}₁, y_{n m}₊ _-₂, ..., y_n₊₁

dan y_n.

D apat disimpulkan bahwa untuk mendapatkan nilai dari y_n harus diketahui n nilai y sebelumnya, yaitu dari nilai y₀ hingga nilai y_n_-₁, dengan n = 1, 2, 3, ...

Proses di atas disebut metode rekursif untuk memperoleh solusi persamaan beda.

[Farlow, 1994] 2.4 Model Kermack – McKendrick

Model Kermack-McKendrick terdiri atas sebuah sistem dari 3 persamaan diferensial biasa taklinear, sebagai berikut:

dS SI dt = −β

dI

SI I dt =β −γ dR

I dt =γ

dengan t adalah waktu, S (t) adalah bany aknya orang sehat yang rentan, I (t) adalah banyaknya orang yang terinfeksi, R (t) adalah banyaknya orang yang telah sembuh dan berkembang menjadi imun terhadap infeksi, β adalah tingkat infeksi, dan γ adalah tingkat penyembuhan.

[Weisstein EW dan Weissten T, 2004]

III PEMBAHASAN

3.1 Diskretisasi Fungsi Eksponensial Fungsi eksponensial pada umumnya berbentuk f

( )

x =ex, dengan e adalah konstanta Euler. Fungsi eksponensial di atas merupakan bentuk solusi untuk sebuah laju pertumbuhan eksponensial (exponential growth). Laju pertumbuhan eksponensial merupakan sebuah model yang terbentuk karena terdapat sebuah variabel yang berkembang secara eksponensial terhadap waktu. Misalkan W adalah sebuah variabel yang berkembang terhadap waktu (t). Hubungan pertumbuhan W terhadap t dapat dituliskan dalam bentuk persamaan diferensial sebagai berikut:

( )

t ...(1.1) dW

k W dt =

dengan k adalah kon stanta proposional yang menggambarkan laju pertumbuhan dari W. Persamaan (1.1) merupakan model pertumbuhan eksponensial dengan solusi:

( )

t ₀ kt ...

( )

1.2

W =W e

dengan W0 adalah kondisi awal dari W (lihat

Lampiran 1).

Untuk mendapatkan bentuk diskret dari fungsi eksponensial pada pesamaan (1.1), akan dilakukan proses transformasi yang disebut diskretisasi. Langkah dari proses diskretisasi adalah sebagai berikut:

Karena dW

dt

adalah laju pertumbuhan W terhadap waktu t, maka :

(

) ( )

( )

0

lim

W t t W t

dW

k W t t

dt t→

+∆ −

= =

∆ ∆

Pada model diskret diambil ∆ =t 1, sehingga

( ) ( )

( )

1 1 1

W t W t

k W t

W t W t k W t

+ − =

Dengan memisalkan W t( )=x_n dan t=n, didapatkan:

( )

(

)

1 1 1 1 1

n n n

n n

t t t k

k

W W k W x x x

x x x

x k x

(13)

D ari proses di atas diperoleh persamaan diskret untuk fungsi eksponensial, sebagai berikut:

( )

1 1 ...(1.3)

n k n

x ₊ = + x

dengan k adalah konstanta proposional yang menggambarkan laju pertumbuhan dari W. Persamaan (1.3) merupakan model diskret pertumbuhan eksponensial dengan solusi:

( )

1 ₀ ...(1.4) n

n k

x = + x

dengan x0 adalah kondisi awal dari

x

n (lihat

Lampiran 2).

Setelah dilakukan diskretisasi pada fungsi eksponensial, akan dilakukan simulasi numerik dengan menggunakan software Mathematica 6 untuk mendapatkan graf ik perkembangan W(t) dan

x

n, sehingga dapat

dibandingkan apakah grafik dari persamaan

diskret hasil transformasi fungsi eksponensial sama dengan grafik dari fungsi aslinya (persamaan (1.1)). Dengan memilih nilai awal untuk W(t) dan

x

n, diambil W(0) =

x

0 = 2,

akan diperlihatkan grafik perkembangan W(t) dan

x

n pada beberapa nilai parameter k

berbeda.

Dengan menggunakan persamaan (1.2) sebagai fungsi kontinu eksponensial:

( )

₀ kt

t

W =W e

dan persamaan (1.4) sebagai fungsi eksponensial diskret:

( )

1 ₀

n

n k

x = + x

Didapatkan grafik perkembangan W(t) dan

x

n

dengan berbagai kasus pada nilai k tertentu, sebagai berikut:

Nilai

k

Fungsi Eksponensial Diskret

( )

1 ₀

n

n k

x = + x

Fungsi Eksponensial Kontinu

( )

₀ kt

t

W =W e

0.2

0

(14)

-1

-1.7

-2

-2.2

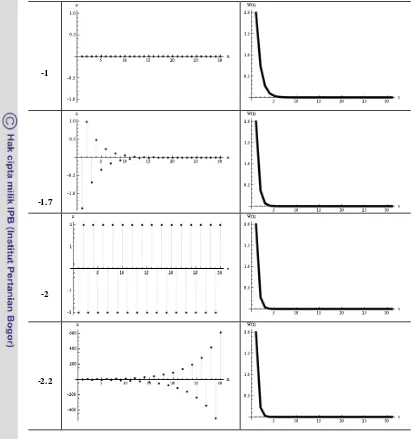
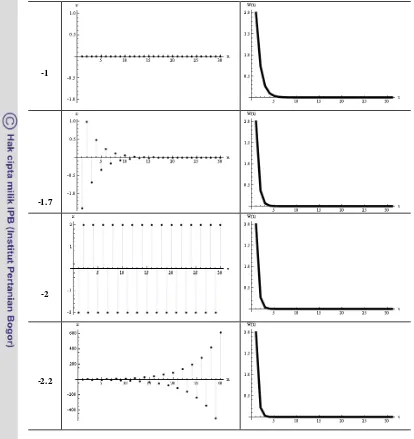
Gambar 1 Perbandingan grafik fungsi eksponensial kontinu dan diskret terhadap k. Secara umum terdapat 3 macam kasus

perkembangan W t( ) berdasarkan batas nilai k pada fungsi eksponensial kontinu (persamaan (1.2)), yaitu:

1. k > 0, perkembangan W t( ) akan terus meningkat hingga mendekati 8 seiring berjalannya waktu (t). Lihat G ambar 1 pada k = 0.2.

2. k = 0, perkembangan W t( ) akan selalu sama dengan nilai awalnya (W0) untuk

setiap t. Lihat G ambar 1 pada k = 0. 3. k < 0, perkembangan W t( ) akan terus

menurun hingga mendekati 0 seiring

berjalannya waktu (t). Lihat G ambar 1 pada k < 0.

(15)

namun terdapat beberapa kasus pada fungsi eksponensial diskret yang tidak terdapat pada fungsi eksponensial kontinu.

Secara umum terdapat 7 kasus khusus perkembangan

x

n berdasarkan batas nilai k

pada fungsi eksponensial diskret (persamaan (1. 4)), yaitu:

1. k > 0, perkembangan

x

n akan terus

meningkat hingga menuju 8 seiring berjalannya waktu (n). Lihat Gambar 1 pada k = 0.2.

2. k = 0, perkembangan

x

n akan selalu sama

dengan nilai awalnya (

x

0) untuk setiap n.

Lihat G ambar 1 pada k = 0.

3. -1 < k < 0, perkembangan

x

n akan terus

menurun hingga mendekati 0 seiring berjalannya waktu (n). Lihat Gambar 1 pada k = -0.3.

4. k = -1, perkembangan

x

n akan selalu

berada pada

x

= 0 untuk setiap n. Lihat Gambar 1 pada k = -1.

5. -2 < k < -1, perkembangan

x

n akan

berosilasi dan konvergen menuju 0 seiring berjalannya waktu (n). Lihat Gambar 1 pada k = -1.7.

6. k = - 2, perkembangan

x

n akan berubah

secara periodik pada

x

= -2 pada n ganjil dan

x

=

2 pada n genap. Lihat G ambar 1 pada k = -2.

7. k < -2, perkembangan

x

n akan berosilasi

dan divergen seiring berjalannya waktu (n). Lihat G ambar 1 pada k = -2.2.

3.2 Diskretisasi Fungsi Logistik Tinjau persamaan berikut :

( ) ( )

' t 1 t (2.1)

dS S S rS dt K = =





−









dengan:

• S

( )

t : banyaknya mangsa pada saat t • r : laju pertumbuhan S terhadap waktu

(t)

• K : daya dukung kondisi lingkungan bagi mangsa

Persamaan (2.1) merupakan fungsi logistik kontinu dengan solusi sebagai berikut:

( )

(

)

...(2.2)

1 rt K S t be− = + (lihat Lampiran 3)

Selanjutnya, dengan menggunakan proses seperti pada fungsi eksponensial , akan dilakukan proses transformasi (diskretisasi) untuk mendapatkan persamaan beda dari

sebuah fungsi logistik kontinu. Langkah dari proses diskretisasi adalah sebagai berikut: Karena dS

dt

adalah laju pertumbuhan S terhadap waktu t, maka:

(

) ( )

( )

lim 1

0

S t t S t

dS S t

rS t t

dt t K

+∆ − = _∆ = − ∆ →













( ) ( )

( )

1 1 1 1 1

S t S t S t

rS t

K

S t

S t S t rS t

K + − = − + − = −

























Dengan memisalkan S t( )=x_n dan t=n, didapatkan:

( )

1 1 1 1 1 1

n n n

t

t t t

xn r K xn r K S

S S rS

K

x x x

+ + +   − = _ − _   → = +  −    − = − →













Dari proses diskretisasi di atas didapatkan fungsi logistik diskret dari persamaan (2.1) adalah:

1 1 ...(2.3)

n

n n r n _K

x x ₊ =x + x





−









Setelah dilakukan diskretisasi pada fungsi logistik kontinu, akan dilakukan simulasi numerik dengan menggunakan software Mathematica 6 untuk mendapatkan grafik perkembangan S(t) dan

x

n, sehingga dapat

dibandingkan apakah grafik dari persamaan diskret hasil transformasi fungsi logistik sama dengan grafik dari fungsi aslinya (persamaan (2.1)). Dengan memilih nilai awal untuk

x

n

dan nilai K, diambil

0

x = 0.5 dan K = 2, akan diperlihatkan grafik perkembangan S(t) dan

x

n

pada beberapa nilai parameter r berbeda. Dengan menggunakan persamaan (2.2) sebagai fungsi logistik kontinu:

_{( )}

(

1 rt

)

K S t

be− =

+

dan persamaan (2.3) s ebagai fungsi logistik diskret:

1 1

n

n n r n _K

x x ₊ =x + x





−









, didapat grafik perkembangan S t( ) dan

x

n pada

(16)

Nilai r

Fungsi Logistik Diskret

1 1

n

n n r n _K

x x ₊ =x + x





−









Fungsi Logistik Kontinu ( )

(

1 rt

)

K S t

be− =

+

r =0

r =0.7

r =1.8

r =2

(17)

r =2.5

r =2.74

r =3

r =3.5

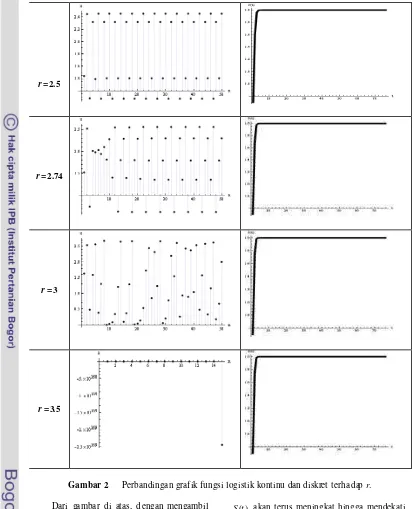
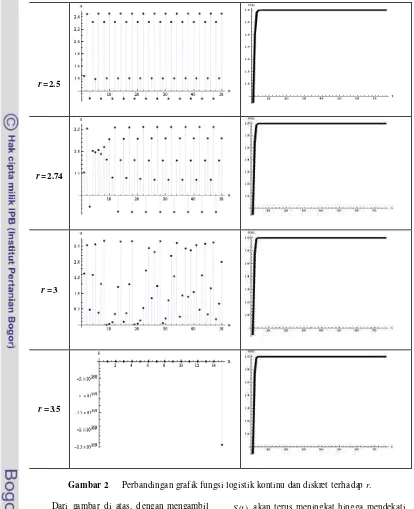
Gambar 2 Perbandingan grafik fungsi logistik kontinu dan diskret terhadap r. Dari gambar di atas, dengan mengambil

sembarang nilai 0

x , S(0), dan K, contoh: 0

x = S(0) = 0.5 dan K = 2, dapat dilihat beberapa perbedaan antara fungsi logist ik kontinu dengan fungsi logistik diskret. Pada fungsi logistik kontinu, dapat dilihat pada Gambar 2, pada r = 0, perkembangan S t( )

selalu berada pada S(0) untuk setiap t, sedangkan pada saat r > 0 pola p erkembangan

( )

S t akan terus meningkat hingga mendekati nilai S t( ) = 2, karena sebelumnya telah diambil nilai K = 2, sebagai batas atas perkembangan S t( ).

Sedangkan pada fungsi logistik diskret, terdapat beberapa perbedaan dibandingkan dengan fungsi logistik kont inu. Sama dengan fungsi logis t ik kont inu, pada r = 0, perkembangan

x

n fungsi logistik diskret juga

akan selalu berada pada

x

0 untuk set iap n.

(18)

khusus yang tidak terjadi pada fungsi logistik kontinu. Secara umum perkembangan

x

n

pada fungsi logistik diskret dapat dikelompokkan dalam beberapa kasus berdasarkan batas r, sebagai berikut:

1. r = 0, perkembangan

x

n akan selalu

berada pada

x

0 untuk s et iap n. Lihat

Gambar 2 pada r = 0.

2. 0 < r < 1.2, perkembangan

x

n akan terus

meningkat hingga mendekati K, lihat Gambar 2 pada r = 0.7.

3. 1.2 = r < 2.1, perkembangan

x

n akan

berosilasi dan konvergen mendekati nilai K seiring berjalannya waktu (n) , lihat Gambar 2 pada r = 1.8 dan r = 2. 4. 2.1 = r < 2.4, perkembangan

x

n akan

berubah berpola periodik.

x

n berada

disekitar K pada n genap dan

x

n berada

disekitar 0 pada n ganjil dan terus berkembang dengan pola yang sama. Lihat G ambar 2 pada r = 2.3.

5. 2.4 = r = 2.6, perkembangan

x

n akan

berubah berpola periodik pada nilai

x

n

tertentu saat n tertentu yang disebut dengan pola periodik stabil periode 2. Lihat G ambar 2 pada r = 2.5.

6. 2.6 < r = 2.85, perkembangan

x

n akan

berubah berpola periodik pada nilai

x

n

tertentu saat n tertentu yang disebut dengan pola periodik stabil periode 4. Lihat G ambar 2 pada r = 2.74.

7. 2.85 < r = 3, perkembangan

x

n akan

berubah berpola acak yang disebut dengan chaos. Kasus ini merupakan kasus unik pada fungsi logistik diskret. Lihat Gambar 2 pada r = 3.

8. r > 3, perkembangan

x

n akan

berkembang terus menurun dan divergen menuju -8 . Lihat G ambar 2 pada r = 3.5. Dapat disimpulakan bahwa, fungsi logistik diskret memiliki semua kasus dalam fungsi logistik kontinu, namun terdapat beberapa kasus pada fungsi logistik diskret yang tidak terdapat pada fungsi logistik kontinu.

3.3 Diskretisasi Sistem Persamaan Diferensial

3.3.1 Model kontinu wabah penyakit

AIDS : Model SIA

Titik pangkal model in i adalah model SIR, yang diperkenalkan pa da t ahun 1927 oleh Kermack dan McKendrick (Weisstein EW dan Weissten T , 2004) . Pada model tersebut, populasi (N) dikelompokkan menjadi 3

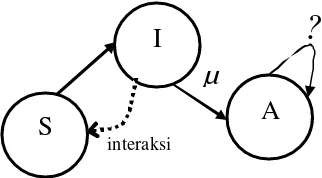
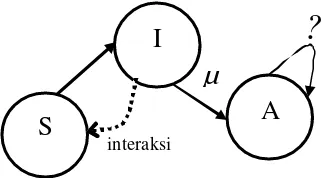
bagi an, yaitu populasi individu rentan terserang infeksi (S), populasi individu terinfeksi dan dapat menginfeksi individu lain (I), dan pop ulasi individu yang telah pulih dari infeksi atau meninggal (R). Namun, berdasarkan model di atas, yang digunakan pada model kali ini adalah model SIA yang juga membagi populasi (N) menjadi 3 bagian, yaitu: Pertama, populasi individu sehat tapi rentan terserang infeksi, (S). Kedua, populasi indiv idu positif terinfeksi HIV, masih berinteraksi dengan individu populasi pertama dan dapat menginfeksi individu populasi tersebut, (I). Ketiga, populasi individu terinfeksi HIV namun tidak dapat menginfeksi individu lainnya (termasuk individu yang telah meninggal) (A), seperti yang ditunjukkan pada Gambar 3.

Peningkatan jumlah individu dalam populasi terinfeksi (I) dan meninggal (A) bergantung pada kuantitas interaksi populasi terinfeksi dengan individu populasi rentan, sehingga dibutuhkan pembatas antara populasi yang satu dengan yang lainnya. Untuk mendapatkan pembatas populasi yang lebih baik, dipengaruhi beberapa asumsi yang tepat, guna membangun model yang lebih baik dan seseder hana mungkin. Asumsi-asumsi yang digunakan adalah:

1. Jumlah awal populasi individu rentan adalah tetap dan akan terus menurun dengan bertambahnya waktu.

2. Efek kematian alami ketiga populasi tersebut dapat diabaikan.

Hubungan ketiga populasi tersebut dapat dituliskan sebagai berikut :

( )

, , .. 3.1

dS dI dA

SI SI I I A

dt= - dt= - m dt=m-l dengan:

m= tingkat kematian individu penderita AIDS

l = tingkat kesembuh an individu penderita AIDS

µ

S

I

A

Gambar 3 Model penyebaran AIDS.

?

(19)

dengan l > m

(

> 0

)

disebabkan karena evolusi terhadap kematian lebih cepat daripada daya tahan leukosit (seropositivity) dalam menghadapi virus HIV.

(Tamizhmani et al, 2004) Model kontinu yang diberikan pada persamaan (3.1) dapat dinyatakan juga sebagai berikut :

(

S+ I

)

'= - mI ...(3.2)

(

S+ I+ A

)

'= -lA ...(3.3) (lihat Lampiran 4)

3.3.2 Diskretisasi Model Kontinu Penyebaran AIDS

Model kontinu yang diberikan dapat dinyatakan dalam model diskret dengan melakukan transformasi dari model kontinu menjadi model diskret yang disebut diskretisasi. Pendekatan dasar yang sama seperti pada persamaan logistik maupun fungsi eksponensial akan digunakan pada model ini. Dimulai dengan persamaan

d S S I d t =

sebelumnya akan dianalogikan

dengan bentuk diskret 1 1 n n n x x y + = +

. Proses diskretisasi tersebut didapat dengan memisalkan x_n =S t( ), y_n=I t( ), z_n=A t( ),

t= n dan memisalkan parameter m= 1- a

dan l =1- b.

Diketahui bahwa dS S'( )t

dt = , maka

dapat dicari analogi diskretnya dengan cara sebagai berikut:

( )

(

) ( )

0 ' lim t

S t t S t S t t ∆ → + ∆ − = ∆

( ) ( )

1 1 1 S S

t S t

+ − =

= + −

Dengan memisalkan x_n=S t( ), y_n=I t( ) dan

t= n maka didapat:

( ) ( )

1 n1 n

n

S t S t x x

x

+

+ − → −

→ ∆

Setelah diketahui S t'

( )

= Dx_n, dari model diskret ₁

1 n n n x x y + = + didapat :

(

)

( )

1 1 1 1 1 1 1 1 1 n n

n n n

n

n n n

n

n n n

n

n n

y

x

x x x

y

x x y x

x x x y

x x y

+ -+ + + + + + + + = = = = -= ® + ® ® ® D

Dengan memisalkan x_n =S t( ), y_n=I t( ) dan

t= n maka didapat:

( )

1 n ' ( 1) ( )

n n

x x y S S t I t

dS SI dt

+

-D = ® = - +

® =

-Dengan ini telah ditunjukkan diskretisasi dari sistem kontinu dS _SI

dt =

menghasilkan

sistem diskret ₁

1 n n n x x y + = +

. Dengan menggunakan persamaan (3.2) dan (3.3) serta melakukan proses diskretisasi yang sama dengan proses di atas, akan didapat bentuk diskret dari persamaan dI _dan dA

dt dt

pada sistem persamaan diferensial (3.1), lihat Lampiran 5.

Model diskret yang menggambarkan penyebaran virus HIV sebagai hasil transformasi dari model kontinunya dituliskan sebagai berikut :

n+1 n

n x

x =

1 + y , n+1 n

n n n x y y = ay +

1 + y ,

(

)

n+1 n n

z

= 1- a y + ß z

…….. (3.4) dengan :

n

x = banyaknya individu populasi rentan pada waktu ke-n

n

y = banyaknya individu populasi terinfeksi pada waktu ke-n

n

z = banyaknya individu populasi meninggal atau telah sembuh pada waktu ke-n

a

= 1- mdan b = 1- l

(20)

Untuk kedua parameter, didapatkan

1

b< a< yang berkorespondensi pada fakta bahwa l > m> 0 pada limit kontinu.

Dengan melakukan simulasi komputer menggunakan software mathematica 6 didapatkan grafik dari model kontinu penyebaran AIDS dan model diskretnya, sehingga dapat dibandingkan antara kedua

model tersebut. Dengan memisalkan nilai awal dari masing – masing varibel adalah

0

(0)

95

x

=

S

=

, y₀

=

I

(0)

=

0.01

, dan

0

(0)

0.01

z

=

A

=

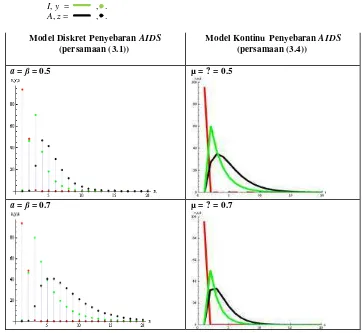
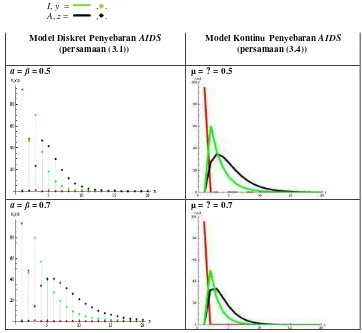
. Didapatkan grafik perkembangan ketiga variabel pada model penyebaran AIDS kontinu dan diskret terhadap beberapa nilai parameter , sebagai berikut:

Keterangan : S, x = , . I, y = , . A, z = , .

Model Diskret Penyebaran AIDS

(persamaan (3.1))

Model Kontinu Penyebaran AIDS (persamaan (3.4))

a = ß = 0.5 µ = ? = 0.5

a = ß = 0.7 µ = ? = 0.7

Gambar 4 Perbandingan grafik m odel penyebaran AIDS kontinu dan diskret. Dapat dilihat pada gambar di atas, bahwa

grafik perkembangan dari x, y, z dari model diskret hasil transformasi model kont inu dari model penyebaran AIDS. Grafik model diskret memperlihatkan bentuk yang sama dengan model asalnya, model kontinu. Tidak terdapat perbedaan yang signifikan antara

(21)

IV SIMPULAN dan SARAN

I. Simpulan

Proses transformasi model kontinu menjadi model diskret disebut diskretisasi. Proses ini dilakukan pada fungsi eksponensial kontinu, fungsi logistik kontinu dan model kontinu penyebaran AIDS pada jurnal (Tamizhmani K. M, 2004), didapatkan fungsi eksponensial diskret, fungsi logistik diskret dan model diskret penyebaran AIDS.

Melalui proses simulasi numerik, dengan menggunakan software Mathematica 6, didapatkan grafik perkembangan setiap variabel dari fungsi eksponensial, fungsi logistik dan model penyebaran AIDS terhadap beberapa parameter tertentu. Dengan membandingkan grafik model kontinu dengan grafik model diskretnya, didapat beberapa perbedaan, terutama pada fungsi eksponensial dan fungsi logistik.

Fungsi eksponensial kontinu memiliki 3 pola perkembangan variabelnya berdasarkan batas parameter k, dengan nilai aw al variabel = 2, yaitu: k > 0, k = 0, k < 0. Fungsi eksponensial dis kret memiliki 7 pola perkembangan variabelnya berdasarkan batas parameter k, dengan nilai awal variabel = 2, yaitu: k > 0, k = 0, -1 < k < 0, k = 1, 2 < k < -1, k = -2, k < -2. Fungsi eksponensial diskret memiliki semua pola perkembangan variabel pada fungsi eksponensial kontinu , namun

fungsi eksponensial kontinu tidak memiliki semua pola perkembangan variabel pada fungsi eksponensial diskret.

Fungsi logistik diskret memiliki semua pola perkembangan variabel pada fungsi logistik kontinu, namun fungsi logistik kontinu tidak memiliki semua pola perkembangan variabel pada fungsi logistik diskret. Fungsi logistik diskret memiliki 8 pola perkembangan variabel berdasarkan parameter laju pertumbuhan (r), dengan nilai awal variabel = 0.5 dan K = 2, yaitu pada: r = 0, 0 < r < 1.2, 1.2= r < 2.1, 2.1= r < 2.4, -2.4 = r = 2.6, 2.6 < r = 2.85, 2.85 < r = 3, dan r > 3.

Pada model penyebaran AIDS terdapat beberapa proses penyederhanaan pesamaan diferensial model aslinya untuk memudahkan dalam proses transformasi untuk mendapatkan model diskretnya. Pada model penyebaran AIDS, model diskret hasil transformasi dapat mengimplementasikan model kontinunya. II. Saran

Apabila ada yang ingin melanjutkan tulisan ini, disarankan agar membahas tentang proses diskretisasi pada fungsi kontinu lain selain fungsi eksponensial dan logistik sehingga dapat diimplement as ikan pada pemodelan fenomena-fenomena diskret.

V DAFTAR PUSTAKA

Farlow SJ. 1994. An Introduction to Differential Equations and Their Applications. McGraw Hill, New York. Kaplan D, Glass L. 1995. Understanding Non

Linear Dynamics. Springer-Verlag. New York

Murray JD. 1993. Mathematical Biology. Springer, Berlin.

Tamizhmani KM, Ramani A, Grammaticos B, Carstea AS. 2004. Modelling AIDS Epidemic and Treatment with Difference Equations. Advance in Difference Equations. 3: 183–193.

(22)

(23)

LAMPIRAN 1 Solusi Persamaan (1.1)

( )

dW

kW t dt =

Dengan menggunakan cara pemisahan variab el didapatkan:

( )

1

dW dW

kW t kdt

dt W t

dW kdt W t

= → =

→ =

Kemudian dengan mengintegralkan kedua ruas persamaan didapatkan:

( )

1 ₁

ln , dengan 0

ln

dW kdt dW kdt

W t W t

W t kt c W t

W t _kt

e e

c kt

W t e e

= →∫ =∫

→ = + >

→ =

Dengan W

( )

0 =ec maka didapat:

( )

c kt

( )

0 kt

W t =e e →W t =W e

Didapat solusi untuk persamaan (1.1) sebagai berikut:

( )

0 kt

W t =W e

LAMPIRAN 2 Solusi Persamaan (1.3)

( )

1 1 1 1

n k n n k n

x ₊ = + x →x = + x ₋

Dengan menggunakan metode rekursif, dengan memasukkan nilai n = 0, 1, 2, 3, ..., m, didapat:

( )

( ) ( )

(

)

( )

( ) ( )

(

)

( )

( ) ( )

(

)

( )

1 1 0

1

2 1

1 1 ₀

2

1 ₀

1

3 2

2

1 1 ₀

3 1

0

1 ₁

1

1 1 ₀

1 0 untuk =0

untuk =1

u n t u k = 2

untuk =

k k

k k x

k k

k k x

k

m m

m

k k x

m k

n x x

x

n x x

x

n m x x

x = + = + = + + = + = + = + + = + = + ₋ − = + + = + → → → →

M

Didapat solusi untuk persamaan (1.3) sebagai berikut:

( )

1

0 n k n

(24)

LAMPIRAN 3 Solusi Persamaan (2.1)

( )

' t 1 t

dS S

S rS

dt = = − K













Dengan menggunakan cara pemisahan variab el didapatkan:

( )

(

( )

)

( )

(

( )

)

1 1

1

dS S t dS

rS t rdt dS r d t

S t S t

K

dt _{S t} _{S t}

K K

dS r d t dS rdt

S t K S t S t K S t

K K K

K K

dS rdt dS r d t

S t _{K S t} _{S t K S t}

 

=  − → _ _= → _ _ =

  ₋ ₋

   

   

→ = → =

−

   

−

   

   

→ = → =

− −

Kemudian dengan mengintegralkan kedua ruas persamaan didapatkan:

( )

(

( )

)

( )

(

( )

)

1 K K

dS rdt dS rdt

S t K S t− = →∫S t K S t− =∫

Dengan m enggunakan fraksi parsial untuk ruas kanan persamaan di atas, didapat:

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

)

( )

(

( )

)

( )

(

( )

)

( )

(

) ( )

( )

)

K A B

K

dS

S t K S t S t K S t S t K S t

A K S t B S t K

S t K S t S t K S t

K AK B A S t

S t K S t S t K S t

→ = +

∫ ₋

− −

− +

→ =

− −

+ −

→ =

− −

Diketahui bahwa K=AK dan

(

B A S t−

) ( )

=0maka didapat:

(

) ( )

(

)

( )

(

)

1

0 0,karena 0

1 0 1

K AK A

B A S t B A S t

B B

= → =

− = → − = ≠

→ − = → =

Dengan memasukkan nilai A dan B didapat:

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

1 1

K A B

K

dS

S t K S t S t K S t S t K S t

K

S t K S t S t K S t

K

dS dS

S t

S t K S t K S t

→ = +

∫

− − −

→ = +

− −

= +

∫ ∫

(25)

( )

(

( )

)

( )

(

( )

)

( )

(

( )

)

( )

(

)

( )

(

)

( )

(

)

( )

(

( )

)

1 1 ln ln ln ln K

dS rdt dS rdt

S t

S t K S t K S t

S t K S t rt c

S t K S t

S t rt c

rt c e e

K S t

S t rt c rt c

e S t K S t e

K S t

= → + = ∫ ₋ ∫ ∫ ₋ ∫ → − − = + − ₊ → = + → = − + + → = → = − −

Karena S t

( )

>0, maka S t

( )

=S t( ), jadi S t( )=

(

K S t−

( )

)

ert c+ . Karena K adalah batas atas perkembangan S(t), maka K > S(t) sehingga

(

K S t−

( )

)

>0, maka

(

K S t−

( )

)

=

(

K S t−

( )

)

, jadi

( )

(

)

( ) rt c

S t = K S t− e + , sehingga

( )

(

)

( )

(

)

( )

(

)

( ) 1 1 rt c

S t K S t e

rt c rt c

S t Ke S t e

rt c rt c

S t S t e Ke

rt c rt c

S t e Ke

rt c Ke S t rt c e + → = − + + → = − + + → + = + + → + = + → = + +

Dengan mem bagi ert c+ dengan ert c+ pada ruas atas dan bawah, didapatkan:

( )

₍ ₎

( )

1

1 ₁

1 1

rt c c rt

rt c e K

rt c _K

e

S t S t

rt c e

rt c

rt c _e

e

K K

S t S t

e− + e− e−

+ + → = ₊ → =  ₊    +   _ ₊ _  +  _ _   → = → = + ₊

Dengan memisalkan e−c= b didapatkan:

( )

1 rt K S t be− = +

(26)

LAMPIRAN 4

Penurunan persamaan (3.2) dan (3.3) dari persamaan (3.1)

Dari persamaan (1.1) diketahui bahwa:

( ) ( )

t t ,

( ) ( )

t t

( )

t ,

( )

t

( )

t

d S d I d A

S I S I I I A

d t = - d t = - m d t = m - l

Dari turunan S terhadap t didapatkan:

dS

SI

S

'

SI

dt

= -

®

= -

, dari turunan I terhadap t

didapatkan: dI SI I

'

I

dt = - m

®

I

=

SI

-

m

. Karena

S

'

= -

SI

sehingga

-

S

'

=

SI

, maka didapatkan:

(

)

... terbukti( )

'

I I

I

SI

I

S

I

S

I

S

m m

m

m ®

® ®

=

-

= -

-+

=

+

=

Lalu dari turunan A terhadap t didapatkan:

dA

I

A

'

I

A

dt

=

m

-

l

®

=

m

-

l

Karena

(

I

+

S

)

'

=

-

mI sehingga

-

(

I

+

S

)

'

=

mI, maka didapatkan:

(

)

(

)

(

)

(

terbukti

)

'

...

A

I

A

I

S

A

I

S

A

I

S

A

m

l

=

-

®

= -

+

-®

+

=

(27)

-LAMPIRAN 5

Penurunan persamaan (3.4) dari persamaan (3.1)

Setelah diketahui S t'

( )

= Dx_n, d ari model diskret ₁ 1 n n n x x y + = + didapat:

(

)

( )

1 1 1 1 1 1 1 1 1 n n

n n n

n

n n n

n

n n n

n

n n

y

x

x x x

y

x x y x

x x x y

x x y

+ -+ + + + + + + + = = = = -= ® + ® ® ® D

Dengan memisalkan x_n =S t( ), y_n=I t( ) dan t= n maka didapat:

( )

1 n ' ( 1) ( )

n n

x x y S S t I t

dS SI dt

+

-D = ® = - +

® =

-Didapat model diskret dari dS SI

dt = - adalah 1 ₁

n n n x x y + = + ( ) ( ) ( ) ( )

(

)

()

(

)

()

0 dan 1 1 ( ), ( ), ( ), danparameter

dengan 1sehinggamenyebabkan 0

denganmemilih 1,maka

1

karena ( ), ( ), ( ), , maka 1

1

lim

n n n

n

S t t S t t t

S t S t

S t y I t z A t t n

dS

dt

t

S t S t

S t y I t z A t t n

S t S t

x

b a l m

m

a

l

b

®

+

+ D -D D

+

-=

= = = =

(28)

( )

(

) (

)

(

)

1 1 1 1 1 1 1 1 1

1

n n n

n n n n n

n

n n n n

n

n n

n n n n

n n

dI

dS

SI

I

I t

dt

dI

dS

I t

dt

y

x

y

x

y

x

y

x

y

x

y

x

y

x

y

x

y

m

+ + + + + + + + +

æ

ö

÷

ç

=

-

Þ

= -

ç

÷

-çè

ø

Þ

+

=

-Þ D

+ D

=

-Þ

-

+

-

=

-Þ

-

+

-

=

-Þ

-

+

-

=

-Þ

-

+

-

=

-+

æ

+

ö

÷

ç

÷

Þ

-

+

-

ç

÷

=

-÷

ç

+

è

+

ø

Þ

-

(

)

(

)

(

)

(

)

(

)

1 1 1 1 1

karena maka sehingga

terbukti

1

...

1

n n n

n n

n n n n

n n n

n

n n

n n n

n

n n

n n n

n n n n n n n n n n n

x

y

x

x y

y

x y

y

x y

y

x y

y

x y

y

m

a

m

(29)

( )

1

dari pembuktian diatas didapatkan bahwa

:

,

maka

n n n n

n

dA

I t

A t

dt

dI

dS

dI

dS

I t

dt

dA

dI

dS

A t

dt

dA

dI

dS

A t

dt

dA

dI

dS

A t

dt

z

y

x

z

m

l

m

l

+

=

-æ

ö

÷

ç

+

= -

ç

çè

+

÷

ø

æ

ö

÷

ç

Þ

= -

ç

çè

+

÷

-ø

æ

ö

÷

ç

Þ

+

ç

+

÷

=

-çè

ø

Þ

+

=

-Þ D + D + D

=

-Þ

(

-

) (

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1 1

1 1 1

0

1

0

1

0

1

0

1

n n n n n n

n n n n n n n

n n n n n n

n n n

n n n n n

n n

n n n

n n

n n n

n n

n

y

x

z

y

x

z

y

x

z

y

x

x y

x

z

y

x

y

x

y

x y

z

y

z

l

a

l

a

l

+ + + + + + + + + + + + + +

+

-

+

-

=

-Þ

-

+

-

+

-

=

-Þ

-

+

-

+

-

+

=

Þ

+

-

+

-

+

-

=

Þ

+

-

+

-

+

-

=

+

-

+

Þ

+

-

+

-

+

=

+

Þ

+

-

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1 1 1 1 1 1

karena maka sehingga

ter

1

0

1

0

1

0

1

...

n n n n n n

n n

n n n n

n n n

n n

n n n

x y

x

x y

z

y

x y

z

y

z

y

z

y

z

y

z

y

z

y

z

a

l

a

l

a

l

a

l

a

l

b

l

a

b

+ + + + + +

-

-+

-

+

=

+

Þ

+

-

+

-

+

-

=

+

Þ

+

-

+

-

=

Þ

= -

-

-Þ

=

-

+

-Þ

=

-

+

-= -

=

(30)

LAMPIRAN 6

Program Mathematica Fungsi Eksponensial Kontinu (1.1)

LAMPIRAN 7

Program Mathematica Fungsi Eksponensial Diskret (1.2)

LAMPIRAN 8

Program Mathematica Fungsi Logistik Kontinu (2.1)

LAMPIRAN 9

(31)

LAMPIRAN 10

(32)

LAMPIRAN 1 1

(33)

DISKRETISASI MODEL DINAMIK KONTINU

G54102014

(34)

M U H A M M A D A R IF TIR TA N A. D iskretisasi M odel D inam ik Kontinu. D ibim bing oleh N G A K A N K O M A N G K U T H A A R D A N A dan A L I K U SN A N T O .

D iskretisasi diperlukan untuk m endapatkan m odel dinam ik diskret dari m odel dinam ik kontinu. Proses tersebut didapat dengan m entransform asi persam aan diferensial pada m odel dinam ik kontinu m enjadi persam aan beda pada m odel dinam ik diskret.

Tulisan ini m em perlihatkan bagaim ana m em peroleh persam aan beda sebagai m odel diskret dari fungsi eksponensial kontinu dan fungsi logistik kontinu. Berdasarkan pola perilaku m odel diskret dan m odel kontinu pada fungsi eksponensial dan fungsi logistik, diperoleh bahw a sem ua pola perilaku pada m odel kontinu dim iliki oleh m odel diskret, tetapi m odel kontinu tidak m em iliki sem ua pola perilaku pada m odel diskret.

Tulisan ini juga m em perlihatkan proses diskretisasi pada sistem persam aan diferensial m enjadi sistem persam aan beda sebagai m odel diskretnya. Berdasarkan perbandingan pola perilaku m odel diskret dan m odel kontinu pada m odel penyebaran A ID S diperoleh bahw a pola perilaku pada m odel diskret m engim plem entasikan pola perilaku pada m odel kontinunya.

(35)

M U H A M M A D A R IF TIR TA N A . D iscretization of Continuous D ynam ic M odel. Supervised by N G A K A N K O M A N G K U T H A A R D A N A and A LI K U SN A N TO .

D iscretization is a process to form a discrete dynam ic m odel from a continuous one. This can be done by transform ing differential equations of continuous m odel into difference equations of discrete m odel.

This paper show s how to get the difference equations from a continuous exponential and a continuous logistic function. Based on the pattern of the continuous and the discrete m odel of exponential and logistic function, it is found that all pattern of continuous m odels are satisfied by discrete m odels, but continuous m odels don’t necessarily have all pattern of discrete m odels.

(36)

M odel matematik telah banyak digunakan pada bidang fisika dan biologi, terutama dalam masalah dinamik. Pemodelan fenomena alam yang terjadi dalam kehidupan nyata secara matematis dapat mempermudah para peneliti untuk menjelajahi efek dari perubahan–perubahan berbagai parameter yang berpengaruh dengan lebih mudah, cepat dan murah dibandingkan bila hany a bereksperimen, selain tidak murah dan memakan waktu yang cukup lama, kadang hasil yang didapat kan tidak fisibel.

Sebagian besar model matematik yang menggambarkan fenomena–fenomena alam dinyatakan dalam model kontinu. Namun, sebagian besar dari fenomena tersebut hanya berubah pada waktu–waktu tertentu dan tidak setiap saat, sehingga penggambaran secara kontinu terasa kurang tepat. Oleh karena itu diperlukan sebuah model diskret untuk mengimplementasikan fenomena–fenomena alam yang hanya berubah pada waktu–waktu tertentu, seperti proses kelahiran atau kematian, penyebaran atau penyembuhan penyakit, dan sebagainya. Meskipun begitu, terdapat beberapa model matematik yang telah menggambarkan fenomena alam secara diskret. Namun, untuk memperoleh model diskret dari sebuah model matematik yang menggambarkan fenomena alam secara

model kontinu menjadi model diskret. Bagaimanapun juga, pembentuka n sec ara eksplisit pada model matematik dibuat dengan analisis yang detail secara matematis melalui proses-proses yang lebih mudah dimengerti. M odel kontinu telah banyak digunakan dalam pemodelan, namun dalam kehidupan nyata sebagian kasus lebih berupa sistem diskret, sehingga akan lebih tepat bila menggunakan model diskret untuk menggambarkan sebagian fenomena–fenomena alam dalam kehidupan nyata. Dalam tulisan ini diperlihat kan cara memperoleh proses transformasi untuk mendapatkan model diskret yang memadai bagi sebuah sistem kontinu .

1.2 Tujuan

Tujuan dari penulisan karya ilmiah ini adalah mempelajari proses transformasi sebuah model kontinu dinamik menjadi sebuah model diskret.

1.3 Ruang Lingkup

Ruang lingkup penulisan karya ilmiah ini mencakup: (1) melakukan proses transformasi fungsi kontinu menjadi fungsi diskret pada fungsi eksponensial dan fungsi logistik; (2) merekonstruksi jurnal Modelling AIDS Epidemic and Treatment with Difference Equations oleh Tamizhmani et al, 2004.

II LANDASAN TEORI

2.1 Persamaan Beda Definisi 1 (Persamaan Beda)

Persamaan beda adalah suatu persamaan yang menghubungkan anggota–anggota yang berbeda dari barisan bilangan

{

y y y0, 1, 2,...,yn,...

}

yang akan dicari dan ditentukan nilainya.

[Farlow, 1994] Definisi 2 (O rde Persamaan Beda)

Orde persamaan beda adalah perbedaan antara indeks tertinggi dengan indeks terendah yang muncul pada persamaan yang diberikan. Misal kan diberikan persamaan seperti di bawah ini:

(

, 1, 2,...,

)

k n k n k n k

y ₊ =F k y _{+ -} y _{+ -} y

Persamaan di atas adalah sebu ah persamaan beda berorde n jika y_k yang muncul dalam fungsi F di sisi kanan adalah y dengan indeks ter endah di sisi kanan dan indeks tertinggi di sisi kanan adalah n – 1.

Contoh 1:

1 2

n n

y ₊ = y + , persamaan beda orde 1.

2 1

n n n

y ₊ = y ₊ + y , persamaan beda orde 2. dengan n = 0, 1, 2, 3, ...

[Farlow, 1994] Definisi 3 (Persamaan Beda Linear)

(37)

M odel matematik telah banyak digunakan pada bidang fisika