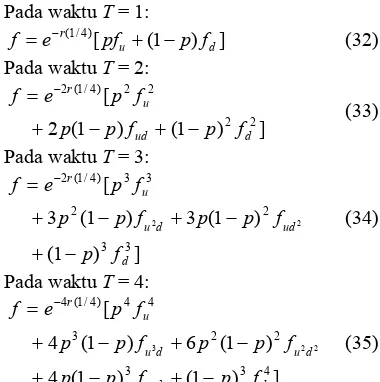Strategi Hedging pada Kontrak Asuransi Jiwa Terkait dengan Ekuitas

DIAN EKAPRATIWI

G54103048

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

DIAN EKAPRATIWI. Hedging Strategy for Equity-Linked Life Insurance Contracts. Under the direction of EFFENDI SYAHRIL and I G. PUTU PURNABA.

In this paper we consider a portofolio of equity-linked life insurance contracts and determine risk-minimizing hedging strategy within a discrete time set-up. The contract that we use is an equity-linked pure endowment contract under which the policy-holder receives max(S_T,K) at time T if he is still alive, where ST is the value of a stock at term T of the contract and K is a guarantee stipulated by the contract. We view the contracts as contingent claims in an incomplete model and discuss the problem of choosing an optimality criterion for hedging strategies.

DIAN EKAPRATIWI. Strategi Hedging pada Kontrak Asuransi Jiwa Terkait dengan Ekuitas. Di bawah bimbingan EFFENDI SYAHRIL dan I G. PUTU PURNABA.

Dalam tulisan ini, akan dibahas sebuah portofolio dari kontrak asuransi jiwa yang terkait dengan ekuitas dan kemudian akan ditentukan strategi hedging dalam waktu diskret yang meminimumkan risiko. Kontrak yang digunakan adalah kontrak endowmen murni yang terkait dengan ekuitas, di mana pemegang polis menerima max(S_T,K) pada waktu T jika ia tetap hidup, di mana ST adalah nilai saham pada waktu T dari kontrak dan K adalah jaminan yang telah ditentukan dalam kontrak. Kontrak dinyatakan sebagai satu kesatuan klaim dalam sebuah model tidak lengkap dan kemudian akan didiskusikan masalah bagaimana memilih kriteria optimal untuk strategi hedging yang biasa digunakan.

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada

Departemen Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

OLEH :

DIAN EKAPRATIWI

G54103048

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Menyetujui :

Pembimbing I,

Drs. Effendi Syahril, Grad. Dipl. NIP. 131 804 163

Pembimbing II,

Dr. Ir. I G. Putu Purnaba, DEA. NIP. 131 878 945

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS. Nip. 131 473 999

Alhamdulillah, puji dan syukur penulis panjatkan kehadirat Allah SWT atas rahmat serta karunia yang telah diberikan kepada penulis selama mengerjakan tugas akhir ini, sehingga penulis dapat menyelesaikannya. Tugas akhir ini berjudul ”Strategi Hedging pada Kontrak Asuransi Jiwa Terkait dengan Ekuitas”.

Selama penyelesaian tugas akhir ini, penulis banyak memperoleh bantuan, dukungan serta sumbang saran dari berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis ingin menyampaikan rasa hormat serta mengucapkan terima kasih kepada :

1. Drs. Effendi Syahril, Grad. Dipl. dan Dr. Ir. I G. Putu Purnaba, DEA., selaku dosen pembimbing atas waktu yang diberikan, kesabaran dan pengertiannya selama membimbing serta atas semangat dan motivasi yang diberikan;

2. Dr. Tony Bakhtiar, M. Sc., selaku dosen penguji atas pengertian, saran dan masukan yang telah diberikan;

3. Bapak, Ibu, Mas Rudi, Mas Dino dan Mas Ferry atas segala yang telah diberikan dan dicurahkan, dukungan, kasih sayang serta doa yang senantiasa diberikan;

4. Septi dan Ifni atas persahabatan, kasih sayang dan semangat yang selalu menyertai;

5. Keluarga besar Edelweiss atas semangat dan semua yang telah dilalui bersama, baik di saat suka maupun duka, serta kecerian yang takkan terlupakan;

6. Civitas matematika angkatan 40, Achie atas dukungan dan motivasinya, Mayang atas waktu dan bantuannya selama ini, Mufti, Mita, Vina, Mika, Abdillah, Rama, Indah dan Ami atas semangatnya, Elis dan Ulfa atas kesediaan serta keikhlasannya, Ari, Uli, Sawa, Gatha dan Walidah atas saran dan masukan yang diberikan, Aam, Lili, Manto, Kafi, Icha, Yuda, ’Nchi, Azis, Prima, Sri, Yudi, Jayadin, Rusli, Berri, Marlin, Dwi, Anton, Dimas, Ali, Rahmat, Metha, Herni, Yusuf, Demi, Nisa dan Putra atas kenangan selama menjalani masa kuliah;

7. Asih, Karin dan Narpendyah beserta keluarga yang telah memberikan semangat dan membantu dalam penyelesaian tulisan;

8. Seluruh Staff Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB atas bantuan yang telah diberikan;

9. Semua pihak yang telah membantu dalam penyelesaian tugas akhir yang tidak dapat disebutkan satu-persatu.

Penulis menyadari dalam karya tulis ini masih terdapat banyak kekurangan baik dalam hal ilmu yang disampaikan maupun dalam teknik penulisan, oleh karena itu penulis menerima kritik dan saran yang dapat membangun. Semoga karya tulis ini dapat bermanfaat bagi pembaca.

Bogor, Juli 2007

Penulis dilahirkan di Jakarta pada tanggal 27 Juni 1985 sebagai anak bungsu dari empat bersaudara pasangan Bapak Slamet Santoso dan Ibu Naniek Indiastuti. Pendidikan penulis, mulai dari SD hingga SMA ditempuh di Jakarta. Diawali dengan bersekolah di SDN 04 Petang Grogol Selatan pada tahun 1991 – 1997 kemudian melanjutkan ke SLTPN 48 Kebayoran Lama pada tahun 1997 – 2000 dan SMAN 70 Jakarta pada tahun 2000 – 2003.

Setelah tamat SMA, penulis diterima di Institut Pertanian Bogor (IPB) melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB) dan terdaftar sebagai mahasiswa Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam. Selama menempuh pendidikan di IPB, penulis aktif baik dalam kegiatan akademis maupun dalam kegiatan kemahasiswaan. Penulis menjadi pengurus Gugus Mahasiswa Matematika (GUMATIKA) pada Departemen Advokasi, Kajian Strategis dan Kesekretariatan periode 2004 – 2005, pengurus Biro Kesekretariatan Badan Eksekutif Mahasiswa (BEM) FMIPA periode 2005 – 2006 serta mengikuti beberapa kepanitian selama periode 2004 – 2006.

DAFTAR TABEL... viii

DAFTAR GAMBAR... ix

DAFTAR LAMPIRAN... x

PENDAHULUAN... 1

Latar Belakang ... 1

Tujuan... 1

LANDASAN TEORI... 2

MANAJEMEN RISIKO DAN KONTRAK OPSI... 3

Manajemen Risiko... 3

Opsi ... 3

Model Cox, Ross, Rubinstein ... 4

Strategi Self-Financing... 5

KONTRAK ASURANSI HIDUP TERKAIT DENGAN EKUITAS... 6

KESIMPULAN... 13

DAFTAR PUSTAKA... 14

Halaman

1. Hasil Perhitungan Varian dari Biaya... 12

2. Hasil Perhitungan Varian dari Total Klaim... 13

3. Rasio antara Varian dari Biaya dan Varian dari Total Klaim... 13

4. Perhitungan Varian dari Biaya untuk μ=0.1... 20

5. Perhitungan Varian dari Biaya untuk μ=0.5... 20

6. Perhitungan Varian dari Biaya untuk μ=1... 20

Halaman

1. Bukti Persamaan Nilai Risiko Netral ... 16

2. Penurunan Persamaan Harga Opsi untuk Waktu Dua Periode... 17

3. Bukti dan Penurunan Persamaan Varian dari Kerugian Pengasuransi ... 18

4. Penurunan Persamaan Nilai Risiko Netral untuk Kontrak ... 19

PENDAHULUAN

Latar Belakang

Asuransi jiwa merupakan perjanjian antara dua pihak, di mana pihak tertanggung (yang mengasuransikan dirinya) membayarkan sejumlah premi kepada pihak penanggung (pengasuransi/perusahaan asuransi) untuk mendapatkan ganti rugi atas meninggal atau hidupnya seseorang yang dipertanggungkan. Biasanya besar premi asuransi jiwa telah disepakati sebelumnya, yang besarnya bergantung pada tingkat bunga, biaya administrasi dan pajak, besarnya santunan yang diinginkan dan peluang meninggal seseorang. Peluang meninggal seseorang sendiri ditentukan berdasarkan jenis kelamin dan umur si tertanggung pada saat polis mulai berlaku. Premi yang dihitung tanpa memperhatikan faktor biaya administrasi dan pajak disebut premi bersih. Berdasarkan pembayaran klaimnya, asuransi jiwa dibedakan kedalam beberapa bentuk, salah satunya adalah endowmen murni di mana klaim akan dibayarkan jika si tertanggung hidup sampai waktu jatuh tempo.

Sesuai dengan perkembangan zaman, saat ini terdapat berbagai macam kontrak asuransi jiwa. Salah satunya adalah asuransi jiwa yang terkait dengan ekuitas seperti saham, indeks saham, dan lain-lain. Biasanya pembayaran premi pada kontrak ini dilakukan sekaligus atau dalam satuan tahun sampai waktu jatuh tempo atau sampai pada saat tertanggung meninggal dalam rentang waktu yang telah ditentukan. Klaim pada kontrak asuransi ini bersifat kontijensi yaitu pembayaran klaim bergantung pada perkembangan nilai ekuitas. Hal itulah yang membedakan tipe kontrak asuransi ini dengan asuransi jiwa tradisional.

Dalam konteks asuransi, risiko merupakan ketidakpastian dari besarnya kerugian. Walaupun terdapat dana cadangan yang telah dipersiapkan untuk digunakan pada tahun-tahun yang buruk atau pada saat semua pemegang polis melakukan klaim, perusahaan asuransi yang mengeluarkan kontrak asuransi jiwa seperti ini juga membutuhkan strategi khusus untuk mengendalikan risiko yang muncul. Strategi tersebut diperlukan karena perusahaan memiliki risiko tambahan, yaitu risiko terhadap perkembangan harga saham.

Dalam manajemen risiko, terdapat dua cara dalam pengendalian risiko yaitu pengendalian fisik (risiko dihilangkan, risiko diminimalisir) dan pengendalian finansial (risiko ditahan, risiko ditransfer). Mengeliminasi atau menghilangkan risiko berarti menghapuskan semua kemungkinan terjadinya kerugian, sedangkan meminimisasi risiko merupakan upaya untuk meminimumkan kerugian.

Salah satu strategi yang dilakukan dalam pengendalian fisik adalah dengan melakukan

strategi lindung nilai (hedging). Karena polis

asuransi jiwa umumnya merupakan kontrak jangka panjang, maka akan sangat sulit untuk

meng-hedge secara sempurna kontrak asuransi

tersebut dengan menggunakan kontrak opsi

yang mempunyai waktu maturity yang sama

panjangnya dengan kontrak asuransi jiwa tersebut (Bacinello, 2006). Dalam penentuan harga opsi, kerangka Black-Scholes mengasumsikan pasar finansial bersifat lengkap. Suatu pasar finansial dikatakan lengkap jika semua klaim kontijensinya dapat di-hedge seluruhnya dan dapat dihargai unik. Akan tetapi, pasar asuransi merupakan pasar tidak lengkap sehingga klaim kontijensi tidak dapat diduplikasi seluruhnya oleh strategi self-financing. Oleh karena itu pasar tidak lengkap dibentuk dari pasar lengkap dengan membuat kesatuan klaim bergantung pada sumber risiko tambahan yang bebas stokastik dari risiko dalam pasar finansial.

Di dalam strategi hedging, terdapat tiga

strategi yang biasa digunakan oleh perusahaan asuransi antara lain yaitu superreplikasi, pendekatan Brennan-Schwartz, dan minimisasi risiko. Dari ketiga strategi di atas akan dicari strategi dengan harga yang paling optimal untuk mengeliminasi atau meminimalkan risiko.

Tujuan

Tujuan dari karya tulis ini adalah

menelaah ulang pencarian strategi hedging

LANDASAN TEORI

Dalam bagian ini akan dijelaskan mengenai definisi dari istilah matematis yang digunakan dalam bagian selanjutnya.

Definisi 1 : Ruang Contoh

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω.

(Grimmet dan Stirzaker, 1992)

Ruang contoh dalam karya tulis ini merupakan himpunan dari semua kemugkinan hasil dari skenario pasar.

Definisi 2 : Medan -σ (σ-algebra)

Misalkan Ω suatu himpunan tak kosong.

Suatu kelas merupakan subset dari Ω

dinamakan medan-σ jika memenuhi syarat

berikut : (i)

φ

∈

(ii) Jika A

∈

maka Ac

∈

(iii) Jika A1, A2, ..., An, ...

∈

maka

∪∞ =

∈

1

i i

A

(Shreve, 1997)

Di mana

φ

merupakan himpunan kosong dan

Ac adalah komplemen dari A.

Definisi 3 : Ukuran Peluang

Misalkan Ω adalah suatu ruang contoh dari

suatu percobaan acak dan merupakan

medan-σ . Suatu fungsi P yang memetakan

unsur-unsur ke gugus bilangan real ℜ, atau

P :

→

ℜ disebut ukuran peluang jika :

1. P tidak negatif, ∀A∈ , P(A)≥0

2. P bersifat aditif tak hingga (aditif

lengkap), yaitu jika A1, ...., An ....

∈

dengan Aj∩Ak =φ,

j

≠

k

maka

∑∞

= ∞

=1 = 1

) ( ) (

n n

n

n P A

A

P ∪

3. P(Ω) = 1

Pasangan (Ω, , P) disebut ruang ukuran

peluang atau ruang peluang dengan P sebagai

fungsi gugus peluang.

(Hogg dan Craig, 1995)

Definisi 4 : Kejadian

Setiap anak gugus dari ruang contoh dinamakan kejadian.

(Grimmet dan Stirzaker, 1992)

Definisi 5 : Kejadian Saling Bebas

Misalkan (Ω, , P) adalah ruang ukuran

peluang dan A, B

∈

. Kejadian A dan B

dikatakan saling bebas jika :

) ( ). ( )

(A B P A P B

P ∩ =

Dalam kasus umum, {A ii: ∈I} dikatakan

saling bebas jika

( )

i i

i J i J

P A P A

∈ ∈

⎛ ⎞₌

⎜ ⎟

⎝

∩

⎠

∏

untuk semua subset berhingga J dari I. (Grimmet dan Stirzaker, 1992)

Definisi 6 : Peubah acak

Misalkan adalah medan-σ dari ruang

contoh Ω. Suatu peubah acak X adalah suatu

fungsi X:Ω →R dengan sifat

( )

{

ω∈ Ω:X ω ≤x

}

∈ untuk setiap x∈R.

(Grimmet dan Stirzaker, 1992)

Definisi 7 : Menyebar Bebas Stokastik Identik (b.s.i)

Barisan X1, X2, ... dari suatu peubah acak disebut menyebar bebas stokastik identik jika kesemua dari barisan tersebut bebas dan memiliki fungsi distribusi yang sama.

(Ghahramani, 2005 )

Definisi 8 : Filtrasi

Misalkan suatu himpunan tak kosong,

untuk setiap t≤T , barisan berhingga

( )

T t≤

≤

0 dikatakan filtrasi dari ruang contoh

Ω jika :

(a) Setiap adalah medan-σ dari subsets

ruang contoh Ω; dan

(b) Jika s < t maka

⊆

.

Dalam tulisan ini merupakan himpunan tak kosong dari semua informasi pada pasar asuransi dan pasar finansial.

Definisi 8 : -- measurable/ Terukur

Misalkan X suatu peubah acak yang telah

didefinisikan sebelumnya,

(

{

ω∈ Ω:X

( )

ω ≤x

}

∈ untuk setiap

x∈R), maka dapat dikatakan bahwa X

adalah t- measurable.

(Grimmet dan Stirzaker, 1992)

Definisi 9 : Ruang State

Misalkan X adalah suatu peubah acak yang

memiliki nilai pada himpunan terhitung S,

maka S dikatakan ruang state.

(Grimmet dan Stirzaker, 1992)

Definisi 10 : Proses Stokastik

Proses stokastik X = {X(t), t∈ T} adalah suatu koleksi dari peubah acak yang memetakan suatu ruang contoh Ω ke suatu ruang stateS.

(Ross, 1996)

Definisi 11 : Adapted

Misalkan Y adalah peubah acak pada ruang

ukuran peluang (Ω, , P), misalkan pula

={ , ,...} adalah filtrasi dari ruang

contoh Ω. Barisan Y ={Yn:n≥0} dikatakan

diadaptasi oleh filtrasi jika Yn adalah n

-measurable untuk semua n.

(Grimmet dan Stirzaker, 1992)

Definisi 12 : Martingale

Suatu proses stokastik {Z nn, ≥1} dikatakan

martingale jika Z_n teradaptasi dan *

1 1 2

[ _n | , ,..., _n] _n

E Z ₊ Z Z Z =Z . (Ross, 1996)

MANAJEMEN RISIKO DAN KONTRAK OPSI

Manajemen Risiko

Manajemen risiko merupakan suatu proses pengelolaan risiko dan perlindungan atas harta benda, keuntungan, serta keuangan suatu badan usaha atau perorangan dari kemungkinan timbulnya suatu kerugian karena adanya risiko tersebut. Sebagai suatu organisasi, perusahaan pada umumnya memiliki tujuan dalam mengimplementasikan manajemen risiko (PT. Asuransi Astra Buana). Tujuan yang ingin dicapai yaitu menekan atau menghapuskan risiko, mengurangi pengeluaran, menaikkan keuntungan perusahaan, menekan biaya produksi dan sebagainya.

Pada dasarnya, manajemen risiko meliputi suatu proses yang mencakup tiga tahapan. Tahap pertama adalah mengidentifikasi terlebih dahulu risiko-risiko yang mungkin

akan dialami oleh perusahaan (risk

identification). Pada tahap ini, manajer risiko berusaha menginventarisasi semua potensi risiko yang akan dihadapi. Perangkat yang dapat digunakan dalam proses identifikasi antara lain : organisational chart, flow chart, check list, dan sebagainya.

Tahap kedua dalam proses manajemen risiko adalah melakukan evaluasi/analisa risiko. Dua faktor penting yang harus diamati

dalam tahap ini adalah frekuensi dan nilai risiko (severity).

Tahap terakhir adalah pengendalian risiko. Pengendalian risiko dapat dilakukan melalui dua macam pendekatan yaitu pendekatan secara fisik dan pendekatan secara finansial. Pendekatan secara fisik dapat dilakukan melalui penghapusan, pengurangan dan pencegahan risiko. Sedangkan retensi risiko (penahanan risiko) dan transfer risiko dapat dilakukan sebagai pendekatan secara finansial dengan pertimbangan-pertimbangan tertentu.

Menahan sendiri risiko yang terjadi berarti menanggung keseluruhan atau sebagian dari risiko, misalnya dengan cara membentuk dana cadangan dalam perusahaan. Sedangkan pengalihan atau transfer risiko dapat dilakukan dengan memindahkan kerugian/risiko yang mungkin terjadi kepada pihak lain. Sebagai contoh, perusahaan asuransi akan mengalihkan risiko kepada perusahaan reasuransi.

Opsi

diantaranya adalah opsi tipe Amerika dan opsi tipe Eropa. Opsi tipe Amerika memberikan hak kepada pemegangnya untuk membeli atau menjual aset dasar pada atau sebelum tanggal jatuh tempo. Sedangkan opsi tipe Eropa memberikan hak kepada pemegangnya untuk menggunakan opsi hanya pada tanggal jatuh tempo (Bodie, Kane, dan Marcus, 2002)

Selain itu, opsi memiliki dua tipe dasar yaitu opsi beli (call option) dan opsi jual (put option). Opsi beli memberikan hak kepada pemegangnya untuk membeli suatu aset pada harga tertentu yang disebut harga eksekusi (exercise/strike price) pada atau sebelum

tanggal jatuh tempo (maturity) yang

ditentukan. Nilai pembayaran opsi beli pada waktu jatuh tempo adalah :

di mana ST merupakan harga saham pada

waktu maturity, sedangkan K adalah harga

eksekusi. Misalkan saham akan naik dengan return sebesar u dan turun dengan return

sebesar d, maka menurut Ren`o (2002), nilai

opsi beli dari portofolio tersebut adalah

((1 ) )

u

C = +u S−K + dengan peluang p dan

((1 ) )

d

C = +d S−K + dengan peluang (1-p).

Harga opsi beli tersebut dikenal dengan premi (premium).

Opsi jual memberikan hak kepada pemegangnya untuk menjual suatu aset dengan harga eksekusi tertentu pada atau sebelum tanggal jatuh temponya. Nilai pembayaran opsi jual pada waktu jatuh tempo adalah :

Sebuah opsi dikatakan in-the-money jika

penggunaannya akan menghasilkan laba dan sebaliknya, jika penggunaan opsi tersebut

tidak menguntungkan maka opsi dikatakan out

of-the-money. Lain lagi jika harga eksekusi sama dengan harga aset atau jika penggunaan opsi tersebut tidak merugikan ataupun menguntungkan, maka opsi tersebut dikatakan at-the-money. Karena nilai sekuritas derivatif bergantung pada nilai sekuritas lainnya, maka akan sangat berguna jika sekuritas ini

digunakan sebagai alat lindung nilai (hedging)

dalam manajemen risiko.

Model Cox, Ross, Rubinstein

Tehnik yang sangat berguna dan sangat populer dalam penetapan harga opsi saham adalah penetapan harga aset binomial (binomial asset pricing). Selain itu, model ini merupakan perluasan dalam bentuk diskret dari model Black-Scholes yang terkenal. Menurut Argesanu (2004), dengan model binomial atau yang lebih dikenal dengan model Cox, Ross, Rubinstein (CRR) ini, pasar finansial memiliki dua aset dasar yaitu aset

bebas risiko (obligasi atau tabungan) B,

dengan proses harga

t

t r

B =(1+ ) , t = 0, 1, ..., T ,

di mana r adalah return pada aset bebas risiko

selama (t-1, t]. Asumsikan bahwa pada setiap

waktu harga saham akan naik dengan returnu

dan turun dengan return d. Kemudian

nyatakan d<r<u untuk menghindari adanya kemungkinan arbitrage.

Aset dasar yang kedua adalah aset berisiko

(saham, indeks saham dan lainnya) S, dengan

proses harga

Misalkan sebuah portofolio dibentuk dari Δ

saham dan sejumlah aset bebas risiko B. Maka

harga dari portofolio tersebut adalah ΔS+B. Setelah mengalami proses harga, maka nilai

portofolio menjadi Δ(1+u)S+B dengan

peluang p dan Δ(1+d)S+B dengan peluang (1-p).

Dengan menotasikan C sebagai harga beli

portofolio, C=ΔS+B, akan didapatkan

kemungkinan risiko netral (risk-neutral

probabilities)

d u

d r p

− − =

*

, dan nilai risiko

netral (risk neutral valuation)

(1)

Penurunan persamaan kemungkinan risiko netral dan nilai risiko netral diatas dapat dilihat pada Lampiran 1.

Nilai risiko netral ini memiliki kaitan erat

dengan pohon binomial. Pohon binomial

merupakan diagram yang merepresentasikan aliran perkembangan saham dengan berbagai kemungkinan yang berbeda. Karena portofolio tidak memiliki risiko atau risiko netral, return yang dihasilkan harus sama dengan suku

) 1 (

) 1

( *

*

r C p C

p

C u d

+ − + =

(1+u)St dengan peluang p

St+1=

(1+d)St dengan peluang (1-p)

ST – K jika ST > K

Payoff =

0 jika ST ≤ K

0 jika ST > K

Payoff =

bunga bebas risiko. Misalkan harga saham

awal dinotasikan dengan S0 dan harga opsi

saham dinotasikan dengan f. Jika harga saham

meningkat menjadi S0(1+u) dan payoff dari

opsi adalah fu maka nilai portofolio pada

akhir masa berlakunya opsi adalah

u f u

S0(1+ )Δ− . Dan sebaliknya, jika harga

saham mengalami penurunan menjadi )

1 (

0 d

S + dan payoff dari opsi adalah fd

maka nilai portofolionya menjadi

d f d

S0(1+ )Δ− . Kedua nilai portofolio

tersebut adalah sama.

u f u

S0(1+ )Δ− =S0(1+d)Δ− fd

Sehingga

d S u S

f

fu d

0 0 −

− =

Δ (2)

Persamaan (2) menunjukkan bahwa Δ adalah

rasio dari perubahan harga opsi terhadap perubahan harga saham.

Kasus binomial ini dapat diperluas menjadi kasus dua langkah. Misalkan rentang

waktu antar setiap langkah adalah δt, akan

didapatkan harga opsi saham untuk dua periode waktu sebagai berikut :

] ) 1 (

) 1 ( 2 [

2 2 2

ud

ud uu

t r

f p

f p p f p e f

− +

− +

= − δ

(3)

di mana penurunan persamaannya dapat

dilihat pada Lampiran 2.

Persamaan tersebut sesuai dengan prinsip risk

neutral valuation sebelumnya. Faktor p, 2p (1-p), dan (1-p)2 adalah kemungkinan titik akhir atas, tengah dan bawah yang akan dicapai.

Gambar 1. Pohon binomial dengan dua

langkah

Strategi Self-financing

Suatu strategi dikatakan self-financing jika tidak ada penambahan dan pengambilan modal sepanjang periode atau dengan kata lain proses nilainya hanya dihasilkan dari keuntungan perdagangan saja. Misalkan payoff dari suatu opsi tipe Eropa adalah h, maka setiap klaim kontijensi dikatakan dapat

direplikasi jika terdapat suatu strategi

self-financing yang dapat mencapai nilai h pada

waktu T. Jika dalam suatu pasar finansial

terdapat klaim yang tidak dapat direplikasi oleh strategi tersebut, maka pasar tersebut dikatakan tidak lengkap.

Notasikan S* sebagai harga saham yang

telah didiskon, dan definisikan nilai diskon pada waktu t oleh persamaan berikut :

t t

t S

V (ϕ)=ξ *+η (4)

dengan ξ merupakan banyaknya saham dan

η merupakan nilai pada tabungan. Proses

(Vt(φ))tє {0,1,...,T} merupakan nilai diskon dari portofolio φt = (ξt, ηt), yaitu di dalam susunan

kekayaannya pengasuransi memiliki ξt saham

di mana ξt adalah t-1-measurable dan ηt

nilai pada tabungan di mana ηt adalah t

-measurable. Nilai diskon portofolio

1 ( t-1, t-1) t

ϕ₋ = ξ η pada waktu t-1, adalah

sebagai berikut :

1 *

1 1 1 1 1 1 1 1

1( ) ( − − − −) − − −

− −

− = t t t + t t = t t + t

t B S B S

V ϕ ξ η ξ η

Pada waktu t, portofolio ϕt−1 akan

disesuaikan sehingga pengasuransi akan memiliki ξt saham dengan membeli ξt −ξt−1

saham. Pembelian saham ini akan memberikan keuntungan sebesar

)

( *1

* −

− t

t t S S

ξ dan menimbulkan biaya sebesar

* 1 1)

(ξt −ξt− St− . Karena menimbulkan biaya,

maka pada waktu t pengasuransi akan

memutuskan untuk melakukan perubahan nilai pada tabungan dari ηt−1Bt menjadi ηtBt.

Berdasarkan informasi tersebut dapat terlihat bahwa

*

1 1 1

* *

1 1

( ) ( ) ( )

( ) ( )

t t t t t

t t t t t

V V S

S S

ϕ ϕ ξ ξ

ξ η η

− − −

− −

− = −

+ − + − (5)

di mana (ξ ξ_t− _t−1)S_t*₋₁ dan (ηt −ηt−1)

merupakan biaya yang dikeluarkan oleh pengasuransi. Dengan demikian biaya pada waktu t adalah

∑

= Δ

−

= t

j j j t

t V S

C

1 *

) ( )

(ϕ ϕ ξ (6)

Sehingga nilai diskon pada waktu t dapat

ditulis dalam bentuk sebagai berikut

* 1

1 1

* 1

1

( ) ( ) ( )

( ) t

t t t j j

j t

t j j

j

C C V S

V S

ϕ ϕ ϕ ξ

ϕ ξ

−

=

−

− =

− = − Δ

⎛ ⎞

−⎜ − Δ ⎟

⎝ ⎠

∑

∑

S0

f

S0u

fu

S0d

fd

S0u2

fuu

S0d2

fdd

S0ud

)) ( ) ( ( ) ( ) ( ) ( 1 * 1 * 1 ϕ ϕ ξ ϕ ϕ − − − − + − + = t t t t t t t C C S S V V (7)

Karena portofolio tidak dipengaruhi oleh arus keluar masuknya modal sepanjang periode, maka biaya awal yang dikeluarkan persis sama dengan jumlah yang diinvestasikan pada

waktu 0. Dengan demikian nilai diskon pada waktu t menjadi

∑

= Δ

+

= t

j j j

t V S

V

1 * 0( )

)

(ϕ ϕ ξ (8)

KONTRAK ASURANSI JIWA TERKAIT DENGAN EKUITAS

Menurut Bacinello (2006) perusahaan

asuransi melakukan hedging tidak secara

terpisah untuk setiap kontrak polis melainkan untuk keseluruhan portofolio. Masalah utama yang dihadapinya adalah bagaimana menentukan harga atau bagaimana

meng-hedge kontrak jika mengeluarkan kontrak

asuransi yang kompleks. Pada kontrak asuransi jiwa yang terkait dengan ekuitas, keuntungan yang didapatkan oleh pemegang polis pada akhir periode terkait dengan portofolio yang direkomendasikan. Dalam hal ini portofolio terbentuk dari kesatuan aset

berupa saham. Misalkan St atau S

melambangkan perkembangan dari harga

saham pada waktu t, maka pembayaran yang

dilakukan oleh perusahaan asuransi adalah

sebesar f(S), jika pemegang polis tetap

hidup pada waktu T. Fungsi f merupakan

fungsi yang bergantung pada perkembangan

harga saham, sebagai contoh, kontrak

equity-linked murni hanya memiliki fungsi dari nilai terminal dari harga saham saja, yaitu

T

S S f( )= ,

sedangkan equity-linked dengan garansi atau

jaminan jika terjadi penurunan harga saham, memiliki fungsi sebagai berikut:

) , max( )

(S S K

f = T (9)

dengan K merupakan garansi. Selain itu,

masih banyak lagi ketergantungan yang kompleks pada kontrak seperti ini, contohnya

terdapat return garansi tahunan. Misalkan

1 1 − − − j j j S S S

adalah return pada tahun ke-j pada

aset S dan δj adalah garansi pada tahun ke-j,

maka pembayaran yang dilakukan oleh pengasuransi menjadi ∏ = ₋ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − + ⋅ = T

j _j j

j j S S S K S f 1 ₁ 1 1 , 1 max ) ( δ

Sebelumnya akan dianalisis terlebih dahulu kerugian yang akan dihadapi oleh

pengasuransi. Notasikan Yt(n) sebagai angka

bertahan hidup pada waktu t dan portofolio

mengandung n pemegang saham yang

membeli kontrak dengan bentuk yang sama yaitu endowmen murni yang terkait dengan saham pada waktu 0. Jika setiap kontrak individu dibayarkan dengan premi tunggal

pada waktu 0 senilai κ, maka nilai saat ini

dari kerugian pengasuransi adalah nilai saat ini dari kontrak dikurangi oleh banyaknya premi asuransi yang telah dibayarkan pada waktu 0, yaitu

κ δ _n e S f Y

L n t

T

n = −

− ) ( ) ( (10)

dengan t

e−δ adalah faktor diskon.

Peubah acak YT(n) dan f(S) didefinisikan

pada ruang ukuran peluang ( , , )Ω P di mana

P merupakan ukuran peluang dari sebaran

bersama (YT(n),f(S)). Karena angka bertahan

hidup dan perkembangan saham adalah bebas stokastik, maka nilai harapan dan varian dari kerugian pengasuransi adalah sebagai berikut:

κ κ δ δ n S f E Y E e n S f Y e E L E n T T n T T n − = − = − − )] ( [ ] [ ] ) ( [ ] [ ) ( ) ( (11) dan 2 ) ( 2 ) ( 2 2 ]) [ )]( ( [ ] [ ] ) ( [ ]] [ [ ] [ [ ] [ n T T n T T n n n Y E S f Var e Y Var S f E e S L E Var S L Var E L Var δ δ − − + = + = (12)

Penurunan rumus untuk persamaan ini dapat dilihat pada Lampiran 3.

Kemudian notasikan fungsi bertahan hidup

bagi seseorang yang berumur x sampai t tahun

dalam notasi aktuaria standar sebagai berikut : P[T1>t] = tpx (13)

Asumsikan bahwa sisa waktu hidup T1,...,Tn

~ b.s.i dan 1{T1>T},...,1{Tn>T}~ b.s.i Bernoulli

yang dapat mencapai nilai 1 dengan peluang

Tpx. Dengan asumsi tersebut dan berdasarkan

x T T

T n

i T T n T p n T T nP E E Y E i i = > = = ⎥⎦ ⎤ ⎢⎣ ⎡ = ∑ ∑ > = > ] [ ] 1 [ 1 ] [ 1 } {

1 { }

) ( (14) dan ) 1 ( ] 1 [ ] [

1 { }

) ( x T x T n

i T T

n T p p n Var Y Var _i − = =∑

= > (15)

Dengan mensubtitusikan (14) dan (15) ke dalam persamaan (11) dan (12), berturut-turut, akan didapatkan hasil sebagai berikut:

(

κ

)

κ δ δ − = − = − − )] ( [ )] ( [ ] [ S f E e p n n S f E p n e L E T x T x T T n (16) dan 2 2 2 2 )] ( [ ) 1 ( ] ) ( [ ] [ x T T x T x T T p n S f Var e p p n S f E e Ln Var δ δ − − + − = (17)

Nilai harapan dari present value kerugian

akan sama dengan 0 jika dan hanya jika

)] ( [f S E e p T x T δ κ₌ − .

Karena klaim pada kontrak asuransi jiwa ini tidak dapat direplikasi seluruhnya, maka untuk strategi yang pertama digunakan strategi superreplikasi. Strategi ini pada dasarnya menentukan bagaimana

mendapatkan strategi self-financing ϕ'

dengan C0(ϕ)=V0(ϕ) dan VT(ϕ')=H'≥H.

Di mana C0(ϕ) merupakan biaya awal dan

) (

0ϕ

V merupakan investasi awal (initial

value). Sedangkan H merupakan present value dari kontrak endowmen murni yang terkait dengan ekuitas yaitu H=YT f(ST)/BT, di

mana harga saham S berdasarkan model Cox,

Ross, Rubinstein yang didefinisikan oleh

1

) 1

( + −

= t t

t S

S ρ , dengan ρ1,...,ρT adalah

barisan dari peubah acak b.s.i dengan

} , {

1∈ a b

ρ dan 0<P(ρ1=b)<1; ρt adalah

return saham per unit selama interval waktu

] , 1

(t− t . St* merupakan nilai diskon dari

saham pada waktu t dengan proses harga

diskon St St/Bt

*₌

di mana t

t r

B =(1+ ) .

Sehingga nilai diskon dari saham pada waktu t

dapat dituliskan dalam bentuk sebagai berikut

* *

1 1

(1 ) (1 )

(1 )

(1 ) (1 )

t t t

t t t t t

S

S S S

r r r ρ ρ − − + + = = = + + +

Syarat alami dalam parameter a, b, dan r adalah −1<a<r<b, yaitu return saham

pada setiap periode harus melebihi return

pada tabungan dengan kemungkinan positif dan sebaliknya (Moller, 2001).

Menurut Argesanu (2004), suatu pasar dapat dikatakan tidak memiliki kemungkinan arbitrage jika dan hanya jika terdapat ukuran

peluang P* yang ekuivalen dengan P di mana

proses harga diskon *

S adalah *

P

-martingale. Akan dibuktikan bahwa

*

S adalah martingale. Definisikan filtrasi

{0,1,..., }

( )t t∈ T

=

 dengan t =σ{ ,....,S1 ST}

di mana  merupakan filtrasi yang terkait

dengan perkembangan saham pada pasar dan

t diinterpretasikan sebagai informasi yang

dihasilkan dari observasi saham S sampai

pada waktu t. Dan filtrasi =( _{t t})_{∈{0,1,..., }T}

dengan t =σ{ ,....,Y₁ YT}. Filtrasi 

merupakan filtrasi yang mengandung informasi tentang pemegang polis, sedangkan

menginterpretasikan angka kematian yang

dialami sampai pada waktu t. Definisikan

{0,1,..., }

( )t t∈ T

=

 sebagai filtrasi tambahan

dengan = ∨ =σ( ∪ ) yang

mengartikan bahwa  meliputi semua

informasi yang tersedia.

Proses harga diskon didefinisikan dalam

ruang ukuran peluang (Ω, , P) dilengkapi

dengan filtrasi . Diasumsikan proses harga

(S, B) diadaptasi, untuk setiap t, St terukur

dalam ( - measurable); B deterministik.

Diasumsikan terdapat ukuran peluang P*

dengan 1 *

* ) ( p a b a r b P = − − = =

ρ dan

T

ρ

ρ1,..., adalah b.s.i dibawah

*

P . Asumsi

b r

a< < menjamin 0_< * _<1

p , sehingga *

p

adalah ukuran peluang yang ekuivalen dengan

P. Ukuran P* disebut ukuran martingale

ekuivalen. Akan dibuktikan bahwa proses

harga saham yang telah didiskon, *

S , adalah

(, *

P )-martingale.

a b

a r E

E t t t ₋

− + = +

=

+ )| ₋] 1 [ ] 1

1

[( 1 *

* ρ ρ r a p b p + = − + + = 1 ) 1 (

1 * *

Menurut Definisi 12 mengenai martingale

terbukti bahwa *

S merupakan (, *

P )-

martingale. Teorema mengenai representasi martingale berikut terkait dengan model CRR yang digunakan.

Teorema 1

Misalkan H sebagai peubah acak T

-measurable P*-integrable. Kemudian, (,P*)

-martingale. N yang didefinisikan oleh

*

[ | ]

t t

N =E H memberikan representasi

khas berikut:

∑

= Δ

+

= t

j j j

t N S

N

1 *

0 α

di mana

α

_j adalah j-1-measurable untuk

setiap j.

Bukti teorema dapat dilihat pada Williams (1991).

Pembentukan harga pada strategi hedging

yang akan dibahas selanjutnya mengikuti teorema di atas.

Dalam strategi self-financing ϕ yang

memiliki nilai terminal Vt(ϕ)=H, nilai awal

) (

0 ϕ

V merupakan satu-satunya harga yang

layak untuk H, dan V0(ϕ) disebut sebagai

harga no-arbitrage dari H.

Dalam strategi superreplikasi, akan dicari

klaim H' di mana klaim tersebut lebih besar

dibandingkan dengan klaim yang sebenarnya.

Misal, klaim H' yang diperoleh dengan

mengganti sejumlah angka bertahan hidup

pada waktu T menjadi n kontrak pemegang

polis yang masuk pada waktu 0, yaitu

T T B S nf

H'= ( )/ . Klaim ini jelas lebih besar

dibandingkan dengan klaim asli selama

n

YT ≤ . Sehingga strategi ϕ' yang

mereplikasi klaim H' yang juga memenuhi

H H

VT(ϕ')= '≥ merupakan strategi

superreplikasi untuk H.

Berdasarkan Teorema 1, nilai diskon dari portofolio tersebut dapat dituliskan dalam bentuk:

* * ( )

[ | ] [ | ]

( )

[ ]

T

t t t

T T

T

f S

V E H E n

B f S

nE B

∗

∗

= =

=

(18)

] ) ( [

T T B

S f

nE∗ merupakan strategi

superreplikasi termurah, karena semua strategi superreplikasi yang lain membutuhkan

investasi awal yang melebihi [ ( )]

T T B

S f

nE∗ .

Sehingga harga premi yang ditawarkan terlalu tinggi dan jika dipaksakan untuk menggunakan strategi ini, maka masih terdapat risiko yang belum tereliminasi, selain itu harga strategi superreplikasi yang sama

dengan harga no-arbitrage untuk ( T)

T f S n

B ini

jelas jauh lebih tinggi dibandingkan dengan harga klaim asli, sehingga strategi ini tidak terlihat sebagai alat yang tepat untuk meng-hedge klaim asuransi jiwa yang terkait dengan saham di mana klaim bergantung pada tambahan sumber risiko yang bebas stokastik dengan pasar finansial.

Strategi yang kedua adalah pendekatan Brennan-Schwartz yang menyarankan untuk mengganti klaim asli dengan klaim

T T T f S B Y

E

H"= [ ] ( )/ , yaitu mengganti

jumlah dari kemungkinan bertahan hidup yang tidak diketahui dengan jumlah yang diketahui.

"

H di sini merupakan opsi tipe Eropa dengan

waktu konstan, oleh karena itu nilainya dapat dicapai dan di-hedge serta dapat dihargai unik. Berdasarkan Teorema 1 dan dengan proses yang sama dengan strategi sebelumnya,

didapatkan harga no-arbitrage untuk H"

yaitu E[YT]E [f(ST)/BT]

∗

. Nyatakan masalah harga dari H" bergantung pada H,

yaitu calon harga dan calon strategi hedging

self-financing untuk H dapat menggunakan harga dan strategi self-financing dari H".

Proses pembentukkan harga klaim pada H"

sangat rumit karena kontrak yang terkait dengan ekuitas dalam prakteknya sering kali melibatkan ketergantungan yang sangat kompleks pada saham atau indeks saham yang ada. Selain itu, pendekatan ini juga masih meninggalkan risiko bagi pengasuransi.

Strategi terakhir adalah strategi hedging

minimisasi risiko. Definisikan dua proses

nilai, yaitu proses πf yang terkait dengan

pasar finansial dan proses M yang terkait

dengan portofolio dari asuransi jiwa. Dengan menggunakan Teorema 1 didapatkan harga

diskon dari pembayaran f(ST) pada waktu t

sebesar

∑

= Δ

+ =

=

t j

j f j T

T T

T f

t

S B

S f E

B S f E

1 * *

*

] ( [

] | ) ( [

α π

(19)

dan proses M didefinisikan oleh:

*

[ | ]

t T t T t x t

yaitu nilai harapan bersyarat dari orang yang bertahan hidup pada waktu T; T−tpx+t adalah

peluang bersyarat dari kemungkinan bertahan

hidup sampai waktu T. Catat bahwa M

berfluktuasi secara khas dan MT = YT.

Berdasarkan kebebasan antara Y dan S,

maka proses harga dapat ditulis sebagai berikut: t f t T T T T T T T T T t M Y E B S f E Y E B S f E B S f Y E V π = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = ] | [ ) ( ] | [ ) ( ) ( * * * * * * (21) Sehingga 1 1 * 1 * * − − − = − − = Δ t f t t f t t t

t V V M M

V π π

1 1

1

1 − − −

− + −

−

= f _t

t t f t t f t t f

t M π M π M π M

π

) (

)

( − −1 −1+ − −1

= t t

f t t f t f

t π M π M M

π

Dan dengan menggunakan persamaan (19)

didapatkan t

f t t f t t

t M S M

V = Δ + Δ

Δ ₋α * π

1 *

.

Proses Vt* =E*[H| t] jika dihubungkan dengan

P*-martingale akan mempunyai dekomposisi yang unik yaitu

H t t j j H j

t V S L

V = +∑ Δ +

=1 * * 0 * ξ (22)

Bukti dapat dilihat pada William (1991). Di

mana ξH dapat diperkirakan (yaitu

H t

ξ adalah t−1-measurable) dan

H

L adalah

P*-martingale yang ortogonal dengan S*, Oleh karena itu, S L* Hjuga P* - martingale.

Catat bahwa f

t t

M −1α adalah ukuran t-1

dan proses ξH didefinisikan oleh

f t t H

t M α

ξ = −1 . Jika dapat ditunjukkan bahwa

∑ = Δ = t j j f j t M L 1

π adalah martingale, maka

dekomposisi (22) telah terpenuhi dan akan didapatkan bentuk:

Untuk menunjukkan bahwa L adalah

martingale, berdasarkan kebebasan antar

 dan  , didapatkan

[

]

[

]

0 ] [ ] [ 1 1 * * 1 * 1 = ∨ Δ = Δ = Δ − − − − t t t f t t t f t t t M E E M E L E π π

karena M adalah martingale dan M bebas

stokastik dari filtrasi  .

Dengan perhitungan yang sama, dapat

ditunjukkan bahwa LS* juga martingale,

karena

( )

t t t t t t t t t t t L S S L S L S L S L LS Δ + Δ + Δ Δ = − = Δ − − − − * 1 * 1 * * 1 1 * *

maka, dapat ditunjukkan bahwa

[

]

0 ] | [ ] | ) ( [ | 1 * 1 * * 1 * 1 * * 1 * * = Δ − Δ = − Δ = Δ Δ − − − − − t t t t t t t t t t t t S L S L E S S L E S L E

Berdasarkan proses biaya yang telah didefinisikan sebelumnya, nyatakan masalah minimisasi sebagai fungsi dari (ξt+1,ηt) yaitu proses meminimumkan nilai harapan

bersyarat di bawah ukuran martingale dari

kuadrat biaya yang muncul selama interval waktu selanjutnya. ] | )) ( ) ( [( ) ( 2 1 * t t t

t E C C

r ϕ = + ϕ − ϕ (23)

Karena H diasumsikan T-measurable maka

H T T j j H j

T V S L

H E

H = = +∑ Δ +

=1 * * 0 * ] | [ ξ

Nilai minimum untuk rt(ϕ) didapatkan

dengan memilih strategi ξ~ dan η~ sehingga

) ~ (ϕ

C adalah martingale, yaitu

] | ) ~ ( [ ) ~ ( 1 * t t

t E C

C ϕ = + ϕ

Hal ini mengakibatkan proses V(ϕ~) juga

martingale. Karena VT(ϕ~)=H maka

H t t j j H j

t V S L

V = +∑ Δ +

=1 * * 0 ) ~

(ϕ ξ (24)

Berdasarkan persamaan (4) maka

didapatkan ~ * ~ *

t t t t V ξ S

η = − . Selanjutnya

masukkan persamaan (6) dan (24) ke dalam persamaan (23) untuk mendapatkan

(

)

_⎥⎦⎤

⎢⎣

⎡ _{− Δ +Δ}

= _{+ + + +} 2

1 * 1 1 1 * ) ~ ( ) ~

( t t Ht

H t

t E S L

r ϕ ξ ξ

(25) ∑ ∑ = = − Δ + Δ + = t j j f j t j j f j j

t V M S M

Karena 1

~

+

t

ξ dan H

t+1

ξ adalah t–measurable

dan

[

1

]

0

* 1

*_{Δ Δ =}

+

+ Ht

t L S

E , serta berdasarkan

keortogonalan dari S* dan LH, persamaan (25) dapat dituliskan ke dalam bentuk

(

)

(

)

(

)

] [ ] [ ~ ) ~ ( 2 1 * 2 * 1 * 2 1 1 t H t t t t H t t L E S E r + + + + Δ + Δ − = ξ ξ ϕ

Di mana akan minimal jika H

t t ξ

ξ~ = dan

* * ~ t H t t V ξt S

η = − .

Berdasarkan perhitungan tersebut maka didapatkan strategi minimisasi risiko untuk kontrak asuransi jiwa yang terkait dengan ekuitas adalah

f t t t M α

ξ = −1 =Yt−1T−(t−1)px+(t−1)αtf (26)

* ) 1 ( ) 1 ( 1 * ) 1 ( ) 1 ( 1 * * t f t t x t T t t x t T t f t t f t t x t T t t f t t t t S p Y p Y S p Y M S V t α π α π ξ η − + − − − + − − + − − − − = − = − = (27)

Dengan menuliskan kembali peluang

) 1 ( ) 1 (− + −

−t x t

T p sebagai 1px+(t−1)T−tpx+t, maka

kerugian selama (t-1, t] adalah

) ( −11 +(−1) +

− −

=

Δ T t x t t t x t

f t

t p Y Y p

L π

Persamaan tersebut menjelaskan bahwa kerugian pengasuransi adalah proporsional

dengan faktor T t x t

f t − p +

π yang merupakan

harga diskon opsi f(ST) pada waktu t dikali

dengan peluang bertahan hidup T−tpx+t.

Jumlah tersebut merepresentasikan cadangan

yang layak pada waktu t untuk seorang

pemegang polis yang hidup pada waktu t.

Faktor kedua (Yt −Yt−11px+(t−1)) merupakan selisih nilai sebenarnya dari yang bertahan hidup dengan nilai harapan bersyarat yang dihitung pada t-1.

Menurut Moller (2001) strategi minimisasi risiko ini dapat menaksir besarnya risiko dari

pengasuransi. Kebebasan antara π f

dan M di

bawah P* dan fakta bahwa perubahan ukuran

dari P ke P* tidak mempengaruhi distribusi

dari sisa waktu hidup, memberikan varian dari biaya sebagai berikut :

( )

( )

( )

∑ ∑ = = Δ = Δ = T t t f t T t t f t T M E E M E C Var 1 2 2 * 1 2 2 * * ] [ ] [ ] [ ] [ π π ϕ (28) T M

Δ dapat dikatakan berkaitan dengan

peluang bertahan hidup. Hal ini dapat terlihat dari perhitungan berikut

[ ]

[

[

]

]

) 1 ( ] ] [ [ ]] [ [ ) 1 ( 1 1 1 1 2 − + + − − + − − − − = = Δ + Δ = Δ t x t x t T x T t t t x t T t t t t t p p p n F Y p Var E F M E Var F M Var E M E

di mana pada persamaan terakhir digunakan YT| t-1 ~ binomial (Yt−1,1px+(t−1)). Varian (28)

sebaiknya dibandingkan dengan total varian

dari klaim H yang merupakan varian dari

kerugian pengasuransi dengan tidak melakukan transaksi yang diberikan oleh persamaan berikut :

(29)

Contoh

Nyatakan bahwa dalam satu tahun terjadi lima kali waktu perdagangan, misalkan

4 , 3 , 2 , 1 , 0 =

k , sehingga T =4. Notasikan

selang waktu antar perdagangan dengan

4 1

=

Δt , yaitu dalam satu tahun terbagi

menjadi 4 periode dengan selang waktu antar periode adalah tiga bulan. Untuk memudahkan perhitungan, asumsikan bahwa sisa waktu bertahan hidup dari pemegang polis adalah bebas dan menyebar eksponen

dengan tingkat hazard (bahaya) μ yang

berbeda-beda. Sehingga peluang bertahan hidup dari pemegang polis adalah

) exp( k t px

k = −μ Δ untuk semua k (dan x).

Misalkan nilai garansi dari kontrak adalah

T r S K ) 2 1 1 ( 0 +

= dengan S0=100.

Peluang *

p adalah nilai peluang yang

ekuivalen dengan peluang p. Dengan

menggunakan persamaan kemungkinan risiko

netral (risk neutral probabilities) akan

didapatkan nilai dari *

p . 46 . 0 25 . 0 115 . 0 ) 1 . 0 ( 15 . 0 ) 1 . 0 ( 015 . 0 * _{= =} − − − − = − − = a b a r p

152.1 152.1

119.0 119.0

93.2 103.4 132.3

132.3

103.5 108.9

81.0

100.9 115.0

117.9

90.0 103.0 100.0

108.2

174.9 174.9

136.9 136.9

107.1 107.1

83.8 103.0

65.6 103.0 101.5

72.9

a -0.1

b 0.15

r 0.015

*

p 0.46

p 0.50

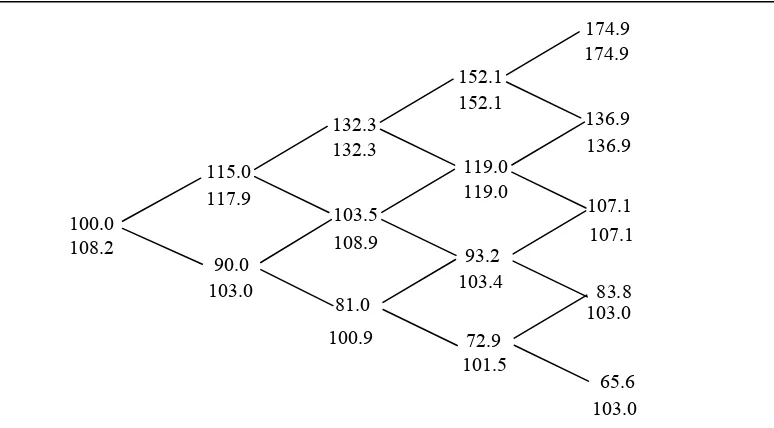
dan dengan menggunakan model CRR, didapatkan perkembangan harga saham dan

proses harga no-arbitrage (risk neutral

valuation) (Gambar 2). Perkembangan harga saham (atas) menggunakan persamaan yang telah didefinisikan sebelumnya yaitu

1

) 1

( + −

= t t

t S

S ρ

Pada waktu k = 1, harga saham mengalami

kenaikan menjadi

0 . 115 100 ) 15 . 0 1 ( ) 1

( + 1 = + =

= k−

u b S

S

dan akan turun menjadi

90 100 ) 1 . 0 1 ( ) 1

( + 1 = − =

= _k−

d a S

S

Dengan meneruskan perhitungan diatas, akan didapatkan pohon binomial untuk perkembangan harga saham (gambar 2).

Sedangkan proses harga no-arbitrage

menggunakan prinsip pada persamaan (1) dengan mengganti harga opsi dengan

max(f(ST), K). Prinsip dalam perhitungan

harga no-arbitrage adalah menghitung dari

belakang dengan menggunakan pohon

Gambar 2. Pohon Binomial untuk perkembangan harga saham (atas) dan proses harga

no-arbitrage untuk kontrak (bawah).

Gambar 3. Hedge untuk f(ST)=max(ST,K) (atas) dan strategi hedging minimisasi risiko untuk

kontrak endowmen murni H untuk kasus satu orang pemegang polis yang bertahan

hidup, dimana μ =1(bawah).

1.000 0.607

0.605 0.367

0.092

0.056 0.811

0.383

0.359

0.170 0.595

0.219

0.779 1.000

1.000 0.779

0.176 0.137

binomial yang telah dibentuk sebelumnya (working backward through the tree). Untuk k = 0, harga no-arbitrage didapatkan dari

* *

1 1 1 1

0 0 (1 ) (1 ) (0.46)117.9 (0.54)103.0 108.2 (1 0.015) f f

f p B p B

B r π π π = + − + + = = +

Untuk mencari strategi hedging bagi opsi beli,

gunakan proses harga no-arbitrage yang telah

dihitung sebelumnya. Misalkan ϕ0(1) sebagai

banyaknya aset bebas risiko pada waktu k=0

dan ϕ1(1) sebagai banyaknya saham yang

dimiliki pada waktu k=0 dan dengan

menggunakan proses harga

) 1 ( ) 1 ( )

(ϕ ϕ1 t tϕ0

t S B

V = + sebelum didiskon,

akan didapatkan proses harga

9 . 117 ) 1 ( 015 . 1 ) 1 (

115ϕ1 + ϕ0 =

0 . 103 ) 1 ( 015 . 1 ) 1 (

90ϕ1 + ϕ0 =

Penyelesaian persamaan diatas, akan menghasilkan ϕ1=0.595 dan ϕ0= −48.72.

Dengan melanjutkan proses tersebut, akan

dihasilkan proses hedging 1(t)

f t ϕ

α = untuk

) , max( )

(S S K

f T = T (Gambar 3).

Berdasarkan persamaan (26) dan (27) maka

akan didapatkan proses hedging untuk living

benefit. Untuk satu orang pemegang polis akan didapatkan

f x T (11)p (11) 1

1 α

ξ = _{− − + − =e}−1(0.595)₌0.219

yaitu pada waktu k = 0 portofolio

mengandung 0.219 saham dan

9 . 17 100 ) 219 . 0 ( ) 2 . 108 ( 1 * 1 1 * 0 0 = − = − = − e S V ξ η

memiliki nilai pada tabungan sebesar 17.9.

Pada waktu k=1 nilai tersebut akan

berubah sesuai dengan nilai saham dan bergantung pada kemungkinan pemegang polis tetap hidup pada waktu tersebut. Jika pemegang polis tidak dapat bertahan sampai dengan k=1, maka ξ2 =0 dan η1=0. Jika ia

tetap hidup pada waktu k=1, dan nilai saham

meningkat (menjadi 115.0), maka ξ2 =0.383

dan 3 / 4

1 e 117.9 0.383 115.0 11.6

μ

η ₌ − _{− ⋅ =}

Cara yang sama dilakukan untuk mendapatkan proses hedge selanjutnya.

Dalam kasus kontrak seperti ini, persamaan (28) dan (29) dapat disederhanakan menjadi

* * 2

1 2 [ ( )] ( [( ) ] (1 )) T f T k k

T t k t t

Var C n E

e μ μ eμ

ϕ π = − Δ + Δ − Δ = ∑ − (30)

dan, dengan H =YTf(ST)/BT,

* * 2

* 2 2

[ ] [( ) ] (1 )

[ ]

f T t T t

T

f T t T

Var H E ne e

Var n e

μ μ μ π π − Δ − Δ − Δ = −

+ (31)

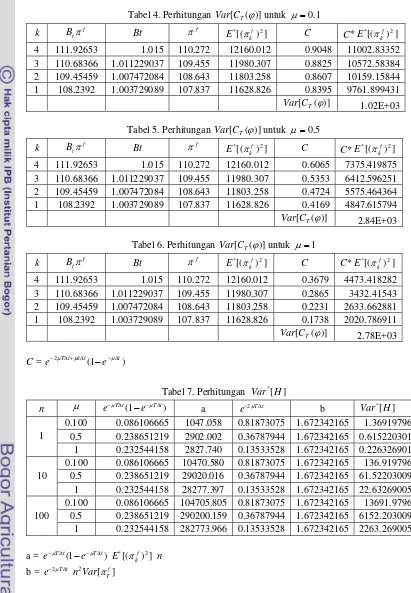
Untuk menghitung *

[ T( )]

Var C ϕ digunakan

harga no-arbitrage yang telah didiskon.

Dengan menggunakan prinsip untuk mencari persamaan (3) sebelumnya dan dengan

mengganti payoff opsi dengan harga

no-arbitrage akan didapatkan harga no-arbitrage

yang telah didiskon pada waktu T = 1, 2, 3

dan 4 sebagai berikut: Pada waktu T = 1:

] ) 1 ( [ ) 4 / 1 ( d u

r _{pf p f}

e

f = − + − (32)

Pada waktu T = 2:

] ) 1 ( ) 1 ( 2 [ 2 2 2 2 ) 4 / 1 ( 2 d ud u r f p f p p f p e f − + − + = − (33)

Pada waktu T = 3:

] ) 1 ( ) 1 ( 3 ) 1 ( 3 [ 3 3 2 2 3 3 ) 4 / 1 ( 2 2 2 d ud d u u r f p f p p f p p f p e f − + − + − + = − (34)

Pada waktu T = 4:

] ) 1 ( ) 1 ( 4 ) 1 ( 6 ) 1 ( 4 [ 4 3 3 2 2 3 4 4 ) 4 / 1 ( 4 3 2 2 3 d ud d u d u u r f p f p p f p p f p p f p e f − + − + − + − + = − (35)

Karena harga saham merupakan martingale,

maka:

f k f

k

E[π +1| ]=π

Sehingga pada waktu T = 4 akan digunakan

harga no-arbitrage pada waktu T = 3. Berikut

merupakan hasil perhitungan *

[ _T( )]

Var C ϕ

untuk beberapa nilai hazard yang berbeda dan

dengan jumlah pemegang opsi yang berbeda:

Tabel 1. Hasil perhitungan *

[ T( )]

Var C ϕ

n

0.1 1.02E+03

0.5 2.84E+03

1

1 2.78E+03

0.1 1.02E+04

0.5 2.84E+04

10

1 2.78E+04

0.1 1.02E+05

0.5 2.84E+05

100

1 2.78E+05

Tabel berikut memperlihatkan hasil

perhitungan *

[ ]

Var H .

μ *[ (ϕ)]

T

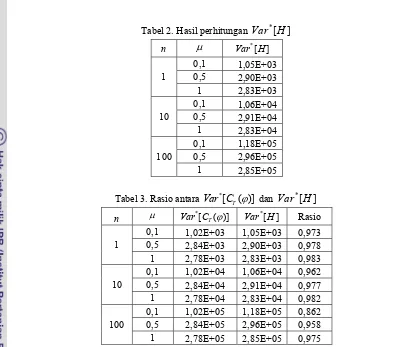
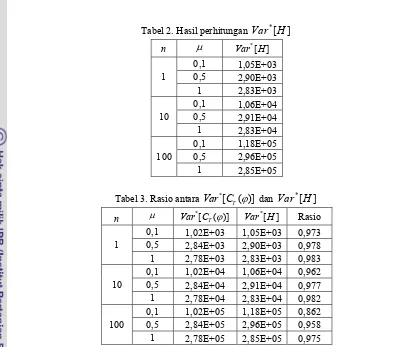
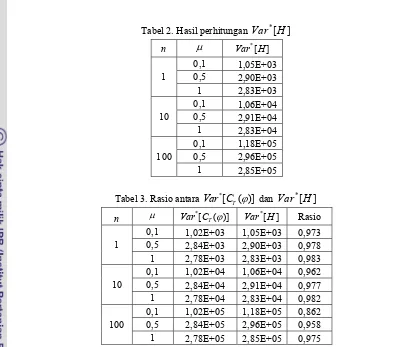
Tabel 2. Hasil perhitungan Var H*[ ]

n

μ

*

[ ]

Var H

0,1 1,05E+03

0,5 2,90E+03

1

1 2,83E+03

0,1 1,06E+04

0,5 2,91E+04

10

1 2,83E+04

0,1 1,18E+05

0,5 2,96E+05

100

1 2,85E+05

Tabel 3. Rasio antara Var C*[ _T( )]ϕ dan

Var H

*

[

]

n μ Var C*[ T( )]ϕ

*

[ ]

Var H Rasio

0,1 1,02E+03 1,05E+03 0,973

0,5 2,84E+03 2,90E+03 0,978

1

1 2,78E+03 2,83E+03 0,983

0,1 1,02E+04 1,06E+04 0,962

0,5 2,84E+04 2,91E+04 0,977

10

1 2,78E+04 2,83E+04 0,982

0,1 1,02E+05 1,18E+05 0,862

0,5 2,84E+05 2,96E+05 0,958

100

1 2,78E+05 2,85E+05 0,975

Dapat terlihat dari tabel 3 diatas bahwa

rasio dari *_{[ ( )]}

T

Var C ϕ dan _{Var H}*_{[ ]}

bergantung pada jumlah pemegang polis dan

nilai hazard (μ). Jika jumlah pemegang polis

bertambah maka rasio akan berkurang, dan

sebaliknya jika nilai hazard bertambah maka

rasio juga akan bertambah. Ketergantungan

terhadap μ dapat diinterpretasikan menjadi,

jika μ meningkat, ketidakpastian terhadap

angka pemegang polis yang dapat bertahan hidup bertambah besar dibandingkan dengan ketidakpastian finansial. Sama halnya dengan

pada saat jumlah pemegang polis (n)

meningkat, bagian yang muncul dalam

*_{[ ]}

Var H yang proporsional terhadap n2

menjadi lebih dominan, oleh karena itu rasio menurun.

KESIMPULAN

Selain melakukan pendekatan finansial, perusahaan asuransi juga melakukan pendekatan fisik untuk mengurangi risiko yang ada, yaitu dengan mencari harga optimal dari kontrak yang diterbitkan. Terdapat tiga strategi yang biasa digunakan dalam mencari harga dari suatu kontrak asuransi jiwa yang terkait dengan ekuitas, dalam hal ini saham, yaitu superreplikasi, pendekatan Brennan-Schwartz dan minimisasi risiko. Dari ketiga strategi tersebut, strategi superreplikasi dan pendekatan Brennan-Schwartz bukanlah

strategi yang tepat untuk digunakan karena harga yang terbentuk terlalu tinggi, selain itu proses dalam pencarian harga tersebut dapat

terbilang rumit. Strategi hedging yang dapat

memberikan harga optimal bagi kontrak

tersebut adalah strategi hedging minimisasi

risiko.

Strategi minimisasi risiko memberikan dua proses nilai, yaitu nilai yang terkait dengan pasar finansial yang merupakan perkalian dari

proses hedging yang telah dilakukan dengan

bertahan hidup pada waktu T. Dan proses nilai lainnya yaitu nilai yang terkait dengan portofolio dari asuransi jiwa, yang merupakan

selisih dari perkalian harga no-arbitrage

dengan nilai harapan bersyarat dari orang

yang bertahan hidup pada waktu T, dengan

nilai yang terkait dengan pasar finansial dikalikan dengan harga saham. Kedua nilai tersebut akan memberikan harga yang optimal untuk kontrak asuransi jiwa yang terkait dengan ekuitas.

Telah ditunjukkan bahwa varian dari biaya memberikan nilai yang lebih kecil dibandingkan dengan varian dari total klaim. Rasio dari keduanya akan meningkat seiring

dengan kenaikan dari nilai hazard (μ), akan

tetapi berbanding terbalik dengan jumlah

pemegang polis (n). Semakin besar jumlah

pemegang polis maka akan semakin kecil rasio keduanya.

DAFTAR PUSTAKA

Argesanu, George. 2004. Risk Analysis and

Hedging in Incomplete Markets. The

Ohio State University. Ohio.

Bacinello, Anna Rita. 2006. Fair Valuation of Life Insurace Contracts with Embedded Options. Association Suisse des Actuaries. Laussane.

Bodie, Z, Kane, A, dan Marcus, A J. 2002. Investments. Ed. ke-6. The McGraw-Hill Companies, Inc. New York.

Ghahramani, Saeed. 2005. Fundamentals of Probability With Stochastic Process. Ed. Ke-2. Prentice Hall, Inc. New Jersey.

Grimmet, G.R. dan D.R. Stirzaker. 1992. Probability and Random Processes. Ed. ke-2. Clarendon Press. Oxford. New York.

Hogg, R.V. dan A.T. Craig. 1995. Introduction to Mathematical Statistics. Ed. ke-5. Prentice-Hall, Inc. New Jersey.

Moller, Thomas. 2001. Hedging Equity-Linked Life Insurance Contracts. North American Actuarial Journal 5(2) (2001), 79-95. Copenhagen.

PT. Asuransi Astra Buana. 2006. Pengertian

dan Prinsip Risiko. http://www.virtual.co.id/. [11 April 2007].

Ren`o, Roberto. 2002. Finance Option Pricing : The CRR Model. Universitas Siena. Siena.

Ross, Sheldon M. 1996. Stochastic Processes. Ed. ke-2. John Wiley & Sons, Inc. Canada.

Shreve, Steven E. 1997. Stochastic Calculus

and Finance. Carnegie Mellon

University.

Lampiran 1.

Bukti persamaan nilai risiko netral (persamaan (1)) :

Misalkan pada waktu 0 harga opsi adalah C0. Jika harga saham meningkat maka payoff-nya adalah (xS0 −K)+ dan sebaliknya, jika harga saham menurun maka payoff-nya menjadi

+

− )

(yS0 K . Pada waktu 0, tidak diketahui apakah harga saham akan naik atau turun, oleh karena itu dilakukan hedging dengan membeli sebanyak Δ0 saham. Jika nilai C0 lebih dari yang dibutuhkan untuk membeli Δ0 saham, maka sisanya akan diinvestasikan pada tingkat suku bunga r. Dengan kata lain C0 −Δ0S0 akan diinvestasikan pada pasar uang.

Jika harga saham meningkat, nilai dari portofolio adalah Δ0Su +(1+r)(C0 −Δ0S0) dan

dibutuhkan Cu, yaitu akan dipilih C0 dan Δ0 sehingga

) )(

1

( 0 0 0

0S r C S

Cu =Δ u + + −Δ (A.1)

Jika harga saham menurun, nilai dari portofolio adalah Δ0Sd +(1+r)(C0 −Δ0S0) dan dibutuhkan

d

C , yaitu akan dipilih C0 dan Δ0 sehingga

) )(

1

( 0 0 0

0S r C S

Cd =Δ d + + −Δ (A.2) Dengan mengurangkan persamaan (A.1) dengan (A.2)

) ( )) )( 1 ( ( ) )( 1 ( 0 0 0 0 0 0 0 0 0 0 0 d u d u d u d u S S S S S C r S S C r S C C − Δ = Δ − Δ = Δ − + + Δ − Δ − + + Δ = −

sehingga didapatkan :

d u d u S S C C − − =

Δ₀ (A.3)

Subtitusi (A.3) ke dalam (A.1) atau (A.2).

0 0 0 0 ) 1 ( ) 1 ( ) 1 ( S S S C C r C r S S S C C S S S C C C r S S S C C C d u d u u d u d d d u d u u d u d u u − − + − + + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − + + − − =

Dengan menyelesaikan persamaan didapatkan :

y x C C r x C C y x C S S S C