Informasi Dokumen
- Sekolah: Universitas
- Mata Pelajaran: Kalkulus
- Topik: Bab 6 Integrasi Numerik
- Tipe: Dokumen
Ringkasan Dokumen
I. Te r a p a n Inte g ra l d a la m Bid a ng Sa ins d a n Re ka ya sa
Integral memiliki banyak aplikasi dalam bidang sains dan rekayasa. Dalam praktik rekayasa, fungsi yang diintegrasikan sering kali adalah fungsi empirik yang diberikan dalam bentuk tabel atau fungsi yang terlalu rumit untuk diintegrasikan secara analitik. Contoh penerapan integral dalam fisika termasuk menghitung jarak total yang ditempuh oleh partikel berdasarkan kecepatan yang merupakan fungsi waktu. Dalam teknik elektro, arus listrik yang berosilasi dapat dianalisis menggunakan integral untuk menghitung nilai rata-rata arus. Data yang ditabulasikan seperti fluks panas matahari juga memerlukan integrasi numerik untuk menghitung total energi yang diserap. Metode numerik menjadi penting karena sering kali fungsi yang diintegrasikan tidak memiliki bentuk analitik yang sederhana.
II. Pe rso a la n Inte g ra si Num e rik
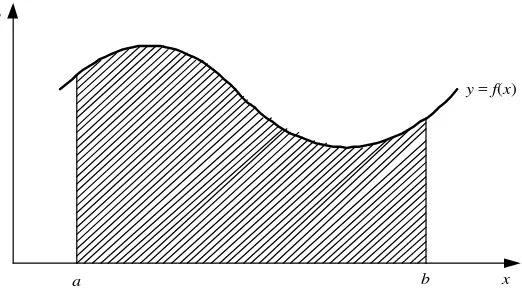
Masalah utama dalam integrasi numerik adalah menghitung nilai integral tentu secara akurat. Terdapat tiga pendekatan utama dalam mengembangkan rumus integrasi numerik: pendekatan geometris, interpolasi polinom, dan evaluasi fungsi di titik tertentu. Pendekatan geometris membagi daerah integrasi menjadi strip atau pias, dan menghitung luasnya. Pendekatan interpolasi menggunakan polinom untuk mendekati fungsi yang diintegrasikan, sedangkan evaluasi fungsi di titik tertentu melibatkan metode seperti Kuadratur Gauss. Setiap pendekatan memiliki kelebihan dan kekurangan tergantung pada sifat fungsi yang diintegrasikan dan tujuan analisis.
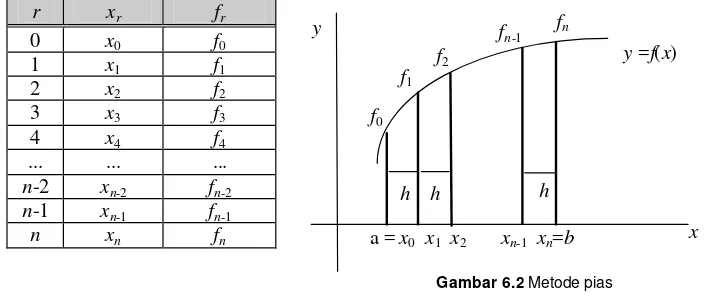
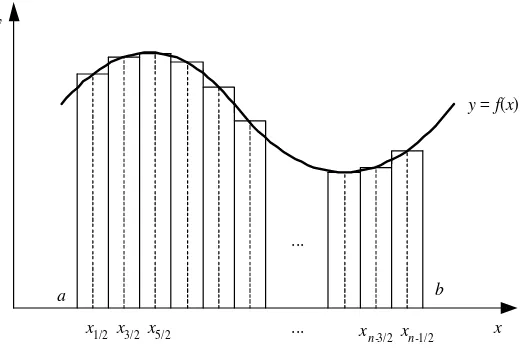
III. Me to de Pia s
Metode pias adalah teknik dasar dalam integrasi numerik yang menggunakan titik diskrit untuk menghitung luas daerah di bawah kurva. Metode ini mencakup kaidah segiempat, trapesium, dan titik tengah. Kaidah segiempat menggunakan pias berbentuk persegi panjang untuk menghampiri luas, sedangkan kaidah trapesium menggunakan bentuk trapesium. Kaidah titik tengah menghampiri luas dengan menghitung nilai fungsi di titik tengah setiap pias. Setiap metode memiliki rumus dan galat yang berbeda, dengan kaidah trapesium dan titik tengah sering digunakan untuk mendapatkan hasil yang lebih baik dibandingkan dengan kaidah segiempat.
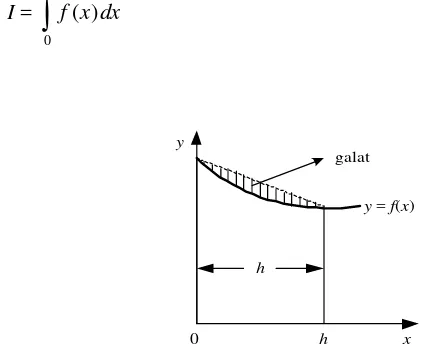
6.3.1 Ka id a h Se g ie m p a t
Kaidah segiempat menghampiri integral dengan menggunakan pias berbentuk persegi panjang. Luas satu pias dapat dihitung dengan mengalikan tinggi pias dengan lebar pias. Kaidah ini dapat diperluas untuk menghitung integral dalam selang [a, b] dengan membagi selang menjadi n pias. Rumus untuk kaidah segiempat gabungan menghasilkan estimasi luas yang lebih akurat dengan menambahkan kontribusi dari setiap pias yang dihitung secara terpisah.
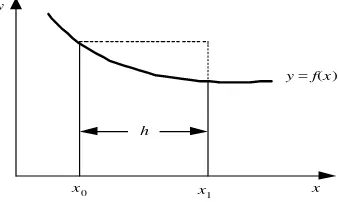
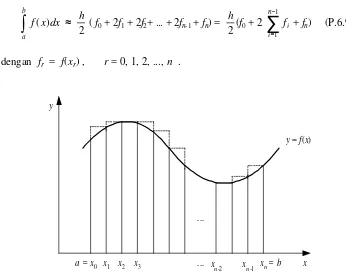
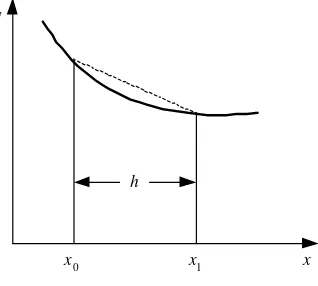
6.3.2 Ka id a h Tra p e sium
Kaidah trapesium menggunakan bentuk trapesium untuk menghampiri luas di bawah kurva. Dengan membagi selang integrasi menjadi n pias trapesium, metode ini menghasilkan rumus yang lebih akurat dibandingkan kaidah segiempat. Galat dari kaidah ini dapat dihitung dan menunjukkan bahwa semakin kecil lebar pias, semakin kecil galat yang dihasilkan.
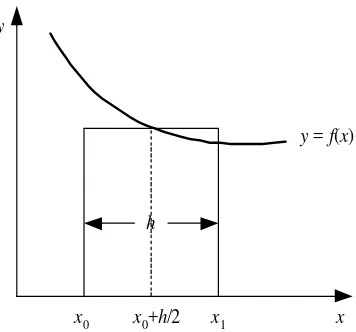
6.3.3 Ka id a h Titik Te ng a h
Kaidah titik tengah menghampiri integral dengan menggunakan nilai fungsi pada titik tengah setiap pias. Metode ini sering kali memberikan hasil yang lebih baik dibandingkan dengan metode trapesium, terutama ketika fungsi yang diintegrasikan adalah fungsi yang halus. Kaidah ini juga memiliki rumus spesifik untuk menghitung luas total dengan menjumlahkan kontribusi dari setiap titik tengah.
IV. Me to de Ne wto n- C o te s
Metode Newton-Cotes adalah pendekatan yang umum digunakan untuk mengembangkan rumus integrasi numerik berdasarkan polinom interpolasi. Metode ini mencakup kaidah trapesium, Simpson 1/3, dan Simpson 3/8, yang masing-masing menggunakan polinom dengan derajat berbeda untuk menghampiri fungsi yang diintegrasikan. Keuntungan dari metode ini adalah kemampuannya untuk memberikan estimasi yang lebih akurat dengan menggunakan lebih banyak titik data. Namun, metode ini juga memiliki batasan, terutama ketika fungsi yang diintegrasikan memiliki perilaku yang kompleks atau tidak terdefinisi di beberapa titik.
6.4.1 Ka id a h Tra p e sium
Kaidah trapesium menghampiri integral dengan menggunakan dua titik data untuk membentuk garis lurus. Ini memberikan estimasi luas yang lebih baik dibandingkan dengan metode pias sederhana. Kaidah ini dapat diperluas untuk menghitung integral dalam selang yang lebih besar dengan menggunakan banyak trapesium yang saling terhubung.
6.4.2 Ka id a h Sim p so n 1/3
Kaidah Simpson 1/3 menggunakan polinom derajat dua untuk menghampiri fungsi yang diintegrasikan, memberikan hasil yang lebih akurat dengan menggunakan tiga titik data. Metode ini sangat efektif ketika jumlah subinterval genap dan memberikan estimasi yang lebih baik dibandingkan kaidah trapesium.
6.4.3 Ka id a h Sim p so n 3/8
Kaidah Simpson 3/8 adalah metode yang lebih kompleks yang menggunakan empat titik data untuk menghampiri fungsi. Metode ini memberikan estimasi yang sangat akurat, terutama ketika jumlah subinterval adalah kelipatan tiga. Meskipun lebih rumit, kaidah ini sangat berguna untuk fungsi yang lebih sulit diintegrasikan secara analitik.
V. Sing ula rita s
Singularitas dalam fungsi dapat menyebabkan kesulitan dalam menghitung integral numerik, terutama jika fungsi tidak terdefinisi pada titik tertentu. Untuk mengatasi masalah ini, teknik manipulasi fungsi perlu diterapkan agar fungsi menjadi tidak singular. Contoh-contoh termasuk perubahan variabel dan pemisahan integral menjadi bagian-bagian yang lebih sederhana. Pemahaman tentang singularitas sangat penting dalam analisis numerik untuk memastikan integrasi yang akurat.
VI. Pe ng g una a n Ekstra po la si untuk Inte g ra si
Ekstrapolasi Richardson adalah teknik yang digunakan untuk meningkatkan akurasi hasil integrasi numerik dengan cara menghitung nilai integrasi pada jarak titik yang berbeda. Dengan menggunakan nilai dari dua jarak yang berbeda, metode ini dapat memberikan estimasi yang lebih baik dengan mengeliminasi galat yang ada. Ekstrapolasi ini dapat diterapkan pada berbagai metode integrasi untuk meningkatkan ketelitian hasil akhir dan mengurangi galat.
Referensi Dokumen
- The Art of Loving ( Erich Fromm )
- MAT93
- CHA91