RINGKASAN
NUNUNG NURSALD. Pendugaan dengan 2 Kondisi Ketakhiasan pada Teknik Cokrigirig. Dibimbing oleh MUHAMMAD NUR AID1 dan RETNO BUDIARTI.
Data spasial adalah data yang dikumpulkan dari lokasi-lokasi yang saling berkorelasi satu sama lain. Persoalan yang ada pada data spasial adalah sulit melakukan pengukuran pada sernua lokasi karena lokasi bersifat kontinu. Oleh karena itn pendugaan titik-titik yang tidak dilaknkan pengukuran sangatlah penting.
Salah satu ilustrasi dalam masalal~ nyata adalah dalam industri minyak. Dipmeter mengukur lubang dan mencari kedalaman, juga terdapat beberapa parameter seperti sifat menyerap (porosily), perrneabilitas dan kejenuhan cairan yang bergantung pada kedalaman.
02-9
PENDUGAAN DENGAN 2 KONDISI KETAKBIASAN
PADA TEKNIK COKRIGING
NUNUNG NURSAID
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN LLMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
DAFTAR PUSTAKA
Chiles, J. P. & P. Delfiner. 1999. Isaaks, E. H. & R.
M.
Srivastava. 1989. Geostalislics Moiielirlg Spalinl Applied Geoslalislics. Oxford Urlcermiilty. John Wiley & Sons, New University Press, Oxford.York. Olea, R. A. 1975. Oplin~rrrii Mnppirrg
Helms, L. L. 1997. I?~lrodrrclio~z lo Techr~iq~ies ~ i s i i ~ g Regiorialized I'robabiliiy Theory with Cor~tmrporary Variable Tt~eory. Empresa Nacional del Applicaio~s. W.H. Freeman and Petroleo, Santiago, Chile.
02-9
PENDUGAAN DENGAN 2 KONDISI KETAKBIASAN
PADA TEKNIK COKRIGING
NUNUNG NURSAID
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN LLMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
RINGKASAN
NUNUNG NURSALD. Pendugaan dengan 2 Kondisi Ketakhiasan pada Teknik Cokrigirig. Dibimbing oleh MUHAMMAD NUR AID1 dan RETNO BUDIARTI.
Data spasial adalah data yang dikumpulkan dari lokasi-lokasi yang saling berkorelasi satu sama lain. Persoalan yang ada pada data spasial adalah sulit melakukan pengukuran pada sernua lokasi karena lokasi bersifat kontinu. Oleh karena itn pendugaan titik-titik yang tidak dilaknkan pengukuran sangatlah penting.
Salah satu ilustrasi dalam masalal~ nyata adalah dalam industri minyak. Dipmeter mengukur lubang dan mencari kedalaman, juga terdapat beberapa parameter seperti sifat menyerap (porosily), perrneabilitas dan kejenuhan cairan yang bergantung pada kedalaman.
PENDUGAAN DENGAN 2 KONDISI KETAKBIASAN
PADA TEKNIK
COKRIGING
NUNUNG NURSAID
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Program Studi Matematika
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTlTUT PERTANlAN BOGOR
Judul
:
Pendugaan dengan 2 Kondisi Ketakbiasan pada Teknik
Cokrrging
Nama
:
Nunung Nursaid
Nrp
:
GO5498022
Jurusan
:Matematika
Menyetujui,
Dr. Muhammad Nur Aidi. MS
Peinbimbing I
\
Ir.
Retno Budiarti, MS
Pembimbing I1
Penulis dilahirkan di Cirebon pada tanggal 26 Juni 1980 sebagai anak ke empat dari delapan bersaudara, anak dari Bapak Sukardi dan Ibu Enin Mu'minin.
Tahnn 1992 penulis lulus dari SD Negeri Cipeujeuh Wetan IV Sindanglaut Cirebon, melanjutkan ke SLTP Negeri I Sindanglaut Cirebon dan lulus pada tahun 1995, dan melanjutkan ke SMU Negeri 6 Cirebon dan lulus pada tahun 1998. Pada tahun yang sama lulus seleksi ~iiasuk IPB melalui jalur Undanyan Seleksi Masuk IPB (USMI). Penulis memilih program studi Matematika denyan minor Industri di Jurusan Matematika, Fakultas Matematika dan llmu Pengetalioan Alam.
Selama masih duduk di banyku kuliah, penulis penah menjadi Asisten Dosen untuk mata kuliah Pengalltar Matematika, Matenlatika Dasar, Kalkulus, Kalkulus I, dan Persalnaan Diferensial Biasa. Juga pernah mengajar di salah satu sekolah menengah di Bogor, pengajar di Bimbingan Belajar l'ri~ate Plus Nurul Ilmi Bogor, dan sekarang masih menjadi pengajar Matematika di Pusat Birnbingan Belajar Ganesha Operation cabang Jabotabek dan Depok.
KATA PENGANTAR
Alhamdulillah penulis panjatkan ke-hadirat Nlah SWT yang telah memberikan rahmat dan hidayah-Nya sehingga pada akhirnya penulis dapat menyelesaikan tugas akhir ini tepat pada waktunya.
Dalam penyusunan tulisan ini, penulis banyak mendapatkan bantuan dari berbagai pihak baik secara langsung maupun tidak langsung. Untuk itu penulis mengucapkan terima kasih ysng tak terhingga kepada :
I . Bapak Dr. Ir. Muhammad Nur Aidi, M S selaku Pemhimbing 1, Ibu Ir. Retno Budiani, MS selaku Pembimbing 2, juga Bapak Dr. I Wayan Mangku selaku dosen penguji.
2. Al-Ustadz K.H Ahmad Zaini Dahlan pimpinan ponpes N-Imdad yang telah membina jasmani dan rohani penulis selama lebih kurang 4 tahun.
3. Penulis nggak pernah lupa untuk ngucapin terima kasih buat anak Matematika 35 y a i g chakep, centil, imut-imut tapi amit-amit '~orry Pris kalo tersinggung), jrtfrkies, ,fmrky, keren abis, gaul, norak, ilyebelin, ngeselin seperti Syauqi yang masih jomblo, Matzech, Pris yang emosinya stabil, Herdyn, Madhi, [Mila (pembahas 11, Liana, Irma
000
yang udah ngebantuin ngumsin transparansi pas mo seminar tms nungguin ampe sidang beres], Lilo, Puji, Sarah (pernbahas 2), Yunita, Samsul, Kiky, [Hepy (pembahas 3), DenBakh yang udah ngasih semangat dan nasihat pas mo seminar tms ngasih tumpangan buat tidur waktu malam lum'at buat persiapan seminar], Berlin, Ingeu, Anna (makasih atas dorongannya yang sangat berarti bagi saya), Indra, Izma, lim, Desi, Dinah (thanks sudah pinjemin printer 0 ) , Imeh dan ... yang penulis tidak bisa sebutkan namanya disini, OK. Terima kasih sekali khususnya buat syauqi 35 yang sudah ngebantu mecahin masalah pake' komputernya yang udah ketinggalan kereta.4. Mahasiswa Matematika angkatan 32, 33, 34, 36, 37 dan 38 yang sudah memberikan kritik dan saran yang membangun bagi penulis, yang sudah meminjamkan buku, dan yang memberikan semangat juang 45 agar penulis bisa lulus secepatnya.
5 . Juga makasih buat santri-santri N-Imdad yang udah banyak ngebantu ngetik, ngeprint, nerjemahin, ataupun hal-ha1 lain dalam penyelesaian tulisan ini seperti Aziz, Faiz, Hadi, BimBim, Khariz. Goten dan semuanya.
6. Juga buat keluarga di rumah yang udah ngasih biaya. Terima kasih penulis ucapkan dari lubuk hati yang paling dalan kepada semuanya temtama Bapak Sukardi, Ibu Enin, Mbak Renih, Mbak Liha, Mbak Atun, Dudi, Yani, Ayu, Toh Gugun, Mas ling, Mas Mul, A Ibro, Mang Aan, Bi Ayi, Baenah, Neneng, Adah, Nia dan yang lainnya yang tidak bisa penulis sebutkan satu per satu disini.
Akhirnya penulis merasa bahwa tulisan ini masih banyak kekurangannya. Untuk itu penulis sangat mengharapkan sekali kritik dan saran yang membangun untuk perbaikan tulisan ini dari para pembaca. Sebelum dan sesudahnya penulis ucapkan terima kasih.
Bogor, Agustus 2002
DAFTAR IS1
PENDAHULUAN
Halaman
... 1
LANDASAN TEORl ... I DRIFT ... 2
COKRIGING ... 2
PEMBAHASAN ... 4
DAFTAR TABEL
DAFTAR LAMPRAN
Bukti Teorema 1 9
Bukti Teorema 3 10
PENDAHULUAN
Latar B e l a h ~ n gData spasial adalah data yang dikumpulkan dari lokasi-lokasi yang saling berkorelasi satu sama lain. Selanjutnya, korelasi suatu peubah U dan lfmenggambarkan hubungan keeratan antara U dan K
Persoalan yang ada pada data spasial adalah sulit melakukan pengukuran pada semua lokasi karena lokasi bersifat kontinu. Oleh karena itu, pendugaan pada titik-titik yang tidak dilakukan pengukuran sangatlah penting.
Metode pendugaan banyak variasinya, diantaranya adalah :
1) Ordinary Kriging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu yang dilakukan dengan mengamati data yang sejenis pada daerah lain.
2) BIok Kriging yaitu pendugaan rata-rata suatu nilai pada suatu area dan area tersebut dipecah-pecah menjadi area-area yang lebih kecil dimana suatu nilai menggambarkan nilai potongan area yang kecil tersebut.
3 ) Cohiging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu menggunakan data lebih dari satu peubah dengan mengamati data yang sejenis pada lokasi yang lain.
Pada beberapa fenomena, misalkan pendugaan terhadap kandungan sumber daya alam (misal : minyak bumi sebagai peubah utama (U)) seringkali menggunakan beberapa parameter yang mempunyai korelasi linear dengan kandungan sumber daya alam tersebut (sebagai peubah pelengkap
(q).
Pada kegiatan pendugaan kandungan sumber daya alam sering menggunakan teknik cokriging. Pada kajian ini dicoba menggunakan cohigi,~g.Salah satu ilustrasi dalam masalah nyata adalah dalam industri minyak. Dipmeter menykur lubang dan mencari kedalaman, juga terdapat beberapa parameter seperti sifat menyerap (porosity), permeabilitas dan kejenuhan cairan yang bergantung pada kedalaman (diambil dari Geosiatislics Modcli,~g Sparial Ut~ceriait~iy oleh Chiles, J. P. dan P. Delfiner).
Tujuan
Membandingkan C o h i g i ~ ~ g dengan kondisi tak bias 1 dan Cokriging dengan kondisi tak bias 2.
LANDASAN TEORI
Berikut ini diberikan beberapa pokok Definisi 2 :
bahasan baik berupa definisi, lemma maupun Jika V(x) suatu peubah acak diskret atau kontinu teorema yang digunakan dalam penyusunan yang mempunyai momen kedua berhingga, maka
tulisan ini. ragam bagi V(x), dilambangkan Varpfx)),
didefinisikan sebagai :
Definisi 1 : Var{V(x)] = E [ ( v ( ~ ) - E [ V ( X ) ] ) ~ ] . Nilai harapan bagi peubah V(r/ dilambangkan
(Helms, 1997), E[V(x)], diddenisikan sebagai :
E[V(x)] = ~ v i p [ v i ] . jika V(x) diskret dengan Definisi 3 :
i=l Jika U(x) dan V(x) mempunyai momen kedua
kemungkinan nilai I>,, r 2 , . .., 11,, dan kngsi berhingga, maka colJarian U(wJ dan V O , massa peluang p[vi] = p ( ~ ( x ) = 1 1 ~ ) . dan dilambangkan Cov(U(x), V(x)), didefinisikan sebagai
COIJ(U(X), V(x)) = C0ll(o; V )
m
q V ( x ) ] = [ilf[v]dv, jika Y(r) kontinu dengan = E [ W ] - E[U]EP/
--
Untuk konstanta c terten:~, Coir(U,cj = 0 danhngsi kepekatan peluang f [ v ] , dimana V(x) Cos(U,
U)
= E[U2] - (E[U])- = VarflJ).(Helms, 1997).
adalah peubah
If
yang tergantung pada lokasi X.Teorema 1 :
Jika Ul, ..., U, mempunyai momen kedua berhingga, maka
1s;<,s,,
Bukti : (Lihat lampiran 1, halaman 9 ).
Corollary 2 :
Jika Ul, ..., U, adalah peubah acak bebas yang mempunyai momen kedua berhingga, maka
Var X U , = C v a r u ,
)
;Il
Bukti :
Untuk i # . I , U i dan U i bebas dan
Teorema 3 :
Misalkan U . U,, V .
,
mempunyai momen kedua berhingga dan misalkana , . a h . . h , adalah bilangan real sembarang. Maka
Bnkti : (Lihat lampiran 2, halaman 10).
Drift
Cokriging
Nilai dugaan cohiging adalah kombinasi linear dari data utama dan data pelengkap seperti yang di tuliskan berikut ini :
dengan
e Uo adalah nilai dugaan U pada lokasi 0
*
U , , U Z ,..., U , adalah data utama pada n lokasi herdekatanV,,V, ,..., V,,, adalah data pelengkap pada ni lokasi yang berdekatan
e al ,a ,,..., a,, dan 6, , b Z , . .
.,
h,,, adalah pembohotcokrigitig yang hams ditentukan
Dengan memberikan h o sebagai parameter
dari pendugaan dengan U,, merupakan dugaan, maka dicoba mencari syarat apa yang hams diberikan agar kondisi tak bias terpenuhi.
Jika
R
adalah peubah galat maka galat dugaanDefinisi 4 :
Misalkan V(x) adalab peubab regional. Maka (2)
driji nz(x) didefinisikan dengan
nt(x) = E/V(x)].
*
w' = (0, ,a2 ,... ,fl,,,bl ,ha ,..., h,,,-l) Yaitu drift pada titik x adalah nilai harapandari peubah regional Vpada titikx. (Olea, 1975).
Definisi 5 :
Misalkan V(x) adalah peubab regional dengan driji nz(x). Maka residrial Y(x) adalah :
0 U I , U , ,..., U,, adalah peubah acak yang
merepresentasikan sifat U pada ti lokasi
dimana U dijadikan sampel data
V 2I , adalah peubah acak yang
merepresentasikan sifat V pada m lokasi berdekatan dimana Vdijadikan sampel data. Persamaan (1) adalah kombinasi linear dari n+m+l peubah acak, yaitu U I ,..., U,,, Vl ,..., V ,
dan U,. Diperoleh ekspresi ragam R sebagai
dengan Cz adalah matriks covariatr dari Z
Dengan memperluas dan menyederhanakan (3) diperoleh suatu ekspresi untuk ragam dari galat pendugaan dalam bagian pembobot
colo.igi,rg dau covariatr antar peubah-peubah acak :
"I
-
2 C bjCo~~(VjUo)+
C U I J ( ~ J ~ U ~ )j=l
(4) (Lihat Lampiran 3, halaman 11)
dengan
*
Cov(U>UJ adalah covarrat~ antara U, danU,
*
Cov(V,VJ adalah covnrratr antara V, danV,
e Cov(U,v adalah cross-co~~artmr antara U, dan
V,
Gugus pembobot cobigitg yang dicari hams memenuhi dua syarat. Pertama, pembobot harus sedemikian rupa sehingga nilai dugaan yang diberikan dalam (1) tak bias. Kedua, pembobot hams sedemikian rupa sehingga ragam galat yang diberikan dalam (4) adalah sekecil mungkin.
Untuk mendaoatkan kondisi tak bias maka :
dimana
E [ u ~ ]
= tt$ danE[v,]=
Dan persamaan ini, terlihat bahwa salah satu cara menjamin ketakbiasan yaitu dengan membuat pembobot pada bagian penjumlahan yang pertama sama dengan 1 sedangkan pada bagian yang kedua sama dengan 0 :
,,,
:ai = l dan C b j = O
i=L j=l
Sekarang dihadapkan dengan masalah minimisasi yang klasik yang bergantung kepada dua kendala. Dicoha mencari y g u s pembobot yang meminimisasi ragam galat yang diberikan dalam (4) dan juga memenuhi dua syarat tak bias. Dengan menggunakan metode pengali Lagrarige
"8
~ a r ( ~ ) = wlCiiv + 2 ~ ~ ( i a , - I ) + 2A2(Cbj)
i=l ,=I
(6)
dengan / I I dan /.2 adalah pengali Lagrntige.
Untuk meminimisasi (6) dihitung turunan parsial dari Var(R) terhadap rionr pembobot dan kedua pengali Lagrallge:
- 2Cov(UjlJ0)+ 2 4
a(Vnr{Rh = 2= bi
col.(vi
vj)
f n i ~ o v ( ~ i ~ j )+
fbicol~(?v,)+
A,db j i=l i=l i=l
= c o v ( v j u o )
+
2?ni CU~J(U~V,)i = ~ untuk j = I, ..,m
- 2 c o v ( v j u n )
+
2A, n, Xui = I dan x b , = Ountuk j= I, ..., m i = ~ j=l
a(vaI'{~}) = ,(f ni -1) (8)
32, i = ~ Minimisasi ragam galat yang berhubungan
(7) dapat dihitung dengan menggunakan (4) atau untuk
a(vnr{~})
= b j , gugus utama dari syarat ketakbiasan, (4) dapat812 j=l disederhanakan dengan membuat subsitusi yang
Sistem cokr.iging akhirnya diperoleh menggunakan pengali Lngt'onge menjadi dengan menyamakan masing-masing ; + m i 2
persamaan ini dengan 0 dan menyusun ulang v ~ ( R ) = C O ~ ~ ( U ~ U ~ ) - A
-
n i ~ o i l ( ~ i ~ o )i=l
masing-masing dengan :
,,,
f n j ~ o v ( ~ i ~ , ) + x b j ~ o v ( ~ , v j ) + A, - bi cov(vi
uo)
j=l j=I j=l
= c o l ~ ( u i u o )
untuk i = I ,..,?I (9)
PEMBAHASAN
Pendugaan titik dilakukan pada gridIOXlO m2 . Radius terbatas sampai 40 m, dan kuadran digunakan untuk mendekati nilai total data dalam setiap kuadran sampai titik lebih dari 6. Dalam setiap kuadran, tidak lebih dari tiga sampel U yang digunakan dan sampel V juga tetap dipakai.
Batasan akhir yang didekati dengan ekstrapolasi peubah utama adalah penempatan
2 data sampel U. Tidak ada titik dugaan yang lebih jauh dari 11 m dari nilai sampel U. Dua
cokrigittg dapat dilakukan dengan masing- masing penggunaan gugus kondisi tak bias yang berbeda. Cokrigitzg pertama
"1 meng~unakan kondisi x n i =I dan x b j =O
i=l j=l
untuk bobot utama dan bobot pelengkap.
Cokrigiilg kedua menggunakan kondisi tak bias 1, yang ditetapkan bahwa penjumlahan semua bobot harus sama dengan I:
Dengan alternatif kondisi ketakbiasan ini, penduga harus sedikit diubah. Nilai U
yang tidak diketahui sekarang diduga sebagai kombinasi linear yang diboboti dari daerah dekat nilai U ditambah kombinasi linear dari
daerah dekat nilai V yang merupakan konstanta sedemikian sehingga meannya sama dengan mean nilai U:
"8
O n = ? a i ~ ,
+
z b j ( v j -mr, + m u )i=l j=l (11)
Penduga ini memerlukan infonnasi tarnbahan, katakanlah menduga mean U dan menduga mean V yang melebihi daerah dugaan.
Satu cara sederhana untuk menduga mean
&v
danmu adalah menghitung rata-rata aritmetik dari 2
nilai sampel U dan bersamaan dengan 2 nilai sampel
dimana niu
=E[u,]
dan E[v,]= niir. Kondisi,,,
Cci,
+
zbj
=l untuk memastikan bahwai=1 j=1
cokrigirig tak bias.
Untuk melakukan pendugaan dengan teknik cohigirig memerlukan model linear coregionalisasi yang diperoleh dari sampel variogram yang diberikan oleh :
yu ( / I ) = 440000
+
70000SphI (/ I ; )+
9500OSph, ( h i ) y, (h) = 22000+40000Sp/1, (11;)+45000Sph, ( h i )
yw (h) = 47000+50000Sph, ( h ; )
t 40000Sphl (hi )
(13)
dimana vektor h:, dihitung sebagai berikut :
hr= jarak dua titik pada sumbu x
h, = jarak dua titik pada sumbu y.
jika h
>
a(16)
dimana h aI ) adalah model spheric01 dan n
adalah range spherical.
Untuk mencari nilai cosorinrl yang terdapat pada matriks cokrigillg menggunakan hubungan :
C w
(h) = YUY ( m f - ~ r n ~ (h)c u (h) = Yu (m)-yu ( 4 (1 7 )
cv
(h) = 71, ( a ) - Y v (h)Contoh perhitungan :
Perhatikan Gambar 1 (data diambil dari Isaaks, E. H. dan R. M. Srivastava dalam Applied Geosm(istics). Pertama menghitung coi,ariat, untuk
UiU2 dan untuk yang lainnya caranya sama sebagai berikut :
=
[::;:]
sehingga hi = 0.5957
sehingga hi = 0.2716
Panjang h; dan hi aloenkan olen :
0.5957 ( o , 5 ( ~ . 5 r 7 ) 3
Sphl (hi) = ( 1 . 5 ) ~ -
-
I
r , % - , \ - 7 -
I (15) sphI(h;) = ( I S ) - - - 0.2716
1
(14) Selanjutnya substitusi ke persamaan (16),
Panjang h; dan hi diberikan oleh :
0.5957 ( o , 5 ( ~ . 5 r 7 ) 3
Sphl (hi) = ( 1 . 5 ) ~ -
-
I
= 0.788
(15) 0.2716
sphI(h;) = ( I S ) - - - 1
Substitusi ke persamaan (13) akan diperoleh :
y , (m) = 440000
+
70000(0.788)+95000(0.397) Cokriging dengan kondisi tak bias 1 :2 3
= 532875 xaiUi = l dan x b j V j = 0
i=O j-1
Dengan cara yang sama akan diperoleh :
yu(h) = 505760 Berdasarkan hasil yang ada di Tabel I
Sehingga Coif7J,Ud = 532875-505760 halaman 13, dengan substitusi ke persamaan (8) =27115 diperoleh matriks coi~aria~? sebagai berikut :
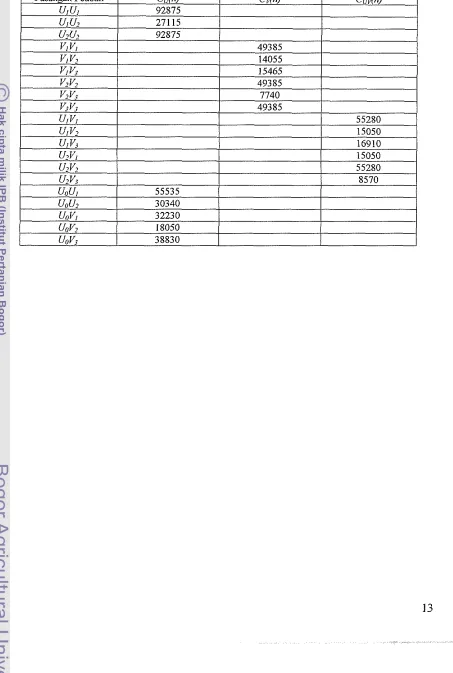
(Lihat Tabel 1 di Lampiran 4 halaman 13)
Gambilr I . Kunligurosi dola cakrirrgi,rg yang mongondunp dua date utama dnn tigo data pelcngkap
LolasilitikBsmpe(
'92875 27115 55280 15050 16910 1 0 27115 92875 15050 55280 8570 1 0 55280 15050 49385 14055 15465 0 1 15050 55280 14055 49385 7740 0 1 16910 8570 15465 7740 49385 0 1 I 1
o
o
o
o o
Dengan menggunakan soflware MapleV
akan diperoleh bobot seperti di Tabel 2 Cokriging dengan kondisi tak bias 2: halaman 7. Dari persamaan (2) diperoleh: 2 3
z
3 x a , + x b , = 1I<= x n , U , + ~ b j V j - U , ;=I j = ~
;=I j = ~ Dan Persamaan 2 diperoleh :
3 &[Uo]= E[640.162]
E[R]=E x n i U i
+
z b j v j;=I
['
j=l EIUo]= 640.162E[u,] = ~[465.11] Dan dari persamaan (1 1) diperoleh : A
E[u,]
= 465.11 Uo = 640.162 sehingga Var(R) = 56405 1.5416'a, a , b, b, h,
-a,
Dan dari persamaan (1) diperoleh :
Uo =465.11 sehingga Vmm) = 34159.82
'I'skl 2. ?hhl perbandingon unluk cukriging dcngan kondisi tali bias I dnn eob.;ging dungan
kondisi talc bins 2
Mungkin ha1 yang penting untuk diperhatikan dalam Tabel 2 adalah dugaan
cc)krigi,g negatif Alasan untuk dugaan negatif
111
mula-mula dengan kondisi tak bias 236, = 0
j = l
Untuk jumlah bobot sama dengan no1 maka beberapa nilai dugaan hams negatif Pada saat bobot yang negatif dikalikan dengan nilai sampel V yang besar, dugaan negatif dapat muncul. Jika hasil kali negatif jumlahnya hesar dalam nilai mutlak dari pada jumlah bobot positif, maka dugaannya negatif.
Cokrigitig dengan kondisi tak bias 1 lehih diterima karena mempunyai galat yang lebih kecil dibandingkan cokriging dengan kondisi tak bias 2.
Pengarub nilai yang lebih kuat dalam pendugaan ini mengacu pada pilihan kondisi tak bias yang menghasilkan hobot lebih yang diberi tanda untuk peubah pelengkap.
Sebagai ringkasan bahwa cokriging dengan kondisi tak bias 2 kurang memuaskan. Misalkan kasus dimana hanya dua nilai data pelengkap yang ditemukan sama jauhnya dari titik pendugaan dan dari semua data utama. Karena dua nilai data pelengkap sama jauhnya, maka hams diberi bobot yang sama. Meskipun solusi ini secara matematika benar, tapi sulit untuk memhayangkan proses fisika yang mana skema bobotnya benar. Melalui metode ini akan menurunkan kebiasan, tapi tidak menurunkan penyebaran galat yang besar.
Menggunakan kondisi tak bias 1, bagaimanapun dapat melakukan perbaikan, tidak hanya dalam kehiasan dan penyebaran galat., tapi juga dalam kejadian dugaan negatif yang lebih rendah. Melalui pendekatan ini diperlukan pendugaan prior dari mean global
U
dan V, ha1 ini jelas bahwa kejadian dengan dugaan yang lebih sederhana dari mean global, kita dapat memperbaiki pendugaan.KESIMPULAN DAN SARAN
Metode pendugaan data spasial dengan cokriging, mempakan suatu metode yang digunakan untuk menduga nilai pada suatu titik yang tidak dilakukan pengamatan dengan mengynakan data lebih dari satu peubah.
C(>krigirig dengan kondisi tak bias 1 mempunyai ragam galat yang lebih kecil dibandingkan cokr~ging dengan kondisi tak
bias 2. Sehingga cokrigi,~g dengan kondisi tak bias 1 lebih diterima daripada cokriging dengan kondisi tak bias 2.
DAFTAR PUSTAKA
Chiles, J. P. & P. Delfiner. 1999. Isaaks, E. H. & R.
M.
Srivastava. 1989. Geostalislics Moiielirlg Spalinl Applied Geoslalislics. Oxford Urlcermiilty. John Wiley & Sons, New University Press, Oxford.York. Olea, R. A. 1975. Oplin~rrrii Mnppirrg
Helms, L. L. 1997. I?~lrodrrclio~z lo Techr~iq~ies ~ i s i i ~ g Regiorialized I'robabiliiy Theory with Cor~tmrporary Variable Tt~eory. Empresa Nacional del Applicaio~s. W.H. Freeman and Petroleo, Santiago, Chile.
Lampiran 1 : Bukti Teorema 1
Karena E
[;I]
U j]
=,
C
plr,,
maka' I
[(
. - ~ ] + ~ $ E [ ( U ~ - ~ ~ I ~ ) ( U , - A ~ ~ ~ ) ]= C
I
7
U , PlIjj=l i=l ,=I
Lampiras 2 : Bukti Teorema 3
Untuk membuktikan teorema diatas, kita gunakan teorema lain yang tidak diberikan buktinya disini, yaitu :
Jika U,, ..., U, adalah peubah acak dengan nilai harapan berhingga dan c,, ..., c, adalah konstanta
-
-
real, maka i c j u j mempunyai nilai harapan berhingga dan E
j=I
Sehingga { = a r U j ] = = ~ ; E [ u ~ ] dan
{e
j=l bjV,] = ~ b j E [ V , ] .,=I
Karena
maka
,,,
+ k f l j u j . ~ b , v , ) i=l j=l
=.[('ajujXfbjvj]]
($~;EI.;I)['~~*I)
,J
,,<
Lampiran 5 : (Bukti yang menjamin nilai ragam galat minimum)
Teorema 4 : (Uji T u r u n a n Pertama untuk Ekstrim Lokal)
Andaikan f kontinu pada selang terbuka (a, b) yang memuat titik kritis c,
I . Jika f'(x) > 0 untuk semua x dalam (a, c) dan f'(x) < 0 untuk semua x dalam (c, b) maka f (c) adalah nilai maksimum lokalf:
2. Jika f'(x) < 0 nntuk semua x dalam (a, c) dan f'(x) > 0 untuk semua x dalam (c, b) maka f (c) adalah nilai minimum lokalf:
3. Jika f'(x) bertanda sama pada kedua pihak c, maka f (c) bukan nmilai ekstrim lokalf:
Teorema 5 : (Uji Turunan Kedua untuk Ekstrim Lokal)
Andaikan f'dan f" ada pada setiap titik dalam selang terbuka (a, b) yang memuat c, dan andaikan f'(c) = 0 .
1. Jika f"(c) > 0 , f(c) adalah nilai minimum lokalf: 2. Jika f"(c) < 0 , f(c) adalah nilai maksimum lokalf:
Bukti :
1. Berdasarkan definisi dan hipotesis, f"(c) =
Lim
f'b-f'(4**C x-C
= Linz f'(x)-0 > 0
X+C X - C
sehingga dapat disimpulkan bahwa terdapat selang
(a,p)
(mungkin pendek) disekitar c dimana f'(x) > o ,-
x-C
Kedua ketaksamaan ini menunjukkan bahwa f'(x) < 0 untuk a < x < c dan f'(x) > 0 untuk c < x
<
p
.
Jadi, menurut Teorema Uji Turunan Pertama, f (c) adalah nilai minimum lokal.CB Terbukti.
2. Bukti serupa dengan (1)
= ~ ( C O V ( U ~ U ~ ) + C O V ( U ~ U ~ ) + C O V ( U ~ U ~ ) ) untuk i = 1,
...,
na 2 ( v a r ( R ) ) = 2=Cov(Vivj) abjz i=l
= 2(cov
(v,
v,
)+
cov (v,v*)+
Cov(v]
v3
)+
Cov(vzvl
)+
cov(v21/*
)+
cov(v2v3))
+
~ ( C O V(v3 v,
)+
cow(v3 v2
)+
Cov(v3
v3
))
untuk j = 1,
...,
m Karena nilai covarian positif dan nilai cross-covarian lebih kecil dari nilai covarian, maka :a2
(vQ~(R)) >,,
dana2
( v a r ( ~ ) ),O,
aaj
2 abiZTeorema 6 :
Matriks A adalah suatu matrik simetrik. Matriks A adalah matriks definit positif jika dan hanya jika semua akar cirinya positif.
Bukti :
(-4
Matriks A adalah matriks definit positif maka x T ~ x > 0 . Akan dibuktin dibuktikan 'm(.Ua akar cirinya positif.
Jika vektor ciri berpadanan dengan A maka berlaku A x = A x sehingga
xTAx maka A=->O
llxl12 .. .. Terbukti A > 0 .
(4
Matriks A mempunyai akar ciri yang semuanya positif. Akan dibuktikan matriks A definit positif.
Menurut teorema bahwa ( Jika A adalah matriks simetrik maka vektor-vektor ciri yang berbeda akan ortogonal) dan dengan menerapkan prosedur Gram-Smith menjamin bahwa vektor-vektor ciri yang didapatkan dengan prosedur ini akan ortonormal.
Misalkan ,x2,...,.x,,) adalah gugus ortonormal dari vektor ciri A. Jika
x
adalah vektor bukan"
T " 2 2no1 dalam %",
x = a l x ,
+ a 2 x 2+...+
a,x, dengan ai =C X
ri
danChi)
=IIxII
.
i=l i=l
Oleh karenUOIeh karena itu, MB : M B :r MB : MB :j
T
x ~ x = ( a ~ x ~ + a 2 x 2 + . . . + a , x , ) T ( a l X 1 ~ I +n2x2A2
+...+
a,,x,,~,)Lampiran 1 : Bukti Teorema 1
Karena E
[;I]
U j]
=,
C
plr,,
maka' I
[(
. - ~ ] + ~ $ E [ ( U ~ - ~ ~ I ~ ) ( U , - A ~ ~ ~ ) ]= C
I
7
U , PlIjj=l i=l ,=I
Lampiras 2 : Bukti Teorema 3
Untuk membuktikan teorema diatas, kita gunakan teorema lain yang tidak diberikan buktinya disini, yaitu :
Jika U,, ..., U, adalah peubah acak dengan nilai harapan berhingga dan c,, ..., c, adalah konstanta
-
-
real, maka i c j u j mempunyai nilai harapan berhingga dan E
j=I
Sehingga { = a r U j ] = = ~ ; E [ u ~ ] dan
{e
j=l bjV,] = ~ b j E [ V , ] .,=I
Karena
maka
,,,
+ k f l j u j . ~ b , v , ) i=l j=l
=.[('ajujXfbjvj]]
($~;EI.;I)['~~*I)
,J
,,<
Lampiran 5 : (Bukti yang menjamin nilai ragam galat minimum)
Teorema 4 : (Uji T u r u n a n Pertama untuk Ekstrim Lokal)
Andaikan f kontinu pada selang terbuka (a, b) yang memuat titik kritis c,
I . Jika f'(x) > 0 untuk semua x dalam (a, c) dan f'(x) < 0 untuk semua x dalam (c, b) maka f (c) adalah nilai maksimum lokalf:
2. Jika f'(x) < 0 nntuk semua x dalam (a, c) dan f'(x) > 0 untuk semua x dalam (c, b) maka f (c) adalah nilai minimum lokalf:
3. Jika f'(x) bertanda sama pada kedua pihak c, maka f (c) bukan nmilai ekstrim lokalf:
Teorema 5 : (Uji Turunan Kedua untuk Ekstrim Lokal)
Andaikan f'dan f" ada pada setiap titik dalam selang terbuka (a, b) yang memuat c, dan andaikan f'(c) = 0 .
1. Jika f"(c) > 0 , f(c) adalah nilai minimum lokalf: 2. Jika f"(c) < 0 , f(c) adalah nilai maksimum lokalf:
Bukti :
1. Berdasarkan definisi dan hipotesis, f"(c) =
Lim
f'b-f'(4**C x-C
= Linz f'(x)-0 > 0
X+C X - C
sehingga dapat disimpulkan bahwa terdapat selang
(a,p)
(mungkin pendek) disekitar c dimana f'(x) > o ,-
x-C
Kedua ketaksamaan ini menunjukkan bahwa f'(x) < 0 untuk a < x < c dan f'(x) > 0 untuk c < x
<
p
.
Jadi, menurut Teorema Uji Turunan Pertama, f (c) adalah nilai minimum lokal.CB Terbukti.
2. Bukti serupa dengan (1)
= ~ ( C O V ( U ~ U ~ ) + C O V ( U ~ U ~ ) + C O V ( U ~ U ~ ) ) untuk i = 1,
...,
na 2 ( v a r ( R ) ) = 2=Cov(Vivj) abjz i=l
= 2(cov
(v,
v,
)+
cov (v,v*)+
Cov(v]
v3
)+
Cov(vzvl
)+
cov(v21/*
)+
cov(v2v3))
+
~ ( C O V(v3 v,
)+
cow(v3 v2
)+
Cov(v3
v3
))
untuk j = 1,
...,
m Karena nilai covarian positif dan nilai cross-covarian lebih kecil dari nilai covarian, maka :a2
(vQ~(R)) >,,
dana2
( v a r ( ~ ) ),O,
aaj
2 abiZTeorema 6 :
Matriks A adalah suatu matrik simetrik. Matriks A adalah matriks definit positif jika dan hanya jika semua akar cirinya positif.
Bukti :
(-4
Matriks A adalah matriks definit positif maka x T ~ x > 0 . Akan dibuktin dibuktikan 'm(.Ua akar cirinya positif.
Jika vektor ciri berpadanan dengan A maka berlaku A x = A x sehingga
xTAx maka A=->O
llxl12 .. .. Terbukti A > 0 .
(4
Matriks A mempunyai akar ciri yang semuanya positif. Akan dibuktikan matriks A definit positif.
Menurut teorema bahwa ( Jika A adalah matriks simetrik maka vektor-vektor ciri yang berbeda akan ortogonal) dan dengan menerapkan prosedur Gram-Smith menjamin bahwa vektor-vektor ciri yang didapatkan dengan prosedur ini akan ortonormal.
Misalkan ,x2,...,.x,,) adalah gugus ortonormal dari vektor ciri A. Jika
x
adalah vektor bukan"
T " 2 2no1 dalam %",
x = a l x ,
+ a 2 x 2+...+
a,x, dengan ai =C X
ri
danChi)
=IIxII
.
i=l i=l
Oleh karenUOIeh karena itu, MB : M B :r MB : MB :j
T
x ~ x = ( a ~ x ~ + a 2 x 2 + . . . + a , x , ) T ( a l X 1 ~ I +n2x2A2
+...+
a,,x,,~,)PENDAHULUAN
Latar B e l a h ~ n gData spasial adalah data yang dikumpulkan dari lokasi-lokasi yang saling berkorelasi satu sama lain. Selanjutnya, korelasi suatu peubah U dan lfmenggambarkan hubungan keeratan antara U dan K
Persoalan yang ada pada data spasial adalah sulit melakukan pengukuran pada semua lokasi karena lokasi bersifat kontinu. Oleh karena itu, pendugaan pada titik-titik yang tidak dilakukan pengukuran sangatlah penting.
Metode pendugaan banyak variasinya, diantaranya adalah :
1) Ordinary Kriging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu yang dilakukan dengan mengamati data yang sejenis pada daerah lain.
2) BIok Kriging yaitu pendugaan rata-rata suatu nilai pada suatu area dan area tersebut dipecah-pecah menjadi area-area yang lebih kecil dimana suatu nilai menggambarkan nilai potongan area yang kecil tersebut.
3 ) Cohiging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu menggunakan data lebih dari satu peubah dengan mengamati data yang sejenis pada lokasi yang lain.
Pada beberapa fenomena, misalkan pendugaan terhadap kandungan sumber daya alam (misal : minyak bumi sebagai peubah utama (U)) seringkali menggunakan beberapa parameter yang mempunyai korelasi linear dengan kandungan sumber daya alam tersebut (sebagai peubah pelengkap
(q).
Pada kegiatan pendugaan kandungan sumber daya alam sering menggunakan teknik cokriging. Pada kajian ini dicoba menggunakan cohigi,~g.Salah satu ilustrasi dalam masalah nyata adalah dalam industri minyak. Dipmeter menykur lubang dan mencari kedalaman, juga terdapat beberapa parameter seperti sifat menyerap (porosity), permeabilitas dan kejenuhan cairan yang bergantung pada kedalaman (diambil dari Geosiatislics Modcli,~g Sparial Ut~ceriait~iy oleh Chiles, J. P. dan P. Delfiner).
Tujuan
Membandingkan C o h i g i ~ ~ g dengan kondisi tak bias 1 dan Cokriging dengan kondisi tak bias 2.
LANDASAN TEORI
Berikut ini diberikan beberapa pokok Definisi 2 :
bahasan baik berupa definisi, lemma maupun Jika V(x) suatu peubah acak diskret atau kontinu teorema yang digunakan dalam penyusunan yang mempunyai momen kedua berhingga, maka
tulisan ini. ragam bagi V(x), dilambangkan Varpfx)),
didefinisikan sebagai :
Definisi 1 : Var{V(x)] = E [ ( v ( ~ ) - E [ V ( X ) ] ) ~ ] . Nilai harapan bagi peubah V(r/ dilambangkan
(Helms, 1997), E[V(x)], diddenisikan sebagai :
E[V(x)] = ~ v i p [ v i ] . jika V(x) diskret dengan Definisi 3 :
i=l Jika U(x) dan V(x) mempunyai momen kedua
kemungkinan nilai I>,, r 2 , . .., 11,, dan kngsi berhingga, maka colJarian U(wJ dan V O , massa peluang p[vi] = p ( ~ ( x ) = 1 1 ~ ) . dan dilambangkan Cov(U(x), V(x)), didefinisikan sebagai
COIJ(U(X), V(x)) = C0ll(o; V )
m
q V ( x ) ] = [ilf[v]dv, jika Y(r) kontinu dengan = E [ W ] - E[U]EP/
--
Untuk konstanta c terten:~, Coir(U,cj = 0 danhngsi kepekatan peluang f [ v ] , dimana V(x) Cos(U,
U)
= E[U2] - (E[U])- = VarflJ).(Helms, 1997).
adalah peubah
If
yang tergantung pada lokasi X.PENDAHULUAN
Latar B e l a h ~ n gData spasial adalah data yang dikumpulkan dari lokasi-lokasi yang saling berkorelasi satu sama lain. Selanjutnya, korelasi suatu peubah U dan lfmenggambarkan hubungan keeratan antara U dan K
Persoalan yang ada pada data spasial adalah sulit melakukan pengukuran pada semua lokasi karena lokasi bersifat kontinu. Oleh karena itu, pendugaan pada titik-titik yang tidak dilakukan pengukuran sangatlah penting.
Metode pendugaan banyak variasinya, diantaranya adalah :
1) Ordinary Kriging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu yang dilakukan dengan mengamati data yang sejenis pada daerah lain.
2) BIok Kriging yaitu pendugaan rata-rata suatu nilai pada suatu area dan area tersebut dipecah-pecah menjadi area-area yang lebih kecil dimana suatu nilai menggambarkan nilai potongan area yang kecil tersebut.
3 ) Cohiging yaitu pendugaan suatu nilai peubah pada suatu titik tertentu menggunakan data lebih dari satu peubah dengan mengamati data yang sejenis pada lokasi yang lain.
Pada beberapa fenomena, misalkan pendugaan terhadap kandungan sumber daya alam (misal : minyak bumi sebagai peubah utama (U)) seringkali menggunakan beberapa parameter yang mempunyai korelasi linear dengan kandungan sumber daya alam tersebut (sebagai peubah pelengkap
(q).
Pada kegiatan pendugaan kandungan sumber daya alam sering menggunakan teknik cokriging. Pada kajian ini dicoba menggunakan cohigi,~g.Salah satu ilustrasi dalam masalah nyata adalah dalam industri minyak. Dipmeter menykur lubang dan mencari kedalaman, juga terdapat beberapa parameter seperti sifat menyerap (porosity), permeabilitas dan kejenuhan cairan yang bergantung pada kedalaman (diambil dari Geosiatislics Modcli,~g Sparial Ut~ceriait~iy oleh Chiles, J. P. dan P. Delfiner).
Tujuan
Membandingkan C o h i g i ~ ~ g dengan kondisi tak bias 1 dan Cokriging dengan kondisi tak bias 2.
LANDASAN TEORI
Berikut ini diberikan beberapa pokok Definisi 2 :
bahasan baik berupa definisi, lemma maupun Jika V(x) suatu peubah acak diskret atau kontinu teorema yang digunakan dalam penyusunan yang mempunyai momen kedua berhingga, maka
tulisan ini. ragam bagi V(x), dilambangkan Varpfx)),
didefinisikan sebagai :
Definisi 1 : Var{V(x)] = E [ ( v ( ~ ) - E [ V ( X ) ] ) ~ ] . Nilai harapan bagi peubah V(r/ dilambangkan
(Helms, 1997), E[V(x)], diddenisikan sebagai :
E[V(x)] = ~ v i p [ v i ] . jika V(x) diskret dengan Definisi 3 :
i=l Jika U(x) dan V(x) mempunyai momen kedua
kemungkinan nilai I>,, r 2 , . .., 11,, dan kngsi berhingga, maka colJarian U(wJ dan V O , massa peluang p[vi] = p ( ~ ( x ) = 1 1 ~ ) . dan dilambangkan Cov(U(x), V(x)), didefinisikan sebagai
COIJ(U(X), V(x)) = C0ll(o; V )
m
q V ( x ) ] = [ilf[v]dv, jika Y(r) kontinu dengan = E [ W ] - E[U]EP/
--
Untuk konstanta c terten:~, Coir(U,cj = 0 danhngsi kepekatan peluang f [ v ] , dimana V(x) Cos(U,
U)
= E[U2] - (E[U])- = VarflJ).(Helms, 1997).
adalah peubah
If
yang tergantung pada lokasi X.Teorema 1 :
Jika Ul, ..., U, mempunyai momen kedua berhingga, maka
1s;<,s,,
Bukti : (Lihat lampiran 1, halaman 9 ).
Corollary 2 :
Jika Ul, ..., U, adalah peubah acak bebas yang mempunyai momen kedua berhingga, maka
Var X U , = C v a r u ,
)
;Il
Bukti :
Untuk i # . I , U i dan U i bebas dan
Teorema 3 :
Misalkan U . U,, V .
,
mempunyai momen kedua berhingga dan misalkana , . a h . . h , adalah bilangan real sembarang. Maka
Bnkti : (Lihat lampiran 2, halaman 10).
Drift
Cokriging
Nilai dugaan cohiging adalah kombinasi linear dari data utama dan data pelengkap seperti yang di tuliskan berikut ini :
dengan
e Uo adalah nilai dugaan U pada lokasi 0
*
U , , U Z ,..., U , adalah data utama pada n lokasi herdekatanV,,V, ,..., V,,, adalah data pelengkap pada ni lokasi yang berdekatan
e al ,a ,,..., a,, dan 6, , b Z , . .
.,
h,,, adalah pembohotcokrigitig yang hams ditentukan
Dengan memberikan h o sebagai parameter
dari pendugaan dengan U,, merupakan dugaan, maka dicoba mencari syarat apa yang hams diberikan agar kondisi tak bias terpenuhi.
Jika
R
adalah peubah galat maka galat dugaanDefinisi 4 :
Misalkan V(x) adalab peubab regional. Maka (2)
driji nz(x) didefinisikan dengan
nt(x) = E/V(x)].
*
w' = (0, ,a2 ,... ,fl,,,bl ,ha ,..., h,,,-l) Yaitu drift pada titik x adalah nilai harapandari peubah regional Vpada titikx. (Olea, 1975).
Definisi 5 :
Misalkan V(x) adalah peubab regional dengan driji nz(x). Maka residrial Y(x) adalah :
0 U I , U , ,..., U,, adalah peubah acak yang
merepresentasikan sifat U pada ti lokasi
dimana U dijadikan sampel data
V 2I , adalah peubah acak yang
merepresentasikan sifat V pada m lokasi berdekatan dimana Vdijadikan sampel data. Persamaan (1) adalah kombinasi linear dari n+m+l peubah acak, yaitu U I ,..., U,,, Vl ,..., V ,
dan U,. Diperoleh ekspresi ragam R sebagai
dengan Cz adalah matriks covariatr dari Z
Dengan memperluas dan menyederhanakan (3) diperoleh suatu ekspresi untuk ragam dari galat pendugaan dalam bagian pembobot
colo.igi,rg dau covariatr antar peubah-peubah acak :
"I
-
2 C bjCo~~(VjUo)+
C U I J ( ~ J ~ U ~ )j=l
(4) (Lihat Lampiran 3, halaman 11)
dengan
*
Cov(U>UJ adalah covarrat~ antara U, danU,
*
Cov(V,VJ adalah covnrratr antara V, danV,
e Cov(U,v adalah cross-co~~artmr antara U, dan
V,
Gugus pembobot cobigitg yang dicari hams memenuhi dua syarat. Pertama, pembobot harus sedemikian rupa sehingga nilai dugaan yang diberikan dalam (1) tak bias. Kedua, pembobot hams sedemikian rupa sehingga ragam galat yang diberikan dalam (4) adalah sekecil mungkin.
Untuk mendaoatkan kondisi tak bias maka :
dimana
E [ u ~ ]
= tt$ danE[v,]=
Dan persamaan ini, terlihat bahwa salah satu cara menjamin ketakbiasan yaitu dengan membuat pembobot pada bagian penjumlahan yang pertama sama dengan 1 sedangkan pada bagian yang kedua sama dengan 0 :
,,,
:ai = l dan C b j = O
i=L j=l
Sekarang dihadapkan dengan masalah minimisasi yang klasik yang bergantung kepada dua kendala. Dicoha mencari y g u s pembobot yang meminimisasi ragam galat yang diberikan dalam (4) dan juga memenuhi dua syarat tak bias. Dengan menggunakan metode pengali Lagrarige
"8
~ a r ( ~ ) = wlCiiv + 2 ~ ~ ( i a , - I ) + 2A2(Cbj)
i=l ,=I
(6)
dengan / I I dan /.2 adalah pengali Lagrntige.
Untuk meminimisasi (6) dihitung turunan parsial dari Var(R) terhadap rionr pembobot dan kedua pengali Lagrallge:
- 2Cov(UjlJ0)+ 2 4
a(Vnr{Rh = 2= bi
col.(vi
vj)
f n i ~ o v ( ~ i ~ j )+
fbicol~(?v,)+
A,db j i=l i=l i=l
= c o v ( v j u o )
+
2?ni CU~J(U~V,)i = ~ untuk j = I, ..,m
- 2 c o v ( v j u n )
+
2A, n, Xui = I dan x b , = Ountuk j= I, ..., m i = ~ j=l
a(vaI'{~}) = ,(f ni -1) (8)
32, i = ~ Minimisasi ragam galat yang berhubungan
(7) dapat dihitung dengan menggunakan (4) atau untuk
a(vnr{~})
= b j , gugus utama dari syarat ketakbiasan, (4) dapat812 j=l disederhanakan dengan membuat subsitusi yang
Sistem cokr.iging akhirnya diperoleh menggunakan pengali Lngt'onge menjadi dengan menyamakan masing-masing ; + m i 2
persamaan ini dengan 0 dan menyusun ulang v ~ ( R ) = C O ~ ~ ( U ~ U ~ ) - A
-
n i ~ o i l ( ~ i ~ o )i=l
masing-masing dengan :
,,,
f n j ~ o v ( ~ i ~ , ) + x b j ~ o v ( ~ , v j ) + A, - bi cov(vi
uo)
j=l j=I j=l
= c o l ~ ( u i u o )
untuk i = I ,..,?I (9)
PEMBAHASAN
Pendugaan titik dilakukan pada gridIOXlO m2 . Radius terbatas sampai 40 m, dan kuadran digunakan untuk mendekati nilai total data dalam setiap kuadran sampai titik lebih dari 6. Dalam setiap kuadran, tidak lebih dari tiga sampel U yang digunakan dan sampel V juga tetap dipakai.
Batasan akhir yang didekati dengan ekstrapolasi peubah utama adalah penempatan
2 data sampel U. Tidak ada titik dugaan yang lebih jauh dari 11 m dari nilai sampel U. Dua
cokrigittg dapat dilakukan dengan masing- masing penggunaan gugus kondisi tak bias yang berbeda. Cokrigitzg pertama
"1 meng~unakan kondisi x n i =I dan x b j =O
i=l j=l
untuk bobot utama dan bobot pelengkap.
Cokrigiilg kedua menggunakan kondisi tak bias 1, yang ditetapkan bahwa penjumlahan semua bobot harus sama dengan I:
Dengan alternatif kondisi ketakbiasan ini, penduga harus sedikit diubah. Nilai U
yang tidak diketahui sekarang diduga sebagai kombinasi linear yang diboboti dari daerah dekat nilai U ditambah kombinasi linear dari
daerah dekat nilai V yang merupakan konstanta sedemikian sehingga meannya sama dengan mean nilai U:
"8
O n = ? a i ~ ,
+
z b j ( v j -mr, + m u )i=l j=l (11)
Penduga ini memerlukan infonnasi tarnbahan, katakanlah menduga mean U dan menduga mean V yang melebihi daerah dugaan.
Satu cara sederhana untuk menduga mean
&v
danmu adalah menghitung rata-rata aritmetik dari 2
nilai sampel U dan bersamaan dengan 2 nilai sampel
dimana niu
=E[u,]
dan E[v,]= niir. Kondisi,,,
Cci,
+
zbj
=l untuk memastikan bahwai=1 j=1
cokrigirig tak bias.
Untuk melakukan pendugaan dengan teknik cohigirig memerlukan model linear coregionalisasi yang diperoleh dari sampel variogram yang diberikan oleh :
yu ( / I ) = 440000
+
70000SphI (/ I ; )+
9500OSph, ( h i ) y, (h) = 22000+40000Sp/1, (11;)+45000Sph, ( h i )
yw (h) = 47000+50000Sph, ( h ; )
t 40000Sphl (hi )
(13)
dimana vektor h:, dihitung sebagai berikut :
hr= jarak dua titik pada sumbu x
h, = jarak dua titik pada sumbu y.
jika h
>
a(16)
dimana h aI ) adalah model spheric01 dan n
adalah range spherical.
Untuk mencari nilai cosorinrl yang terdapat pada matriks cokrigillg menggunakan hubungan :
C w
(h) = YUY ( m f - ~ r n ~ (h)c u (h) = Yu (m)-yu ( 4 (1 7 )
cv
(h) = 71, ( a ) - Y v (h)Contoh perhitungan :
Perhatikan Gambar 1 (data diambil dari Isaaks, E. H. dan R. M. Srivastava dalam Applied Geosm(istics). Pertama menghitung coi,ariat, untuk
UiU2 dan untuk yang lainnya caranya sama sebagai berikut :
=
[::;:]
sehingga hi = 0.5957
sehingga hi = 0.2716
Panjang h; dan hi aloenkan olen :
0.5957 ( o , 5 ( ~ . 5 r 7 ) 3
Sphl (hi) = ( 1 . 5 ) ~ -
-
I
r , % - , \ - 7 -
I (15) sphI(h;) = ( I S ) - - - 0.2716
1
(14) Selanjutnya substitusi ke persamaan (16),
Panjang h; dan hi diberikan oleh :
0.5957 ( o , 5 ( ~ . 5 r 7 ) 3
Sphl (hi) = ( 1 . 5 ) ~ -
-
I
= 0.788
(15) 0.2716
sphI(h;) = ( I S ) - - - 1
Substitusi ke persamaan (13) akan diperoleh :
y , (m) = 440000
+
70000(0.788)+95000(0.397) Cokriging dengan kondisi tak bias 1 :2 3
= 532875 xaiUi = l dan x b j V j = 0
i=O j-1
Dengan cara yang sama akan diperoleh :
yu(h) = 505760 Berdasarkan hasil yang ada di Tabel I
Sehingga Coif7J,Ud = 532875-505760 halaman 13, dengan substitusi ke persamaan (8) =27115 diperoleh matriks coi~aria~? sebagai berikut :
(Lihat Tabel 1 di Lampiran 4 halaman 13)
Gambilr I . Kunligurosi dola cakrirrgi,rg yang mongondunp dua date utama dnn tigo data pelcngkap
LolasilitikBsmpe(
'92875 27115 55280 15050 16910 1 0 27115 92875 15050 55280 8570 1 0 55280 15050 49385 14055 15465 0 1 15050 55280 14055 49385 7740 0 1 16910 8570 15465 7740 49385 0 1 I 1
o
o
o
o o
Dengan menggunakan soflware MapleV
akan diperoleh bobot seperti di Tabel 2 Cokriging dengan kondisi tak bias 2: halaman 7. Dari persamaan (2) diperoleh: 2 3
z
3 x a , + x b , = 1I<= x n , U , + ~ b j V j - U , ;=I j = ~
;=I j = ~ Dan Persamaan 2 diperoleh :
3 &[Uo]= E[640.162]
E[R]=E x n i U i
+
z b j v j;=I
['
j=l EIUo]= 640.162E[u,] = ~[465.11] Dan dari persamaan (1 1) diperoleh : A
E[u,]
= 465.11 Uo = 640.162 sehingga Var(R) = 56405 1.5416'a, a , b, b, h,
-a,
Dan dari persamaan (1) diperoleh :
Uo =465.11 sehingga Vmm) = 34159.82
'I'skl 2. ?hhl perbandingon unluk cukriging dcngan kondisi tali bias I dnn eob.;ging dungan
kondisi talc bins 2
Mungkin ha1 yang penting untuk diperhatikan dalam Tabel 2 adalah dugaan
cc)krigi,g negatif Alasan untuk dugaan negatif
111
mula-mula dengan kondisi tak bias 236, = 0
j = l
Untuk jumlah bobot sama dengan no1 maka beberapa nilai dugaan hams negatif Pada saat bobot yang negatif dikalikan dengan nilai sampel V yang besar, dugaan negatif dapat muncul. Jika hasil kali negatif jumlahnya hesar dalam nilai mutlak dari pada jumlah bobot positif, maka dugaannya negatif.
Cokrigitig dengan kondisi tak bias 1 lehih diterima karena mempunyai galat yang lebih kecil dibandingkan cokriging dengan kondisi tak bias 2.
Pengarub nilai yang lebih kuat dalam pendugaan ini mengacu pada pilihan kondisi tak bias yang menghasilkan hobot lebih yang diberi tanda untuk peubah pelengkap.
Sebagai ringkasan bahwa cokriging dengan kondisi tak bias 2 kurang memuaskan. Misalkan kasus dimana hanya dua nilai data pelengkap yang ditemukan sama jauhnya dari titik pendugaan dan dari semua data utama. Karena dua nilai data pelengkap sama jauhnya, maka hams diberi bobot yang sama. Meskipun solusi ini secara matematika benar, tapi sulit untuk memhayangkan proses fisika yang mana skema bobotnya benar. Melalui metode ini akan menurunkan kebiasan, tapi tidak menurunkan penyebaran galat yang besar.
Menggunakan kondisi tak bias 1, bagaimanapun dapat melakukan perbaikan, tidak hanya dalam kehiasan dan penyebaran galat., tapi juga dalam kejadian dugaan negatif yang lebih rendah. Melalui pendekatan ini diperlukan pendugaan prior dari mean global
U
dan V, ha1 ini jelas bahwa kejadian dengan dugaan yang lebih sederhana dari mean global, kita dapat memperbaiki pendugaan.KESIMPULAN DAN SARAN
Metode pendugaan data spasial dengan cokriging, mempakan suatu metode yang digunakan untuk menduga nilai pada suatu titik yang tidak dilakukan pengamatan dengan mengynakan data lebih dari satu peubah.
C(>krigirig dengan kondisi tak bias 1 mempunyai ragam galat yang lebih kecil dibandingkan cokr~ging dengan kondisi tak
bias 2. Sehingga cokrigi,~g dengan kondisi tak bias 1 lebih diterima daripada cokriging dengan kondisi tak bias 2.
'I'skl 2. ?hhl perbandingon unluk cukriging dcngan kondisi tali bias I dnn eob.;ging dungan
kondisi talc bins 2
Mungkin ha1 yang penting untuk diperhatikan dalam Tabel 2 adalah dugaan
cc)krigi,g negatif Alasan untuk dugaan negatif
111
mula-mula dengan kondisi tak bias 236, = 0
j = l
Untuk jumlah bobot sama dengan no1 maka beberapa nilai dugaan hams negatif Pada saat bobot yang negatif dikalikan dengan nilai sampel V yang besar, dugaan negatif dapat muncul. Jika hasil kali negatif jumlahnya hesar dalam nilai mutlak dari pada jumlah bobot positif, maka dugaannya negatif.
Cokrigitig dengan kondisi tak bias 1 lehih diterima karena mempunyai galat yang lebih kecil dibandingkan cokriging dengan kondisi tak bias 2.
Pengarub nilai yang lebih kuat dalam pendugaan ini mengacu pada pilihan kondisi tak bias yang menghasilkan hobot lebih yang diberi tanda untuk peubah pelengkap.
Sebagai ringkasan bahwa cokriging dengan kondisi tak bias 2 kurang memuaskan. Misalkan kasus dimana hanya dua nilai data pelengkap yang ditemukan sama jauhnya dari titik pendugaan dan dari semua data utama. Karena dua nilai data pelengkap sama jauhnya, maka hams diberi bobot yang sama. Meskipun solusi ini secara matematika benar, tapi sulit untuk memhayangkan proses fisika yang mana skema bobotnya benar. Melalui metode ini akan menurunkan kebiasan, tapi tidak menurunkan penyebaran galat yang besar.
Menggunakan kondisi tak bias 1, bagaimanapun dapat melakukan perbaikan, tidak hanya dalam kehiasan dan penyebaran galat., tapi juga dalam kejadian dugaan negatif yang lebih rendah. Melalui pendekatan ini diperlukan pendugaan prior dari mean global
U
dan V, ha1 ini jelas bahwa kejadian dengan dugaan yang lebih sederhana dari mean global, kita dapat memperbaiki pendugaan.KESIMPULAN DAN SARAN
Metode pendugaan data spasial dengan cokriging, mempakan suatu metode yang digunakan untuk menduga nilai pada suatu titik yang tidak dilakukan pengamatan dengan mengynakan data lebih dari satu peubah.
C(>krigirig dengan kondisi tak bias 1 mempunyai ragam galat yang lebih kecil dibandingkan cokr~ging dengan kondisi tak
bias 2. Sehingga cokrigi,~g dengan kondisi tak bias 1 lebih diterima daripada cokriging dengan kondisi tak bias 2.