Metode Goal Linear Programming Untuk Menentukan Regresi Berganda

METODE GOAL LINEAR PROGRAMMING UNTUK MENENTUKAN REGRESI BERGANDA

SKRIPSI

EVI YULLY DESNA NABABAN 080823025

DEPARTEMEN PENDIDIKAN NASIONAL

FAKULTAS MATEMATIKA DAN ILMU PNGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2010

METODE GOAL LINEAR PROGRAMMING UNTUK MENENTUKAN REGRESI BERGANDA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

EVI YULLY DESNA NABABAN 080823025

DEPARTEMEN PENDIDIKAN NASIONAL

FAKULTAS MATEMATIKA DAN ILMU PNGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2010

PERSETUJUAN

Judul : METODE GOAL LINEAR PROGRAMMING

UNTUK MENENTUKAN REGRESI BERGANDA

Kategorik : SKRIPSI

Nama : EVI YULLY DESNA NABABAN Nomor Induk Mahasiswa : 080823025

Program Studi : SARJANA (SI) MATEMATIKA

Fakultas : MATEMATIKA DAN ILMUPENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, November 2010

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Bambang Irawan, M.Sc Drs. Marwan Harahap,M.Eng NIP. 194704211976031001 NIP.194612251974031001

Diketahui oleh

Departemen Matematika FMIPA USU Ketua

PERNYATAAN

METODE GOAL LINEAR PROGRAMMING UNTUK MENENTUKAN REGRESI BERGANDA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, November 2010

PENGHARGAAN

Puji dan syukur penulis kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah karunia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan.

Abstrak

Di dalam upaya penentuan persamaan estimasi linear dengan metode garis lurus akan menghasilkan persamaan yang baik, semua titik yang mencerminkan pasangan data berada di sekitar garis lurus tersebut. Namun, jika titik-titik pasangan data tersebut satu sama lain, maka persamaan linear yang baik untuk mengestimasi nilai variabel dependen adalah persamaan linear yang kurvanya mempunyai kesalahan yang minimum antara titik estimasi dengan titik sebenarnya. Penelitian ini menerangkan bagaimana cara untuk mendekati garis regresi dengan metode goal linear programming.

Bentuk umum persamaan regresi linear sederhana yang menunjukkan hubungan antara dua variabel, yaitu variabel X sebagai variabel bebas dan variabel Y sebagai variabel tak bebas adalah:

i i e X

Y =β0 +β1 + untuk i=1,...,n

Keterangan:

Y = varibel tak bebas

i

X = variabel bebas

0

β = intersep (titik potong kurva terhadap sumbu Y)

1

β = kemiringan (slope) i

e = kesalahan

Abstract

In determining equation of linear estimation with the straight line method will produce good equation. All point reflected couple data are in the straight line. But, if the couple points are each other, so good equation of linear to etimate variable value dependent is curve equation of linear which has minimal false between estimation point with real point. The research explains how the way to approach the linear regression with goal linear programming method.

General shape of equation simple linear regression that shows the correlation between two variables, they are X variable as independent variable and variable

Y as dependent variable is.

i i e X

Y =β₀ +β₁ + for i=1,...,n

Remark:

Y = is dependent variable i

X = is independent variable

0

β = is intercept (curve cut point to axis Y)

1

β = is inclination (slope) i

e = error

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel viii

Daftar Gambar x

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Tujuan Penelitian 2

1.4 Kontribusi Penelitian 3

1.5 Tinjauan Pustaka 3

1.6 Metode Penelitian 4

BAB 2 LANDASAN TEORI 5

2.1 Analisa Regresi 5

2.1.1 Regresi Linear Sederhana 5

2.1.2 Regresi Linear Berganda 6

2.1.3 Penduga Parameter 7

2.1.4 Meminimalkan Jumlah Deviasai (Regresi Kuadrat Terkeci) 8 2.1.5 Regresi Berganda dengan Cara Matrix 9

2.1.6 Uji Keberartian Regresi 10

2.2 Konsep-konsep dan Unsur-unsur Goal Programming 11 2.2.1 Unsur-unsur Linear Goal Programming 12

2.2.1.1 Kendala Tujuan 13

2.2.1.2 Kendala Non Negarif 14

2.2.1.3 Kendala Struktural 14

2.3 Model Goal Programming 14

2.4 Urutan Prioritas 16

BAB 3 PEMBAHASAN 19

3.1 Penggunaan Goal Linear Programming dengan Metode Simpleks 19 3.2 Komputasi Linear Programming dengan Sistem Lindo 30 3.2.1 Langkah-langkah Pengerjaan Program Lindo 30 3.3 Menentukan Persamaan Regresi Berganda dengan Cara Matrix 33

3.4 Uji Keberartian 36

3.5 Ringkasan 37

BAB 4 KESIMPULAN DAN SARAN 38

4.1 Kesimpulan 38

4.2 saran 38

DAFTAR TABEL

Halaman

Tabel 2.1 Jenis-jenis Kendala Tujuan 13

Tabel 2.2 Tabel Awal Goal Linear Programming 17

Tabel 3.1 Awal Simpleks 21

Tabel 3.2 Simpleks 23

Tabel 3.3 Simpleks 25

Tabel 3.4 Simpleks 27

Tabel 3.5 Simpleks 29

Tabel 3.6 Penentu nilai d _i 30

DAFTAR GAMBAR

Halaman

Gambar 3.1 Tampilan Sementara Program Lindo 30

Gambar 3.2 Tampilan File yang Tersedia di Program Lindo 31

Gambar 3.3 Tampilan Untuk Mengisi Angka-angka Sesuai dengan Soal 31

Abstrak

Di dalam upaya penentuan persamaan estimasi linear dengan metode garis lurus akan menghasilkan persamaan yang baik, semua titik yang mencerminkan pasangan data berada di sekitar garis lurus tersebut. Namun, jika titik-titik pasangan data tersebut satu sama lain, maka persamaan linear yang baik untuk mengestimasi nilai variabel dependen adalah persamaan linear yang kurvanya mempunyai kesalahan yang minimum antara titik estimasi dengan titik sebenarnya. Penelitian ini menerangkan bagaimana cara untuk mendekati garis regresi dengan metode goal linear programming.

Bentuk umum persamaan regresi linear sederhana yang menunjukkan hubungan antara dua variabel, yaitu variabel X sebagai variabel bebas dan variabel Y sebagai variabel tak bebas adalah:

i i e X

Y =β0 +β1 + untuk i=1,...,n

Keterangan:

Y = varibel tak bebas

i

X = variabel bebas

0

β = intersep (titik potong kurva terhadap sumbu Y)

1

β = kemiringan (slope) i

e = kesalahan

Abstract

In determining equation of linear estimation with the straight line method will produce good equation. All point reflected couple data are in the straight line. But, if the couple points are each other, so good equation of linear to etimate variable value dependent is curve equation of linear which has minimal false between estimation point with real point. The research explains how the way to approach the linear regression with goal linear programming method.

General shape of equation simple linear regression that shows the correlation between two variables, they are X variable as independent variable and variable

Y as dependent variable is.

i i e X

Y =β₀ +β₁ + for i=1,...,n

Remark:

Y = is dependent variable i

X = is independent variable

0

β = is intercept (curve cut point to axis Y)

1

β = is inclination (slope) i

e = error

BAB 1

PENDAHULAN

1.1Latar Belakang

Dalam banyak hal yang berkaitan dengan kegiatan perusahaan dan perekonomian mungkin perlu diketahui hubungan antara 2 (dua) variabel atau lebih variabel, dan hubungan ini dapat digunakan untuk memperkirakan nilai rata-rata dari satu variabel yang dinamakan variabel tidak bebas (dependent variable), dan variabel bebas (independent variable). Misalnya diketahui data tentang pengeluaran untuk iklan berdasarkan volume penjualan, memperkirakan pengeluaran untuk keperluan pokok keluarga berdasarkan pendapatan keluarga itu, meramalkan hasil tanaman kacang tanah berdasarkan banyak pupuk yang digunakan tiap hektar, daya tahan papan kayu A terhadap bobot tertentu ditinjau dari tebalnya, dan masih banyak contoh lain lagi yang dapat dikemukakan. Untuk menjawab hal-hal yang seperti dicontohkan, perlu dibahas mengenai bentuk hubungan dan keeratan hubungan. Bila ingin mengetahui bentuk hubungan dua variabel atau lebih, maka digunakan analisa regresi. Kemudian bila ingin melihat keeratan hubungan, maka digunakan analisa korelasi.

Kata regresi diperkenalkan pertama kali oleh Sir Francis Galton tahun 1877 pada bukunya tentang hereditas. Ia menemukan bahwa tinggi badan anak dari orang tua yang tinggi cenderung memendek menuju tinggi rata-rata populasi. Garis matematis yang dikembangkan dikenal sebagai garis regresi. Istilah garis regresi (line of regression) lebih sering digunakan walaupun sebenarnya yang lebih tepat adalah istilah persamaan prediksi (predictive equation) atau persamaan penduga (estimating equation).

Secara umum, tujuan dari regresi linear berganda adalah untuk menemukan baris yang memprediksi terbaik Y dari X. Regresi linear memerlukan hal ini dengan mencari baris yang meminimalkan jumlah kuadrat jarak dari kesalahan (the error

sum of square).

Goal linear programming merupakan perluasan dari model linear programming. Charles D dan Timothy Simpson (2002), dalam paper “Goal Programming Application in Multidisciplinary Design Optimization” goal progmming sangat cocok digunakan untuk masalah multi tujuan karena melalui variabel deviasinya, goal programming secara otomatis memberi informasi tentang pencapaian relatif dari tujuan-tujuan yang ada. Oleh karena itu solusi optimal yang diberikan dapat dibatasi pada solusi fisibel yang menggabungkan ukuran-ukuran performasi yang diinginkan.

Dari uraian di atas penulis mengambil judul: Metode Goal Linear Programming untuk Menentukan Regresi Berganda.

1.2Perumusan Masalah

1.3Tujuan Penelitian

Tujuan penelitian ini untuk menguraikan cara mendekati garis regresi dengan meminimumkan jumlah dari selisih nilai deviasi dengan metode goal linear programming.

1.4Kontribusi Penelitian

Manfaat penelitian ini agar dapat diketahui mengenai penerapan pemrograman matematika statistik terhadap regresi berganda dengan menggunakan goal linear programming dalam masalah optimisasi.

1.5Tinjauan Pustaka

• Draper, Norman dan Harry Smith. 1992. Analisis Regresi Terapan. Edisi kedua. Jakarta: Penerbit Gramedia Pustaka utama.

Dari buku ini ditinjau bentuk umum persamaan regresi linear berganda yang menunjukkan hubungan antara dua atau lebih variabel, yaitu variabel X sebagai variabel bebas dan variabel Ysebagai variabel tak bebas:

ε β

β β

β + + + + +

= 0 1X1 2X2 ... n−1Xn−1

Y Keterangan:

Y = variabel tak bebas

X = varibel bebas

0

β = konstanta merupakan titik potong kurva terhadap sumbu Y

1

β = kemiringan kurva linear ε = nilai kesalahan

• Han-Lin Li. Januari 1998. Solve Least Absolute Value Regression Problem

Using Modified Goal Programming Techniques, Computer Ops Res. Vol. 25

No. 12, pp. 1137-1143, 1998. © 1998 Elsivier Science Ltd Dari jurnal ini ditinjau metode goal linear programming yaitu:

Minimumkan

∑

= n i

i

d

dengan kendala y b x bj di i n

m j

ij

i ( ) 0, 1,2,...,

1

0 + − ≥ =

−

∑

=

y b x bj di i n

m j

ij

i ( ) 0, 1,2,...,

1

0 + + ≤ =

−

∑

=

a_i ≥0dan b_j∈F

• Arthanari, T. S. dan Yadollah Dodge. 1980. Mathematical Programming in

Statistics. New York: Wiley.

Dari buku ini ditinjau meminimalkan jumlah selisih absolut antar deviasi yaitu:

Minimalkan

∑

[

]

<j − i

j i d

d

dari rumus

∑

[

]

<j − i

j i d

d untuk d ,_i d_jdiperoleh:

∑

[

]

<j − i

j i d

d

∑

[

]

< − − − − −

= j i

j j

i

i X Y X

Y ) ( )

( β0 β1 β0 β1

=

∑

[

]

<j − − − i

j i j

i Y X X

Y ) ( )

( β₁

misalkan Yij =Yi −Yjdan Xij = Xi −X j,i< jdiperoleh:

∑

[

]

<j − i

j i d

d =

∑

[

]

<j − i

ij ij X

Y β₁

1.6Metode Penelitian

Metode yang digunakan dalam penelitian adalah sebagai berikut:

• Memaparkan metode goal linear programming untuk menentukan regresi berganda.

• Membentuk persamaan regresi berganda dari jumlah deviasi kuadrat (regresi kuadrat terkecil).

• Membentuk persamaan regresi berganda dari metode goal linear programming dengan meminimumkan mean absolut deviasi (MINMAD).

BAB 2

LANDASAN TEORI

2.1 Analisa Regresi

Analisa regresi adalah teknik statistik yang berguna untuk memeriksa dan memodelkan hubungan di antara variabel-variabel. Analisa regresi berguna dalam menelaah hubungan dua variabel atau lebih dan terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan sempurna, sehingga dalam penerapanya lebih bersifat eksploratif.

2.1.1 Regresi Linear Sederhana

Regresi linear sederhana adalah analisis regresi yang melibatkan hubungan antara satu variabel tak bebas dihubungkan dengan satu variabel bebas.

Variabel tak bebas adalah variabel yang nilainya selalu bergantung dengan nilai variabel lain dalam hal ini variabel tak bebas nilainya selalu dipengaruhi oleh variabel bebas, sehingga sering disebut dengan variabel terikat sedangkan variabel bebas adalah variabel yang nilainya tidak bergantung dengan nilai varibel lain. Biasanya variabel tak bebas dinotasikan dengan Ydan variabel bebas dinotasikan dengan X . Hubungan itu dinyatakan dalam model matematis akan memberikan persamaan tertentu.

Model matematis dalam menjelaskan hubungan antar variabel dalam analisis regresi menggunakan persamaan regresi. Persamaan regresi adalah suatu persamaan matematis yang mendefinisikan hubungan antar dua variabel. Persamaan regresi digunakan untuk membuat taksiran mengenai nilai variabel tak bebas yang disebut dengan persamaan regresi estimasi.

Bentuk umum persamaan regresi linear sederhana yang menunjukkan hubungan antara dua variabel, yaitu variabel X sebagai variabel bebas dan variabel

Ysebagai variabel tak bebas adalah:

i i e X

Keterangan:

Y = varibel tak bebas

i

X = variabel bebas

0

β = intersep (titik potong kurva terhadap sumbu Y)

1

β = kemiringan (slope)

e = kesalahan pada pengamatan _i

2.1.2 Regresi Linear Berganda

Regresi linear berganda adalah analisis regresi yang melibatkan hubungan dari dua atau lebih variabel bebas.

Adakalanya persamaan regresi dalam menganalisis hubungan antar variabel tak bebas hanya dipengaruhi oleh faktor atau variabel bebas tapi dapat pula dipegaruhi oleh dua atau lebih faktor yang mempengaruhinya. Regresi linear yang mengandung lebih dari satu variabel bebas digunakan regresi linear berganda. Jadi model ini dikembangkan untuk mengestimasi nilai variabel tak bebas Y dengan menggunakan lebih dari satu variabel bebas (X1,X2,...,Xn).

Model regresi linear berganda merupakan suatu model yang dapat dinyatakan dalam persamaan linear yang memuat variabel dan parameter. Parameter ini umumnya tidak diketahui dan dapat ditaksir. Hubungan linear lebih dari dua variabel dinyatakan dalam bentuk persamaan matematisnya adalah:

ε β

β β

β + + + + +

= 0 1X1 2X2 ... n−1Xn−1

Y untuk i =1,...,n

Keterangan:

Y = variabel tak bebas X = varibel bebas

0

β = konstanta merupakan titik potong kurva terhadap sumbu Y

1

2.1.3 Penduga Parameter β₀ dan β₁

Populasi dari seluruh pasangan nilai (X_i,Y_i) diketahui, dapat menghitung nilai sebenarnya dari parameter β₀ dan β₁. Dalam prakteknya, tidak diketahui nilai parameter tersebut, akan tetapi dapat diperkirakan dengan menggunakan data empiris, yakni hasil observasi berdasarkan sampel yang ditarik dari populasi yang tidak terbatas (infinite population). Data empiris tersebut sering berupa data deret berkala (time series data):

n

i X

X X

X1, 2,..., ,..., dan Y1,Y2,...,Yi,...,Yn

Untuk memperkirakan β₀ dan β₁, dipergunakan metode kuadrat terkecil. Metode kuadrat terkecil adalah suatu metode untuk menghitung β₀ dan β₁ sebagai perkiraan β₀ dan β₁, sedemikian rupa sehingga jumlah kesalahan kuadrat memiliki nilai terkecil. Dengan bahasa matematik, dapat dinyatakan sebagai berikut:

n i

e X

Y_i =β₀ +β_{1 i} + _i, =1,..., )

( _{0 1 i} i

i Y X

e = − β +β kesalahan ke-i

[

]

2

1 0 2

) (

∑

∑

ei = Yi − β +β Xi jumlah kesalahan kuadrat.

Metode kuadrat terkecil adalah metode untuk menghitung β₀ dan β₁ sehingga

∑

e_i2 terkecil (minimum). Caranya ialah dengan membuat turunan parsial (partial differential) dari

∑

2

i

e mula-mula terhadap a kemudian terhadap b dan menyamakan dengan nol.

[

( )

]

( 1) 0 ...(2.1)

2 _{0 1 0 1}

0 2

∑

∑

∑

∑

_{= − + − = ⇒ = +}

∂ ∂

i i

i i

i

X n

Y X

Y e

β β β

β β

[

( )

]

( ) 0 ...(2.2)

2 _{0 1 0 1} 2

1 2

∑

∑

∑

∑

∑

_{= − + − = ⇒ = +}

∂ ∂

i i

i i i

i i

i

X X

Y X X

X Y

e

β β

β β β

Persamaan (2.1) dibagi dengan

n X

n n n

Y

n⇒

∑

i = β0 +

∑

i

sehingga;

Y

= 0

β -β1X

Masukkan β0 ke persamaan (2.2)

Y Y X_{i i} =(

∑

-X

1

β )

∑

_i + ₁

∑

_i2 ⇒

∑

_{i i} =(

∑

i − ₁

∑

i)

∑

X_i + ₁

∑

X_i2 n X n Y Y X X

X β β β

∑

∑

∑ ∑

∑

= − + 2

1 2 1 ) ( i i i i i i X n X n Y X Y

X β β

n Y X Y X n X

X_i i

∑

_{i i}

∑ ∑

i i

∑

∑

= −         − 1 2

2 ( )

β sehingga;

∑

∑

∑

∑ ∑

∑

∑

∑

∑ ∑

− − = − −

= 2 2 2 2

1 ) ( / ) ( / i i i i i i i i i i i i X X n Y X Y X n n X X n Y X Y X β

2.1.4 Meminimalkan Jumlah Deviasi Kuadrat (Regresi Kuadrat Terkecil)

Metode ini didasarkan pada pemilihan β₀ dan β₁ sehingga meminimalkan jumlah kuadrat deviasi vertikal titik-titik data dari garis yang disamakan.

Jumlah dari kuadrat deviasi (SSD) dari garis adalah:

= =

∑

= n i i e SSD 1

2

(

)

2 1 1 0

∑

Y_i −β −β X ………(2.3)

Kemudian akan dipilih taksiran β₀ dan β₁ taksiran ini disubsitusikan ke dalam persamaan (2.3) jumlah deviasi kuadrat menjadi minimum. Dengan mendiferensialkan (2.3) terhadap β₀ dan β₁ menetapkan derivatif yang dihasilkan sama dengan nol, diperoleh:

) (

2 _{0 1}

1 0 i n i i X Y SSD β β β =− − − ∂ ∂

∑

= ) (

2 0 1

1 1 i i n i

i Y X

karena,

(

)

0

1

1

0 − =

−

∑

₌n

i

i

i X

Y β β

0 ) (

1

1

0 − =

−

∑

₌ i

n i

i

i Y X

X β β ……….(2.5)

Dari persamaan (2.5), diperoleh:

∑

₌ =

∑

₌ + n i n i i i

i X Y

X n 1 1 1 0 β β i n i i n i i n i

i X X Y

X

∑

∑

∑

₌ + ₌ = ₌ 1 1 2 1 1 0 β β ………(2.6)

Persamaan (2.6) disebut persamaan normal. Dari persamaan (2.6) diperoleh:

1 ∧ β =

∑

∑

∑

∑ ∑

− − n X X n Y X Y X i i i i i i / ) ( / ) )( ( 2 2

dan β∧0 =Y−−β∧1, di mana

−

Y dan

−

X adalah

∑

n_i=1Yi / dan n

∑

₌ n

i1Xi / . n

∧

0

β dan ∧

1

β yang diperoleh dengan cara ini disebut taksiran kuadrat terkecil masing-masing dari β₀ dan β₁. Dengan demikian, taksiran persamaan regresi dapat ditulis sebagai,

∧ ∧ ∧

+

= _{0 1}X,

Y β β yang disebut persamaan prediksi.

2.1.5 Regresi Berganda dengan Cara Matrix

Untuk mencari nilai estimasi parameter β₀,β_1, β₂,β₃ dapat juga dicari dengan cara matrix. Langkah-langkahnya sebagai berikut:

1. Mencari matrix X'X di mana

         

∑

∑

∑

∑

∑

∑

∑

∑

2 1 2 1 2 2 1 2 1 1 2 1 X X X X X X X X X X n

2. Kemudian dicari nilai determinan matrix X'X

13 13 12 12 11

11A a A a A

a

3. Setelah itu dicari matrix kofaktor dari matrix X'X yang disebut sebagai “Adjoint Matrix” di mana:

Adj. X'X =

    

    

−

− −

−

33 32 31

23 22

21

13 12 11

A A A

A A

A

A A A

4. Kemudian dicari invers matrix (X'X) di mana:

(X'X) D 1

1=

− _{. Adj X}'_X

5. Dicari juga nilai dari X'Y yang besarnya

Y X' =

  

 

  

 

∑

∑

∑

2 1

YX YX Y

6. Sehingga nilai koefisien β₀,β_1, β₂,β₃ di dapat dengan cara

  

 

  

  =

    

    

∑

∑

∑

2 1 '

2 1 0

. .

1

YX YX Y

X X Adj D ββ β

2.1.6 Uji Keberartian Regresi

Pengujian ini digunakan untuk mengetahui ada tidaknya linear antara variabel tak bebas Y dengan variabel bebas X1, X2, X3,...,Xn, hipotesa yang digunakan adalah:

0 ..

... ...

, _{2 3}

1

0 = = = = = n =

H β β β β

H₁ =β_i ≠0, untuk paling sedikit satu nilai

Penolakan H0 =βi =0 menginformasikan bahwa paling sedikit satu variabel bebas X₁, X₂, X₃,...,X_n, memiliki sumbangan yang nyata pada model tersebut:

∑

∑

∑

+ + +

= X Y X Y k XkiYi

Jkreg β_{1 1 1} β_{2 2 2} ... β

2

) (

∑

− ∧

= Y Y

) 1 /(

/ − − =

k n Jkres

k Jkreg F_hitung

F_tabel =(α;k,n−k−1)

2.2 Konsep-Konsep dan Unsur-Unsur Goal Programming

Agar memahami dengan baik bidang yang dipelajari, pembaca selalu harus mengerti istilah-istilah dan lambang-lambang yang digunakan orang dalam bidang studi itu. Berikut ini adalah definisi dari beberapa istilah dan lambang yang biasa digunakan dalam goal programming.

Goal programming dilambangkan dengan x_j, untuk ( j =1,2,...,n) yang akan dicari nilainya (variabel keputusan).

Right hand side values (RHS): nilai-nilai yang biasanya menunjukkan ketersediaan

sumber daya (dilambangkan dengan b ) yang akan ditentukan kekurangan atau _i

kelebihan penggunanya (nilai sisi kanan).

Goal: keinginan untuk meminimumkan angka penyimpangan dari suatau nilai RHS

pada suatu goal constraint tertentu (tujuan).

Goal Constraint: sinonim dari istilah goal equation, yaitu suatu tujuan yang

diekspresikan dalam persamaan matematik yang memasukkan variabel simpangan (kendala tujuan).

Preemtive priority factor: suatu sistem urutan yang dilambangkan dengan p , di _k

mana k =1,2,...,k dan k menunjukkan banyaknya tujuan dan model yang memungkinkan tujuan-tujuan disusun secara ordinal dalam model linear goal programming. Sistem urutan ini menempatkan tujuan-tujuan dalam susunan dengan hubungan sebagai berikut:

1

P >P >>>₂ P _k

Keterangan:

P merupakan tujuan yang paling penting ₁

2

P merupakan tujuan yang kurang penting dan seterusnya

Deviational variable: variabel-variabel yang menunjukkan kemungkinan

RHS (dilambangkan dengan d_i+ variabel-variabel ini sama dengan slack variable dalam linear goal programming (variabel simpangan).

Differential weight: timbangan matematika yang diekspresikan dengan angka

kardinal (dilambangkan dengan w di mana _ki k =1,2,...,k;i=1,2,...,m)dan digunakan untuk membedakan variabel simpangan i di dalam suatu tingkat prioritas k (bobot).

Techological coefficient: nilai-nilai numerik (dilambangkan dengan a_ij) yang menunjukkan penggunaan nilai b per unit untuk menciptakan _i x_j (koefisien teknologi).

2.2.1 Unsur-Unsur Linier Goal Programming

Setiap model linear goal programming paling sedikit terdiri dari tiga komponen, yaitu: sebuah fungsi tujuan, kendala-kendala tujuan dan kendala non negatif.

Minimumkan

∑

=

+ − ₊ = m

i

i i d

d Z

1

Minimumkan

∑

=

+ − ₊ = m

i

i i k d d

P Z

1

)

( untuk k =1,2,...,K

Minimumkan

∑

=

+ − ₊ = m

i

i i k

kiP d d

w Z

1

)

( untuk k =1,2,...,K

Fungsi tujuan yang pertama digunakan jika variabel simpangan dalam suatu masalah tidak dibedakan menurut prioritas atau bobot. Fungsi tujuan ke dua digunakan dalam suatu masalah di mana urutan tujuan diperlukan, tetapi variabel simpangan di dalam setiap tingkat prioritas memiliki kepentingan yang sama. Dalam fungsi tujuan ke tiga, tujuan-tujuan diurutkan dan variabel simpangan pada setiap tingkat prioritas dibedakan dengan menggunakan bobot berlainan w . Jadi, _ki

fungsi tujuan yang digunakan akan tergantung pada situasi masalahnya.

positif dari nilai RHS kendala tujuan. Linear programming mencari nilai solusi x_j secara langsung melalui minimasi penyimpangan-penyimpangan dari nilai RHSnya.

2.2.1.1 Kendala Tujuan

Ada enam jenis kendala tujuan yang berlainan. Maksud setiap jenis kendala itu ditentukan oleh hubungannya dengan fungsi tujuan. Pada Tabel 2.1 disajikan ke enam jenis kendala itu. Terlihat bahwa setiap jenis kendala tujuan harus punya satu atau dua variabel simpangan yang ditempatkan pada fungsi tujuan. Adanya kendala-kendala yang tidak memiliki variabel simpangan. Kendala-kendala ini sama seperti kendala-kendala yang tidak memiki variabel simpangan. Kendala-kendala ini sama seperti Kendala-kendala-Kendala-kendala persamaan linear. Persamaan pertama pada Tabel 2.1 maknanya sama dengan kendala pertidaksamaan ≤ dalam masalah program linear maksimasi. Persamaan ke dua maknanya sama dengan kendala pertidaksamaan ≥ pada masalah program linear minimasi. Persamaan ke tiga, ke empat dan ke lima semuanya memperbolehkan penyimpangan dua arah, tetapi persamaan ke lima mencari penggunaan sumber daya yang diinginkan sama dengan

i

b . Ini sama dengan kendala persamaan dalam linear programming, tetapi tidak

selalu pada solusi, karena dimungkinkan adanya penyimpangan negatif dan positif. Jika kendala persamaan di anggap perlu dalam perumusan model linear goal programming, maka dapat dimasukkan dengan menempatkan ke tiga dan ke empat memperbolehkan adanya penyimpangan positif dan negatif RHSnya. Dalam kendala linear programming tak ada pembanding untuk persamaan ke tiga dan ke empat.

Tabel 2.1 Jenis-Jenis Kendala Tujuan Kendala Tujuan Variabel

Simpangan

Dalam Fungsi Tujuan

Kemungkinan Simpangan

Penggunaan Nilai RHS yang Diinginkan

i i j

ijx d b

a + − = di− Negatif =bi

i i j

ijx d b

a − + = di+ Positif =b i

i i i j

ijx d d b

Positif

i i i j

ijx d d b

a + − − + = di− Negatif dan

Positif

i

b atau kurang

i i i j

ijx d d b

a + − − + = di−dan + i

d Negatif dan Positif

i

b =

i i j

ijx d b

a − + = di+(artf) Tidak ada pas = b i

2.2.1.2Kendala Non-Negatif

Seperti dalam linear programming variabel-variabel model linear goal programming biasanya bernilai lebih besar atau sama dengan nol. Semua model linear goal programming terdiri dari variabel simpangan dan variabel keputusan, sehingga pernyataan non negatif dilambangkan sebagai: xj,di−,di+ ≥0.

2.2.1.3 Kendala Struktural

Di samping ke tiga komponen yang telah disebutkan itu, dalam model linear goal programming kadang-kadang terdapat komponen yang lain, yaitu, kendala struktural artinya kendala-kendala lingkungan yang tidak berhubungan langsung dengan tujuan-tujuan masalah yang dipelajari. Variabel simpangan tidak dimasukkan dalam kendala ini, karena itu kendala ini tidak disertakan fungsi tujuan.

2.3 Model Goal Programming

Goal programming merupakan pengembangan proses linear dan non linear, karena model pemrograman linear biasa tidak mampu menyelesaikan masalah manajemen yang menghendaki sasaran-sasaran tertentu secara simultan. Model goal programming merupakan perluasan dari model program linear, sehingga seluruh asumsi, notasi, formulasi model matematika, prosedur perumusan model dan penyelesainnya tidak berbeda. Perbedannya hanya terletak pada kehadiran sepasang variabel devisional yang akan muncul di fungsi tujuan dan fungsi-fungsi kendala.

skala utama rangking yang diurutkan biasanya diaplikasikan ke tujuan lain. Goal programming sering disebut prosedur yang memuaskan yang mana pendekatannya menghasilkan keputusan dalam suatu proses usaha untuk mencapai feasibility tingkat multiple objektif dari pada hasil yang optimal untuk tujuan tunggal.

Charnes dan Cooper (2002) yang mengembangkan goal programming sebagai pendekatan untuk menyelesaikan masalah yang infeasibility (tidak layak) pada program linier yang disebabkan oleh tujuan yang bertentangan. Ijiri dan Jaaskelainen kemudian melanjutkan dan melengkapinya sehingga dapat dipakai secara operasional. Lee mengkontribusikan menjadi ke tingkat yang lebih baik cara kerjanya, prestasi dari goal programming, pada bagian P selalu lebih besar dari ₁

bagian prioritas merangking yang lebih rendah P . Ignizio (2002) membentuk dan ₂

mengaplikasikan bilangan bulat yang tepat pada algoritma goal programming dan juga mampu bekerja dalam program non linear.

Goal programming berusaha untuk meminimumkan deviasi atau simpangan di antara berbagai tujuan atau sasaran yang telah ditetapkan sebagai targetnya, artinya nilai ruas kiri suatu persamaan kendala sebisa mungkin mendekati nilai ruas kanannya.

Dalam goal programming terdapat dua tipe kendala yaitu kendala teknologi (technological constraint) yang merupakan permasalahan kapasitas sumber dan kendala lainnya yang bukan terhadap tujuan, kendala tujuan (goal constraint) yang mewakili atau menggambarkan target dari objek-objek dalam urutan prioritas.

Minimumkan

∑

=

− + ₊ = m

i

i i i d d

w Z

1

) (

=

∑

Wi+di+ +Wi−di− Syarat ikatan:

(kendala tujuan) i

m i

i i j

ijx d d b

a + − =

∑

₌ − +

1

untuk i=1,2,...,m

0 , , i− i+ ≥ j d d x

0

=

+ +

Keterangan: +

i

d dan d_i− = jumlah unit deviasi yang kekurangan (-) atau kelebihan (+) terhadap tujuan (b _i)

+ i

W dan W = timbangan atau bobot yang diberikan terhadap suatu unit deviasi _i−

yang kekurangan atau kelebihan terhadap tujuan (b i) ij

a =koefisien teknologi fungsi kendala tujuan, yaitu yang berhubungan dengan tujuan peubah pengambilan keputusan (x_j)

j

x = variabel pengambilan keputusan i

b = tujuan atau target yang ingin dicapai

Model tersebut merupakan perluasan pengoptimuman untuk meminimumkan jumlah dari semua deviasi positif dan negatif yang individual dari tujuan yang telah ditetapkan.

Dalam perumusan goal programming dapat dimasukkan satu tujuan atau lebih yang langsung berhubungan dengan fungsi objektif dalam bentuk variabel deviasi.

Algoritma simpleks menjamin persyaratan non negatif. Berhubungan tidak dapat mencapai plus dan deviasi minus dari tujuan atau target yang ditetapkan secara sekaligus atau simultan, salah satu dari variabel deviasi atau ke dua-duanya akan menjadi nol (0), yang berarti target terpenuhi dengan sangat memuaskan dan dapat dinyatakan sebagai berikut:

et t di jikaZ jikaZ Z1, arg

, 1 , , 1

, 1 ,

0 =

= − > ≤ −

tujuan Z

di = ZjikajikaZ Z = ≥

< − + 0, 1, ,

, , 1 , 1 ,

2.4 Urutan Prioritas

Misalnya untuk faktor prioritas, diberikan simbol P (di mana i=1,2,…..,m). _i

Faktor-faktor prioritas tersebut memiliki hubungan sebagai berikut: 0

.... ₁

3 2

1 >>>P >>>P >>> >>>Pi >>>Pi+ >

P

di mana P >>> berarti jauh lebih tinggi dari pada ₁ P . Hubungan tersebut _i+1

menjelaskan bahwa masing-masing faktor tersebut tidak akan berubah urutan prioritasnya meskipun digandakan dengan sembarang konstanta. Tujuan yang paling diutamakan ditetapkan sebagai prioritas utama (P1), tujuan yang lebih

rendah ditetapkan sebagai prioritas ke dua (P2), demikian selanjutnya untuk tujuan dengan tingkat prioritas yang lebih rendah berikutnya.

Dengan demikian, model umum dari goal programming yang memiliki struktur timbangan pegutamaan (Preemptive weights) dengan urutan ordinal dapat dirumuskan sebagai berikut:

Minimumkan

∑

=

− − +

+ ₊

= m i

i s i s i y i

yW d PW d

P Z

1

) (

Syarat ikatan:

(kendala tujuan)

∑

+ − − + = n

i i i j

ijx d d b

a

Untuk i=1,2,…..,m Untuk k=1,2,…..,p J=1,2,…..,n dan x_j,d_i−,d_i+ ≥0

di−,di+ =0

Keterangan: d ,_i− d_i+ =deviasi plus dan minus dari tujuan atau target ke-i P ,y Px = faktor-faktor prioritas

W_i+,_y = timbangan relatif dari

+ i

d dalam urutan ke y Wi+,x = timbangan relatif dari

− i

d dalam urutan ke x

[image:30.595.89.503.160.435.2]

variabel d_i+(yaitu variabel dasar). Kendala tujuan tidak memiliki variabel d_i+, diberikan variabel artifisial dengan prioritas 0.

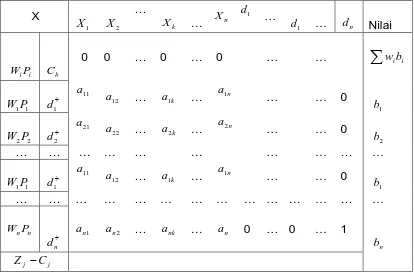
Tabel 2.2 Tabel Awal Goal Programming

X

1

X X₂

…

Xk … n

X d1

… d1 … dn Nilai

i iP

W Cb

0 0 … 0 … 0 … …

∑

wibi

1 1P

W d₁+

11

a

a12 … a1k …

n

a₁

… … 0

1

b

2

2P

W d₂+

21

a

a22 … a2k …

n

a2

… … 0

2

b

… … … … … … … … … …

1 1P

W d1+ 11

a

a12 … a1k …

n

a₁

… … 0

1

b

… … … … … … …

n nP

W

+ n d

1

n

a a_n2 … ank … an 0 … 0 … 1 n

b

j j C

Z −

Baris 1 : Variabel keputusan X_j dan variabel deviasi d_i− Kolom 5 : Nilai sebelah kanan

Kolom 3 : Koefisien variabel keputusan aij

Kolom 4 : Matriks identitas menunjukkan pemasukan variabel deviasi negatif −

i d

Kolom 1 : Faktor prioritas P dan bobot i W untuk setiap variabel deviasi positif i (yakni variabel basis) dan memasukkan variabel deviasi artifisial seperti ditampilkan dalam kolom 2.

Kolom 2 : Nilai total deviasi absolut, yang mewakili jumlah total deviasi dari semua tujuan untuk tiap tabel sebagai iterasi proses pendapatan. Baris 2 : Vektor baris dan penunjuk nol pada proses perhitungan.

Baris 3 : Bobot W untuk setiap variabel deviasi yang dimasukkan dalam _i

BAB 3

PEMBAHASAN

3.1 Penggunaan Goal Linear Programming dengan Metode Simpleks

Dalam pembahasan ini, dibahas goal linear programming untuk menentukan persamaan regresi berganda dan goal linear programming diselesaikan dengan menggunakan metode simpleks.

Andaikan suatau persoalan dalam produksi bawang dilakukan 5 observasi, karektristik yang diuji dalam observasi ini adalah:

) ( ) (

) (

) (

3 3

2 1

m hujan curah

X

kg pupuk X

hektar lahan

luas X

ton bawang produksi

Y

= = = =

Tabel Produksi Bawang dengan Menggunakan Metode Simpleks Observasi Produksi bawang

(Y)

Luas lahan (X ) ₁

Pupuk (X ) ₂

Curah hujan (X₃)

1 89 7 71 1 2 71 1 61 2 3 103 6 80 3 4 98 8 62 5 5 95 8 66 3 Total 456 30 340 14

dengan menentukan regresi MINMAD yang terdiri dari ,

3 3 2 2 1 1

0 x x x

Y =β +β +β +β estimasi β₀,β₁,β₂,β₃.

[ ]

di =d1i +d2i i i

i d d

Bentuk umum

Minimum : Z =

∑

d1i +

∑

d2i Kendala : Xβ+d₁−d₂ =Y

Bentuk standart

Minimum : Z =d₅ +d₆ +d₇ +d₈ +d₉ +d₁₀+d₁₁+d₁₂ +d₁₃+d₁₄

Kendala :

95 3 66 8 98 5 62 8 103 3 80 6 71 2 61 89 71 7 14 9 3 2 1 0 13 8 3 2 1 0 12 7 2 1 0 11 6 3 2 1 0 10 5 3 2 1 0 = − + + + + = − + + + + = − + + + + = − + + + + = + + + + − d d d d d d d d d d β β β β β β β β β β β β β β β β β β β β Misalkan: 4 3 3 2 2 1 1 0 X X X X = = = = β β β β 9 9 8 8 7 7 6 6 5 5 X d X d X d X d X d = = = = = 14 14 13 13 12 12 11 11 10 19 X d X d X d X d X d = = = = = Fungsi tujuan

Minimum :

Z

=

X₅ +X₆ +X₇ +X₈ +X₉ +X₁₀+ X₁₁+X₁₂+X₁₃+X₁₄

Kendala :

95 3 66 8 98 5 62 8 103 3 80 6 71 2 61 89 71 7 19 9 4 3 2 1 18 8 4 3 2 1 17 7 4 3 2 1 16 6 4 3 2 1 15 5 4 3 2 1 = − + + + + = − + + + + = − + + + + = − + + + + = + + + + − X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X

[image:33.595.86.503.108.518.2]

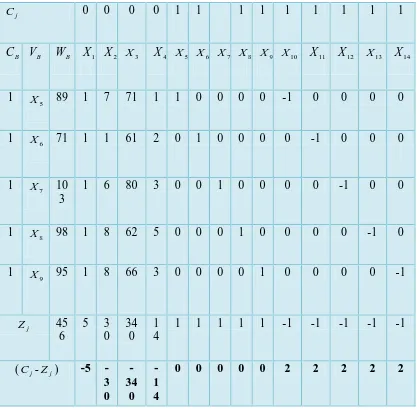
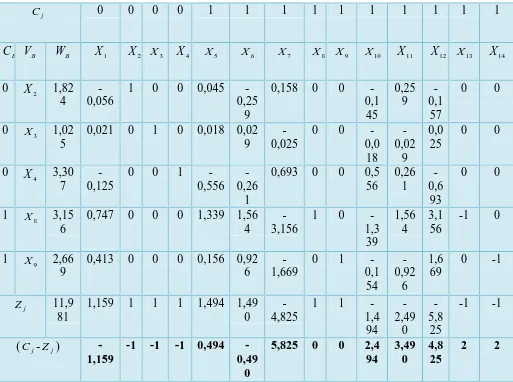
Tabel Awal Simpleks

j

C 0 0 0 0 1 1 1 1 1 1 1 1 1

B

C V _B W_B X₁ X₂ X 3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14

1 X₅ 89 1 7 71 1 1 0 0 0 0 -1 0 0 0 0

1 X₆ 71 1 1 61 2 0 1 0 0 0 0 -1 0 0 0

1 X₇ 10 3

1 6 80 3 0 0 1 0 0 0 0 -1 0 0

1 X₈ 98 1 8 62 5 0 0 0 1 0 0 0 0 -1 0

1 X₉ 95 1 8 66 3 0 0 0 0 1 0 0 0 0 -1

j

Z 45

6

5 3 0

34 0

1 4

1 1 1 1 1 -1 -1 -1 -1 -1

(C_j-Z_j) -5 -3 0

-34

0 -1 4

Pada tabel dapat dilihat bahwa nilai (C_j −Z_j)yang negatif terbesar adalah (-340) dengan demikian kolom kuncinya adalah X , dan rasio yang positif paling kecil ₃

dari X yaitu: 89/71 71/61 103/80 98/62 95/66 untuk itu baris kunci adalah ₃ X . ₆

Sehingga demikian X mengganti ₆ X variabel dasar. ₃

Baris 1 baru = baris 1 lama – 71/61 (baris kunci lama) − − − − − − − = 0 0 0 164 , 1 1 0 0 0 164 , 1 1 328 , 1 0 836 , 5 164 , 0 361 , 6 ) 0 0 0 0 1 0 0 0 0 1 0 2 61 1 1 ( 61 / 71 ) 0 0 0 1 0 0 0 0 1 1 1 71 7 1 89 (

Baris 2 baru = 1/pivot ×(baris kunci lama)

= 1/61 (71 1 1 61 2 0 1 0 0 0 0 -1 0 0 0 0)

= 0,016 0,016 1 0,033 0 0 0,164 0 0 0 0 0 -0,016 0 0 0 1,164

Baris 3 baru = baris 3 lama - 80/61 (baris kunci lama)

− − − − − − = 0 0 1 312 , 1 0 0 0 1 312 , 1 0 377 , 0 0 689 , 4 312 , 0 885 , 9 ) 0 0 0 1 0 0 0 0 1 0 2 61 1 1 71 ( 61 / 80 ) 0 0 1 0 0 0 0 1 0 0 3 80 6 1 103 (

Baris 4 baru = baris 4 lama - 62/61 (baris kunci lama) − − − − − − = 0 1 0 016 , 1 0 0 1 0 016 , 1 0 967 , 2 0 984 , 6 016 , 0 836 , 25 ) 0 0 0 1 0 0 0 0 1 0 2 61 1 1 71 ( 61 / 62 ) 0 1 0 0 0 0 1 0 0 0 5 62 8 1 98 (

[image:35.595.31.523.98.494.2]

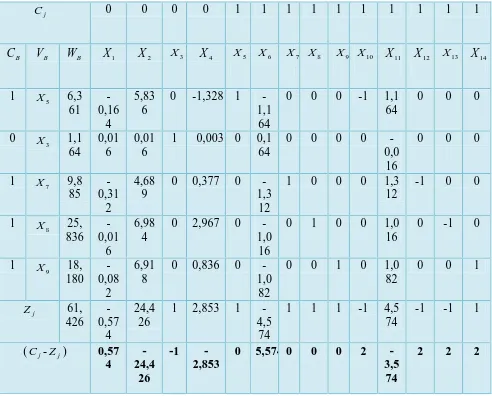
Tabel 2 Simpleks

j

C 0 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C V _B W _B X ₁ X ₂ X₃ X ₄ X₅ X ₆ X₇ X ₈ X₉ X₁₀ X₁₁ X₁₂ X₁₃ X₁₄

1 X ₅ 6,3 61

-0,16

4

5,83 6

0 -1,328 1 -1,1

64

0 0 0 -1 1,1 64

0 0 0

0 X ₃ 1,1 64

0,01 6

0,01 6

1 0,003 0 0,1 64

0 0 0 0 -0,0

16

0 0 0

1 X ₇ 9,8 85

-0,31

2

4,68 9

0 0,377 0 -1,3

12

1 0 0 0 1,3 12

-1 0 0

1 X ₈ 25, 836

-0,01

6

6,98 4

0 2,967 0 -1,0

16

0 1 0 0 1,0 16

0 -1 0

1 X ₉ 18, 180

-0,08

2

6,91 8

0 0,836 0 -1,0

82

0 0 1 0 1,0 82

0 0 1

j

Z 61,

426 -0,57

4

24,4 26

1 2,853 1 -4,5

74

1 1 1 -1 4,5 74

-1 -1 1

(C_j-Z_j) 0,57 4

-24,4

26

-1 -2,853

0 5,574 0 0 0 2 -3,5

74

Pada tabel dapat dilihat bahwa nilai (Cj −Zj)yang negatif terbesar adalah (-24,426) dengan demikian kolom kuncinya adalah X , dan rasio yang positif paling ₂

kecil dari X , yaitu: 6,361/5,836 1,164/0,016 9,885/4,689 25,836/6,984 ₂

18,180/6,918 untuk itu baris kunci adalah X₅. Sehingga demikian X5 mengganti

2

X variabel dasar.

Baris 1 baru = 1/pivot ×(baris kunci lama)

= 1/5,836 (6,361 -0,16 5,836 0 -1,328 1 -1,164 0 0 0 -1 1,164 0 0 0 0)

= 1,089 -0,028 1 0 -0,028 0,171 -0,199 0 0 0 -0,171 0,199 0 0 0

Baris 2 baru = baris 2 lama – 0,016/5,836

− − − − − − − − = 0 0 0 019 , 0 003 , 0 0 0 0 019 , 0 003 , 0 037 , 0 1 0 017 , 0 146 , 1 ) 0 0 0 164 , 1 1 0 0 0 164 , 1 1 328 , 1 0 836 , 5 16 , 0 361 , 6 ( 836 , 5 / 016 , 0 ) 0 0 0 016 , 0 0 0 0 0 164 , 0 0 033 , 0 1 016 , 0 016 , 0 164 , 1 (

Baris 3 baru = baris 3 lama – 4,689/5,836 (baris kunci lama) − − − − − − − − − − − − = 0 0 1 376 , 0 803 , 0 0 0 1 376 , 0 803 , 0 444 , 1 0 0 018 , 0 775 , 4 ) 0 0 0 164 , 1 1 0 0 0 164 , 1 1 328 , 1 0 836 , 5 16 , 0 361 , 6 ( 836 , 5 / 689 , 4 ) 0 0 1 312 , 1 0 0 0 1 312 , 1 0 377 , 0 0 689 , 4 312 , 0 885 , 9 (

Baris 4 baru = baris 4 lama – 6,989/5,836 (baris kunci lama) − − − − − − − − − − − = 0 1 0 376 , 0 197 , 1 0 1 0 376 , 0 197 , 1 556 , 4 0 0 018 , 0 225 , 18 ) 0 0 0 164 , 1 1 0 0 0 164 , 1 1 328 , 1 0 836 , 5 16 , 0 361 , 6 ( 836 , 5 / 984 , 6 ) 0 1 0 016 , 1 0 0 1 0 016 , 1 0 967 , 2 0 984 , 6 016 , 0 836 , 25 (

[image:37.595.35.552.104.516.2]

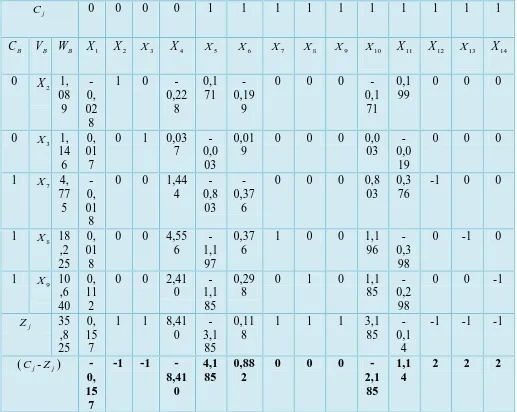
Tabel 3 Simpleks

j

C 0 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C V_B W_B X₁ X₂ X₃ X ₄ X ₅ X ₆ X ₇ X ₈ X ₉ X₁₀ X₁₁ X₁₂ X₁₃ X₁₄

0

2

X 1, 08 9

-0, 02 8

1 0

-0,22 8

0,1 71

-0,19

9

0 0 0

-0,1 71

0,1 99

0 0 0

0 X₃ 1, 14 6

0, 01 7

0 1 0,03 7

-0,0

03

0,01 9

0 0 0 0,0

03 -0,0

19

0 0 0

1 X₇ 4, 77 5

-0, 01 8

0 0 1,44 4

-0,8

03 -0,37

6

0 0 0 0,8

03 0,3

76

-1 0 0

1 X₈ 18 ,2 25

0, 01 8

0 0 4,55 6

-1,1

97

0,37 6

1 0 0 1,1

96 -0,3

98

0 -1 0

1 X₉ 10 ,6 40

0, 11 2

0 0 2,41 0

-1,1

85

0,29 8

0 1 0 1,1

85 -0,2

98

0 0 -1

j

Z 35

,8 25

0, 15 7

1 1 8,41 0

-3,1

85

0,11 8

1 1 1 3,1

85 -0,1

4

-1 -1 -1

(Cj-Zj) -0, 15 7

-1 -1 -8,41

0

4,1 85

0,88 2

0 0 0

-2,1 85

1,1 4

Pada tabel dapat dilihat bahwa nilai (Cj −Zj)yang negatif terbesar adalah (-8,410) dengan demikian kolom kuncinya adalah X , dan rasio yang positif paling kecil ₄

dari X yaitu: 1,089/-0,228 1,146/0,037 4,775/1,444 18,225/4,556 10,640/2,410 ₄

untuk itu baris kunci adalah X₇. Sehingga demikian X₇ mengganti X variabel ₄

dasar.

Baris 1 baru = baris 1 lama – (-0,228)/1,444 (baris kunci lama) − − − − − − − − − − − − − = 0 0 259 , 0 145 , 0 0 0 158 , 0 259 , 0 045 , 0 0 0 1 056 , 0 824 , 1 ) 0 0 1 376 , 0 803 , 0 0 0 1 376 , 0 803 , 0 444 , 1 0 0 018 , 0 775 , 4 ( 444 , 1 / 228 , 0 ) 0 0 0 199 , 0 171 , 0 0 0 0 199 , 0 171 , 0 228 , 0 0 1 028 , 0 089 , 1 (

Baris 2 baru= baris 2 lama- 0,037/1,444 (baris kunci lama) − − − − − − − − − − = 0 0 025 , 0 029 , 0 018 , 0 0 0 025 , 0 029 , 0 018 , 0 0 1 0 021 , 0 025 , 1 ) 0 0 1 376 , 0 803 , 0 0 0 1 376 , 0 803 , 0 444 , 1 0 0 018 , 0 775 , 4 ( 444 , 1 / 037 , 0 ) 0 0 0 019 , 0 003 , 0 0 0 0 019 , 0 003 , 0 037 , 0 1 0 017 , 0 146 , 1 (

Baris 3 baru = 1/pivot × (baris kunci lama) 0 0 693 , 0 261 , 0 556 , 0 0 0 693 , 0 261 , 0 556 , 0 1 0 0 125 , 0 307 , 3 ) 0 0 1 376 , 0 803 , 0 0 0 1 376 , 0 803 , 0 444 , 1 0 0 018 , 0 775 , 4 ( 44 , 1 / 1 − − − − = − − − − =

Baris 4 baru = baris 4 lama – 4,556/1,444 (baris kunci lama) − − − − − − − − − − − = 0 1 156 , 3 564 , 1 339 , 1 0 1 156 , 3 564 , 1 339 , 1 0 0 0 747 , 0 156 , 3 ) 0 0 1 376 , 0 803 , 0 0 0 1 376 , 0 803 , 0 444 , 1 0 0 018 , 0 775 , 4 ( 444 , 1 / 037 , 0 ) 0 0 0 019 , 0 003 , 0 0 0 0 019 , 0 003 , 0 037 , 0 1 0 017 , 0 146 , 1 (

Baris 5 baru = baris 5 lama – 2,410/1,444 (baris kunci lama)

[image:39.595.61.574.97.479.2]

Tabel 4 Simpleks

j

C 0 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C V _B W _B X ₁ X₂ X₃ X₄ X ₅ X ₆ X ₇ X₈ X ₉ X₁₀ X ₁₁ X₁₂ X₁₃ X ₁₄

0

2

X 1,82

4 -0,056

1 0 0 0,045 -0,25

9

0,158 0 0 -0,1

45

0,25 9

-0,1

57

0 0

0 X ₃ 1,02 5

0,021 0 1 0 0,018 0,02 9

-0,025

0 0

-0,0 18

-0,02

9 0,0

25

0 0

0

4

X 3,30

7 -0,125

0 0 1 -0,556

-0,26

1

0,693 0 0 0,5 56

0,26 1

-0,6

93

0 0

1 X ₈ 3,15 6

0,747 0 0 0 1,339 1,56 4

-3,156

1 0

-1,3 39

1,56 4

3,1 56

-1 0

1 X ₉ 2,66 9

0,413 0 0 0 0,156 0,92 6

-1,669

0 1

-0,1 54

-0,92

6 1,6

69

0 -1

j

Z 11,9

81

1,159 1 1 1 1,494 1,49 0

-4,825

1 1

-1,4 94

-2,49

0 -5,8

25

-1 -1

(C_j-Z_j) -1,159

-1 -1 -1 0,494 -0,49

0

5,825 0 0 2,4 94

3,49 0

4,8 25

Pada tabel dapat dilihat bahwa nilai (Cj −Zj)yang negatif terbesar adalah (-1,159) dengan demikian kolom kuncinya adalah X , dan rasio yang positif paling kecil ₁

dari X yaitu: 1,824/-0,056 1,025/0,021 3,307/-0,125 3,156/0,747 2,669/0,413 ₁

untuk itu baris kunci adalah X₈. Sehingga demikian X₈ mengganti X variabel ₁

dasar.

Baris 1 baru = baris 1 lama – (-0,056)/0,747 (baris kunci lama)

− − − − − − − − − − − − − − − = 0 049 , 0 0 184 , 0 112 , 0 0 049 , 0 0 181 , 0 112 , 0 0 0 1 019 , 0 080 , 2 ) 0 1 156 , 3 564 , 1 339 , 1 0 1 156 , 3 564 , 1 339 , 1 0 0 0 747 , 0 307 , 3 ( 747 , 0 / 056 , 0 ) 0 0 157 , 0 259 , 0 145 , 1 0 0 158 , 0 259 , 0 045 , 0 0 0 1 056 , 0 824 , 1 (

Baris 2 baru = baris 2 lama – 0,021/0,747 (baris kunci lama) − − − − − − − − − − − − = 0 008 , 0 0 017 , 0 007 , 0 0 008 , 0 0 017 , 0 007 , 0 0 1 0 015 , 0 935 , 0 ) 0 1 156 , 3 564 , 1 339 , 1 0 1 156 , 3 564 , 1 339 , 1 0 0 0 747 , 0 307 , 3 ( 747 , 0 / 021 , 0 ) 0 0 025 , 0 029 , 0 018 , 0 0 0 025 , 0 029 , 0 018 , 0 0 1 0 021 , 0 025 , 1 (

Baris 3 baru = baris 3 lama – (-0,125/0,747 (baris kunci lama)

− − − − − − − − − − − − − − = 0 219 , 0 0 083 , 0 263 , 0 0 219 , 0 0 083 , 0 263 , 0 1 0 0 039 , 0 833 , 3 ) 0 1 156 , 3 564 , 1 339 , 1 0 1 156 , 3 564 , 1 339 , 1 0 0 0 747 , 0 307 , 3 ( 747 , 0 / 125 , 0 ) 0 0 693 , 0 261 , 0 556 , 0 0 0 693 , 0 261 , 0 556 , 0 1 0 0 125 , 0 307 , 3 (

Baris 4 baru = 1/pivot × (baris kunci lama) 0 317 , 0 1 496 , 0 424 , 0 0 317 , 0 1 496 , 0 424 , 0 0 0 0 237 , 0 224 , 4 ) 0 1 156 , 3 564 , 1 339 , 1 0 1 156 , 3 564 , 1 339 , 1 0 0 0 747 , 0 307 , 3 ( 747 , 0 / 1 − − − − = − − − − =

[image:41.595.44.544.90.593.2]

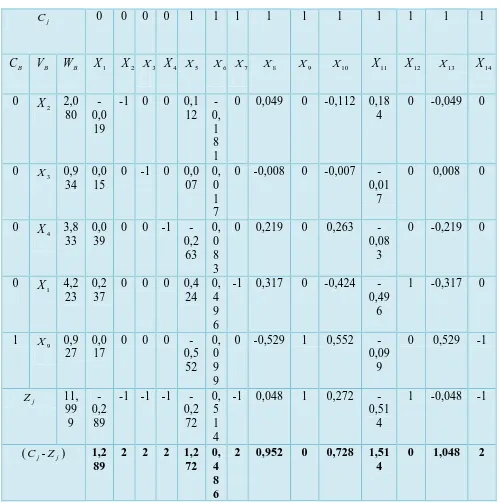
Tabel 5 Simpleks

j

C 0 0 0 0 1 1 1 1 1 1 1 1 1 1

B

C V _B W_B X ₁ X₂ X₃ X₄ X ₅ X₆ X₇ X ₈ X ₉ X ₁₀ X ₁₁ X₁₂ X ₁₃ X₁₄

0

2

X 2,0

80 -0,0

19

-1 0 0 0,1 12

-0,

1 8 1

0 0,049 0 -0,112 0,18 4

0 -0,049 0

0 X₃ 0,9 34

0,0 15

0 -1 0 0,0 07

0, 0 1 7

0 -0,008 0 -0,007 -0,01

7

0 0,008 0

0

4

X 3,8

33 0,0

39

0 0 -1 -0,2

63 0,

0 8 3

0 0,219 0 0,263 -0,08

3

0 -0,219 0

0

1

X 4,2

23 0,2

37

0 0 0 0,4 24

0, 4 9 6

-1 0,317 0 -0,424 -0,49

6

1 -0,317 0

1 X₉ 0,9 27

0,0 17

0 0 0 -0,5

52 0,

0 9 9

0 -0,529 1 0,552 -0,09

9

0 0,529 -1

j

Z 11,

99 9

-0,2

89

-1 -1 -1 -0,2

72 0,

5 1 4

-1 0,048 1 0,272 -0,51

4

1 -0,048 -1

(Cj-Zj) 1,2 89

2 2 2 1,2 72

0, 4 8 6

2 0,952 0 0,728 1,51 4

Dari hasil metode simpleks diperoleh:

833 , 3 ;

934 , 0 ;

080 , 2 ;

223 ,

4 _{2 1 3 2 4 3}

0

1 =β = X =β = X =β = X =β =

X

Persamaan regresi berganda adalah:

3 2

1 0,934 3,833

080 , 2 223 ,

4 X X X

[image:42.595.122.466.189.315.2]

Y∧ = + + +

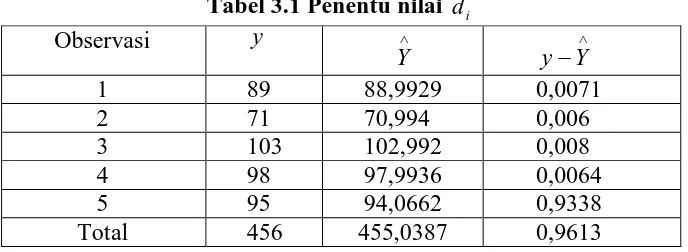
Tabel 3.1 Penentu nilai d _i

Observasi y

Y ∧ y−Y∧

1 89 88,9929 0,0071 2 71 70,994 0,006 3 103 102,992 0,008 4 98 97,9936 0,0064 5 95 94,0662 0,9338 Total 456 455,0387 0,9613

3.2 Komputasi Linear Programming dengan Sistem Lindo

Analisa perhitungan atau komputasi persoalan linear yang ukuranya kecil dapat dilakukan dengan tangan atau kalkulator biasa. Semakin besar persoalan linear programming diperlukan bantuan komputer digital karena cara manual sudah tidak efisien dan tidak layak dilakukan.

3.2.2 Langkah-langkah pengerjaan program Lindo

Tampilan sementara setelah program Lindo dijalankan tampak pada gambar 3.2

[image:43.595.87.502.134.271.2]

Setelah tampilan sementara berakhir, akan muncul tampilan awal seperti gambar 3.2 yang berarti program sudah siap untuk menjalankan modul-modul yang akan dipilih. Kemudian pilih file New seperti gambar 3.3

[image:43.595.88.503.340.543.2]

Selesaikan persoalan dengan mengklik tombol step pada toolbar ,akan muncul pengerjaan linear programming yang terlihat pada gambar 3.5

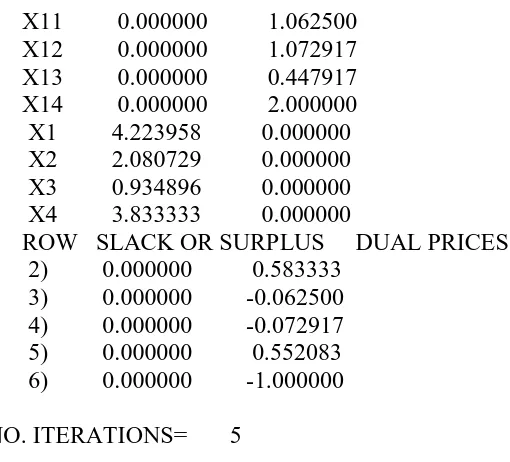
LP OPTIMUM FOUND AT STEP 5 OBJECTIVE FUNCTION VALUE 1) 0.9270833

VARIABLE VALUE REDUCED COST X5 0.000000 1.583333

X11 0.000000 1.062500 X12 0.000000 1.072917 X13 0.000000 0.447917 X14 0.000000 2.000000 X1 4.223958 0.000000 X2 2.080729 0.000000 X3 0.934896 0.000000 X4 3.833333 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 0.583333

3) 0.000000 -0.062500 4) 0.000000 -0.072917 5) 0.000000 0.552083 6) 0.000000 -1.000000

NO. ITERATIONS= 5

3.3 Menentukan Persamaan Regresi Berganda dengan Matrix

Setelah menentukan persamaan regresi berganda dengan metode goal linear programming, kemudian dengan metode yang berbeda untuk menentukan persamaan regresi berganda dengan matrix. Misalnya dalam produksi bawang dilakukan 5 observasi, karektristik yang diuji dalam observasi ini adalah:

) ( ) (

) (

) (

3 3

2 1

m hujan curah

X

kg pupuk X

hektar lahan

luas X

ton bawang produksi

Y

[image:45.595.100.355.68.299.2]

= = = =

Tabel Produksi Bawang dengan Menggunakan Matrix Observasi Produksi bawang

(ton)

Luas lahan (hektar)

Pupuk (kg)

Curah hujan (m3)

Langkah-langkahnya adalah:

1. y =

                95 98 103 71 89                 = 3 66 8 5 62 8 3 80 6 2 61 1 1 71 7 x             = 3 2 1 0 β ββ β β 2.             = 3 5 3 2 1 66 62 80 61 71 8 8 6 1 7 1 1 1 1 1 ' X X                 × 3 66 8 1 5 62 8 1 3 80 6 1 2 61 1 1 1 71 7 1 =             48 941 91 14 941 23362 2062 340 91 2062 214 30 14 340 30 5

3. Determinan X'X

X X' =

            48 941 91 14 941 23362 2062 340 91 2062 214 30 14 340 30 5 =               91 14 2062 340 214 30 30 5 48 941 91 14 941 23362 2062 340 91 2062 214 30 14 340 30 5

= (5×214×23362×48)+(30×2062×941×14)+(340×91×340×91) = - (14×2062×2062×14)−(5×91×23362×91)−(30×30×941×941) = 243936

4. Setelah itu dicari matrix kofaktor dari matrix X'X yang disebut sebagai “Adjoint Matrix”

Adj. X'X =

=                                         − + − + − + − + − + − + − + − + 23362 2062 340 2062 214 30 340 30 5 941 2062 340 91 214 30 14 30 5 941 23362 340 91 2062 30 14 340 5 941 23362 2062 91 2062 241 14 340 30 941 91 14 2062 214 30 340 30 5 48 91 14 91 214 30 14 30 5 48 941 14 91 2062 30 14 340 5 48 941 91 941 2062 241 14 340 30 941 91 14 23362 2062 340 340 30 5 48 91 14 941 2062 340 14 30 5 48 941 14 941 23362 340 14 340 5 48 941 91 941 23362 2062 14 340 30 941 91 14 23362 2062 340 2062 214 30 48 91 14 941 2062 340 91 241 33 48 941 14 941 23362 340 91 2062 30 48 941 91 941 23362 2062 91 2062 214 =             − − − − − − − − 38720 2640 9680 229856 2640 1251 1353 84342 9680 1353 10043 58850 229856 84342 58850 6074540

5. Kemudian dicari invers natrix X'X di mana:

(X'X)− = ×

D

1

1

AdjX'X

= 243936 1 ×             − − − − − − − − 38720 2640 9680 229856 2640 1251 1353 84342 9680 1353 10043 58850 229856 84342 58850 6074540 =             − − − − − − − − − − 15873 , 0 01082 , 0 03968 , 0 94228 , 0 01082 , 0 000512 , 0 00554 , 0 34575 , 0 03968 , 0 00554 , 0 04117 , 0 24125 , 0 94227 , 0 34575 , 0 24125 , 0 90218 , 24

6. Nilai dari X'Y

Y X' =

=             1315 31236 2856 456

7. Sehingga nilai koefisien β₀,β₁,β₂,β₃didapat dengan cara:

            3 2 1 0 β ββ β = × D 1

AdjX'X ×

            ∑ ∑ ∑ ∑ 3 2 1 YX YX YX Y = 243936 1 ×             − − − − − − − − 38720 2640 9680 229856 2640 1251 1353 84342 9680 1353 10043 58850 229856 84342 58850 6074540 ×             1315 31236 2856 456 =             769 , 3 909 , 0 160 , 2 323 , 5

Persamaan regresi bergandanya:

3 2

1 0,909 3,769

160 , 2 323 ,

5 X X X

[image:48.595.90.428.68.413.2]

Y∧ = + + +

Tabel 3.3 Penentu nilai d _i

Observasi y

Y ∧ y−Y∧

3.4 Uji Keberartian Regresi

Pengujian ini digunakan untuk mengetahui ada tidaknya hubungan linear antara variabel tak bebas Ydengan variabel bebas X1,X2,X3,...,Xn, hipotesa yang digunakan adalah:

0 ..

... ...

, _{2 3}

1

0 = = = = = n =

H β β β β

0

1 = i ≠

H β , untuk paling sedikit satu nilai

Penolakan H0 =βi =0 menginformasikan bahwa paling sedikit satu variabel bebas X₁,X₂,X₃,...,X_n memiliki sumbangan yang nyata pada model tersebut:

∑

∑

∑

+ + +

= X Y X Y k XkiYi<