PENGEMBANGAN UJI PORTMANTEAU
UNTUK DIAGNOSTIK MODEL DERET WAKTU
YULITASARI
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
YULITASARI. Pengembangan Uji Portmanteau untuk Diagnostik Model Deret Waktu.Dibimbing oleh KUSMAN SADIK dan YENNI ANGRAINI.
Kecukupan model deret waktu dapat diperiksa berdasarkan sisaannya. Jika model layak maka fungsi autokorelasi sisaan contoh tidak berbeda nyata dengan nol untuk semua lag lebih besar dari satu. Uji yang digunakan untuk memeriksa apakah k pertama autokorelasi sisaan sama dengan nol adalah uji portmanteau yang diperkenalkan pertama kali oleh Box-Pierce pada tahun 1970. Dalam perkembangannya, uji ini mengalami perbaikan dan menerima usulan antara lain oleh Ljung-Box (1978), Monti (1994) dan Pena-Rodriquez (2002).
Penelitian ini bertujuan untuk melihat kesensitifan ketiga uji portmanteau yaitu uji portmanteau Ljung-Box (QLB), uji portmanteau Monti (QMT) dan uji portmanteau Pena-Rodriquez (Dm).
Penelitian dilakukan dengan simulasi dengan membangkitkan 36 model ARMA (p,q) dengan ukuran contoh 100 dan 30 sebanyak 10 000 ulangan. Hasil memperlihatkan dari 36 model ARMA (p,q) yang di-fit dengan model AR (1) atau MA (1) atau ARMA (1,1), uji Dm merupakan uji yang
paling sensitif dibandingkan dengan kedua uji yang lain. Uji QLB memberikan hasil yang hampir
sama dengan uji QMT untuk lag kecil dan hasil yang lebih sensitif pada lag besar. Tetapi uji QMT
PENGEMBANGAN UJI PORTMANTEAU
UNTUK DIAGNOSTIK MODEL DERET WAKTU
YULITASARI
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PRAKATA
Skripsi dengan judul Pengembangan Uji Portmanteau untuk Diagnostik Model Deret Waktu ini diinspirasikan oleh penelitian yang dilakukan oleh Daniel Pena dan Julio Rodriquez. Hasil penelitian mereka dapat dilihat pada jurnal Journal of the American Statistical Association (JASA) 97:601-610 tahun 2002 dengan judul “A Powerful Portmanteau Test of Lack of Fit for Time Series”. Disamping menggunakan 24 model ARMA (p,q) yang digunakan pada penelitian terdahulu, penulis juga menambahkan 12 model ARMA (p,q) yang di-fit dengan model ARMA (1,1).
Terselesaikannya skripsi ini adalah dengan penuh perjuangan. Empat tahun lamanya terkatung-katung sampai akhirnya dapat tertuntaskan. Perjuangan panjang ini tak lepas dari bantuan banyak pihak. Orang tua di rumah yang selalu percaya pada anaknya. Pak Kusman Sadik dan Bu Yenni Angraini selaku pembimbing skripsi. Dudi atas saran penggunaan R 2.4.0. Marta, Nono, Rani, Itut dan semua teman yang yang tak tersebut yang tak lelah terus memberi semangat. Syukur nikmat ini sungguh tak terbilang.
Bogor, Agustus 2007
RIWAYAT HIDUP
Penulis merupakan anak kedua dari pasangan Drs. Noor Siswanto, S.H dan Siti Samsilah. Penulis dilahirkan di Wonosari, Gunung Kidul pada tanggal 7 Juli 1982. Masa kecil dilewatkannya di beberapa kota mengikuti orangtuanya yang pindah tugas.
Pendidikan dasar diselesaikan di tiga sekolah dan akhirnya tahun 1994 penulis lulus dari SDN 3 Toma Lima, Passo, Ambon. Sempat bersekolah di SMP Negeri 1 Lateri Ambon sebelum menyelesaikan pendidikan menengahnya di SMP Negeri 11 Pontianak pada tahun 1997. Setelah menghabiskan masa kelas 1 dan 2 di SMU Negeri 1 Pontianak, penulis lulus dari SMU Negeri 1 Karanganom, Klaten pada tahun 2000. Pada tahun yang sama penulis diterima di Departemen Statistika FMIPA IPB melalui jalur UMPTN.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ··· vii
DAFTAR LAMPIRAN ··· viii
PENDAHULUAN Latar Belakang ··· 1
Tujuan ··· 1
TINJAUAN PUSTAKA Metode Simulasi ··· 1
Deret Waktu ··· 1
Koefisien Autokorelasi ··· 2
Proses Auto Regresi ··· 2
Proses Moving Average ··· 2
Uji Portmanteau ··· 3
Uji Portmanteau Ljung-Box (QLB) ··· 3
Uji Portmanteau Monti (QMT) ··· 3
Uji Portmanteau Pena dan Rodriquez (DM) ··· 3
METODE ANALISIS ··· 4
HASIL DAN PEMBAHASAN Pemerikasaan Program ··· 5
Program Pembangkitan Data ··· 5
Program perhitungan QLB, QMT, dan Dm ··· 7
Kelayakan Model ··· 7
Pembangkitan dan Pengolahan Data ··· 8
SIMPULAN DAN SARAN Simpulan ··· 9
Saran ··· 9
DAFTAR PUSTAKA ··· 9
DAFTAR GAMBAR
Halaman
1 Plot Normal Galat yang Dibangkitkan dengan rnorm ··· 5
2 Plot Data Bangkitan Terhadap Waktu ··· 5
3 Plot ACF Data Bangkitan ··· 6
4 Plot PACF Data Bangkitan ··· 6
5 Pendugaan Parameter dengan Model MA (2) ··· 6
6 Plot Sisaan Model MA (2) Terhadap Waktu ··· 6
7 Plot ACF Sisaan Model MA (2) ··· 6
8 Plot PACF Sisaan Model MA (2) ··· 6
9 Pendugaan Parameter dengan Model AR (3) ··· 7
10 Plot Sisaan Model AR (3) Terhadap Waktu··· 7
11 Plot ACF Sisaan Model AR (3)··· 7
12 Plot PACF Sisaan Model AR (3) ··· 7
13 Plot ACF Sisaan Model AR (3)··· 8
DAFTAR LAMPIRAN
Halaman
1 Perintah Pembangkitan Deret Waktu dengan R 2.4.0 ··· 11
2 Model ARMA (p,q) yang Dibangkitkan ··· 14
3 Pembuktian Teorema dan Pendekatan Sebaran ··· 15
4 Nilai QLB dengan MINTAB dan R 2.4.0 ··· 17
5 Nilai Dm dengan R 2.4.0 dan Secara Manual ··· 17
6 P-value untuk Dm, QLB, serta QMT dengan Minitab dan R 2.4.0 ··· 17
7 P-value Uji Portmanteau ··· 18
8 Persentase series (deret 1, deret 2, … deret 10000) dengan sisaan berkorelasi ketika data di-fit dengan model AR(1), MA(1) dan ARMA(1,1) pada beberapa model ARMA(p,q) dengan uji DM, QLB dan QMT pada n=100 ··· 19
9 Persentase series (deret 1, deret 2, … deret 10000) dengan sisaan berkorelasi ketika data di-fit dengan model AR(1), MA(1) dan ARMA(1,1) pada beberapa model ARMA(p,q) dengan uji DM, QLB dan QMT pada n=30 ··· 20
10 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QLB pada N=100 ··· 22
11 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QMT pada N=100 ··· 23
12 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji Dm pada N=100 ··· 24
13 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QLB pada N=30 ··· 25
14 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QMT pada N=30 ··· 26
1
PENDAHULUAN
Latar Belakang
Data yang dikumpulkan berdasarkan urutan waktu atau biasa disebut data deret waktu dapat digunakan untuk melakukan pendugaan kejadian yang akan datang yang disebut dengan peramalan. Jenis data ini sering dijumpai di berbagai bidang.
Peramalan merupakan satu elemen penting dalam pengambilan keputusan dan penentuan kebijakan. Dengan peramalan kerugian akibat ketidakpastian dalam pengambilan keputusan dapat dikurangi. Peramalan dapat dilakukan dengan melakukan pemulusan terhadap data dan pemodelan. Ketepatan peramalan dapat ditingkatkan dengan menyediakan lebih banyak data, tetapi sering kali data yang tersedia tidak cukup banyak untuk membangun sebuah model pendugaan yang baik.
Pemodelan data deret waktu dilakukan dalam tiga tahap yaitu penentuan model tentatif, pendugaan parameter dan analisis diagnostik terhadap kelayakan model. Ketiga tahapan ini dikenal sebagai metode Box-Jenkins.
Model dikatakan layak jika sisaannya saling bebas, mempunyai sebaran identik serta menyebar normal dengan rataan nol dan ragam σe2 (Cryer 1986). Sisaan tidaklah selalu saling bebas, pada beberapa kasus terjadi autokorelasi. Jika hal ini diabaikan maka akan menyebabkan ketidakkonsistenan pendugaan galat baku, ketidaktepatan uji hipotesis dan ketidakefisienan pendugaan koefisien regresi. Uji formal yang digunakan untuk menguji apakah sisaan saling bebas atau tidak adalah uji portmanteau (statistik Q) yang diperkenalkan pertama kali oleh Box-Pierce pada tahun 1970. Uji portmanteau dirumuskan sebagai perkalian ukuran contoh dan jumlah kuadarat k autokorelasi sisaan contoh pertama. Statistika Q akan menyebar mengikuti sebaran khi-khuadrat dengan derajat bebas k-p-q jika H0 benar dengan hipotesis nol sisaan saling
bebas.
Dalam perkembangannya, uji portmanteau mengalami perbaikan dan menerima usulan antara lain oleh Ljung-Box (1978), Monti (1994) dan Pena-Rodriquez (2002). Uji portmanteau Pena-Rodriquez (Dm) dipercaya
lebih sensitif untuk mendeteksi adanya autokorelasi pada sisaan terutama pada n kecil. Uji ini memisalkan sisaan sebagai contoh dari
data multivariat dengan perilaku sebaran peluang tertentu.
Tujuan
Tujuan penelitian ini adalah membandingkan kesensitifan tiga uji portmanteau yaitu uji portmanteau Pena-Rodriquez (Dm), uji portmanteau Ljung-Box
(QLB) dan uji portmanteau Monti (QMT).
TINJAUAN PUSTAKA
Metode Simulasi
Simulasi dalam statistika dapat diartikan sebagai kumpulan teknik yang berguna yang kesemuanya berhubungan dengan meniru perilaku suatu model (Morgan 1984). Simulasi tidak hanya dapat menerangkan model itu sendiri, tetapi juga untuk menyelidiki bagaimana perilaku model dapat berubah mengikuti perubahan di dalam model. Metode simulasi dapat memberikan efisiensi dan kemudahan dalam menganalisis suatu model matematika. Sekarang kebanyakan simulasi dalam statistika dilakukan dengan bantuan perangkat komputer.
Deret Waktu
Deret waktu adalah suatu gugus tatanan nilai-nilai pengamatan sifat kuantitatif suatu individu atau kumpulan individu yang diamati pada titik-titik waktu berbeda. Biasanya jarak titik-titik waktu tersebut dibuat sama.
Deret waktu dapat dimodelkan dalam bentuk umum :
t k k t bz t b z t b z t
X = 1 1()− 2 2()+L+ ()+ε keterangan :
bt = parameter
zt(t) = fungsi matematik dari t t
ε = galat acak
Dua tujuan utama dari analisis deret waktu adalah memodelkan proses stokastik yang membangkitkan pengamatan deret waktu dan memprediksi atau meramalkan kejadian mendatang berdasarkan data terdahulu.
2
Koefisien Autokorelasi
Koefisien autokorelasi adalah ukuran seberapa besar korelasi antara data yang berdekatan pada data deret waktu Xt (Pindyck
dan Rubinfield 1997). Korelasi antara Xt dan
Xt+k yang terpisahkan oleh k interval waktu
disebut autokorelasi lag k dan didefinisikan sebagai: 2 2 ) [( ] ) [( )] )( [( X X E X X E X X X X E k t t k t t k − − − − = + + ρ k t t X X k t t X X Cov + − = σ σ ) , (
Pada proses yang konstan, ragam pada waktu t akan sama besar dengan ragam pada waktu t + k, sehingga koefisien autokorelasi akan menjadi: 0 2 ) , (( γ γ σ ρ k x k t t k X X Cov = = −
Autokorelasi bernilai antara -1 dan 1. Nilai autokorelasi yang mendekati ±1 mengin- dikasikan adanya hubungan yang kuat dan nilai autokorelasi mendekati nol menunjukan tidak adanya hubungan.
Koefisien autokorelasi dapat diduga dengan koefisien autokorelasi contoh (rk)
(Pindyck dan Rubinfield 1997).
∑ ∑ = = + = − n t t n k t t t k k a a a r 1 2 1
Kesulitan pengidentifikasian nilai p pada proses autoregresi dapat ditanggulangi dengan penggunaan autokorelasi parsial. Autokorelasi parsial (πˆ ) dapat diartikan sebagai korelasi k antara Xt dan Xt-k setelah pengaruh
pembalikan peubah Xt-1, Xt-2, ..., Xt-k+1
dihilangkan pada data deret waktu yang konstan (Cryer 1986).
Proses Autoregresi
Prose autoregresi ordo p (AR (p)) dimodelkan sebagai: t p t p t t
t X X X
X =ξ+φ1 −1+φ2 −2+L+φ − +ε
Persamaan ini disebut autoregresi karena pengamatan aktual Xt diregresikan pada
pengamatan sebelumnya Xt-1, Xt-2, ..., Xt-p
dalam deret waktu yang sama (Montgomery et all 1990). Proses AR (p) dapat dituliskan dalam bentuk operator backward-shift:
t t p B X ε φ ( ) =
Proses AR (p) dapat diterapkan untuk proses yang stasioner maupun tidak stasioner. Proses AR (p) akan stasioner jika akar dari
polinomial φp (B) berada diluar unit lingkaran.
Proses AR (p) memiliki fungsi autokorelasi (ACF) yang berpola polinomial dan fungsi autokorelasi parsial (PACF) yang terpotong pada lag p.
Model AR yang paling sederhana adalah AR (1) :
t t
t X a
X =μ+φ −1+
dimana peristiwa pada waktu t hanya bergantung pada peristiwa pada waktu t-1 dan bebas terhadap peristiwa waktu t-2, t-3, ..., t0. Proses ini disebut juga proses Markov. Proses ini akan stasioner jika dan hanya jika |φ| < 1. Nilai tengah dari model ini nol, ragamnya
) 1 /( 2
2 φ
σa − dan autokorelasi untuk lag k sama dengan φk.
Proses Moving Average
Model umum proses moving average ordo q (MA (q)) dapat ditulis sebagai:
q t q t t t t
X =ε +θ1ε −1+θ2ε −2+L+θ ε − Terminologi moving average berasal dari fakta bahwa Xt dibangun dengan
membobotkan 1,-φ1, -φ2, ..., -φq, pada variabel t, t-1, t-2, ...,t-p kemudian mengerakkan
pembobot yang sama satu periode waktu kebelakangdan membobotkannya pada t+1, t,
t-1, ..., t-p+1 untuk mendapatkan Xt+1 (Cryer
1986). Proses MA (q) dapat ditulis dalam bentuk operator backward-shift sebagai:
t q
t B
X =μ+θ ( )ε
Untuk kondisi tertentu proses MA (q) dapat ditulis ke dalam bentuk AR (∞). Kondisi ini disebut invertibility bagi MA (q). Syarat agar proses MA (q) dapat dirubah menjadi proses AR (∞) adalah akar dari polinomial θq
(B) = 0 berada diluar unit lingkaran. Proses MA (q) dapat dikenali dengan melihat plot ACF yang terpotong pada lag q dan plot PACF yang berpola polinomial. Dapat disimpulkan bahwa proses tidak memiliki korelasi setelah lag q.
Proses MA yang paling sederhana adalah MA (1) yang di modelkan sebagai:
1
−
+ = t t t
X ε θε
Nilai tengah model ini bernilai nol, ragamnya (1+θ2) σ2 dan autokorelasi lag 1 sama dengan -θσ2 serta autokorelasi untuk lag k, k > 1 akan bernilai nol.
3
campuran autoregresi-moving average order (p,q) (ARMA (p,q)) dapat dituliskan sebagai :
q t q t t t p t p t t
t X X X
X − − − − − − − − − − + + + + + = ε θ ε θ ε θ ε φ φ φ ξ L L 2 2 1 1 2 2 1 1
Model campuran ini akan stasioner jika akar dari polinomial φp (B) berada diluar unit
lingkaran dan invertible jika akar dari polinomial θq (B) = 0 berada diluar unit
lingkaran.
Uji Portmanteau
Ada dua cara untuk melihat asumsi kebebasan galat. Pertama dengan melihat plot sisaan dengan waktu. Jika plot ini tidak berpola maka dapat disimpulkan bahwa sisaan bebas. Yang kedua melihat ACF sisaan. Jika autokorelasi sisaan bernilai nol maka dapat dikatakan sisaan saling bebas.
Uji formal untuk menguji asumsi kebebasan galat adalah uji portmanteau. Uji ini pertama kali diperkenalkan oleh Box-Pierce pada tahun 1970 berdasarkan pada autokorelasi sisaan yang dirumuskan sebagai:
∑ = m=
k rk
n
Q 1
2
Jika model ARMA(p,q) teridentifikasi dengan benar maka untuk n yang besar Q akan menyebar khi-kuadrat dengan derajat bebas m-p-q. Hipotesis yang digunakan adalah sisaan saling bebas melawan sisaan tidak bebas (berkorelasi).
Uji Portmanteau Ljung-Box (QLB)
Persoalan muncul jika n tidak besar. Ljung dan Box (1978) menunjukan bahwa untuk n = 100 pun pendekatan Q ke sebaran khi-kuadrat tidak memuaskan. Uji portmanteau kemudian diperbaiki menjadi uji portmanteau Ljung-Box (QLB) dengan mengantikan koefisien
autokorelasi sisaan (rk) dengan nilai
standarnya (r~ ) (Pena dan Rodriguez 2002). k
2 2 ) ( ) 2 ( ~ k k r k n n r − + = sehingga
∑
= − − + = m k kLB nn n k r
Q ( 2) 1( ) 1 2
QLB menyebar khi-kuadrat dengan derajat
bebas m-p-q. Ljung (1986) dalam Pena dan Rodriguez (2002) memperlihatkan bahwa menghitung QLB dengan banyak autokorelasi
sisaan dapat mengurangi kekuatan ujinya.
Uji Portmanteau Monti (QMT)
Monti (1994) memperkenalkan uji portmanteau QMT yang berdasarkan pada
autokorelasi parsial (πˆ ). k
∑
= − −+
= m
k k
MT nn n k
Q ( 2) 1( ) 1πˆ2
QMT menyebar khi khuadrat dengan derajat
bebas m-p-q. Melalui simulasi, Monti (1994) menunjukan bahwa ketika alternatif model memiliki ordo moving average yang lebih tinggi, QMT lebih sensitif dibandingkan
dengan QLB. Kwan dan Wu (1997) dalam
Pena dan Rodriquez (2002) mengevaluasi via simulasi Monte Carlo untuk data bangkitan dengan siklus bulanan dan menemukan perbedaan yang kecil antara kekuatan uji QLB
dan QMT.
Uji Portmanteau Pena dan Rodriquez Adanya fakta bahwa berkurangnya kekuatan uji QLB dengan bertambahnya lag
serta hanya terdapat sedikit perbedaan kekuatab uji QLB dan QMT mendorong Pena
dan Rodriquez mengusulkan sebuah uji portmanteau yang baru. Uji yang diusulkan pada tahun 2002 ini menggunakan transformasi dari determinan Rˆm untuk menguji adanya autokorelasi pada sisaan. Dimana Rˆm adalah matriks korelasi sisaan data deret waktu stasioner ordo m yang didefinisikan sebagai: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = − − 1 1 1 ˆ 1 1 1 1 L M O M M L L m m m m m r r r r r r R
Uji portmanteau Pena-Rodriquez dirumuskan sebagai: ] | ˆ | 1 [
ˆ 1/m
m
m n R
D = −
Determinan Rˆm akan bernilai 1 dan Dˆ m bernilai 0 ketika r1 = r2 = ... = rm = 0. Ketika r1
= r2 = ... = rm = 1, determinanRˆmakan bernilai
0 danDˆm bernilai n. Untuk semua nilai rk, m
Dˆ bernilai lebih dari sama dengan nol.
Misalkan rˆ(m) =(r1,r2,K,rm)' , maka
matriks korelasi dapat ditulis sebagai:
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ′ = −1 ) ( ) ( ˆ ˆ ˆ 1 ˆ m m m m R r r R
Dengan menggunakan sifat determinan matriks terbagi didapatkan |Rˆm|=
) 1 ( | ˆ
|Rm−1 −Rm2 dimana Rm2 rˆ(m)Rˆm11rˆ(m)
− − ′ =
adalah perkalian koefisien korelasi yang dikuadratkan dari model linear εˆt =
. ˆ
1
4 m m i i m m R R / 1 1 2 / 1 ) 1 ( | ˆ | ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − =
∏
=dan 1−|Rˆm|1/m dapat dinteprestasikan sebagai rataan kuadrat koefisien korelasi (Pena dan Rodriguez2002).
m
Dˆ dapat pula ditafsirkan berdasarkan koefisian autokorelasi parsial. Perhatikan bahwa 1 - Ri2 = JKG(1,i)/JKT dan dengan cara
yang sama didapatkan 1 – Ri-12 = JKG(1, i-1)/
JKT sehingga ) ˆ 1 ( ) 1 , 1 ( ) , 1 ( 1 1 2 2 1 2 i i i i JKG i JKG R
R = −π
− = − − − Dimana ) 1 , 1 ( ) , 1 ( ) 1 , 1 ( ˆ2 − − − = i JKG i JKG i JKG i
π adalah
kuadrat koefisien autokorelasi ke-i. Sehingga determinan Rˆmdapat dituliskan sebagai
m i m m i i m m R / ) 1 ( 1 2 /
1 (1 ˆ )
| ˆ | − + −
∏
− = πJika model teridentifikasi dengan benar maka Dˆm akan menyebar secara asymtot
sebagai
∑
mi=1λiχ12.i (Lampiran 3). Peluang Pr(Dˆ > m x) dapat dievaluasi dengan membalikfungsi karateristik dari
∑
im=1λiχ12.i (Imhof 1961). Pendekatan sebaran λiχ12.i dilakukanoleh sebaranaχb2 dengan mean dan ragam yang sama dengan sebaran yang sebenarnya serta derajat bebas b yang berupa pecahan. Akan didapatkan bahwa a =
∑
λi2/∑
λi dan b = (∑
λi)2/∑
λ2i .Sebaran Dˆm dapat didekati dengan
sebaran gamma, Γ (α=b/2, β=1/2a) dengan parameter yang didefinisikan sebagai:
)] ( 12 ) 1 2 )( 1 ( 2 [ 2 )] ( 2 ) 1 [( 3 2 q p m m m q p m m + − + + + − + = α dan ) ( 12 ) 1 2 )( 1 ( 2 )] ( 2 ) 1 [( 3 q p m m m q p m m + − + + + − + = β
Sebaran ini memiliki rataan α/ β = (m+1)/ 2 – (p+q) dan ragam α/ β2 = (m+1)(2m+1)/ 3m –
2(p + q).
Pendekatan di atas akan lebih baik jika menggunakan koefisien autokorelasi yang distandarkan (r~ ) sehingga uji portmanteau k terbaru menjadi ] | ~ | 1
[ m 1/m
m n R
D = −
m
R~ adalah matriks korelasi yang dibangun
berdasarkan ~rk. Pendekatan Dm lebih baik
dibandingkan Dˆm , terutama untuk contoh berukuran kecil (Pena dan Rodriguez 2002). Nilai Dm akan bernilai lebih dari sama dengan
nol untuk semua nilai rk.
METODE ANALISIS
Penelitian dilakukan dengan melakukan simulasi. Pembangkitan data dilakukan dengan bantuan perangkat lunak R 2.4.0. Model yang dibangkitkan adalah model deret waktu ARMA(p,q)
Xt = φ1Xt-1 + φ2Xt-2 + ... + φpXt-p +at - θ1at-1 -θ2at-2 - ... - θqat-q
Dimana p dan q bernilai (0,1,2), at ~ N(0, σa2)
dan bebas stokastik identik. Koefisien autoregresi (φ) dan koefisien moving average (θ) dipilih sedemikian sehingga model yang dibangkitkan stasioner dan invertible. Pengulangan dilakukan sebanyak 10 000 kali. Ukuran contoh (n) yang digunakan adalah 30 dan 100. Evaluasi uji dilakukan pada lag 6, 12, 18, dan 24 untuk n = 30, sedangkan pada n = 100 dilakukan pada lag 12, 24, 36 dan 48 dengan taraf nyata uji α = 0.05. Penentuan n dan lag evaluasi dilakukan secara subjektif oleh penulis.
Langkah-langkah simulasi yang dilakukan adalah:
1. Dibangkitkan at yang menyebar normal
dengan rataan 0 dan ragam 1.
2. Data deret waktu di bangun dengan model dan parameter yang telah ditetapkan (Lampiran 2) dengan at sebagai galatnya.
3. Data deret waktu di-fit dengan model AR (1) atau MA (1) atau ARMA (1,1) (Lampiran 2). Sisaan contoh di hitung dengan rumus:
t q p
t ˆ (B)ˆ(B)X
ˆ φ 1 θ ε = −
4. Nilai autokorelasi sisaan contoh (rk) dan
autokorelasi parsial sisaan contoh (πˆ ) k dicari.
5. Uji QLB dihitung berdasarkan nilai
koefisien autokorelasi sisaan contoh (rk).
∑ −
+
= m= −
k k
LB nn n k r
Q ( 2) 1( ) 1 2
6. Peluang QLB dihitung dengan merujuk
pada persentil sebaran Khi-Khuadrat dengan derajat bebas m-p-q.
7. Uji QMT dilakukan berdasarkan nilai
koefisien autokorelasi parsial sisaan contoh (πˆ ). k
∑
= − −+
= m
k k
MT nn n k
5
8. Peluang QMT dihitung dengan merujuk
pada persentil sebaran Khi-Khuadrat dengan derajat bebas m-p-q.
9. Uji Dm dilakukan berdasarkan autokorelasi
sisaan contoh yang telah distandarkan (r~ ). k
] | ~ | 1
[ m 1/m
m n R
D = −
10.Peluang Dm dihitung mengunakan
pendekatan sebaran gamma Γ(α, β) dengan parameter: )] ( 12 ) 1 2 )( 1 ( 2 [ 2 )] ( 2 ) 1 [( 3 2 q p m m m q p m m + − + + + − + = α dan ) ( 12 ) 1 2 )( 1 ( 2 )] ( 2 ) 1 [( 3 q p m m m q p m m + − + + + − + = β
11.Jika nilai peluang kurang dari α maka tolak H0 yaitu autokorelasi sisaan contoh
berbeda nyata dengan nol
12.Langkah 1-11 dilakukan sebanyak 10 000 kali ulangan.
13.Langkah 1-12 diulang untuk setiap model.
HASIL DAN PEMBAHASAN
Pemeriksaan Program
Pemeriksaan program dilakukan untuk melihat apakah program yang digunakan telah berjalan dengan baik dan memberikan hasil benar. Perintah pelaksanaan simulasi pada perangkat lunak R 2.4.0 dapat dilihat pada Lampiran 1.
Program Pembangkitan Data
Program pembangkitan data yang baik dan benar akan menghasilkan keluaran sesuai dengan yang diinginkan. Hal ini sangatlah penting karena sangat berpengaruh pada hasil yang akan dicapai. Jika data yang dibangkitkan salah maka akan salah pula kesimpulan yang kita ambil.
Sebagai ilustrasi diberikan gambaran pembangkitan untuk model 16 yaitu model MA (2) dengan θ1 = 0.80 dan θ2 = -0.50.
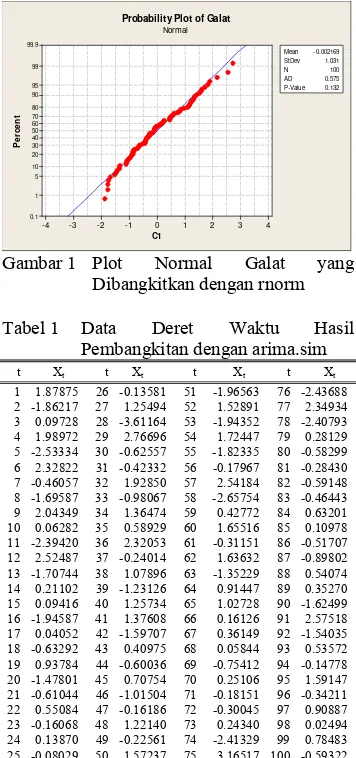
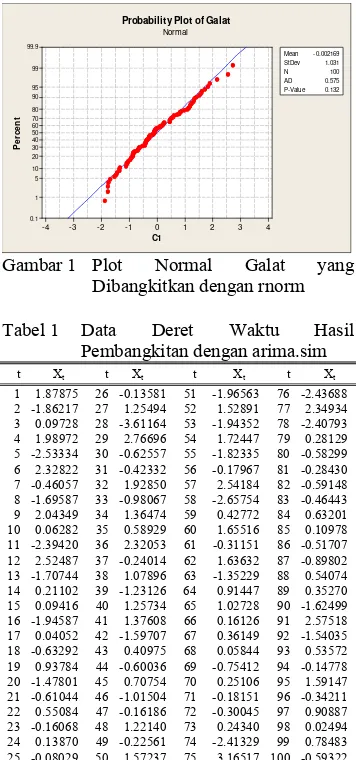
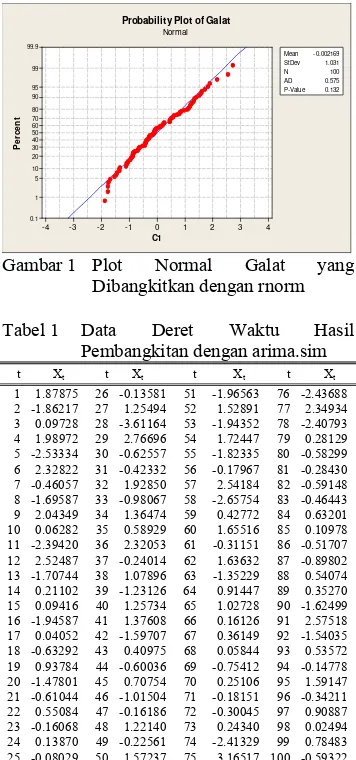
Pembangkitan data dilakukan dengan R 2.4.0. Galat yang menyebar normal dengan rataan nol dan ragam satu dibangkitkan dengan perintah rnorm. Dari plot normal Anderson-Darling (Gambar 1) didapatkan nilai AD sebesar 0.575 dengan peluang 0.132. Hal ini menunjukkan bahwa tidak cukup bukti untuk menyatakan bahwa galat yang dibangkitkan tidak menyebar normal dengan selang kepercayaan 95%. Berdasarkan galat ini, data deret waktu dibangkitkan dengan perintah
arima.sim. Hasil bangkitan dapat dilihat pada Tabel 1. C1 P e rc e n t 4 3 2 1 0 -1 -2 -3 -4 99.9 99 95 90 80 70 60 50 40 30 20 10 5 1 0.1 Mean 0.132 -0.002169 StDev 1.031 N 100 AD 0.575 P-Value
Probability Plot of Galat
Normal
Gambar 1 Plot Normal Galat yang Dibangkitkan dengan rnorm
Tabel 1 Data Deret Waktu Hasil Pembangkitan dengan arima.sim
t Xt t Xt t Xt t Xt
1 1.87875 26 -0.13581 51 -1.96563 76 -2.43688 2 -1.86217 27 1.25494 52 1.52891 77 2.34934 3 0.09728 28 -3.61164 53 -1.94352 78 -2.40793 4 1.98972 29 2.76696 54 1.72447 79 0.28129 5 -2.53334 30 -0.62557 55 -1.82335 80 -0.58299 6 2.32822 31 -0.42332 56 -0.17967 81 -0.28430 7 -0.46057 32 1.92850 57 2.54184 82 -0.59148 8 -1.69587 33 -0.98067 58 -2.65754 83 -0.46443 9 2.04349 34 1.36474 59 0.42772 84 0.63201 10 0.06282 35 0.58929 60 1.65516 85 0.10978 11 -2.39420 36 2.32053 61 -0.31151 86 -0.51707 12 2.52487 37 -0.24014 62 1.63632 87 -0.89802 13 -1.70744 38 1.07896 63 -1.35229 88 0.54074 14 0.21102 39 -1.23126 64 0.91447 89 0.35270 15 0.09416 40 1.25734 65 1.02728 90 -1.62499 16 -1.94587 41 1.37608 66 0.16126 91 2.57518 17 0.04052 42 -1.59707 67 0.36149 92 -1.54035 18 -0.63292 43 0.40975 68 0.05844 93 0.53572 19 0.93784 44 -0.60036 69 -0.75412 94 -0.14778 20 -1.47801 45 0.70754 70 0.25106 95 1.59147 21 -0.61044 46 -1.01504 71 -0.18151 96 -0.34211 22 0.55084 47 -0.16186 72 -0.30045 97 0.90887 23 -0.16068 48 1.22140 73 0.24340 98 0.02494 24 0.13870 49 -0.22561 74 -2.41329 99 0.78483 25 -0.08029 50 1.57237 75 3.16517 100 -0.59322
Keterangan : Xt adalah model MA (2) dengan θ1 = 0.80
dan θ2 = -0.50)
Gambar 2 Plot Data Bangkitan Terhadap Waktu
6
sesuai dengan apa yang diharapkan. Proses ini dilakukan dengan melihat plot data terhadap waktu, plot ACF, plot PACF, pendugaan parameter dan analisis sisaannya.
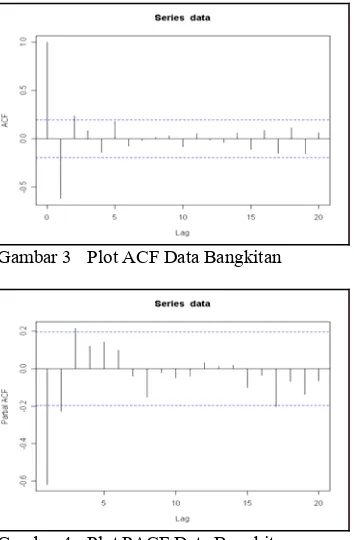
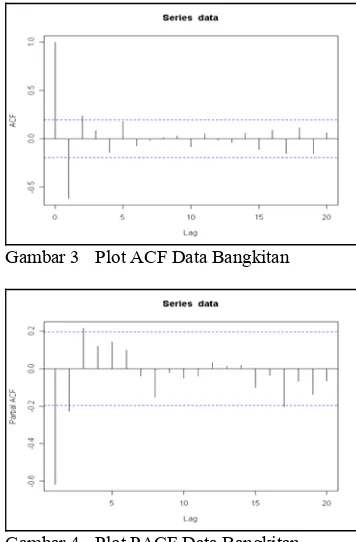
Plot data bangkitan terhadap waktu (Gambar 2) memperlihatkan kestasioneran, baik pada rataan maupun pada ragam, sehingga tidak perlu dilakukan pembedaan pada data. Plot ACF dan plot PACF data (Gambar 3 dan Gambar 4) dapat digunakan sebagai dasar penentuan model tentatif. Dari plot ACF yang memperlihatkan hanya autokorelasi pada lag 1 dan lag 2 yang berbeda nyata dengan nol dan plot PACF yang turun secara lambat, dapat kita tentukan model tentatifnya adalah MA (2). Jika dianggap plot PACF nyata untuk lag 1, lag 2 dan lag 3 dan plot ACF turun secara lambat maka model tentatif data diatas adalah AR (3).
Gambar 3 Plot ACF Data Bangkitan
Gambar 4 Plot PACF Data Bangkitan
Pendugaan parameter dengan model MA (2) memperlihatkan bahwa nilai dugaan parameter θˆ1 = 0.8117 dan θˆ2 = -0.4906 mendekati nilai parameter aslinya θ1 = 0.80
dan θ2 = -0.50 (Gambar 5). Secara visual
dapat diperlihatkan bahwa sisaan model telah saling bebas, karena plot residual terhadap waktu (Gambar 6) tidak memperlihatkan adanya pola. Hal ini diperkuat dengan plot ACF sisaan (Gambar 7) dan plot PACF sisaan (Gambar 8) yang memperlihatkan tidak
adanya autokorelasi sisaan dan autokorelasi parsial sisaan yang berbeda nyata dari nol. Sehingga dapat disimpulkan bahwa model MA (2) layak.
Gambar 5 Pendugaan Parameter Model MA (2)
Gambar 6 Plot Sisaan Model MA (2) Terhadap Waktu
Gambar 7 Plot ACF Sisaan Model MA (2)
Gambar 8 Plot PACF Sisaan Model MA (2)
Call:
arima(x = data, order = c(0, 0, 2))
Coefficients:
ma1 ma2 intercept
0.8117 -0.4906 0.0402
s.e. 0.1004 0.0843 0.0694
sigma^2 estimated as 1.049:
7
Hasil pendugaan parameter untuk model AR (3) dapat dilihat pada Gambar 9. Nilai
dugaan parameternya adalah φˆ1= -0.7117,
2 ˆ
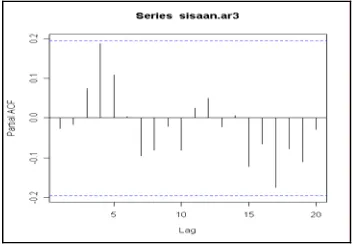
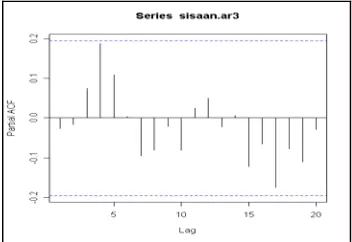
φ = -0.0471, dan φˆ3 = 0.02318 dengan dugaan ragam sebesar 1.069. Plot sisaan terhadap waktu yang tidak berpola (Gambar 10), serta tidak adanya autokorelasi sisaan (Gambar 11) dan parsial autokorelasi sisaan (Gambar 12) yang berbeda nyata dengan nol menandakan sisaan model AR (3) telah saling bebas. Berdasarkan hal ini dapat disimpulkan bahwa model AR (3) juga layak.
Gambar 9 Pendugaan Parameter Model AR (3)
Gambar 10 Plot Sisaan Model AR (3) Terhadap Waktu
Gambar 11 Plot ACF Sisaan Model AR (3)
Dikarenakan kedua model terbukti layak, maka harus dipilih salah satu sebagai model terbaik. Model terbaik untuk data deret waktu diatas adalah MA (2), karena model ini adalah
model yang paling sederhana dengan nilai AIC = 297.46 lebih kecil dibandingkan dengan nilai AIC model AR (3) = 301.26.
Gambar 12 Plot PACF Sisaan Model AR (3)
Keseluruhan proses di atas memperlihatkan pembangkitan data dengan model MA (2) memberikan hasil yang baik dan benar. Model terbaik yang didapatkan sesuai dengan model pembangkit dengan dugaan parameter yang mendekati paameter aslinya. Hal ini membuktikan bahwa program pembangkitan telah terbukti baik dalam membangkitkan model sesuai dengan yang diinginkan.
Program Perhitungan QLB, QMT, dan Dm
Pada dasarnya program perhitungan QMT
dan QLB adalah sama. Perbedaannya adalah
QLB dihitung berdasarkan nilai ACF dan QMT
dengan nilai PACF. Perhitungan QLB untuk
sisaan model MA (2) dengan MINITAB dan R 2.4.0 tidak memperlihatkan adanya perbedaan (Lampiran 4) menandakan program perhitungan QLB dan QMT telah berjalan baik.
Pemeriksaan program perhitungan Dm
dilakukan dengan membandingkan hasil perhitungan program R 2.4.0 dengan hasil perhitungan secara manual. Perhitungan secara manual dilakukan karena belum tersedianya perangkat lunak yang menyediakan program perhitungan Dm. Tidak
adanya perbedaan nilai Dm untuk sisaan model
MA (2) yang dihitung secara manual dan dengan R 2.4.0. (Lampiran 5) mengindikasikan bahwa program perhitungan Dm telah berjalan baik.
P-value uji portmanteau dihitung berdasarkan pada fungsi kepekatan peluang bersama. Peluang QMT dan QLB dihitung
berdasarkan pada sebaran khi-khuadrat, sedangkan peluang Dm dihitung berdasarkan
sebaran gamma. Hasil yang didapatkan dari perhitungan dengan MINITAB sama dengan hasil yang diperoleh dari program R 2.4.0 (Lampiran 6).
Call:
arima(x = data, order = c(3, 0, 0))
Coefficients:
ar1 ar2 ar3 intercept
-0.7117 -0.0471 0.2318 0.0386 s.e. 0.0966 0.1206 0.0973 0.0678
sigma^2 estimated as 1.069:
8
Kelayakan Model
Uji diagnostik terhadap kelayakan model MA (2) untuk data Tabel 1 dengan menggunakan ketiga uji portmanteau memberikan kesimpulan bahwa model MA (2) layak. Dimana P-value untuk Dm, QLB, dan
QMT untuk sisaan model MA (2) bernilai lebih
dari α = 0.05 untuk semua lag k (k = 6, 12, 18, 24, 30, 36, 42, 48) (Lampiran 7). Model AR (3) juga merupakan model yang layak untuk data Tabel 1 berdasarkan pada uji QLB, QMT,
dan Dm, dimana ketiga uji memperlihatkan
nilai yang lebih dari α = 0.05 untuk semua lag k (k = 6, 12, 18, 24, 30, 36, 42, 48) (Lampiran 7).
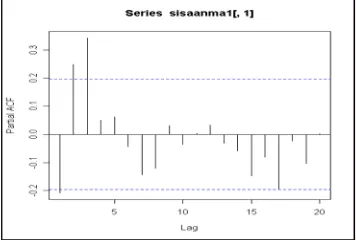
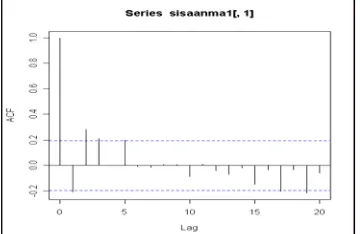
Ketika data tersebut di-fit dengan model yang salah misalnya model MA (1), terlihat bahwa sisaannya tidak saling bebas dan model tidak layak. Hal ini dapat dilihat jelas dari plot ACF sisaan (Gambar 13) dan plot PACF sisaan (Gambar 14) yang tidak berbeda nyata dengan nol serta diperkuat oleh ketiga uji portmanteau dengan P-value yang kurang dari α = 0.05 untuk semua lag k (k = 6, 12, 18, 24, 30, 36, 42, 48) kecuali dengan uji Dm pada lag
36 dan 42 (Lampiran 7).
Gambar 13 Plot ACF Sisaan Model MA (1)
Gambar 14 Plot PACF Sisaan Model MA (1)
Kelayakan sebuah model ARMA (p,q) dapat dengan mudah dilihat dari plot ACF sisaan dan plot PACF sisaan. Tetapi tidak
selamanya kedua plot tersebut dapat dijadikan patokan layak atau tidaknya sebuah model ARMA (p,q), sehingga perlu dilakukan uji portmanteau.
Pembangkitan dan Pengolahan Data
Jika program telah berjalan dengan benar, maka keseluruhan simulasi dapat dilakukan. Tahap pertama yang dilakukan dalam pembangkitan dan pengolahan data adalah membangkitkan data deret waktu ARMA (p,q). Data ini lalu di-fit dengan model AR (1) atau MA (1) atau ARMA (1,1) (Lampiran 2). Dari pem-fit-an model akan didapatkan sisaan contoh.
Tahap selanjutnya adalah menghitung nilai ACF sisaan contoh dan PACF sisaan contoh. Perhitungan uji portmanteau didasarkan pada kedua nilai ini. Koefisien autokorelasi sisaan contoh menjadi dasar perhitungan QLB dan Dm.
Sedangkan QMT dihitung berdasarkan pada
koefisien autokorelasi parsial sisaan contoh. Peluang dari masing-masing uji didapatkan dengan menghitung persentil sebaran asymtot-nya. Jika P-value kurang dari α maka tolak H0, yang berarti model tidak
layak karena sisaannya berkorelasi. Hal ini dilakukan sebanyak 10 000 kali untuk tiap-tiap model ARMA (p,q) dan ukuran contoh, sehingga total deret yang dibangkitkan sejumlah 720 000 deret waktu.
Tujuan dari uji portmanteau adalah untuk melihat ada atau tidaknya autokorelasi yang nyata pada sisaan. Jika model tepat, maka tidak ada autokorelasi pada sisaan (Box dan Pierce 1970). Pada penelitian ini dilakukan hal yang sebaliknya. Model sebenarnya dari data telah diketahui kemudian dilakukan pem-fit -an deng-an model y-ang salah. Hasil y-ang diharapkan adalah adanya korelasi pada sisaan, yang menandakan bahwa model yang digunakan tidak layak. Ketiga uji portmanteau diharapkan dapat mendeteksi adanya autokorelasi pada sisaan ini. Semakin banyak series yang dinyatakan memiliki sisaan berkorelasi maka semakin sensitif uji tersebut.
Persentase banyaknya series yang modelnya dinyatakan tidak layak oleh uji QMT
semakin menurun dengan semakin besarnya lag baik untuk n=100 maupun n=30 (Lampiran 11 dan 14). Ini sesuai dengan yang diharapkan bahwa kesensitifan uji akan semakin menurun dengan bertambahnya lag. Hasil yang sama ditunjukan oleh uji QLB dan
uji Dm pada sebagian besar model pada n=100
9
oleh uji QLB dan uji Dm untuk beberapa model
pada n=30 (Lampiran 13 dan 15).
Persentase banyaknya series (series 1 – series 10000) dengan sisaan berkorelasi dengan uji Dm pada n=100 dan lag 12 berkisar
antara 9.12% – 99.99%, lag 24 antara 14.45% – 99.96%, lag 36 18.39% – 99.87%, dan untuk lag 48 antara 22.58% – 99.77%. Untuk n=30, persentase ini menurun yaitu untuk lag 6 berkisar antara 2.02% – 81.71%, untuk lag 12 antara 10.71% – 83.34%, lag 18 antara 15.05% – 78.22%, dan lag 24 selang 12.71% – 71.91% (Lampiran 8 dan 9).
Dari 10000 series, series yang dinyatakan modelnya tidak layak oleh uji QLB pada n=100
dan lag 12 adalah antara 3.25% – 94.44% series, untuk lag 24 antara 4.68% – 98.65% series, lag 36 selang 5.66% – 98.07%, dan lag 48 antara 5.92% – 97.53%. Untuk n=30 lag 6 jumlah series dengan model tidak layak berjumlah antara 2.14% – 68.50% series, untuk lag 12 berkisar antara 2.81% – 63.62% series, lag 18 selang 2.67% – 63.70%, dan lag 24 antara 2.58% – 63.84% (Lampiran 8 dan 9).
Series dengan sisaan berkorelasi dengan uji QMT pada n=100 lag 12 berkisar 3.32% –
99.98%, lag 24 berkisar 3.45% – 99.82%, lag 36 selang 2.88% – 99.1%, dan lag 48 antara 1.44% – 96.51%. Untuk n=30 lag 6 persentasenya berkisar antara 2.99% – 83.74%, lag 12 antara 2.76% – 66.13%, lag 18 selang 1.77% – 50.3%, dan lag 24 antara 2.24% – 34.7% (Lampiran 8 dan 9).
Ketiga uji lebih sensitif pada n=100 dibandingkan dengan n=30 kecuali untuk model ARMA (p,q) dengan θ1 = 0.75 yang
di-fit dengan ARMA (1,1). Pada n=100 lag 12, banyaknya series yang dinyatakan modelnya tidak layak sebanyak 9.17 %, sedangkan pada n=30 sebanyak 78.91% (Lampiran 8 dan 9).
Uji Dm memberikan jauh lebih banyak
series dengan model yang tidak layak dibandingkan dengan kedua uji lainnya untuk semua lag dan semua model kecuali untuk n=30 lag 6). Untuk n=30 lag 6 pada model ARMA (p,q) yang di-fit dengan ARMA (1,1), ketiga uji memberikan hasil yang sebanding (Lampiran 9). Uji QLB lebih sensitif dibanding
uji QMT untuk n=100 lag 24, 36 dan 48 serta
n=30 lag 12,18, dan 24 kecuali pada model ARMA (p,q) dengan θ1 ≤ -0.60 yang di-fit
dengan AR (1). Pada n=100 lag 12 dan n=30 lag 6, uji QLB dan uji QMT memberikan hasil
yang relatif sama (Lampiran 8 dan 9).
SIMPULAN DAN SARAN
Simpulan
Dari 36 model ARMA (p,q) yang di-fit dengan model AR (1) atau MA (1) atau ARMA (1,1) dapat disimpulkan bahwa uji Dm
merupakan uji yang paling sensitif. Kesensitifan ini terlihat dari jumlah series yang dinyatakan modelnya tidak layak oleh uji Dm lebih banyak dibandingkan kedua uji
portmanteau lainnya. Perbedaan kesensitifan ini tergantung kepada model dan ukuran contoh, dimana kesensitifan uji Dm mencapai
30% lebih sensitif dibanding uji QLB dan uji
QMT. Uji QLB memberikan hasil yang sama
sensitifnya dengan uji QMT untuk lag kecil dan
hasil yang lebih sensitif pada lag besar. Tetapi uji QMT terbukti lebih sensitif ketika model
sebenarnya memiliki order MA yang lebih tinggi.
Saran
Beberapa saran untuk penelitian lanjutan antara lain :
1. Pembuatan program perhitungan Dm yang
lebih terintegrasi dan efisien yaitu program dengan running time yang lebih singkat.
2. Metode untuk membandingkan kesensitifan uji QLB, QMT, dan Dm untuk
data deret waktu yang tidak stasioner maupun yang memiliki siklus musiman. 3. Metode untuk membandingkan
kesensitifan uji QLB, QMT, dan Dm untuk
data deret waktu yang berupa peubah ganda.
DAFTAR PUSTAKA
Arnold SF. 1990. Mathematical Statistics. Englewood Cliffs, NJ: Prentice Hall International.
Box GEP dan Pierce DA. 1970. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J Amer Statist Assoc 65:1509-25.
Cryer JD. 1986. Time Series Analysis. Boston: Duxbury Press.
10
Imhof JP. 1961. Computing the distribution of quadratic form in normal variables. Biometrika 48: 419-26.
Ljung GM. 1986. Diagnostic testing of univariate time series models. Biometrika 73:725-730.
Ljung GM dan Box GEP. 1978. On a measure of mack of fit in time series models. Biometrika 65:297-303.
Monti AC. 1994. A Proposal for a residual autocorrelation test in linear models. Biometrika 81:776-80.
McLeod AI. 1978. On the distribution of residual autocorrelation in Box-Jenkin models. J R Statist Soc 40:296-302.
Montgomery DC, Johnson LA, Gardiner JS. 1990. Forecasting and Time Series Analysis. Ed ke-2. Singapore: McGraw-Hill. Inc.
Morgan JT. 1984. Element of Simulation. New York: Chapman and Hall Ltd.
Pena D, Rodriguez J. 2002. A powerful portmanteau test of lack of fit for time series. J Amer Statist Assoc 97:601-610.
Pindyck RS, Rubinfield DL. 1997. Econometric Model and Economic Forecats. Edisi ke-4. Singapura: Mgraw-Hill.
11
Lampiran 1 Perintah Pembangkitan Deret Waktu dengan R 2.4.0
#pembangkitan data deret waktu ARMA (p,q) dengan φ =p, θ=q dan n=nbar sebanyak nkol x.arima<-function(nbar,nkol,p,q){
x.arima<-matrix(0,nrow=nbar,ncol=nkol) for(i in 1:nkol){
rand.ita<-function(n)rnorm(n,0,1)
x.arima[,i]<-arima.sim(nbar,model=list(ar=p,ma=q),rand.gen=rand.ita) }
return(x.arima) }
#pem-fit-an dengan model arima = model #x adalah matriks data deret waktu x.residual<-function(x,model){ nkol<-ncol(x) nbar<-nrow(x)
x.residual<-matrix(0,nrow=nbar,ncol=nkol) for(i in 1:nkol){
ita<-arima(x[,i],order=model) x.residual[,i]<-ita$residuals }
return(x.residual) }
#menghitung acf residual
#x adalah matriks sisaan data deret waktu x.acf<-function(x,nlag){
x.acf<-matrix(0,nrow=nlag+1,ncol(x)) for(i in 1:ncol(x)){
ita<-acf(x[,i],lag.max=nlag,plot=FALSE) x.acf[,i]<-ita$acf
}
return(x.acf) }
#menghitung pacf residual
#x adalah matriks sisaan data deret waktu x.pacf<-function(x,nlag){
x.pacf<-matrix(0,nrow=nlag,ncol(x)) for(i in 1:ncol(x)){
ita<-pacf(x[,i],lag.max=nlag,plot=FALSE) x.pacf[,i]<-ita$acf
}
return(x.pacf) }
#menghitung acf/pacf yang distandarkan
#x adalah matriks acf/pacf sisaan data deret waktu x.standar<-function(x,n){
x.standar<-matrix(0,nrow(x),ncol(x)) indek<-vector()
for(i in 1:nrow(x)){
indek[i]<-(n+2)/(n-i) }
x<-x^2 for(j in 1:ncol(x)){
x.standar[,j]<-sqrt(x[,j]*(indek)) }
12
#menghitung portmanteau Monti (QMT)
#x adalah matriks pacf sisaan data deret waktu x.qmt<-function(x,n){
x.qmt<-matrix(0,nrow(x),ncol(x)) x<-x.standar(x,n)
x<-x^2 for(j in 1:ncol(x)){ kolom<-vector() kolom<-x[,j]
for (i in 1:nrow(x)){
x.qmt[i,j]<-sum(kolom[1:i]) }
}
x.qmt<-n*x.qmt return(x.qmt) }
#menghitung portmanteau Ljung-Box (QLB)
#x adalah matriks acf sisaan data deret waktu x.qlb<-function(x,n){
x<-x[-1,] x<-x.qmt(x,n) return(x) }
#menghitung portmanteau Pena-Rodriquez (Dm)
#x adalah matriks acf sisaan data deret waktu x.dm<-function(x,n){
x<-x[-1,] x<-x.standar(x,n)
x.dm<-matrix(0,nrow(x),ncol(x)) for(l in 1:ncol(x)){
for(p in 2:nrow(x)+1){ rm<-diag(1,p)
for(j in 1:p){ for(i in 1:p){ b<-abs(j-i)
if(b!=0){ rm[i,j]<-x[b,l]
} } }
x.dm[p-1,l]<-n*(1-((abs(det(rm)))^(1/(p-1)))) }
}
return(x.dm) }
#Menghitung peluang sebaran khi-khuadrat #x adalah matriks nilai QLB atau QMT
x.chisquare<-function(x){ x.chisquare<-vector() chisquare<-vector()
for(i in 2:ncol(x)){
chisquare<-pchisq(x[,i],(i-1))
x.chisquare<-cbind(x.chisquare,chisquare) }
13
#Menghitung peluang sebaran gamma #x adalah matriks nilai Dm
x.gamma<-function(x,p,q){ x.gamma<-vector() gamma<-vector()
for(i in 1:ncol(x)){
alpha<-((((i+1)-2*(p+q))**2)*3*i)/((2*(i+1)*(2*i+1)-12*i*(p+q))*2) beta<-(((i+1)-2*(p+q))*3*i)/(2*(i+1)*(2*i+1)-12*i*(p+q))
gamma<-pgamma(x[,i],alpha,beta) x.gamma<-cbind(x.gamma,gamma) }
return(x.gamma) }
#Perintah untuk memanggil program
ita1<-x.arima(100,10000,c(0.90,-0.40),c(-1.20,0.30)) ita2<-x.residual(ita1,c(1,0,0))
ita3<-x.acf(ita2,50) ita4<-x.pacf(ita2,50) ita5<-x.qlb(ita3,100) ita6<-x.qmt(ita4,100) ita7<-x.dm(ita3,100) ita8<-t(ita5)
ita8<-1-x.chisquare(ita8) ita9<-t(ita7)
ita9<-1-x.gamma(ita9,1,0)
14
Lampiran 2 Model ARMA (p,q) yang Dibangkitkan
Di-fit dengan AR(1) 1. Zt = at + 0.50a t-1
2. Zt = at + 0.80at-1
3. Zt = at + 0.60a t-1 - 0.30at-2
4. Zt = 0.10Zt-1 + 0.30Z t-2 + at
5. Zt = 1.20Zt-1 – 0.40Z t-2 + at
6. Zt = 0.70Zt-1 + at + 0.40at-1
7. Zt = 0.70Zt-1 + at + 0.90at-1
8. Zt = 0.40Zt-1 + at + 0.60at-1 – 0.30at-2
9. Zt = 0.70Zt-1 + at – 0.70at-1 + 0.15at-2
10.Zt = 0.70Zt-1 + 0.20Zt-2 + at – 0.50at-1
11.Zt = 0.70Zt-1 – 0.20Zt-2 + at + 0.50at-1
12.Zt = 0.90Zt-1 – 0.40Zt-2 + at –1.20at-1 + 0.30at-2
Di-fit dengan MA(1) 13.Zt = 0.50Zt-1 + at
14.Zt = 0.80Zt-1 + at
15.Zt = 1.10Zt-1 – 0.35Zt-2 + at
16.Zt = at – 0.80at-1 + 0.50at-2
17.Zt = at + 0.60at-1 – 0.30at-2
18.Zt = 0.50Zt-1 + at + 0.70at-1
19.Zt = -0.50Zt-1 + at – 0.70at-1
20.Zt = 0.30Zt-1 + at – 0.80at-1 + 0.50at-2
21.Zt = 0.80Zt-1 + at + 0.50at-1 – 0.30at-2
22.Zt = 1.20Zt-1 – 0.50Zt-2 + at – 0.90at-1
23.Zt = 0.30Zt-1 - 0.20Zt-2 + at + 0.70at-1
24.Zt = 0.90Zt-1 – 0.40Zt-2 + at – 1.20at-1 + 0.30at-2
Di-fit dengan ARMA(1,1) 25.Zt = 0.50Zt-1 + at
26.Zt = 0.90Zt-1 – 0.30Zt-2 + at
27.Zt = –1.20Zt-1 – 0.80Zt-2 + at
28.Zt = at – 0.75at-1
29.Zt = at – 1.10at-1 + 0.80at-2
30.Zt = at + 0.60at-1 + 0.30at-2
31.Zt = 0.40Zt-1 + at + 0.60at-1 + 0.30at-2
32.Zt = 0.70Zt-1 + at + 0.70at-1 – 0.20at-2
33.Zt = 1.20Zt-1 – 0.50Zt-2 + at + 0.90at-1
34.Zt = 0.30Zt-1 – 0.20Zt-2 + at + 0.70at-1
35.Zt = 0.90Zt-1 – 0.40Zt-2 + at – 1.20at-1 + 0.30at-2
15
Lampiran 3 Pembuktian Teorema dan Pendekatan Sebaran.
Pembuktian Teorema
Misalkan hipotesis nol adalah Dˆm menyebar secara asimtot sebagai peubah acak X. Dengan menerapkan – method (Arnold 1990) pada g(x) = log (1-x) maka –nlog|Rm|1/m juga menyebar
secara asimtot sebagai X. Sehingga persamaan
m i m m i i m m R / ) 1 ( 1 2 /
1 (1 ˆ )
| ˆ | − + −
∏
−= π dapat dituliskan
sebagai
∑
= − + − − = − m i i m m m i m n R n 1 2 / 1 ) ˆ 1 log( 1 ) | ˆlog(| π (A.1)
Untuk mencari sebaran dari (A.1), misalkan ( ˆ , ˆ22, , ˆ2)
2
1 n n m
nπ π L π menyebar secara asimtot sebagai Y. Kemudian dengan menerapkan multivariate – method (Arnold 1990) pada
) ˆ , , ˆ , ˆ
(n 12 n 22 n m2
g π π L π = −
∑
im=1 m−i+ m − i2) ˆ 1 log( ) / ) 1
(( π didapatkan
Y m m m m i m n m i i ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − → − + − −
∑
= 1 , , 1 , 1 ) ˆ 1 log( 1 1 2 Lπ (A.2)
Dimana Æ adalah lambang konvergen dalam sebaran.
Dengan teorema Cramer-Wold (Arnold 1990) didapatkan bahwa
Y m m m n n n m m m m ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − → ′ ⎟ ⎠ ⎞ ⎜ ⎝
⎛ − 1
, , 1 , 1 ) ˆ , , ˆ , ˆ ( 1 , , 1 ,
1 L π12 π22 L π2 L (A.3)
Dengan fakta bahwa n1/2πˆ(m) menyebar secara asimtot sebagai N(0, Im - Qm) dan teorema bentuk
kuadrat (Box 1954) menyebabkan
∑
= → = ′ ⎟ ⎠ ⎞ ⎜ ⎝⎛ − m
i i i m
m
m n W
n n n m m m 1 2 . 1 ) ( ) ( 2 2 2 2
1, ˆ , , ˆ ) ˆ ˆ
ˆ ( 1 , , 1 ,
1 L π π L π π π λχ (A.4)
dari (A.3) dan (A.4) didapatkan
∑
= → ⎟ ⎠ ⎞ ⎜ ⎝⎛ − m
i i i
Y m m m 1 2 . 1 1 , , 1 ,
1 L λχ
Dan dari (A.2) didapatkan
∑
=→ m i i i m D 1 2 . 1 ˆ λχ
Pendekatan Sebaran Dˆm
Box-Pierce (1970) dan McLeod(1978) mendekati matriks Qm = XmV-1Xm' dengan matriks proyeksi
Qm = Xm(Xm'Xm)-1Xm' ketika m cukup besar. Pendekatan ini amat berguna untuk menghitung nilai
dari a dan b yang tidak tergantung pada parameter φ dan θ dari model ARMA. Diketahui
) ( ) / 1 ( ) ( ) ( ) ) (( 1 m m m m m m m m i
i=tr I −Q W =trW −tr Q + mtr Q C
∑
=
λ (A.5)
Dimana Cm adalah matriks diagonal dengan elemen ci = i, i = 0, ... , (m-1) dan
) ( ) / 1 ( ) ( ) ( ) / 2 ( ) ( ) / 2 ( ) ( ) ) (( 1 m m m m m m m m m m m m i i C Q tr m Q tr C Q tr m C Q tr m W tr W Q I tr + − − + = − =
∑
= λ (A.6)Pernyataan alternatif untuk Σλi dan Σλi2 dapat diperoleh dengan penguraian Cholesky pada matriks
(Im – Qm) (Velilla 1994). Karena Qm adalah matriks idempoten tingkat p+q, (A.5) dan (A.6) dapat
ditulis sebagai fungsi dari p, q, m, qii dan qij dimana qijadalah elemen dari Qm.
∑
∑
= − + + = − + = m i m i iii i q
m q p m 1 2 ) 1 ( 1 ) ( 2 1
λ (A.7)
16
Akan diperlihatkan bahwa hubungan dalan (A.8) yang tergantung pada qij akan mendekati nol jika
m meningkat. Sadari rangkaian ai = i dan bi=(i-1)qii. Maka
∑
= i− q i≤∑
im= qii=p+q<∞ mi1( 1) ii/ 1
ketika mÆ ∞ dan dengan lemma Kronecker’s (Davidson 1997) didapatkan bahwa
0 ) 1 ( ) / 2
( m
∑
mi=1 i− qii→ . Dengan argumen yang sama dan sifat dari matriks idempoten,∑
=+
= m
i ij ii
ii q q
q 2 1 2 , dapat ditunjukan bahwa (2/m2)
∑
mi=2(i−1)2qii →0 dan 0) 1 )( 1 ( )
/ 1
( m2
∑ ∑
im=2 m2 i− j− qij2→ . Untuk m yang besar persamaan (A.7) dan (A.8) dapat didekati sebagai∑
= − +
+ = m
i i
q p m
1
) ( 2
1
λ (A.9)
) ( ) 1 2 )( 1 ( 6
1
1 2
q p m
m m
m
i
i = + + − +
∑
17
Lampiran 4 Nilai QLB dengan Minitab dan R 2.4.0
lag MINITAB R 2.4.0 6 4.04436 4.04436 12 5.22066 5.22066 18 9.76794 9.76794 24 21.14837 21.14837 30 25.99563 25.99563 36 38.00570 38.00570 42 40.79568 40.79568 48 49.19603 49.19603
Keterangan : untuk sisaan model MA (2)
Lampiran 5 Nilai Dm dengan R 2.4.0 dan secara Manual
lag R 2.4.0 MANUAL 6 1.46916 1.46916 12 2.92072 2.92072 18 3.93665 3.93665 24 6.45886 6.45886 30 8.79726 8.79726 36 12.29416 12.29416 42 16.36345 16.36345 48 20.31015 20.31015
Keterangan : untuk sisaan model MA (2)
Lampiran 6 P-value untuk Dm, QLB, serta QMT dengan Minitab dan R 2.4.0
lag MINITAB R 2.4.0
Dm QLB QMT Dm QLB QMT
6 0.4206 0.5430 0.5595 0.4206 0.5430 0.5595 12 0.7379 0.9200 0.8668 0.7379 0.9200 0.8668 18 0.9056 0.9131 0.8503 0.9056 0.9131 0.8503 24 0.8829 0.5720 0.6963 0.8829 0.5720 0.6963 30 0.8855 0.6257 0.7396 0.8855 0.6257 0.7396 36 0.8199 0.3341 0.4095 0.8199 0.3341 0.4095 42 0.7182 0.4796 0.2411 0.7182 0.4796 0.2411 48 0.6331 0.3853 0.2070 0.6331 0.3853 0.2070
18
Lampiran 7 P-value Uji Portmanteau
Lag Dm P-Value QLB P-Value QMT P-Value
MA(2) 6 1.4692 0.4206 4.0444 0.5430 3.9306 0.5595 12 2.9207 0.7379 5.2207 0.9200 6.0978 0.8668 18 3.9367 0.9056 9.7679 0.9131 11.1192 0.8503 24 6.4589 0.8829 21.1484 0.5720 19.0855 0.6963 30 8.7973 0.8855 25.9956 0.6257 23.7816 0.7396 36 12.2942 0.8199 38.0057 0.3341 36.2633 0.4095 42 16.3635 0.7182 40.7957 0.4796 46.9701 0.2411 48 20.3101 0.6331 49.1960 0.3853 54.6410 0.2070 AR(3) 6 2.4754 0.0000 5.1411 0.3989 5.7135 0.3351 12 3.9303 0.3435 6.4426 0.8423 8.5605 0.6624 18 5.1317 0.6624 11.6138 0.8229 15.4240 0.5650 24 7.0252 0.7590 21.4136 0.5558 21.2000 0.5689 30 8.5045 0.8557 24.8685 0.6851 27.4212 0.5490 36 11.6301 0.8102 41.4281 0.2106 39.0344 0.2933 42 14.7778 0.7725 44.5839 0.3235 50.6533 0.1435 48 17.6835 0.7584 50.8879 0.3232 57.0685 0.1491 MA(1)
6 12.3870 0.0005* 21.8722 0.0006* 24.3285 0.0002*
12 14.7655 0.0047* 22.9331 0.0181* 28.5979 0.0026*
18 16.5621 0.0205* 31.5191 0.0173* 37.2680 0.0031*
24 20.8344 0.0195* 49.7452 0.0010* 42.1248 0.0088*
30 25.9619 0.0125* 54.3781 0.0029* 46.1628 0.0226*
36 25.9599 0.0517 59.1095 0.0066* 57.9068 0.0088*
42 25.9469 0.1468 63.6724 0.0132* 69.7904 0.0033*
48 27.5321 0.0055* 75.2801 0.0055* 79.5698 0.0021*
Keterangan : Data = Tabel 1
Model Pem-fit : MA(2), AR(3) dan MA (1)
19
Lampiran 8 Persentase series (deret 1, deret 2, … deret 10000) dengan sisaan berkorelasi pada beberapa model ARMA (p,q) ketika di-fit dengan model AR(1), MA(1) dan ARMA(1,1) dengan uji Dm, QLB dan QMT
Model Pembangkit Model Pem-Fit
lag 12 lag 24 lag 36 lag 48
φ1 φ2 θ1 θ2 Dm QLB QMT Dm QLB QMT Dm QLB QMT Dm QLB QMT
0.50 ARMA11 0.0912 0.0325 0.0372 0.1510 0.0468 0.0369 0.1938 0.0579 0.0307 0.2258 0.0627 0.0162
0.50 MA1 0.5739 0.2623 0.2269 0.5141 0.2403 0.1552 0.4904 0.2439 0.1155 0.4947 0.2515 0.0758
0.80 MA1 0.9981 0.9743 0.9603 0.9956 0.9512 0.9027 0.9927 0.9355 0.8368 0.9906 0.9298 0.7549
0.10 0.30 AR1 0.7769 0.4067 0.3712 0.7151 0.3543 0.2534 0.6847 0.3452 0.1774 0.6727 0.3464 0.1205
1.20 -0.40 AR1 0.9694 0.8109 0.7867 0.9446 0.7248 0.6313 0.9253 0.6922 0.5108 0.9059 0.6765 0.4032
0.90 -0.30 ARMA11 0.2020 0.0762 0.0764 0.2391 0.0852 0.0636 0.2638 0.0943 0.0472 0.2936 0.0987 0.0295
-1.20 -0.80 ARMA11 0.9990 0.9944 0.9922 0.9988 0.9865 0.9724 0.9983 0.9807 0.9416 0.9977 0.9753 0.8974
1.10 -0.35 MA1 0.9997 0.9938 0.9937 0.9991 0.9811 0.9747 0.9987 0.9692 0.9375 0.9976 0.9623 0.8824
-0.50 AR1 0.5854 0.2433 0.2567 0.5121 0.2246 0.1764 0.4847 0.2254 0.1274 0.4848 0.2300 0.0831
-0.80 AR1 0.9829 0.6864 0.9362 0.9459 0.5767 0.7994 0.9142 0.5382 0.6608 0.8857 0.5277 0.5304
0.75 ARMA11 0.0917 0.0342 0.0332 0.1445 0.0470 0.0345 0.1839 0.0566 0.0288 0.2258 0.0592 0.0144
-0.60 0.30 AR1 0.9881 0.7164 0.9773 0.9649 0.5997 0.8982 0.9383 0.5681 0.7927 0.9098 0.5503 0.6667
1.10 -0.80 ARMA11 0.4162 0.1718 0.1989 0.3864 0.1689 0.1399 0.3831 0.1697 0.0990 0.3930 0.1808 0.0667
-0.60 -0.30 ARMA11 0.2694 0.0937 0.0937 0.2976 0.1034 0.0763 0.3185 0.1090 0.0545 0.3410 0.1194 0.0362
0.80 -0.50 MA1 0.9800 0.7879 0.9045 0.9443 0.6684 0.7607 0.9118 0.6255 0.6218 0.8830 0.6212 0.4925
-0.60 0.30 MA1 0.7574 0.3649 0.4162 0.6622 0.3157 0.2889 0.6171 0.3072 0.2183 0.6043 0.3078 0.1500
0.70 -0.40 AR1 0.8664 0.5060 0.5487 0.7794 0.4335 0.3888 0.7324 0.4173 0.2955 0.7112 0.4097 0.2046
0.70 -0.90 AR1 0.9999 0.9746 0.9998 0.9996 0.9004 0.9982 0.9971 0.8550 0.9910 0.9906 0.8363 0.9651
0.50 -0.70 MA1 0.9770 0.8439 0.8202 0.9576 0.7719 0.6728 0.9367 0.7354 0.5514 0.9200 0.7242 0.4345
-0.50 0.70 MA1 0.9822 0.8655 0.8409 0.9661 0.7966 0.6968 0.9525 0.7575 0.5799 0.9411 0.7405 0.4667
0.40 -0.60 0.30 AR1 0.9951 0.7825 0.9940 0.9777 0.6613 0.9621 0.9517 0.6156 0.8949 0.9268 0.6015 0.7961
0.70 0.70 -0.15 AR1 0.4553 0.1666 0.1412 0.4220 0.1667 0.1076 0.4193 0.1752 0.0817 0.4314 0.1862 0.0527
0.40 -0.60 -0.30 ARMA11 0.3526 0.1529 0.1547 0.3501 0.1461 0.1128 0.3607 0.1543 0.0808 0.3824 0.1585 0.0492
0.70 -0.70 0.20 ARMA11 0.1124 0.0487 0.0504 0.1482 0.0576 0.0434 0.1801 0.0722 0.0353 0.2165 0.0788 0.0203
0.30 0.80 -0.50 MA1 0.9124 0.5729 0.6921 0.8442 0.4796 0.5112 0.8053 0.4602 0.3866 0.7695 0.4554 0.2812
0.80 -0.50 0.30 MA1 0.9955 0.9727 0.9470 0.9909 0.9496 0.8831 0.9885 0.9399 0.8117 0.9853 0.9345 0.7337
0.70 0.20 0.50 AR1 0.9163 0.7106 0.7010 0.8641 0.6173 0.5472 0.8254 0.5895 0.4326 0.8016 0.5853 0.3299
0.70 -0.20 -0.50 AR1 0.9996 0.9546 0.9884 0.9963 0.8892 0.9383 0.9902 0.8444 0.8620 0.9785 0.8251 0.7694
1.20 -0.50 -0.90 ARMA11 0.7410 0.3288 0.6259 0.7278 0.2863 0.4692 0.7056 0.2824 0.3478 0.6718 0.2866 0.2418
0.30 -0.20 -0.70 ARMA11 0.2952 0.1369 0.1140 0.2924 0.1334 0.0829 0.3034 0.1431 0.0624 0.3349 0.1520 0.0401
1.20 -0.50 0.90 MA1 0.8162 0.4341 0.6728 0.7683 0.3688 0.5099 0.7346 0.3532 0.3766 0.6997 0.3512 0.2659
20
Lampiran 8 Lanjutan
Model Pembangkit Model Pem-Fit
lag 12 lag 24 lag 36 lag 48
φ1 φ2 θ1 θ2 Dm QLB QMT Dm QLB QMT Dm QLB QMT Dm QLB QMT
0.90 -0.40 1.20 -0.30 AR1 0.9827 0.6460 0.9572 0.9498 0.5349 0.8408 0.9146 0.4995 0.7053 0.8724 0.4975 0.5729
0.90 -0.40 1.20 -0.30 ARMA11 0.6259 0.3714 0.3373 0.5993 0.3200 0.2292 0.5815 0.3112 0.1655 0.5750 0.3117 0.1118
0.30 -0.70 -0.20 -0.30 ARMA11 0.9833 0.9193 0.8922 0.9780 0.8682 0.7819 0.9687 0.8362 0.6768 0.9588 0.8227 0.5696
0.90 -0.40 1.20 -0.30 MA1 0.9781 0.7176 0.9019 0.9445 0.5953 0.7608 0.9105 0.5538 0.6148 0.8764 0.5471 0.4824
Keterangan : n=100, α = 0.05
Lampiran 9 Persentase series (deret 1, deret 2, … deret 10000) dengan sisaan berkorelasi pada beberapa model ARMA (p,q)ketika di-fit dengan model AR(1), MA(1) dan ARMA(1,1) dengan uji Dm, QLB dan QMT
Model Pembangkit Model Pem-Fit
lag 6 lag 12 lag 18 lag24
φ1 φ2 θ1 θ2 Dm QLB QMT Dm QLB QMT Dm QLB QMT Dm QLB QMT
0.50 ARMA11 0.0202 0.0214 0.0299 0.1098 0.0281 0.0276 0.1505 0.0267 0.0177 0.1271 0.0258 0.0224
0.50 MA1 0.2015 0.0773 0.0863 0.2439 0.0914 0.0629 0.2739 0.0985 0.0376 0.2257 0.0988 0.0402
0.80 MA1 0.6711 0.4412 0.3939 0.6516 0.4235 0.2804 0.6334 0.4593 0.1976 0.5657 0.4853 0.1744
0.10 0.30 AR1 0.2659 0.0900 0.1006 0.3070 0.1038 0.0698 0.3303 0.1054 0.0412 0.2699 0.1002 0.0448
1.20 -0.40 AR1 0.6380 0.3752 0.3349 0.6017 0.3540 0.2343 0.5769 0.3482 0.1611 0.4840 0.3386 0.1447
0.90 -0.30 ARMA11 0.0412 0.0410 0.0538 0.1496 0.0520 0.0404 0.1935 0.0477 0.0245 0.1570 0.0442 0.0289
-1.20 -0.80 ARMA11 0.6907 0.6850 0.6285 0.7983 0.6362 0.4899 0.7822 0.6370 0.3810 0.7191 0.6384 0.3470
1.10 -0.35 MA1 0.8171 0.6031 0.5891 0.7811 0.5544 0.4358 0.7397 0.5749 0.3264 0.6464 0.5944 0.2943
-0.50 AR1 0.2928 0.1228 0.1358 0.3147 0.1233 0.0878 0.3269 0.1260 0.0540 0.2720 0.1255 0.0579
-0.80 AR1 0.5671 0.2646 0.3991 0.5355 0.2596 0.2730 0.5124 0.2605 0.1760 0.4230 0.2525 0.1600
0.75 ARMA11 0.7891 0.5807 0.8374 0.8334 0.5022 0.6613 0.7669 0.5001 0.5030 0.6314 0.5031 0.4341
-0.60 0.30 AR1 0.6148 0.2704 0.4375 0.6013 0.2627 0.3125 0.5742 0.2616 0.2060 0.4581 0.2594 0.1817
1.10 -0.80 ARMA11 0.3385 0.2685 0.3763 0.5154 0.2480 0.2783 0.5127 0.2453 0.2023 0.4091 0.2402 0.1906
-0.60 -0.30 ARMA11 0.0483 0.0388 0.0500 0.1690 0.0516 0.0386 0.2163 0.0498 0.0255 0.1666 0.0456 0.0318
0.80 -0.50 MA1 0.5059 0.2372 0.3154 0.4901 0.2415 0.1988 0.4785 0.2404 0.1225 0.4010 0.2371 0.1167
-0.60 0.30 MA1 0.3014 0.1171 0.1610 0.3060 0.1277 0.1100 0.3210 0.1220 0.0679 0.2619 0.1223 0.0671
0.70 -0.40 AR1 0.4464 0.2229 0.2279 0.4248 0.2181 0.1517 0.4213 0.2210 0.0961 0.3469 0.2127 0.0884
0.70 -0.90 AR1 0.8498 0.4840 0.7618 0.7704 0.4485 0.5855 0.7230 0.4478 0.4433 0.5962 0.4425 0.3770
0.50 -0.70 MA1 0.6207 0.3602 0.2991 0.5783 0.3400 0.1982 0.5500 0.3605 0.1310 0.4765 0.3747 0.1178
-0.50 0.70 MA1 0.7506 0.4859 0.3979 0.7076 0.4387 0.2841 0.6765 0.4359 0.1928 0.5988 0.4442 0.1708
0.40 -0.60 0.30 AR1 0.6200 0.2976 0.5216 0.5848 0.2875 0.3711 0.5591 0.2859 0.2510 0.4452 0.2868 0.2131
21
Lampiran 9 Lanjutan
Model Pembangkit Model Pem-Fit
lag 6 lag 12 lag 18 lag24
φ1 φ2 θ1 θ2 Dm QLB QMT Dm QLB QMT Dm QLB QMT Dm QLB QMT
0.40 -0.60 -0.30 ARMA11 0.0575 0.0611 0.0703 0.1774 0.0685 0.0504 0.2209 0.0650 0.0311 0.1787 0.0619 0.0379
0.70 -0.70 0.20 ARMA11 0.0235 0.0322 0.0363 0.1071 0.0414 0.0281 0.1626 0.0409 0.0183 0.1399 0.0415 0.0225
0.30 0.80 -0.50 MA1 0.3534 0.1404 0.2024 0.3708 0.1535 0.1200 0.3892 0.1500 0.0735 0.3167 0.1507 0.0737
0.80 -0.50 0.30 MA1 0.7190 0.5102 0.4048 0.6846 0.4863 0.2911 0.6664 0.5137 0.2072 0.6067 0.5467 0.1818
0.70 0.20 0.50 AR1 0.2692 0.0923 0.0992 0.2879 0.0956 0.0702 0.3119 0.1165 0.0406 0.2627 0.1225 0.0419
0.70 -0.20 -0.50 AR1 0.2173 0.4920 0.5755 0.2530 0.4381 0.4130 0.2757 0.4406 0.2979 0.2268 0.4328 0.2607
1.20 -0.50 -0.90 ARMA11 0.0983 0.0700 0.1295 0.2821 0.0855 0.0994 0.3062 0.0798 0.0638 0.2252 0.0738 0.0669
0.30 -0.20 -0.70 ARMA11 0.1192 0.1109 0.1415 0.2476 0.1163 0.1018 0.2778 0.1181 0.0677 0.2343 0.1155 0.0669
1.20 -0.50 0.90 MA1 0.3072 0.1323 0.1748 0.3678 0.1338 0.1306 0.3754 0.1301 0.0820 0.2903 0.1233 0.0840
0.30 -0.20 -0.70 MA1 0.3127 0.1359 0.1298 0.3158 0.1397 0.0873 0.3210 0.1408 0.0562 0.2713 0.1427 0.0543
0.90 -0.40 1.20 -0.30 AR1 0.5422 0.2131 0.3602 0.5467 0.2038 0.2508 0.5078 0.2019 0.1586 0.3977 0.1939 0.1407
0.90 -0.40 1.20 -0.30 ARMA11 0.1616 0.1685 0.1489 0.3003 0.1633 0.1003 0.3298 0.1606 0.0656 0.2759 0.1589 0.0602
0.30 -0.70 -0.20 -0.30 ARMA11 0.4968 0.4540 0.4137 0.6196 0.4094 0.2790 0.5829 0.4034 0.1985 0.4695 0.4019 0.1787
0.90 -0.40 1.20 -0.30 MA1 0.4653 0.1716 0.2851 0.4572 0.1786 0.1959 0.4435 0.1726 0.1220 0.3483 0.1706 0.1126
22
Lampiran 10 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QLB pada N=100
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
12 24 36 48
Lag
P
e
rsen
ta
se
Model 1
Model 2
Model 3
Model 4
Model 5
Model 6
Model 7
Model 8
Model 9
Model 10
Model 11
Model 12
Model 13
Model 14
Model 15
Model 16
Model 17
Model 18
Model 19
Model 20
Model 21
Model 22
Model 23
Model 24
Model 25
Model 26
Model 27
Model 28
Model 29
Model 30
Model 31
Model 32
Model 33
Model 34
Model 35
23
Lampiran 11 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QMT pada N=100
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
12 24 36 48
Lag
P
e
rs
en
ta
se
Model 1
Model 2
Model 3
Model 4
Model 5
Model 6
Model 7
Model 8
Model 9
Model 10
Model 11
Model 12
Model 13
Model 14
Model 15
Model 16
Model 17
Model 18
Model 19
Model 20
Model 21
Model 22
Model 23
Model 24
Model 25
Model 26
Model 27
Model 28
Model 29
Model 30
Model 31
Model 32
Model 33
Model 34
Model 35
24
Lampiran 12 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji Dm pada N=100
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
12 24 36 48
Lag
P
e
rs
en
ta
se
Model 1
Model 2
Model 3
Model 4
Model 5
Model 6
Model 7
Model 8
Model 9
Model 10
Model 11
Model 12
Model 13
Model 14
Model 15
Model 16
Model 17
Model 18
Model 19
Model 20
Model 21
Model 22
Model 23
Model 24
Model 25
Model 26
Model 27
Model 28
Model 29
Model 30
Model 31
Model 32
Model 33
Model 34
Model 35
25
Lampiran 13 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QLB pada N=30
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
6 12 18 24
Lag
P
e
rs
en
ta
se
Model 1
Model 2
Model 3
Model 4
Model 5
Model 6
Model 7
Model 8
Model 9
Model 10
Model 11
Model 12
Model 13
Model 14
Model 15
Model 16
Model 17
Model 18
Model 19
Model 20
Model 21
Model 22
Model 23
Model 24
Model 25
Model 26
Model 27
Model 28
Model 29
Model 30
Model 31
Model 32
Model 33
Model 34
Model 35
26
Lampiran 14 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji QMT pada N=30
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
6 12 18 24
Lag
P
e
rs
en
ta
se
Model 1
Model 2
Model 3
Model 4
Model 5
Model 6
Model 7
Model 8
Model 9
Model 10
Model 11
Model 12
Model 13
Model 14
Model 15
Model 16
Model 17
Model 18
Model 19
Model 20
Model 21
Model 22
Model 23
Model 24
Model 25
Model 26
Model 27
Model 28
Model 29
Model 30
Model 31
Model 32
Model 33
Model 34
Model 35
27
Lampiran 15 Grafik Persentase Banyaknya Series yang Modelnya Dinyatakan Tidak Layak dengan Uji Dm pada N=30
0.0 0.1 0.2 0.3 0.4 0.5