DAFTAR PUSTAKA
[1] Mohammad, R. A,2015, membangun indonesia melalui pengembangan teknologi energi alternatif, dari :
http://writingcontesttotal.bisnis.com/artikel/read/20150320/404/413945/mem bangun-indonesia-melalui-pengembangan-teknologi-energi-alternatif [2] Wibowo, A. S, 2012, makalah energi angin menjadi energi listrik http://anangsetiyowibowo.blogspot.co.id/2012/04/makalah-energi-angin- menjadi-energi.html
[3] TunggaBhimadiKaryasa,2010,Dasar-dasargetaranmekanis.CV. Andi Offset
[4] Yefri Chan. UniversitasDarmaPersada. Diktat GetaranMekanik
[5] MarizkaLustiaDewi, Tahun 2010, Penelitian “ANALISA KINERJA TURBIN ANGIN POROS VERTIKAL DENGAN MODIFIKASI ROTOR SAVONIUS L UNTUK OPTIMASI KINERJA TURBIN” Mahasiswa F-MIPA UniversitasSebelasMaret Surakarta.
[6] Martinus, M.Sc, Tahun 2010, Penelitian
“PembuatandanStudiKelayakanEkonomi Prototype TurbinAnginTipe Helix SebagaiAlternatifPembangkitListrikdenganStudiKasus Daerah Bandar Lampung-Indonesia”. F-TeknikMesinUniversitas Lampung [7] M. Alexin Putra, Mulyadi, GanjarPribadi, TaufiqMawardinata, Tito
Santika. Thn 2011. Penelitian “UJI EXPERIMENTAL ROTOR HELICAL SAVONIUS DIBANDINGKAN DENGAN ROTOR SAVONIUS”.
MahasiswaFakultasTeknologiIndustriInstitutTeknologiNasional.
[8] AdityoPutranto (L0E 008 007), AndikaPrasetyo (L0E 008 014), AriefZatmiko U. (L0E 008 021). Tahun 2011. Penelitian “RANCANG BANGUN TURBIN ANGIN VERTIKAL UNTUK PENERANGAN
RUMAHTANGGA”.
MahasiswaFakultasTeknikUnuversitasDiponegoro.
[10] Mittal, Neeraj. 2001. Investigation of Performance Characteristics of a Novel VAWT. Thesis. UK: Departement of Mechanical Engineering University ofStrathclyde
[11] Dutta, Animesh. 2006. Basics of Wind Technology. Asian Institute of Technology, Thailand. 6 Juli 2006
[12] Daryanto, Y., 2007. Kajian Potensi Angin Untuk Pembangkit Listrik Tenaga Bayu. Balai PPTAGG - UPT-LAGG
[13] Mittal, Neeraj. 2001. Investigation of Performance Characteristics of a Novel VAWT. Thesis. UK: Departement of Mechanical Engineering University ofStrathclyde
[14] Dutta, Animesh. 2006. Basics of Wind Technology. Asian Institute of Technology, Thailand. 6 Juli 2006
[15] Fisika Jilid – I, Endarko, dkk
Diterbitkan oleh ; Direktorat Pembinaan Sekolah Menengah Kejuruan Direktorat Jenderal Manajemen Pendidikan Dasar dan Menengah Departemen Pendidikan Nasional, Tahun 2008
[16] ITS, Jurusan Teknik Mesin, Fakultas Teknologi Industri. Diktat Fundamentals of Vibration,
[17] Scheffer, C. dan Girdhar P. Practical Machinery Vibration Analysis and Predictive Maintenance. Netherlands, IDC Technologies. 2004.
[18]
[19]
[20]
Mohammed Hadi Ali Lecturer University of Mustansiriya. Experimental Comparison Study for Savonius Wind Turbine of Two & Three Blades At Low Wind Speed. International Journal of Modern Engineering Research (IJMER) www.ijmer.com Vol. 3, Issue. 5, Sep - Oct. 2013 pp-2978-2986 ISSN: 2249-6645
Robert K. Vierck, Analisis Getaran 190-191.Penerjemah ; DR. Dicky Rezady Munaf, MS. MSCE
BAB III
METODOLOGI PENELITIAN
3.1 Tempat dan Waktu Penelitian
Penelitian dilaksanakan sejak tanggal pengesahan usulan oleh pengelola program studi sampai dinyatakan selesai dan direncanakan berlangsung selama 2 s/d 6 bulan. Tempat pelaksanaan penelitian di Program Magister Teknik Mesin, Fakultas Teknik, Laboratorium Teknik Mesin Universitas Sumatera Utara.
Tabel 3.1 Jadwal Penelitian diletakkan dalam model instalasi sederhana wind tunnel skala laboratorium seperti terlihat pada Gambar 3.2.
Gambar 3.1. (1)Perangkat Wind Tunnel, (2)Turbin angin. 1
3.3 Prosedur Penelitian
5 variasi kecepatan angin (4, 4.5, 5, 5.5, & 6)
Kec. Putaran rotor (100 detik) Arus dan Tegangan (100
detik)
Analisa Data
Menghitung kec. Sudut, dan frekuensi Menghitung nilai perpindahan,
Penelitian ini dilakukan dengan menggunakan turbin angin savonius tipe rotor helix,seperti terlihat pada Gambar 3.3.
Gambar 3.3 Turbin angin savonius tipe “helix” 3.4 Bahan
Beberapa bahan dari pada komponen turbin angin savonius tipe rotor helix ini, anatara lain:
1. Dudukan lengan sudu.
Dudukan lengan sudu ke dua turbin angin berbentuk silinder berbahan besi dengan ketebalan 10 mm, dan diameter luarnya 20 mm serta diameter dalam 10 mm, seperti terlihat pada Gambar 3.4.
Gambar 3.4. Bentuk dudukan lengan sudu
2. Lengan sudu
Gambar 3.5. Lengan sudu
3. Sudu
Sudu kedua turbin angin berbahan pelat aluminium dengan ketebalan 0,3 mm, seperti yang diperlihatkan pada Gambar 3.6.
Gambar 3.6. Bahan pelat Aluminium untuk sudu
4. Poros
.
Gambar 3.7. Poros 5. Bantalan
Bearing (bantalan) adalah elemen mesin yang menumpu poros yang mempunyai beban, sehingga putaran atau gerakan bolak-baliknya dapat berlangsung secara halus, aman, dan mempunyai umur yang panjang. Bearing harus cukup kokoh untuk memungkinkan poros serta elemen mesin lainnya bekerja dengan baik, seperti pada Gambar 3.8.
.
Gambar 3.8. Bantalan
6. Transmisi Daya
Dalam penelitian ini roda gigi digunakan untuk mentransmisikan daya dan
putaran. Roda gigi memiliki gigi di sekelilingnya, sehingga penerusan daya
dilakukan oleh gigi-gigi kedua roda yang saling berkait. Diameter luar roda
gigi pada poros 120 mm, dan diameter luar roda gigi pada poros motor DC 10
(a) (b)
Gambar 3.9. (a) Roda Gigi pada Poros Turbin dan (b) Pada Poros motos DC
7. Generator Listrik
Generator listrik yang akan digunakan dalam penelitian ini adalah 12V 100mA, seperti Gambar 3.10.
Gambar 3.10. Generator Listrik
8. Bola lampu dan wayar
Bola lampu yang akan digunakan adalah jenis bola lampu LED seperti pada Gambar 3.11.
3.5 Peralatan
Peralatan yang akan digunakan dalam pelaksanaan penelitian ini antara lain: 1. Wind Tunnel, dengan menggunakan wind tunnel maka relative dapat di
setting kecepatan angin dan kestabilannya sesuai dengan kebutuhan penelitian, seperti pada Gambar 3.12.
Gambar 3.12. Perangkat Wind Tunnel.
(1).Compressor,(2).Test section, (3).Diffuser, (4).Kain penghubung, (5).Drive section
2. Inverter, inverter adalah salah satu alat untuk mengubah arus AC ke DC untuk me-nyupllay listrik ke dinamo motor dengan arus DC, jadi alat ini aslinya mempunyai multi fungsi, merubah AC ke DC kemudian mengeluarkannya dengan arus AC kembali, inverter diperlihatkan pada Gambar 3.13.
Gambar 3.13. Inverter
1
3 4 5
3. Vibrometer, Vibrometer VQ – 400 - A, Alat ini digunakan untuk mengukur kecepatan permukaan getaran, juga dapat digunakan untuk mendapatkan waktu putar sehingga dapat diketahui kecepatan putar suatu benda atau bahan uji. Seperti pada Gambar 3.14.
Gambar 3.14. Alat Vibrometer
4. Tachometer, Tachometer adalah alat untuk mengukur kecepatan putaran yang dikopel langsung dengan poros. Seperti pada Gambar 3.15.
Spesifikasi Digital Photo Contact Tachometer sebagai berikut: Name : Digital Photo Contact Tachometer
Display : Photo Tach (5 to 99,999 rpm) Contact Tach (0,5 to 19,999 rpm) Resulotion : Photo Tach/Contact Tach
0,1 rpm (0,5 to 999,9 rpm) 1 rpm (over 1,000 rpm) Accuracy : ± (0,05 % + 1 Digit)
Sampling Time : Photo Tach (1 sec over 60 rpm) Contact Tach (1 sec over 6 rpm) Battery : 4 x 1,5 V AA (UM-3) Battery Size : 215 x 65 x 38 mm
Weight : 300 g (0,66 lb)/including Battery
5. Multi tester digital. Hasil ukur yang ditampilkan pada multitester digital merupakan hasil yang telah sesuai, sehingga tidak perlu dilakukan lagi perhitungan antara hasil ukur dan batas ukur.
Fungsi Multi tester yang dimiliki setiap multi tester ada beberapa macam tergantung tipe dan merk multi tester. Akan tetapi pada umumnya setiap multitester memiliki 3 fungsi ukur utama yaitu sebagai alat ukur arus, tegangan dan resistansi seperti yang diperlihatkan pada Gambar 3.16.
6. Anemometer,fungsi anemometer yaitu sebagai perangkat atau alat yang digunakan untuk mengukur kecepatan angin. Dengan anemometer kita dapat memperkirakaan cuaca pada hari itu. Selain itu anemometer juga dapat difungsikan sebagai alat pendeteksi cuaca buruk seperi angin topan ataupun badai. Pada dasarnya anemometer adalah alat untuk mengukur kecepatan udara atau kecepatan gas dalam fenomena terjadinya hembusan angin, contohnya untuk mengkur aliran udara di dalam saluran, atau juga pengukuran arus terbatasi, seperti angin atmosfer. Untuk menentukan kecepatan, anemometer mendeteksi perubahan di beberapa sifat fisik dari fluida atau efek fluida pada alat mekanis dimasukkan ke dalam aliran seperti pada Gambar 3.17.
7.
Gambar 3.17. Alat Anemometer
Gambar 3.18. Alat Labjack
9. Lavtop (PC), PC laptop, digunakan untuk menampilkan dan menyimpan hasil serta pengolahan data yang di dapat dari pengukuran getaran.
10. Alat tulis dan kamera digital. Alat tulis digunakan untuk mencatat data hasil penelitian dan kamera digital akan digunakan untuk mengabadikan proses eksperimental atau sebagai dokumentasi.
3.6 Metodologi Penelitian
Metode yang dilakukan dalam penelitian ini adalah metode eksperimental. Kegiatannya meliputi:
1. Pengambilan data 5 variasi, masing-masing variasi kecepatan angin akan dilakukan pencatatan 5 kali yaitu pada selang waktu 20, 40, 60, 80, 100 detik, hal ini guna memperoleh rata getaran putaran poros (rpm), rata-rata tegangan (V), dan rata-rata-rata-rata arus (A).
2. Pengambilan data dilakukan dengan melakukan 5 variasi putaran electro motor pada wind tunnel guna memperoleh 5 variasi kecepatan angin pada kedua tipe turbin tersebut, dan penyetelan putaran menggunakan alat inverter yang ada pada wind tunnel.
Tabel 3.2. Lembar kerja pengambilan data Turbin angin Savonius tipe “Helix” pada kecepatan angin = 4 m/s
No. Test-1
Turbin angin Savonius tipe “Helix” pada kecepatan angin = 4,5 m/s No. Test-2
Dan seterusnya sampai test-5 pada kecepatan angin 6 m/s, hal yang sama dilakukan pada turbin angin Savonius tipe “Helix”.
3.7 Set Up Alat
3.7.1. Set up alat uji wind tunnel
Perlu dilakukan set up alat uji wind tunnel. Berikut ini langkah –langkah set up yang dilakukan :
1. Periksa kondisi wind tunnel hingga siap untuk pengujian.
2. Periksa kondisi elektro motor yang ada di drive suction pada wind tunnel hingga siap untuk berputar.
4. Sambungkan arus listrik ke inverter hingga lampu merah aktif menyala.
3.7.2. Set up alat ukur penelitian
Perlu dilakukan set up alat ukur penelitian, berikut ini langkah–langkah set up yang dilakukan:
1. Letakkan turbin angin savonius pada test suction wind tunnel.
Gambar 3.19. turbin angin savonius pada test suction wind tunnel.
2. Pasang kabel pada generator ke lampu LED.
3. Pasang kabel multitester.
Gambar 3.21. Pemasangan kabel multitester.
4. Setel posisi anemometer.
Gambar 3.22. Posisi anemometer
5. Setel posisi vibrometer laser pada posisi yang tepat (lampu laser berwarna merah tepat kena ujung poros bagian atas turbin agin, hal ini untuk pengambilan data.
6. Pastikan vibrometer terhubung dengan labjack dan laptop, hal ini untuk melihat grafik.
Gambar 3.24. Memastikan vibrometer berfungsi
7. Atur posisi untuk pengambilan kecepatan putar poros turbin angin dengan menggunakan tachometer.
Gambar 3.25. Posisi tachometer
8. Jalankan Wind tunnel melalui inverter. 9. Siapkan alat tulis dan kamera digital.
Gambar 3.26. Chanel penyetelan
11. Catat data kecepatan angin, arus, tegangan listrik, suhu udara, kecepatan poros turbin, tekanan udara dan juga getaran yang terjadi di poros turbin.
BAB IV
HASIL DAN PEMBAHASAN
Hasil pengukuran yang diperoleh berupa kecepatan relatif. Instrumen pengujian getaran dalam penelitian ini dengan menggunakan alat ukur vibrometer.
4.1.Amplitudo getaran pada Turbin Angin Savonius
Pencatatan variabel penelitian dilakukan pada 5 variasi kecepatan angin dan disetiap rentang waktu 20 detik dengan menggunakan Laser vibrometer, dan dilakukakan vibration source seperti diperlihatkan pada Gambar 4.1.
Gambar 4.1. Vibration source Tipe rotor Helix
4.1.1. Pengambilan data pada kecepatan angin 4 m/s
Setelah dilakukan pengukuran pada kecepatan angin 4 m/s selama 100 detik didapat hasil putaran, Arus dan tegangan yang dihasilkan setiap 20 detik dapat dilihat pada tabel 4.1 berikut :
Tabel 4.1 Data kecepatan angin 4 m/s
t(s) Rpm Arus(mA) Tegangan (V)
20 19 0,6 2,20
60 20 0,7 2,29
80 22 0,8 2,64
100 19 0,6 2,21
Rata-rata 20,40 0,70 2,40
Dari tabel 4.1 rata-rata putaran per menit adalah 20,40 rpm, rata arus yang dihasilkan 0,7 mA dan tegangan rata-rata 20,40 Amper.Dari putaran poros turbin angin maka dapat diperoleh kecepatan sudut, frekuensi dan perioda sebagai berikut :
Kecepatan sudut dihitung sebagai berikut:
x n =
x 20,40 = 2,1352 rps Frekuensi rotor dihitung sebagai berikut:
f =
Velocity pada detik ke-1 didapat dari data :
(pada lampiran 1)
Amplitudo di hitung sebagai berikut :
= -0,2775 mm
Perhitungan diatas diteruskan untuk setiap nilai amplitudo pada data 100 detik. Untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan pada lampiran 1, sehingga di peroleh amplitudo rata-rata:
Gambar 4.2. Velocity getaran pada kecepatan angin 4 m/s
Dari grafik amplitudo velocity diatas, dapat dilihat bahwa pada poros turbin angin savonius rotor tipe Helix mengalami kecepatan getaran pada puncak atas sebesar 0,5273 mm/s. Dimana berdasarkan ISO 10816-3 sebagai indikator tingkat vibrasi menyatakan bahwa getaran dari poros turbin angin savonius rotor tipe Helix dalam batas toleransi dan hanya dapat dioperasikan dalam waktu yang terbatas. Terlihat pada Gambar 4.2.
Displacement dihitung sebagai berikut :
(Pada lampiran 1)
Gambar 4.3 Displacement getaran pada kecepatan angin 4 m/s
Dari grafik amplitudo displacement diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 64 sebesar 0,2408 mm dan puncak bawah terjadi pada detik ke 89 sebesar -0,2407 mm. Terlihat pada Gambar 4.3.
Acceleration dihitung sebagai berikut:
(Pada lampiran 1)
Gambar 4.4 Acceleration getaran pada kecepatan angin 4 m/s
Grafik amplitudo acceleration diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor Helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 64 sebesar 1,0978 mm/s2 dan puncak bawah terjadi pada detik ke 39 sebesar -1,0975 mm/s2. Terlihat pada Gambar 4.4.
Setelah perhitungan pada kecepatan angin 4 m/s selama 100 detik, maka dapat kita lihat grafik perbandingan amplitudo getaran serta puncak atas dan puncak bawah dari masing-masing getaran, seperti terlihat pada Table 4.2.dibawah ini.
Tabel 4.2. Indikasi puncak amplitudo pada Kecepatan angin 4 m/s No Indikasi Amplitudo
Pada 100 detik
Tipe Helix
Peak atas Peak bawah
1. PuncakPerpindahan Terjadi pada
0,2408 Detik Ke-64
2 Puncak Kecepatan
4.1.2. Pengambilan data pada kecepatan angin 4,5 m/s
Pada kecepatan angin 4,5 m/s selama 100 detik didapat putaran, Arus dan tegangan yang dihasilkan setiap 20 detik dapat dilihat pada tabel 4.3 berikut :
Tabel 4.3 Data kecepatan angin 4,5 m/s
t(s) Rpm Arus(mA) Tegangan (V)
Kecepatan sudut dihitung sebagai berikut :
x n =
x 23,20 = 2,4283 rps Frekuensi rotor dihitung sebagai berikut :
f =
=
= 0,38 Hz Perioda rotor dihitung sebagai berikut :: T = =
Velocity pada detik ke-1 didapat dari data :
(pada lampiran 2)
Amplitudo di hitung sebagai berikut :
=
= -0,1896 mm
Perhitungan diatas diteruskan untuk setiap nilai amplitudo pada data 100 detik. Untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan pada lampiran 2, sehingga di peroleh amplitudo rata-rata:
A0 = - 0,1683mm (pada lampiran 2)
Gambar 4.5. Velocity getaran pada kecepatan angin 4,5 m/s
Helix dalam batas toleransi dan hanya dapat dioperasikan dalam waktu yang terbatas. Terlihat pada Gambar 4.5.
Displacement dihitung sebagai berikut :
(Pada lampiran 2)
Perhitungan displacement diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan pada hasil dalam bentuk grafik pada gambar 4.6 berikut :
Gambar4.6. Displacement getaran pada kecepatan angin 4,5 m/s
Dari grafik amplitudo displacement diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 33 sebesar 0,1683 mm dan puncak bawah terjadi pada detik ke 11 sebesar -0,1683 mm. Terlihat pada Gambar 4.6.
Acceleration dihitung sebagai berikut
Perhitungan Acceleration diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan dalam bentuk grafik pada gambar 4.7. berikut :
Gambar 4.7. Acceleration getaran pada kecepatan angin 4,5 m/s
Grafik amplitudo acceleration diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor Helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 33 sebesar 0,9921 mm/s2 dan puncak bawah terjadi pada detik ke 11 sebesar -0,9924 mm/s2. Terlihat pada Gambar 4.7.
Setelah perhitungan pada kecepatan angin 4,5 m/s selama 100 detik, maka dapat kita lihat perbandingan grafik amplitudo getaran pada Table 4.4 puncak atas dan puncak bawah dari masing-masing getaran, seperti terlihat dibawah ini.
2 Puncak Kecepatan
4.1.3. Pengambilan data pada kecepatan angin 5 m/s
Setelah dilakukan pengukuran pada kecepatan angin 5 m/s selama 100 detik didapat putaran, Arus dan tegangan yang dihasilkan setiap 20 detik dapat dilihat pada tabel 4.5 berikut :
Tabel 4.5. Data kecepatan angin 5 m/s
t(s) Rpm Arus(mA) Tegangan (V)
Kecepatan sudut dihitung sebagai berikut :
x n =
x 28,60 = 2,9935 rps Frekuensi rotor dihitung sebagai berikut ::
f = =
= 0,43 Hz Perioda rotor dihitung sebagai berikut ::
T = =
Velocity pada detik ke-1 didapat dari data :
(pada lampiran 3)
Amplitudo di hitung sebagai berikut :
=
= -0,1710 mm
Perhitungan diatas diteruskan untuk setiapnilai amplitudo pada data 100 detik. Untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan pada lampiran 3, sehingga di peroleh amplitudo rata-rata :
A0 = - 0,2374mm (pada lampiran 3)
Gambar 4.8. Velocity getaran pada kecepatan angin 5 m/s
Helix dalam batas toleransi dan hanya dapat dioperasikan dalam waktu yang terbatas. Terlihat pada Gambar 4.8.
Displacement dihitung sebagai berikut :
(Pada lampiran 3)
Perhitungan displacement diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan pada hasil dalam bentuk grafik pada gambar 4.9 berikut : Amplitudo di hitung sebagai berikut :
Gambar 4.9. Displaciment getaran pada kecepatan angin 5 m/s
Dari grafik amplitudo displacement diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 96 sebesar 0,2366 mm dan puncak bawah terjadi pada detik ke 53 sebesar -0,2374 mm. Terlihat pada Gambar 4.9.
Acceleration dihitung sebagai berikut
Perhitungan Acceleration diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan dalam bentuk grafik pada Gambar 4.10. berikut :
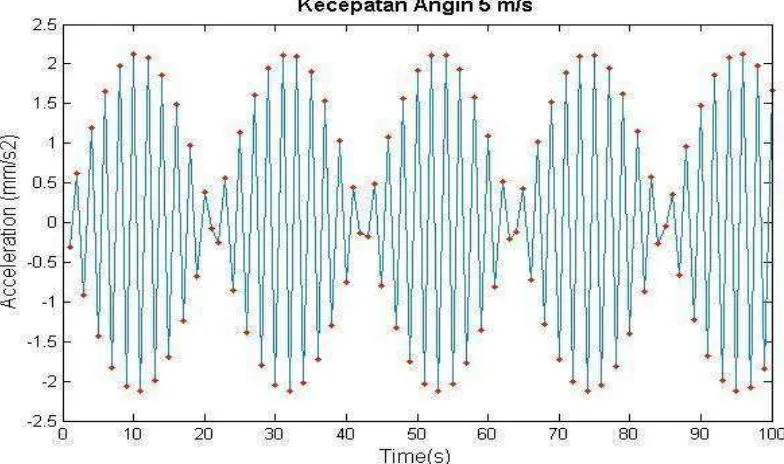
Gambar 4.10. Acceleration getaran pada kecepatan angin 5 m/s
Grafik amplitudo acceleration diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor Helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 11 sebesar 2,1206 mm/s2 dan puncak bawah terjadi pada detik ke 53 sebesar -2,1273 mm/s2. Terlihat pada Gambar 4.10.
Setelah perhitungan pada kecepatan angin 5 m/s selama 100 detik, maka dapat kita lihat perbandingan grafik amplitudo getaran pada table 4.6 serta puncak atas dan puncak bawah dari masing-masing getaran, seperti terlihat dibawah ini:
2 Puncak Kecepatan
4.1.4. Pengambilan data pada kecepatan angin 5,5 m/s
Setelah dilakukan pengukuran pada kecepatan angin 5,5 m/s selama 100 detik didapat putaran, Arus dan tegangan yang dihasilkan setiap 20 detik dapat dilihat pada tabel 4.7 berikut :
Tabel 4.7. Data kecepatan angin 5,5 m/s
t(s) Rpm Arus(mA) Tegangan (V)
Kecepatan sudut dihitung sebagai berikut :
x n =
x 32 = 3.4331rps Frekuensi rotor dihitung sebagai berikut :
f = =
= 0,55 Hz Perioda rotor dihitung sebagai berikut ::
T = =
Velocity pada detik ke-1 didapat dari data :
(pada lampiran 4)
Amplitudo di hitung sebagai berikut :
=
= -0,0820 mm
Perhitungan diatas diteruskan untuk setiapnilai amplitudo pada data 100 detik. Untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan pada lampiran 4, sehingga di peroleh amplitudo rata-rata :
A0 = 0,0963 mm (pada lampiran 4)
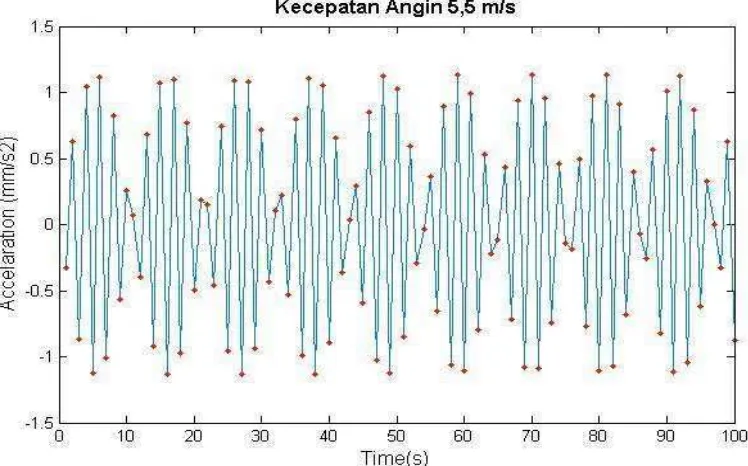
Gambar 4.11. Velocity kecepatan angin 5,5 m/s
Helix dalam batas toleransi dan hanya dapat dioperasikan dalam waktu yang terbatas. Terlihat pada Gambar 4.11.
Displacement dihitung sebagai berikut :
(Pada lampiran 4)
Perhitungan displacement diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel dan diperlihatkan pada hasil dalam bentuk grafik pada gambar 4.12 berikut
Gambar 4.12. Displacement getaran pada kecepatan angin 5,5 m/s
Dari grafik amplitudo displacementdiatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 70 sebesar 0,0963 mm dan puncak bawah terjadi pada detik ke 23 sebesar -0,0963 mm. Terlihat pada Gambar 4.12.
Acceleration dihitung sebagai berikut
Perhitungan Acceleration diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan dalam bentuk grafik pada gambar 4.13. berikut :
Gambar 4.13. Acceleration getaran pada kecepatan angin 5,5 m/s
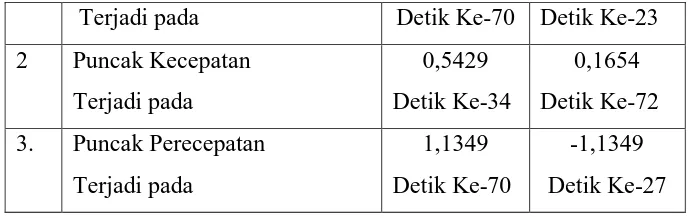
Grafik amplitudo acceleration diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor Helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 70 sebesar 1,1349 mm/s2 dan puncak bawah terjadi pada detik ke 27 sebesar -1,1349 mm/s2. Terlihat pada Gambar 4.13.
Setelah perhitungan pada kecepatan angin 5,5 m/s selama 100 detik, maka dapat kita lihat perbandingan grafik amplitudo getaran pada table 4.8 berupapuncak atas dan puncak bawah dari masing-masing getaran, seperti terlihat dibawah ini.
Tabel 4.8. Indikasi puncak amplitude pada kecepatan angin 5,5 m/s
No Indikasi Amplitudo Pada 100 detik
Tipe Helix
Peak atas Peak bawah
Terjadi pada Detik Ke-70 Detik Ke-23
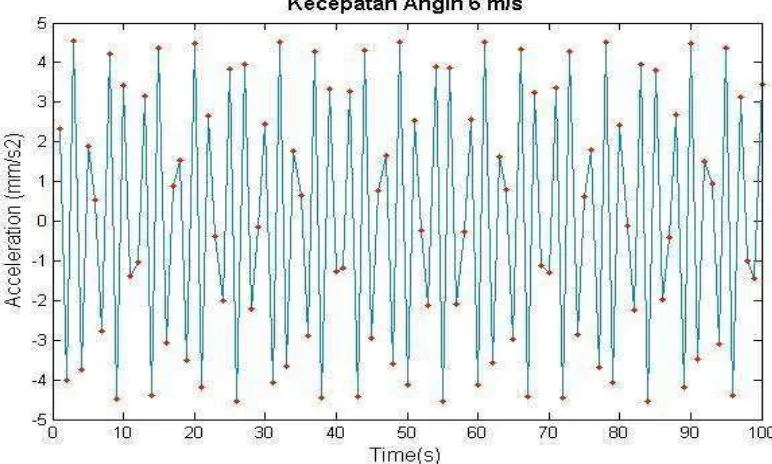
4.1.5. Pengambilan data pada kecepatan angin 6 m/s
Setelah dilakukan pengukuran pada kecepatan angin 6 m/s selama 100 detik didapat putaran, Arus dan tegangan yang dihasilkan setiap 20 detik dapat dilihat pada tabel 4.9 berikut :
Tabel 4.9. Data kecepatan angin 6 m/s
t(s) Rpm Arus(mA) Tegangan (V)
Dari tabel 4.9 rata-rata putaran per menit adalah 20,40 rpm, rata arus yang dihasilkan 0,7 mA dan tegangan rata-rata 2,40 Amper.Dari putaran poros turbin angin maka dapat diperoleh :
Kecepatan sudut dihitung sebagai berikut :
x n =
Frekuensi rotor dihitung sebagai berikut : f =
=
= 0,59 Hz Perioda rotor dihitung sebagai berikut ::
T = =
=1,70s
Velocity pada detik ke-1 didapat dari data :
(pada lampiran 5)
Amplitudo di hitung sebagai berikut :
=
= -0,0788 mm
Perhitungan diatas diteruskan untuk setiapnilai amplitudo pada data 100 detik. Untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan pada lampiran 5, sehingga di peroleh amplitudo rata-rata :
A0 = 0,3343 mm (pada lampiran 5)
Dari grafik amplitudo velocity diatas, dapat dilihat bahwa pada poros turbin angin savonius rotor tipe Helix mengalami kecepatan getaran pada puncak atas sebesar 0,5279 mm/s. Dimana berdasarkan ISO 10816-3 sebagai indikator tingkat vibrasi menyatakan bahwa getaran dari poros turbin angin savonius rotor tipe Helix dalam batas toleransi dan hanya dapat dioperasikan dalam waktu yang terbatas. Terlihat pada Gambar 4.14.
Displacement dihitung sebagai berikut :
(Pada lampiran 5)
Perhitungan displacement diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan pada hasil dalam bentuk grafik pada gambar 4.15 berikut
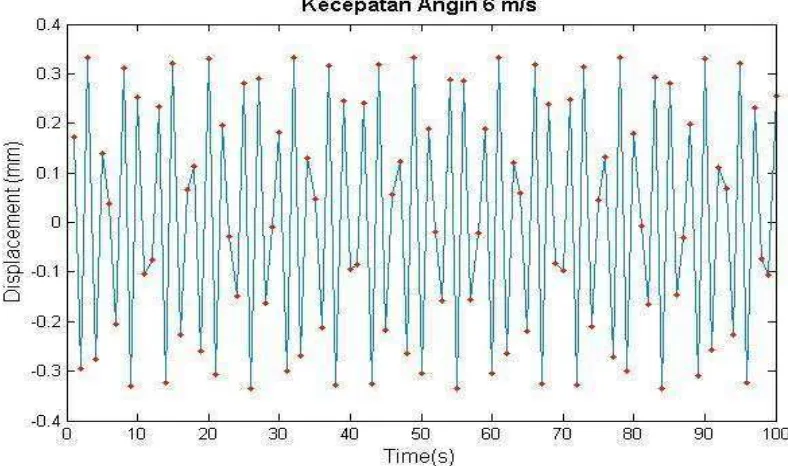
Gambar 4.15. Displacement getaran pada kecepatan angin 6 m/s
puncak bawah terjadi pada detik ke 55 sebesar -0,3343 mm/s2. Terlihat pada Gambar 4.15.
Acceleration dihitung sebagai berikut
(Pada lampiran 5)
Perhitungan Acceleration diatas diteruskan pada data 100 detik, dan untuk mempercepat penghitungan dilakukan dengan menggunakan program microsoft excel yang diperlihatkan dalam bentuk grafik pada gambar 4.16. berikut :
Gambar 4.16. Acceleration getaran pada kecepatan angin 6 m/s
Grafik amplitudo acceleration diatas, dapat dilihat bahwa pada poros turbin savonius tipe rotor Helix mengalami perpindahan yang cukup stabil. Dengan perpindahan puncak atas pada detik ke 3 sebesar 4,5304 mm/s2 dan puncak bawah terjadi pada detik ke 55 sebesar -4,3078 mm/s2. Terlihat pada Gambar 4.16.
berupapuncak atas dan puncak bawah dari masing-masing getaran, seperti terlihat dibawah ini
Tabel 4.10 Indikasi Puncak amplitude pada kecepatan angin 6 m/s
No Indikasi Amplitudo
4.2.Hubungan variasi puncak amplitudo dengan variasi kecepatan angin
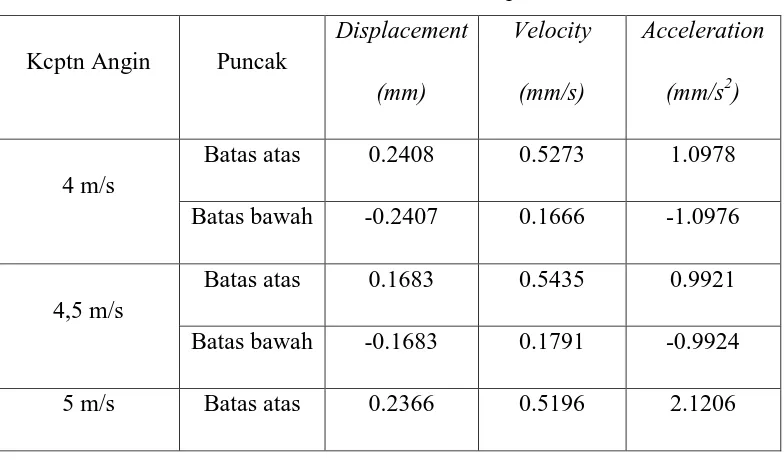
Akibat dari variasi kecepatan angin maka mengakibatkan terjadinya variasi pada puncak amplitudo. Tabel 4.11. memperlihatkan hasil perhitungan yang telah dilakukan dan diperoleh masing-masing puncak atas serta puncak bawah getaran pada displacement, velocity, dan pada Acceleration.
Batas bawah -0.2374 0.1594 -2.1273 Displacemen, yang terjadi pada Acceleration, dan yang terjadi pada velocity pada turbin angin savonius tipe “Helix”.
Dari hasil pengukuran, displacement getaran Turbin angin Savanius tipe rotor helix pada 5 (lima) vareasi kecepatan angin amplitude displacement cenderung stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 6 m/s dan mempunyai amplitude sebesar 0,3338 mm. Untuk puncak bawah terjadi pada kecepatan angin 6 m/s dan mempunya nilai amplitudo sebesar -0.3343 mm. Velocity getaran Turbin angin Savanius tipe rotor helix pada 5 (lima) vareasi kecepatan angin mempunyai amplitude velocity relative stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 4,5 m/s dan amplitude sebesar 0.5435 cm/s. Untuk puncak bawah terjadi pada kecepatan angin 4,5 m/s dan mempunya nilai amplitudo0.1791 cm/sAcceleration getaran Turbin angin Savanius tipe rotor helix pada 5 (lima) vareasi kecepatan angin mempunyai amplitude acceleration relative stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 6 m/s dan amplitude sebesar 4.5304 cm²/s. Untuk puncak bawah terjadi pada kecepatan angin 6 m/s dan mempunya nilai amplitudo-4.5378 cm/s.
4.3. Data Hasil Fast Fourier Transform
respon yang diukur oleh vibrometer. Setiap respon yang tercatat oleh vibrometer merupakan respon sejarah waktu karena itu output yang tercatat pada tiap channel akan dilakukan FFT untuk mengubahnya menjadi frekuensi domain. Berikut merupakan data hasil hasil FFTnya.
4.3.1. FFT pada kecepatan angin 4 m/s
Berdasarkan fungsi karakter perpindahan, dengan bantuan softwareMatlab R2012a maka frekuensi dapat digambarkan melalui FFT perpindahan partikel yang bergetar. Perpindahan getaran pada displacementuntuk turbin angin savonius tipe helix pada kecepatan angin 4 m/s dapat dilihat Gambar 4.17.di bawah.
Gambar 4.17. Hasil FFT poros turbin pada displacement getaran kecepatan angin 4 m/s
Dari hasil FFT poros turbin angin savonius tipe rotor helix pada dicplacement kecepatan angin 4 m/s diindikasikan mengalami gejala misalignment dikarenakan pada getaran dari grafik FFT yang dihasilkan terdapat getaran yang lebih besar dari keadaan normal 2 x RPM terlihat pada Gambar 4.17. diatas.
Frekuensi poros turbin hasil FFT pada velocity untuk turbin angin savonius tipe helix pada kecepatan angin 4 m/s dapat dilihat pada Gambar 4.18. dibawah.
Gambar 4.18. Hasil FFT poros turbin pada velocity getaran kecepatan angin 4 m/s
Dari hasil FFT poros turbin angin savonius tipe rotor helix pada velocity kecepatan angin 4 m/s diindikasikan mengalami gejala misalignment dikarenakan pada getaran dari grafik FFT yang dihasilkan terdapat getaran yang lebih besar dari keadaan normal 2 x RPM terlihat pada Gambar 4.18. diatas.
Berdasarkan fungsi karakter perpindahan, dengan bantuan software Matlab R2012a maka frekuensi dapat digambarkan melalui FFT perpindahan partikel yang bergetar. Perpindahan getaran pada acceleration untuk turbin angin savonius tipe helix pada kecepatan angin 4 m/s.
Gambar 4.19. Hasil FFT poros turbin pada acceleration getaran kecepatan angin 4 m/s
Dari hasil FFT poros turbin angin savonius tipe rotor helix pada acceleration kecepatan angin 4 m/s diindikasikan mengalami gejala misalignment dikarenakan pada getaran dari grafik FFT yang dihasilkan terdapat getaran yang lebih besar dari keadaan normal 2 x RPM terlihat pada Gambar 4.19. diatas.
4.3.2. FFT pada kecepatan angin 4,5 m/s
Gambar 4.20. Hasil FFT poros turbin angin pada displacement getaran kecepatan angin 4,5 m/s
Frekuensi poros turbin hasil FFT pada velocity untuk turbin angin savonius tipe helix pada kecepatan angin 4,5 m/s.
Gambar 4.21. Hasil FFT poros turbin angin pada velocitygetaran kecepatan angin 4,5 m/s
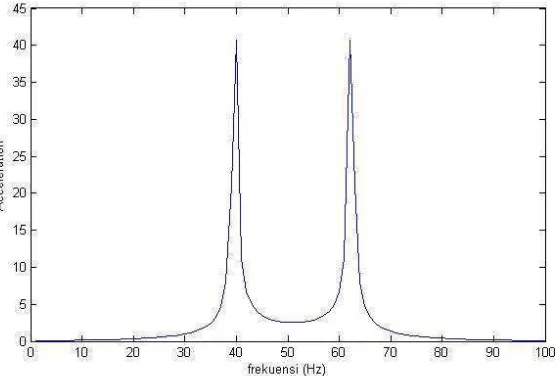
Gambar 4.22. Hasil FFT poros turbin angin pada accelerationgetaran kecepatan angin 4,5 m/s
4.3.3. FFT pada kecepatan angin 5 m/s
Berdasarkan fungsi karakter perpindahan, dengan bantuan software Matlab R2012a maka frekuensi dapat digambarkan melalui FFT perpindahan partikel yang bergetar. Perpindahan getaran pada displacementuntuk turbin angin savonius tipe helix pada kecepatan angin 5 m/s dapat dilihat Gambar 4.23. di bawah.
Frekuensi poros turbin hasil FFT pada velocity untuk turbin angin savonius tipe helix pada kecepatan angin 4,5 m/s.
Gambar 4.24. Hasil FFT poros turbin angin pada velocity getaran kecepatan angin 5 m/s
Frekuensi poros turbin hasil FFT pada acceleration untuk turbin angin savonius tipe helix pada kecepatan angin 5 m/s.
4.3.4. FFT pada kecepatan angin 5,5 m/s
Berdasarkan fungsi karakter perpindahan, dengan bantuan software Matlab R2012a maka frekuensi dapat digambarkan melalui FFT perpindahan partikel yang bergetar. Perpindahan getaran pada displacementuntuk turbin angin savonius tipe helix pada kecepatan angin 5,5 m/s dapat dilihat Gambar 4.26.di bawah.
Gambar 4.26. Hasil FFT poros turbin angin dicplacement getaran pada kecepatan angin 5,5 m/s
Frekuensi poros turbin hasil FFT pada velocity untuk turbin angin savonius tipe helix pada kecepatan angin 5,5 m/s.
Frekuensi poros turbin hasil FFT pada acceleration untuk turbin angin savonius tipe helix pada kecepatan angin 5,5 m/s.
Gambar 4.28. Hasil FFT poros turbin pada acceleration getaran kecepatan angin 5,5 m/s
4.3.5. FFT pada kecepatan angin 6 m/s
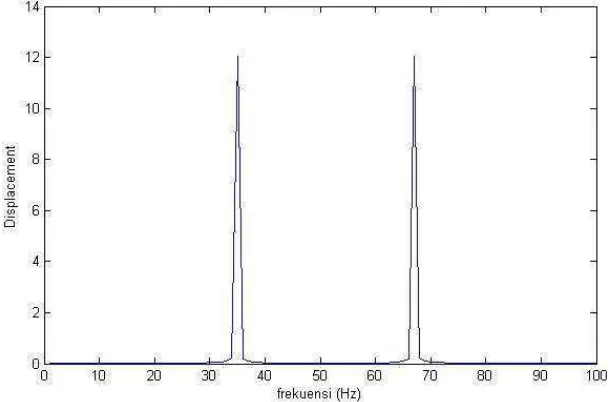
Berdasarkan fungsi karakter perpindahan, dengan bantuan software Matlab R2012a maka frekuensi dapat digambarkan melalui FFT perpindahan partikel yang bergetar. Perpindahan getaran pada displacementuntuk turbin angin savonius tipe helix pada kecepatan angin 6 m/s dapat dilihat Gambar 4.29.di bawah.
Frekuensi poros turbin hasil FFT pada velocity untuk turbin angin savonius tipe helix pada kecepatan angin 6 m/s.
Gambar 4.30. Hasil FFT poros turbin pada velocity getaran kecepatan angin 6 m/s
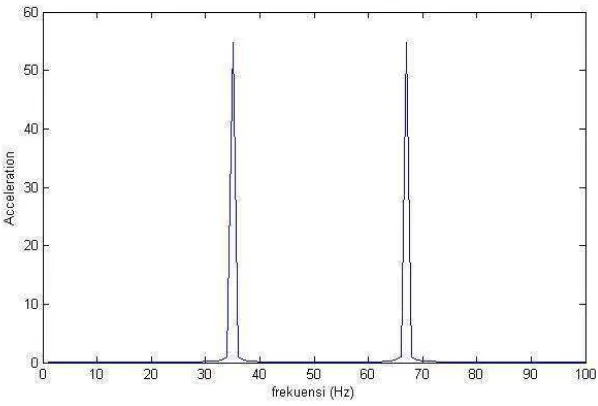
Frekuensi poros turbin hasil FFT pada acceleration untuk turbin angin savonius tipe helix pada kecepatan angin 6 m/s.
Dari seluruh grafik frekuensi pada kecepatan angin 4 m/s, 4,5 m/s, 5 m/s, 5,5 m/s, dan 6 m/s yang telah dikomputasi dengan metode FFT dengan menggunakan bantuan sofware MatLab R2012a dapat disimpulkan bahwa terjadi fenomena misaligment. Hal ini disebabkan karena tidak terlalu besar pengaruh putaran yang terjadi pada poros turbin sehingga getaran yang dihasilkan oleh poros turbin juga tidak menunjukan pengaruh yang signifikan.
4.4. Perbandingan Hasil FFT dan Lintasan Orbit
Dari pengukuran vibrasi turbin angin savonius tipe rotor helix kemudian data itu di olah secara FFT dan secara analisa lintasan orbit dengan menggunkan matlab, sehingga didapatkan perbandingan data berupa grafik spektrum dan data lintasan orbit yang merupakan grafik perbandingan frekuensi dan amplitudo, dan dari grafik itu dapat dianalisa jenis kerusakan turbin dan tingkat kerusakan.
4.4.1. Lintaasan orbit Displacement
Berdasarkan fungsi karakteristik perpindahan maka dengan bantuan softwate Matlab 6.1 maka energi yang didisipasi dapat digambarkan melalui orbit perpindahan partikel yang bergetar. Perpindahan getaran pada tes-I arah radial, mengikuti persamaan karakteristik perpindahan getaran :
Gambar 4.33. Lintasan orbit pada kecepatan angin 4,5 m/s karakteristik perpindahan
Gambar 4.35. Lintasan orbit pada kecepatan angin 5,5 m/s karakteristik perpindahan
Gambar 4.36. Lintasan orbit radial pada kecepatan angin 6 m/s karakteristik perpindahan
4.4.2. Lintaasan orbit Velocity
Berdasarkan fungsi karakteristik kecepatan maka dengan bantuan softwate Matlab 2014 maka energi yang didisipasi dapat digambarkan melalui orbit perpindahan partikel yang bergetar.
Gambar 4.37. Lintasan orbit radial velocity pada kecepatan angin 4 m/s
Gambar 4.39. Lintasan orbit radial velocity pada kecepatan angin 5 m/s
Gambar 4.41. Lintasan orbit radial velocity pada kecepatan angin 6 m/s
Dari bentuk lintasan orbit pada kecepatan angin 6 m/s terlihst semakin luasnya bentuk elips dari lintasan orbit. Dari keseluran bentuk lintsana orbit menindiksasikan terjadi misaligment.
4.4.3. Lintaasan orbit Accelaration
Berdasarkan fungsi karakteristik Percepatan maka dengan bantuan softwate Matlab 2014 maka energi yang didisipasi dapat digambarkan melalui orbit perpindahan partikel yang bergetar.
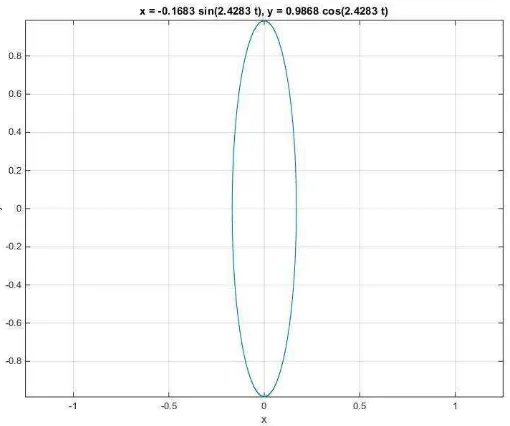
Gambar 4.43. Lintasan orbit radial Accelaration pada kecepatan angin 4,5 m/s
Gambar 4.45. Lintasan orbit radial Accelaration pada kecepatan angin 5,5 m/s
Gambar 4.46. Lintasan orbit radial Accelaration pada kecepatan angin 6 m/s
BAB V
KESIMPULAN & SARAN
5.1Kesimpulan
1. Displacement getaran Turbin angin Savonius tipe rotor helix pada 5 (lima) vareasi kecepatan angin amplitude displacement cenderung stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 6 m/s dan mempunyai amplitude sebesar 0,3338 mm. Untuk puncak bawah terjadi pada kecepatan angin 6 m/s dan mempunya nilai amplitudo sebesar -0.3343 mm. 2. Velocity getaran Turbin angin Savonius tipe rotor helix pada 5 (lima) vareasi
kecepatan angin mempunyai amplitude velocity relative stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 4,5 m/s dan amplitude sebesar 0.5435 mm/s. Untuk puncak bawah terjadi pada kecepatan angin 4,5 m/s dan mempunya nilai amplitudo0.1791 mm/s
3. Acceleration getaran Turbin angin Savonius tipe rotor helix pada 5 (lima) vareasi kecepatan angin mempunyai amplitude acceleration relative stabil dengan puncak atas gelombang getaran terjadi pada kecepatan angin 6 m/s dan amplitude sebesar 4.5304 cm²/s.. Untuk puncak bawah terjadi pada kecepatan angin 6 m/s dan mempunya nilai amplitudo -4.5378 mm/s2.
4. Dari seluruh grafik fast fourier transform (FFT) dan lintasan orbit pada kecepatan angin 4 m/s, 4,5 m/s, 5 m/s, 5,5 m/s, dan 6 m/s yang telah dikomputasi dengan metode FFT dengan menggunakan bantuan sofware MatLab dapat disimpulkan bahwa terjadi fenomena misaligment. Hal ini disebabkan karena tidak terlalu besar pengaruh putaran yang terjadi pada poros turbin sehingga getaran yang dihasilkan oleh poros turbin juga tidak menunjukan pengaruh yang signifikan.
5.2Saran
Saran dari penelitian ini untuk kelanjutan penelitian penulis adalah sebagai berikut:
1. Untuk melihat fenomena/karakteristik pada grafik FFT yang lebih banyak seharusnya menambahkan jumlah vareasi kecepatan angin, hal ini akan membantu untuk melihat fenomena/karakteristik grafik FFT yang lebih dominan.
BAB II
TINJAUAN PUSTAKA
2.1 Literature Review
Dari studi literature yang dilakukan, semakin besar sudut kelengkungan turbin, maka semakin besar jari-jari turbin, akibatnya gaya hambat yang dialami turbin semakin besar sehingga kecepatan putar turbin berkurang. Kecepatan putar turbin bertambah sebanding dengan bertambahnya kecepatan angin. Semakin besar jari-jari turbin, semakin besar pula torsinya, namun putaran yang dihasilkan turbin semakin kecil[5].
Pembuatan turbin angin tipe rotor helix dengan sistem modul dapat diaplikasikan, dengan setiap sambungannya dengan menggunakan mekanisme baut, sehingga turbin angin tipe helix mudah ditransportasikan. Semakin tinggi kecepatan angin yang melintas di turbin angin tipe helix ini, baik yang bersudu lurus maupun yang bersudu setengah lingkaran, maka semakin tinggi daya yang dihasilkan oleh generator. Untuk menghasilkan daya minimum 300 Watt baik yang bersudu lurus atau pun yang bersudu setengah lingkaran, turbin angin menggunakan empat buah turbin angin dengan tipe yang sama dengan kecepatan angin rata-rata 4 m/s[6].
Semakin pendek ukuran lengan, putaran generator yang dihasilkan semakin besar. Semakin pendek ukuran lengan, daya yang dihasilkan semakin besar. Semakin besar rasio gear yang digunakan, semakin besar putaran generator yang dihasilkan[7].
2.2 Turbin Angin
pengairan. Desain turbin angin yang ada saat ini terbagi menjadi dua, yaitu turbin angin sumbu mendatar (HAWT) dan turbin angin sumbu vertikal (VAWT)[8]. Bagian-bagian turbin angin dapat dilihat pada Gambar 2.1.
Gambar 2.1. Konstruksi turbin angin[8] Keterangan gambar :
1. Arah angin pada HAWT tipe upwind 2. Diameter rotor
3. Hub height 4. Rotor blade 5. Gear box 6. Generator 7. Nacelle
8. Tower pada HAWT
9. Arah angin pada HAWT tipe downwind 10. Tinggi rotor
11. Tower pada VAWT 12. Equator height
Pemanfaatan energi angin telah dilakukan sejak lama. Pertama kali digunakan untuk menggerakan perahu di sungai Nil sekitar 5000 tahun lalu SM. Penggunaan kincir sederhana sudah dimulai sejak permulaan abad ke-7 dan tersebar di berbagai negara seperti Persia, Mesir, dan Tiongkok dengan berbagai desain. Di Eropa, kincir angin mulai dikenal sekitar abad ke-11 dan berkembang pesat saat revolusi industri pada awal abad ke-19. Kini turbin angin lebih banyak digunakan untuk mengakomodasi kebutuhan listrik masyarakat, dengan menggunakan prinsip konversi energi dan menggunakan sumber daya alam yang dapat diperbaharui yaitu angin. Walaupun sampai saat ini pembangunan turbin angin masih belum dapat menyaingi pembangkit listrik konvensional (Contoh: PLTD,PLTU,dll), turbin angin masih lebih dikembangkan oleh para ilmuwan karena dalam waktu dekat manusia akan dihadapkan dengan masalah kekurangan sumber daya alam tak terbaharui (Contoh : batubara, minyak bumi) sebagai bahan dasar untuk membangkitkan listrik[8].
Salah satu komponen yang dapat meningkatkan safety dan efisiensi dari turbin angin adalah rotor. Rotor ini berfungsi sebagai perubah gerak linier angin menjadi gerak putar sudu turbin. Untuk klasifikasi berdasarkan fungsi gaya aerodinamisnya, merujuk pada gaya utama yang menyebabkan rotor berputar. Berdasarkan fungsi dari gaya aerodinamis, rotor terbagi menjadi dua, yaitu rotor tipe drag dan rotor tipe lift[9].
1. Rotor tipe drag, memanfaatkan efek gaya hambat atau drag sebagai gaya penggerak rotor.
2. Rotor tipe lift, memanfaatkan efek gaya angkat sebagai gaya penggerak rotor. Gaya ini terjadi akibat angin yang melewati rotor.
Turbin angin sumbu vertikal/tegak (VAWT) memiliki poros/sumbu rotor utama yang disusun tegak lurus. Kelebihan utama susunan ini adalah turbin tidak harus diarahkan ke angin agar menjadi efektif. Kelebihan ini sangat berguna di tempat-tempat yang arah anginnya sangat bervariasi. VAWT mampu mendayagunakan angin dari berbagai arah[9].
keperluan perawatan/pemeliharaan. Tapi ini menyebabkan sejumlah desain menghasilkan tenaga putaran yang tidak stabil. Drag (gaya yang menahan pergerakan sebuah benda padat melalui fluida (zat cair atau gas) bisa saja tercipta saat kincir berputar. Karena sulit dipasang di atas menara, turbin sumbu tegak sering dipasang lebih dekat ke dasar tempat ia diletakkan, seperti tanah atau puncak atap sebuah bangunan. Kecepatan angin lebih pelan pada ketinggian yang rendah, sehingga tersedia energi angin yang sedikit. Jika tinggi puncak atap yang dipasangi menara turbin kira-kira 50% dari tinggi bangunan, ini merupakan titik optimal bagi energi angin yang maksimal dan turbulensi angin yang minimal[9]. Ada tiga tipe rotor pada turbin angin jenis ini, yaitu: Savonius, Darrieus, dan Helix rotor. Turbin Savonius memanfaatkan gaya drag sedangkan Darrieus dan Helix rotor memanfaatkan gaya lift. Turbin angin sumbu vertical dapat dilihat pada Gambar 2.2.
Gambar 2.2. Turbin angin sumbu vertical[9]
2.2.1. Teori Momentum Elementer Betz
Gambar 2.3. Teori A. Betz[10]
Dalam sistem konversi energi angin, energi mekanik turbin hanya dapat diperoleh dari energi kinetik yang tersimpan dalam aliran angin, berarti tanpa perubahan aliran massa udara, kecepatan angin di belakang turbin haruslah mengalami penurunan. Dan pada saat yang bersamaan luas penampang yang dilewati angin haruslah lebih besar, sesuai dengan persamaan kontinuitas. Jika
kecepatan angin di depan rotor, Vkecepatan angin saat melewati rotor, dankecepatan angin di belakang rotor, maka daya mekanik turbin diperoleh dari selisih energi kinetik angin sebelum dan setelah melewati turbin, proil kecepatan angin melewati penampang rotor dapat dilihat pada Gambar 2.4[10].
Gambar 2.4. Profil kecepatan angin melewati penampang rotor[10]
2.2.2. Rotor
Bagian dari turbin angin yang mengumpulkan energi dari angin disebut dengan rotor (blade/baling-baling). Rotor biasanya terdiri dari dua atau lebih sudu yang terbuat dari kayu, fiberglass atau logam berkeliling sumbu (horizontal atau vertikal). Sudu-sudu dipasang pada naf (hub), yang menempel pada poros utama. Rotor didesain berdasarkan prinsip dasar drag dan lift[9].
menggerinda (di Belanda), pertanian (windmills). Sudu lift dikembangkan sama dengan prinsip dasar yang dimiliki pesawat, layangan dan burung untuk terbang. Sudu sebagai airfoil, atau sayap. Ketika udara melewati sudu, kecepatan angin dan perbedaan tekanan terjadi antara permukaan atas dan permukaan bawah sudu. Tekanan pada bagian bawah lebih besar dan mengakibatkan sudu terangkat. Ketika sudu-sudu dipasang pada sumbu utama, sama seperti baling-baling kincir angin, gaya angkat diubah menjadi putaran. Jenis lift ini memiliki putaran(rpm) yang lebih tinggi dari jenis drag[9].
Jumlah sudu rotor dan luas total yang ditutup sudu mempengaruhi performansi kincir angin. Untuk jenis baling-baling lift untuk mengefektifkan fungsinya, angin harus mengalir perlahan terhadap sudu. Untuk mencegah turbulen, ruang antara sudu harus lebih besar maka satu sudu tidak akan menghalangi aliran, aliran udara lemah disebabkan sudu telah dilewati sebelumnya[9].
2.2.3. Turbin Angin Savonius
Salah satu jenis turbin angin sumbu vertikal (VAWT) yang dapat digunakan pada angin dengan kecepatan rendah. Turbin ini ditemukan oleh sarjana Finlandia bernama Sigurd J. Savonius pada tahun 1922. Konstruksi turbin sangat sederhana, tersusun dari dua buah sudu setengah silinder[11]. Pada perkembangannya turbin Savonius ini banyak mengalami perubahan bentuk rotor, seperti yang terlihat pada Gambar 2.5.
2.3 Gerak dan Gaya
Suatu benda dikatakan bergerak jika benda tersebut berubah kedudukannya setiap saat terhadap titik acuannya (titik asalnya). Sebuah benda dikatakan bergerak lurus atau melengkung, jika lintasan berubah kedudukannya dari titik asalnya berbentuk garis lurus atau melengkung[12].
Kinematika dan Dinamika, kinematika adalah ilmu yang mempelajari gerak tanpa mengindahkan penyebabnya, sedangkan dinamika adalah ilmu yang mempelajari gerak dan gaya-gaya penyebabnya[12].
2.3.1. Hukum Newton Tentang Gerak.
Bila penyebab gerak diperhatikan disebut dinamika, melibatkan besaran-besaran fisika yang disebut gaya. Gaya adalah suatu tarikan atau dorongan yang dapat menimbulkan perubahan gerak. Dengan demikian jika benda ditarik/didorong maka pada benda bekerja gaya dan keadaan gerak benda dapat berubah. Gaya adalah dengan nol ( F=0) maka benda tersebut ;
1. Jika dalam keadaan diam akan tetap diam, atau
2. Jika dalam keadaan bergerak lurus beraturan akan tetap bergerak lurus beraturan[12].
2.3.2 Gerak Melingkar
Gambar 2.6. Gerak melingkar[12]
Kecepatan pada gerak melingkar beraturan besarnya selalu tetap namun arahnya selalu berubah, arah kecepatan selalu menyinggung lingkaran, maka v selalu tegak lurus garis yang ditarik melalui pusat lingkaran ke sekeliling lingkaran tersebut terlihat pada Gambar 2.6.[12].
2.3.3 Radian
1 (Satu) radian adalah besarnya sudut tengah lingkaran yang panjang busurnya sama dengan jari-jarinya. Besarnya sudut seperti diperlihatkan pada Gambar 2.7.[12]
Gambar. 2.7. Ilustrasi radian[12]
2.3.4. Frekuensi dan perioda dalam gerak melingkar beraturan
Waktu yang diperlukan sebuah titik P untuk satu kali berputar mengelilingi lingkaran di sebut waktu edar atau perioda dan diberi notasi T. Banyaknya putaran per detik disebut frekuensi dan diberi notasi f. Satuan frekuensi ialah Hertz atau cps (cycle per second). Jadi antara f danTkita dapatkan hubungan [12]:
2.3.5. Kecepatan linier dan kecepatan sudut
Jika dalam waktu T detik ditempuh lintasan sepanjang keliling lingkaran sebesar s= 2 R, maka kelajuan partikel P untuk mengelilingi lingkaran dapat dirumuskan: v = ecepatan ini disebut kecepatan linier dan diberi notasi v.[12]
Kecepatan anguler (sudut) diberi notasi adalah perubahan dari perpindahan sudut persatuan waktu (setiap saat). Biasanya dinyatakan dalam radian/s, derajat per sekon, putaran per sekon (rps) atau putaran per menit (rpm). Bila benda melingkar beraturan dengan sudut rata-rata ( ) dalam radian per
Suatu peralatan yang berputar sebaiknya memiliki suatu nilai getaran standart dan batasan getaran yang diperbolehkan (dibuat oleh pabrik) sehingga apabila nilai getaran yang terjadi diluar batasan yang diizinkan maka peralatan tersebut harus menjalani tindakan perawatan. Semua mesin memiliki tiga sifat fundamental yang berhubungan untuk menentukan bagaimana mesin akan bereaksi terhadap kekuatan-kekuatan yang menyebabkan getaran-getaran, seperti sistem pegas-massa yaitu: [13]
1) Massa (m) : merupakan inersia untuk tetap dalam keadaan semula atau gerak. Sebuah gaya mencoba untuk membawa perubahan dalamkeadaan istirahat atau gerak, yang ditentang oleh massa dan satuannya dalam kg. 2) Kekakuan/stiffness (k) : ada kekuatan tertentu yang dipersyaratkan membengkokkan atau membelokkan struktur dengan jarak tertentu. Ini mengukur gaya yang diperlukan untuk memperoleh defleksi tertentu disebut kekakuan, satuannya dalam N / m.
untuk memperlambat gerak (kecepatan). Karakteristik ini untuk mengurangi kecepatan gerakan disebut redaman, satuannya dalam N /(m/s)[13].
Sebagaimana disebutkan di atas, efek gabungan untuk menahan pengaruh kekuatan karena massa, kekakuan dan redaman menentukan bagaimana suatu sistem akan merespon yang diberikan kekuatan eksternal. Sederhananya, cacat dalam mesin membawa gerakan getaran. Massa, kekakuan dan redaman mencoba untuk melawan getaran yang disebabkan oleh cacat. Jika getaran akibat cacat jauh lebih besar dari pada tiga karakteristik tersebut maka getaran yang dihasilkan akan lebih tinggi dan cacat dapat terdeteksi[13].
2.4.1 Konsep Analisa Getaran
Data getaran yang biasanya diperoleh dalam bentuk sinyal (analog) listrik yang kontinyu yang dihasilkan dari tranducer, dimana masing-masing sinyal analog tersebut menunjukan besar regangan, tegangan, gaya, atau parameter gerakan sesaat (displacement, velocity, dan acceleration ) sebagai fungsi waktu. Sinyal yang demikian disebut sebagai time history. Suatu sample data didefinisikan sebagai time history dari pengukuran getaran tunggal x(t) dalam durasi tertentu[14].
Getaran diartikan sebagai gerak osilatif disekitar posisi tertentu. Untuk getaran sebuah titik akibat operasi mesin, analisa getaran didasarkan pada peristiwa gerak osilatif yang periodik. Gerak periodik adalah suatu gerak gelombang yang berulang dalam selang waktu tertentu. Bentuk paling sederhana dari gerak periodik adalah gerak harmonik [14].
2.4.2 Karakteristik Getaran
Gambar 2.8. Sistem Getaran Sederhana[15]
Kondisi suatu mesin dan masalah-masalah mekanik yang terjadi dapat diketahui dengan mengukur karakteristik getaran pada mesin tersebut. Karakteristik getaran yang penting antara lain adalah:[15]
1) Frekuensi adalah jumlah siklus pada tiap satuan waktu. Besarnya dapat dinyatakan dengan siklus per detik (cycles per second/cps) atau siklus per menit (cycles per minute/cpm). Frekuensi juga bisa diartikan sebagai karakteristik dasar yang digunakan untuk mengukur dan menggambarkan getaran. Frekuensi getaran penting diketahui dalam analisis getaran mesin untuk menunjukkan masalah yang terjadi pada mesin tersebut. Dengan mengetahui frekuensi getaran, akan memungkinkan untuk dapat mengidentifikasikan bagian mesin yang salah (fault) dan masalah yang terjadi.
2) Perpindahan adalah gerakan suatu titik dari suatu tempat ke tempat lain yang mengacu pada suatu titik tertentu yang tidak bergerak (tetap). Dalam pengukuran getaran mesin, sebagai standar digunakan jarak perpindahan puncak ke puncak (peak to peak displacement). Perpindahan juga dapat mengindikasikan berapa jauh suatu objek bergetar.
4) Percepatan adalah perubahan kecepatan per satuan waktu. Percepatan berhubungan erat dengan gaya. Gaya yang menyebabkan getaran pada bantalan mesin atau bagian-bagian lain dapat ditentukan dari besarnya getaran. Juga dapat mengindikasikan suatu objek bergetar terkait dengan gaya penyebab getaran.
5) Phase mengindikasikan bagaimana suatu bagian bergetar relatif terhadap bagian yang lain, atau untuk menentukan posisi suatu bagian yang bergetar pada suatu saat, terhadap suatu referensi atau terhadap bagian lain yang bergetar dengan frekuensi yang sama. Fasa menunjukkan perbedaan awal siklus terjadi. Hubungan fasa antara perpindahan, kecepatan, dan percepatan diilustrasikan pada Gambar 2.9. kecepatan puncak maju (peak forward velocity) terjadi pada 900 sebelum puncak perpindahan positif (peak positive displacement). Dengan kata lain, kecepatan mendahului 900 terhadap perpindahan, sedangkan percepatan tertinggal 1800 terhadap perpindahan[15].
Gambar 2.9. Beda fasa antara perpindahan, kecepatan, dan percepatan[15]
Hubungan antara perpindahan dan waktu untuk gerak harmonic dapat dinyatakan secara matematik sebagai berikut :
………...(2.3)
Dimana perpindahan maksimum diekspresikan sebagai A
dengan differensiasi. Dengan menggunakan notasi titik untuk turunannya, maka
Dengan amplitudo maka dapat terbaca indikasi beratnya kerusakan pada mesin dan juga dapat digunakan untuk mengukur beberapa masalah getaran, yang menunjukkan Displacement dan Frequency.
Gambar 2.10. Hubungan phasa perpindahan, kecepatan, dan percepatan pada gerak harmonik[15]
2.4.3 Standard Getaran (Vibrasi) Untuk Pompa Sentrifugal
Sampai saat ini sangat sulit untuk mendapatkan standart vibrasi untuk pompa sentrifugal, bahkan pabrikan pembuat pompa tidak dapat memberikan standar vibrasi dari pompa buatannya. Demikian juga dengan vibrasi yang timbul akibat kesalahan perencanaan dan pengoperasian, seperti tinggi tekan dan kapasitas pompa jauh lebih besar dari tinggi tekan sistem atau instalasi. Sehingga pengoperasian yang dilakukan dengan mengatur secara paksa tinggi tekan dan kapasitas yang akan menimbulkan vibrasi yang besar. Berdasarkan standart ISO 10816-3 untuk standart vibrasi, memberikan batasan-batasan vibrasi berdasarkan kecepatan (velocity) yang dikategorikan dalam beberapa zona dan warna seperti ditunjukkan pada Gambar 2.11. [16]
Gambar 2.11.ISO 10816-3 Untuk Vibrasi [16]
Keterangan Gambar di atas sebagai berikut :
1. Zona A bewarna hijau, getaran dari mesin sangat baik dan di bawah getaran
yang diijinkan.
2. Zona B bewarna hijau muda, getaran dari mesin baik dan dapat dioperasikan
tanpa larangan.
3. Zona C bewarna kuning, getaran dari mesin dalam batas toleransi dan hanya
dioperasikan dalam waktu terbatas.
Zona D bewarna merah, getaran dari mesin dalam batas berbahaya dan dapat terjadi
kerusakan sewaktu-waktu.
2.5 Modal Analisis (Mode Superposition Methods)
Modal analisis adalah suatu proses penentuan karakteristik dinamik dari suatu sistem. Modal analisis menjadi dasar mangapa respon getaran suatu sistem dapat di ekspresikan sebagai kombinasi linier dari respon kordinat modalnya. Modal ini mencakup instrumentasi, pengolahan sinyal, estimasi parameter, dan analisis vibrasi [16].
menghasilkan input gaya pada struktur. Transducers berfungsi untuk mengkonversi gerakan mekanik pada struktur ke sinyal electric, signal conditioning. Amplifier untuk mencocokkan karakteristik transducers dengan input elektronik data digital, dan analyzer, di mana terdapat program komputer pemrosesan sinyal dan modal analisis. Skema penyusunan perangkat tersebut di ilustrasikan pada Gambar 2.12. [17].
Gambar 2.12. Skema Modal Testing [17]
Getaran pada suatu sistem yang akan di tentukan secara eksperimen pada umumnya terdiri dari tiga mekanisme pengukuran : (1) mekanisme eksitasi; (2) mekanisme pembacaan; (3) mekanisme akuisisi data dan pengolahan. Mekanisme eksitasi di tentukan dari sistem yang menyediakan input gerakan terhadap struktur dalam analisis, umumnya berupa gaya yang di berikan pada koordinat tertentu. Mekanisme pembacaan pada dasarnya di gunakan sensing device yang di kenal sebagai force transduces. Banyak variasi dari alat tersebut dan biasanya di gunakan pada eksperimental modal analisys adalah piezoelectric transducers baik untuk mengujur eksitasi gaya (force transducers) atau mengukur respon percepatan (accelerometers) [17].
terlihat frekuensi alami struktur setiap mode yang di asosiasikan dengan frekuensi nilai puncak. Periode getar struktur kemudian dapat ditentukan yang merupakan invers dari frekuensi alaminya terlihat pada Gambar 2.13. [17].
Gambar 2.13. Contoh respon jembatan akibat beban impuls dalam, (a) time domain; (b) frequency domain [17]
Simpangan struktur total merupakan kontribusi dari respon setiap mode (modal displacement). Simpangan kontribusi setiap mode dapat dihitung dengan melalui integrasi numerik atas persamaan independen. Apabila simpangan untuk setiap mode pada massa tertentu sudah diperoleh maka simpangan total massa yang bersangkutan merupakan superposisi atau penjumlahan dari simpangan tiap-tiap mode tersebut. Simpangan massa yang lain dapat dicari dengan cara yang sama. Berikut contoh modal analisis dari sistem derajat kebebasan banyak (MDOF) yang di modelkan sebagai bangunan geser, dengan menggunakan program MatLab, seperti pada Gambar 2.13. [17].
2.6 MatLab (Matrix Laboratory)
Gambar 2.14. Contoh modal analisis dari sistem derajat kebebasan [17]
Matlab yang merupakan singkatan dari Matrix Laboratory, merupakan bahasa pemrograman yang dikembangkan oleh The Mathwork Inc. yang hadir dengan fungsi dan karakteristik yang berbeda dengan bahasa pemrograman lain yang sudah ada lebih dahulu seperti Delphi, Basic maupun C++.
Pada awalnya program aplikasi MATLAB ini merupakan suatu interface untuk koleksi rutin-rutin numerik dari proyek LINPACK dan EISPACK, dan dikembangkan dengan menggunakan bahasa FORTRAN, namun sekarang ini MATLAB merupakan produk komersial dari perusahaan Mathworks, Inc.
Yang dalam perkembangan selanjutnya dikembangkan dengan menggunakan bahasa C++ dan assembler, (utamanya untuk fungsi-fungsi dasar MATLAB). MATLAB telah berkembang menjadi sebuah environment pemprograman yang canggih yang berisi fungsi-fungsi built-in untuk melakukan tugas pengolahan sinyal, aljabar linier, dan kalkulasi matematis lainnya. MATLAB juga menyediakan berbagai fungsi untuk menampilkan data, baik dalam bentuk dua dimensi maupun dalam bentuk tiga dimensi.
dibutuhkan tidak terlalu sulit bila kita telah memiliki pengalaman dalam pemrograman bahasa lain seperti C, PASCAL, atau FORTRAN.
MATLAB (Matrix Laboratory) yang juga merupakan bahasa pemrograman tingkat tinggi berbasis pada matriks, sering kita gunakan untuk teknik komputasi numerik, yang kita gunakan untuk menyelesaikan masalah-masalah yang melibatkan operasi matematika elemen, matrik, optimasi, aproksimasi dll [18].
2.7 Analisa Vibrasi dengan Fast Fourier Transform(FFT)
Analisa fourier terbagi atas dua yakni deret fourier untuk sinyal periodik dan trasformasi fourier untuk sinyal aperiodik. Setiap sinyal periodik dapat dinyatakan atas jumlah komponen-komponen sinyal sinusoidal dengan frekuensi yang berbeda (distinct). Jika ada sebuah fungsi f(t) yang kontinyu periodik dengan periode T yang bernilai tunggal terbatas pada suatu interval terbatas, dan memiliki diskontinyuitas yang terbatas jumlahnya dalam interval tersebut serta dapat diintegralkan secara mutlak, maka f(t) dapat dinyatakan dengan deret fourier. Dengan menggunakan software komputer, komputasi FFT menjadi lebih mudah dan cepat. Contoh sederhana FFT pada matlab sebuah fungsi f(t) dari time domain menjadi frequency domain diperlihatkan pada Gambar2.15. [19].
Gambar 2.15.Hasil FFT dari Data Vibrasi [19]
FFT merupakan elemen pemrosesan sinyal pada pengukuran vibrasi. Pada pengukuran vibrasi ada empat tahapan untuk merubah sinyal vibrasi menjadi spektrumnya. Algoritma FFT untuk analisa vibrasi tersebut adalah sebagai berikut:
Sistem akuisisi menghasilkan spektrum yang menunjukkan perbandingan waktu dengan percepatan.
Hasil spektrum diolah menggunakan software lain dengan menggunakan Fast Fourier Transform.
Hasil pengolahan menggunakan FFT akan berupa grafik perbandingan frekuensi dengan amplitudo yang menunjukkan jenis kerusakan dan tingkat kerusakan mesin [19].
2.8 Diagnosa Kerusakan Mesin Melalui Spectrum Analysis
Setiap bagian dari mesin yang berputar mempunyai tingkat vibrasi yang berbeda tergantung pada letaknya dan gaya yang diterima. Tingkat vibrasi inilah yang bisa dijadikan sebagai pendeteksi keadaan dari suatu kondisi mesin apakah ada kerusakan atau tidak. Kerusakan umum yang biasa terjadi pada pompa dan mesin-mesin berputar adalah ketidakseimbangan atau unbalance, misalingment, kerusakan bearing dan mechanical looseness. Kerusakan-kerusakan tersebut dapat dideteksi dari spektrum vibrasi. Kerusakan – kerusakan yang sering terjadi pada mesin berputar yaitu : [19]
a. Unbalance
normal ≥ 80% dari amplitudo keseluruhan ketika masalah dipastikan unbalance terlihat pada Gambar 2.16. [19].
Gambar 2.16. Pola Spektrum Vibrasi Unbalance [19]
b. Misalignment
Ketidaklurusan (misalignment) terjadi ketika frekuensi shaft yang berputar satu kali putaran atau dapat juga terjadi dua dan tiga kali putaran. Normalnya disebabkan adanya getaran yang tinggi pada axial dan radial.
Misalignment terjadi saat getaran yang dihasilkan lebih besar dari keadaan normal di 2x RPM. Jika misalignment menjadi semakin buruk hal ini dapat disebabkan besarnya nilai harmonik dimana akan menghasilkan spektrum nampak seperti masalah looseness terlihat pada Gambar 2.17.[19].
Gambar 2.17.Pola Spektrum Vibrasi Misalignment [19]
2.9 Metode Lintasan Orbit (Pola Lissajous)