Penyelesaian Clustered Travelling Salesman Problem Dengan Algoritme Lexisearch

(1)

PENYELESAIAN

CLUSTERED TRAVELLING SALESMAN

PROBLEM

DENGAN ALGORITME

LEXISEARCH

FIKRI HIDAYAT

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Clustered Travelling Salesman Problem dengan Algoritme Lexisearch adalah benar karya saya dengan arahan dari dosen pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Maret 2016

Fikri Hidayat

(4)

ABSTRAK

FIKRI HIDAYAT. Penyelesaian Clustered Travelling Salesman Problem dengan Algoritme Lexisearch. Dibimbing oleh FARIDA HANUM dan ELIS KHATIZAH.

Clustered Travelling Salesman Problem (CTSP) merupakan salah satu varian dari TSP. Pada model CTSP pelanggan dikelompokkan menjadi beberapa cluster. Cluster pada CTSP dibentuk berdasarkan kedekatan yang sama pada tiap

cluster. CTSP menghasilkan rute berjarak minimum yang mengunjungi setiap pelanggan pada cluster yang sama terlebih dahulu, setelah itu pelanggan pada

cluster lain. Tujuan penelitian ini ialah menyelesaikan Clustered Travelling Salesman Problem dengan Algoritme Lexisearch dan mengaplikasikannya pada masalah distribusi pengiriman ayam broiler pada sejumlah kandang di wilayah Cikarang-Bekasi, Jakarta, dan Kabupaten Bogor. Solusi terbaik atau optimal dari permasalahan ini ialah rute dengan jarak terpendek yang mengunjungi pelanggan-pelanggan di setiap cluster dengan urutan cluster yang telah ditentukan.

Kata kunci: algoritme lexisearch, cluster, Clustered Travelling Salesman Problem, optimal, rute

ABSTRACT

FIKRI HIDAYAT. The Solution of the Clustered Travelling Salesman Problem

with Lexisearch Algorithm. Supervised by FARIDA HANUM and ELIS KHATIZAH.

Clustered Travelling Salesman Problem (CTSP) is one variant of TSP. In the model of CTSP, customers are grouped into several clusters. Clusters on CTSP are organized based on the proximity of clusters. CTSP produces a route with minimum distance which visiting each customer on the same clusters. Then it is visiting other customers on the other clusters. The purpose of this research is to find the solution of the Clustered Travelling Salesman Problem with

Lexisearch Algorithm and to apply it to the distribution problems of the delivery broiler chickens in the several hencoops in Cikarang-Bekasi, Jakarta, and Kabupaten Bogor.The best solution or optimal solution of this problem is a route with the shortest distance that visiting customers in each cluster with the order of the clusters appointed.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENYELESAIAN

CLUSTERED TRAVELLING SALESMAN

PROBLEM

DENGAN ALGORITME

LEXISEARCH

FIKRI HIDAYAT

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah Subhanahu Wa Ta’ala atas segala karuniaNya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Penyelesaian Clustered Travelling Salesman Problem dengan Algoritme

Lexisearch”. Selawat serta salam senantiasa diucapkan kepada Nabi Muhammad SAW sebagai pemimpin dan suri teladan terbaik bagi umatnya. Penyusunan karya ilmiah ini tidak lepas dari peranan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1 keluarga tercinta: Abdul Basit dan Siti Nihayah selaku orang tua, serta keluarga yang telah mendoakan, memberikan semangat dan motivasi,

2 Dra Farida Hanum, MSi selaku dosen pembimbimg I yang selalu sabar dalam membimbing, memberi motivasi, semangat dan doa,

3 Elis Khatizah, SSi, MSi selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya,

4 Drs Prapto Tri Supriyo, MKom selaku dosen penguji yang telah memberikan kritik dan saran serta doanya

5 para dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan,

6 para staf Departemen Matematika, terima kasih atas bantuan yang telah diberikan selama ini,

7 Indri Juliyanti dan keluarga yang selalu memberikan motivasi, mendoakan, memberikan dukungan dan perhatiannya,

8 teman-teman Matematika 47, 48, dan 49 yang selalu mendukung agar terus berkembang dan telah menjadi keluarga selama di Bogor,

9 Gumatika yang telah memberikan banyak pengalaman yang berkesan, 10 teman-teman Mengejar Sarjana yang selalu mengingatkan dan menyemangati, 11 teman yang membantu dalam proses kelulusan Ando, Rendi, Ika, Son, Imad,

Bella, Tuty, Mira, Ale, Putri P, Rizky, Eric, Kamil, Kiki dan Syafii,

12 teman-teman yang selalu menyemangati Novan, Galih, Ichwan, Zeddy, Anbiya, Bian, Aldi, Bani, Apro,

13 semua pihak yang telah membantu, mendukung dan mendoakan dalam penyusunan karya ilmiah ini.

Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.

Bogor, Maret 2016

(9)

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

TINJAUAN PUSTAKA 1

Konsep-konsep dalam Teori Graf 1

Travelling Salesman Problem 2

Clustered Travelling Salesman Problem 3

Modifikasi Matriks Jarak 3

Bias dari Matriks 3

Tabel Alfabet 4

Blok Kata 5

Batas Bawah 5

Penyelesaian Clustered Travelling Salesman Problem dengan Algoritme

Lexisearch 5

APLIKASI 7

Penyelesaian CTSP dengan Algoritme Lexisearch 8

SIMPULAN DAN SARAN 13

Simpulan 13

Saran 13

DAFTAR PUSTAKA 13

LAMPIRAN 15

(10)

DAFTAR TABEL

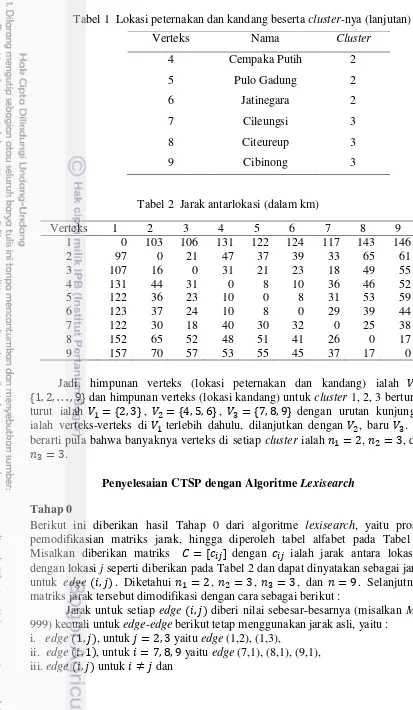
1. Lokasi peternakan dan kandang beserta cluster-nya 7

2. Jarak antarlokasi (dalam km) 8

3. Modifikasi matriks jarak dan minimal baris 9

4. Modifikasi matriks jarak dan minimal kolom 9

5. Matriks jarak yang direduksi 10

6. Tabel alfabet 10

7. Tabel pencarian 11

DAFTAR GAMBAR

1. Peta Subang, Cikarang, Bekasi, Jakarta, dan Kabupaten Bogor 7

(11)

PENDAHULUAN

Latar Belakang

Distribusi barang merupakan suatu kegiatan yang bertujuan mempermudah kegiatan penyaluran barang dari pihak produsen ke pihak konsumen. Masalah yang sering muncul dalam proses pendistribusian barang adalah menentukan rute terpendek tur yang efisien dan efektif untuk sampai tujuan. Permasalahan distribusi dapat dimodelkan sebagai masalah penentuan rute terpendek pada graf yang merupakan modifikasi dan pengembangan dari model Travelling Salesman Problem (TSP). TSP dapat diilustrasikan sebagai perjalanan seorang salesman

dimulai dari suatu kota yang harus melalui semua kota yang dituju dengan jarak terpendek sehingga setiap kota hanya boleh dilalui satu kali dan kembali ke kota awal perjalanan. Solusi dari TSP ialah jalur yang dilalui oleh salesman tersebut. Tentunya solusi terbaik atau optimal dari permasalahan ini ialah jalur dengan jarak terpendek atau dapat disebut juga dengan rute perjalanan minimum.

Salah satu varian dari TSP adalah Clustered Travelling Salesman Problem

(CTSP). Model CTSP dibentuk berdasarkan kedekatan yang sama pada tiap

cluster. Contoh aplikasi dalam kehidupan nyata, misalnya: dalam perencanaan produksi, operasional komputer, jadwal ujian, dsb. Masalah CTSP dapat diselesaikan dengan beberapa metode, antara lain mentransformasikan CTSP menjadi TSP dengan cara memodifikasi matriks jarak (Chisman 1975) dan menyelesaikannya dengan algoritme branch and bound; atau dengan beberapa algoritme heuristik seperti dalam (Anily et al. 1996), dan (Guttmann-Beck et al.

2000), algoritme tabu search (Laporte et al. 1996), dan algoritme genetik 2 tingkat (Ding et al. 2007). Dalam karya ilmiah ini, masalah CTSP diselesaikan dengan algoritme lexisearch. Sumber utama karya ilmiah ini ialah artikel yang berjudul An exact algorithm for the clustered travelling salesman problem

(Ahmed 2013).

Tujuan Penelitian

Tujuan penulisan karya ilmiah ini ialah menyelesaikan Clustered Travelling Salesman Problem dengan Algoritme Lexisearch dan mengaplikasikannya pada masalah distribusi pengiriman ayam broiler pada sejumlah kandang di wilayah Cikarang-Bekasi, Jakarta, dan Kabupaten Bogor.

TINJAUAN PUSTAKA

Konsep-konsep dalam Teori Graf

(12)

2

kemudian dikemasnya dalam bentuk buku yang diterbitkan pada tahun 1936. Dalam periode yang sangat singkat, teori graf kini mengalami perkembangan yang sangat pesat (Chartrand & Oellermann 1993). Berikut ini akan dijelaskan beberapa konsep-konsep dalam teori graf.

Definisi 1 (Graf)

Suatu graf adalah pasangan terurut dengan adalah himpunan berhingga dan takkosong dari elemen-elemen graf yang disebut verteks (node, simpul) dan adalah himpunan pasangan yang menghubungkan dua elemen subhimpunan dari yang biasa disebut sisi (edge, line). dapat dituliskan dan , setiap sisi , pada dapat dinotasikan dengan atau . Banyaknya verteks dari graf disebut order dari dan banyaknya sisi dari graf disebut size dari graf (Chartrand & Zhang 2009).

Definisi 2 (Walk)

Suatu walk W pada graf G adalah barisan bergantian antara verteks dan sisi yang dimulai dan diakhiri oleh verteks. Walk yang dimulai dari dan berakhir di disebut walk dan walk W mempunyai panjang n karena melalui n sisi (tidak harus berbeda) (Chartrand & Oellermann 1993).

Definisi 3 (Jalur/path)

Path adalah walk dengan tidak ada verteks yang diulang (Chartrand & Oellermann 1993).

Definisi 4 (Cycle)

Cycle adalah walk tertutup, yang memuat sedikitnya tiga verteks, dan semua verteks pada walk tersebut berbeda (Foulds 1992).

Definisi 5 (Graf lengkap)

Graf lengkap adalah graf dengan � verteks sehingga terdapat tepat satu sisi yang menghubungkan tiap pasang verteks (Chartrand & Oellermann 1993). Definisi 6 (Cycle Hamilton)

Cycle Hamilton adalah sebuah jalur/path pada suatu graf yang berawal dan berakhir pada verteks yang sama dan menyinggahi semua verteks tepat satu kali (Foulds 1992).

Travelling Salesman Problem

Menurut Fournier (2009), Travelling Salesman Problem (TSP) dapat dipandang sebagai permasalahan penentuan cycle Hamilton pada suatu graf yaitu

(13)

3

kota, berangkat dari sembarang kota awal, melewati setiap kota tepat sekali, dan terakhir kembali ke kota di mana ia berangkat. Penentuan rute ditetapkan berdasarkan jarak minimum yang akan ditempuh.

Clustered Travelling Salesman Problem

Clustered travelling salesman problem (CTSP) adalah sebuah variasi dari

Travelling Salesman Problem (TSP). Masalah CTSP ini diperkenalkan dalam (Chisman 1975) yang dapat didefinisikan sebagai berikut. Misalkan merupakan suatu graf lengkap tak berarah dengan adalah himpunan verteks yang telah dikelompokkan dalam m buah cluster

kecuali verteks awal (depot = ). Misalkan banyaknya verteks di dalam cluster 1 sampai m berturut-turut dinyatakan sebagai � � � . Himpunan

ialah kumpulan dari sisi. Matriks menyatakan biaya, waktu, atau jarak tur yang didefinisikan di E. Dimulai dari depot , masalah CTSP merupakan masalah menentukan sebuah cycle Hamilton pada dengan jarak/biaya minimum sehingga semua verteks dari setiap cluster

dikunjungi satu per satu. Dalam karya ilmiah ini, diasumsikan bahwa setiap

cluster dikunjungi secara berurutan dengan urutan : Modifikasi Matriks Jarak

Misalkan himpunan verteks dari suatu graf lengkap tak berarah ialah : � , dan adalah matriks jarak berukuran n × n

dan merupakan jarak dari verteks ke , dan misalkan verteks 1 sebagai depot. Kecuali verteks 1, misalkan himpunan verteks dipartisi menjadi mcluster dengan urutan indeks menaik dan banyaknya verteks dalam cluster

berturut-turut ialah � � � . Matriks jarak yang telah diberikan, dimodifikasi dengan cara menetapkan jarak untuk setiap edge (i, j) dengan nilai sebesar-besarnya (misalkan ), yang menyatakan verteks yang tak boleh dikunjungi berdasarkan urutan kunjungan cluster, kecuali edge berikut ini:

i. edge , untuk �

ii. edge , untuk � � � � iii. edge untuk dan

a.) � � �

b.) � � � � � � � c.) � � � � � � � �

� � � ; dan seterusnya; hingga

d.) � � � � � � �

�.

Bias dari Matriks

(14)

4

{ } �

Kemudian setiap elemen pada baris ke-i di matriks C dikurangi dengan sehingga didapatkan matriks baru, ̅ ̅ , dengan

̅ , untuk setiap �; � (1.2) Setelah itu, ditentukan elemen terkecil pada setiap kolom dari matriks ̅, yaitu

̅ �

Selanjutnya, setiap elemen pada kolom ke-j dikurangi dengan sehingga didapatkan matriks modifikasi ̿ ̿ , dengan

̿ ̅ untuk �; � (1.4) Bias dari matriks C didefinisikan sebagai

Bias = ∑ ∑ . (1.5)

(Ahmed 2011) Matriks jarak yang dimodifikasi/direduksi ̿ merupakan matriks taknegatif dengan setidaknya satu elemen yang bernilai nol di setiap baris dan di setiap kolom. Dalam masalah penugasan (assignment problem), dengan menambah atau mengurangi suatu konstanta untuk setiap elemen dari baris atau kolom dalam matriks jarak, maka penugasan yang meminimumkan total jarak pada salah satu matriks juga meminimumkan total jarak pada matriks lainnya. Karena TSP merupakan kasus khusus dari AP (Assignment Problem) maka untuk menyelesaikan TSP dapat digunakan matriks jarak yang dimodifikasi (Ahmed 2011).

Tabel Alfabet

Matriks alfabet, , adalah matriks segi berordo n yang dibentuk berdasarkan posisi elemen dari matriks jarak termodifikasi berukuran n, yaitu

̿ ̿ . Baris ke-i pada matriks A terdiri atas posisi dari elemen-elemen pada baris ke-i dari matriks C ketika elemen-elemen tersebut diatur dalam urutan tidak menurun. Jika menyatakan elemen dengan urutan ke-j pada baris ke-i dari matriks A, maka menyatakan posisi elemen terkecil di baris i pada matriks

̿. Isi tabel alfabet pada baris ke-i dan kolom ke-j ditampilkan dalam bentuk

(15)

5

Blok Kata

Misalkan suatu kata lengkap terdiri atas n huruf, maka

�, menyatakan kata yang taklengkap. Suatu kata yang taklengkap dapat dipandang sebagai tur parsial yang terdiri dari beberapa verteks. Kata taklengkap juga merepresentasikan blok dari kata dengan kata taklengkap ini sebagai leader blok. Sebagai ilustrasi, say merupakan leader

dari blok kata-kata: saya, sayap, sayang, sayup, sayur dan sebagainya.

Untuk CTSP, setiap verteks dianggap sebagai huruf dalam alfabet dan setiap tur dapat direpresentasikan sebagai sebuah kata dalam alfabet. Dengan demikian himpunan kata dalam kamus (yang merepresentasikan himpunan solusi) dipartisi ke dalam blok-blok. Sebagai contoh, blok B dengan leader ( )

Penentuan batas bawah nilai fungsi objektif untuk setiap leader pada CTSP saat ini masih sangat sulit (Ahmed 2013). Oleh karena itu, pada karya ilmiah ini digunakan batas bawah nilai fungsi objektif TSP sebagai batas bawah nilai fungsi objektif CTSP. Langkah-langkah untuk menentukan batas bawah tersebut adalah sebagai berikut. Misalkan diberikan tur parsial dan verteks dipilih untuk dirangkaikan ke dalam tur parsial. Sebelum dibentuk rangkaian, terlebih dahulu diperiksa batas untuk tur . Untuk itu, dimulai dari baris ke-2 pada tabel alfabet sampai baris ke n jumlahkan nilai-nilai (jarak) untuk verteks yang tidak termasuk dalam tur parsial, termasuk verteks 1 (depot), dan tidak termasuk baris dan . Jumlah ini adalah batas bawah untuk leader

.

Penyelesaian Clustered Travelling Salesman Problem dengan Algoritme Lexisearch

Salah satu cara untuk menyelesaikan clustered travelling salesman problem

(16)

6

Menurut Ahmed (2013) langkah-langkah dalam algoritme lexisearch untuk menentukan cycle Hamilton pada suatu graf (yaitu cycle yang melewati semua verteks dari graf tersebut tepat satu kali) ialah sebagai berikut.

Misalkan ialah matriks jarak dan misalkan banyaknya verteks pada clusteri ialah � dengan .

Tahap 0 : Biasdari matriks jarak dihilangkan dan konstruksi tabel alfabet yang didasarkan pada matriks jarak yang telah dimodifikasi. “Solusi terbaik” diberi nilai sebesar-besarnya (misalkan M). Karena verteks 1 adalah verteks awal, maka penghitungan dilakukan dari baris pertama pada tabel alfabet. Nilai awal “tur parsial” = 0, = 1 dan beralih ke Tahap 1.

Tahap 1 : Pergi ke elemen kepada baris matriks (misalkan verteks ) dengan jarak verteks sesuai dengan “jarak verteks saat ini”. Jika (jarak tur parsial + jarak verteks saat ini) lebih besar atau sama dengan “jarak solusi terbaik”, maka dilanjutkan ke Tahap 9. Jika tidak, beralih ke Tahap 2.

Tahap 2 : Jika verteks membentuk suatu subtur atau melanggar aturan urutan kunjungan cluster, maka verteks v tidak digunakan dan . Kemudian beralih pada Tahap 7. Jika tidak, proses dilanjutkan ke Tahap 3.

Tahap 3 : Jika semua verteks telah dikunjungi, ditambahkan suatu edge yang menghubungkan verteks dengan verteks 1. Jarak tur yang lengkap dihitung dan dilanjutkan ke Tahap 4. Jika tidak, proses dilanjutkan ke Tahap 5.

Tahap 4 : Jika jarak tur yang lengkap lebih besar atau sama dengan jarak solusi terbaik, lanjut ke Tahap 9; jika tidak, jarak tur diganti sebagai jarak solusi terbaik dan beralih ke Tahap 9.

Tahap 5 : Hitung batas bawah nilai fungsi objektif untuk leader blok yang

Tahap 8 : Beralih ke subblok, yaitu baris ke pada tabel alfabet. Jika panjang tur parsial lebih besar atau sama dengan (∑� ), maka nilai

∑ � . Jika tidak, , dan proses dilanjutkan ke Tahap 1.

(17)

7

Tahap 10 : Nilai solusi terbaik merupakan nilai solusi optimal relatif terhadap matriks yang tereduksi. Bias matriks ditambahkan pada nilai solusi optimal agar diperoleh nilai solusi optimal terhadap matriks jarak awal, dan beralih ke Tahap 11.

Tahap 11: Tur yang ada saat ini merupakan tur optimal relatif terhadap matriks jarak awal/asli dan kemudian proses dihentikan.

APLIKASI

Kebutuhan pokok manusia meliputi pangan, sandang dan papan. Untuk mendapatkan segala sesuatu yang dibutuhkan, diperlukan pendistribusian dari produsen ke konsumen. Sebagai contoh, kasus pendistribusian pengiriman ayam broiler dari peternakan di Subang ke sejumlah kandang di wilayah Cikarang, Bekasi, Jakarta, dan Kabupaten Bogor yang denahnya diberikan pada Gambar 1 berikut.

Gambar 1 Peta Subang, Cikarang, Bekasi, Jakarta, dan Kabupaten Bogor

Daerah lokasi kandang dibagi menjadi tiga cluster, yaitu Cikarang-Bekasi, Jakarta, dan Kabupaten Bogor dengan detail lokasi kandang di tiap cluster

diberikan pada Tabel 1 dan jarak antarlokasi diberikan di Tabel 2. Tabel 1 Lokasi peternakan dan kandang beserta cluster-nya

Verteks Nama Cluster

1 Subang Depot

2 Cikarang 1

(18)

8

Tabel 1 Lokasi peternakan dan kandang beserta cluster-nya (lanjutan)

Verteks Nama Cluster

4 Cempaka Putih 2

5 Pulo Gadung 2

6 Jatinegara 2

7 Cileungsi 3

8 Citeureup 3

9 Cibinong 3

Tabel 2 Jarak antarlokasi (dalam km)

Verteks 1 2 3 4 5 6 7 8 9

1 0 103 106 131 122 124 117 143 146

2 97 0 21 47 37 39 33 65 61

3 107 16 0 31 21 23 18 49 55

4 131 44 31 0 8 10 36 46 52

5 122 36 23 10 0 8 31 53 59

6 123 37 24 10 8 0 29 39 44

7 122 30 18 40 30 32 0 25 38

8 152 65 52 48 51 41 26 0 17

9 157 70 57 53 55 45 37 17 0

Jadi, himpunan verteks (lokasi peternakan dan kandang) ialah

dan himpunan verteks (lokasi kandang) untuk cluster 1, 2, 3 berturut-turut ialah , , dengan urutan kunjungan ialah verteks-verteks di terlebih dahulu, dilanjutkan dengan , baru . Ini berarti pula bahwa banyaknya verteks di setiap cluster ialah � , � , dan

� .

Penyelesaian CTSP dengan Algoritme Lexisearch

Tahap 0

Berikut ini diberikan hasil Tahap 0 dari algoritme lexisearch, yaitu proses pemodifikasian matriks jarak, hingga diperoleh tabel alfabet pada Tabel 6. Misalkan diberikan matriks dengan ialah jarak antara lokasi i

dengan lokasi j seperti diberikan pada Tabel 2 dan dapat dinyatakan sebagai jarak untuk edge . Diketahui � , � , � , dan � . Selanjutnya, matriks jarak tersebut dimodifikasi dengan cara sebagai berikut :

Jarak untuk setiap edge diberi nilai sebesar-besarnya (misalkan M = 999) kecuali untuk edge-edge berikut tetap menggunakan jarak asli, yaitu :

i. edge , untuk yaitu edge (1,2), (1,3),

(19)

9

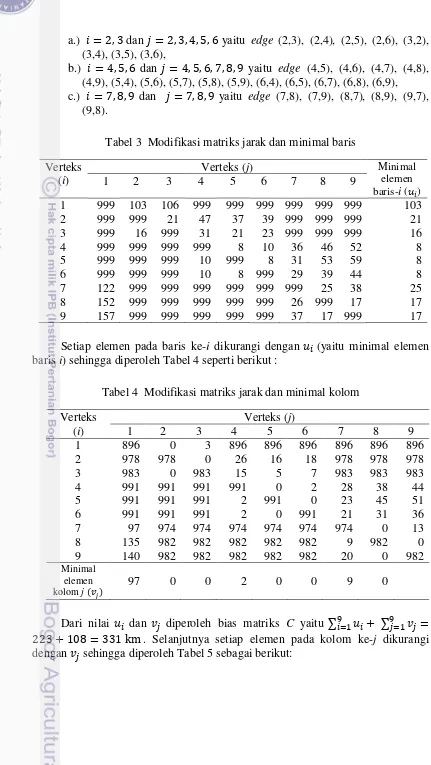
Tabel 3 Modifikasi matriks jarak dan minimal baris Verteks baris i) sehingga diperoleh Tabel 4 seperti berikut :

Tabel 4 Modifikasi matriks jarak dan minimal kolom

(20)

10

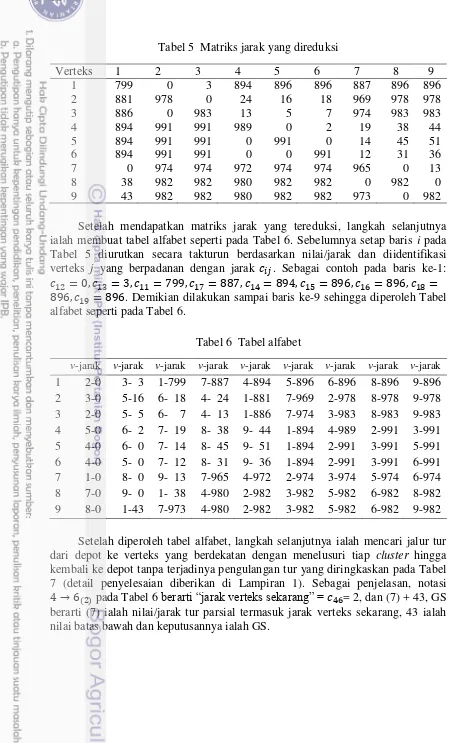
Tabel 5 Matriks jarak yang direduksi

Verteks 1 2 3 4 5 6 7 8 9

1 799 0 3 894 896 896 887 896 896

2 881 978 0 24 16 18 969 978 978

3 886 0 983 13 5 7 974 983 983

4 894 991 991 989 0 2 19 38 44

5 894 991 991 0 991 0 14 45 51

6 894 991 991 0 0 991 12 31 36

7 0 974 974 972 974 974 965 0 13

8 38 982 982 980 982 982 0 982 0

9 43 982 982 980 982 982 973 0 982

Setelah mendapatkan matriks jarak yang tereduksi, langkah selanjutnya ialah membuat tabel alfabet seperti pada Tabel 6. Sebelumnya setap baris i pada Tabel 5 diurutkan secara takturun berdasarkan nilai/jarak dan diidentifikasi verteks j yang berpadanan dengan jarak . Sebagai contoh pada baris ke-1:

. Demikian dilakukan sampai baris ke-9 sehingga diperoleh Tabel alfabet seperti pada Tabel 6.

Tabel 6 Tabel alfabet

v-jarak v-jarak v-jarak v-jarak v-jarak v-jarak v-jarak v-jarak v-jarak

1 2-0 3- 3 1-799 7-887 4-894 5-896 6-896 8-896 9-896 2 3-0 5-16 6- 18 4- 24 1-881 7-969 2-978 8-978 9-978 3 2-0 5- 5 6- 7 4- 13 1-886 7-974 3-983 8-983 9-983 4 5-0 6- 2 7- 19 8- 38 9- 44 1-894 4-989 2-991 3-991 5 4-0 6- 0 7- 14 8- 45 9- 51 1-894 2-991 3-991 5-991 6 4-0 5- 0 7- 12 8- 31 9- 36 1-894 2-991 3-991 6-991 7 1-0 8- 0 9- 13 7-965 4-972 2-974 3-974 5-974 6-974 8 7-0 9- 0 1- 38 4-980 2-982 3-982 5-982 6-982 8-982 9 8-0 1-43 7-973 4-980 2-982 3-982 5-982 6-982 9-982 Setelah diperoleh tabel alfabet, langkah selanjutnya ialah mencari jalur tur dari depot ke verteks yang berdekatan dengan menelusuri tiap cluster hingga kembali ke depot tanpa terjadinya pengulangan tur yang diringkaskan pada Tabel 7 (detail penyelesaian diberikan di Lampiran 1). Sebagai penjelasan, notasi

(21)

(22)

12

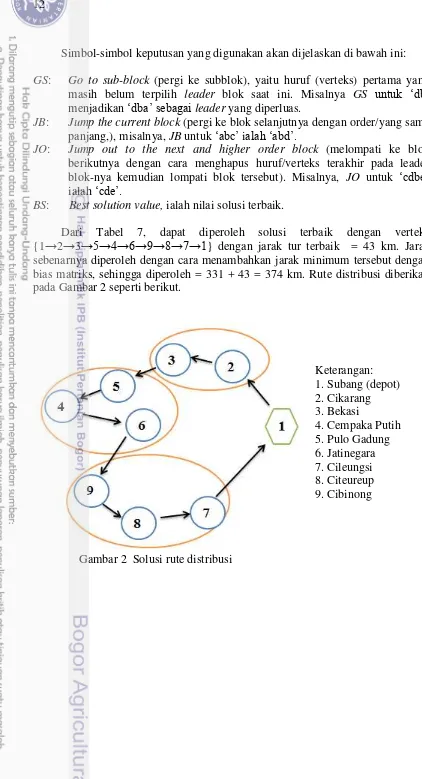
Simbol-simbol keputusan yang digunakan akan dijelaskan di bawah ini:

GS: Go to sub-block (pergi ke subblok), yaitu huruf (verteks) pertama yang masih belum terpilih leader blok saat ini. Misalnya GS untuk „db‟

menjadikan „dba‟ sebagai leader yang diperluas.

JB: Jump the current block (pergi ke blok selanjutnya dengan order/yang sama panjang,), misalnya, JB untuk „abc‟ ialah „abd‟.

JO: Jump out to the next and higher order block (melompati ke blok berikutnya dengan cara menghapus huruf/verteks terakhir pada leader blok-nya kemudian lompati blok tersebut). Misalnya, JO untuk „cdbe‟ ialah „cde‟.

BS: Best solution value, ialah nilai solusi terbaik.

Dari Tabel 7, dapat diperoleh solusi terbaik dengan verteks {1→2→3→5→4→6→9→8→7→1} dengan jarak tur terbaik = 43 km. Jarak sebenarnya diperoleh dengan cara menambahkan jarak minimum tersebut dengan bias matriks, sehingga diperoleh = 331 + 43 = 374 km. Rute distribusi diberikan pada Gambar 2 seperti berikut.

Keterangan: 1. Subang (depot) 2. Cikarang 3. Bekasi

4. Cempaka Putih 5. Pulo Gadung 6. Jatinegara 7. Cileungsi 8. Citeureup 9. Cibinong

(23)

13

SIMPULAN DAN SARAN

Simpulan

Masalah Clustered Travelling Salesman Problem (CTSP) dapat diselesaikan menggunakan algoritme lexisearch. Telah diperlihatkan bahwa masalah CTSP dapat diterapkan pada pendistribusian ayam broiler dari Subang ke wilayah-wilayah yang terdapat di wilayah-wilayah Cikarang-Bekasi, Jakarta, dan beberapa wilayah-wilayah di Kabupaten Bogor. Hasil yang didapatkan yaitu jarak tur optimal dengan matriks jarak yang sebenarnya = bias matriks + jarak tur terbaik = 331 + 43 = 374 km.

Saran

Karya ilmiah ini menggunakan metode lexisearch, untuk karya ilmiah selanjutnya dapat menggunakan metode lain seperti algoritme branch and bound; atau dengan beberapa algoritme heuristik, dan membangun software yang dapat menerapkan metode heuristik tersebut.

DAFTAR PUSTAKA

Ahmed ZH. 2010. A lexisearch algorithm for the bottleneck travelling salesman problem. International Journal of Computer Science and Security (IJCSS). 3(6):569-577.doi: 10.1016/j.jda.2008.11.007.

Ahmed ZH. 2011. A data-guided lexisearch algorithm for the asymmetric travelling salesman problem. Mathematical Problem in Engineering. 2011:1-18.doi:10.1155/2011/750968.

Ahmed ZH. 2013. An exact algorithm for the clustered travelling salesman problem. Opsearch. 50(2):215-228.doi:10.1007/s12597-012-0107-0.

Anily S, Bramel J, Hertz A. 1996. A 5/3-approximation algorithm for the clustered traveling salesman tour and path problems. Operations Research Letters. 24:29-35. Chartrand G, Oellermann OR. 1993. Applied and Algorithmic Graph Theory. New

York (US): McGraw-Hill.

Chartrand G, Zhang P. 2009. Chromatic Graph Theory. London (GB): CRC Pr. Chisman JA. 1975. The clustered travelling salesman problem. Computers &

Operations Research. 2(2):115-119.

Ding C, Cheng Y, He M. 2007. Two-level genetic algorithm for clustered traveling salesman problem problem with application in large-scale TSPs. Tsinghua Science

and Technology. 12(4):459-465.

Foulds LR. 1992. Graph Theory Applications. New York (US): Springer-Verlag. Fournier JC. 2009. Graph Theory and Applications. New Jersey (US): John Wiley &

(24)

14

Guttmann-Beck N, Hassin R, Khuller S, Raghavachari B. 2000. Approximation algorithms with bounded performance guarantees for the clustered traveling salesman problem. Algorithmica. 28(4):422-437.doi: 10.1007/s004530010045. Laporte G, Potvin JY, Quilleret F. 1996. A tabu search heuristic using genetic

(25)

15

Tahap 5: Leader blok saat ini: (1, 2). Batas bawah nilai fungsi objektif ialah Batas = + + + + + + Tahap 8: Pergi ke subblok, yaitu baris ke-2 pada tabel alfabet.

Panjang tur taklengkap = 2 < 9 maka p = 1 dan ke Tahap 1 untuk iterasi

Tahap 5: Leader blok saat ini: (1, 2, 3). Batas bawah nilai fungsi objektif ialah Batas = + + + + + + Tahap 8: Pergi ke subblok, yaitu baris ke-3 pada tabel alfabet.

Tahap 2: Verteks 2 membentuk subtur, maka verteks 2 tidak dapat digunakan dan

(26)

16

Tahap 5: Leader blok saat ini: (1, 2, 3, 5). Batas bawah nilai fungsi objektif ialah Batas = + + + + + Tahap 8: Pergi ke subblok, yaitu baris ke-5 pada tabel alfabet.

Tahap 3: Belum semua verteks dikunjungi.

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4). Batas bawah nilai fungsi objektif Tahap 8: Pergi ke subblok, yaitu baris ke-4 pada tabel alfabet.

Tahap 2: Verteks 5 membentuk subtur, maka verteks 5 tidak dapat digunakan dan

p← 1+ 1 = 2 beralih ke Tahap 7.

(27)

17

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6). Batas bawah nilai fungsi objektif Tahap 8: Pergi ke subblok, yaitu baris ke-6 pada tabel alfabet.

Panjang tur taklengkap = 6 < 9 maka p = 1 dan ke Tahap 1 untuk iterasi Tahap 2: Verteks 4 membentuk subtur, maka verteks 4 tidak dapat digunakan dan

p ← 1 + 1 = 2 beralih ke Tahap 7. Tahap 2: Verteks 5 membentuk subtur, maka verteks 5 tidak dapat digunakan dan

p ← 2 + 1 = 3 beralih ke Tahap 7.

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 7). Batas bawah nilai fungsi objektif ialah

Batas = + + = + +

(28)

18

Tahap 6: Karena (batas + Sol + jarak) = 0 + 7 + 12 = 19 < BS, verteks 7 diterima untuk tur parsial {1→2→3→5→4→6→7}.

“Jaraktur parsial” = Sol ← Sol + jarak = 7 + 12 = 19. Tahap 8: Pergi ke subblok, yaitu baris ke-7 pada tabel alfabet.

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 7, 8). Batas bawah nilai fungsi Tahap 8: Pergi ke subblok, yaitu baris ke-8 pada tabel alfabet.

p ← 1+ 1 = 2 beralih ke Tahap 7.

Tahap 7: ∑� untuk cluster ketiga, panjang tur taklengkap {1→2→3→5→4→6→7→8} adalah 8 ≤ 9 dan elemen ke 2 < 9, maka proses dilanjutkan ke Tahap 1.

Tahap 1: Dilanjutkan ke elemen ke-2 pada baris ke-8 tabel alfabet dengan

dan “jarak verteks sekarang” = jarak = = 0 dan sesuai dengan urutan kunjungan cluster; (Sol + jarak) = 19 + 0 = 19 < BS. Tahap 2: Verteks 9 tidak membentuk subtur dan tidak melanggar urutan

(29)

19

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 7, 8, 9). Batas bawah nilai fungsi Tahap 8: Pergi ke subblok, yaitu baris ke-9 pada tabel alfabet.

Panjang tur taklengkap = 9 ≤ 9 maka p = 1 dan ke Tahap 1 untuk iterasi ke 2 < 9, maka proses dilanjutkan ke Tahap 1.

(30)

20

“Jarak tur parsial” = Sol ← Sol + jarak = 19 + 13 = 32. Tahap 8: Pergi ke subblok, yaitu baris ke-9 pada tabel alfabet.

Panjang tur taklengkap = 8 ≤ 9 maka p = 1 dan ke Tahap 1 untuk iterasi

Panjang tur taklengkap = 9 ≤ 9 maka p = 1 dan ke Tahap 1 untuk iterasi ke 2 < 9, maka proses dilanjutkan ke Tahap 1.

Tahap 1: Dilanjutkan ke elemen ke-2 pada baris ke-8 tabel alfabet dengan ke 3 < 9, maka proses dilanjutkan ke Tahap 1.

dan “jarak verteks sekarang” = jarak = = 38 dan sesuai dengan urutan kunjungan cluster; (Sol + jarak) = 32 + 38 = 70 > BS. Karena jarak turlengkap lebih besar dibanding 62, maka tidak diterima dan lanjut ke Tahap 9.

(31)

21

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 8). Batas bawah nilai fungsi Tahap 8: Pergi ke subblok, yaitu baris ke-8 pada tabel alfabet.

(32)

22

dan “jarak verteks sekarang” = jarak = = 0 dan sesuai dengan urutan kunjungan cluster; (Sol + jarak) = 38 + 0 = 38 < BS. Tahap 2: Verteks 8 membentuk subtur, maka verteks 8 tidak dapat digunakan dan

Tahap 7: ∑� untuk cluster ketiga, panjang tur taklengkap {1→2→3→5→4→6→8→7} adalah 8 ≤ 9 dan elemen ke 3 < 9, maka proses dilanjutkan ke Tahap 1.

dan “jarak verteks sekarang” = jarak = = 13 dan sesuai dengan urutan kunjungan cluster; (Sol + jarak) = 38 + 13 = 51 < BS. Tahap 2: Verteks 9 tidak membentuk subtur dan tidak melanggar urutan

kunjungan cluster.

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 8, 7, 9). Batas bawah nilai fungsi objektif ialah

Batas = = = 43.

Tahap 6: Karena (batas + Sol + jarak) = 43 + 38 + 13 = 94 > BS, jarak turlengkap lebih besar dibanding 62, maka tidak diterima dan lanjut ke Tahap 9. Tahap 9: Lompati blok ini dan pindah ke blok dengan level lebih tinggi.

Misalkan lompat ke blok dengan leader (1, 2, 3, 5, 4, 6), berarti pindah ke baris ke-6 dan p ← 5.

Tahap 5: Leader blok saat ini: (1, 2, 3, 5, 4, 6, 9). Batas bawah nilai fungsi Tahap 8: Pergi ke subblok, yaitu baris ke-9 pada tabel alfabet.

(33)

23

Tahap 2: Verteks 8 tidak membentuk subtur dan tidak melanggar urutan kunjungan cluster.

(34)

24

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 6 November 1992 sebagai anak ketiga dari tiga bersaudara, anak pasangan Drs Abdul Basit, M.Ag dan Siti Nihayah, S.Pd.I. Tahun 2004 penulis lulus dari SD Negeri Cipinang Muara 05 PG Jakarta, tahun 2007 penulis lulus dari SMP Negeri 27 Jakarta, tahun 2010 penulis lulus dari SMA Negeri 44 Jakarta. Penulis diterima di Institut Pertanian Bogor pada tahun 2010 melalui jalur Undangan Seleksi Masuk IPB (USMI) dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.