KONTROL OPTIMUM VAKSINASI DAN PENGOBATAN
PADA PENYAKIT MENULAR TIPE
SIR
FARICHATUL IVADA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Kontrol Optimum Vaksinasi dan Pengobatan pada Penyakit Menular Tipe SIR adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
FARICHATUL IVADA. Kontrol Optimum Vaksinasi dan Pengobatan pada Penyakit Menular Tipe SIR. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan FARIDA HANUM.
Saat ini terdapat banyak penyakit menular di masyarakat yang menyebabkan epidemi dalam populasi. Oleh karena itu, diperlukan program yang tepat untuk menanggulangi penyebaran penyakit menular tersebut seperti vaksinasi dan pengobatan. Penyebaran penyakit menular dapat digambarkan dengan model SIR. Pada penelitian ini dipaparkan model SIR, dianalisis dinamika populasinya, serta dilakukan optimalisasi pengendalian penyebaran penyakit menular melalui vaksinasi dan pengobatan. Hasil dari analisis, terdapat dua titik tetap yaitu titik tetap bebas penyakit dan titik tetap endemik penyakit. Selain itu, dari analisis model didapat pula bilangan reproduksi, ℛ0. Jika ℛ0 1 maka titik tetap bebas penyakit bersifat stabil global asimtotik, sedangkan jika ℛ0 > 1 maka titik tetap endemik bersifat global asimtotik. Kontrol optimum pada penelitian ini menggunakan pendekatan prinsip minimum Pontryagin dengan variabel kontrol berupa vaksinasi dan pengobatan. Tujuan pengendalian pada penelitian ini adalah mencari kombinasi yang optimal dari vaksinasi dan pengobatan sehingga dapat meminimumkan biaya total dari kedua kontrol sekaligus meminimumkan jumlah individu yang terinfeksi di akhir waktu.
Kata kunci: kontrol optimum, model SIR, pengobatan, prinsip minimum Pontryagin, vaksinasi. population. Therefore, an effective program is required to eliminate the infectious diseases, such as vaccination and treatment. The spread of infectious diseases can be modeled by SIR model, in which it enables us to predict the outbreak and the control rate. In this research, the SIR model is applied to analyze the population dynamic and to optimize the control of the outbreak with vaccination and treatment. As the result, the model provides two equilibrium points, i.e. dieases-free and diseases-endemic equilibrium points. Moreover, the analysis show that if the reproduction number or ℛ0 is less than or equal 1, then the disease-free equilibrium point is globally asymptotically stable. While if ℛ0 is more than 1, then the disease-endemic equilibrium point is globally asymptotically stable. In this research the optimal control uses Pontryagin’s minimum principle with vaccination and treatment as control measures. The control objective is to find the optimal combination of vaccination and treatment that minimizes the cost of the two control measures as well as the number of infected individuals at the end of control period.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
KONTROL OPTIMUM VAKSINASI DAN PENGOBATAN
PADA PENYAKIT MENULAR TIPE
SIR
FARICHATUL IVADA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Kontrol Optimum Vaksinasi dan Pengobatan pada Penyakit Menular Tipe SIR
Nama : Farichatul Ivada NIM : G54100006
Disetujui oleh
Dr Ir Endar H. Nugrahani, MS Pembimbing I
Dra Farida Hanum, MSi Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Alhamdulillahirabbil’alamiin. Segala puji bagi Allah SWT karena atas rahmat dan karunia-Nya penulis dapat menyelesaikan karya ilmiah ini. Shalawat dan salam terucap pula kepada Nabi Muhammad SAW yang telah membawa umat manusia dari kegelapan kepada cahaya yang terang benderang. Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih yang sebesar-besarnya kepada semua pihak yang telah mendukung dan membantu penulis, antara lain:
1 Alm. Bapak Marji dan Ibu Sumarti tercinta yang senantiasa mendoakan penulis dalam setiap kesempatan. Do’a yang selalu menjadi penerang jalan penulis. 2 Ibu Dr. Ir. Endar H. Nugrahani, MS dan Ibu Dra. Farida Hanum, M.Si selaku
dosen pembimbing. Terima kasih atas waktu, ilmu yang diberikan, dan kesabarannya dalam membimbing penulis.
3 Bapak Dr. Paian Sianturi selaku dosen penguji atas kesediaan waktu dan saran kepada penulis.
4 Keluarga tercinta Mbak Mas’uda, Mbak Masruroh, Kak Noer, Kak Ucuph, Bang Ady, adik Titah, dan si kecil Faiz yang selalu membuat penulis bersemangat.
5 Sahabat dan teman-teman Matematika 47 dan 46, Ponpesma Al Iffah, Berkah Crew, SERUM G, dan JCC yang selalu memberi semangat dan motivasi kepada penulis. Khususnya kepada Ceu Lia, Uci, Hasanah, Lilis, Mute, Dince, Dea, Peni, dan Desty.
6 Beasiswa Bidik Misi yang telah mendanai studi penulis selama di IPB.
Penulis menyadari bahwa karya ilmiah ini masih banyak kekurangannya, untuk itu kritik dan saran yang konstruktif sangat penulis harapkan demi perbaikan tulisan selanjutnya. Penulis berharap semoga karya ilmiah ini dapat bermanfaat.
Bogor, Juli 2014
DAFTAR ISI
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
Sistem Persamaan Diferensial dan Solusi Keseimbangan 2
Masalah Kontrol Optimum 4
Model SIR 5
HASIL DAN PEMBAHASAN 6
Model SIR dengan Vaksinasi 6
Titik Tetap Model 8
Bilangan Reproduksi 9
Analisis Kestabilan Titik Tetap 9
Konstruksi Matriks Jacobi 9
Kestabilan Lokal Titik Tetap 10
Kestabilan Global Titik Tetap 11
Masalah Kontrol Optimum 11
Fungsi Objektif 11
Fungsi Kendala 12
Prinsip Minimum Pontryagin 12
Simulasi Penerapan Kasus 13
SIMPULAN 19
DAFTAR PUSTAKA 20
LAMPIRAN 21
DAFTAR GAMBAR
1 Konsep kestabilan 4
2 Skema model SIR 6
3 Skema model SIR dengan pengaruh vaksinasi 7
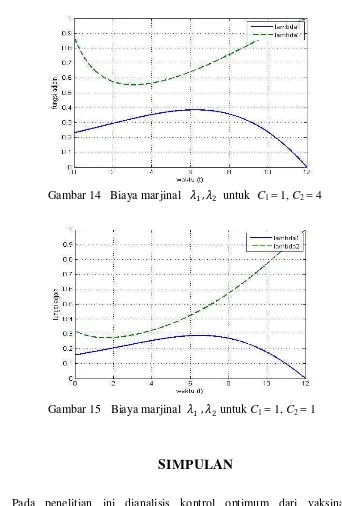
4 Dinamika populasi dengan ketiadaan vaksinasi dan pengobatan 14 5 Dinamika populasi ketika 1 = 0.02 dan 2 = 0.02 15 6 Dinamika populasi ketika 1 = 0.2 dan 2 = 0.06 15 7 Fungsi kontrol 1, 2 untuk C1 = 4, C2 = 1 16 8 Fungsi kontrol 1, 2 untuk C1 = 1, C2 = 4 16 9 Fungsi kontrol 1, 2 untuk C1 = 1, C2 = 1 16 10Suppopulasi S dan I untuk C1 = 4, C2 = 1 17 11Suppopulasi S dan I untuk C1 = 1, C2 = 4 17 12Suppopulasi S dan I untuk C1 = 1, C2 = 1 17 13Biaya Marjinal 1, 2 untuk C1 = 4, C2 = 1 18 14Biaya Marjinal 1, 2 untuk C1 = 1, C2 = 4 19 15Biaya Marjinal 1, 2 untuk C1 = 1, C2 = 1 19
DAFTAR LAMPIRAN
1 Pencarian solusi khusus ( ) 21
2 Pencarian titik tetap �0 dari sistem persamaan (6) 21 3 Pencarian titik tetap �1 dari sistem persamaan (6) 21 4 Pembuktian titik tetap �0 bersifat stabil lokal asimtotik jika ℛ0< 1 22 5 Perhitungan nilai eigen titik tetap endemik penyakit (dengan software
Maple) 23
6 Pembuktian titik tetap �1 bersifat stabil lokal asimtotik jika ℛ0 > 1 24 7 Simulasi bidang solusi dinamika populasi tanpa kontrol vaksinaasi dan
pengobatan (dengan software Maple) 25
8 Simulasi bidang solusi dinamika populasi dengan 1 = 2 = 0.02
(dengan software Maple) 25
9 Simulasi bidang solusi dinamika populasi dengan 1 = 0.2 dan
2 = 0.04 (dengan software Maple) 26
10 M-File Matlab untuk solusi numerik model SIR 26 11 M-File Matlab untuk plot fungsi kontrol, fungsi keadaan, dan fungsi
adjoint pada kasus I yaitu C1 = 4 dan C2 = 1 28 12 M-File Matlab untuk plot fungsi kontrol, fungsi keadaan, dan fungsi
adjoint pada kasus II yaitu C1 = 1 dan C2 = 4 28 13 M-File Matlab untuk plot fungsi kontrol, fungsi keadaan, dan fungsi
PENDAHULUAN
Latar Belakang
Seiring dengan perkembangan ilmu pengetahuan dan teknologi khususnya di bidang kesehatan, pengendalian penyebaran penyakit menular dapat dilakukan secara langsung dan tidak langsung. Secara langsung, terhadap individu yang rentan dapat dilakukan vaksinasi sedangkan terhadap individu yang telah terinfeksi dapat dilakukan pengobatan. Adapun pengendalian penyebaran penyakit menular secara tidak langsung dapat dilakukan dengan tindakan persuasif seperti edukasi baik di sekolah maupun di instansi pendidikan, kampanye pemahaman perihal penyebab, gejala penyakit, dan cara penularan. Individu yang telah terinfeksi penyakit menular harus segera mendapatkan pengobatan karena dapat berujung pada kematian apabila tidak segera diberi pengobatan secara tepat. Pengobatan penyakit menular dapat dilakukan dengan menggunakan antitoksik dan antibodi serta perawatan secara intensif. Selain dilakukan pengobatan, upaya pencegahan juga diperlukan untuk menanggulangi permasalahan ini agar tidak terulang kembali. Pencegahan penyakit ini dapat dilakukan dengan pemberian vaksinasi terhadap individu yang rentan.
Perkembangan ilmu pengetahuan di bidang matematika juga turut memberikan peranan penting dalam mencegah meluasnya penyebaran penyakit menular. Peranan tersebut berupa model matematika yang mempelajari penyebaran penyakit. Matematika memberikan salah satu solusi penyelesaian penyebaran penyakit menular. Pertama, pola endemik bisa digambarkan secara matematis dengan mendekati keadaan sebenarnya melalui suatu model matematika. Kedua, dengan matematika akan dianalisis pola endemik melalui model yang telah dirumuskan berdasarkan suatu asumsi.
Berdasarkan teori epidemik dari Kermark & McKendrick yang dikemukakan pertama kali pada tahun 1927, penyebaran penyakit menular biasanya dapat digambarkan secara matematis oleh model-model kompartemen seperti model SIR dengan setiap huruf mengacu pada kompartemen di mana individu dapat berada. Model SIR (Susceptibles, Infected, Recovered) ini dapat mentransformasikan kejadian epidemik suatu penyakit menular ke dalam model matematika sehingga laju penyebaran dan kepunahan suatu wabah penyakit dalam populasi dapat diketahui. Dari model ini dapat ditentukan solusi analitis dan titik kesetimbangannya, yang selanjutnya dianalisis sesuai permasalahan yang sesungguhnya dalam kehidupan nyata. Analisis ini meliputi perilaku penyebaran penyakit terhadap dinamika populasi serta eksistensinya pada kondisi bebas penyakit dan endemik penyakit. Selain menentukan laju penyebaran dan kepunahan, dari model matematika ini dapat dicari pula optimalisasi dari pengendalian penyebaran penyakit yakni vaksinasi dan pengobatan. Optimalisasi pada sistem dinamik pada umumnya menggunakan kontrol optimum (Tu 1994), dengan salah satu metode penyelesaian masalah kontrol optimum yang banyak digunakan adalah pendekatan prinsip maksimum atau minimum Pontryagin.
2
tidak konstan serta dilakukan penyelesaian masalah kontrol optimum dengan pendekatan prinsip minimum Pontryagin dengan kontrol berupa vaksinasi dan pengobatan.
Tujuan Penelitian
Tujuan dari penulisan penelitian ini ialah merekonstruksi model SIR dari penyakit menular yang telah dilakukan oleh Yusuf dan Benyah pada tahun 2012. Dari model ini akan dilakukan analisis dinamika populasi dengan menentukan titik tetap dan kestabilannya kemudian dilakukan optimalisasi tingkat vaksinasi dan pengobatan pada suatu populasi yang terkena wabah penyakit menular dengan pendekatan prinsip kontrol optimum, serta dilakukan simulasi terhadap nilai-nilai parameter yang memengaruhinya.
TINJAUAN PUSTAKA
Sistem Persamaan Diferensial dan Solusi Keseimbangan
Pemodelan matematika dapat digunakan untuk mengamati penyebaran suatu penyakit, khususnya penyakit menular. Salah satu model yang digunakan adalah dengan pendekatan SIR. Persamaan yang digunakan pada pendekatan SIR adalah sistem persamaan diferensial taklinear.
Diberikan sistem persamaan diferensial (SPD) sebagai berikut:
= , ,
= , .
Titik ( ∗, ∗) disebut titik tetap jika memenuhi ( ∗, ∗ ) = 0 dan ( ∗, ∗ ) = 0. Titik tetap disebut juga titik kritis atau titik kesetimbangan. Untuk selanjutnya akan digunakan istilah titik tetap. Untuk menganalisis kestabilan titik tetap dari suatu SPD taklinear, dapat dilakukan dengan pelinearan pada sistem persamaan diferensialnya. Andaikan ( ∗, ∗) adalah titik tetap dari persamaan di atas, maka ∗, ∗ = 0 dan ∗, ∗ = 0. Misalkan = − ∗ dan = − ∗ maka didapatkan:
=
= ( ∗+ , ∗+ )
= ∗, ∗ + + + ( 2, 2, )
= + + ( 2, 2, )
serta,
=
= ( ∗+ , ∗+ )
= ∗, ∗ + + + ( 2, 2, )
3 Dalam bentuk matriks:
= + 2, 2, .
Matriks �= disebut matriks Jacobi pada titik tetap ∗, ∗ . Karena ( 2, 2, )→ 0 maka dapat diabaikan sehingga didapat persamaan linear:
= .
(Strogatz 1994) Selain pelinearan, dibahas pula penentuan kestabilan dari suatu titik tetap. Kestabilan titik tetap dapat bersifat lokal dan global. Titik tetap bersifat stabil lokal jika kestabilan tersebut hanya berlaku untuk nilai awal di sekitar titik tetap, sedangkan kestabilan titik tetap bersifat global jika kestabilan berlaku untuk semua nilai awal pada daerah asal sehingga ketika → ∞, semua solusi akan menuju titik tetap. Berikut Definisi dari titik tetap stabil, stabil asimtotik lokal, dan stabil asimtotik global.
Definisi 1 Titik Tetap Stabil
Misalkan ∗ adalah titik tetap dari SPD dan merupakan solusi yang memenuhi kondisi awal 0 = 0 dengan 0 ≠ ∗. Titik tetap ∗ dikatakan stabil jika terdapat �0 > 0 yang memenuhi sifat yakni untuk setiap 0 < �1 <�0, terdapat �0 > 0 sedemikian sehingga jika ∗− 0 <� maka ∗− ( ) < �1, untuk > 0.
Definisi 2 Titik Tetap Stabil Lokal Asimtotik
Titik tetap ∗ dikatakan stabil lokal asimtotik jika titik ∗ stabil dan terdapat �> 0 sedemikian sehingga ∗− 0 <� maka lim →∞ ( ) = ∗, dengan 0 = 0.
Definisi 3 Titik Tetap Stabil Global Asimtotik
Titik tetap ∗ dikatakan stabil global asimtotik jika titik ∗ stabil dan terdapat 0 Ω ⊆ , lim→∞ ( ) = ∗, dengan 0 = 0.
4
Gambar 1 Konsep kestabilan
(Szidarovszky & Bahill 1997) Selain menggunakan Definisi, kestabilan titik tetap dapat ditentukan dengan mencari nilai eigen yang diperoleh dari penyelesaian solusi taknol matriks yang berukuran × . Misalkan � adalah matriks berukuran × dan adalah matriks identitas berukuran × , maka nilai eigen dari matriks � mempunyai solusi taknol jika dan hanya jika:
det � − = 0.
Dari persamaan di atas diperoleh nilai eigen, dengan = 1,2,3,… . Penentuan kestabilan titik tetap berdasarkan nilai eigen secara umum mempunyai perilaku sebagai berikut:
1 Stabil, jika
a) Setiap nilai eigen real adalah negatif ( < 0 untuk setiap i).
b) Setiap komponen bagian real dari nilai eigen kompleks, lebih kecil atau sama dengan nol, (Re( ) 0 untuk setiap i).
2 Stabil asimtotik, jika
a) Setiap nilai eigen real adalah negatif ( < 0 untuk setiap i).
b) Setiap komponen bagian real dari nilai eigen kompleks, lebih kecil dari nol, (Re < 0 untuk setiap i).
3 Takstabil, jika
a) Setiap nilai eigen real adalah positif ( > 0 untuk setiap i).
b) Setiap komponen bagian real dari nilai eigen kompleks lebih besar dari nol, (Re( ) > 0 untuk setiap i).
4 Sadel, jika perkalian dua buah nilai eigen real tertentu adalah negatif ( < 0 untuk suatu i dan j).
(Tu 1994)
Masalah Kontrol Optimum
Masalah kontrol optimum adalah masalah menentukan peubah kontrol yang dapat mengendalikan suatu proses sedemikian sehingga memenuhi beberapa kendala fisik dan dalam waktu yang sama mengoptimumkan kriteria tertentu. Masalah kontrol optimum dirumuskan sebagai berikut.
opt = , ,
5 Dari kontrol optimum ini ditentukan admissible control u*(t) yang dapat mengendalikan sistem dinamik
= , , ,
sedemikian sehingga mampu mengikuti admissible trajectory x*(t) dalam interval waktu [0,T] dan mengoptimumkan fungsional objektif
= , + , , 0
,
dengan adalah peubah keadaan atau variabel state dan fungsi , didefinisikan sebagai fungsi scrap. Fungsi scrap adalah fungsi yang menggambarkan keadaan sistem di akhir periode.
Syarat perlu untuk meminimumkan suatu besaran dalam masalah kontrol optimum adalah terpenuhinya prinsip minimum Pontryagin. Pendekatan prinsip minimum Pontryagin banyak menggunakan teknik dalam kalkulus variasi. Perhatikan masalah kontrol optimum berikut: Dalam masalah kontrol optimum terdapat fungsi Hamilton yang dapat memaksimumkan atau meminimumkan fungsi objektif dengan kendala berupa persamaan diferensial. Fungsi Hamilton didefinisikan sebagai:
, , , ≔ , , + , , , (1)
∗, ∗, ∗, , , , ,
dengan merupakan “pengali Hamilton” atau atau variabel adjoint. Syarat perlu optimalitas masalah kontrol optimum adalah,
1 ( ) meminimumkan fungsi Hamilton H yaitu, = 0 ⟺ = 0,
6
tersebut terdiri dari kelas individu S yang rentan terserang penyakit, kelas individu I yang terinfeksi penyakit, dan kelas individu R yang telah sembuh. Dalam penyebaran penyakit, diasumsikan bahwa penyakit menular melalui kontak langsung antara individu rentan dengan individu terinfeksi dengan laju sebesar serta laju penyembuhan individu terinfeksi dilambangkan dengan . Individu yang terinfeksi kemudian sembuh dan memiliki kekebalan yang tetap sehingga tidak akan terjangkit penyakit kembali. Berikut adalah ilustrasi gambar penyebaran penyakit tipe SIR.
Gambar 2 Skema model SIR
Persamaan diferensial yang dibuat Kermack dan McKendrick untuk penyakit yang diilustrasikan dalam Gambar 2 sebagai berikut.
= − ,
= − ,
= .
HASIL DAN PEMBAHASAN
Model SIR dengan Vaksinasi
Model endemik SIR dengan memperhatikan faktor vaksinasi diturunkan ulang dari model endemik SIR klasik. Model penyebaran penyakit diturunkan menggunakan asumsi atau batasan tertentu. Pada pembentukan model SIR ini diberikan berbagai asumsi, yaitu
1 jumlah populasi diasumsikan cukup besar, 2 populasi tertutup (tidak ada proses migrasi),
3 terjadi proses kelahiran dan kematian namun dengan kelajuan yang berbeda sehingga jumlah populasi tidak konstan,
4 setiap individu yang belum terserang penyakit masuk ke subpopulasi susceptible (rentan terserang),
5 penyakit dapat disembuhkan,
6 individu yang sembuh mempunyai kekebalan tetap,
7 penyakit menular melalui kontak langsung antara individu rentan dengan penderita.
Selanjutnya program vaksinasi diperhatikan dalam model. Diasumsikan bahwa keefektifan vaksinasi adalah 100% sehingga setiap individu yang telah mendapatkan vaksinasi akan kebal dari penyakit. Kekebalan yang terjadi karena vaksinasi bersifat permanen. Individu yang memperoleh vaksinasi kebal dari penyakit dan memasuki subpopulasi sembuh.
7 Pada model SIR ini laju kelahiran dilambangkan dengan . Karena laju kelahiran tidak sama dengan laju kematian maka laju kematian alami dilambangkan dengan yang besarnya sama untuk setiap subpopulasi. Setiap individu yang lahir dalam populasi akan memasuki subpopulasi rentan. Pada subpopulasi rentan dalam jangka waktu tertentu, individu yang tidak memperoleh vaksinasi akan memasuki subpopulasi yang terinfeksi sedangkan individu yang mendapatkan vaksinasi akan memasuki subpopulasi yang sembuh. Laju penularan penyakit dilambangkan dengan sedangkan laju vaksinasi dilambangkan dengan 1. Pada subpopulasi yang terinfeksi penyakit, individu yang mendapatkan pengobatan dapat sembuh dari penyakit namun yang tidak mendapatkan pengobatan dapat mengalami kematian akibat penyakit tersebut. Laju pengobatan dilambangkan dengan 2 sedangkan laju kematian akibat penyakit dilambangkan dengan . Subpopulasi yang sembuh, terdiri dari individu rentan yang mendapatkan vaksinasi dan individu yang terinfeksi yang telah mendapatkan pengobatan. Berikut ini gambar skema penyebaran penyakit tipe SIR dengan pengaruh vaksinasi.
Dari Gambar 3 maka model endemik SIR dengan mempertimbangkan pengaruh vaksinasi selengkapnya dapat diekspresikan dengan persamaan-persamaan sebagai berikut. Pertama, laju perubahan individu rentan atau susceptible dapat dinyatakan sebagai:
= − − 1 − . (2)
Kedua, laju perubahan individu terinfeksi atau infected diekspresikan dengan
= − 2 − − . (3)
Serta yang ketiga, laju perubahan individu yang sembuh dari penyakit atau recovered adalah
= 1 + 2 − . (4)
dengan parameter-parameter , , , > 0, batas laju vaksinasi dan pengobatan adalah 0 1 1, dan 0 2 1 serta batas jumlah individu di setiap subpopulasi sebesar 0 0, (0) 0, dan (0) 0.
Karena dalam asumsi dinyatakan bahwa laju kelahiran dengan laju kematian tidak sama maka total populasi bersifat tidak konstan. Dengan memperhatikan bahwa = + + maka didapat persamaan laju perubahan total populasi yakni
= − − . (5)
Dari persamaan (2)-(5) dapat diperhatikan bahwa pada persamaan (2) dan (3), variabel R tidak muncul. Hal ini menunjukkan bahwa jumlah individu pada
8
subpopulasi R tidak memengaruhi laju perubahan jumlah individu pada subpopulasi S maupun I, sehingga untuk penyelesaian R dapat diperoleh dari
= − − , jika nilai S, I, dan N sudah diperoleh. Dengan demikian persamaan (2)-(5) dapat direduksi sebagai berikut.
= = − − 1 −
= = − 2 − −
= = − − .
(6)
Pada keadaan bebas penyakit yaitu ketika jumlah individu terinfeksi dalam populasi tidak ada, dengan kata lain = 0, maka = − . Dengan melakukan perhitungan kalkulus diperoleh penyelesaian
= 1− − − 0 − (perhitungan disajikan dalam Lampiran 1).
Jika membesar maka diperoleh lim →∞ ( ) = , sehingga dapat dijelaskan bahwa dalam jangka waktu yang panjang, total populasi manusia akan menuju kapasitas batas yakni . Namun ketika terjadi endemik penyakit maka total populasi akan berubah hingga titik tertentu sehingga daerah solusi model sebagai berikut
Ω= � = ( , , ) ∈ 3| 0, 0, + , (7)
dengan � merupakan ruang skalar bilangan real yang berelemen tiga.
Titik Tetap Model
Analisis titik tetap pada sistem persamaan diferensial sering digunakan untuk menentukan suatu solusi yang tidak berubah terhadap waktu (solusi konstan). Titik tetap dari persamaan (6) dapat diperoleh dengan menentukan = 0, = 0, dan = 0. Dengan menyelesaikan persamaan secara bersamaan maka akan diperoleh dua titik tetap.
Titik yang pertama disebut sebagai titik tetap bebas penyakit. Dikatakan demikian karena dalam populasi tidak terdapat individu yang terinfeksi dengan kata lain = 0. Dengan kondisi ini didapat titik tetap bebas penyakit sebagai berikut.
�0 = 0, 0, 0 = 1+
,0,
(penurunan persamaan diberikan pada Lampiran 2).
9
Bilangan Reproduksi
Bilangan reproduksi atau dikenal dengan ℛ0 menunjukkan bentuk kuantitatif atau indikator dari tingkat penyebaran penyakit. Menurut Hethcote (2000), bilangan reproduksi merupakan bilangan yang menunjukkan jumlah individu susceptible yang dapat menderita penyakit yang diakibatkan oleh satu individu infected. ℛ0 merupakan rasio antara jumlah individu susceptible pada kondisi bebas penyakit dengan jumlah individu susceptible pada kondisi endemik penyakit. Selanjutnya bilangan reproduksi dalam tulisan ini merupakan bilangan reproduksi pada kasus yang memperhatikan faktor vaksinasi dan pengobatan yang dinyatakan sebagai
ℛ0 = 0∗ = 1+ 2+ + . (8)
Ketika ℛ0 < 1, satu individu infected hanya akan menularkan penyakit kepada kurang dari satu individu susceptible atau dengan kata lain tidak ada individu baru yang tertular sehingga penyakit akan menghilang dalam populasi, sedangkan ketika ℛ0 > 1, satu individu infected akan menularkan penyakit kepada lebih dari satu individu susceptible sehingga penyakit akan berkembang menjadi endemik dalam populasi.
Bilangan reproduksi ini akan berkaitan dengan analisis kestabilan dari titik tetap yang ada baik lokal maupun global karena bilangan reproduksi merupakan ambang batas (threshold) terjadinya penyebaran penyakit. Menurut Giesecke (1994) beberapa kondisi yang ditimbulkan oleh ℛ0
1 Jika ℛ0 < 1, maka penyakit akan menghilang dalam populasi (bebas penyakit), 2 Jika ℛ0 = 1, maka penyakit akan menetap dalam populasi,
3 Jika ℛ0 > 1, maka penyakit akan meningkat menjadi wabah dalam populasi (endemik penyakit).
Berikut bentuk lain dari titik tetap endemik dengan melibatkan ekspresi ℛ0 ∗ = 1
Analisis kestabilan ditentukan berdasarkan nilai eigen dari matriks Jacobi yang diperoleh dari metode linearisasi. Misalkan
, , = − − 1 − ,
, , = − 2 − − ,
, , = − − .
10
Dari persamaan (9) akan diperoleh matriks Jacobi sebagai berikut:
= =
1 Titik tetap bebas penyakit �0
Dengan menyubstitusikan titik �0 =
1+ ,0,
Nilai eigen dari matriks Jacobi 0 diperoleh dengan menggunakan persamaan |0 − | = 0 yaitu lokal asimtotik, sehingga dapat disimpulkan bahwa titik tetap bebas penyakit �0 akan stabil lokal asimtotik jika ℛ0 < 1 yaitu pada kondisi penyakit telah menghilang dalam populasi.
2 Titik tetap endemik penyakit �1
Pelinearan pada titik tetap �1 akan menghasilkan matriks Jacobi sebagai
dengan menghitung |1− | = 0, maka didapat nilai eigen 1 = − ,
2,3 =
−ℛ0 1+ ± ℛ02 1+ 2−4 ℛ0−1 1+ ( 2+ + ) 2
(bukti pada Lampiran 5).
11 (penyakit bersifat endemik). Berikut adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh.
Tabel 1 Kondisi kestabilan lokal titik tetap
Kondisi �0 �1
ℛ0 < 1 Stabil asimtotik Tidal stabil ℛ0 > 1 Tidak stabil Stabil asimtotik
Tabel 1 menunjukkan bahwa dinamika sistem ditentukan oleh bilangan reproduksi dasar. Ketika ℛ0 < 1 titik tetap bebas penyakit akan stabil lokal asimtotik yang berarti bahwa penyakit tidak akan menyebar dalam populasi atau dengan kata lain pada akhirnya penyakit akan hilang dari populasi. Ketika ℛ0 > 1 titik tetap endemik penyakit akan stabil lokal asimtotik yang berarti bahwa penyakit akan tetap ada dan menyebar dalam populasi.
Kestabilan Global Titik Tetap
Menurut Yusuf dan Benyah (2012) kestabilan global titik tetap pada persamaan (8) dipengaruhi oleh bilangan reproduksi sebagai berikut.
1 Jika ℛ0 1, maka titik tetap bebas penyakit bersifat stabil global asimtotik. Pada kondisi ℛ0 1 maka dalam populasi tidak terdapat penyakit atau = 0. Ketika = 0 disubstitusikan ke persamaan dan , akan diperoleh nilai
→
1+ dan → ketika → ∞
, sehingga didapat tititk tetap ε0. Titik tetap bebas penyakit bersifat global asimtotik artinya bahwa setiap nilai awal � 0 ∈ Ω maka setiap solusi � yang dihasilkan akan menuju titik tetap ε0 untuk t → ∞.
2 Jika ℛ0 > 1, maka titik tetap endemik penyakit bersifat global asimtotik. Jika ℛ0 > 1 yang artinya dalam populasi terdapat endemik penyakit maka setiap solusi dari sistem persamaan (8), dengan nilai awal � 0 ∈ Ω akan mendekati titik tetap �1 untuk t → ∞. Oleh karena itu, jika ℛ0 > 1 dalam jangka waktu yang panjang populasi akan selalu terjangkit penyakit dan setiap subpopulasi susceptible, infected, recovered, maupun populasi total akan mendekati titik tetap ε1.
Masalah Kontrol Optimum
Pada bagian ini akan dibahas model masalah kontrol optimum dengan tiga bahasan yaitu, model fungsi objektif dan fungsi kendala serta penyelesaian dengan prinsip minimum Pontryagin.
Fungsi Objektif
12
penyebaran penyakit dengan cara pemberian vaksinasi dan pengobatan. Diasumsikan sumber daya (keuangan) terbatas dan fungsi biaya berbentuk kuadrat sehingga pada tingkat tertentu laju kontrol vaksinasi 1 dan laju kontrol pengobatan 2 dapat meminimumkan total biaya sekaligus meminimumkan jumlah individu yang terinfeksi. Bentuk �1 12 menyatakan fungsi biaya dari vaksinasi dan bentuk �2 22 merupakan fungsi biaya dari pengobatan.
Fungsi objektif Z dari kontrol optimum ini secara matematik dapat
Dari hasil observasi diperoleh informasi bahwa tingkat vaksinasi dan pengobatan masing-masing mempengaruhi jumlah individu susceptible dan infected. Semakin besar tingkat vaksinasi yang diberikan maka jumlah individu susceptible semakin berkurang. Begitu pula ketika tingkat pengobatan diperbesar maka jumlah individu yang terinfeksi pun akan semakin berkurang. Dengan kata lain, jumlah individu susceptible dan infected dipengaruhi atau dikontrol langsung oleh tingkat vaksinasi dan pengobatan sehingga fungsi kendala dapat dinyatakan sebagai,
= − − 1 − ,
= − 2 − − . (12)
Jumlah individu recovered tidak secara langsung memengaruhi tingkat vaksinasi maupun pengobatan. Jumlah individu recovered merupakan akibat dari pemberian vaksinasi terhadap individu susceptible dan pemberian pengobatan terhadap individu infected sehingga tidak perlu disertakan dalam fungsi kendala. Adapun total populasi ( ) juga tidak termasuk fungsi kendala pada masalah maka diperoleh fungsi Hamilton yang dinyatakan sebagai
ℋ =1
2(�1 1 2+�
2 22) + 1 − − 1 − + 2 − 2 − − . (13) Penyelesaian masalah kontrol optimum dengan menerapkan prinsip minimum Pontryagin memberikan syarat optimalitas (1), yaitu meminimumkan fungsi Hamilton dengan cara ℋ = 0 dengan = 1,2 sehingga didapat 1 = 1
13 berkorespondensi terhadap variabel keadaan ∗, ∗ yang meminimumkan fungsi objektif, maka terdapat variabel adjoint 1 dan 2 yang memenuhi serta diperoleh pula variabel S dan I yang merupakan fungsi kendala, yakni
= ℋ Dari persamaan (14) dan (15) serta syarat transversalitas persamaan (16) dan syarat batas di atas maka sistem optimal dari masalah kontrol optimum ini dapat dituliskan sebagai berikut.
14
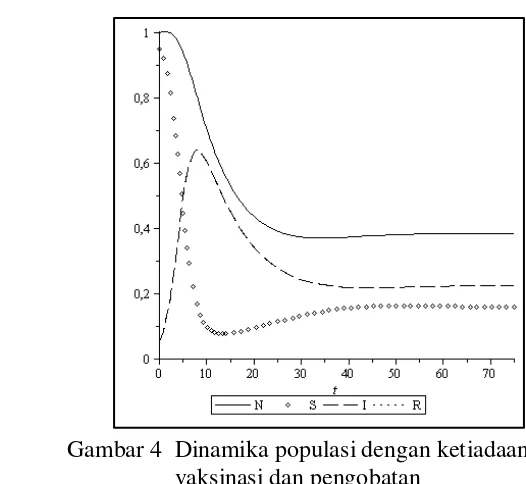
Gambar 4 Dinamika populasi dengan ketiadaan vaksinasi dan pengobatan
Gambar 4 menunjukkan proporsi individu susceptible, infected, recovered, dan total populasi di mana pemberian vaksinasi dan pengobatan ditiadakan ( 1 = 0 dan 2 = 0). Subpopulasi susceptible mengalami penurunan cukup signifikan pada beberapa tahun pertama sedangkan proporsi individu infected mengalami kenaikan yang cukup signifikan pada waktu 10. Hal ini terjadi karena individu susceptible mulai terinfeksi penyakit dan memasuki subpopulasi infected akibat dari tidak adanya penanganan berupa vaksinasi subpopulasi infected semakin bertambah. Begitu pula dengan ketiadaan pengobatan sehingga subpopulasi recovered sama dengan nol akibatnya subpopulasi infected hanya akan meninggalkan subpopulasinya jika mengalami kematian saja. Hal ini mengakibatkan total populasi pun menurun proporsinya secara signifikan. Namun, pada waktu t menuju takhingga ( 50), jumlah individu pada subpopulasi susceptible dan infected serta total populasi tidak mengalami perubahan. Pada keadaan tersebut sistem berada pada kondisi setimbang. Pada kondisi tersebut, penyakit akan selalu ada sampai waktu yang tak terbatas, dengan kata lain penyakit bersifat endemik dalam populasi. Kondisi setimbang tersebut dicapai pada ε1 = (0.16, 0.223, 0.383 ). Dari kesetimbangan ini terlihat penurunan proporsi pada total populasi tidak akan menyebabkan populasi mengalami kepunahan.
Pengendalian dianggap berhasil jika pada waktu tertentu penyakit menghilang dari populasi. Bilangan reproduksi dapat digunakan untuk menentukan apakah penyakit telah menghilang atau bersifat endemik dalam populasi. Penyakit dikatakan menghilang jika ℛ0 < 1 sedangkan penyakit dikatakan endemik jika ℛ0 > 1. Adapun dari persamaan (8) diketahui nilai
ℛ0 =
1+ 2+ + .
Dengan menyubstitusikan nilai-nilai parameter yang diberikan maka didapat proporsi 1 = 0.0225
15 jika tingkat vaksinasi atau pengobatan diberikan lebih besar dari nilai tersebut maka penyakit akan menghilang dalam populasi karena ℛ0 < 1. Kedua kondisi ini diilustrasikan dalam Gambar 5 dan Gambar 6.
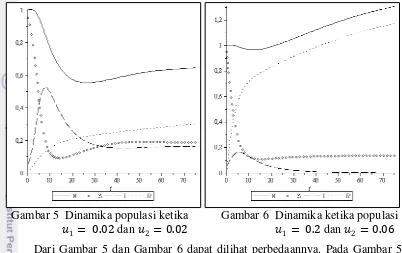
Gambar 5 Dinamika populasi ketika Gambar 6 Dinamika ketika populasi 1 = 0.02 dan 2 = 0.02 1 = 0.2 dan 2 = 0.06 Dari Gambar 5 dan Gambar 6 dapat dilihat perbedaannya. Pada Gambar 5 ketika nilai 1 dan 2 dibuat lebih kecil dari 1 dan 2 , hingga waktu tak terbatas ( > 50) penyakit selalu ada dalam populasi atau penyakit bersifat endemik. Hal ini menunjukkan program vaksinasi dan pengobatan belum berhasil memusnahkan penyakit. Sedangkan Gambar 6 menunjukkan bahwa penyakit akan menghilang dalam kurun waktu kurang dari 50 tahun ketika diberikan nilai 1 > 1 dan 2 > 2 . Hal ini menunjukkan bahwa pengendalian penyebaran penyakit berhasil memusnahkan penyakit dalam populasi.
Selanjutnya akan diberikan simulasi tiga kasus di mana setiap kasus memiliki kombinasi bobot relatif dari biaya setiap kontrol kemudian dianalisis pengaruhnya terhadap variabel kontrol ( 1, 2), variabel adjoint ( 1, 2), dan terhadap dinamika populasinya (S,I). Kasus 1 bobot relatif dari biaya vaksinasi dibuat lebih besar dari biaya pengobatan yakni C1 = 4, C2 = 1, kasus II bobot relatif dari biaya pengobatan lebih besar dari vaksinasi atau C1 = 1, C2 = 4, dan kasus III di mana kedua biaya kontrol memiliki bobot relatif yang sama yakni C1=C2 = 1.
16
17
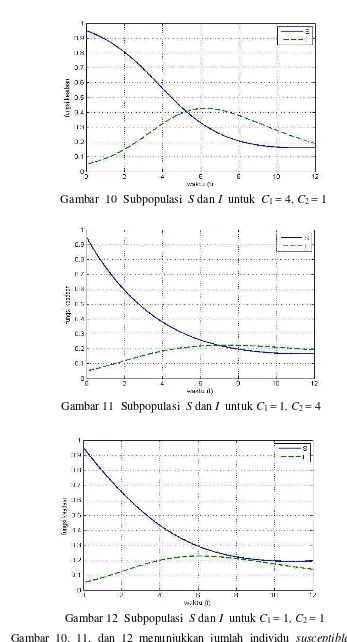
Gambar 10, 11, dan 12 menunjukkan jumlah individu susceptible yang semakin berkurang sedangkan jumlah individu infected mengalami kenaikan. Pada Gambar 10, untuk pengoptimuman diterapkan kontrol pengobatan lebih
18
banyak karena bobot relatif biaya dari pengobatan yang lebih kecil daripada vaksinasi. Namun, penerapan kontrol pengobatan yang lebih banyak tidak secara signifikan menurunkan jumlah individu infected dengan titik puncak masih mencapai 0.4, dibandingkan dengan kasus ketika menerapkan lebih banyak vaksinasi, titik puncak jumlah individu infected hanya mencapai 0.2. Begitu pula ketika bobot relatif dari biaya kontrol sama, puncak jumlah individu infected tidak jauh berbeda dengan kasus bobot relatif dari biaya vaksinasi yang lebih kecil daripada bobot relatif dari biaya pengobatan.
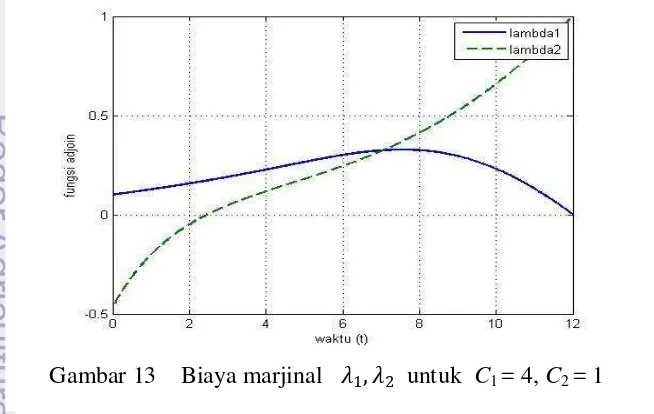
Gambar 13, 14, dan 15 menunjukkan solusi numerik dari nilai adjoint 1 dan 2. Dalam masalah kontrol optimum, nilai adjoint menunjukkan nilai marjinal dari fungsi objektif akibat dari perubahan variabel state atau variabel keadaan. Karena fungsi objektif dalam penelitian ini berkaitan dengan fungsi biaya dan dinamika variabel keadaan (individu susceptible dan infected) dikontrol oleh tingkat vaksinasi dan pengobatan maka dalam penelitian ini merepresentasikan biaya marjinal dari tiap kontrol yakni 1 untuk biaya marjinal dari kontrol vaksinasi dan 2 untuk biaya marjinal dari kontrol pengobatan. Biaya marjinal dalam masalah kontrol optimum ini menunjukkan peningkatan atau penurunan total biaya akibat dari penambahan atau pengurangan kontrol vaksinasi maupun pengobatan.
Gambar 13 yakni ketika C1= 4 dan C2 = 1, biaya marjinal untuk vaksinasi dan pengobatan mengalami kenaikan. Namun setelah perpotongan, biaya marjinal dari vaksinasi mengalami penurunan sedangkan biaya marjinal dari pengobatan semakin meningkat. Peningkatan biaya marjinal pada kedua kontrol menyebabkan biaya yang dikeluarkan tidak ekonomis. Kasus C1 = 1 dan C2 = 4, pada beberapa awal tahun pengendalian biaya marjinal dari vaksinasi meningkat secara perlahan sedangkan biaya marjinal dari pengobatan mengalami penurunan, namun terjadi sebaliknya pada beberapa akhir tahun pengendalian. Kedua biaya marjinal tidak mengalami overlapping (tumpang tindih), hal ini menunjukkan bahwa lebih ekonomis untuk memperbesar jumlah vaksinasi daripada pengobatan karena bobot relatif dari vaksinasi lebih rendah dari pengobatan. Pada kasus C1 = C2 = 1, Gambar 15 menunjukkan pola yang sama dengan kasus C1 = 1 dan C2 = 4.
19
SIMPULAN
Pada penelitian ini dianalisis kontrol optimum dari vaksinasi dan pengobatan terhadap model epidemik SIR dengan jumlah populasi tidak konstan. Berdasarkan hasil dan pembahasan, hasil analisis yang telah dilakukan pada model matematika ini diperoleh dua titik tetap yaitu titik tetap bebas penyakit dan titik tetap endemik penyakit. Dari analisis kestabilan baik lokal maupun global, dinamika populasi bergantung pada bilangan reproduksi dasar. Ketika bilangan reproduksi dasarnya kurang dari satu maka titik tetap bebas penyakit akan stabil asimtotik yang berarti bahwa penyakit tidak akan menyebar dalam populasi atau pada akhirnya penyakit akan hilang dari populasi. Jika bilangan reproduksi dasarnya lebih dari satu maka titik tetap endemik akan stabil asimtotik yang berarti bahwa penyakit akan tetap ada dan menyebar dalam populasi.
20
Selanjutnya, dari analisis kontrol optimum secara matematis dan simulasi terhadap strategi kontrol vaksinasi dan pengobatan dengan beberapa tingkat biaya diperoleh kesimpulan sebagai berikut:
1 Pada kasus di mana bobot relatif dari biaya vaksinasi lebih besar dari biaya pengobatan, sumber daya (keuangan) sebaiknya lebih banyak digunakan untuk biaya pengobatan hingga penyakit mulai menurun penyebarannya, namun pilihan ini tidak menurunkan jumlah subpopulasi yang rentan secara signifikan sehingga jumlah subpopulasi yang terinfeksi tetap tinggi.
2 Pada kasus di mana bobot relatif dari biaya vaksinasi lebih kecil dari biaya pengobatan, sumber daya (keuangan) sebaiknya lebih banyak digunakan untuk biaya vaksinasi. Hal ini mengakibatkan penurunan jumlah subpopulasi yang rentan yang juga mengakibatkan penurunan jumlah subpopulasi yang terinfeksi secara signifikan.
3 Pada kasus di mana kedua biaya memiliki bobot relatif sama, sumber daya (keuangan) sebaiknya pada awal tahun terjadinya epidemik lebih banyak digunakan untuk biaya vaksinasi sehingga mendorong penurunan tingkat epidemik penyakit hingga batas waktu tertentu kemudian diterapkan lebih banyak pengobatan daripada vaksinasi.
DAFTAR PUSTAKA
Giesecke J. 1994. Modern Infectious Disease Epidemiology. New York (US): Oxford Univ Pr.
Hethcote HW. 2000. The mathematics of infectious diseases. SIAM Rev. 42(4):599-653. 10.1137/S0036144500371907
Strogatz SH. 1994. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. Massachusete (US): Addison-Wesley. Szidarovszky F, Bahill AT. 1997. Linear System Theory. Ed ke-2. Florida (US):
CRC Press.
Tu PNV. 1993. Introductory Optimization Dynamics: Optimal Control with Economics and Management Applications. Second Revised and Enlarged Edition.
Heidelberg (DE): Springer-Verlag.
21 Lampiran 1 Pencarian solusi khusus
Laju perubahan total populasi pada t tertentu adalah = − − . Pada keadaan bebas penyakit, = 0, maka
= − . (18)
Dari persamaan (18) dilakukan perhitungan kalkulus dengan mengintegralkan kedua ruas menjadi
Maka diperoleh titik tetap bebas penyakit �0 =
1+ ,0,
Lampiran 3 Pencarian titik tetap �1 dari sistem persamaan (6) Titik tetap endemik penyakit �1 = ( ∗, ∗, ∗)
Karena keadaannya adalah penyakit bersifat endemik maka solusi yang berlaku adalah = 2+ +
= 0
22 Maka titik tetap penyakit bersifat endemik adalah
�1 = 2
Matriks Jacobi dari titik tetap bebas penyakit
0 =
23
1+ −
( 2+ + ) < 0
1+
< ( 2+ + )
1+
( 2+ + )< 1
1+ 2+ +
< 1
ℛ0< 1
24
Lampiran 6 Pembuktian titik tetap �1 bersifat stabil lokal asimtotik jika ℛ0 > 1
Matriks Jacobi dari titik tetap endemik penyakit
1 =
ℛ0−1 1 +
− 1 − − 2 + +
0
ℛ0−1 1
+ 2+ +
− 2− − 0
0 − −
=
−ℛ0 1+ 2 + + 0 ℛ0−1 1+ 0 0
0 − −
Nilai eigen dicari dengan menyelesaikan solusi persamaan taknol 1− � = 0
−ℛ0 1+ − 2+ + 0 ℛ0−1 1+ − 0
0 − − −
= 0
Dari perhitungan menggunakan Maple 13 (lihat Lampiran 5), diperoleh nilai eigen 1 = −
2,3 = −ℛ0 1+ ± ℛ02 1+ 2−4 ℛ0−1 1+ ( 2+ + ) Agar �1 bersifat stabil lokal asimtotik maka < 0 untuk i = 1, 2, 3, sehingga
1< 0, karena > 0. Maka 2,3 < 0 sehingga 2 < 0
−ℛ0 1+ + ℛ02 1+ 2−4 ℛ0−1 1+ 2+ + < 0
−ℛ0 1+ < − ℛ02 1+ 2−4 ℛ0−1 1+ 2+ +
25 Karena ℛ02 1+ 2 > 0 dan 4 1+ 2+ + > 0, agar terpenuhi kondisi di atas maka (ℛ0−1) > 0, sehingga ℛ0 > 1
Begitu pula dengan
3 < 0
−ℛ0 1+ − ℛ02 1+ 2−4 ℛ0−1 1+ 2+ + < 0
ℛ0 1+ + ℛ02 1+ 2−4 ℛ0−1 1+ 2+ + > 0
ℛ0 1+ > − ℛ02 1+ 2 −4 ℛ0−1 1+ 2+ +
Karena ℛ02 1+ 2 > 0 dan 4 1+ 2+ + > 0, agar terpenuhi kondisi di atas maka (ℛ0−1) > 0, sehingga ℛ0 > 1
Lampiran 7 Simulasi bidang solusi dinamika populasi tanpa kontrol vaksinasi dan pengobatan (dengan menggunakan software Maple)
>
>
> >
Lampiran 8 Simulasi bidang solusi dinamika populasi dengan 1 = 0.02 dan 2 = 0.02 (dengan software Maple)
26
>
Lampiran 9 Simulasi bidang solusi dinamika populasi dengan 1 = 0.2 dan 2 = 0.04 (dengan software Maple)
>
>
> >
Lampiran 10 M-File Matlab untuk solusi numerik model SIR
function [u1,u2,S,I,lambda1,lambda2,J] =
SIR_withcontrol(beta,alfa,gama,mu,S0,I0,C1,C2,t0,tf,n)
tol = 0.01; err1= tol + 1; err2= tol + 1; hasilc=[]; h = (tf-t0)/n; S = zeros(1,n+1); I = zeros(1,n+1);
lambda1 = zeros(1,n+1); lambda2 = ones(1,n+1);
u1 = zeros(1,n+1)+0.05; u2 = zeros(1,n+1)+0.05; S(1) = S0;
I(1) = I0;
28
grid; xlabel('waktu (t)'); ylabel('fungsi kontrol');
hold on
figure(2)
plot(t,S,t,I,'--','LineWidth',2); legend('S','I');
grid; xlabel('waktu (t)'); ylabel('fungsi keadaan');
hold on
figure(3)
plot(t,lambda1,t,lambda2,'--','LineWidth',2);
legend('lambda1','lambda2');
grid; xlabel('waktu (t)'); ylabel('fungsi adjoin');
29
grid; xlabel('waktu (t)'); ylabel('fungsi kontrol');
hold on
figure(2)
plot(t,S,t,I,'--','LineWidth',2); legend('S','I');
grid; xlabel('waktu (t)'); ylabel('fungsi keadaan');
hold on
figure(3)
plot(t,lambda1,t,lambda2,'--','LineWidth',2);
legend('lambda1','lambda2');
grid; xlabel('waktu (t)'); ylabel('fungsi adjoin');
hold on
grid; xlabel('waktu (t)'); ylabel('fungsi kontrol');
hold on
figure(2)
plot(t,S,t,I,'--','LineWidth',2); legend('S','I');
grid; xlabel('waktu (t)'); ylabel('fungsi keadaan');
hold on
figure(3)
plot(t,lambda1,t,lambda2,'--','LineWidth',2);
legend('lambda1','lambda2');
grid; xlabel('waktu (t)'); ylabel('fungsi adjoin');
30
RIWAYAT HIDUP
Penulis lahir di Lamongan, Jawa Timur pada tanggal 9 Mei 1993 dari pasangan Bapak Marji dan Ibu Sumarti. Penulis merupakan anak keenam dari enam bersaudara. Tahun 2004 penulis lulus dari SDN Kanugrahan, kemudian melanjutkan studi di SMPN 1 Maduran, Lamongan dan lulus pada tahun 2007. Tahun 2010 penulis berhasil menamatkan studi di SMAN 1 Gresik yang kemudian melalui jalur Undangan Saringan Masuk IPB (USMI) penulis dapat melanjutkan pendidikan sarjana di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor (IPB).