Kajian Simplicial Complex dan kth Betti Number pada cakupan jaringan penguat sinyal GSM Indoor

KAJIAN

SIMPLICIAL COMPLEX

DAN

K

TH

BETTI NUMBER

PADA CAKUPAN JARINGAN PENGUAT

SINYAL GSM

INDOOR

FACHRI ADITYA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Kajian Simplicial Complex dan kth Betti Number pada Cakupan Jaringan Penguat Sinyal GSM Indoor adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

ABSTRAK

FACHRI ADITYA. Kajian Simplicial Complex dan kth Betti Number pada Cakupan Jaringan Penguat Sinyal GSM Indoor. Dibimbing oleh SUGI GURITMAN dan FARIDA HANUM.

Sinyal perangkat mobile sering kali menghilang saat memasuki gedung beratap. Masalah tersebut dapat diatasi dengan menambahkan penguat sinyal di dalam gedung beratap. Tujuan penelitian ini ialah mengonstruksi cakupan jaringan penguat sinyal dalam suatu ruangan dengan konsep simplicial complex dan kth Betti number. Simplicial complex adalah objek amatan yang berada pada ruang topologi dan kth Betti number merupakan ciri atau karakteristik dari objek amatan yang berada pada ruang topologi. Dengan software Matlab R2008b yang terintegrasi JPlex dan Wolfram Mathematica7, cakupan jaringan penguat sinyal dalam suatu ruangan dapat dikonstruksi. Langkah-langkah yang dilakukan ialah: memasukkan koordinat titik, memberikan diameter cakupan jaringan penguat sinyal, dan menganalis koordinat titik dengan konsep simplicial complex dan kth Betti number. kth Betti number dari suatu simplicial complex dilambangkan dengan β_k. Nilai β₀ adalah jumlah unit yang terhubung dari suatu simplicial complex dan nilai β₁ adalah jumlah lingkaran lubang dari suatu simplicial complex.

Kata kunci: kth Betti number, simplicial complex, topologi

ABSTRACT

FACHRI ADITYA. Study of Simplicial Complex and kth Betti Number on Coverage of Indoor GSM Signal Booster Network. Supervised by SUGI GURITMAN and FARIDA HANUM.

The mobile devices signal often disappear when entering the building. The problem could be solved by equipping the building with a signal amplifier. The purpose of this study is to construct a network coverage signal booster in a room with the concept of simplicial complex and kth Betti number. Simplicial complex is observed objects in the topological space and the kth Betti number is a trait or characteristic of the observed objects in the topological space. Using integrated Matlab R2008 with JPlex and Wolfram Mathematica7, the network coverage in an indoor signal booster can be constructed. The performed steps are: enter the coordinates of points, give the diameter of network coverage signal amplifier, and analyze coordinates of points the concept of simplicial complex and kth Betti number. kth Betti number of a simplicial complex is denoted by β_k. β₀ denotes the number of connected units of a simplicial complex and β₁ denotes the number of circular holes of a simplicial complex.

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

KAJIAN

SIMPLICIAL COMPLEX

DAN

K

TH

BETTI NUMBER

PADA CAKUPAN JARINGAN PENGUAT

SINYAL GSM

INDOOR

FACHRI ADITYA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Kajian Simplicial Complex dan kth Betti Number pada Cakupan Jaringan Penguat Sinyal GSM Indoor berhasil diselesaikan.

Terima kasih penulis ucapkan kepada Bapak Dr Sugi Guritman dan Ibu Dra Farida Hanum, MSi selaku pembimbing, serta Bapak Muhammad Ilyas, MSc MSi yang telah banyak memberi saran. Ungkapan terima kasih juga disampaikan

kepada kedua orangtua penulis, Bapak Wana’I dan Ibu Siti Masngudah, kedua

adik Nofika Aisyah dan Riza Fathoni, serta seluruh keluarga atas doa dan kasih sayangnya. Terima kasih juga disampaikan kepada seluruh dosen dan staf penunjang Departemen Matematika atas segala ilmu dan bantuannya, Qowiyyul Amin Siregar dan Syaepul Anwar atas bantuan dan dukungannya, teman-teman Matematika 46 dan Jakarta Community 46 atas doa dan kebersamaannya.

Semoga karya ilmiah ini bermanfaat.

DAFTAR ISI

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

LANDASAN TEORI 2

Matriks dan Sistem Persamaan 2

Ruang Vektor 2

Simplicial Complex dan Betti Number 2

BAHAN DAN METODE 4

Bahan 4

Metode 4

HASIL DAN PEMBAHASAN 4

Penyusun Konsep Simplicial Complex dan kthBetti Number 4

Mengonstruksi Cakupan Jaringan Penguat Sinyal 13

SIMPULAN DAN SARAN 15

Simpulan 15

Saran 15

DAFTAR PUSTAKA 16

LAMPIRAN 17

DAFTAR GAMBAR

1 Metodologi penelitian 4

2 Bentuk simplicial complex 5

3 Plot {a₀, a₁} dengan koordinat titik pusat yang berbeda 6

4 Penjumlahan a₀+a₁ 7

5 Pengurangan a₁−a₀ 7

6 Plot {a₀} dengan koordinat titik pusat yang berbeda 8

7 Kombinasi t₀ pada 0-simplex 8

8 Perkalian t₀a₀ dengan nilai skalar t₀ = 2 9

9 Kombinasi t_j pada 1-simplex 11

10 Kombinasi t_j pada 2-simplex 12

11 Kombinasi t_j pada 3-simplex 12

12 Contoh dari simplicial complex 13

13 Nilai kth Betti number 13

14 Pembangkitan koordinat titik 14

15 Pemberian diameter setiap titik 14

16 Bentuk simplicial complex 14

DAFTAR LAMPIRAN

1 Pembuatan gambar q-simplex dan simplicial complex 17

2 Pembuktian simplicial complex pada Gambar 12 18

PENDAHULUAN

Latar Belakang

Sinyal perangkat mobile sering kali menghilang saat memasuki gedung beratap. Masalah tersebut dapat diatasi dengan menambahkan penguat sinyal di dalam gedung beratap. Jika perangkat mobile berada pada sudut yang tidak berhadapan langsung dengan penguat sinyal maka tetap saja akan sulit mendapatkan sinyal di dalam gedung tersebut. Solusi yang ditawarkan kepada orang-orang yang berada di dalam gedung yang memiliki penguat sinyal ialah memosisikan perangkat mobile yang dimiliki agar berada dalam cakupan area penguat sinyal. Cakupan area penguat sinyal biasanya berupa bola besar. Penguat sinyal merupakan sebuah perangkat elektronik yang menerima isyarat dan mentransmisikan kembali isyarat tersebut dengan daya yang lebih tinggi. Penguat sinyal memudahkan para pengguna perangkat mobile untuk mendapatkan sinyal yang baik dan kuat dengan jaringan nirkabel atau wireless, sehingga komunikasi menjadi lebih baik.

Dari masalah tersebut, terlihat bahwa penting sekali menentukan letak penguat sinyal dalam sebuah ruangan atau gedung beratap. Salah satu cara untuk menentukan letak penguat sinyal adalah dengan melihat cakupannya menggunakan konsep topologi. Konsep topologi adalah ilmu tentang properti yang mempertahankan bentuk asli dari perubahan kontinu seperti direnggangkan dan diputar tetapi tidak dihancurkan, dipisahkan, disambungkan dan disatukan (Munkres 2000). Secara formal konsep topologi dapat dikatakan sebagai ilmu tentang properti yang dilihat secara kualitatif terhadap objek-objek yang tidak berubah dalam beberapa macam dari transformasi (Zomorodian 2005). Untuk lebih sederhana konsep topologi adalah ilmu tentang kekontinuan dan keterhubungan. Jika suatu bentuk dapat diubah menjadi bentuk lain dikatakan bahwa bentuk-bentuk tersebut adalah ekuivalen secara topologi (topologically equivalent) (Munkres 2000). Contoh bentuk yang ekuivalen secara topologi (topologically equivalent) ialah sebuah cangkir kopi dan sebuah bentuk donat (torus).

Pada karya ilmiah ini penulis menggunakan konsep simplicial complex dan kth Betti number yang diambil dari artikel de Silva dan Ghrist (2006) untuk melihat cakupan jaringan penguat sinyal dalam suatu bangunan. Konsep simplicial complex adalah objek amatan yang berada pada ruang topologi sedangkan kth Betti number merupakan ciri atau karakteristik dari objek amatan yang berada pada ruang topologi (Munkres 2000). Setelah itu akan dilakukan simulasi untuk melihat cakupan jaringan penguat sinyal dalam suatu ruangan.

Tujuan Penelitian

2

LANDASAN TEORI

Matriks dan Sistem Persamaan

Definisi (Operasi Baris Elementer)

I Pertukaran dua baris.

II Kalikan suatu baris dengan bilangan real bukan nol.

III Ganti suatu baris dengan hasil penjumlahannya dengan kelipatan dari baris lain (Leon 2001).

Definisi (Bentuk Eselon Baris)

Suatu matriks dikatakan memiliki bentuk eselon baris jika (i) entri bukan nol pertama dalam setiap baris adalah 1

(ii) jika baris k tidak seluruhnya mengandung nol, maka banyaknya entri nol di bagian muka pada baris k + 1 lebih besar dari banyaknya entri nol di bagian muka pada baris k

(iii)jika terdapat baris-baris yang entrinya semuanya nol, maka baris-baris ini berada di bawah baris-baris yang memiliki entri bukan nol (Leon 2001). Berikut adalah beberapa contoh matriks eselon baris tereduksi

1 4 2

Simplicial Complex dan Betti Number

Definisi (Bebas Secara Geometri)

3 Suku q_{j= 1}t_j a_j −a₀ merupakan vektor-vektor a_j −a₀ yang saling bebas linear, sehingga ketika dijumlahkan dengan suku q_{j= 0}t_j a₀ himpunan titik {a₀, a₁,…, a_q} merupakan himpunan yang bebas secara geometri di ℝ�.

Definisi (q-simplex)

Jika himpunan titik {a₀, a₁, …, a_q} bebas secara geometri di ℝ� maka didefinisikan q-simplex yang direntangkan oleh a₀, a₁,…, a_q menjadi himpunan semua titik x di ℝ� sehingga:

�= t_ja_j

q

j=0

dengan t_j

q

j=0 = 1

dan 0≤ t_j≤ 1 untuk j= 0, 1, …, q (Munkres 2000). Kumpulan q-simplex disebut simplicies atau simplicial dan himpunan titik {a₀, a₁,…, a_q} q-simplex disebut simpul-simpul (Zomorodian 2005).

Definisi (Face, Coface)

Suatu q-simplex adalah rentangan � = {a₀, a₁,…, a_q} yang dilambangkan dengan � = {a₀, a₁,…, a_q}. Suatu q-simplex atau � memiliki coface � dan � disebut face dari � (Zomorodian 2005).

Dapat diartikan bahwa coface adalah himpunan bagian yang dimiliki oleh �, himpunan bagian tersebut dilambangkan � = a₀, a₁,…, a_q dengan � ⊆ �. Face adalah elemen pada himpunan titik � terdapat juga pada himpunan titik � dengan � ⊆ �. Contoh � = a₀, a₁, a₂ memiliki coface � = { a₀,a₁ , a₀,a₂ , a₁,a₂ ,

a₀ , a₁ , a₂ } dan � disebut face dari �. Pada contoh tersebut � merupakan 2-simplex dan � merupakan simplicial terdiri dari 0-simplex dan 1-simplex.

Definisi (Simplicial Complex)

Sebuah koleksi berhingga K dari kumpulan simplicial di ℝ� dikatakan simplicial complex jika memenuhi dua kondisi berikut:

1 �∈�, jika � ⊆ � maka �∈�

2 jika �∈� dan �′∈� maka � ∩ �′=∅ atau � ∩ �′ merupakan face dari � dan �′ (Zomorodian 2005).

kth Betti Number

kth Betti number adalah ciri atau karakteristik dari objek amatan yang berada pada ruang topologi. kth Betti number dilambangkan dengan β_k dari suatu simplicial complex �. Secara intuitif kth Betti number dapat dijelaskan sebagai berikut:

 β₀ adalah jumlah unit yang terhubung dari suatu simplicial complex �

 β₁ adalah jumlah lingkaran lubang dari suatu simplicial complex �

4

BAHAN DAN METODE

Bahan

Bahan yang digunakan dalam penelitian ini ialah data simulasi berupa koordinat titik yang menunjukkan lokasi penempatan penguat sinyal. Dalam karya ilmiah ini akan dilakukan simulasi untuk 2 contoh lokasi penempatan penguat sinyal. Pada setiap contoh, banyaknya koordinat titik yang dibangkitkan adalah 19 titik yang terdiri atas 14 titik tetap dan 5 titik tambahan. Analisis cakupan jaringan penguat sinyal dilakukan menggunakan Software Matlab R2008b yang terintegrasi dengan JPlex dan Wolfram Mathematica7.

Metode

Tahapan-tahapan yang dilakukan dalam mengonstruksi cakupan jaringan penguat sinyal dalam suatu ruangan ialah:

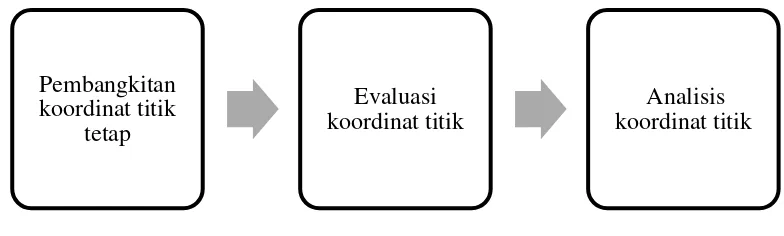
Dalam metodologi penelitian pada Gambar 1, cakupan daerah yang akan dianalisis berukuran 13×13 dengan setiap titik penguat sinyal berdiameter 4 satuan. Konsep simplicial complex dan kth Betti number digunakan untuk mengetahui apakah 19 titik koordinat yang dibangkitkan pada setiap contoh telah mencakup daerah yang berukuran 13×13. Koordinat titik dievaluasi menggunakan sistem JPlex. Sistem JPlex menerima masukan berupa koordinat titik dalam sebuah bidang dua dimensi. Koordinat titik tersebut akan diproses dengan cara memberikan diameter setiap titik. Pada sistem tersebut juga dibuat simplicial complex dan dihitung kth Betti number-nya.

HASIL DAN PEMBAHASAN

Penyusun Konsep Simplicial Complex dan kthBetti Number

Pada karya ilmah ini akan dibahas cakupan jaringan penguat sinyal dalam suatu ruangan dengan konsep simplicial complex dan kth Betti number serta

Gambar 1 Metodologi penelitian Pembangkitan

koordinat titik tetap

Evaluasi koordinat titik

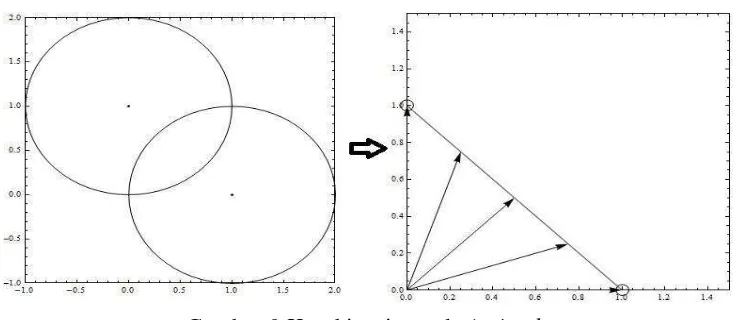
5 mengonstruksi cakupan jaringan penguat sinyal dalam suatu ruangan. Pada Gambar 2 diperlihatkan contoh suatu bentuk simplicial compex dengan nilai β₀= 1 dan β₁= 2 yang diambil dari artikel de Silva dan Ghrist (2006).

Pada Gambar 2 nilai kth Betti number tersebut menunjukkan bahwa bentuk yang diperoleh adalah 1 unit yang terhubung tetapi terdapat 2 lubang pada cakupannya. Berikut ini dijelaskan terlebih dahulu jenis-jenis q-simplex yang merupakan penyusun konsep simplicial complex dan kth Betti number.

Jenis-jenis q-simplex

Nilai q = 0, 1, 2, …, q dalam suatu q-simpex adalah banyaknya simpul-simpul. Diasumsikan banyaknya simpul-simpul tersebut adalah jumlah penguat sinyal. Jenis-jenis q-simplex yang akan dibahas ialah 0-simplex, 1-simplex, 2-simplex, dan 3-simplex. Titik, yaitu 0-2-simplex, menunjukkan bahwa penguat sinyal tersebut tidak beririsan dengan penguat sinyal lain. Garis, yaitu 1-simplex, menunjukkan bahwa terdapat 2 penguat sinyal yang saling beririsan. Segitiga, yaitu 2-simplex, menunjukkan bahwa terdapat 3 penguat sinyal yang saling beririsan. Bidang empat beraturan (tetrahedron), yaitu 3-simplex, menunjukkan bahwa terdapat 4 penguat sinyal yang saling beririsan.

Berikut ini akan diperlihatkan penafsiran secara geometri pada 0-simplex, 1-simplex, 2-1-simplex, dan 3-simplex yang bebas secara geometri. Agar lebih mudah penafsiran secara geometri yang dilakukan adalah dengan memberikan contoh koordinat titik pada 0-simplex, 1-simplex, 2-simplex dan 3-simplex. Himpunan koordinat titik yang digunakan ialah sebagai berikut:

6

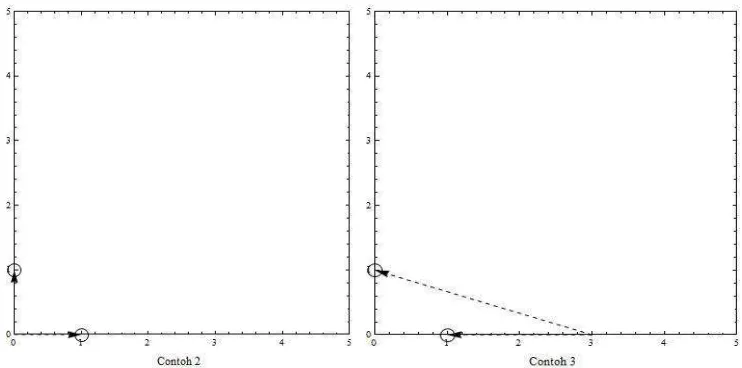
Gambar 3 Plot a₀, a₁ dengan koordinat titik pusat yang berbeda

Operasi-operasi pengurangan dan penjumlahan di himpunan titik berbeda dengan operasi himpunan vektor. Hal tersebut dikarenakan jika letak plot gambar hasil dari operasi-operasi pengurangan dan penjumlahan di himpunan titik dengan koordinat titik pusat yang berbeda adalah sama maka operasi-operasi di himpunan titik dapat ditentukan. Dapat ditentukan yang dimaksud adalah letak plot gambar himpunan titik dengan koordinat titik pusat yang berbeda menghasilkan plot gambar yang sama.

Berikut ini akan diperlihatkan penafsiran secara geometri pada operasi-operasi pengurangan dan penjumlahan di himpunan titik dengan koordinat titik pusat yang berbeda. Untuk membuktikannya diberikan koordinat titik pusat yang berbeda. Koordinat titik pusat yang digunakan ialah sebagai berikut:

Contoh 2

koordinat titik pusat = 0 0 .

Contoh 3

koordinat titik pusat = 3 0 .

Pada Gambar 3 diplotkan a₀, a₁ dengan kooordinat titik pusat yang berbeda menggunakan himpunan koordinat titik pada Contoh 1 bagian 1-simplex. Sintaks program pembangkitan gambar seperti yang ada di Gambar 3, Gambar 4 dan Gambar 5 dapat dilihat pada Lampiran 1.

Pada Gambar 3 koordinat titik a₀ dan a₁ dengan koordinat titik pusat yang berbeda menghasilkan vektor � ₀ dan � ₁ yang berbeda. Pada Contoh 2, � ₀ = 1

0 dan � ₁ = 0

1 dan pada Contoh 3, � 0 = − 2

0 dan � 1 = − 3

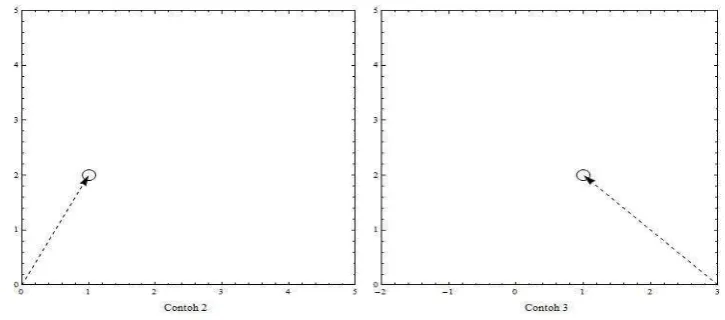
1 . Pada Gambar 4 diplotkan hasil operasi pengurangan a₁−a₀ pada setiap contoh. Pada Contoh 2,

a₁−a₀ = � ₁− � ₀ = 0 1 −

1 0 = −

1

1 dan pada Contoh 3, a1−a0 = � 1− � 0 = −₁3 − −₀2 = −1

1 . Hasil operasi pengurangan a1−a0 pada Gambar 4 Contoh 2 dan Contoh 3 sama yaitu vektor −1

7

Gambar 4 Pengurangan a₁−a₀

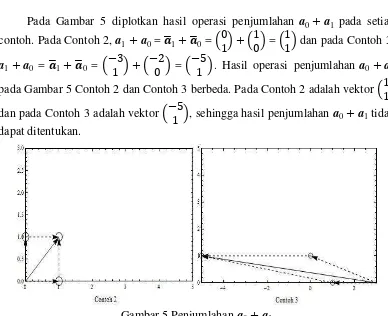
Gambar 5 Penjumlahan a₀+a₁

Pada Gambar 5 diplotkan hasil operasi penjumlahan a₀+a₁ pada setiap contoh. Pada Contoh 2, a₁+a₀ = � 1+� 0 = 0₁ + 1₀ = 1₁ dan pada Contoh 3,

a₁+a₀ = � ₁+� 0 = −₁3 + −₀2 = −5

1 . Hasil operasi penjumlahan a0+a1 pada Gambar 5 Contoh 2 dan Contoh 3 berbeda. Pada Contoh 2 adalah vektor 1

1 dan pada Contoh 3 adalah vektor −5

1 , sehingga hasil penjumlahan a0+a1 tidak dapat ditentukan.

 0-simplex

8

Gambar 6 Plot {a₀} dengan koordinat titik pusat yang berbeda Pada Gambar 6 koordinat titik 0-simplex = {a₀}= 1

2 . Koordinat titik

a₀ dengan koordinat titik pusat yang berbeda menghasilkan vektor � ₀ yang berbeda. Pada Contoh 2, � ₀ = 1

2 dan pada Contoh 3, � 0 = − 2

2 . Hasil operasi perkalian t₀a₀ dengan nilai skalar t₀ = 0 pada Contoh 2 dan Contoh 3 sama yaitu vektor 0

0 . Pada Contoh 2, t0a0 = t0� 0 = 0 1 2 =

0

0 dan pada Contoh 3, t0a0 = t₀� ₀ = 0 −2

2 = 0

0 . Hasil operasi tersebut menunjukkan bahwa 0-simplex bebas secara geometri.

Hasil operasi perkalian t₀a₀ dengan nilai skalar t₀ = 1 pada Contoh 2 dan Contoh 3 sama yaitu titik a₀ = 1

2 . Pada Contoh 2, t0a0 = t0� 0 = 1 1 2 =

1 2 dan pada Contoh 3, t₀a₀ = t₀� ₀ = 1 −2

2 = − 2

2 . Hasil operasi tersebut menunjukkan bahwa 0-simplex yang direntangkan oleh a₀ menjadi titik a₀ sendiri. Pada Gambar 7 akan diperlihatkan kombinasi t₀ pada 0-simplex.

Pada Gambar 8 akan diplotkan hasil operasi perkalian t₀a₀ dengan nilai skalar t₀ ≠ 0 dan t₀ ≠ 1. Misalkan t₀ = 2 pada Contoh 2 dan Contoh 3. Pada Contoh 2, t₀a₀ = t0� 0 = 2 1₂ = ₄2 dan pada Contoh 3, t0a0 = t0� 0 = 2 −₂2 =

9 −₄4 . Hasil operasi perkalian skalar antara t₀a₀ dengan t₀ = 2 pada Gambar 8 Contoh 2 dan Contoh 3 berbeda. Hasil perkalian dengan skalar antara t₀a₀ dengan nilai skalar t₀ = 2 tidak dapat ditentukan.

Bebas secara geometri pada himpunan titik yang elemennya lebih dari 1 sulit untuk diperiksa. Untuk itu persamaan bebas secara geometri q_{j= 0}t_ja_j = 0 dapat diubah menjadi:

t_j

q

j= 0

a₀ + t_j

q

j= 1

a_j −a₀ = 0………(1)

Pada Persamaan (1) suku pertama nilai t_j hanya ada 2 kemungkinan, yaitu t_j = 0 atau 1. Pada suku pertama nilai skalar t₀ harus sama dengan 0 mengakibatkan a₀

adalah koordinat titik pusat 0 ⋮ 0

. Suku kedua, yaitu q_{j= 1}t_j a_j −a₀ , merupakan vektor-vektor a_j −a₀ yang saling bebas linear, sehingga ketika dua suku tersebut dijumlahkan himpunan titik {a₀,a₁,…,a_q} merupakan himpunan yang bebas secara geometri di ℝ�.

Berikut ini akan dibuktikan bahwa vektor- vektor a₁ − a₀,a₂ −a₀,…,a_q− a₀ pada 1-simplex, 2-simplex, dan 3-simplex adalah bebas linear. Pembuktian tersebut menggunakan himpunan koordinat titik pada Contoh 1.

 1-simplex

a₁−a₀= 1 -1 ; t₁ 1

-1 = 0

0 →

1

-1 t1 = 0 0

Dengan operasi baris elementer, dapat diperoleh: 1

-1 0 0 �

21 1 ~

1 0

0 0

Jadi t₁= 0; terbukti a₁−a₀ bebas linear.

10 Dengan operasi baris elementer, dapat diperoleh:

1 Dengan operasi baris elementer, dapat diperoleh:

1 simplex, 2-simplex, dan 3-simplex adalah bebas linear maka menurut definisi bebas secara geometri himpunan titik {a₀,a₁,…,a_q} pada 1-simplex, 2-simplex,

11

0 }. Pada Gambar 9 diperlihatkan transformasi dua jaringan penguat sinyal yang saling beririsan menjadi kombinasi t_j pada 1-simplex.

Pada Gambar 9 terlihat bahwa kombinasi t_j membentuk kumpulan titik suatu garis sehingga dapat dikatakan bahwa 1-simplex adalah garis.

 2-simplex jaringan penguat sinyal yang saling beririsan menjadi kombinasi t_j pada 2-simplex.

12

Gambar 11 Kombinasi t_j pada 3-simplex Gambar 10 Kombinasi t_j pada 2-simplex

Pada Gambar 10 terlihat bahwa kombinasi t_j membentuk kumpulan titik suatu segitiga sehingga dapat dikatakan bahwa 2-simplex adalah segitiga.

 3-simplex

Nilai 3_j=0t_j= 1 merupakan kombinasi antara t₀, t₁, t₂, t₃ yang jumlahnya harus sama dengan 1.

x = t₀

Plot Gambar 11 menggunakan perintah GraphPlot. Pada Gambar 11 diperlihatkan transformasi empat jaringan penguat sinyal yang saling beririsan menjadi kombinasi t_j pada 3-simplex.

Pada Gambar 11 terlihat bahwa kombinasi t_j membentuk kumpulan titik suatu bidang empat beraturan (tetrahedron) sehingga dapat dikatakan bahwa 3-simplex adalah bidang empat beraturan (tetrahedron).

Konsep Simplicial Complex dan kthBetti Number

13

Gambar 12 Contoh dari simplicial complex

contoh tersebut terdapat 6 jaringan penguat sinyal dengan diameter yang sama dan 14 q-simplex atau �= 14. Sintaks program pembangkitan gambar seperti yang ada di Gambar 12 dapat dilihat pada Lampiran 1.

Pada Gambar 12 didapat himpunan titik K = v₀, v₁, v₂, v₃, v₄, v₅ . Jika ditransformasikan ke dalam bentuk simplicial complex maka simplicial complex K = {∅, {v₀}, {v₁}, {v₂}, {v₃}, {v₄}, {v₅}, {v₀, v₁}, {v₀, v₂}, {v₁, v₂}, {v₂, v₃}, {v₃,

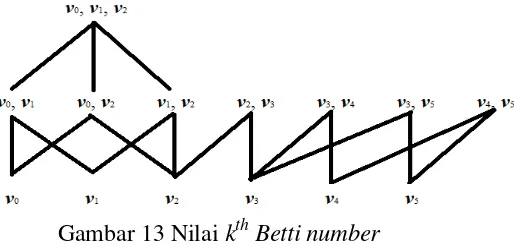
v₄}, {v₃, v₅}, {v₄, v₅}, {v₀, v₁, v₂}}. Pembuktian simplicial complex pada Gambar 12 dapat dilihat pada Lampiran 2. Pada Gambar 13 diberikan nilai kth Betti number dengan mengkaji simplicial complex K.

Baris pertama pada Gambar 13 merupakan himpunan 0-simplex yaitu {{v₀}, {v₁}, {v₂}, {v₃}, {v₄}, {v₅}}, baris kedua himpunan 1-simplex yaitu {{v₀, v₁}, {v₀,

v₂}, {v₁, v₂}, {v₂, v₃}, {v₃, v₄}, {v₃, v₅}, {v₄, v₅}} dan baris ketiga himpunan 2-simplex yaitu {v₀, v₁, v₂} yang merupakan anggota K. Perhatikan bahwa pada Gambar 10 bentuk tersebut saling terhubung yang berarti nilai β₀= 1. Melihat pada bagian {v₃, v₄}, {v₃, v₅}, dan {v₄, v₅} dengan {v₃}, {v₄}, dan {v₅} bila garisnya ditarik akan membentuk sebuah lingkaran, hal itu menunjukkan bahwa nilai β₁= 1. Dilihat dari nilai kth Betti number dapat disimpulkan bahwa, terdapat sebuah ruang yang belum tercakup oleh penguat sinyal. Jadi, jika β

1= 0 maka daerah tersebut telah tercakup oleh penguat sinyal.

Mengonstruksi Cakupan Jaringan Penguat Sinyal

Membangkitkan dan Mengevaluasi Koordinat Titik

Pada proses ini akan dilakukan pembangkitan 19 koordinat titik yang terdiri dari 14 koordinat titik tetap (berwarna biru) dan 5 koordinat titik tambahan (berwarna merah). Koordinat titik tetap adalah kumpulan titik yang menunjukkan bahwa titik-titik tersebut mencakup batasan daerah berukuran 13×13. Koordinat

14

Gambar 16 Bentuk simplicial complex

titik tambahan adalah kumpulan titik yang menunjukkan bahwa titik-titik tersebut menutup daerah cakupan koordinat titik tetap. Pada penelitian ini diberikan 2 macam koordinat titik tambahan yang berbeda, sehingga menghasilkan Gambar 14. Sintaks program untuk pembangkitan gambar seperti yang ada di Gambar 14, Gambar 15, dan Gambar 16 dapat dilihat pada Lampiran 3.

Setelah membangkitkan koordinat titik, langkah selanjutnya ialah memberikan diameter setiap titik pada Contoh 1 dan Contoh 2, sehingga akan menghasilkan Gambar 15.

Dalam Gambar 15 sulit melihat daerah mana yang tidak tercakup jaringan penguat sinyal dalam suatu bangunan. Agar lebih mudah melihat cakupan jaringan penguat sinyal maka lingkaran cakupan setiap titik yang terdapat pada Contoh 1 dan Contoh 2 akan dikonversi ke dalam bentuk simplicial complex sehingga akan menghasilkan Gambar 16.

15 Setelah dikonversi dalam bentuk simplicial complex akan dihitung nilai kth Betti number setiap contoh. Pada Contoh 1 β₀= 1 dan β₁= 1, sedangkan pada Contoh 2

β₀= 1 dan β₁= 0.

Analisis koordinat titik

Nilai kth Betti number dapat mengidentifikasi cakupan sinyal dalam suatu bangunan. Pada Contoh 1, nilai kth Betti number yang diperoleh ialah β₀= 1 dan

β₁= 2; itu berarti bahwa bentuk yang diperoleh adalah 1 unit yang terhubung tetapi terdapat 2 lubang pada cakupannya. Pada Contoh 2, nilai kth Betti number yang diperoleh ialah β₀= 1 dan β₁= 0. Itu berarti bahwa bentuk yang diperoleh adalah 1 unit yang terhubung dengan tidak ada lubang pada cakupannya.

Dengan melihat hasil kth Betti number pada dua contoh tersebut dapat dilihat bahwa Contoh 2 lebih baik dibandingkan dengan Contoh 1. Hal tersebut disebabkan karena pada Contoh 2, bentuk yang dihasilkan adalah 1 unit yang terhubung dengan tidak adanya lubang, sedangkan pada Contoh 1 terdapat satu lubang. Lubang tersebut menyatakan bahwa masih ada ruang yang belum tercakup oleh penguat sinyal.

SIMPULAN DAN SARAN

Simpulan

Konsep simplicial complex dan kth Betti number dapat digunakan untuk melihat cakupan jaringan penguat sinyal dalam sebuah wilayah. Konsep simplicial complex adalah objek amatan yang berada pada ruang topologi dan kth Betti number merupakan ciri atau karakteristik dari objek amatan yang berada pada ruang topologi. Dengan software Matlab R2008b yang terintegrasi JPlex dan Wolfram Mathematica7 dapat direkontruksi cakupan jaringan penguat sinyal dalam suatu ruangan. Langkah-langkah yang dilakukan ialah: memasukkan koordinat titik, memberikan diameter cakupan jaringan penguat sinyal, dan menganalis koordinat titik dengan konsep simplicial complex dan kth Betti number.

Saran

16

DAFTAR PUSTAKA

De Silva V, Ghrist R. 2006. Coordinate-free coverage in sensor networks with controlled boundaries via homology. Intl J Robotics Research. 25(12):1205-1222.doi:10.1177/0278364906072252.

Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Ed ke-5. Bondan A, penerjemah. Jakarta (ID): Penerbit Erlangga. Terjemahan dari: Linear Algebra with Applications.

Munkres J R. 2000. Topology. Ed ke-2. New Jersey (US): Prentice Hall.

17 Lampiran 1 Pembuatan gambar q-simplex dan simplicial complex

Gambar 3

a=Arrow[{{0,0},{1,0}}];b=Arrow[{{0,0},{0,1}}];c=Circle[{1,0} ,.1];d=Circle[{0,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{c},{d}},Frame True,PlotRange{{0,5},{0,5}}],Text["Contoh 2"]]

a=Arrow[{{3,0},{1,0}}];b=Arrow[{{3,0},{0,1}}];c=Circle[{1,0} ,.1];d=Circle[{0,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{c},{d}},Frame True,PlotRange{{0,5},{0,5}}],Text["Contoh 3"]]

Gambar 4

a=Arrow[{{0,0},{1,0}}];b=Arrow[{{0,0},{0,1}}];c=Arrow[{{1,0} ,{0,1}}];d=Circle[{1,0},.1];e=Circle[{0,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{c},{d},{e}},Frame True,PlotRange{{0,5},{0,5}}],Text["Contoh 2"]]

a=Arrow[{{3,0},{1,0}}];b=Arrow[{{3,0},{0,1}}];c=Arrow[{{1,0} ,{0,1}}];d=Circle[{1,0},.1];e=Circle[{0,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{c},{d},{e}},Frame True,PlotRange{{-2,3},{0,5}}],Text["Contoh 3"]]

Gambar 5

a=Arrow[{{0,0},{1,0}}];b=Arrow[{{0,0},{0,1}}];c=Arrow[{{1,0} ,{1,1}}];d=Arrow[{{0,1},{1,1}}];e=Arrow[{{0,0},{1,1}}];f=Cir cle[{1,0},.1];g=Circle[{0,1},.1];h=Circle[{1,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{Dashed,c},{Dashed,d },{e},{f},{g},{h}},Frame

True,PlotRange{{0,5},{0,3}}],Text["Contoh 2"]]

a=Arrow[{{3,0},{1,0}}];b=Arrow[{{3,0},{0,1}}];c=Arrow[{{1,0}

,{-5,1}}];d=Arrow[{{0,1},{-5,1}}];e=Arrow[{{3,0},{- 5,1}}];f=Circle[{1,0},.1];g=Circle[{0,1},.1];h=Circle[{-5,1},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{Dashed,c},{Dashed,d },{e},{f},{g},{h}},Frame

True,PlotRange{{-5,3},{0,5}}],Text["Contoh 3"]]

Gambar 6

d=Circle[{1,2},.1];

Labeled[Graphics[{{d}},Frame

True,PlotRange{{0,5},{0,5}}],Text["Contoh 2"]] d=Circle[{1,2},.1];

Labeled[Graphics[{{d}},Frame True,PlotRange{{-2,3},{0,5}}],Text["Contoh 3"]]

Gambar 7

a=Arrow[{{0,0},{1,2}}];d=Circle[{1,2},.1]; Labeled[Graphics[{{Dashed,a},{d}},Frame

True,PlotRange{{0,5},{0,5}}],Text["Contoh 2"]] a=Arrow[{{3,0},{1,2}}];d=Circle[{1,2},.1];

18

Gambar 8

a=Arrow[{{0,0},{1,2}}];b=Arrow[{{0,0},{2,4}}];d=Circle[{1,2} ,.1];e=Circle[{2,4},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{d},{e}},Frame True,PlotRange{{0,5},{0,5}}],Text["Contoh

2"]]a=Arrow[{{3,0},{1,2}}];b=Arrow[{{3,0},{-1,4}}];d=Circle[{1,2},.1];e=Circle[{-1,4},.1];

Labeled[Graphics[{{Dashed,a},{Dashed,b},{d},{e}},Frame True,PlotRange{{-2,3},{0,5}}],Text["Contoh _3”]]

Gambar 9

e=Point[{1,0}]

;f=Point[{0,1}];g=Circle[{1,0},1];h=Circle[{0,1},1];

Graphics[{{e},{f},{g},{h}},Frame True,PlotRange{{-1,2},{-1,2}}]

a=Arrow[{{0,0},{0,1}}];b=Arrow[{{0,0},{1,0}}];c=Arrow[{{0,0},{1/2, 1/2}}];d=Arrow[{{0,0},{1/4,3/4}}];e=Arrow[{{0,0},{3/4,1/4}}];f=Lin e[{{0,1},{1,0}}];g=Circle[{1,0},.03];h=Circle[{0,1},.03];

Graphics[{{a},{b},{c},{d},{e},{f},{g},{h}},Frame

True,PlotRange{{0,1.5},{0,1.5}}]

Gambar 10

a=Arrow[{{0,0,0},{0,1,1}}];b=Arrow[{{0,0,0},{1,0,1}}];c=Arrow[{{0, 0,0},{1,1,0}}];d=Arrow[{{0,0,0},{2/3,2/3,2/3}}];e=Arrow[{{0,0,0},{ 3/4,3/4,1/2}}];f=Polygon[{{1,1,0},{0,1,1},{1,0,1}}];i=Sphere[{1,1, 0},.05];j=Sphere[{0,1,1},.05];k=Sphere[{1,0,1},.05];

Graphics3D[{{a},{b},{c},{d},{e},{f},{i},{j},{k}},AxesTrue,PlotRa

nge{{0,1},{0,1},{0,1}}]

i=Sphere[{0,1,1},1]; j= Sphere[{1,0,1},1];k=Sphere[{1,1,0},1];

Graphics3D[{{i},{j},{k}},AxesTrue,PlotRange

{{-1,2},{-1,2},{-1,2}}]

Gambar 11

GraphPlot[{{0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0}},VertexRenderin gFunction({Yellow,EdgeForm[Black],Disk[#,0.7],Red,Text[#2,#1]}&) ]

GraphPlot[{{0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0}},VertexRenderin gFunction({Yellow,EdgeForm[Black],Disk[#,0.1],Red,Text[#2,#1]}&) ]

GraphPlot[{{0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0}},VertexRenderin gFunction({Yellow,EdgeForm[Black],Disk[#,0.1],Red,Text[#2,#1]}&) ,PlotStyle Dashed]

Gambar 12

GraphPlot[{0

1,02,12,23,34,35,45},VertexRenderingFunction({Yellow,Edge Form[Black],Disk[#,0.7],Red,Text[#2,#1]}&)]

Lampiran 2 Pembuktian simplicial complex pada Gambar 12

Diketahui: simplicial complex K = {∅, {v₀}, {v₁}, {v₂}, {v₃}, {v₄}, {v₅}, {v₀, v₁}, {v₀, v₂}, {v₁, v₂}, {v₂, v₃}, {v₃, v₄}, {v₃, v₅}, {v₄, v₅}, {v₀, v₁, v₂}}

19 Bukti:

Jika poin 1 dan poin 2 terpenuhi maka Gambar 12 adalah simplicial complex � pada simplicial complex K berjumlah 14

Poin 1: �∈�, jika � ⊆ � maka �∈�

�1 = {v0, v1, v2}, �1 ∈ � dengan τ1 = {{v0}, {v1}, {v2}, {v0, v1}, {v0, v2}, {v1,

v₂}}, τ₁ ∈�

�2 = {v4, v5}, �2 ∈� dengan τ2 = {{v4}, {v5}}, τ2 ∈� �3 = {v3, v5}, �3 ∈� dengan τ3 = {{v3}, {v5}}, τ3 ∈� �4 = {v3, v4}, �4 ∈� dengan τ4 = {{v3}, {v4}}, τ4 ∈� �5 = {v2, v3}, �5 ∈� dengan τ5 = {{v2}, {v3}}, τ5 ∈� �6 = {v1, v2}, �6 ∈� dengan τ6 = {{v1}, {v2}}, τ6 ∈� �7 = {v0, v2}, �7 ∈� dengan τ7 = {{v0}, {v2}}, τ7 ∈� �8 = {v0, v1}, �8 ∈� dengan τ8 = {{v0}, {v1}}, τ8 ∈� �9 = {v5}, �9 ∈� dengan τ9 = ∅, τ9 ∈�

�10 = {v4}, �10 ∈� dengan τ10 = ∅, τ10 ∈� �11 = {v3}, �11 ∈� dengan τ11 = ∅, τ11 ∈� �12 = {v2}, �12 ∈� dengan τ12 = ∅, τ12 ∈� �13 = {v1}, �13 ∈� dengan τ13 = ∅, τ13 ∈� �14 = {v0}, �14 ∈� dengan τ14 = ∅, τ14 ∈�

Poin 2: jika �∈� dan �′∈� maka � ∩ �′= ∅ atau � ∩ �′ merupakan face dari � dan �′

Terbukti Gambar 12 adalah simplicial complex

∩ �1 �2 �3 �4 �5 �6 �7 �8 �9 �10 �11 �12 �13 �14

�1 ∅ ∅ ∅ {v2} {v1,

v2}

{v₀,

v2}

{v₀,

v1}

∅ ∅ ∅ {v₂} {v₁} {v₀}

�2 ∅ {v5} {v4} ∅ ∅ ∅ ∅ {v5} {v4} ∅ ∅ ∅ ∅

�3 ∅ {v5} {v3} {v3} ∅ ∅ ∅ {v5} ∅ {v3} ∅ ∅ ∅

�4 ∅ {v4} {v3} {v3} ∅ ∅ ∅ ∅ {v4} {v3} ∅ ∅ ∅

�5 {v2} ∅ {v3} {v3} {v2} {v2} ∅ ∅ ∅ {v3} {v2} ∅ ∅

�6 {v1,

v2}

∅ ∅ ∅ {v2} {v2} {v1} ∅ ∅ ∅ {v2} {v1} ∅

�7 {v0,

v2}

∅ ∅ ∅ {v₂} {v₂} {v₀} ∅ ∅ ∅ {v₂} ∅ {v₀}

�8 {v0,

v1}

∅ ∅ ∅ ∅ {v₁} {v₀} ∅ ∅ ∅ ∅ {v₁} {v₀}

�9 ∅ {v5} {v5} ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅

�10 ∅ {v4} ∅ {v4} ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅

�11 ∅ ∅ {v3} {v3} {v3} ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅

�12 {v2} ∅ ∅ ∅ {v2} {v2} {v2} ∅ ∅ ∅ ∅ ∅ ∅

�13 {v1} ∅ ∅ ∅ ∅ {v1} ∅ {v1} ∅ ∅ ∅ ∅ ∅

20

Lampiran 3 Rekontruksi cakupan jaringan penguat sinyal

%% Gambar14 dan Gambar16 %% Membuka Javaplex

startJPlex

%% Membangkitkan koordinat titik tetap

x = [1 6 8.5 10.5 11 12 10 7 5 1.4 1.9 1.2 12 3]; y = [2 2 1.5 2.5 6.5 9.5 11 12 10 11 9 6 4 3];

%% Membangkitkan koordinat titik tambahan dan menggabungkan dengan titik tetap

%tambah = [4 6.4;6 5;6.8 8;8.5 5;8.5 8.6];

tambah = [4 6.4;6 5;6.8 8;8.5 5;8 8];

tambahan = [[x;y]'; tambah];

cover = EuclideanArrayData(tambahan);

ripscover = Plex.RipsStream(0.001, 3, 4, cover);

intervals = Plex.Persistence.computeIntervals(ripscover); Plex.FilterInfinite(intervals)

Plex.plot(intervals, 'ripscover', 4)

scatter(tambahan(:,1),tambahan(:,2),'filled')

xmin=a1 - r0;xmax=a1 + r0; x1=xmin:0.01:xmax;

y1= b1 + sqrt(r0^2-(x1-a1).^2); x2=xmin:0.01:xmax;

y2=b1 - sqrt(r0^2-(x2-a1).^2);

xmin=a3 - r0;xmax=a3 + r0; x3=xmin:0.01:xmax;

y3= b3 + sqrt(r0^2-(x3-a3).^2); x4=xmin:0.01:xmax;

y4=b3 - sqrt(r0^2-(x4-a3).^2);

xmin=a5 - r0;xmax=a5 + r0; x5=xmin:0.01:xmax;

y5= b5 + sqrt(r0^2-(x5-a5).^2); x6=xmin:0.01:xmax;

y6=b5 - sqrt(r0^2-(x6-a5).^2);

xmin=a21 - r0;xmax=a21 + r0; x21=xmin:0.01:xmax;

y21= b21 +

sqrt(r0^2-(x21-a21).^2);

x22=xmin:0.01:xmax;

y22=b21 -

sqrt(r0^2-(x22-a21).^2);

xmin=a23 - r0;xmax=a23 + r0; x23=xmin:0.01:xmax;

y23= b23 +

sqrt(r0^2-(x23-a23).^2);

x24=xmin:0.01:xmax;

y24=b23 -

sqrt(r0^2-(x24-a23).^2);

21

xmin=a7 - r0;xmax=a7 + r0; x7=xmin:0.01:xmax;

y7= b7 + sqrt(r0^2-(x7-a7).^2); x8=xmin:0.01:xmax;

y8=b7 - sqrt(r0^2-(x8-a7).^2);

xmin=a9 - r0;xmax=a9 + r0; x9=xmin:0.01:xmax;

y9= b9 + sqrt(r0^2-(x9-a9).^2); x10=xmin:0.01:xmax;

y10=b9 - sqrt(r0^2-(x10-a9).^2);

xmin=a11 - r0;xmax=a11 + r0; x11=xmin:0.01:xmax;

y11= b11 +

sqrt(r0^2-(x11-a11).^2);

x12=xmin:0.01:xmax;

y12=b11 -

sqrt(r0^2-(x12-a11).^2);

xmin=a13 - r0;xmax=a13 + r0; x13=xmin:0.01:xmax;

y13= b13 +

sqrt(r0^2-(x13-a13).^2);

x14=xmin:0.01:xmax;

y14=b13 -

sqrt(r0^2-(x14-a13).^2);

xmin=a15 - r0;xmax=a15 + r0; x15=xmin:0.01:xmax;

y15= b15 +

sqrt(r0^2-(x15-a15).^2);

x16=xmin:0.01:xmax;

y16=b15 -

sqrt(r0^2-(x16-a15).^2);

xmin=a17 - r0;xmax=a17 + r0; x17=xmin:0.01:xmax;

y17= b17 +

sqrt(r0^2-(x17-a17).^2);

x18=xmin:0.01:xmax;

y18=b17 -

sqrt(r0^2-(x18-a17).^2);

xmin=a19 - r0;xmax=a19 + r0; x19=xmin:0.01:xmax;

y19= b19 +

sqrt(r0^2-(x19-a19).^2);

x20=xmin:0.01:xmax;

y20=b19 -

sqrt(r0^2-(x20-a19).^2);

x25=xmin:0.01:xmax;

y25= b25 +

sqrt(r0^2-(x25-a25).^2);

x26=xmin:0.01:xmax;

y26=b25 -

sqrt(r0^2-(x26-a25).^2);

xmin=a27 - r0;xmax=a27 + r0; x27=xmin:0.01:xmax;

y27= b27 +

sqrt(r0^2-(x27-a27).^2);

x28=xmin:0.01:xmax;

y28=b27 -

sqrt(r0^2-(x28-a27).^2);

xmin=a29 - r0;xmax=a29 + r0; x29=xmin:0.01:xmax;

y29= b29 +

sqrt(r0^2-(x29-a29).^2);

x30=xmin:0.01:xmax;

y30=b29 -

sqrt(r0^2-(x30-a29).^2);

xmin=a31 - r0;xmax=a31 + r0; x31=xmin:0.01:xmax;

y31= b31 +

sqrt(r0^2-(x31-a31).^2);

x32=xmin:0.01:xmax;

y32=b31 -

sqrt(r0^2-(x32-a31).^2);

xmin=a33 - r0;xmax=a33 + r0; x33=xmin:0.01:xmax;

y33= b33 +

sqrt(r0^2-(x33-a33).^2);

x34=xmin:0.01:xmax;

y34=b33 -

sqrt(r0^2-(x34-a33).^2);

xmin=a35 - r0;xmax=a35 + r0; x35=xmin:0.01:xmax;

y35= b35 +

sqrt(r0^2-(x35-a35).^2);

x36=xmin:0.01:xmax;

y36=b35 -

sqrt(r0^2-(x36-a35).^2);

xmin=a37 - r0;xmax=a37 + r0; x37=xmin:0.01:xmax;

y37= b37 +

sqrt(r0^2-(x37-a37).^2);

x38=xmin:0.01:xmax;

y38=b37 -

22

23

RIWAYAT HIDUP

Penulis dilahirkan di Madiun pada tanggal 6 Februari 1991 sebagai anak pertama dari dua bersaudara, dengan ayah bernama Wana’I, SE dan ibu bernama Dra. Siti Masngudah.

Pada tahun 2009, penulis lulus dari SMA Negeri 47 Jakarta Selatan dan pada tahun yang sama diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI).

Selama mengikuti perkuliahan di IPB, penulis pernah menjadi pengurus GUMATIKA divisi Kewirausahaan pada tahun 2011. Penulis aktif dalam OMDA Jakarta Community (J-Co) sebagai ketua divisi Akademik periode 2011/2012 dan aktif dalam beberapa kepanitiaan di kampus dan di organisasi.