0-1 Programing Menentukan Shortest Path yang Memenuhi Kendala

0-1 PROGRAMMING MENENTUKAN SHORTEST PATH YANG

MEMENUHI KENDALA

SKRIPSI

ASTRI WULAN SARI

060823012

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

0-1 PROGRAMMING MENENTUKAN SHORTEST PATH YANG

MEMENUHI KENDALA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

ASTRI WULAN SARI

060823012

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

PERSETUJUAN

Judul : 0-1 PROGRAMMING MENENTUKAN SHORTEST

PATH YANG MEMENUHI KENDALA

Kategori : SKRIPSI

Nama : ASTRI WULAN SARI

Nomor Induk Mahasiswa : 060823012

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Juni 2009 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Syahriol Sitorus, S.Si, M.IT Drs. Marwan Harahap, M.Eng

NIP. 132 174 687 NIP.130 422 437

Diketahui oleh :

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

0-1 PROGRAMMING MENENTUKAN SHORTEST PATH YANG MEMENUHI KENDALA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2009

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT, dengan limpahan dan karunia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan.

ABSTRAK

ABSTRACK

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

Bab 1. Pendahuluan 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 4

1.3 Tujuan Penelitian 4

1.4 Kontribusi penelitian 4

1.5 Tinjauan Pustaka 5

1.6 Metode Penelitian 6

Bab 2. Landasan Teori 7

2.1 Konsep Dasar Graph 7

2.2 Graph Terhubung 10

2.3 Graph Berlabel 11

2.4 Shortest Path 14

2.5 0-1 Programming 16

2.6 Knapsack 18

2.7 Pengenalan Program LINDO 19

Bab 3. Pembahasan 21

3.1 Permasalahan Lintasan Terpendek 21

3.2 Metode Balas 22

3.2.1 Beberapa Defenisi dan Notasi 26

3.3.1 Penyelesaian Shortest Path Berkendala pada Permasalahan Knapsack dengan 0-1 Programming 41 3.3.2 Langkah-langkah Penyelesaian dengan Menggunakan

Program LINDO 43

Bab 4. Kesimpulan dan Saran 48

4.1 Kesimpulan 48

4.2 Saran 49

DAFTAR TABEL

Halaman Tabel 3. 1 Penyelesaian Sebagian Secara Lengkap 27

Tabel 3. 2 Complete Enumeration 28

DAFTAR GAMBAR

Halaman Gambar 1.1 Contoh ilustrasi masalah shortest path yang berkendala 2

Gambar 2.1 Graph dengan 6 verteks dan 6 edge 8

Gambar 2.2 Graph dengan loop dan edge sejajar 8 Gambar 2.3 Graph dengan walk yang bergaris tebal 9

Gambar 2.4 Graph dnegan 5 verteks dan 6 edge 9

Gambar 2.5 Graph tak terhubung 10

Gambar 2.6 Graph terhubung 11

Gambar 2.7 Graph jaringan listrik di 8 kota 13

Gambar 2.8 Shortest path 14

Gambar 2.9 Sistem jalan di taman Seervada 15

Gambar 2.10 Tampilan awal program LINDO 20

Gambar 3.1 Suatu graph berarah dan tidak berbobot 21

Gambar 3.2 Shortest path 28

Gambar 3.3 Flowcahrt metode Balas 31

Gambar 3.4 Representasi graph pada pengiriman barang 40 Gambar 3.5 Representasi graph pada jaringan komunikasi 41 Gambar 3.6 Penyelesaian menggunakan 0-1 Programming program LINDO 45

Gambar 3.7 Hasil akhir 46

ABSTRAK

ABSTRACK

BAB 1

PENDAHULUAN

1.1Latar Belakang

Masalah dalam menentukan rantaian terpendek diantara pasangan node (titik) tertentu dalam suatu graph telah banyak menarik perhatian. Persoalan dirumuskan sebagai kasus khusus dari persoalan aliran biaya minimal, dan algoritma efisien yang tersedia untuk menghitung lintasan terpendek dan biaya minimum. Shortest path yang diperoleh akan meminimumkan fungsi linear yang khusus (fungsi) dari path seperti biaya, jarak atau waktu. Perumusan persoalan ini akan menjadi salah satu kegunaan dari lintasan dengan jarak (waktu) diminimumkan terhadap biaya yang dianggarkan.

Algoritma Dijkstra merupakan dasar pemikiran untuk menentukan suatu lintasan terpendek dalam suatu graph berarah dari suatu titik awal (sumber) ke suatu titik akhir (tujuan), bilamana pada setiap node dan arc menotasikan suatu ukuran atau bobot yang tidak negatif. Algoritma ini juga untuk menentukan lintasan terpendek untuk setiap pasangan lintasan yang diinginkan. Pada umumnya algoritma Dijkstra digunakan hanya untuk menentukan lintasan terpendek pada suatu graph. Tetapi bilamana shortest path tersebut harus memenuhi kendala-kendala linear yang ditentukan, algoritma tersebut tidak dapat digunakan.

Masalah khusus dari persoalan graph ini adalah mendapatkan suatu lintasan dengan jarak minimum yang memenuhi terhadap (subject to) kendala anggaran (budgetary). Kemungkinan masalah lainnya adalah path juga merupakan minimasi biaya yang harus memenuhi kendala waktu. Andaikan diberikan sebuah graph G dengan node (titik) N = 1,2,…,i dan arc (garis) F = 1,2,…,j serta a(x,y) dan b(x,y) adalah jarak (waktu) dan biaya.yang dihubungkan dengan tiap garis (i,j) dalam graph G. Masalahnya adalah menentukan lintasan terpendek dari titik 1 (sumber) ke titik n

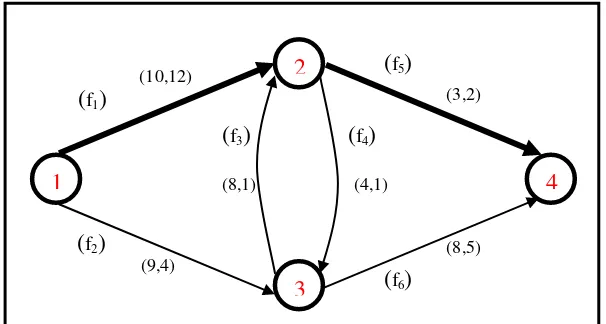
Gambar 1.1 Contoh ilustrasi masalah shortest path yang berkendala.

Gambar diatas menerangkan sebuah graph G dimana (a,b) = 10, 12 dinyatakan sebagai jarak (waktu) dan biaya yang dihubungkan tiap garis F(i,j), dan node 1, 2, 3, 4 adalah node-node N yang ditentukan pada graph. Dan pada gambar juga diperlihatkan yang bergaris tebal adalah merupakan lintasan terpendek yang harus dilewati dari sumber (node 1) ke tujuan (node 4). Pada persoalan ini diandaikan biaya sebagai kendala, dan ditentukan pula biaya berbanding terbalik dengan jarak atau keduanya bernilai sama.

Menentukan jarak terpendek yang memenuhi kendala biaya yang dianggarkan pada suatu graph adalah merupakan salah satu tipe masalah Integer Knapsack, yaitu dimana kita diminta untuk memilih bobot minimum yang akan dimasukkan kedalam

knapsack (karung) yang mempunyai bobot maksimum tertentu. Persoalan ini disebut

Integer Knapsack karena tiap objek hanya memiliki dua status yaitu terpilih atau tidak. Untuk permasalahan knapsack pada suatu graph, bobot minimum yang dipilih adalah merupakan lintasan terpendek yang harus dilewati dari titik sumber ke titik

2

4

3 1

(10,12)

(9,4)

(8,5) (3,2)

(8,1) (4,1)

(f1)

(f2)

(f3) (f4)

(f5)

Masalah knapsack ini dapat dirumuskan dengan memberi nilai 1 sampai n dan memperkenalkan suatu vektor variabel biner xj (j = 1,…,n) dengan arti sebagai

berikut :

     =

0 1 j

x

Jika pj merupakan ukuran kelayakan yang diberikan oleh objek j, wj adalah

besarannya dan K adalah bobot maksimum dari knapsack, masalahnya akan terpilih, diantara semua semua vektor biner x (0–1) yang akan memenuhi kendala

∑

=

≤ n

j j jx K

w

1

Dimana salah satu fungsi objektif di maksimumkan

∑

=

n

j j jx

p

1

0–1 Programming adalah salah satu metode yang dipergunakan untuk menyelesaikan masalah Knapsack, dimana keadaan tertentu terjadi dan masing-masing keadaan mempunyai sebuah nilai yang dihubungkan dengan besarannya. Secara nyata bahwa solusi optimal dari masalah Knapsack akan menunjukkan kemungkinan yang terbaik. Oleh sebab itu penulis berkeinginan untuk membahas bagaimana metode 0-1 Programming dalam menyelesaikan masalah lintasan terpendek yang memenuhi kendala-kendala yang telah ditentukan, serta menerapkannya dengan menggunakan program LINDO .

Jika objek j dipilih

1.2 Perumusan Masalah

Masalah yang dibahas adalah bagaimana menentukan lintasan terpendek yang merupakan masalah knapsack dari titik sumber ke titik tujuan pada suatu graph yang memenuhi kendala biaya yang dianggarkan (budgetary) dengan menggunakan 0-1 Programming.

1.3Tujuan Penelitian

Problem shortest path diantara dua node tertentu dalam sembarang graph umumnya dapat diselesaikan dengan menggunakan Dijkstra Algorithm. Tetapi bilamana shortest path tersebut harus memenuhi kendala-kendala linear yang ditentukan, algoritma tersebut pada umumnya tidak dapat digunakan. Penelitian bertujuan untuk memperlihatkan dan menerangkan suatu konsep algoritma untuk penyelesaian dalam

menentukan shortest path yang memenuhi kendala-kendala yang ditentukan, dengan

menerapkan 0-1 programming.

1.4 Kontribusi Penelitian

1.5Tinjauan Pustaka

Teori graf merupakan pokok bahasan yang sudah tua usianya namun memiliki banyak terapan sampai saat ini. Graf digunakan untuk mempresentasikan objek-objek diskrit [10] dan hubungan antara objek-objek tersebut. Reprentasikan visual dari graf adalah dengan menyatakan objek dinyatakan sebagai noktah, bulatan, atau titik, sedangkan hubungan antara objek dinyatakan dengan garis. Salah satu contoh yaitu sebuah peta jaringan jalan raya yang menghubungkan sejumlah provinsi, dimana sesungguhnya peta tersebut adalah sebuah graf, di dalam hal ini kota dinyatakan sebagai bulatan sedangkan jalan dinyatakan sebagai garis. Dengan pencarian jalur terpendek maka kita dapat mengetahui perjalanan yang singkat dari satu kota ke kota yang lainnya.

Integer Programming 0-1 adalah suatu linier programming dengan tambahan persyaratan bahwa semua atau beberapa variabel bernilai bulat nonnegatif, tetapi tidak perlu bahwa parameter model juga bernilai bulat.Ada banyak kasus dalam masalah

integer programming yang membatasi variabel model bernilai nol atau satu. Dalam kasus demikian, persoalan lintasan hanya memiliki dua pilihan yaitu masuk atau keluar dari jaringan. Jika variabel ini bernilai satu, persoalan masuk, dan jika variabel bernilai nol, persoalan keluar [4].

akan terdorong untuk menyelesaikan suatu persoalan dalam menentukan lintasan terpendek pada suatu distribusi aliran. Pendekatan yang sederhana dapat dimasukkan ke dalam program komputer untuk memeriksa semua harga 0-1 yang mungkin, dipilih yang terbaik yang memenuhi kendala [3] .

1.6Metode Penelitian

Secara umum penelitian yang dilakukan dengan beberapa tahapan, yaitu :

1. Menguraikan teori dasar graph dan terminologi-terminologi graph yang menunjang terhadap pembahasan.

2. Menguraikan tentang konsep lintasan terpendek serta 0-1 Programming pada permasalahan Knapsack pada sembarang graph.

3. Menjelaskan penggunaan dan pengembangan 0-1 Programming untuk menentukan path yang memungkinkan dari sumber ke tujuan.

4. Menyelesaikan permasalahan shortest-path yang memenuhi kendala-kendala tertentu

BAB 2

LANDASAN TEORI

Pada bab ini akan diuraikan mengenai teori dan terminologi graph, yaitu bentuk-bentuk khusus suatu graph dan juga akan diuraikan penjelasan mengenai shortest path.

2.1 Konsep Dasar Graph

Definsi 2.1

Graph G adalah pasangan (V(G),E(G)) di mana:

1. V(G) adalah sebuah himpunan tak kosong yang berhingga, yang anggota-anggotanya disebut vertek.

2. E(G) adalah sebuah himpunan yang berhingga, yang terdiri atas pasangan-pasangan tak berurut yang tertentu dari verteks V, yang disebut edge.

Atau dengan kata lain V(G) adalah himpunan vertek dari G dan E(G) adalah himpunan edge dari G. Selanjutnya, keduanya cukup disingkat V dan E, dan graph G=(V,E).

edge disebut dengan graph (p,q) ditulis dengan g(p,q). Untuk lebih mudahnya (p,q) biasa ditulis pq.

Secara umum graph dapat digambarkan dengan suatu diagram dimana verteks ditunjukkan sebagai titik yang ditulis dengan vi, i = 1,2,...,p dan edge digambarkan dengan sebuah garis lurus atau garis melengkung yang menghubungkan dua verteks (vi, vj) dan ditulis ek, k = 1,2,...,q disebut vertek-vertek ujung dari ek. Sebagai contoh dapat dilihat Gambar 2 dan Gambar 3 yaitu sebuah graph dengan 6 verteks dan 6 edge, maka dapat ditulis dengan G(6,6).

Gambar 2.1 Graph dengan 6 verteks dan 6 edege v3

e3

V4

V5

V6

V1

e6

e5

e4

e1

V2

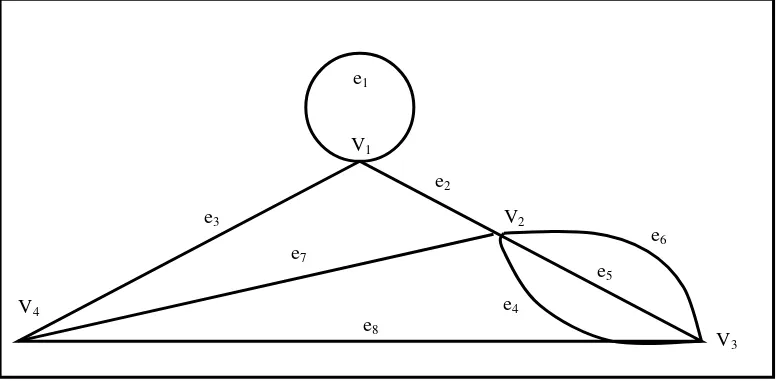
Gambar 2.2 Graph dengan loop dan edge sejajar Defenisi 2.2

Suatu edge yang menghubungkan pasangan verteks yang sama yakni (vi, vi) disebut loop dan dua atau lebih edge yang mempunyai vertek-vertek ujung yang sama yaitu (vi, vi) disebut dengan edge sejajar. Jika sebuah graph G yang didalamnya tidak terdapat loop dan edge sejajar disebut graph sederhana.

Definisi 2.3

Suatu walk dinyatakan sebagai barisan alternatif berhingga dari vertek-vertek dan edge yang diawali dan diakhiri dengan verteks yang sedemikian hingga tiap-tiap edge insiden dengan verteks yang terdahulu dan dengan vertek yang berikutnya. Vertek yang merupakan vertek awal dan vertek akhir disebut dengan terminal vertek.

Pada Gambar 4 dapat dipilih sebuah walk yaitu v1, e3, v5, e7, v6, e8, v3, e9, v7, e6 dan v4, dimana vertek terminalnya adalah v1 dan v4.

e1

V1

e3

V4 e4

V3

e6

e5

V2

e2

e7

Gambar 2.3 Graph dengan walk yang bergaris tebal

Dapat juga sebuah walk dimulai dan diakhiri oleh verteks yang sama, walk yag demikan disebut dengan close walk. Sebaliknya sebuah walk yang tidak tertutup disebut open walk. Sebuah close walk dapat juga disebut cycle.

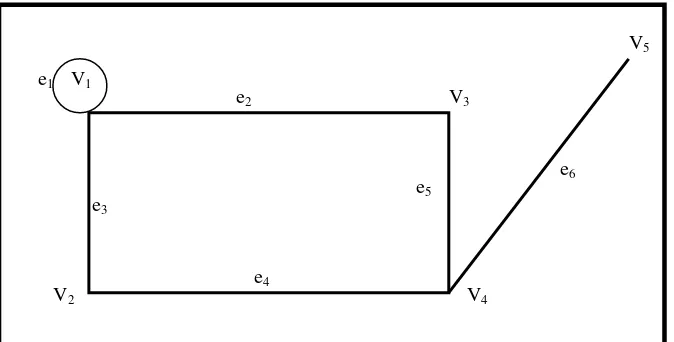
Gambar 2.4 Graph dengan 5 verteks dan 6 edge V1

e2 V3

V5

V4

V2

e5

e6

e3

e4

e1

V1

V2

V3

V4

V5 V6

e2 e8

e4

e11

e6

e12

e5

e7

e3

V7

Sebuah open walk yang didalamnya tidak ada verteks yang muncul lebih dari satu kali disebut sebagai sebuah lintasan (path) atau lintasan sederhana atau sebuah lintasan dasar. Pada Gambar 5 dapat diambil sebuah lintasan v1, e1, v2, e4, v4, e6, v5 sebagai contoh . Tapi pada Gambar 4 dapat dilihat v1, e3, v5, e7, v6, e8, v3, e9, v7, e4, v6, e5, v2, e12, v4 bukan merupakan lintasan karena terdapat verteks yang muncul lebih dari satu kali. Dengan kata lain, sebuah lintasan, verteks dan edgenya tidak beririsan dengan verteks dan edge sendiri.

Jumlah dari edge-edge dalam sebuah lintasan disebut dengan panjang dari lintasan. Sebuah edge yang bukan loop dapat dimasukkan didalam sebuah walk, tapi tidak termasuk lintasan. Verteks terminal dalam suatu lintasan mempunyai derajat lanjutan satu dan verteks lainnya yang disebut dengan verteks lanjutan mempunyai derajat dua. Derajat-derajat ini dihitung hanya verteks yang berhubungan dengan edge-edge yang ada lam lintasan dan bukannya seluruh lintasan dalam graph.

2.2 Graph Terhubung

Secara intuisi, konsep-konsep tentang keterhubungan suatu graph telah jelas. Sebuah graph dikatakan terhubung jika terdapat sebuah verteks yang terhubung menuju vertek-vertek lainnya sepanjang jalur edge.

V1

V3

V4

Gambar 2.5 Graph tak terhubung

Gambar 2.6 Graph terhubung

Definisi 2.4

Sebuah graph G dikatakan terhubung (connected) jika ada sedikitnya satu lintasan antara setiap pasangan verteks dalam graph G. Sebaliknya graph G adalah tak terhubung (disconnected). Contoh masing-masing untuk graph terhubung dan tak terhubung dapat dilihat pada Gambar 6 dan Gambar 7.

2.3 Graph Berlabel

Hubungan antar verteks-verteks dalam graph perlu diperjelas. Hubungan tidak cukup V1

V2 V5

V3

V4

V7

suatu daerah. Verteks-verteks pada graph menyatakan kota-kota yang ada di daerah tersebut, dan edge-edge dalam graph menyatakan jalan yang menghubungkan kota-kota tersebut.

Informasi tentang peta daerah perlu diperjelas dengan mencantumkan jarak antara 2 kota yang berhubungan. Informasi tentang jarak dibutuhkan karena dalam graph, letak verteks dan panjang edgenya tidak menyatakan jarak 2 kota yang sebenarnya seperti halnya dengan peta yang sebenarnya. Jadi setiap garis dalam graph berhubungan dengan suatu label yang menyatakan bobot garis tersebut.

Definisi 2.5

Graph Berlabel (weighted graph) adalah suatu graph tanpa edge paralel dimana setiap edgenya berhubungan dengan suatu bilangan riil tak negatif yang menyatakan bobot edge (w(e)) tersebut. Jumlah bobot semua edge disebut Total Bobot.

Matriks yang bersesuaian dengan graph berlabel G adalah matriks hubung A = (aij) dengan aij = bobot edge yang menghubungkan verteks vi dengan verteks vj. Jika verteks vi tidak berhubungan langsung dengan verteks vj maka aij = ∞, dan aij = 0 jika i = j.

Contoh 2.1

Edge Kota yang dihubungkan Biaya per satuan e4 e7 e2 e8 e9 e1 e3 e10 e5 e11 e6

v2 – v3 v4 – v6 v1 – v7 v3 – v4 v3 – v5 v1 – v2 v1 – v4 v6 – v8 v7 – v8 v5 – v6 v6 – v7

3 4 5 5 5 15 15 15 15 15 18

a. Graph berlabel untuk menyatakan jaringan listrik di 8 kota dapat digambarkan pada gambar 2.3. dibawah ini. Angka dalam kurung menyatakan bobot edge yang bersangkutan. Bobot tersebut menyatakan biaya pengadaan jaringan listrik.

v1 v4 v6 v8 v7 v2 v3 v5 e2 (5) _{e3 (15)}

e5 (15)

e6 (18)

e7 (4)

e8 (5)

e9 (5) e4 (3) e1 (15)

e10 (15)

Gambar 2.7 Graph Jaringan listrik di 8 kota

b. Matriks hubung untuk menyatakan graph berlabel pada gambar 2.3. adalah matriks

A = (aij) dengan aij =

Jarak verteks vi dengan vj jika ada edge yang menghubungkan verteks vi dengan vj

∞ Jika tidak ada edge yang menghubungkan verteks vi dengan vj

0 jika i = j

v1 v2 v3 v4 v5 v6 v7 v8

v1 0 15 ∞ 15 ∞ ∞ ∞ ∞

v2 15 0 3 ∞ ∞ ∞ ∞ ∞

v3 ∞ 3 0 5 5 ∞ ∞ ∞

A = v4 15 ∞ 5 0 ∞ 4 ∞ ∞

v5 ∞ ∞ 5 ∞ 0 15 ∞ ∞

v6 ∞ ∞ ∞ 4 15 0 18 15

v7 5 ∞ ∞ ∞ ∞ 18 0 15

v8 ∞ ∞ ∞ ∞ ∞ 15 15 0

Setiap path dalam digraph (directed graph) mempunyai nilai yang dihubungkan dengan nilai path tersebut, yang nilainya adalah jumlah dari nilai edge path tersebut. Dari ukuran dasar ini dapat dirumuskan masalah seperti “ mencari lintasan terpendek antara dua vertek dan meminimumkan biaya”.

Banyak bidang penerapan mensyaratkan untuk menentukan lintasan terpendek berarah dari asal ke tujuan di dalam suatu distribusi aliran berarah. Algoritma yang diberikan dapat dimodifikasi dengan mudah untuk menghadapi lintasan berarah pada setiap iterasinya.

Suatu versi yang lebih umum dari masalah lintasan terpendek adalah menentukan lintasan terpendek dari sembarang verteks menuju ke setiap verteks lainnya. Pilihan lain adalah membuang kendala tak negatif bagi “jarak”. Suatu kendala lain dapat juga diberlakukan dalam suatu masalah lintasan terpendek.

Definisi 2.6

Lintasan terpendek antara dua verteks dari s ke t dalam jaringan adalah lintasan graph berarah sederhana dari s ke t dengan sifat dimana tidak ada lintasan lain yang memiliki nilai terendah.

[image:31.595.126.508.140.320.2]

Gambar 2.8 Shortest path (garis tebal)

Pada Gambar 9 dapat dilihat bahwa setiap edge terletak pada path-path dari titik 1 ke titik 4. Edge merepresentasikan saluran dengan kapasitas tertentu (contohnya, air) dapat dialirkan melalui saluran. Sedangkan verteks merepresentasikan persimpangan saluran. Air mengalir melalui verteks pada verteks yang dilalui

Lintasan terpendek dari verteks pada graph di atas adalah P = {1 – 2, 2 – 4} dengan kapasitas 4.

Contoh 2.3

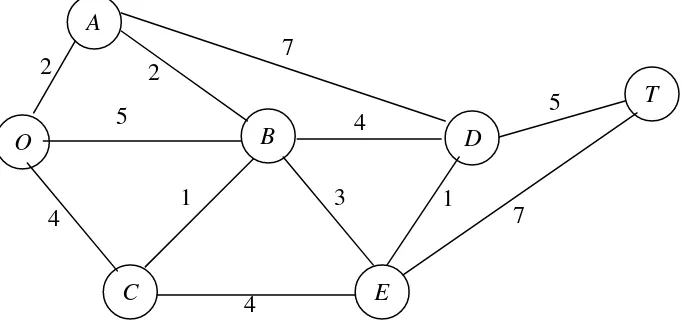
Taman Seervada diciptakan sebagai tempat untuk berdarmawisata dan pendakian bukit dengan jumlah yang terbatas. Mobil tidak diizinkan untuk masuk ke dalam taman, tetapi disana terdapat suatu sistem jalan sempit berliku untuk trem dan jeep petugas taman. Sistem jalan tersebut ditunjukkan (tanpa lengkungan) dalam gambar 2.9 dimana O adalah pintu masuk taman sedangkan abjad lain diperuntukkan bagi pos penjagaan (dengan beberapa fasilitas yang terbatas). Angka-angka pada gambar menunjukkan jarak tempuh antara pos-pos tersebut dalam satuan mil.

1

2

3 4

3X1

5X3

2X2 1X4

[image:32.595.137.479.262.428.2]

Taman tersebut memiliki pemandangan yang sangat indah di pos T. Sejumlah kecil trem digunakan sebagai sarana transportasi para pelancong dari pintu masuk taman menuju pos T dan sebaliknya. Pengelola taman ini menghadapi suatu permasalahan yaitu menentukan lintasan dengan jarak tempuh terpendek dari pintu masuk menuju pos T dalam upaya mengoperasikan trem.

Gambar 2.9 Sistem Jalan di Taman Seervada

Perhatikan suatu jaringan kerja tak berarah yang terhubungkan dengan dua buah verteks istimewa yang disebut sebagai verteks asal dan tujuan. Berpadanan dengan setiap link (garis tak berarah) terdapat jarak tak negatif. Tujuannya adalah menentukan lintasan terpendek (lintasan dengan total jarak terpendek) dari asal menuju tujuan.

2.5 0-1 Programming (Binary Integer)

A

O B D

T

C E

2 ₂

5

4

1

4 7

4

3 1

5

Model 0-1 Programming biasanya dipilih untuk permasalahan yang variabel variabelnya tidak dimungkinkan bertipe bilangan tidak bulat, misalnya : variabel jumlah orang.

0-1 Programming adalah program linear (Linear Programming) dengan tambahan persyaratan bahwa semua atau beberapa variabel bernilai bulat nonnegatif, tetapi tidak perlu bahwa parameter model juga bernilai bulat. 0-1 Programming

digunakan untukmemodelkan permasalahan yang variabel-variabelnya tidak mungkin berupa bilangan yang tidak bulat (bilangan real), seperti variabel yang merepresentasikan jumlah orang, karena jumlahorang pasti bulat dan tidak mungkin berupa pecahan. 0-1 Programming juga biasanya lebih dipilih untuk memodelkan suatu permasalahan karena program linear dengan variabel berupa bilangan real

kurang baik dalam memodelkan permasalahan yangmenuntut solusi berupa bilangan integer, misalnya keuntungan produksi 3 pesawat dibandingkan dengan keuntungan produksi 3,5 pesawat akan menghasilkanselisih keuntungan yang signifikan.

Ada banyak kasus dalam masalah 0-1 Programming yang membatasi variabel model bernilai nol atau satu. Dalam kasus demikian, persoalan lintasan hanya memiliki dua pilihan yaitu masuk atau keluar dari jaringan. Jika variabel Xj bernilai satu, persoalan masuk, dan jika variabel Xj bernilai nol, persoalan keluar.

Dalam masalah 0-1 Programming, jika persoalan mengharapkan semua variabel basis bernilai bulat positif atau nol, dinamakan pure(all) integer programming. Jika persoalan hanya mengharapkan variabel-variabel tertentu bernilai

Pemrograman bulat dibutuhkan ketika keputusan harus dilakukan dalam bentuk bilangan bulat (bukan pecahan yang sering terjadi bila kita gunakan metode simpleks). Model matematis dari pemrograman bulat sebenarnya sama dengan model linear programming, dengan tambahan batasan bahwa variabelnya harus bilangan bulat.

Terdapat 3 macam permasalahan dalam pemrograman bulat, yaitu:

1. Pemrograman bulat murni, yaitu kasus dimana semua variabel keputusan harus berupa bilangan bulat.

2. Pemrograman bulat campuran, yaitu kasus dimana beberapa, tapi tidak semua, variabel keputusan harus berupa bilangan bulat

3. Pemrograman bulat biner, kasus dengan permasalahan khusus dimana semua variabel keputusan harus bernilai 0 dan 1

Walaupun persoalan umum 0–1 linear programming dapat diselesaikan dengan algoritma cutting plane atau branch-and-bound, Blintasan Force mengembangkan suatu algoritma enumerative yang efisien dan menarik untuk menyelesaikan persoalan ini. Sangat singkat sebagai dasar integer nonlinear programming. Fungsi digunakan untuk menyamaratakan kesalahan metode untuk menyelesaikan persoalan all integer dan mixed-integer nonlinear programming.

Xj =   

tidak keputusan

untuk

ya keputusan untuk

, 0

, 1

Model ini seringkali disebut sebagai model pemrograman bulat biner .

2.6 Knapsack

Algoritma 0 – 1 Programming merupakan salah satu tipe masalah Knapsack dimana keadaan tertentu terjadi, masing-masing keadaan mempunyai sebuah nilai yang dihubungkan dengan besarannya. Secara nyata bahwa solusi optimal dari masalah knapsack akan menunjukkan kemungkinan yang terbaik.

Pada masalah ini akan terdorong untuk menyelesaikan suatu persoalan dalam menentukan lintasan terpendek pada suatu distribusi aliran. Pendekatan yang sederhana dapat dimasukkan ke dalam program komputer untuk memeriksa semua harga 0-1 yang mungkin, dipilih yang terbaik yang memenuhi kendala.

Contoh 2.4 Persoalan Knapsack

Seorang pendaki gunung ingin membawa semua peralatan yang ia perlukan dalam satu kantong (sack) saja. Misalkan ada sejumlah n peralatan yang diperlukan, tetapi ia tidak ingin berat seluruhnya melebihi b kg. Bila berat peralatan ke – j adalah aj kg dan harganya adalah Cj maka persoalan yang dihadapi ialah memaksimumkan harga semua peralatan tanpa melebihi batas berat, yakni b kg. Misalkan jenis peralatan ialah Xj dan,

Xj =

0 bila alat ke – j tidak ikut

Berdasarkan keterangan diatas, persoalan dapat dirumuskan sebagai berikut :

Max. f = c1 X1 + c2 X2 + ….. + cn Xn Dengan kendala :

a1 X1 + a2 X2 + ….. + an Xn ≤ b X1 , X2 , ………. Xn = 0 atau 1

Persoalan ini merupakan persoalan Knapsack sebagai persoalan nol satu (0-1).

0 - 1 atau biner, Persoalan Knapsack yaitu masukan dari n item dan suatu

knapsack, dengan

pj = keuntungan dari item j,

wj = bobot dari item j,

c = kapasitas dari knapsack

pilih subset dari item sebagai

maksimumkan _j

j jx

p z

∑

=

= 1

dengan kendala ,

1

c x w _j

n

j

j ≤

∑

=

xj 0 atau 1, j ε N {1,…..,n}

     =

0 1 j

x

2.7 Pengenalan Program LINDO

LINDO (Linier, Interaktip, dan Discrete Optimizer) adalah suatu alat yang mudah, tangguh untuk memecahkan permasalahan linear, bilangan bulat, dan permasalahan pemrograman kuadratik. Permasalahan ini terjadi di dalam bidang-bidang untuk urusan(bisnis, industri, riset dan pemerintah. Bidang-bidang-bidang aplikasi-aplikasi spesifik di mana LINDO sudah terbukti penggunaannya dalam memasukkan distribusi produk, campuran ramuan, penjadwalan produksi dan personil, manajemen inventori. Perangkat lunak LINDO dirancang bersifat sederhana untuk belajar dan untuk digunakan.

Jika objek j memenuhi

[image:38.595.134.500.144.396.2]

BAB 3

PEMBAHASAN

3.1 Permasalahan Lintasan Terpendek

Ada beberapa macam persoalan lintasan terpendek, antara lain:

a. Lintasan terpendek antara dua buah simpul tertentu (a pair shortets path). b. Lintasan terpendek antara semua pasangan simpul (all pairs shortest path). c. Lintasan terpendek dari simpul tertentu ke semua simpul yang lain (

single-source shortest path).

[image:39.595.157.468.440.543.2]

d. Lintasan terpendek antara dua buah simpul yang melalui beberapa simpul tertentu (intermediate shortest path).

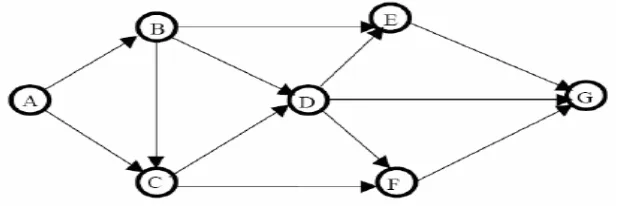
Gambar 3.1 Menunjukkan suatu graf ABCDEFG yang berarah dan tidak berbobot.

Pada Gambar 12. misalkan dari kota A ingin menuju Kota G. Untuk menuju kota G, dapat dipilih beberapa jalur yang tersedia :

A  B  C  D  F  G A  B  C  D  G A  B  C  F  G A  B  D  E  G A B D  F  G A B  D  G A B  E  G A C  D  E  G A C  D  F  G A C  D  G A C  F  G

Berdasarkan data diatas, dapat dihitung jalur terpendek dengan mencari jarak antara jalur-jalur tersebut. Apabila jarak antar jalur belum diketahui, jarak dapat dihitung berdasarkan koordinat kota-kota tersebut, kemudian menghitung jalur terpendek yang dapat dilalui.

3.2 Metode Balas

Sejak algoritma cutting plane dan branch and bound berkembang terutama untuk memecahkan suatu bilangan integer yang umum pada masalah LP, mereka tidak pernah mengambil keuntungan dari laporan khusus pada permasalahan nol-satu LP. Dengan begitu beberapa metoda-metoda yang telah diusulkan pada permasalahan nol-satu LP bisa lebih secara efisien. Pada bagian ini suatu algoritma yang di kembangkan oleh Balas (tahun 1965) dalam memecahkan permasalahan LP dengan variabel-variabel yang biner saja.

Egon Balas mengembangkan suatu cara atau algoritma untuk menyelesaikan persoalan program linier hanya dengan variabel biner nol-satu (0-1). Pendekatan yang digunakan adalah pendekatan enumerasi, baik yang total maupun implicit, terhadap setiap kombinasi variabel yang diatur sama dengan nol dan satu. Kombinasi 0 dan 1 yang memenuhi semua kendala dan meminimumkan fungsi tujuan dinyatakan sebagai jawab optimal.

Jika ada variabel-variabel biner n pada suatu masalah, satu proses enumerasi eksplisit akan melibatkan percobaan 2n kemungkinan penyelesaian berlawanan yang dinyatakan sebagai batasan dan fungsi objektif. Di Metode Balas, semua kemungkinan pemecahan 2n disebut enumerasi eksplisit atau secara implisit. Efisiensi dari metoda muncul karena strategi yang pandai yang mengadopsi di dalam memilih hanya sedikit solusi-solusi untuk proses enumerasi eksplisit.

Metoda mulai dengan pengaturan semua n variabel sepadan dengan kosong, dan terdiri atas suatu prosedur yang sistematis berturut-turut menugaskan kepada variabel-variabel yang tertentu bernilai 1, sedemikian sehingga setelah mencoba

salah satu yang manapun suatu pemecahan optimal atau bukti dari fakta bahwa tidak ada penyelesaian layak ada. Satu-satunya operasi yang diperlukan di dalam perhitungan itu adalah penambahan-penambahan dan pengurangan-pengurangan dan karenanya menyelesaikan error tidak akan terjadi di sana. Untuk alasan ini, metoda itu biasa dikenal sebagai algoritma aditif.

Untuk menguraikan algoritma itu maka di pertimbangkan, menganggap bentuk umum berikut suatu masalah LP dengan peubah nol-satu :

a) Tentukan X =               n x x x ' 2 1 minimumkan (maksimumkan)

F(X) = CT X

dengan kendala

A X ≥ B

dan

xi= 0 atau 1, i = 1,2,...,n.

C =                     n c c c . . . 2 1

dan B =

                    o m b b b . . . 2 1

Permasalahan ini dapat selalu diubah jadi suatu bentuk di mana semua batasan akan menjadi bentuk ≤, dan semua koefisien dari fungsi objektif (untuk yang diperkecil) menjadi tidak negatif., ini dapat dicapai oleh operasi yang berikut :

− Rubah tanda dari fungsi objektif jika masalah berasal dari tipe maksimalisasi.

− Ganti semua persamaan kendala oleh dua ketidaksamaan, salah satu bentuk ≤, dan yang lain dari bentuk ≥.

− Kalikan oleh -1 semua ketidaksamaan bentuk ≥ untuk merubah mereka kepada bentuk ≤..

− Bentuk variabel-variabel baru x1 seperti :

   < − ≥ = 0 1 0 i i i i i c if x c if x

x in the minimization problem

Tentukan X =               n x x x ' 2 1 seperti

F (X) = CT X minimum

dengan kendala

A X + Y = B

Xi= 0 atau 1

dan

Y ≥ 0 dimana

C =               n c c c ' 2 1

≥ 0, Y =               m y y y ' 2 1

, B =               m b b b ' 2 1 dan

A =

                mn m m n n a a a a a a a a a ... . . . . . . . . ... ... 2 1 2 22 21 1 12 11

c) (yj)baru = (yj)ada – ajs xs

0 1 = − ≤

+ k k

k

j jEJ

j

k c x

f

k

∑

=

* f c f_k + _s ≥

d) Pk = jk – ( Nk ∪ Mk ) = R – Jk – (Nk ∪ Mk)

e)

∑

∈

>

k

P

k j js y

a

f)

( )

k

s k

t I

I =max seperti x_s ∈P_k

3.2.1 Beberapa Definisi dan Notasi pada Metode Balas

(i) Penyelesaian sebagian

Jika beberapa (tidak semua) dari n variabel tiap-tiap xidiberikan nilai 0 atau 1,

selanjutnya solusi ini dinamakan penyelesaian sebagian J. Demikian jika n = 5, solusinya

J = (x1= 1, x3 = 1, x4 = 0) (a)

Dapat dikatakan partial solution. Untuk penulisan notasi yang sebaiknya, berturut-turut kita gunakan symbol i dan –i untuk mewakili xi = 1 dan xi = 0.

Menurut notasi ini, partial solution diatas dapat ditulis menjadi

J = (1, 3, -4)

(ii) Variabel Bebas

Variabel yang tidak dimasukkan dalam partial solution ( J ) dinamakan variabel bebas. Sebagai contoh, untuk partial solution ditunjukkan contoh (a), variabel x2 dan x5 menjadi variabel bebas. Ini dikatakan variabel bebas selama kita memberikan tiap-tiap pilihan nilai 0 atau 1. Selanjutnya kita akan mengambil semua variabel bebas sama dengan nol dan sebaliknya kecuali kalau ditetapkan.

(iii) Penyelesaian Sebagian Secara Lengkap

Jika tiap-tiap variabel bebas dari partial solution (J) diberikan nilai 0 atau 1, kemudian kumpulan variabel lengkap (masukkan partial solution) dinamakan

[image:46.595.108.528.531.687.2]

Penyelesaian Sebagian Secara Lengkap. Demikian, untuk partial solution yang ditetapkan pada contoh (b), ada 4 kemungkinan penyelesaian seperti yang ditunjukkan dibawah ini :

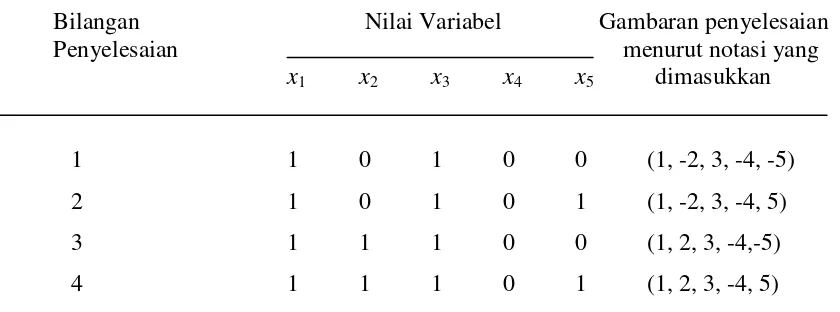
Tabel 3.1 Penyelesaian Sebagian Secara Lengkap

Bilangan Nilai Variabel Gambaran penyelesaian

Penyelesaian menurut notasi yang

x1 x2 x3 x4 x5 dimasukkan

1 1 0 1 0 0 (1, -2, 3, -4, -5)

2 1 0 1 0 1 (1, -2, 3, -4, 5)

Diketahui, pada ke empat penyelesaian, nilai x1, x3, dan x4 menjadi 1, 1, dan 0 berturut-turut ditetapkan oleh partial solution J pada contoh (b).

(iv) Awal Penyelesaian Sebagian

Untuk menyelesaikan persoalan yang ditetapkan pada contoh (a) kita mulai dengan awal penyelesaian sebagian yang diberikan variabel, jadi, semua variabel merupakan variabel bebas dengan nilai nol. Awal penyelesaian sebagian ini ditunjukkan sebagai J0.

(v) Solusi Explicit dan Implicit Enumeration

Jika persoalan hanya meliputi 2 atau 3 variabel biner, semua solusi yang mungkin dapat disebutkan satu persatu dengan jelas seperti dibawah ini :

Persoalan 2 variabel Persoalan 3 variabel

( Bilangan solusi = 22 = 4 ) ( Bilangan solusi = 23 = 8 )

1, 1 1, 1, 1

1, 0 1, 1, 0

0, 1 1, 0, 1

0, 0 0, 1, 1

[image:48.595.253.421.162.311.2]

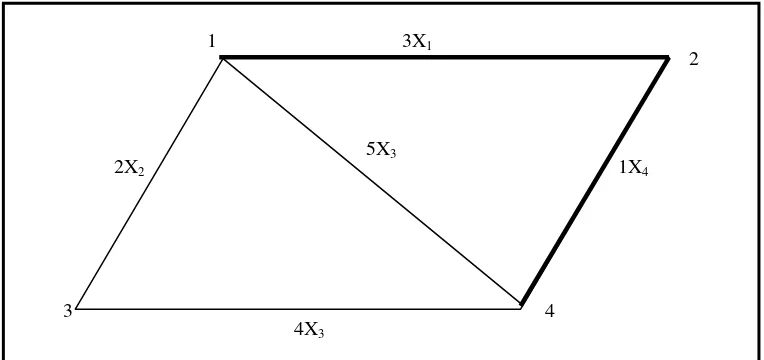
Gambar 3.2 Shortest Path

Pada contoh kasus ini terdapat 8 variabel, sehingga ada 256 kemungkinan yang layak. Evaluasi semua kemungkinan ini adalah :

Tabel 3.2 Complete Enumeration Kemungkinan

Ke X1 X2 X3 X4 X5 X6 X7 X8 Kelayakan Nilai Z

1 0 0 0 0 0 0 0 0 - 0

2 0 0 0 0 0 0 0 1 - 5

3 0 0 0 0 0 0 1 0 - 3

4 0 0 1 0 0 1 0 0 Ya 4

5 0 0 0 0 1 0 0 0 - 4

6 0 0 0 1 0 0 0 0 - 1

7 0 1 0 0 0 0 1 0 Ya 5

8 0 1 0 0 0 0 0 0 - 2

1 2

3

4 5

2 x1

2 x2 _{4 x}

5

1 x6

5 x8

3 x7

1 x4

[image:48.595.116.532.435.688.2]

10 1 0 0 0 0 0 0 1 Ya 7

11 0 1 1 0 0 0 0 0 - 5

12 0 0 1 1 0 0 0 0 - 4

13 0 0 0 1 1 0 0 0 - 5

14 0 0 1 1 0 0 1 0 Ya 7

15 0 0 0 0 0 1 1 0 - 4

16 0 1 0 0 1 0 0 1 Ya 11

17 1 0 1 0 0 0 0 0 - 5

18 0 1 0 1 0 0 0 0 - 3

19 0 0 1 0 1 0 0 0 - 7

20 0 0 1 1 1 0 0 1 Ya 13

. . .

256 1 1 1 1 1 1 1 1 - 21

Diantara 256 kemungkinan solusi hanya ada 6 kemungkinan yang memenuhi, yang lain melanggar salah satu atau beberapa kendala. Diantara solusi yang layak, kemungkinan ke 4 adalah lintasan terpendek dan memberikan biaya termurah.

Sehingga diperoleh lintasan terpendek pada distribusi aliran ini, yaitu :

X3 – X6 = 4

X2 – X7 = 5

X1 – X8 = 7

X2 – X5 – X8 = 11 X3 – X4 – X5 – X8 = 13

Biaya termurah dari lintasan terpendek ini adalah X3 – X6 = 4

Dimana harga seluruhnya dari lintasan terpendek ini adalah : Z = 2X1 + 2X2 + 3X3 + 5X8 + 4X5 + 3X7 + X4 + X6

= 2 + 2 + 3 + 5 + 4 + 3 + 1 + 1 = 21

Beberapa notasi yang digunakan pada presentasi metode Balas :

Jk = set dari variabel yang telah diberikan suatu nilai dari 0 atau 1 di iterasi kth. Itu menandai (adanya) variabel melibatkan di suatu solusi yang parsial di iterasi kth.

Jo = set dari variabel melibatkan di dalam solusi awal parsial . Itu diambil sebagai

suatu himpunan nol.

R = set dari semua variabel n pada permasalahan. =

−

= _k

k R J

J

_

set dari peubah bebas yang tidak tercakup di solusi yang parsial selama iterasi kth. Seperti yang dinyatakan di definisi, semua peubah bebas diasumsikan untuk menjadi nol, dinyatakan selainnya.

Pk = set tertentu (tidak harus semua) dari peubah bebas yang mungkin untuk

variabel-= k o

I suatu ukuran dari infeasibilitas yang total pada masalah ketika variabel-variabel xs adalah suatu nilai 1 di dalam iterasi kth.

= k

f nilai dari fungsi objektif pada awal iterasi kth. =

o

J nilai paling sedikit dari fungsi objektif yang dicapai sejauh ini. kita ingin memperbaiki solusi lebih lanjut, jika mungkin.

[image:52.595.67.555.71.707.2]

Gambar 3.3 Flow chart metode Balas

Masukan k = 0, Jk = null, R = (x1, x2, …, xn), y (k)

= B, fk = 0, f* = ~

Bentuk masukan Nk dan Mk

digambarkan padalangkah 1(a)

Cari penyelesaian sebagian baru Jk+1 dengan

menambahkan xt = .1 untuk

penyelesaian Jk

Masukkan Pk menggunakan

persamaan Cari masukan variabel

bebas Jk = R - Jk

f* = fk Berhenti,

nilai optimum dicapai fmin

= f*

dan xopt. = sesuai dengan f*

Cari variabel xt yang paling

sesuai yang digunakan dalam persamaan

Berhenti Jk adalah

penyelesaian optimum Ganti nilai variabel paling

kanan yang mempunyai nilai 1 menjadi 0 dan hapus semua variabel dikanannya, jika ada. Ini diberikan pada solusi baru Jk+1. Hitung nilai yj

k+1

dan fk+1

Masukkan k = k + 1

Hitung yk_jdengan menggunakan penyelesaian

yang ada Jk

∑

= cJ x j j k j x c f

Masukkan k = k + 1 Apakah semua variabel Jk

sama dengan 0 ? Apakah k = 0 ?

Apakah Pk null ?

Apakah yj k_{≥ 0 ?}

i = 1 sampai m

Apakah persamaan diterima ? Atau

Apakah Pk ditolak ?

3.2.2 Penyelesaian 0-1 Programming dengan Metode Balas.

Minimumkan f =−5x₁ +7x₂ +10x₃ −3x₄ +x₅

dengan kendala x₁+3x₂ −5x₃ +x₄ +4x₅ ≤0 4 2 2 3 6

2x₁+ x₂ − x₃ + x₄ + x₅ ≥

2

2 _{3 4 5}

2 − x −x +x ≤−

x

0 1 =

x or 1, f = 1 to 5

Solusi:

Langkah (i): nyatakan masalah yang diberi di dalam bentuk baku. Untuk ini, digambarkan variabel-variabel baru xi seperti :

4 4

3 3 2 2 1

1 1 x ,x x ,x x ,x 1 x

x = − = = = − and x₅ = x₅

Dengan subtituting xi dalam permasalahan menjadi seperti berikut :

Minimumkan f =5x₁+7x₂ +10x₃ +3x₄ +x₅

dengan kendala −x₁ +3x₂ −5x₃ −x₄ +4x₅ +y₁ =−2 0 2

2 3 6

2x₁− x₂ + x₃ + x₄ − x₅ + y₂ =

1

2 _{3 4 5 3}

2 − x +x +x + y =−

x

0 1 =

x or 1, f = 1 to 5

di mana y1,y2 dan y3 adalah variabel tidak negatif dan suku tetap itu dilalaikan di (E2)

Pada persamaan (E2) dapat di diperlihatkan pada bentuk matriks seperti :

Minimumkan f =CTX dengan kendala AX + Y = B

xi = 0 or 1, Y ≥ 0

dimana           − − − − − − = 1 1 2 1 0 2 2 3 6 2 4 1 5 3 1 A                 = 1 3 10 7 5 C           − − =           = 1 0 2 3 2 1 b b b B                 = 5 4 3 2 1 x x x x x

X dan

          = 3 2 1 y y y Y

Langkah (ii) : temukan solusi awal, dari sistim kanonik pada persamaan (E2) diperoleh solusi. , 1 , 0 ,

2 _{2 3}

1 =− y = y =−

y x₁ = x₂ =x₃ =x₄ = x₅ =0, f =0

Solusi ini membuat ukuran optimal yang sesuai (semua cj > 0) tetapi bukan syarat kelayakan (tidak semua bi > 0).

Oleh pengaturan iterasi jumlah k = 0 , kita mempunyai :

0 , 1 0 2 0 0 3 0 2 0 1 ) 0 ( ₌           − − =           = f y y y

Y and fo= ∞ ;

Langkah (iii) : karena sumber y₁0 adalah negative, diperoleh bentuk variabel bebas seperti :

J0 = R – J0 = (1,2,3,4,5)

Langkah (iv) : menurut bentuk N0pada langkah i (a) , diperoleh y10 and 0 2

y adalah negatif dan diantara a1dan a2, adalah positif hanya untuk s = 2 dan 5. Karena Nhberisi

x1dan x2.

∴ N0 = (2,5)

Seperti f0 =∞, dimana tidak ada variabel x2 , yang berhubungan dengan f0+ c2≥

*

f dan karena

Langkah (v) : temukan set P0, seperti :

) 5 , 2 ( ) 5 , 4 , 3 , 2 , 1 ( )

( _{0 0}

0

0 = J − N ∪M = − P

= (1,3,4)

Langkah (vi) : karena P0 bukanlah himpunan nol, dicari apakah dicukupi atau tidak.

Untuk Yj = Y1 : 1 5 1 7

0 − = − − − =

∑

P js

a > y₁(0) =−2

Untuk Yj = Y3 : 2

0 − =

∑

P js

a > (0) 1

3 =− y

Ini memperlihatkan P0 tidak dapat ditolak.

) , 0 min( ) , 0 min( ) , 0

min( ₁0 ₁₁ 0_{2 21 3}0 ₃₁

) 0 (

1 y a y a y a

I = − + − + −

= min( 0, -2+1) + min(0, 0-2) + min (0, -1-0) = -1 -2 -1 = -4

) , 0 min( ) , 0 min( ) , 0

min( ₁0 _{13 2}0 _{23 3}0 ₃₃

) 0 (

3 y a y a y a

I = − + − + −

= min( 0, -2+5) + min(0, 0-3) + min (0, -1+2) = 0 -3 + 0 = -3

) , 0 min( ) , 0 min( ) , 0 min( 34 0 3 24 0 2 14 0 1 ) 0 (

4 y a y a y a

I = − + − + −

= min( 0, -2+1) + min(0, 0-2) + min (0, -1-1) = -1 -2 -2 = -5

Karena I₃(0)adalah nilai maksimum yang dihasilkan dari I₁(0),I₃0 and I₄(0), maka nilai t = 3.

Langkah (vii) : masukkan x3= 1 ke J0 untukmemproleh solusi parsial baru J1 seperti

:

J1= (3)

Langkah (viii) : set jumlah iterasi seperti k = 1.

Langkah (ix) : hitung nilai baru dari yf dan f seperti :

3 5 2 13 ) 0 ( 1 ) 1 (

1 = y −a =− + = y 3 3 0 23 ) 0 ( 1 ) 1 (

2 = y −a = − =− y 1 2 1 33 ) 0 ( 3 ) 1 (

3 = y −a =− + = y 10 10 0 3 0

1 = f +c = + =

Langkah (x) : karena beberapa dari y(_j1) adalah negatif, akan di proses untuk solusi parsial baru selanjutnya. Untuk itu ,pertama diperoleh :

) 5 , 4 , 2 , 1 ( ) 3 ( ) 5 , 4 , 3 , 2 , 1 ( 1

1 =R−J = − =

J

Langkah (xi) : untuk memperoleh set N1, ditandai bahwa y₂(1) adalah negatif, dan a_2s

adalah positif untuk s = 1 dan 4. ∴N1= (1,4)

Seperti f1= 10 , dan f0 = ∞ , tidak ada variabel xs yang memuaskan pada

hubungan f₁+c_s > f0 dan karena : M1 = φ = null set

Langkah (xii) : temukan set P1:

) 5 , 2 ( ) 4 , 1 ( ) 5 , 4 , 2 , 1 ( )

( _{1 1}

1

1 = J − N ∪M = − =

P

Langkah (xiii) : karena P1 bukan null set , dicoba untuk y2.Disini diberikan :

8 2 6

1

2 =− − =−

∑

∈P x

s

s

c > y₂(1) =−3

dan c_2s <0

ini memperlihatkan bahwa P1 tidak dapat ditolak.

Langkah (xiv) : untuk menemukan variabel yang paling menjanjikan, hitung :

) , 0 min( ) , 0 min( ) , 0

min( ₁1 ₂₃ 1_{2 24 3}1 ₂₅

) 1 (

2 y a y a y a

I = − + − + −

) , 0 min( ) , 0 min( ) , 0

min( ₁1 ₂₅ 1_{2 24} 1_{3 25}

) 1 (

5 y a y a y a

I = − + − + −

= min( 0, 3-4) + min(0, -3+2) + min (0, 1-1) = -1-1+0 = -2

Karena I₂(1) adalah nilai dari I₂(1) dan I5(1), maka t = 2.

Langkah (xv) : solusi parsial J2yang diperoleh adalah :

J2 = (3,2)

Langkah (xvi) : set iterasi berikutnya k = 2

Langkah (xvii) : nilai baru dari yi dan f dihitung seperti :

0 3 3 13 ) 2 ( 1 ) 2 (

1 = y −c = − = y 3 6 3 23 ) 2 ( 2 ) 2 (

2 = y −c =− + = y 0 1 1 33 ) 2 ( 3 ) 2 (

3 = y −c = − = y 17 7 10 2 1

2 = f +c = + =

f

Karena semua y(_j2) ≥0, set f 0 = f₂ =17 dan proses untuk menghasilkan solusi parsial baru dengan cara mengulang kembali.

Langkah (xviii) : tukar nilai pada beberapa variabel yang kanan (x0) di J3 seperti :

− =(3, 3

J χ) Hitung nilai baru dari yj dan f dari

Karena J3 adalah x1 =x2 = x4 =x5 =0 dan x3=1, diperoleh : 3 5 2 3 13 ) 3 ( 1 ) 3 (

1 = y −a x =− + = y

y₂(3) = y₂(3) −a₂₃x₃ =0−3=−3 1 2 1 3 33 ) 3 ( 3 ) 3 (

3 = y −a x =− + = y

10 2 2

3 =c +x =

f

Langkah (xix) : set iterasi baru dengan k=3.

Langkah (xx) : karena beberapa y3_j adalah negatif, didapatkan :

= − − =

−

= ₃ (1,2,3,4,5) (3, 2) 3 R J

J set dari variabel R.

yang tidak termasuk kedalam J3 = (1,4,5)

langkah (xxi) : untuk bentuk set N3 menurut pada langkah 1, ditemukan y3(3) adalah negatif dan a_3sadalah positif dari s = 1 dan 4.

∴ N3 = (1,4)

f3 = 10 dan f* = 17, diperoleh tidak ada variabel xs termasuk dari set J₃

* 3 c f f + s ≥

= =φ 3

M null set

Langkah (xxii) : karena P3 bukan null set, lihat apakah dicukupi atau tidak, seperti 0

) 3 ( 2 ≤

y , diperoleh :

3

2 ₂(3)

2

2 =a =− > y =−

Ini menunjukkan bahwa Ps dapat ditolak. Hal ini juga menunjukkan bahwa J3

diukur dan karenanya proses untuk menghasilkan solusi parsial baru dengan cara mundur.

Langkah (xxiv) : seperti k ≠ 0 dan ,semua variabel dari J3 ≠ 0 , ubah nilai dari

kebanyakan variabel yang mempunyai nilai 1 di J3 ke 0 dan menghapus variabel di

sebelah kanan untuk memperoleh J4 seperti :

J4 = (-3)

Hitung nilai baru dari yj dan f :

s n s js j k

j y a x

y

∑

= + _{= −} 1 ) 0 ( ) 1 ( s n s s

k c x

f

∑

= + =

1 1

Karena J4 memberikan x1 =x2 = x3 =x4 =x5 =0, diperoleh : 2 ) 0 ( 1 ) 4 (

1 = y =−

y 0 ) 0 ( 2 ) 4 (

2 = y =

y 1 ) 0 ( 3 ) 4 (

3 = y =− y

0 4 =

f

Langkah (xxv) :set iterasi berikutnya k = 4

Langkah (xxvi) : karena beberapa y(_j4) adalah negatif , diperoleh :

) 3 ( ) 5 , 4 , 3 , 2 , 1 ( 4

4 =R−J = − −

J

Langkah (xxvii) : untuk bentuk set N4, diperoleh bahwa y1(4) dan ) 4 ( 5

y adalah negatif dan diantara a_1s dan a_3s adalah positif untuk s = 2 dan 5.

N4 = (2,5)

Seperti f4 = 0 dan f* = 17 , tidak ada variabel xs yang sesuai pada relasi

* f c

f_k + _s≥ dan karena

= =φ

4

M null set

Langkah (xxviii) : temukan set P4 seperti :

) 4 , 1 ( ) 5 , 2 ( ) 5 , 4 , 2 , 1 ( )

( _{4 4}

4

4 = J − N ∪M = − =

P

Langkah (xxix) : karena P4 tidak null set coba untuk :

: ) 4 ( 1

y

∑

a_1s =−1−1=−2> y₁(4)=-2 :

) 4 ( 3

y

∑

a_2s =0> y₃(4) =−1 Karena P4 tidak dapat ditolak.

Langkah (xxx) : seperti k ≠ 0 dan semua variabel dari J4 adalah 0, prosedur mundur kembali melengkapi dan solusi jumlah maksimum diberi oleh :

fmin = nilai akhir of f0 = 17

dan solusi parsial yang sesuai , Js = (3,2)

Nilai-nilai jumlah maksimum dari variabel-variabel yang asli xi dapat diperbaiki

seperti :

0 ,

1 1

, 1 ,

1 ,

1

1 _{1 2 2 3 3 4 4 5 5}

1 = −x = x =x = x = x = x = −x = x =x =

x

yang memberi nilai jumlah maksimum dari fungsi objektif yang asli adalah seperti : fmin = 9

3.3 Analisis Knapsack pada Permasalahan Shortest Path

Masalah knapsack ini dapat dirumuskan secara matematika dengan memberi nilai pada objek dari 1 sampai n dan memperkenalkan suatu vektor dari variabel biner

xj(j = 1,…,n)yang memiliki arti sebagai berikut :

     =

0 1 j

x

Jika pj merupakan ukuran dari kelayakan yang diberikan oleh objek j, wj

adalah besarannya dan c adalah besaran dari knapsack, masalahnya akan terpilih, diantara semua semua vektor biner x (0–1) yang akan memenuhi kendala

∑

=

≤ n

j j jx c

w

1

,

xj = 0 atau 1, j ε N {1,…,n}

Dimana salah satu fungsi objektif di maksimumkan

Jika objek j memenuhi

∑

=

n

j j jx

p

1

Dalam permasalahan shortest path berkendala ini, untuk arc yang terpilih akan bernilai 1 dan arc yang tidak terpilih bernilai 0, sedangkan kendala B (biaya) dianggap sebagai knapsack (karung) yang memiliki bobot tertentu yang harus dipenuhi, sehingga akan didapat lintasan terpendek yang optimal sesuai dengan biaya yang dianggarkan. Persoalan ini disebut permasalahan knapsack karena tiap lintasan yang terpilih hanya memiliki dua status yaitu terpilih atau tidak.

Contoh 3.2 Persoalan lintasan terpendek diimplementasikan ke dalam Knapsack.

[image:64.595.184.428.155.305.2]

Gambar 3.4 Representasi graph pada lintasan pengiriman barang dari kota S ke kota T

Pada gambar graph diatas andaikan a(x,y) merupakan jarak(waktu) melintasi sepanjang arc f(x,y) dan b(x,y) merupakan biaya yang dianggarkan pada pemindahan satu unit flow sepanjang arc ini, maka model matematika shortest path berkendala pada permasalahan knapsack diformulasikan sebagai berikut :

Minimumkan Z1(f) =

∑

A y x f y x

a( , ). ( , )

Dengan kendala      ≠ = − = = −

∑

∑

∈ ∈ s x jika t x jika s x jika x y f y x f N y N y 0 1 1 ) , ( ) , (

dan

∑

≤

A B y x f y x

b( , ). ( , )

dimana a(x,y) = 3 dan b(x,y) = 5 dinyatakan sebagai jarak (waktu) dan biaya yang dihubungkan tiap garis F(x,y), dan node s,a,b,c,t adalah node-node N yang ditentukan pada graph.

[image:65.595.119.507.271.621.2]

3.3.1 Penyelesaian Shortest Path Berkendala pada Permasalahan Knapsack dengan 0-1 Programming

Gambar 3.5 Representasi graph pada jaringan komunikasi

komunikasi adalah kecepatan transmisi data dan biaya dari gedung asal (sumber) ke gedung tujuan. Permasalahan jaringan komunikasi pada gambar 3.5 adalah menentukan lintasan terpendek yang harus dilewati untuk mengrimkan data dari gedung a/0 (sumber) ke gedung j/9 (tujuan) dengan biaya tertentu sesuai anggaran [12]. Tabel berikut merupakan keterangan pada gambar 3.5.

Node Nama Lintasan Waktu Biaya

a/0 (sumber) A : a-d 4 5

b/1 B : d-h 1 8

c/2 C : a-h 10 2

d/3 D : h-e 5 5

e/4 E : a-e 1 2

f/5 F : e-f 3 6

g/6 G : h-i 9 10

h/7 H : i-f 1 7

i/8 I : i-j 2 9

j/9 (tujuan) J : j-g 1 3

K : f-g 7 8

L : f-b 1 3

M : f-c 3 8

[image:66.595.142.472.256.582.2]

N : b-c 2 4

Tabel 3.3 Keterangan gambar graph pada jaringan komunikasi

Minimumkan Z1(f) =

∑

A y x f y x

a( , ). ( , )

Dengan kendala      ≠ = − = = −

∑

∑

∈ ∈ s x jika t x jika s x jika x y f y x f N y N y 0 1 1 ) , ( ) , (

Dan

∑

≤

A B y x f y x

b( , ). ( , )

f(x,y) = 0 atau 1

Karena persoalan knapsack untuk mencari persoalan 0 dan 1, dan kendala diatas

fxy= 0 atau 1, maka persoalan ini dinamakan persoalan knapsack.

Dari formulasi diatas andaikan a(x,y) merupakan jarak(waktu) melintasi sepanjang arc f(x,y) dan b(x,y) merupakan biaya yang dianggarkan pada pemindahan satu unit flow sepanjang arc ini, maka :

Minimumkan Z₁(f)=

∑

a(x,y).f(x,y)

=

∑

+ + + + + + A G F E D C B

A 1 10 5 1 3 9 4 N M L K J I

H 2 1 7 1 3 2

1 + + + + + +

dengan kendala      ≠ = − = = −

∑

∑

∈ ∈ s x jika t x jika s x jika x y f y x f N y N y 0 1 1 ) , ( ) , (

pada node (g) : J – K = 0

pada node (h) : G – B – C - D = 0 pada node (i) : G + I – H = 0 pada node (j) : - I – J = -1

dan

∑

≤

A B y x f y x

b( , ). ( , )

∑

+ + + + + + A G F E D C B

A 8 2 5 2 6 10 5

7H +9I +3J +8K+3L+8M +4N ≤40

3.3.2 Langkah – langkah Penyelesaian dengan Menggunakan Program LINDO

Untuk menyelesaikan soal diatas dengan menggunakan program LINDO langkah-langkahnya adalah sebagai berikut ini :

Langkah (i) : Membuat model persamaan pada permasalahan knapsack dengan memasukkan nilai-nilai yang ada pada network, yaitu :

Minimumkan Z₁(f)=

∑

a(x,y).f(x,y)

=

∑

+ + + + + + A G F E D C B

A 1 10 5 1 3 9 4 N M L K J I

H 2 1 7 1 3 2

1 + + + + + +

pada node (c) : N – M = 0 pada node (d) : B – A = 0 pada node (e) : D + F – E = 0 pada node (f) : H + M – F – L = 0 pada node (g) : J – K = 0

pada node (h) : G – B – C - D = 0 pada node (i) : G + I – H = 0 pada node (j) : - I – J = -1

dan

∑

≤

A

B y x f y x

b( , ). ( , )

∑

+ + + + + +

A

G F E D C B

A 8 2 5 2 6 10 5

7H +9I+3J +8K +3L+8M +4N ≤40

Langkah (ii) : Masukkan persamaan diatas sesuai dengan bahasa yang dimengerti program LINDO, yaitu :

MIN 4A + 1B + 10C + 5D + 1E + 3F + 9G + 1H + 2I + 1J + 7K + 1L + 3M + 2N

SUBJECT TO

2) A + E + C = 1 3) L – N = 0 4) N – M = 0 5) B- A = 0 6) D + F - E = 0 7) H + M – F - L = 0 8) J – K = 0

11) –I – J = -1 END

INTE 14

Langkah (iii) : Persamaan diatas dapat langsung di jalankan untuk mendapatkan jawaban yang dicari.

[image:70.595.106.524.349.634.2]

Adapun hasil dari penyelesaian pencarian lintasan terpendek pada permasalahan 0-1 Programming yang diselesaikan dengan program LINDO sebagai berikut :

[image:71.595.107.523.139.612.2]

Gambar 3.7 Hasil akhir

bernilai 1 sedang yang lain bernilai 0. Dengan demikian jelas bahwa lintasan terpendek dari a (sumber) ke j (tujuan) yang harus dipilih adalah melalui :

- Jalur E - Jalur F - Jalur H - Jalur I

[image:72.595.117.507.309.656.2]

Pada gambar diperlihatkan yang bergaris tebal adalah merupakan lintasan terpendek terpilih yang harus dilewati untuk mengrimkan data dari gedung a/0 (sumber) ke gedung j/9 (tujuan) dengan biaya yang dianggarkan. Lintasan tependek yang terpilih yaitu :

Nama Lintasan Kota yang dilalui Bobot jarak(waktu) Bobot biaya

E a → e 1 2

F e → f 3 6

H i → f 1 7

I i → j 2 9

[image:73.595.113.521.246.382.2]

Total Bobot 7 24

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dari penelitian ini dapat disimpulkan beberapa hal mengenai penerapan 0-1 programming pada permasalahan shortest path yang berkendala yaitu :

1. Persoalan ini untuk menyelesaikan masalah pendekatan sederhana, yang dapat dimasukkan ke dalam program komputer untuk memeriksa semua nilai 0 dan 1 yang mungkin, dan dipilih yang terbaik yang memenuhi kendala. Kombinasi 0 dan 1 yang memenuhi semua kendala dan meminimumkan fungsi tujuan dinyatakan sebagai jawab optimal.

2. Dalam menyelesaikan suatu persoalan untuk menentukan lintasan terpendek berkendala dari sumber s sampai ke tujuan t pada suatu jaringan kerja dapat diselesaikan dengan menggunakan 0-1 programming.

4.2Saran

Sebagai saran yang ditujukan kepada pembaca yang ingin menggunakan 0-1 Programming agar dapat mengembangkan metode ini lebih luas lagi, disini Penulis hanya menyelesaikan dalam cakupan kecil yang dapat dikerjakan secara manual dan mengimplementasikannya pada software yang sudah ada.

Diharapkan dengan mengembangkan hasil analisa ini, dalam menentukan lintasan terpendek agar dapat membuat ide yang lebih baik dalam metode ini, agar cabang-cabang dan node-node yang diberikan dalam bentuk sebuah graf baik dalam jumlah kecil maupun jumlah yang besar, lintasan terpendeknya dapat di tentukan atau didapatkan dengan lebih baik.

DAFTAR PUSTAKA

[1] Aneja, Y.P. and Nair, K.P.K., (1982), The Constrained Shortest Path Problem, University of New Brunswick.

[2] Bazaraa, Mokhtar, S. and Jarvis, John, S. (1977), Linear Programming And Network Flows.

[3] Danzig, G.B., (1966), Linear Programming and Extensions, Princeton University Press.

[4] Luenberger G., David (1973), Linear and Nonlinear Programming, Addison Wesley Publishing Company.

[5] Evans, J.R., Minieka, E., (1992), Optimization Algorithm for Network and Graphs, Marcel Dekker, inc.

[6] Ford, L. R. Jr. and D.R. Fulkerson (1970), Flows in Networks, Princeton University Press.

[7] Martello, S. and Toth, P., (1990), Knapsack Problems, Jhon Wiley and Sons. [8] Minoux, M. (1986), Mathematical Programing Theory and Algorithms, Jonh

Wiley and Sons.

[9] Rao, S.S., (1978), Optimization, Second Edition, Wiley Eastern Limited New Delhi.

[10] Rinaldi Munir. 2007. Matematika Diskrit Edisi Ketiga.Informatika. Bandung. [11] Suryadi. H.S. 1995. Teori Graf Dasar. Guna Darma.