Pemrograman 0-1 Pada Penentuan Minimum Spanning Tree Yang Memenuhi Kendala Biaya

(1)

PEMROGRAMAN 0-1 PADA PENENTUAN MINIMUM SPANNING TREE

YANG MEMENUHI KENDALA BIAYA

SKRIPSI

FIRDAUS SAFRAN

050803053

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

PEMROGRAMAN 0-1 PADA PENENTUAN MINIMUM SPANNING TREE

YANG MEMENUHI KENDALA BIAYA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

FIRDAUS SAFRAN

050803053

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : PEMROGRAMAN 0-1 PADA PENENTUAN

MINIMUM SPANNING TREE YANG MEMENUHI

KENDALA BIAYA

Kategori : SKRIPSI

Nama : FIRDAUS SAFRAN

Nomor Induk Mahasiswa : 050803053

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Falkultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juni 2011 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Drs. Marwan Harahap, M.Eng

NIP. 19630405 198811 2 001 NIP. 19461225 197403 1 001

Diketahui Oleh :

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

(4)

PERNYATAAN

PEMROGRAMAN 0-1PADA PENENTUAN MINIMUM SPANNING TREE YANG MEMENUHI KENDALA BIAYA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2011

(5)

PENGHARGAAN

Dengan puji dan syukur kepada Allah SWT, karena berkat dan rahmat- Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul

“PEMROGRAMAN 0-1 PADA PENENTUAN MINIMUM SPANNING TREE YANG MEMENUHI KENDALA BIAYA” ini dengan baik. Dalam menyelesaikan skripsi ini penulis banyak sekali menerima bantuan dan masukan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih sebesar-besarnya kepada:

1. Bapak Drs. Marwan Harahap, M.Eng, selaku dosen pembimbing I, Dra. Mardiningsih, M.Si selaku dosen pembimbing II, Drs. Bambang Irawan, M.Sc dan Drs. Suwarno Ariswoyo, M.Si yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini.

2. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

3. Bapak Prof. Dr. Tulus, M.Si, selaku Ketua Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

5. Ayahanda (Alm) Hadri Rhozali dan Ibunda tercinta Mardiana IS, kakak tercinta Irda Haryanti, dan Mardalisna serta abangda tercinta Agus Satria Putra dan Alfi Syahrin yang selalu memberikan dukungan moril dan material serta doa yang tiada henti kepada penulis.

Terima kasih buatnya “my best” Taufik Zuhri, Astri Syafrianti, Kiki winarti, dan Fitriyanti, Juanda, Haris, dan Haikal yang telah menjadi sahabat terdekat selama menimba ilmu di USU. Abangda Saffaruddin, K’nova, B’Anton yang terus memberi motifasi kepada penulis. Teman seperjuangan, Rifyal, Tasvin, Aan, Tedy, HN Leily. Adik adik terbaikku Noza, Jebi, Del, Rozha, dan Ahyan serta keluarga besar FKPPM-ABDYA Medan. Kepada guru-guru dan kawan-kawan sewaktu duduk di bangku SD, SMP, dan SMA, juga tidak lupa kiranya penulis mengucapkan terimakasih atas didikan dan persahabatan selama ini.

Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.

Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi yang membutuhkan.

Medan, Juni 2011 Penulis,

(6)

ABSTRAK

(7)

ABSTRACK

An undirected graph G ( ,V E)with sets of vertex V and sets edge E, where

each edge associate with distance (d_e) and cost (c_e). This article studies about

(8)

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACK v

DAFTAR ISI vi

DAFTAR TABEL viii

DAFTAR GAMBAR ix

BAB 1. PENDAHULUAN

1.1Latar Belakang 1

1.2Perumusan Masalah 4

1.3Pembatasan Masalah 4

1.4Tujuan Penelitian 4

1.5Kontribusi Penelitian 4

1.6Metode Penelitian 5

BAB 2. LANDASAN TEORI

2.1 Definisi Graph 6

2.2 Terminologi Dasar Graph 8

2.3 Trees 8

2.4 Minimum Spanning Tree 12

2.5 Integer Programming 16

2.6 Metode Balas (Balas Additive Algorithm) 17

2.7 Program QM for Windows 22

BAB 3. PEMBAHASAN

3.1 Kondisi Minimum Spanning Tree yang Memenuhi Kendala

Biaya 24

3.2 Kondisi Minimum Spanning yang Memenuhi Kendala Biaya

Dalam Bentuk Pemrograman 0-1 27

3.3 Kelayakan Nilai Biaya Dalam Penentuan Minimum Spanning

Tree yang Memenuhi Kendala Biaya 28

3.4 Kompleksitas 29

(9)

3.6 Penyelesaian Permasalahan Minimum Spanning Tree yang Memenuhi Kendala Biaya dengan Menggunakan

Program QM for Windows 41

BAB 4. KESIMPULAN DAN SARAN

4.1 Kesimpulan 45

4.2 Saran 46

(10)

DAFTAR TABEL

Halaman Tabel 3.1 Input koefisien fungsi objektif dan kendala dari permasalahan

pemrograman 0-1 pada QM for Windows 42 Tabel 3.2 Input koefisien fungsi objektif dan kendala serta solusi

optimal dari permasalahan pemrograman 0-1 pada QM for

Windows 43

Tabel 3.3 Jumlah iterasi penyelesaian pemrograman 0-1 pada Simulasi 1

(11)

DAFTAR GAMBAR

Halaman Gambar 1.1 Graph G= (V,E) dengan edge diberikan 2 (dua) nilai 1 Gambar 1.2 Graph G= (11,18) dengan setiap edge mempunyai 2 nilai

(d_e,c_e) 2

Gambar 1.3 Minimum spanning tree dengan mengabaikan kendala

biaya (c_e) 2

Gambar 1.4 Minimum spanning tree dengan d T( ) 24 yang memenuhi

kendala biaya c T( ) 33 3

Gambar 2.1 Contoh graph ( )a simple graph, ( )b multi graph,

( )c pseudograph 7

Gambar 2.2 Directed graph 7

Gambar 2.3 Sebuah graph yang merupakan tree 9

Gambar 2.4 Graph G dengan 6 verteks dan 7 edge 11 Gambar 2.5 Spanningtree yang dibentuk dari graph pada Gambar 2.4 11 Gambar 2.6 Graph G dengan 6 verteks dan 7 edge 12

Gambar 2.7 Distance graph 12

Gambar 2.8 Penyelesaian integer programming dengan menggunakan

metode grafik 16

Gambar 2.9 Tree enumerasi secara lengkap 18

Gambar 2.10 Tampilan awal program QM for Windows 23 Gambar 3.1 Graph tak-berarah dengan setiap edge diberikan nilai jarak

(d_e) dan biaya (c_e) 24

Gambar 3.2 Graph G dengan setiap edge diberikan nilai jarak (d_e) dan

biaya (c_e) 29

Gambar 3.3 Graph yang dibentuk dari permasalahan Knapsack 31 Gambar 3.4 Graph tak-berarah dengan 5 verteks dan 6 edge 32 Gambar 3.5 Minimum spanning tree terhadap nilai biaya dari graph

Gambar 2.4 32

Gambar 3.6 Iterasi 1 33

(12)

Gambar 3.23 Minimum spanning tree dengan total jarak d T( ) 33 yang

memenuhi kendala biaya c T( ) 15 41

(13)

ABSTRAK

(14)

ABSTRACK

An undirected graph G ( ,V E)with sets of vertex V and sets edge E, where

each edge associate with distance (d_e) and cost (c_e). This article studies about

(15)

BAB 1

PENDAHULUAN

1.1Latar Belakang

Minimum spanning tree (MST) merupakan sebuah permasalahan dalam suatu

graph yang mana banyak aplikasinya baik secara langsung maupun tidak langsung yang telah dipelajari. Salah satu contoh aplikasi secara langsung adalah permasalahan pemasangan jaringan dengan meminimasi jumlah penggunaan kabel/pipa untuk menghubungkan n bangunan secara bersamaan (connected). Untuk aplikasi secara tidak langsung termasuk seperti mereduksi data storage dan cluster analisys. Beberapa permasalahan jaringan juga bisa direduksi ke dalam permasalahan minimum

spanning tree kemudian diselesaikan dengan cara tersebut. Permasalahan minimum

spanning tree juga bisa digunakan untuk menyelesaikan permasalahan graph yang

lain, seperti travelling salesman problem (TSP).

(16)

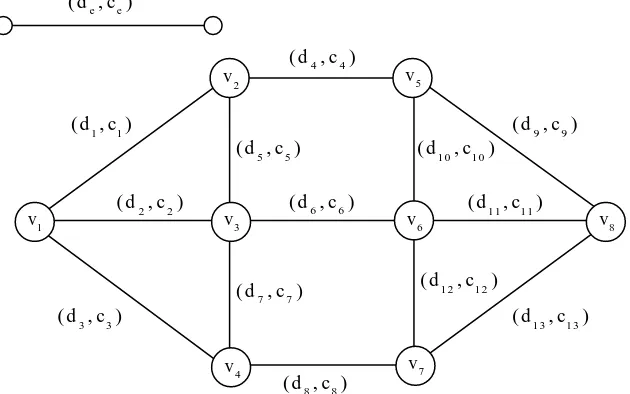
Diberikan sebuah graph tak-berarah G ( ,V E)dengan himpunan verteks V dan himpunan edge E, yang mana masing masing edge e E mempunyai 2 (dua) nilai yaitu jarak (d_e) dan biaya (c_e).

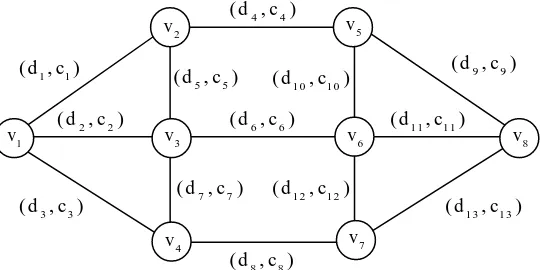
Contoh 1.1 Diberikan sebuah graph G= (V,E):

Gambar 1.2 Graph G= (V,E) dengan setiap edge mempunyai 2 nilai (d_e,c_e)

Sebuah minimum spanning tree dengan mengabaikan kendala biaya adalah:

Gambar 1.3 Minimum spanning tree dengan mengabaikan kendala biaya (c_e)

Spanning tree yang dihasilkan mempunyai total jarak d T( ) 20dan total

biaya c T( ) 48. Jika ingin dibentuk sebuah spanning tree dengan anggaran biaya ( ) 33

c T , maka spanning tree di atas tidak fisibel. Sebuah solusi optimal yang memenuhi c T( ) 33 adalah seperti spanning tree di bawah ini, di mana

( ) 24

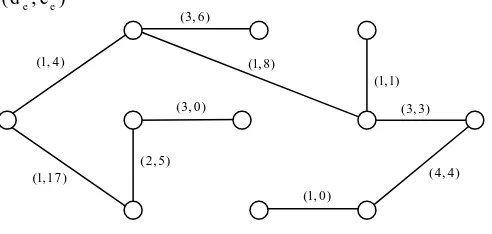
d T dan c T( ) 33: (d_e,c_e)

(1, 4)

(8, 0)

(1,17 )

(2, 5)

(5, 2) (1, 0)

(4, 4) (6, 8) (2, 9)

(4, 8)

(3, 0) (15,15)

(1, 8)

(3, 6) (5, 6)

(1,1) (9, 7)

(3, 3)

(d_e,c_e)

(1, 4)

(1,17 )

(2, 5)

(1, 0)

(4, 4) (3, 0)

(1, 8) (3, 6)

(1,1)

(17)

Gambar 1.4 Minimum spanning tree dengan d T( ) 24 yang memenuhi kendala biaya c T( ) 33

Permasalahan minimum spanning tree yang memenuhi kendala biaya yang dianggarkan pada suatu graph merupakan permasalahan yang termasuk salah satu tipe masalah integer Knapsack. Pada integer Knapsack akan diminta untuk memilih sejumlah barang yang memiliki nilai (c_i) d a n b o b o t (w_i) ke dalam sebuah karung

(knapsack) yang memiliki daya tampung (W). Untuk permasalahan Knapsack pada

minimum spanning tree, akan menimimumkan (c_i) dengan memenuhi kendala biaya

(W)yang telah dianggarkan.

Pemrograman 0-1 merupakan salah satu metode yang digunakan dalam penyelesaian Knapsack problem. Pemrograman 0-1 merupakan bagian dari linier

programming (LP) yang mempunyai kendala tambahan yaitu semua variabel basisnya

harus bernilai integer (bilangan bulat positif atau nol). Dalam linier programming

salah satu asumsi yang melandasinya adalah divisibilitas dari variabel dan kendalanya. Dengan demikian, pada linier programming permasalahan akan dihadapkan pada variabel basis yang bersifat kontinyu sedangkan dalam integer

programming permasalahan akan dihadapkan pada variabel basis yang bersifat diskrit.

Pada dasarnya algoritma yang sudah ada (Prim, Kruskal dan lain sebagainya) merupakan algoritma yang cukup efesien untuk menentukan minimum spanning tree.

Namun apabila permasalahan minimum spanning tree harus memenuhi kendala yang telah ditentukan (C), secara umum algoritma tersebut akan gagal dalam menentukan nilai optimal pada permasalahan.

(d_e,c_e)

(1, 4)

(2, 5)

(5, 2) (1, 0)

(4, 4) (3, 0)

(3, 6)

(1,1)

(18)

1.2Perumusan Masalah

Masalah yang dibahas dalam penelitian ini adalah bagaimana menentukan

minimum spanning tree yang memenuhi kendala biaya (C) dengan menggunakan

pemrograman 0-1 serta mengimplementasikannya pada program QM for Windows.

1.3 Pembatasan Masalah

Dalam penyelesaian permasalahan minimum spanning tree yang memenuhi kendala dilakukan beberapa batasan sebagai berikut:

1. Graph yang digunakan pada penelitian ini adalah graph sederhana, tidak berarah dan pada setiap edge diberikan dua nilai (d_e,c_e) untuk e E . 2. Pemberian nilai (d_e) bersifat keterbalikan terhadap (c_e) guna melihat

seberapa besar pengaruh biaya dalam penyelesaian minimum spanning tree

yang memenuhi kendala biaya.

3. Penelitian ini bersifat simulasi, dalam artian penulis memaparkan beberapa contoh simulasi dengan jumlah variabel yang tidak terlalu banyak.

1.4Tujuan Penelitian

Penelitian ini bertujuan untuk menyelesaikan permasalahan minimum

spanning tree dengan memenuhi batasan kendala biaya dengan menggunakan

pemrograman 0-1.

1.5 Kontribusi Penelitian

(19)

1.6 Metode Penelitian

Secara umum penelitian dilakukan dengan beberapa tahapan, yaitu:

i. Menjelaskan konsep minimum spanning tree dan integer programming.

ii. Memodelkan permasalahan ke dalam bentuk optimisasi:

Minimum spanning tree diformulasikan ke dalam bentuk pemrograman 0-1.

iii. Menyelesaikan permasalahan minimum spanning tree pada graph tak-berarah dengan model pemrograman 0-1.

(20)

BAB 2

LANDASAN TEORI

Pada bab ini akan diuraikan mengenai teori dan terminologi graph, yaitu bentuk-bentuk khusus suatu graph. Di sini juga akan dijelaskan mengenai minimum

spanning tree, pemrograman 0-1, dan aplikasi QM for Windows.

2.1 Definisi Graph

Sebuah graph G didefinisikan sebagai pasangan himpunan (V,E) di mana V

merupakan himpunan verteks v v₁, ₂, ...,v_n dan E merupakan himpunan edge yang menghubungkan sepasang verteks e e₁, ₂, ...,e_n atau dapat ditulis dengan notasi

G= (V,E).

Berdasarkan ada tidaknya loop atau multi egde pada suatu graph, secara umum graph dapat digolongkan menjadi dua jenis, yaitu simple graph dan unsimple graph.

Definisi 2.1 Simple graph

Sebuah graph G dikatakan simple graph jika apabila graph tersebut tidak terdapat multiple edge maupun loop. Dikatakan multiple edge karena terdapat lebih dari dua edge yang menghubungkan pasangan verteks yang sama, sedangkan loop

adalah edge yang menghubungkan verteks yang sama v v_i, _i . Gambar 2.1( )a merupakan simple graph.

Definisi 2.2 Unsimple graph

Sebuah graph G dikatakan unsimple graph apabila pada graph terdapat

multiple edge, maupun loop. Apabila graph tersebut mengandung multiple edge,

(21)

(pseudograph). Pada Gambar 2.1( )c merupakan pseudograph karena terdapat loop pada e v₂,v₂ .

Gambar 2.1 Contoh graph ( )a simple graph, ( )b multi graph, ( )c pseudograph

Berdasarkan orientasi arah pada setiap edge, secara umum graph dibedakan menjadi graph tak-berarah (undirected graph) dan graph berarah (directed graph atau

digraph).

Definisi 2.3 Graph tak-berarah (undirected graph)

Graph yang setiap edge-nya tidak mempunyai orientasi arah disebut dengan graph tak-berarah. Pada graph tak-berarah urutan pasangan verteks tidak diperhatikan sehingga u v, v u, . Gambar 2.1( )a ,( )b , dan ( )c disebut juga dengan undirected graph.

Definisi 2.4 Graph berarah (directed graph)

Untuk graph yang setiap edge-nya mempunyai orientasi arah disebut dengan graph berarah. Pada graph berarah urutan pasangan verteks diperhatikan sehingga

, ,

u v v u . Gambar 2.2 merupakan contoh dari directed graph.

(22)

2.2 Terminologi Dasar Graph

Definisi 2.5 Adjancent

Dua buah verteks pada undirected graph, u adjancent dengan v dengan ( , )u v adalah edge pada graph tersebut.

Definisi 2.6 Incident

Sebuah sembarang edge e u v, dikatakan incident dengan verteks u dan v.

Definisi 2.7 Path

Sebuah path adalah sebuah barisan dari himpunan verteks v v₁, ₂, ...,v_n dengan

1 , 1

n n

v v n n

e v v E untuk semua n 1, ...,n .

Definisi 2.8 Cycle

Sebuah cycle adalah sebuah path v v₁, ₂, ...,v_n dengan edge

1, 2 , 2, 3 , ..., n 1, n

v v v v v v sekaligus dengan edge v_n,v₁ .

Definisi 2.9 Connected

Sebuah graph tak-berarah G disebut connected graph untuk setiap pasang verteks u dan v di dalam himpunan V terdapat path dari u ke v.

Definisi 2.10 Cut-set

Cut-set dari connected graph G adalah himpunan edge. Jika salah satu edge

tersebut tidak terdapat di G akan menyebabkan G tidak terhubung. Jadi, cut-set selalu menghasilkan dua buah komponen terhubung.

2.3 Trees

Tree adalah bentuk khusus dari graph. Adapun definisi dari tree adalah

(23)

Definisi 2.11 Tree

Sebuah graph T V E, disebut sebuah tree apabila memenuhi kondisi di bawah ini:

1. T merupakan connected graph 2. T tidak mengandung cycle

Sebuah graph T V E, yang merupakan tree dicontohkan pada Gambar 2.3 di bawah ini:

Gambar 2.3 Sebuah graph yang merupakan tree

Untuk selanjutnya akan dijelaskan beberapa sifat-sifat (properties) pada tree.

Teorema 2.1 Misalkan T V E, adalah sebuah tree dengan paling sedikit 2 (dua)

verteks, untuk setiap pasangan verteks yang berbeda x y, V , terdapat unique path

(lintasan khusus) di T dari x ke y.

Bukti

Selama T connected, terdapat sebuah path dari x ke y, misalkan menjadi

0( ), 1, ..., r( ) (1)

v x v v y

Kemudian anggap keterbalikan dari kondisi ini sehingga terdapat path yang berbeda

0( ), 1, ..., s( ) (2)

u x u u y

Di sini akan diperlihatkan T akan mempunyai cycle. Path (1) dan (2) merupakan path yang berbeda, untuk i N sedemikian hingga

0 0, 1 1, ..., i i i 1 i 1

v u v u v u te ta p i v u

1

v v₄

7 v 5

v v₈

3 v 6

v

(24)

Perhatikan himpunan verteks v_i ₁,v_i ₂, ...,v_r. Selama kedua path

(1)dan(2)berakhir di y, maka kedua path tersebut akan bertemu kembali di y,

sehingga untuk setiap j i 1,i 2, ...,r sedemikian hingga vj ul untuk setiap 1, 2, ...,

l i i s . Maka kedua path tersebut akan membentuk cycle. Hal ini kontradiktif dengan syarat T adalah sebuah tree.

Teorema 2.2 Misalkan T V E, adalah sebuah tree dengan paling sedikit 2 (dua) verteks. Kemudian graph yang diperoleh dari T dengan menghapus sebuah edge

sehingga menjadi dua komponen, masing-masing komponen tersebut adalah tree.

Bukti

Diberikan u v, E , di mana T V E, . Kemudian edge ini dihapus, sehingga terdapat G V E, , di mana E E \ u v, . Didefinisikan relasi R pada

V sebagai berikut. Dua verteks x y, V memenuhi xRy jika dan hanya jika x y atau merupakan unique path di T dari x ke y dan tidak termasuk edge u v, . Di sini diperlihatkan R adalah relasi yang ekuivalen pada V, dengan dua golongan ekuivalen u dan v . Di sini juga diperlihatkan u dan v merupakan dua komponen dari G,

juga selama T tidak mempunyai cycle, akan terbentuk dua komponen.

Teorema 2.3 Jika T V E, adalah sebuah tree , maka E V 1.

Bukti

Pembuktian akan dilakukan dengan menginduksi jumlah verteks dari ,

T V E . Jelas hasil adalah benar untuk V 1. Misalkan hasil adalah benar untuk V k . Misalkan T V E, dengan V k 1. Jika dihapus sembarang edge dari T,

(25)

1 1, 1

Definisi 2.12 Spanning tree

,

G V E merupakan sebuah connected graph, maka sebuah subset T dari E

disebut sebuah spanning tree dari G apabila T memenuhi dua kondisi berikut:

1. Setiap verteks di V terhubung oleh tepat satu edge di T.

2. Edge di T memenuhi kondisi tree.

Contoh 2.1 Diberikan sebuah graph seperti gambar di bawah ini:

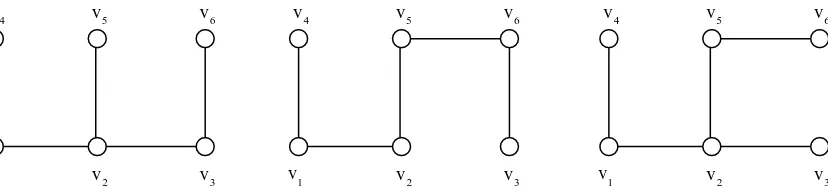
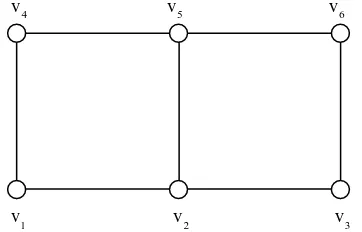
Gambar 2.4 Graph G dengan 6 verteks dan 7 edge

Dari graph Gambar 2.4 bisa dibentuk beberapa spanning tree sebagai berikut:

(26)

2.4 Minimum Spanning Tree

Definisi 2.13 Graph berjarak (distance graph)

Misalkan G V E, kemudian terdapat sebuah fungsi d :E N yang disebut fungsi jarak. Graph G bersama dengan fungsi jarak d :E N , disebut

dengan graph berjarak (distance graph).

Contoh 2.2 Diberikan sebuah graph seperti gambar di bawah ini:

Gambar 2.6 Graph G dengan 6 verteks dan 7 edge

distance dari graph:

Gambar 2.7 Distance graph

(27)

Definisi 2.14 Jarak spanning tree (distance of spanning tree)

Misalkan sebuah graph G V E, , bersama dengan fungsi jarakd :E N . Untuk selanjutnya G merupakan connected, dan T merupakan spanning tree dari G,

maka nilai:

( ) _e

e T

d T d

merupakan penjumlahan seluruh jarak pada semua edge di T, disebut dengan jarak

spanning tree.

Untuk setiap graph G adalah sebuah graph berjarak (distance graph). Jelas, untuk setiap spanning tree T dari G akan mempunyai total jarak d T( ). Dari semua

spanning tree T dari G, terdapat spanning tree yang mempuyai jarak d T( ) minimum.

Definisi 2.15 Minimum spanning tree

Sebuah graph G V E, , bersama dengan fungsi jarak d :E N , membentuk sebuah distance graph. Selanjutnya G connected, sebuah spanning tree

dengan jarak d T( ) minimum dari semua spanning tree di G disebut dengan minimum spanning tree.

Permasalahan minimum spanning tree bisa dirumuskan seperti di bawah ini: m in _e

e T d

T S T G

dengan ketentuan S T G adalah himpunan spanning tree dari graph.

Untuk persoalan minimum spanning tree akan diformulasikan dua kondisi optimal pada persoalan minimum spanning tree.

Teorema 2.4 Kondisi optimal cut (cut optimality condition)

Sebuah spanning tree *

T adalah minimum spanning tree jika dan hanya jika untuk

setiap edge *

(28)

Bukti

Asumsikan terdapat sebuah minimum spanning tree T yang tidak memenuhi kondisi ini, maka akan diperoleh sebuah edge e T dan sebuah edge

, \

e e

f X V X dengan de df. Selanjutnya edge e digantikan dengan edge f,

sehingga diperoleh sebuah spanning tree dengan

\ _e _f

d T e f d T d d d T . Hal ini kontradiktif dengan nilai optimal dari T.

Pada bagian ini akan diperlihatkan bahwa untuk setiap spanning tree * T yang memenuhi kondisi di atas adalah optimal. Asumsikan T adalah minimum spanning

tree dan *

T T . Kemudian terdapat paling sedikit satu edge *

e T sehingga e T .

Jika edge ini dimasukkan ke dalam T , maka T e akan membentuk cycle

,

C T e dengan sebuah edge f e di mana f mempunyai satu titik di X_e dan \ _e

V X . Selama T optimal, maka df de. Untuk selanjutnya edge e dihapus kemudian memasukkan edge f pada *

T , sehingga diperoleh * \

T e f , dengan total jarak:

* * *

\

e f

d T d T d d d T e f

Spanning tree T*\ e f mempunyai sebuah tambahan edge yang sama dengan

T dan memenuhi kondisi optimal cut. Hal ini diulangi sampai akhirnya didapatkan *

T T dengan d T( *) d T( ) sehingga T* juga minimum spanning tree.

(29)

Teorema 2.5 Kondisi optimal path (path optimality condition)

T adalah minimum spanning tree jika dan hanya jika untuk

setiap edge f k l, yang tidak termasuk dalam spanning tree di mana de df

untuk setiap edge e yang merupakan bagian path di *

T yang menghubungkan k dan l.

Bukti

Diberikan sebuah minimum spanning tree *

T dan edge e i j, bagian dari path

di *

T yang menghubungkan k dan l. Edge f k l, dan df de, selanjutnya dilakukan pertukaran edge e dan f. Dari pertukaran ini dihasilkan sebuah spanning

tree baru dengan jarak lebih pendek dari *

T . Hal ini kontradiktif dengan optimal T*.

Diberikan sebuah edge e i j, dan misalkan X_e dan V\ X_e merupakan himpunan verteks yang dihasilkan dengan menghapus edge e. Selanjutnya diberikan

edge k l, dengan k X_e dan l V \ X_e. Sejak *

T memuat sebuah lintasan khusus

(unique path) dari k ke l dan e adalah edge yang menghubungkan himpunan verteks

e

X dan \ e

V X , e adalah bagian dari path yang menghubungkan k dan l. Dari Kondisi

optimal path diketahui bahwa de df di mana f k l, . Kondisi ini berlaku untuk

setiap edge f k l, berada dalam cut {X_e,V \ X_e} untuk setiap *

e T . Jadi * T

memenuhi kondisi optimal cut dan dari teorema 2.4 *

T adalah minimum spanning tree.

Secara umum ada beberapa metode penyelesaian pada permasalahan

minimum spanning tree. Vojtech Jarnik (tahun 1930) dan Robert C.Prim (1975)

secara terpisah menemukan sebuah algoritma untuk menyelesaikan persoalan

minimum spanning tree. Algoritma ini kemudian disebut dengan dengan algoritma

(30)

2.5 Integer programming

Integer programming merupakan bentuk khusus atau variasi dari linier

programming, di mana salah satu atau lebih peubah-peubahnya dalam vektor

penyelesaiannya memiliki nilai integer.

Dalam linier programming, salah satu asumsi yang melandasinya adalah divisibilitas dari peubah dan kendalanya. Dengan demikian, pada linier programming

permasalahan dihadapkan pada kegiatan-kegiatan dan variabel yang bersifat kontinyu, sedangkan pada integer programming setiap variabel akan bersifat diskrit.

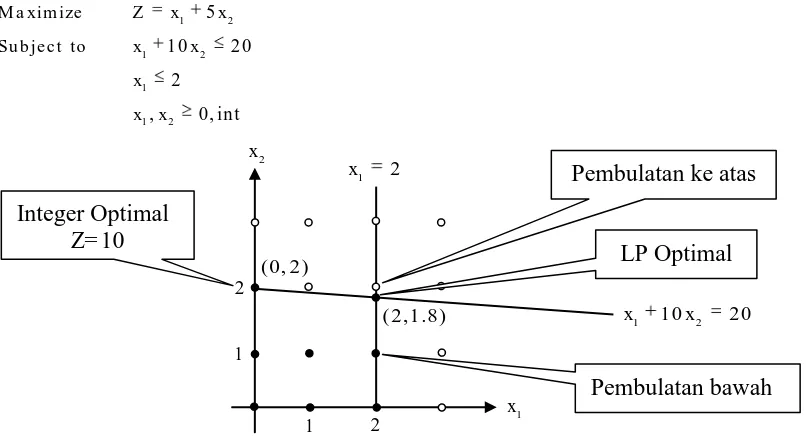
Contoh 2.3 Permasalahan integer programming dengan 2 (dua) variabel basis

1 2

Gambar 2.8 Penyelesaian integer programming dengan metode grafik

Solusi untuk linier programming pada permasalahan di atas adalah Z 1 1 di mana x1 2 dan x2 1, 8. Hal pertama yang dilakukan untuk mendapatkan solusi

integer adalah dengan melakukan pembulatan nilai dari variabel yang tidak integer,

misalkan akan dilakukan pembulatan pada x₂ sehingga (2, 2) namun pembulatan ini 2

Pembulatan ke atas

(31)

melanggar kendala pertama. Kemudian coba dilakukan pembulatan ke bawah pada x₂ sehingga (2,1) dengan Z 7, tetapi nilai Z 7 bukanlah solusi integer optimal dari permasalahan ini karena solusi integer optimal dari permasalahan ini adalah (0, 2) dengan Z 1 0.

Nilai integer optimal terletak begitu jauh dari solusi LP optimal dan tidak memungkinkan hasil integer optimal ini didapat dengan cara melakukan pembulatan dari LP optimal. Hal yang dilakukan dalam menemukan solusi integer optimal adalah dengan cara mengenumerasikan semua solusi yang mungkin dan memilih satu solusi terbaik. Cara ini tentu mudah apabila permasalahan yang dihadapi tidak terlalu rumit, di mana tidak banyak variabel yang terlibat namun hal ini akan berbeda jika permasalahan yang dihadapi melibatkan variabel yang banyak. Misalkan terdapat sebuah permasalahan yang berbentuk pemrograman 0-1 yang melibatkan 20 variabel, maka banyaknya enumerasi yang mungkin di bentuk adalah 20

2 1.048.576 dan ini masih memungkinkan apabila menggunakan bantuan komputer. Jika dihadapkan pada 100 variabel, maka 100 30

2 1.268 10x yang mana hampir tidak memungkinkan apabila dikerjakan pada komputer tercepat sekalipun.

2.6 Metode Balas (Balas Additive Algorithm)

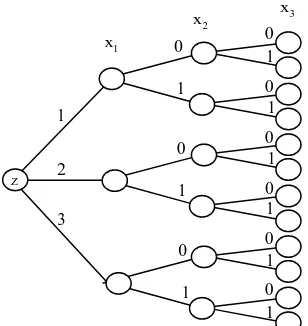
Branch and bound merupakan salah metode dalam menyelesaikan

permasalahan integer programming. Dasar dari metode ini adalah dengan cara mengenumerasi semua solusi integer yang mungkin dalam bentuk struktur tree.

(32)

Gambar 2.9 Tree enumerasi secara lengkap

Ide utama dari metode branch and bound adalah menghindari pembentukan seluruh cabang tree yang mungkin karena hal ini akan sangat rumit jika berhadapan dengan permasalahan dengan variabel yang banyak. Dalam metode branch and bound

pembentukan cabang pada setiap tingkatan hanya akan dilakukan pada node yang memberi harapan dan memungkinkan mendapatkan solusi optimal. Dalam penentuan

node yang lebih menjanjikan untuk mendapatkan solusi optimal adalah dengan

melakukan pendekatan terhadap batas pada nilai terbaik dari fungsi objektif. Metode ini disebut dengan percabangan. Percabangan (branching) adalah membangun node

terpilih untuk selanjutnya akan cabangkan lagi ke tingkat selanjutnya yang merupakan anak dari node yang telah dibentuk sehingga diharapkan pada penyelesaian akhir hanya sedikit bagian dari enumerasi secara lengkap yang dibentuk.

Hal terpenting dalam metode branch and bound adalah penghentian percabangan, yang mana akan dilakukan pemotongan secara permanen dan tidak dilakukan percabangan lagi pada node yang sudah ditentukan. Penghentian percabangan ini dilakukan jika bisa dipastikan bahwa untuk percabangan pada tingkat selanjutnya tidak akan memperoleh hasil yang fisibel maupun optimal. Penghentian percabangan ini merupakan bagian yang paling penting guna menghindari percabangan yang terlalu banyak pada tree.

(33)

Dalam pendeskripsian metode branch and bound secara detil akan dilakukan pendefinisian terhadap beberapa terminologi:

Node: Solusi sebagian atau solusi lengkap. Sebagai contoh, sebuah node pada

tingkatan ke dua dari permasalahan yang melibatkan 5 variabel akan di presentasikan sebagai solusi sebagian (3,17,x₃,x₄,x₅) yang mana variabel pertama bernilai 3 dan variabel ke dua bernilai 17, sedangkan nilai untuk tiga variabel belum diberikan dan dianggap sebagai variabel bebas.

Leaf (Leaf Node): Sebuah solusi lengkap yang mana semua variabel telah di

ketahui nilainya.

Bud (bud node): Sebuah solusi sebagian baik itu fisibel maupun tidak yang

selanjutnya masih akan dilakukan percabangan lagi.

Bounding function (fungsi pembatas): Metode dalam pendekatan nilai terbaik

dari fungsi objektif yang dihasilkan pada saat bud node dicabangkan. Hanya

bud node yang mempunyai nilai fungsi pembatas.

Branching (percabangan): proses pembentukan anak dari node untuk setiap

bud node. Sebuah anak dari node dibentuk untuk setiap variabel selanjutnya

yang mungkin.

Incumbent: Penyelesaian terbaik yang telah didapatkan sejauh percabangan

yang sudah dibentuk. Pada saat pertama dimulai proses pencarian solusi belum ditentukan nilai incumbent. Dalam kasus ini solusi fisibel pertama akan menjadi incumbent sampai ditemukan solusi fisibel yang lebih baik dari nilai

incumbent yang ada dan menggantikan posisi incumbent itu. Sampai tidak ada

lagi node yang bisa dicabangkan, nilai incumbent ini menilai nilai solusi optimal.

Ada beberapa aturan dalam pemilihan node untuk memilih bud node

selanjutnya dalam percabangan selanjutnya:

Best-first or global bud node selection: Pemilihan bud node dilakukan dengan

memilih bud node yang memiliki nilai terbaik bagi fungsi objektif. Pada kasus

minimize ini berarti akan dipilih bud node yang mempunyai nilai fungsi

(34)

Depth-first: Pemilihan akan hanya dilanjutkan pada bud node yang telah di bentuk kemudian memilih bud node yang mempunyai nilai terbaik dari bud

node yang lain pada tingkatan yang sama. Pemilihan secara depth-first terarah

pada penelusuran terhadap satu bud node sehingga hal ini memungkinan lebih cepat mendapatkan penyelesaian secara lengkap (leaf). Setelah didapatkan leaf

percabangan akan dilanjut kan pada bud node di tingkatan atas yang belum dicabangkan.

Breadth-first: Percabangan bud node dilakukan pada tingkatan yang sama di

mana bud node itu dibentuk pertama kali.

Salah satu variasi dari metode Branch and Bound adalah metode Balas. Egon Balas mengembangkan suatu cara atau algoritma untuk menyelesaikan persoalan pemrograman 0-1. Pendekatan yang dilakukan adalah pendekatan enumerasi, baik secara total maupun secara implicit terhadap setiap kombinasi variabel yang diatur sama dengan 0 dan 1.

Pada dasar nya algoritma Balas bekerja adalah sebagai berikut: 1. Bentuk umum dari algoritma Balas adalah:

1

1 2

1, 2, ...,

0 ...

n j j j

ij j i

n M in im ize c x

Su b je c t to a x b

i m

j n

c c c

Kondisi yang tidak mengikuti bentuk umum dari algoritma Balas akan dilakukan beberapa perubahan, antara lain:

Fungsi objektif yang setiap variabel xj mempunyai nilai koefisien negatif, untuk variabel xj diganti menjadi (1 xj ).

(1 )

j j

(35)

Kendala i dengan pertidaksamaan , pertidaksamaan ini akan diubah kedalam bentuk dengan cara mengalikan ruas kiri dan kanan dengan

( 1).

ij j i ij j i

a x b a x b

Kendala yang merupakan bentuk persamaan, diubah ke dalam bentuk pertidaksamaan.

2. Fungsi objektif berbentuk minimalisasi, dan semua koefisien pada fungsi objektif harus bernilai nonnegative. Untuk mendapatkan nilai terkecil dari Z hal yang dilakukan adalah dengan memberikan nilai 0 pada semua variabel

j x .

3. Pemberian nilai 0 pada semua variabel xj ternyata melanggar salah satu atau lebih dari kendala yang telah ditentukan, akan dilakukan percabangan dengan memberikan nilai 0 dan 1 pada setiap cabang yang dibentuk.

4. Penentuan nilai fungsi pembatas dari percabangan yang telah dibentuk: 1

x = variabel yang diberikan nilai pada level percabangan tertentu, dan *

Z = nilai fungsi pembatas

5. Untuk menentukan apakah solusi yang diberikan oleh fungsi pembatas fisibel atau tidak dilakukan dengan mengambil semua variabel x_N (ketika x_N 1) atau x_N ₁ (ketika x_N 0) dan variabel bebas yang akan diberikan nilai 0 kemudian diuji terhadap kendala yang ada. Jika semua kendala terpenuhi pada solusi yang diberikan oleh fungsi pembatas, maka node tersebut terukur

(36)

lebih baik pada node tersebut apabila node tersebut dicabangkan lagi. Dengan adanya solusi fisibel yang diberikan oleh fungsi pembatas yang memenuhi kendala maka nilai fungsi pembatas ini disebut dengan solusi sementara

(incumbent). Untuk solusi fisibel selanjutnya yang didapatkan akan di

bandingkan dengan solusi sementara yang ada. Jika solusi baru yang dihasilkan lebih baik dari solusi sementara yang ada, maka nilai incumbent

akan digantikan oleh solusi yang baru, begitu seterusnya sampai didapatkan solusi yang optimal.

6. Sebuah bud node dikatakan terukur (fathomed) infisibel jika percabangan yang dilakukan pada bud node tersebut tidak akan menghasilkan solusi yang fisibel. Hal ini bisa dilakukan dengan menguji setiap kendala dengan memberikan nilai 1 pada semua variabel bebas yang memiliki koefisien positif dan nilai 0 pada varibel bebas yang koesifien bernilai negatif. Apabila nilai sisi kiri dari pertidaksamaan kendala ternyata masih lebih kecil dari nilai sisi kanan, kendala tersebut tidak akan bisa memenuhi, sehingga node tersebut bisa dieleminasi sebagai “imposible”.

7. Algoritma Balas menggunakan strategi depth-first node selection untuk pemilihan node dalam percabangan.

2.7 Program QM for Windows

Software POM/QM for Windows adalah sebuah software yang dirancang

untuk melakukan perhitungan yang diperlukan pihak manajemen untuk mengambil keputusan di bidang produksi dan pemasaran. Software ini dirancang oleh Howard J.

Weiss tahun 1996 untuk membantu menejer produksi khususnya dalam menyusun

prakiraan dan anggaran untuk produksi bahan baku menjadi produk jadi atau setengah jadi dalam proses pabrikasi.

(37)

Gambar 2.10 Tampilan awal program QM for Windows

1. Pentium I (minimal 100 MHz)

2. Tersedia ruang kosong di Hardisk minimal 20 MB (Mega Byte)

3. Memori 16 MB (Mega Byte)

4. Printer

Sistem operasi minimal yang digunakan adalah Windows 3.11. Disarankan minimal menggunakan Windows 95 ke atas. Program ini mampu menyelesaikan beberapa persoalan yang berhubungan dengan pengambilan keputusan seperti permasalahan assignment, game theory, goal programming, inventory, linier

programming, integer programming, dan lain-lain. Dalam hal ini penulis

(38)

BAB 3

PEMBAHASAN

Pada bab ini akan lebih difokuskan pada permasalahan minimum spanning tree

yang memenuhi kendala biaya. Oleh karena itu akan dibentuk sebuah graph ( , )

G V E dengan himpunan verteks V {1, 2, ..., }n dan himpunan egde E , yang mana pada setiap edge e E mempunyai dua nilai yaitu jarak (d_e) dan biaya (c_e).

3.1 Kondisi minimum spanning tree yang memenuhi kendala biaya

Gambar 3.1 Graph tak-berarah dengan setiap edge diberikan nilai jarak (d_e) dan biaya (c_e)

Permasalahannya adalah menemukan sebuah spanning tree dengan d T( ) minimum di bawah kendala biaya di mana tidak boleh lebih besar dari kendala (C) biaya.

(39)

Lemma 3.1

Tanpa kehilangan keumuman, diasumsikan semua nilai dari jarak dan biaya bernilai

positif.

(40)

Selama T juga fisibel untuk permasalahan baru (dengan argumen yang sama) maka ini kontradiktif dengan pengoptimalan *

T .

Kondisi optimal pada permasalahan minimum spanning tree (Teorema 2.4 dan Teorema 2.5) dapat digunakan untuk memformulasikan kondisi optimal dari penyelesaian permasalahan minimum spanning tree yang memenuhi kendala biaya.

Teorema 3.1 Kondisi optimal cut (cut optimality condition) untuk permasalahan minimum spanning tree yang memenuhi kendala biaya.

T adalah minimum spanning tree yang memenuhi kendala

biaya jika untuk setiap edge *

e T dan untuk setiap f X_e,V \X_e dengan df de

dimana memenuhi biaya c T( ) c_e c_f C.

Bukti

Misalkan teorema di atas tidak memenuhi. Selanjutnya dilakukan pertukaran

edge , *

T exch a n g e [ ,e f] sehingga didapatkan sebuah tree dengan

* * *

( \ { } { }) ( ) _e _f ( )

d T e f d T d d d T

dan

* *

( \ { } { }) ( ) _e _f

c T e f c T c c C

hal ini kontradiktif dengan pengoptimalan dari * T .

Teorema 3.2 Kondisi optimal path (path optimality condition) untuk permasalahan minimum spanning tree yang memenuhi kendala biaya.

T adalah optimal untuk permasalahan minimum spanning tree

yang memenuhi kendala biaya jika untuk setiap edge yang tidak termasuk dalam *

T

{ , }

f k l dengan df de untuk setiap edge e terdapat dalam lintasan di

*

T menghubungkan k dan l, harus memenuhi *

( ) _e _f

(41)

Bukti

Anggap teorema tersebut tidak memenuhi. Kemudian akan dilakukan pertukaran e dengan f dalam *

T dan kemudian akan didapatkan sebuah tree dengan

* * *

hal ini kontradiktif dengan pengoptimalan * T .

Corollary 3.1

Misalkan *

T merupakan solusi optimal dari permasalahan minimum spanning tree.

Untuk setiap *

Misalkan teorema tidak benar, setiap tree yang dihasilkan dari *

T exch a n g e

dan merubah nilai * ( )

d T . Hal ini kontradiktif dengan pengoptimalan * T .

3.2 Kondisi minimum spanning tree yang memenuhi kendala biaya dalam bentuk pemrograman 0-1

Hal utama dari pembahasan ini adalah memformulasikan kondisi minimum

spanning tree yang memenuhi kendala biaya ke dalam bentuk pemrograman 0-1.

Permasalahan 1 Subtour elimination formulation

(42)

Untuk S adalah himpunan dari semua subgraphs yang memungkinkan membentuk

Kendala (3.4) merupakan batasan biaya yang sudah ditentukan. Pada pertidaksamaan (3.3) merupakan kendala untuk menghindari terjadinya cycle dan pada persamaan (3.2) akan memastikan bahwa setiap jumlah egde dari setiap tree

adalah (n 1) dan setiap verteks connected.

3.3 Kelayakan nilai biaya dalam penentuan minimum spanning tree yang memenuhi kendala biaya

Dalam penentuan minimum spanning tree yang memenuhi kendala biaya, batasan biaya yang diberikan dalam permasalahan sangat menentukan akan minimum

spanning tree yang akan dihasilkan.

(43)

Dengan mengabaikan nilai jarak (d_e) akan dibentuk sebuah minimum

spanning tree terhadap nilai biaya (c_e). Permasalahan minimum spanning tree

terhadap nilai biaya bisa dirumuskan seperti di bawah ini: m in _e

e T c

T S T G

Sehingga dalam penentuan minimum spanning tree yang memenuhi kendala biaya (C) , terdapat kendala biaya minimum yang menjamin akan terbentuknya

minimum spanning tree di mana nilai:

m in _e e T

C c

T S T G

Dengan ketentuan S T G adalah himpunan spanning tree dari graph.

3.4 Kompleksitas

Permasalahan Minimum spanning tree biasanya bisa diselesaikan dengan menggunakan beberapa algoritma seperti algoritma Prim dan Kruskal. Pada permasalahan minimum spanning tree yang memenuhi kendala biaya hasil ini akan benar hanya untuk N P P . Arggarwal, Aneja dan Nair telah membuktikan bahwa permasalahan minimum spanning tree dengan kendala biaya termasuk dalam NP-hardness

Teorema 3.3 NP-Hardness

Permasalahan minimum spanning tree dengan memenuhi kendala biaya termasuk ke

dalam NP-hardness.

Bukti

(44)

Bentuk umum permasalahan Knapsack:

Tanpa kehilangan keumuman, asumsikan bahwa semua nilai a_i positif. (dengan kata lain di definisikan a_i : a_i m in₁ _{i n} a_i . Sebuah nilai optimal dari xuntuk permasalahan dengan nilai biaya a_i juga merupakan solusi optimal dari permasalahan awal). Menggunakan identifikasi maxcx min( c x) dapat ditranfromasikan ke dalam permasalahan Knapsack menjadi:

1

Kemudian akan dibentuk sebuah graph ( ,V E) dengan himpunan verteks 1, 1 , 2, 2 , ..., 1, 1

V n n

dan himpunan edge

1 ,1 , 1 , 2 , 1, 2 , 2, 2 , 2, 3 , 2, 3 , ..., , 1 , , 1 , 1, 1

(45)

Gambar 3.3 Graph yang dibentuk dari permasalahan Knapsack

Jika permasalahan minimum spanning tree yang memenuhi kendala biaya diselesaikan pada graph Gambar 3.3, maka semua edge i i, masuk ke dalam solusi optimal. Untuk mendapatkan struktur spanning tree telah dimiliki untuk setiap

1, ...,

i n maka berkesempatan untuk memilih edge i i, 1 atau edge i i, 1 .

Salah satu edge i i, 1 adalah bagian dari solusi optimal *

T dari permasalahan

minimum spanning tree yang memenuhi kendala biaya pada graph di atas, maka

Permasalahan Knapsack bisa direduksi kedalam permasalahan minimum

spanning tree yang memenuhi kendala biaya. Selama permasalahan knapsack adalah

NP-Hard, maka permasalahan minimum spanning tree dengan memenuhi kendala biaya juga termasuk dalam NP-Hard.

3.5 Kondisi minimum spanning tree yang memenuhi kendala biaya dengan menggunakan algoritma Balas

(46)

Gambar 3.4 Graph tak-berarah dengan 5 verteks dan 6 edge

Graph pada Gambar 3.4 adalah sebuah bentuk simulasi dari permasalahan

minimum spanning tree yang memenuhi kendala biaya. Graph tersebut mempunyai 5

verteks dan 6 edge. Pada setiap edge diberikan dua nilai sekaligus yaitu (d_e,c_e) di mana d_e merupakan jarak dan c_e merupakan biaya pada masing-masing edge dan untuk selanjutnya akan ditemukan nilai optimal dari minimum spanning tree yang memenuhi kendala biaya yang telah ditentukan dan dalam simulasi ini telah ditetapkan jumlah biaya (C) =15.

Untuk menentukan nilai kelayakan biaya (C), harus memenuhi m in _e

e T

C c

T S T G

Minimum spanning tree terhadap nilai biaya dari Gambar 3.4 adalah :

(47)

Dengan jumlah total biaya adalah 13, di mana memenuhi kelayakan nilai biaya e

C c pada kondisi minimum spanning tree yang memenuhi kendala biaya. Untuk selanjutnya permasalahan diformulasikan ke dalam bentuk umum pemrograman 0-1 seperti di bawah ini:

1 2 3 4 5 6

Dalam penyelesaian permasalahan pemrograman 0-1 dengan menggunakan metode Balas terlebih dulu menformulasi permasalahan kedalam bentuk umum metode Balas, sehingga didapat model baru yaitu:

5 4 1 3 2 6

Iterasi 1: Karena model berbentuk minimalisasi dan semua koefisien dari setiap

variabel bernilai nonnegative sehingga untuk mendapatkan nilai Z minimal semua variabel diberi nilai x_e 1 sehingga fungsi pembatas *

0

Z dan infisibel pada kendala (1) maka harus dilakukan percabangan pada variabel x₅.

(48)

Iterasi 2: Percabangan di x₅ 1 menghasilkan fungsi pembatas *

juga infisibel pada kendala (1). Untuk selanjutnya akan dilakukan percabangan pada variabel x₄ di bud node yang memiliki fungsi pembatas *

Z minimum.

Gambar 3.7 Iterasi 2

Iterasi 3: Percabangan di x₄ 1 menghasilkan fungsi pembatas Z* 6 dan imposible

pada kendala (5). Hal ini dikarenakan untuk percabangan selanjutnya pada node ini tidak akan membuat kendala (5) fisibel sehingga node ini disebut terukur (fathomed). Sedangkan untuk x₅ 0 menghasilkan fungsi pembatas Z* 7 juga infisibel pada kendala (1). Dalam dalam pemilihan percabangan motode balas menggunakan sistem

depth-first node selection, selanjutnya percabangan akan dilakukan pada bud node

5 0

x oleh variabel x₁.

Iterasi 4:

(49)

Iterasi 5:

Iterasi 6:

Iterasi 7:

(50)

Iterasi 8:

Iterasi 9:

(51)

Iterasi 10:

Iterasi 11:

(52)

Iterasi 12:

Iterasi 13:

(53)

Iterasi 14:

Iterasi 15:

(54)

Iterasi 16:

Iterasi 17:

(55)

Dari penyelesaian didapat fungsi pembatas * 33

Z , di mana

1 0, 2 1, 3 1, 4 1, 5 0, 6 1

x x x x x x pada iterasi ke-13 yang kemudian fungsi pembatas ini berperan sebagai incumbent. Pada iterasi-17 juga didapatkan sebuah fungsi pembatas yang fisibel namun karena nilai fungsi pembatas *

34

Z maka

fungsi pembatas tersebut terleminasi oleh incumbent yang mempunyai nilai lebih baik

sehingga ditemukan fungsi objektif Z 3 3 di mana

1 0, 2 1, 3 1, 4 1, 5 0, 6 1

x x x x x x . Adapun spanning tree yang terbentuk adalah:

Gambar 3.23 Minimum spanning tree dengan total jarak d T( ) 33 yang memenuhi kendala biaya c T( ) 15

Apabila permasalahan dienumerasi secara lengkap, maka terdapat 6 2 64

solusi yang mungkin, tetapi dengan menggunakan algoritma Balas akan hanya menghasilkan solusi sebagian dan solusi secara lengkap. Dalam penyelesaian permasalahan di atas terdapat total 33 node yang dihasilkan, sehingga didapatkan

3 3 / 6 4 5 1 % jika dibandingkan dengan enumerasi secara lengkap.

3.6 Penyelesaian permasalahan minimum spanning tree yang memenuhi kendala biaya dengan menggunakan program QM for Windows

Permasalahan minimum spanning tree yang memenuhi kendala biaya juga bisa diselesaikan dengan mengimplementasikan bentuk pemrograman 0-1 dari permasalahan minimum spanning tree yang memenuhi kendala biaya pada program

QM for Windows. Dengan menggunakan contoh yang sama pada simulasi 1 dimana

nilai biaya dibatasi (C= 15), akan dilakukan penyelesaian persoalan pemrograman 0-1 pada permasalahan minimum spanning tree yang memenuhi kendala biaya dengan

(56)

menggunakan program QM for Windows. Adapun langkah-langkah dalam penyelesaian adalah:

1. Bentuk umum pemrograman 0-1 pada permasalahan minimum spanning tree

yang memenuhi kendala biaya pada persoalan simulasi 1.

1 2 3 4 5 6

4 5 6

1 2 3 4

1 2 3 4 5 6

5 1 0 8 4 2 1 1

4

2

3

6 2 4 7 9 1 5

0,1 , {1, 2, 3, ..., 6}

e

M in im ize Z x x x x x x

Su b je c t to x x x x x x

x x x

x x x x

x x x x x x

x e

2. Memasukkan semua nilai koefisien dari fungsi objektif dan kendala pada pemrograman 0-1 kedalam program QM for Windows dan menentukan tipe dari setiap variabel yaitu 0 atau 1, seperti Tabel 3.1:

X1 X2 X3 X4 X5 X6 RHS

Minimize 5 10 8 4 2 11

Constraint 1 1 1 1 1 1 1 = 4

Constraint 2 0 0 0 1 1 1 <= 2

Constraint 3 1 1 1 1 0 0 <= 3

Constraint 4 6 2 4 7 9 1 <= 15

Variable type O/1 O/1 O/1 O/1 O/1 O/1 Tabel 3.1 Input koefisien fungsi objektif dan kendala dari permasalahan

pemrograman 0-1 pada QM for Windows

(57)

X1 X2 X3 X4 X5 X6 RHS

Minimize 5 10 8 4 2 11

Constraint 1 1 1 1 1 1 1 = 4

Constraint 2 0 0 0 1 1 1 <= 2

Constraint 3 1 1 1 1 0 0 <= 3

Constraint 4 6 2 4 7 9 1 <= 15

Variable type O/1 O/1 O/1 O/1 O/1 O/1

Solution-> 0 1 1 1 0 1 Z-> 33

Tabel 3.2 Input koefisien fungsi objektif dan kendala serta solusi optimal dari permasalahan pemrograman 0-1 QM for Windows

4. Tabel 3.3 merupakan jumlah iterasi pada penyelesaian permasalahan.

Itr Level

Add

const Type Value X1 X2 X3 X4 X5 X6

Optimal 33 0 1 1 1 0 1

1 0 NONinteger 31.3333 1 1 0.33 0.67 0 1

2 1 X3<= 0 Infeasible

3 1 X3>= 1 NONinteger 31.6 1 0.6 1 0.4 0 1

4 2 X2<= 0 Infeasible

5 2 X2>= 1 NONinteger 31.75 1 1 1 0 0.25 0.75

6 3 X5<= 0 INTEGER 33 0 1 1 1 0 1

7 3 X5>= 1 Infeasible

Tabel 3.3 Jumlah iterasi penyelesaian pemrograman 0-1 pada simulasi 1 dengan menggunakan QM for Windows

5. Dari penyelesaian permasalahan pemrograman 0-1 dengan menggunakan program QM for Windows dihasilkan nilai Z=33 dengan

1 0, 2 1, 3 1, 4 1, 5 0, 6 1

x x x x x x . Minimum spanning tree yang

(58)

Gambar 3.24 Minimum spanning tree dengan total jarak d T( ) 33 yang memenuhi kendala biaya c T( ) 15

A (d_e,c_e)

E D

C

B

2 x

4 x

6 x

3 x (10, 2)

(4, 7)

(8, 4)

(11,1) e

(59)

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dari penelitian ini dapat disimpulkan beberapa hal mengenai penerapan pemrograman 0-1 pada permasalahan minimum spanning tree yang memenuhi kendala biaya yaitu:

1. Sebuah graph tak-berarah G= (V,E) di mana setiap edge mempunyai mempunyai 2 nilai, jarak (d_e) dan biaya (c_e). Permasalahan minimum

spanning tree yang memenuhi kendala biaya (C) dapat diselesaikan dengan

mengubah permasalahan ke dalam bentuk umum pemrogramman 0-1 yang kemudian diselesaikan dengan metode Balas (Balas additive algorithm) yang merupakan variasi dari metode Branch and bound.

2. Permasalahan minimum spanning tree yang memenuhi kendala biaya juga bisa diselesaikan menggunakan program QM for Windows di mana program ini akan menentukan solusi optimal dari permasalahan minimum spanning tree

yang memenuhi kendala biaya yang telah diformulasikan kedalam bentuk umum pemrograman 0-1.

3. Dalam penentuan minimum spanning tree yang memenuhi kendala biaya (C),

untuk setiap graph tak-berarah G= (V,E) di mana setiap edge mempunyai nilai jarak (d_e) dan biaya (d_e), maka jumlah biaya (C) minimum agar minimum

spanning tree yang memenuhi kendala biaya bisa dibentuk adalah:

m in _e e T

C c

T S T G

(60)

4.2 Saran

Pada penelitian ini penulis meminimumkan 1 (satu) fungsi objektif dengan biaya sebagai kendala tambahan. Diharapkan kepada pembaca dapat mengembangkan permasalahan ini menjadi lebih kompleks, seperti untuk setiap edge diberikan tiga parameter nilai, sehingga akan dilakukan optimisasi terhadap satu fungsi objektif dengan 2 kendala tambahan sekaligus, dan lain sebagainya.

Diharapkan dengan mengembangkan penelitian ini, untuk selanjutnya dalam penentuan minimum spanning tree yang memenuhi kendala biaya dapat dikembangkan lebih baik guna menyelesaikan permasalahan minimum spanning tree

(61)

DAFTAR PUSTAKA

Aggarwal. V, Aneja, K. P. K. Nair. 1980; Minimal spanning tree subject to a side

constraint, Comput. Oper. Res. 9 (4) , 287-296.

Ahuja R K, Magnanti T L, and Orlin, J B. 1993; Network Flows Theory, Algorithms

and Appliactions.Prentice-Hall.

Bruce A. McCarl, Thomas H. Spreen. 1997; Applied Mathematical Programming

Using Algebraic Systems.

Bazlamacci C F and K S Hindi. 2001; Minimum-weight spanning tree algorithms; a

survey and empirical study. Computers & Operations Research, 28:767-785.

Chen W W L. 1992; Discreate Matematics.

Chinneck Jhon W. 2009; Practical Optimization.