ALGORITMA UNTUK DEGREE CONSTRAINED MINIMUM SPANNING TREE
SKRIPSI
NURLINDA SARI BUTARBUTAR 060803011
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2011
ALGORITMA UNTUK DEGREE CONSTRAINED MINIMUM SPANNING TREE
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
NURLINDA SARI BUTARBUTAR 060803011
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2011
i
PERSETUJUAN
Judul : ALGORITMA UNTUK DEGREE CONS-TRAINED MINIMUM SPANNING TREE
Kategori : SKRIPSI
Nama : NURLINDA SARI BUTARBUTAR Nomor Induk Mahasiswa : 060803011
Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Oktober 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Marwan Harahap, M.Eng Dr. Saib Suwilo, M.Sc. NIP.19461225 197403 1 001 NIP. 19640109 198803 1 004
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
Dr. Tulus, M.Si
NIP. 19620901 198803 1 002
ii
PERNYATAAN
ALGORITMA UNTUKDEGREE CONSTRAINED MINIMUM SPANNING TREE
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Oktober 2011
NURLINDA SARI BUTARBUTAR 060803011
iii
PENGHARGAAN
Segala puji bagi AllahSubhanallahu wa ta’ala seluas langit dan seluas bumi serta seluas apa yang ada diantara keduanya, karena rahmat dan hidayahNya se-hingga penulis dapat menyelesaikan skripsi yang berjudul” ALGORITMA UN-TUK DEGREE CONSTRAINED MINIMUM SPANNING TREE” ini dengan baik. Allahumma shalli ’ala Muhammad wa ’ala ali Muhammad, shalawat beri-ring salam kepada Nabi Muhammadshallallahu ’alaihi wa sallambeserta keluarga dan sahabat-sahabat beliau.
Dalam menyelesaikan skripsi ini penulis banyak sekali menerima dukungan dan masukan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan Jazakumullah Khairan Katsiran kepada:
1. Bapak Prof. Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
2. Bapak Dr. Tulus, M.Si, dan Ibu Mardiningsih, M.Si selaku Ketua dan Sekre-taris Departemen Matematika di FMIPA USU Medan.
3. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Drs. Marwan Harahap, M.Eng selaku dosen pembimbing II yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini.
4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
5. Para guru yang telah memberikan warna mereka pada kehidupan penulis, yaitu: guru-guru di MIS NU Tg. Mulia terkhusus kepada bapak M. Pasti Sembiring, BA, guru-guru di MTs. N L. Pakam, guru-guru di SMA N 1 L. Pakam terkhusus kepada bapak Dekson, SPd.
6. Ibunda Nurhasni Naibaho dan ayahanda tercinta Maksum Butarbutar, abang-da abang-dan kakanabang-da terkasih, Andi Marta Dinata Butarbutar, Romeyta Sakun-tala Butarbutar, dan Suryadi Harahap, serta adinda-adinda tersayang Sri Rahayu Butarbutar dan Muhammad Aidil Akbar Butarbutar yang selalu memberikan motivasi dan do’a tiada hentinya kepada penulis, tak lupa kepa-da kedua keponakan penulis Laila Harahap kepa-dan Ridho Ahmad Harahap yang menceriakan hari-hari penulis.
7. Nurul Hidayati dan Tuti Larasati yang menemani penulis dalam suka dan duka. Serta seluruh keluarga mereka yang mendukung dengan setulus hati, papa, ibu, mama, dan bapak,Ma’a syukri tiada tara.
iv
9. Terkhusus sahabat-sahabat penulis yang ada di asrama putri: Ratika Can-dra, Juriah, Ismatul Husna, Eva Khairani, Lia, Hikmah, Siti, dkk atas per-saudaraannya selama ini. Tak lupa juga kepada Putri Kartika, Monda Mo-rina Harahap, Jaya Bahagia, Tuti Prihatini, dan Kiki. Juga kepada K’Nelly, K’Ayu, K’Rahma, Hanim, dan Fajar.
10. Saudara-saudaraku di IM3 dan UKMI ALFALAK. Senior-senior ’02, ’03, ’04, ’05, K’Tri, K’Diana, B’Topik Zuhri dan K’Yuni atas bantuan dan se-mangatnya. Kepada teman-teman seperjuangan anak Operasi Riset ’06 dan buat teman-teman stambuk 2006, adik-adik ’07, ’08, dan ’09 terima kasih. Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu saran dan kritik yang membangun dari pembaca sangat penulis harapkan. Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini bermanfaat bagi yang membutuhkan.
Medan, Oktober 2011 Penulis,
Nurlinda Sari Butarbutar
iv
ABSTRAK
PermasalahanDegree Constrained Minimum Spanning Tree(DCMST) pada graph G(V, E) berbobot terhubung tak berarah merupakan permasalahan untuk mene-mukanspanning tree T diGdengan total panjang edge yang minimum dan degree dari setiap verteks vi di T dibatasi oleh bi dimana dT(vi) ≤ bi. Untuk menyele-saikan permasalahandegree constrained minimum spanning treedilakukan dengan memodifikasi algoritma Kruskal, dimana sebuah edge diterima di T, jika edge tidak membentukcyclepada edge terdahulu yang berada diT dan verteks-verteks ujungnya memenuhi batas maksimum degree yang diberikan, yaitu dT(v
j) ≤ bj dan dT(vk)≤ bk.
v
ALGORITHM FOR DEGREE CONSTRAINED MINIMUM
SPANNING TREE
ABSTRACT
The Degree Constrained Minimum Spanning Tree (DCMST) on undirected weight-ed connectweight-ed graphG(V, E) is a problem to find a spanning treeT inGwith whose total edge length is minimal and the degree of each vertexvi inT at most a given value bi where dT(vi) ≤ bi. For solving this problem, we modified Kruskal algo-rithm, an edge received inT, if an edge did not produce any cycle with preceding edge in T and a both endpoints should not exceed some given maximum degrees thatdT(vj)≤bj and dT(vk)≤bk.
vi
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang 1
1.2. Perumusan Masalah 2
1.3. Tujuan Penelitian 2
1.4. Manfaat Penelitian 2
1.5. Metodologi Penelitian 2
2. DEGREE CONSTRAINED MINIMUM SPANNING TREE 4
2.1. Konsep Dasar Graph 4
2.2. Tree 11
2.3. Degree Constrained Minimum Spanning Tree 16
3. ALGORITMA UNTUKDEGREE CONSTRAINED MINIMUM
SPANNING TREE 21
3.1. Algoritma untuk Degree Constrained Minimum Spanning
Tree 21
4. KESIMPULAN DAN SARAN 33
4.1. Kesimpulan 33
4.2. Saran 34
DAFTAR PUSTAKA 35
vii
DAFTAR GAMBAR
Gambar Halaman
2.1 Graph 4
2.2 Graph Berbobot 5
2.3 (a)Graph Lengkap dan (b) Graph Sederhana 5
2.4 verteks ujung dan verteks terisolasi 6
2.5 (5,8) Graph 8
2.6 (G) Graph dan (T) Subgraph 9
2.7 (a) Graph terhubung dan (b) Graph tak berhubung 10
2.8 Bridge 11
2.9 Tree 12
2.10 Spanning tree dari G 15
2.11 DCST dariG 16
3.1 Graph G 24
3.2 Hasil Program Integer 0-1 untuk DCMST 29
3.3 Graph G 30
3.4 Hasil Algoritma Kruskal DCMST 32
iv
9. Terkhusus sahabat-sahabat penulis yang ada di asrama putri: Ratika Can-dra, Juriah, Ismatul Husna, Eva Khairani, Lia, Hikmah, Siti, dkk atas per-saudaraannya selama ini. Tak lupa juga kepada Putri Kartika, Monda Mo-rina Harahap, Jaya Bahagia, Tuti Prihatini, dan Kiki. Juga kepada K’Nelly, K’Ayu, K’Rahma, Hanim, dan Fajar.
10. Saudara-saudaraku di IM3 dan UKMI ALFALAK. Senior-senior ’02, ’03, ’04, ’05, K’Tri, K’Diana, B’Topik Zuhri dan K’Yuni atas bantuan dan se-mangatnya. Kepada teman-teman seperjuangan anak Operasi Riset ’06 dan buat teman-teman stambuk 2006, adik-adik ’07, ’08, dan ’09 terima kasih. Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu saran dan kritik yang membangun dari pembaca sangat penulis harapkan. Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini bermanfaat bagi yang membutuhkan.
Medan, Oktober 2011 Penulis,
Nurlinda Sari Butarbutar
iv
ABSTRAK
PermasalahanDegree Constrained Minimum Spanning Tree(DCMST) pada graph G(V, E) berbobot terhubung tak berarah merupakan permasalahan untuk mene-mukanspanning tree T diGdengan total panjang edge yang minimum dan degree dari setiap verteks vi di T dibatasi oleh bi dimana dT(vi) ≤ bi. Untuk menyele-saikan permasalahandegree constrained minimum spanning treedilakukan dengan memodifikasi algoritma Kruskal, dimana sebuah edge diterima di T, jika edge tidak membentukcyclepada edge terdahulu yang berada diT dan verteks-verteks ujungnya memenuhi batas maksimum degree yang diberikan, yaitu dT(v
j) ≤ bj dan dT(vk)≤ bk.
v
ALGORITHM FOR DEGREE CONSTRAINED MINIMUM
SPANNING TREE
ABSTRACT
The Degree Constrained Minimum Spanning Tree (DCMST) on undirected weight-ed connectweight-ed graphG(V, E) is a problem to find a spanning treeT inGwith whose total edge length is minimal and the degree of each vertexvi inT at most a given value bi where dT(vi) ≤ bi. For solving this problem, we modified Kruskal algo-rithm, an edge received inT, if an edge did not produce any cycle with preceding edge in T and a both endpoints should not exceed some given maximum degrees thatdT(vj)≤bj and dT(vk)≤bk.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dalam berbagai situasi kehidupan kita, banyak diantaranya yang dapat kita pre-sentasikan secara grafik yang terdiri atas titik-titik dan garis-garis yang menghu-bungkan titik-titik tersebut. Misalnya, titik-titik tersebut mewakili kota, dengan garis-garis mewakili jalan yang menghubungkan kota tersebut dengan kota lainnya atau bisa juga titik-titik itu mewakili manusia dengan garis mewakili hubungan manusia tersebut dengan manusia yang lainnya. Pada matematika, hubungan titik
dan garis yang demikian diamati oleh suatu objek yang disebut dengan graph.
Teori graph dimulai pada tahun 1736 ketika seorang matematikawan Swiss, Leonhard Euler mempublikasikan tulisan yang berisi solusi untuk menyelesaikan masalah jembatan Konigsberg di Prussia (sekarang Kaliningrad di Russia)(Susanna, 2010). Sejak itu, penelitian terhadap graph terus mengalami perkembangan sei-ring dengan semakin bervariasinya masalah yang dihadapi. Salah satu diantaranya adalah permasalahan degree constrained minimum spanning tree (DCMST).
Permasalahan DCMST pada graph merupakan permasalahan untuk mene-mukanspanning tree dengan total bobot minimum dan memenuhi batasan degree yang diinginkan. Garey dan Jhonson (1979) menyatakan bahwa DCMST meru-pakan NP-hard, karenanya diperlukan suatu metode pendekatan untuk menyele-saikannya.
2
dan metode Branch and Bound. Wamiliana (2004) menggunakan metode Tabu dan modifikasi pencarian penalti. Binh dan Nguyen (2008) menggunakan algo-ritma partikel Swarm, algoalgo-ritma ini menggunakan beberapa metode baru untuk memilih vektor dari partikelnya.
Ning, Ma, dan Xiong (2008) menggunakan teknik reduksi terlebih dahulu untuk mengurangi ukuran graph, kemudian menyelesaikan DCMST dengan meng-gunakan algoritma Kruskal. Tanpa mengmeng-gunakan teknik reduksi terlebih dahulu, penelitian ini akan memodifikasi algoritma Kruskal untuk menyelesaikan DCMST.
1.2 Perumusan Masalah
Permasalahan degree constrained minimum spanning tree merupakan permasala-han untuk menemukan spanning tree dengan total panjang edge yang minimum dan setiap verteks memenuhi batas maksimum degree yang diberikan. Masalah dari penelitian ini adalah bagaimana menyelesaikandegree constrained minimum spanning tree dengan memodifikasi algoritma Kruskal.
1.3 Tujuan Penelitian
Adapun tujuan penelitian ini yaitu menerapkan modifikasi algoritma Kruskal un-tuk menyelesaikandegree constrained minimum spanning tree.
1.4 Manfaat Penelitian
Penelitian ini bermanfaat untuk memperkaya literatur dalam bidang degree cons-trained minimum spanning tree.
1.5 Metodologi Penelitian
Untuk menyelesaikan Degree constrained minimum spanning tree dengan modi-fikasi algoritma Kruskal dilakukan dengan cara sebagai berikut:
1. Memodifikasi algoritma Kruskal, dimana sebuah edge diterima dalam T bila memenuhi dua kondisi berikut:
3
PENEMUAN(vj)6= PENEMUAN(vk).
b. Verteks-verteks ujungnya (verteksvj danvk) memenuhi batasan degree bi, yaknidT(vj)≤bj dan dT(vk)≤bk .
2. Membandingkan hasil yang diperoleh modifikasi algoritma Kruskal dengan Program Integer 0-1 yang dalam penyelesaiannya menggunakan bantuan pro-gram LINDO versi 6.1. Untuk mengetahui keoptimalan hasil yang telah diperoleh.
BAB 2
DEGREE CONSTRAINED MINIMUM SPANNING TREE
Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teo-rema sebagai landasan berfikir dalam melakukan penelitian ini dan akan memper-mudah dalam hal pembahasan hasil utama pada bab berikutnya. Konsep dasar tersebut berkaitan dengan masalah yang dibahas dalam penelitian ini, yakni: kon-sep dasar graph,tree, dan degree constrained tree minimum spanning tree.
2.1 Konsep Dasar Graph
Istilah baku graph diadopsi dari Vasudev, 2006. Suatu graph G = (V, E) meru-pakan himpunan objekV ={v1, v2, v3, ...}disebut verteks (disebut juga pointatau node) dan himpunan E = {e1, e2, ...} yang elemennya disebut edge (disebut juga lineatau arc), sehingga untuk setiap edge em dikenal sebagai penghubung pasang-an verteks (vi, vj). Verteks vi, vj yang dihubungkan oleh edgeem disebut verteks ujung dariem. Suatu graph dapat direpresentasikan secara grafis dengan cara se-tiap verteks direpresentasikan sebagai titik dan sese-tiap edgevivj sebagai garis dari titikvi ke titikvj.
Contoh 2.1a: Berikut diberikan representasi dari graph.
s
s
s s
✒✑ ✓✏
✒✑ ✓✏ v1
v2
v3
v4
Gambar 2.1 : Graph
Dari gambar 2.1a dapat diketahui bahwa V(G) = {v1, v2, v3, v4} dan E(G)
5
={v1v1, v1v2, v1v3, v1v4, v2v3, v2v4, v3v3, v3v4}.
Berdasarkan definisi, edge merupakan penghubung pasangan verteks vj, vk. Untuk suatu edge yang memiliki kedua verteks ujung yang sama disebut loop. Dari gambar 2.1a dapat dilihat bahwa edgev1 dan v3 merupakanloop. Jika untuk
setiap edge pada graph G diberi suatu nilai atau bobot W = {w1, w2, ..., wm}, maka graph tersebut dikatakan graph berbobot.
Contoh 2.1b: Berikut diberikan representasi dari graph berbobot.
s
s s
s v1
v2
v3
v5
e1 =w1
e2 =w2
e3 =w3 e4 =w4
e5 =w5
Gambar 2.2 : Graph Berbobot
Graph yang tidak memiliki loop ataupun edge ganda disebut graph seder-hana. Graph sederhana, dimana setiap verteks dihubungkan tepat satu edge ke verteks lainnya disebut graph lengkap.
Contoh 2.1c: Berikut diberikan representasi dari gaph sederhana dan graph lengkap.
v1 v2
v4 v3
s s
s
s s
s
s s
s v5
v2
v4
v1
v3
a b
Gambar 2.3 : (a)Graph Lengkap dan (b) Graph Sederhana
6
2.1.1 Incident dan Degree
Ketika verteksvi merupakan verteks ujung dari beberapa edge ej, vi dan ej dikatakan incident satu sama lain. Dua edge nonparalel dikatakan adjacent jika mereka incident pada verteks yang sama. Dengan cara yang sama, dua verteks dikatakan adjacent jika mereka merupakan verteks ujung dari edge yang sama. Sebagai contoh pada gambar 2.1a dapat dilihat bahwav1v2,v1v3, v1v4 merupakan
incident pada v1. Adjacent untuk v1 adalah v2, v3, v4. Sedangkan, v1 dan v3
adjacent untuk diri mereka sendiri.
Jumlah edge incident dari suatu verteks vi, dengan edge yang merupakan loop dihitung 2 disebut degree dari verteks tersebut. Degree dari suatu verteks dinotasikan dengandegG(vi) atau degvi atau d(vi) atau d(v). Verteks yang tidak memiliki edgeincidentdisebut verteks terisolasi. Sedangkan verteks yang berdegree satu disebut vertekspendent atau verteks ujung.
Contoh 2.1.1: Berikut diberikan representasi dari verteks ujung dan verteks terisolasi
v1 v2
v4 v3
v5
s s
s s
s
Gambar 2.4 : verteks ujung dan verteks terisolasi
Adapun degree dari setiap verteks pada gambar 2.3, d(v1) = 1, disebut
pen-dant verteks, dan d(v2) = 3, d(v3) = 2, d(v4) = 3, dan d(v5) = 0 karena tidak
memiliki edgeincident (v5 disebut verteks terisolasi).
7
Bukti: Diberikan graph G dengan n verteks v1, v2, ..., vn dan e edge. Karena setiap edge memiliki tepat dua verteks vi dan vj (untuk loop, i = j), maka edge memberikan kontribusi 2degree, yakni 1degreeuntuk verteksvidan 1degreeuntuk verteksvj. Hal ini mengakibatkan penjumlahan degree dari seluruh verteks di G adalah dua kali dari edge di G, yaitu
n X
i=1
d(vi) = 2e
Teorema 2.2 Banyak verteks berdegree ganjil pada suatu graph selalu genap.
Bukti: Dari teorema 2.1, diketahui bahwa n X
i=1
d(vi) = 2e
Jika verteks yang berdegree ganjil dan berdegree genap dipisahkan, maka per-samaan diatas dapat dibentuk menjadi
n X
i=1
d(vi) = X even
d(vj) + X
odd d(vk)
Karena Pn
i=1d(vi) adalah genap, dan P
evend(vj) juga genap, maka P
oddd(vk) juga suatu bilangan genap. Karena d(vk) adalah ganjil, maka syarat agar jumlah seluruh d(vk) genap, banyaknya vk haruslah genap. Hal ini membuktikan bahwa banyak verteks berdegree ganjil pada suatu graph selalu genap.
2.1.2 Walk, Path, dan Cycle
Diberikan graphG dengan verteksvdan w. Sebuah walkdengan panjang m dari v kew didefinisikan sebagai barisan edge dan dituliskan sebagai berikut:
(v0, v1),(v1v2), ...,(vm−1vm)
8
Sebuah trail dari v ke w adalah walk dari v ke w tanpa perulangan edge. Sebuah path didefinisikan sebagai sebuah trail tanpa perulangan verteks. Path tertutup adalahpathyang dimulai dan diakhiri dengan verteks yang sama. Sebuah cycle merupakan sebuah path tertutup, dan sebuah loopmerupakan sebuah cycle dengan panjang 1.
Contoh 2.1.2: Sebagai contoh masing-masing untuk walk, trail, path, cycle, dan loopdapat dilihat pada gambar berikut:
s s
s
s s
✒✑ ✓✏ ✒✑
✓✏ v4
v1
v5
v2 v3
Gambar 2.5 : (5,8) Graph
a. v1 →v3 →v5 →v3→v2 →v4 disebut walk.
b. v1 →v2 →v3 →v5→v2 →v4 disebut trail, walk tanpa perulangan edge.
c. v1 →v2 →v4 →v5 disebut path, walktanpa perulangan edge dan verteks.
d. v1 → v2 → v4 → v5 → v3 → v1 disebut cycle, Karena adanya perulangan
pada verteks awal dan akhir disebut juga ⁀path tertutup.
e. v1 →v1 dan v3 →v3 disebut loop,cycle dengan panjang 1. .
2.1.3 Subgraph
Suatu subgraph dari G adalah graph yang memiliki verteks dan edge yang ada di G. Jika G dan T merupakan dua graph dengan himpunan verteks V(T),
9
V(G) dan himpunan edge E(T) dan E(G) sehingga V(T) ⊆ V(G) dan E(T) ⊆
E(G), maka T disebut subgraph Gatau G disebut supergraph T.
Contoh 2.1.3: Berikut diberikan representasi dari subgraph G.
v1 s vs2
v4 s
v5
s s v6
v3
s
G :
v1 s
v5 s v2
s
v6 s
v3
s
T :
Gambar 2.6 : (G) Graph dan (T) Subgraph
Berdasarkan definisi, dapat dikatakan bahwa:
1. Setiap graph merupakan subgraph itu sendiri.
2. Sebuah subgraph dari subgraph G merupakan subgraph G.
3. Sebuah verteks tunggal di G merupakan subgraph G.
4. Sebuah edge tunggal di G, bersama dengan verteks ujungnya, juga meru-pakan subgraph G.
2.1.4 Graph Terhubung, Graph Tidak Terhubung, dan Komponen Diberikan graph G dengan v dan w merupakan dua verteks diG. Graph G dikatakan terhubung jika dan hanya jika diberikan sebarang dua verteksv dan w diGsedemikian hingga terdapat paling sedikit satu path dari v kew. Selebihnya,
Gdikatakan tidak terhubung.
Pada gambar 2.6 menunjukkan bahwa (a) adalah graph terhubung karena terdapat path dari satu verteks ke verteks yang lainnya, dan (b) adalah graph tak berhubung karena tidak terdapat path dari v1 ke v3. Dari gambar 2.3 dapat
10
verteksv1,v2 dengan edgev1v2, sedangkan bagian kedua adalah verteksv3, v4,dan
v5, dengan edgev3v4,v3v5, danv4v5. Masing-masing bagian ini disebut komponen.
Contoh 2.1.4: Berikut diberikan representasi dari 2 buah graph terhubung dan tidak terhubung.
s
s
s
s s s s
s s
v1 v1
v5 v5
v2 v2
v3 v3
v4 v4
v6 v7
v8 v9
s s
s
s s
a b
Gambar 2.7 : (a) Graph terhubung dan (b) Graph tak berhubung
Teorema 2.3 Suatu graphGdikatakan tidak terhubung jika dan hanya jika verteks himpunan V dapat dibagi ke dalam dua komponen tak kosong, himpunan bagian
V1 danV2 terpisah, sehingga tidak ada edge di G yang memiliki satu verteks ujung
di dalam himpunan bagian V1 begitu juga di himpunan bagian V2.
Bukti: Andaikan komponen ada. Anggap dua sembarang verteks a dan b di G, sehingga a ∈ V1 dan b ∈ V2. Tidak ada path yang bisa diantara verteks a dan b;
sebaliknya terdapat paling sedikit satu edge dimiliki verteks ujungV1 dan lainnya
diV2. Akibatnya jika komponen ada, G tidak terhubung.
Dan sebaliknya, andaikanGmenjadi graph tidak terhubung. Anggap sebuah verteksadi G. AndaikanV1 menjadi himpunan seluruh verteks yang dihubungkan
oleh path ke a. Karena G tidak terhubung, maka V1 tidak memasukkan semua
verteksG. Selebihnya verteks akan berbentuk(tak kosong) himpunan V2. Tidak
ada verteks diV1 yang dihubungkan ke sebarang V2 dengan sebuah edge. Hal ini
11
Teorema 2.4 Jika suatu graph memiliki tepat dua verteks berdegree ganjil, pasti terdapat path yang menyertai dua verteks tersebut.
Bukti: Andaikan Gsebuah graph dengan seluruh verteksnya berdegree genap ke-cuali verteks v1 dan v2, yang berdegree ganjil. Berdasarkan teorema 2.2, hal ini
berlaku untuk seluruh graph, oleh karenanya untuk setiap komponen graph tak terhubung, tak ada graph yang bisa memiliki jumlah ganjil dari verteks ganjil. Karenanya, di graph G v1 dan v2 harus berada pada komponen yang sama,
aki-batnya pasti ada pathdiantara mereka.
2.1.5 Bridge
Suatu edgevivj pada graph Gterhubung dikatakan bridge jika penghapusan edge vivj mengakibatkan G menjadi tidak terhubung.
Contoh 1.1.5: Berikut diberikan representasi dari bridge.
v1 v2
v4
v3
s s
s
s s
s
s
s v5
v7
v9
v6
v8
Gambar 2.8 : Bridge
v3v5 merupakan bridge karena penghapusan edge v3v5 akan menyebabkan graph
menjadi tak terhubung.
2.2 Tree
12
Contoh 2.2a: Berikut diberikan representasi dari tree.
s s
s s
s s
s s s
s s s
s
s
s s s
a b c
Gambar 2.9 : Tree
Teorema 2.5 Hanya ada satu path antara setiap pasangan verteks di tree T.
Bukti: Karena T terhubung, maka terdapat paling sedikit satu path diantara semua pasangan verteks diT. Sekarang anggap bahwa diantara dua verteksadan b di T terdapat path yang berbeda. Penggabungan dari dua path yang berbeda akan menghasilkan cycle, karenanya T bukanlah tree.
Sebaliknya,
Teorema 2.6 Jika pada graph G hanya ada satu path diantara setiap pasangan verteks, maka G merupakan tree.
Bukti: Adanya path diantara setiap pasangan verteks menjamin bahwa G ter-hubung. Suatu cycle diG (dengan dua atau lebih verteks) secara tidak langsung menyatakan bahwa terdapat paling sedikit satu pasangan verteks a, b sehingga terdapat dua path yang berbeda antara a dan b. Karena G hanya memiliki satu path diantara setiap pasangan verteks, maka G tidak bisa memiliki cycle. Oleh karena itu,G merupakan tree.
Teorema 2.7 Suatu tree dengan n verteks memiliki n−1 edge.
Bukti: Hasilnya akan diperlihatkan dengan induksi. Andaikan ek menjadi edge diT dengan verteks ujungvi danvj, berdasarkan teorema 2.3, tidak adapathlain
13
diantara vi dan vj, kecuali ek. Oleh karenanya jika ek dihapus, maka T menjadi graph tak terhubung. Selanjutnya,T −ek akan membentuk dua komponen, dan karena tidak adacycle di T, maka masing-masing komponen tersebut merupakan tree. Kedua treet1 dan t2, masnning-masing memiliki lebih sedikit darin verteks,
oleh karenanya dengan induksi, masing-masing memiliki edge lebih sedikit dari jumlah verteks di dalamnya. Dengan demikian T −ek mengandung n −2 edge. Hal ini berakibat T memiliki tepat n−1 edge.
Teorema 2.8 Untuk sebarang graph terhubung dengan n verteks dan n−1 edge merupakan tree.
Bukti: Berdasarkan definisi graph terhubung, terdapat paling sedikit satu path di G, berdasarkan teorema 2.3 tidak ada path lain diantara vi dan vj, kecualiek, berdasarkan definisi suatu tree merupakan graph terhubung tanpa adanya cycle. karenanya berdasarkan teorema 2.5, suatu tree dengan n verteks memiliki n −
1 edge. Hal ini berakibat graph terhubung dengan n verteks dan n −1 edge merupakan tree.
Teorema 2.9 Suatu graph merupakan tree jika dan hanya jika terhubung.
Bukti: Andaikan graph Gmerupakan tree, berdasarkan definisi suatu tree meru-pakan graph terhubung tanpa adanya cycle. Andaikan G tidak terhubung, maka berdasarkan teorema 2.1 graph bukanlah tree. Hal ini berakibat bahwa untuk graph yang merupakantree, haruslah graph terhubung.
Teorema 2.10 Suatu graph G dengan n verteks, n −1 edge, dan tanpa cycle adalah terhubung.
14
sedikit komponen cycle. Tanpa kehilangan sifat umumnya, andaikan G memiliki komponeng1 dang2. Lalu tambahkan sebuah edgeedintara suatu verteksv1 dig1,
dan v2 di g2. Karena tidak ada path diantara v1 dan v2 di G, tambahkan e tanpa
membentukcycle. Dengan demikianG∪ememilikicyclesedikit, graph terhubung darin verteks dann edge, yang tidak mungkin trejadi. Hal ini berakibat graph G dengan n verteks,n−1 edge, dan tanpa cycle adalah terhubung.
Berdasarkan teorema-teorema diatas, dapat disimpulkan bahwa suatu graph
Gdengan n verteks disebut tree, jika:
1. Gterhubung dan tanpa cycle, atau
2. Gterhubung dan memilikin−1 edge, atau
3. Gtanpa cycle dan memilikin−1 edge, atau
4. Tepat terdapat satu path diantara setiap pasangan verteks diG, atau
5. Gpaling tidak merupakan graph terhubung.
2.2.1 Verteks Ujung dalam Tree
Verteks ujung merupakan verteks dengan jumlah degreeadalah 1.
Teorema 2.11 Pada sebarang tree (dengan dua atau lebih verteks), terdapat pal-ing sedikit dua verteks ujung.
Bukti: Karena treeyang memilikinverteks dan n−1 edge, maka 2(n−1) degree terbagi diantara n verteks. Karenanya tidak akan bisa ada verteks yang tidak memilikidegree, paling tidak harus memiliki dua verteks yang berdegree 1 dalam degree. Tentu saja ini hanya berlaku jika n≥2.
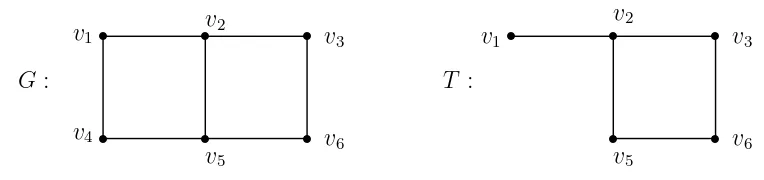
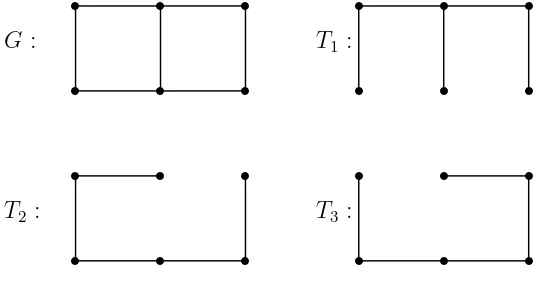
2.2.2 Spanning tree
15
subgraphGdanT mengandung seluruh verteksG. Dengan kata lain,T dikatakan spanning tree jika T terhubung, mengandung n verteksG dan n−1 edge.
Contoh 2.2.2: Berikut diberikan representasi dari spanning tree.
s s
s
s s
s G:
s s
s
s s
s T1 :
s s
s
s s
s T2 :
s s
s
s s
s T3 :
Gambar 2.10 : Spanning tree dari G
Dari gambar 2.9, untuk (6,7) graph menghasilkan spanning tree dengan 6 verteks dan 5 edge. Untuk menemukan spanning tree dari graph G terhubung dapat dilakukan dengan cara yang sederhana. Jika G tidak memiliki cycle, maka
Gmerupakan spanning tree itu sendiri. Jika G memilikicycle maka hapus semua edge yang membentukcycle, denganG masih terhubung.
Proposisi 2.12
Setiap graph terhubung memiliki paling sedikit satu spanning tree.
Bukti: Andaikan Gadalah suatu graph terhubung. Jika G bebas cycle, maka G itu sendiri merupakan spanning tree. Jika tidak, G memiliki paling sedikit satu cycle C1. Dengan teorema 1.8 subgraph G tetap terhubung meski satu edge C1
dihapus. Jika subgraph bebascycle, maka subgraph tersebut merupakanspanning tree. Jika tidak, maka paling sedikit ada satu cyclediC2, dan seperti sebelumnya,
hapus edge di C2 untuk memperoleh spanning tree. Jika tidak, lakukan seperti
sebelummya hingga diperoleh subgraphT dariG yang terhubung dan bebascycle.
16
Oleh karenanya T merupakan spanning tree untuk G.
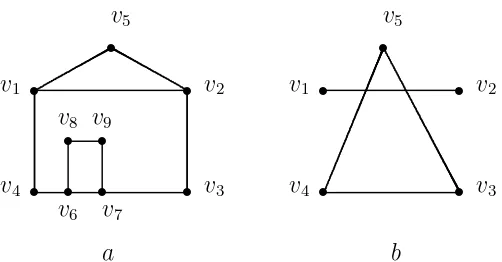
2.3 Degree Constrained Minimum Spanning Tree
Andaikan G merupakan graph terhubung, T merupakan subgraph dari G, dT(v i) merupakandegree dari verteksvi yang ada diT, dan bi merupakan batasan degree di T. Degree constrained spanning tree T adalah menemukan spanning tree T di
G, sehingga dT(v
i)≤bi, untuk setiap verteks vi di T.
Contoh 1.2.4Berikut diberikan graph Gdimana T merupakan DCST dari G.
s
s
s
s s
s s
s
s s
s s s
s s
s s s
s s
G dT(v
i)≤2
dT(vi)≤3 dT(vi)≤4 T1 :
T2 : T3 :
Gambar 2.11 : DCST dariG
Andaikan G = (V, E) adalah suatu graph berbobot terhubung tak berarah di-mana V = {v1, v2, ..., vn} adalah himpunan verteks dan E = {e1, e2, ..., em} him-punan edge di G. Andaikan W = {w1, w2, ..., wm} mewakili bobot dari setiap edge, dimana bobot merupakan bilangan real nonnegatif. Subgraph dari G bisa dideskripsikan menggunakan vektor X = {x1, x2, ..., xm}, dimana setiap element
17
xi didefenisikan oleh:
xi =
1, jika edge terpilih
0, jika tidak terpilih.
Andaikan T menjadi subgraph G, T dikatakan spanning tree dari G jika T terhubung, mengandung seluruh verteks G, dan tidak cycle. Kemudian anggap
d(vi) degree dari verteks vi di G dan K(vi) himpunan degree pada G serta bi merupakan batasan degreedT(v
i) diT, permasalahandegree constrained minimum spanning tree dapat diformulasikan ke dalam program integer sebagai berikut: Fungsi Tujuan:
Min z(x) = m X
i=1
wixi
Kendala:
m X
i=1
xi =|V| −1 (1)
m X
i=1
xi ≤ |N| −1, ∀N ⊂V,|N| ≥3 (2)
X xi∈K(vi)
xi≤bi, 1≤bi ≤ |V| −1, i= 1,2, ..., n (3)
xi ∈ {0,1}, xi ∈E (4)
Dari formulasi diatas, kendala pertama menyatakan bahwa hanya ada n−1 edge yang terpilih, karenanya kendala kedua menjamin bahwa edge yang dipero-leh akan menghubungkan seluruh verteks tanpa terjadi cycle, sedangkan kendala ketiga merupakan batasdegree yang dikehendaki.
Untuk menyelesaikan DCMST yang diformulasikan diatas, maka untuk graph lengkap akan ada 2n − 1− n
2
kendala. Bagaimanapun, untuk n = 30, cara ini sangat tidak praktis. Misalnya untuk graph lengkap dengan 30 verteks akan ada 230 − 1− 30
2
∼
18
dapat ditemukan dalam sepersepuluh detik, maka paling tidak akan dibutuhkan waktu 3,4 tahun untuk dapat menuliskan seluruh kendala sebelum perhitungan dilakukan.
Pada dasarnya persoalan DCMST merupakan perkembangan dari permasala-hanminimum spanning treedengan syarat memenuhi batasandegreeyang diberikan. Karenanya algoritma yang biasa digunakan untuk menyelesaikanminimum span-ning treedapat pula digunakan untuk menyelesaikan permasalahan DCMST. Salah satunya adalah algoritma Kruskal. Ning, Ma, dan Xiong (2008) menggunakan algoritma Kruskal untuk menyelesaikan permasalahan DCMST dengan terlebih dahulu menggunakan teknik reduksi untuk mengurangi ukuran graph dengan cara menghilangkan edge yang dianggap tidak perlu.
Algoritma Kruskal pertama kali diperkenalkan pada tahun 1956 oleh Joseph Kruskal untuk menyelesaikanminimum spanning tree. Algoritma Kruskal ditulis kembali pada tahun 1957 oleh Loberman dan Weinberger, namun pencantuman nama mereka ditolak (Erickson, 2011).
Pada algoritma Kruskal, awalnya seluruh edge diurutkan mulai bobot terkecil hingga terbesar. Lalu pemilihan edge dimulai dari bobot yang terkecil tersebut. Seluruh verteks vi yang ada di G dimasukkan ke T tanpa memasukkan edge, dengan kata lain pada awalnya tidak ada edge di T. Karena pemilihan edge berdasarkan nilai dari bobot setiap edge, maka pada prosesnya akan dihasilkan beberapa tree (forest). Untuk setiap edge (vj, vk) yang telah terurut dilakukan hal berikut, jika verteks vj dan vk berada pada dua tree yang berbeda, maka tambahkan (vj, vk) keforest, kombinasikan dua treeke dalamtreetunggal. Proses dihentikan jika edge (vj, vk) tepat berjumlah |V| −1.
19
Berikut diberikan algoritma Kruskal(Erickson, 2011):
KRUSKAL (V,E):
Mulai:
1. Urutkanei ∈E berdasarkan ukuran bobot 2. T ←(V,∅)
3. untuk setiap verteks vi ∈V MASUKKANHIMPUNAN(V)
4. untuki←1 ke |E|
a. (vj, vk) ← tandai edge keidiE
b. jika PENEMUAN(vj)6= PENEMUAN(vk) GABUNGKAN(vj, vk)
tambahkan (vj, vk) ke T c. jika|(vj, vk)|=|V| −1
hasilT
Akhir
Waktu terburuk yang diperlukan algoritma Kruskal untuk melakukan proses dari tahap awal hingga menghasilkan minimum spanning treeadalah O(ElogV).
Teorema 2.13 Untuk graphG berbobot terhubung, algoritma Kruskal menghasil-kan minimum spanning tree.
Bukti: Andaikan G graph berbobot terhubung dengan p edge, dan andaikan T subgraph yang dihasilkan oleh algoritma Kruskal. Pasti, T merupakan spanning treeG (karenanya memilikip−1 edge), katakanlah:
E(T) = {e1, e2, ..., ep−1}.
dimanaw(e1)≤w(e2)≤...≤w(ep−1).Sehingga bobot T adalah:
w(T) = p−1
X i=1
20
Andaikan sebaliknya, bahwa T bukan merupakan minimum spanning tree. Maka diGmasih terdapat minimum spanning tree, pilih salah satu, katakanlah H yang memiliki jumlah edge paling mirip dengan T. Ini berarti tree H dan T tidak identik. Jadi, terdapat paling sedikit satu edge diT yang tidak ada diH. Andaikan
ei(1 ≤ i ≤ p −1) menjadi edge pertama T yang tidak di H, dan definisikan G0 =H +ei, maka G0 memiliki tepat satu cycle C. Karena T tidak cycle, maka
terdapat e0 diC yang tidak ada di T. Graph T0 =G0−e0 juga spanning treedi
Gdan
w(T0) =w(H) +w(ei)−w(e0)
Karena w(H) ≤ w(T0), maka w(e0) ≤ w(ei). Oleh algoritma Kruskal, ei meru-pakan edge dengan bobot paling minimum sehinggah{e1, e2, ..., ei−1} ∪ {ei}itidak cycle. Bagaimanapun h{e1, e2, ..., ei−1, e0}i adalah subgraph H dan tidak cycle,
sehingga w(ei) = w(e0). Hal ini berakibat w(T0) = w(H), yang secara tidak
langsung menyatakan bahwa T0 juga minimum spanning tree G. Akan tetapi T0
memiliki lebih banyak edge yang sama dengan T daripada H dengan T, yang
kontradiksi dengan asumsi. .
Karena permasalahan dari DCMST merupakan permasalahan menemukan spanning treeT di G dengan total panjang edge minimum dan degree dari setiap verteks memenuhi batas maksimum yang diberikan, maka untuk menyelesaikan DCMST dengan algoritma Kruskal perlu dilakukan modifikasi.
BAB 3
ALGORITMA UNTUK DEGREE CONSTRAINED MINIMUM SPANNING TREE
Pada bab ini akan diperlihatkan pemodifikasian algoritma Kruskal sehingga dapat diterapkan untuk menyelesaikandegree constrained minimum spanning tree.
3.1 Algoritma untuk Degree Constrained Minimum Spanning Tree
Permasalahan degree constrained minimum spanning tree secara sederhana dapat dijelaskan sebagai berikut, diberikan graph G berbobot terhubung tak berarah, temukanspanning tree T dengan total edge minimal dan d(vi) ≤bi, untuk setiap verteksvi di T.
Berikut diberikan algoritma Kruskal sebelum dilakukan pemodifikasian.
KRUSKAL (V,E):
Mulai:
1. Urutkanei ∈E berdasarkan ukuran bobot 2. T ←(V,∅)
untuk setiap verteksvi ∈V
MASUKKANHIMPUNAN(V)
3. untuki←1 ke |E|
a. (vj, vk) ← tandai edge keidiE
b. jika PENEMUAN(vj)6= PENEMUAN(vk) GABUNGKAN(vj, vk)
tambahkan (vj, vk) ke T c. jika|(vj, vk)|=|V| −1
hasilT
22
Penjelasan:
Berikut penjelasan dari algoritma Kruskal diatas.
1. Seluruh edge ei yang ada di E diurutkan berdasarkan nilai bobot, dimana w(e1)≤w(e2)≤...≤w(em).
2. Seluruh verteksvi di V dimasukkan ke T.
3. Untuk edge awal diT merupakan edge dengan nilai bobot paling minimum.
a. Untuk edgevj, vk selanjutnya yang akan dimasukkan keT, periksavjvk terlebih dahulu, jika verteksvj tidak berada dalam treeyang sama de-ngan verteks vk (edge vjvk tidak membentuk cycle), maka gabungkan edge vjvk, lalu tambahkan vjvk keT.
b. Jika jumlah edge yang ada di T = |V| −1, maka hentikan pencarian edge vj, vk karena sudah menghasilkan minimum spanning treeT
Permasalahan degree constrained minimum spanning tree pada graph G ter-hubung tak berarah merupakan permasalahan menemukan spanning tree T di G dengan total panjang edge yang minimum dan degree setiap verteks vi di T me-menuhi bi yang diberikan (dT(vi) ≤ bi). Karena adanya pembatasan degree dari setiap verteks vi di T, untuk memodifikasi algoritma Kruskal ada beberapa hal yang perlu diperhatikan, yaitu:
1. PembatasandegreevidiT, untuk kasus tertentu pada graphGyang memiliki beberapa bridge, menyebabkan T tidak dapat ditemukan. Untuk itu, semua edge vj, vk yang merupakan brigeharus dimasukkan kedalam T.
2. Suatu edge vj, vk diterima pada T jika vj, vk tidak membentuk cycle dengan edge terdahulu yang ada diT dan (dT(v
j)≤bj) dan (dT(vk)≤bk).
23
Berikut diberikan algoritma Kruskal DCMST:
KRUSKAL DCMST (V,E),d(vi)≤bi : Mulai:
1. T ←(V,∅)
untuk setiap verteksvi ∈V
MASUKKANHIMPUNAN(vi) 2. ∀(vj, vk)∈E yang merupakan bridge
tambahkan (vj, vk) ke T
3. Urutkan ei ∈E yang bukan bridge berdasarkan bobot 4. a. (vj, vk) ← tandai edge keidiE
b. jika PENEMUAN(vj) 6= PENEMUAN(vk) dan (dT(vj) ≤bj ,dT(vk)≤bk) GABUNGKAN(vj, vk)
tambahkan (vj, vk) ke T c. jika|(vj, vk)|=|V| −1
hasilT
Akhir
Penjelasan:
1. Seluruh verteksvi di V dimasukkan ke T.
2. Masukkan semua edgevj, vk ∈E yang merupakan bridge diG.
3. Urutkan edge ei ∈ E yang bukan bridge berdasarkan nilai bobot, dimana w(e1)≤w(e2)≤...≤w(em).
4. Pilih edge vj, vk dengan nilai bobot paling minimum.
24
maka gabungkan edge vj, vk, lalu tambahkan vj, vk ke T.
b. Jika jumlah edge yang ada diT =|V|−1, maka hentikan pencarian edge
vj, vk karena sudah menghasilkandegree constrained minimum spanning tree T
Waktu terburuk yang diperlukan oleh algoritma Kruskal untuk melakukan proses dari tahap awal hingga menghasilkandegree constrained minimum spanning treeadalah O(ElogV).
3.1.1 Hasil Percobaan dan Analisis.
Contoh 3.1: Berikut diberikan graph G = (8,17). Temukan spanning tree T dengan total panjang edge yang minimal dandegree dari setiap verteks tidak lebih dari 3, (1≤bi ≤3).
✈ ✈
✈ ✈
✈ ✈
✈ ✈
v1 v3
v2 v5
v8 v6
v4 v7
4
5 10
7
12
5
6
8 7
9
10
12 8 6
7
9 4
Gambar 3.1 : Graph G
Analisis:
a. Dengan Program Integer 0-1
Seperti yang telah disinggung pada Bab 2, bahwa untuk menyelesaikan DCMST bisa dilakukan dengan terlebih dahulu memodelkan graphGke dalam program in-teger 0,1, dimana setiap edge bisa dianggap sebagai sebuah vektorX ={x1, ..., xn},
25
dimana setiap elementxi didefinisikan oleh:
xi =
1, jika edge terpilih
0, jika tidak terpilih.
Adapun bentuk umum pemodelan DCMST adalah sebagai berikut: Fungsi Tujuan:
Min z(x) = m X
i=1
wixi
Kendala:
m X
i=1
xi =|V| −1 (1)
m X
i=1
xi ≤ |N| −1, ∀N ⊂V,|N| ≥3 (2)
X xi∈K(vi)
xi≤bi, 1≤bi ≤ |V| −1, i= 1,2, ..., n (3)
xi ∈ {0,1}, xi ∈E (4)
maka bentuk persoalan pada graph G adalah:
Fungsi Tujuan:
Min z(x) = 4x1+ 5x2+ 10x3+ 7x4+ 12x5+ 6x6+ 8x7+ 7x8+ 5x9+ 4x10+ 9x11+
6x12+ 9x13+ 8x14+ 7x15+ 10x16+ 12x17
Kendala:
• UntukPm
i=1xi =|V| −1
4x1+ 5x2+ 10x3+ 7x4 + 12x5+ 6x6+ 8x7+ 7x8+ 5x9+ 4x10+ 9x11+ 6x12+ 9x13+ 8x14+ 7x15+ 10x16+ 12x17 = 7
• UntukPm
i=1xi ≤ |N| −1,∀N ⊂V,|N| ≥3 (Terbentuknyacycle)
1. Untuk edge yang menghubungkan 3 verteks
x2+x3+x7≤ 2
x1+x2+x4≤ 2
26
x4+x5+x8≤ 2
x4+x8+x9≤ 2
x5+x8+x13≤2
x8+x9+x13≤2
x7+x10 +x12 ≤2
x7+x9+x11≤2
x9+x10+x15≤2
x11+x12+x15 ≤2
x13+x14+x16 ≤2
x13+x16+x17 ≤2
2. Untuk edge yang menghubungkan 4 verteks x4+x5+x6+x8+x9+x13≤3
x7+x9+x10+x11+x12+x15≤3 x1+x2+x3+x4+x7 ≤3
x13+x14+x15+x16+x17≤3 x1+x2+x4+x6+x9 ≤3 x8+x9+x13+x14+x16≤3 x9+x10+x15+x16+x17≤3 x4+x6+x7+x9+x11≤3 x8+x9+x10+x13+x15≤3 x11+x12+x16+x17≤3 x5+x6+x14+x16≤3 x1+x2+x5+x8 ≤3
x2+x3+x10+x12≤3
x4+x6+x10+x15≤3
x7+x8+x11+x13≤3
x8+x10+x14+x17≤3
27
x2+x3+x7+x9+x11≤3
3. Untuk edge yang menghubungkan 5 verteks
x1+x2+x3+x4+x6+x7+x9 +x11 ≤4
x6+x9+x10+x13+x14+x15+x16+x17≤4
x4+x5+x6+x8+x9+x10+x13+x15≤4
x4+x5+x6+x7+x8+x9+x11+x13 ≤4
x4+x6+x7+x9+x10+x11+x15≤4
x7+x8+x9+x10+x11+x12+x13+x15 ≤4
x1+x2+x5+x6+x8+x9+x13 ≤4
x4+x5+x6+x8+x9+x13+x14+x16≤4 x2+x3+x7+x9+x10+x11+x12+x15≤4 x7+x9+x10+x11+x12+x15+x16+x17≤4 x4+x5+x7+x8+x10+x12≤4
x5+x6+x11+x12+x13≤4
4. Untuk edge yang menghubungkan 6 verteks
x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x15≤5
x1+x2+x4+x5+x6+x8+x9 +x13+x14+x16 ≤5
x2+x3+x7+x9+x10+x11+x12+x15+x16+x17 ≤5
x6+x7+x8+x9+x10+x11+x12+x14+x15+x16 ≤5
x1+x2+x3+x4+x6+x7+x9 +x10+x11+x12+x15 ≤5
x4+x5+x6+x8+x9+x10+x14+x15+x16+x17≤5
x1+x2+x3+x12+x14+x17 ≤5
x1+x2+x3+x4+x5+x6+x7 +x8+x9+x10+x13≤5
x5+x6+x11+x12+x13+x14+x15+x16+x17≤5
x1+x2+x3+x4+x5+x7+x8 +x10+x12 ≤5
28
5. Untuk edge yang menghubungkan 7 verteks
x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17≤6
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10 +x11 +x12+x13+x15≤6
x2+x3+x4+x7+x9+x10+x11+x12+x13+x14+x15+x16+x17≤6
x1+x2+x3+x4+x6+x7+x10+x11+x12+x15+x16+x17≤6
x1+x2+x3+x4+x6+x7+x8+x9+x11+x13+x14+x15+x16≤6
x1+x2+x4+ 5x+x6+x8+x10+x13+x14+x15+x16+x17 ≤6
x1+x3+x5+x6+x11+x12+x13+x14+x15+x16+x17 ≤6
x1+x2+x3+x4+x5+x7+x8 +x10+x12+x14+x17 ≤6
6. Untuk edge yang menghubungkan 8 verteks
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+
x15+x16+x17 ≤7
• Untuk edge yang merupakan degreedari verteks vi,
X xi∈K(vi)
xi≤bi,1≤bi ≤ |V| −1, i = 1,2, ..., n
.
x1+x2+x3 ≤3
x10+x15+x17≤3
x1+x4+x5+x6 ≤3
x2+x4+x7+x8+x9+x10≤3
x3+x7+x11+x12≤3
x5+x8+x13+x14≤3
x6+x9+x11+x13+x15+x16≤3
x14+x16+x17≤3
x1+x2+x3 ≥1
x10+x15+x17≥1
x1+x4+x5+x6 ≥1
29
x2+x4+x7+x8+x9+x10≥1
x3+x7+x11+x12≥1
x5+x8+x13+x14≥1
x6+x9+x11+x13+x15+x16≥1
x14+x16+x17≥1
Dengan menggunakan bantuan program LINDO versi 6.1 diperoleh jumlah seluruh bobot adalah 44 dengan edge v1v2, v1v4, v3v5, v3v6, v3v7, v4v7, dan v5v8.
t
t
t
t
t
t t
t v1
v4 v3
v2 v5
v6
v7
v8
Gambar 3.2 : Hasil Program Integer 0-1 untuk DCMST
b. Dengan Algoritma Kruskal DCMST
Dari graph G= (8,17). Berikut langkah-langkah algoritma Kruskal DCMST un-tuk menyelesaikan DCMST pada graph G.
1. Masukkan seluruh verteks vi ∈V kedalamT, T = (V,∅)
2. Karena tidak ada edge vj, vk yang merupakan bridge, lakukan tahap selan-jutnya.
3. Urutkan edge ei ∈E berdasarkan nilai bobot, dimanaw(e1)≤w(e2)≤...≤
w(em)
a. Pilihv1v2, karenav1v2 adalah e1 = 4, edge paling minimal di E.
30 ② ② ② ② ② ② ② ② v1 v3
v2 v5
v8
v6
v4 v7
4 = e1
5 =e3
10 =e14
7 =e7
12 =e16
5 =e4
6 =e5
8 =e10 7 = e8
9 = e12 10 = e15
12 =e17
8 = e14
6 =e6
7 =e9
9 =e13
4 =e2
Gambar 3.3 : Graph G
c. Pilih e3 = 5, yaitu v1v3
d. Pilihe4 = 5, yaitu v3v6
e. Pilih e6 = 7, yaitu v4v7, karena jika edge e5 dimasukkan akan terjadi
cycle.
f. Pilihe11= 8, yaitu v5v8, karena jika dimasukkan e7, e9, e10 akan terjadi
cycle. Sedangkan e8 meski tidak membentukcycle, e8, yaituv3v5 tidak
memenuhi batasan degree yang dikehendaki karena jumlah dTv
3 = 3,
sudah memenuhi batas maksimum (dTv
3 ≤3).
g. Pilihe13= 9, yaitu v5v6, karena e13 jika dimasukkan akan terjadicycle. Karena edge telah diperoleh 7 edge, maka pemilihan edge dihentikan.
Diperoleh spanning tree T memenuhi syarat degree (1 ≤ bi ≤ 3), dengan total jumlah panjang edge adalah 41.
Untuk lebih jelasnya, langkah-langkah tersebut dapat dilihat pada gambar
31
Contoh 3.2: Langkah-langkah algoritma KruskalDCMST:
t t t t t t t t v1 v4 v3
v2 v5
v6 v7 v8 t t t t t t t t v1 v4 v3
v2 v5
v6
v7
v8
T = (V,∅) Pilihv1v2
t t t t t t t t v1 v4 v3
v2 v5
v6 v7 v8 t t t t t t t t v1 v4 v3
v2 v5
v6
v7
v8
Pilihv3v7 Pilihv1v3
t t t t t t t t v1 v4 v3
v2 v5
v6 v7 v8 t t t t t t t t v1 v4 v3
v2 v5
v6
v7
v8
Pilihv3v6 Pilihv4v7
32
t
t
t
t
t
t t
t v1
v4 v3
v2 v5
v6
v7
v8
t
t
t
t
t
t t
t v1
v4 v3
v2 v5
v6
v7
v8
Pilihv5v8 Pilihv5v6
Gambar 3.4 : Hasil Algoritma Kruskal DCMST
Dari sini dapat dilihat bahwa dengan menggunakan algoritma Kruskal DCMST diperoleh jumlah bobot(41) lebih minimum daripada dengan menggunakan LIN-DO versi 6.1 (44), karenanya penggunaan algoritma Kruskal untuk menyelesaikan DCMST adalah layak untuk dipergunakan.
BAB 4
KESIMPULAN DAN SARAN
Pada bab ini akan diberikan kesimpulan yang diperoleh dari hasil penelitian pada bab sebelumnya. Selanjutnya akan diberikan saran untuk penelitian lebih lanjut.
4.1 Kesimpulan
Permasalahandegree constrained minimum spanning treepada graphGterhubung tak berarah merupakan permasalahan menemukan spanning tree T di G dengan total panjang edge yang minimum dan degree setiap verteks vi di T memenuhi bi yang diberikan (dT(vi) ≤ bi). Karena adanya pembatasan degree dari setiap verteks vi di T, untuk memodifikasi algoritma Kruskal ada beberapa hal yang perlu diperhatikan, yaitu:
1. PembatasandegreevidiT, untuk kasus tertentu pada graphGyang memiliki beberapa bridge, menyebabkan T tidak dapat ditemukan. Untuk itu, semua edge vj, vk yang merupakan brigeharus dimasukkan kedalam T.
2. Untuk edge vj, vk selanjutnya yang akan dimasukkan ke T, periksa vj, vk terlebih dahulu, jika verteks vj tidak berada pada tree yang sama dengan verteks vk (edge vj, vk tidak membentuk cycle) dan degree verteks vj di T memenuhibj(dT(vj)≤bj) sertadegreeverteksvkdiT memenuhibk(dT(vk)≤ bk), maka gabungkan edgevj, vk, lalu tambahkan vj, vk keT.
34
4.2 Saran
Penelitian ini telah menyelesaikan degree constrained minimum spanning tree de-ngan menggunakan algoritma Kruskal yang telah dimodifikasi. Namun, belum dapat dipastikan apakah algoritma Kruskal DCMST cukup efisien untukn beruku-ran cukup besar . Dibutuhkan penelitian lebih lanjut untuk menyelesaikandegree constrained minimum spanning treedengan metode lain yang mungkin lebih efektif dan efisien.
35
DAFTAR PUSTAKA
Vasudev C. 2006. Graph Theory with Applications. New Delhi: New age in-ternational publisher.
Deo N. 1986. Graph Theory with Applications to Engineering and Computer Science. New Delhi: Prentice Hall of India.
Wu B.Y dan Chao K.M. 2004. Spanning Tree and Optimization Problems. Chapman and Hall/CRC.
Garey M.R dan Johnson D.S. 1979. Computers and Intractability, A guide to the theory of NP-completeness. New York: W. H Freeman and Com-pany.
Ribiero C.C dan Souza M.A. 2002. Variable neighbourhood search for the degree constrained minimum spanning tree problem.Descrete applied mathematics, 118; 43-54.
Khrishnamoorthy M dan Ernst A. 2001. Comparison of algorithms for the degree constrained minimum spanning tree. Journal of Heuristic, 7; 587-611.
Wamiliana. 2004. Solving the degree constrained minimum spanning tree problem using tabu and modified penalty search methods. Jurnal Teknik Industri, 6 (2004), 1-9.
Cunha A dan Lucena A. 2005. Algorithms for the degree constrained minimum spanning tree problem. Electronic Notes in DESCRETE MATHE-MATICS, 19; 403-409.
Ning A, Ma L, dan Xiong X. 2008. A new algorithm for degree constrained minimum spanning tree based on the reduction technique.Progress in Natural Science, 18 (2008), 495-499.
Binh H.T.T dan Nguyen T.B. 2008. New particle swarm optimization algo-rithm for solving degree constrained minimum spanning tree. LNAI, 5351 (2008), 1077-1085.
Erickson J. 2011. Algorithms. Departement of Computer Science University of Illinois, Urbana-Champaign.
Eiselt H.A dan SanblomC.L . 2007.Linear Programming and its Applications. Canada: Springer.