ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 142
PENERAPAN TEORI GRAF UNTUK MENYELESAIKAN
MASALAH
MINIMUM SPANNING TREE(
MST) MENGGUNAKAN
ALGORITMA KRUSKAL
Swaditya Rizki
Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Metro, Lampung
Email: [email protected]
ABSTRACT: One of useful graph theory to solve the real problems is Minimum Spanning Tree (MST). MST is network optimization problems that can be applied in many fields such as transportations problems and communication network design (Gruber and Raidl, 2005). MST begins from tree namely a connected graph ha s no circuits. From the graph, there is a sub-graph that has all the vertex or spanning tree. If that graph has the weight/cost, then the spanning tree that has the smallest weight/cost is called Minimum Spanning Tree. Basic algorithm used to determine the MST is Kruskal’s algorithm. This algorithm is known as one of the best algorithms for the optimization problems, especially for MST. In this paper is developed a source code program to determine MST using Kruskal’s algorithm and then implemented on several data representing a complete graph.
Keywords: Graph, Tree, Minimum Spanning Tree (MST), Kruskal’s Algorithm.
1. Latar Belakang dan Masalah
Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami peningkatan yang signifikan. Para peneliti terus melakukan penelitian untuk selalu memunculkan penemuan-penemuan baru yang dapat memberikan sumbangan ilmu pengetahuannya sebagai penunjang berkembangnya ilmu-ilmu lain. Salah satunya adalah ilmu-ilmu matematika yang sudah ditemukan oleh ilmuan-ilmuan ratusan tahun yang lalu, sekarang sangat berguna dalam perkembangan teknologi yang sampai
saat ini dapat memudahkan manusia dalam menyelesaikan permasalahan yang ada. Teknologi komputer sendiri pembuatannya sebagian besar menggunakan logika matematika yang sampai saat ini terus berkembang pesat, sehingga ilmu matematika dapat digunakan untuk menyelesaikan berbagai permasalah-an dalam dunia nyata.
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 143 penduduk kota tersebut ingin melewati
jembatan tersebut tepat satu kali dan kembali lagi ke tempat awal keberangkatan. Dari permasalahan tersebut, seorang matematikawan Swiss, Leonard Euler menemukan jawaban dari permasalahan tersebut yaitu memodelkan masalah ini dengan cara merepresentasikan ke dalam graf. Dengan representasi tersebut dapat mempermudah menganalisis dan menemukan solusi dari suatu permasalahan yang sangat membutuhkan dana besar dan waktu lama untuk membuktikannya secara langsung.
Graf juga mempunyai banyak manfaat untuk optimasi dalam membangun jalan raya, rel kereta api, desain jaringan komunikasi, dll. Sebagai contoh, untuk membangun sebuah jalan raya yang menghubungkan beberapa kota, sangat dibutuhkan suatu desain dalam graf agar dapat mengoptimalkan pembangunan suatu jalan tersebut dengan dana yang minimal. Masalah ini dapat direpresentasikan ke dalam graf yaitu dengan menyatakan kota-kota sebagai titik/node/vertex, jalan raya sebagai garis/edge, dan biaya pembangunan jalan raya sebagai bobot dalam graf.
Penelitian ini berfokus pada algoritma Kruskal untuk masalah Minimum Spanning Tree (MST) yang terkait tentang optimasi dalam permasalahan transportasi khususnya pembuatan jalan raya yang menghubungkan lebih dari n kota dan permasalahan desain jaringan komunikasi untuk kecepatan transfer data. Permasalahan ini direpresentasi-kan ke dalam suatu graf, kemudian dicari pohon merentang minimum (Minimum Spanning Tree) menggunakan algoritma Kruskal.
2. Tujuan Penelitian
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 144 v5
e7
mendapatkan solusi dari permasalahan tersebut.
3. Graf (Graph)
Graf G adalah suatu struktur (V,E) dimana V = {v1, v2, …} himpunan tak
kosong dengan elemen-elemennya disebut vertex (titik), sedangkan E = {e1,
e2, …} (mungkin kosong) adalah
himpunan pasangan tak terurut dari elemen-elemen di V(G). Anggota dari E(G) disebut edge (sisi). Secara geometri graf digambarkan sebagai sekumpulan noktah (simpul) di dalam bidang dua dimensi yang dihubungkan dengan sekumpulan garis (sisi).
v1 e3 v2 e1
karena ia berawal dan berakhir pada titik yang sama (Deo, 1989).
Definisi 1 Graf Lengkap (Complete
Graph)
Graf lengkap adalah graf sederhana yang setiap titiknya mempunyai sisi ke semua titik lainnya atau graf yang setiap titiknya saling bertetangga. Graf dengan n buah titik dilambangkan dengan Kn.
Setiap titik pada Kn berderajat n-1. K1
sampai K5adalah contoh graf lengkap.
Gambar 2. Graf Lengkap K1– K5.
Definisi 2 Graf Berbobot (Weighted
Graph)
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 145 Definisi 3 Sirkuit (Cycle)
Lintasan yang berawal dan berakhir pada simpul yang sama disebut sirkuit atau siklus (Munir, 2001).
a. Pohon (Tree)
Definisi 4 Pohon
Tree adalah graf terhubung yang tidak mengandung sirkuit (Deo, 1989).
Gambar 3. Pohon (Tree).
Sifat-sifat dari pohon (tree) adalah sebagai berikut:
Misalkan G = (V, E) adalah graf tak-berarah sederhana dan jumlah simpulnya n. Semua pernyataan di bawah ini adalah ekivalen: penambahan satu sisi pada graf akan membuat hanya satu sirkuit.
6. G terhubung dan semua sisinya adalah jembatan (jembatan adalah sisi yang bila dihapus menyebabkan graf terbagi menjadi dua komponen) (Munir, 2001).
b. Pohon Merentang (Spanning Tree)
Misalkan G graf terhubung. Tree T dikatakan spanning tree dari G jika T adalah subgraf dari G yang memuat semua titiknya (Deo, 1989).
Misalkan G = (V,E) adalah graf tak-berarah terhubung yang bukan pohon, artinya pada G terdapat sirkuit. G dapat diubah menjadi pohon T = (V,E) dengan cara memutuskan sirkuit-sirkuit yang ada. Caranya yaitu dengan memutuskan salah satu sisi pada sirkuit hingga tidak ada sirkuit pada G. Jika di G tidak ada lagi sirkuit maka pohon T ini disebut dengan pohon merentang (spanning tree). Disebut merentang karena semua simpul pada pohon T sama dengan simpul pada graf G, dan sisi pada T sisi pada G, dengan kata lain V1 = V dan
E1 E (Munir, 2001).
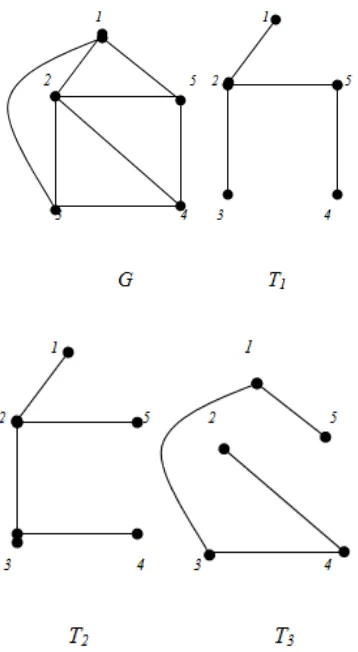
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 146 Gambar 4. Graf dan tiga buah spanning
tree T1, T2, T3.
c. Minimum Spanning Tree (MST)
Jika G pada merupakan graf berbobot, maka bobot pohon merentang T1 atau T2 didefinisikan sebagai jumlah
bobot semua sisi di T1 atau T2. Di antara
pohon merentang yang ada pada G, yang paling penting adalah pohon merentang dengan bobot minimum. Pohon merentang dengan bobot minimum ini disebut dengan pohon merentang minimum atau Minimum Spanning Tree (MST). Contoh aplikasi MST yang sering
digunakan adalah masalah transportasi seperti pemodelan proyek pembangunan jalan raya menggunakan graf. MST digunakan untuk memilih jalur dengan bobot terkecil yang akan meminimalkan biaya pembangunan jalan.
Contoh graf dan pohon berbobot:
Gambar 5. G graf berbobot, T1 danT2
rentang pohon berbobot.
Dari graf berbobot G, akan ditentukan pohon merentang mana yang paling minimum. Apakah T1 atau T2?. Hal
tersebut yang akan dicari dengan membangun pohon merentang minimum.
G
T1
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 147 4. Algoritma Kruskal
Adapun langkah-langkah algoritma Kruskal yaitu sebagai berikut:
1. Urutkan (sorting) biaya/bobot setiap edge dari biaya yang terkecil ke biaya terbesar.
2. Kemudian pilih edge terkecil dan pasang ke dalam tree.
3. Cek apakah jumlah E V 1. Jika tidak, ke Langkah 4. Jika ya, stop.
4. Pilih edge berikutnya dalam sorting.
5. Cek apakah pemasangan edge tersebut menyebabkan sirkuit/cycle. Jika tidak, masukkan edge ke dalam tree dan ke Langkah 6.
Jika ya, ke Langkah 7. 6. Kembali ke Langkah 3.
7. Buang edge pada Langkah 5 dan kembali ke Langkah 4.
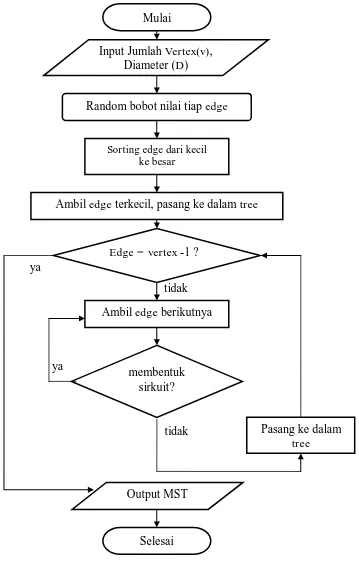
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 148 Diagram alir Minimum Spanning Tree (MST) adalah sebagai berikut:
Gambar 6. Diagram alir (flowcha rt) MST. tidak
ya
tidak ya
Mulai
Edge = vertex -1 ?
Ambil edge terkecil, pasang ke dalam tree
Ambil edge berikutnya
membentuk sirkuit?
Pasang ke dalam tree
Selesai
Random bobot nilai tiap edge
Output MST Input Jumlah Vertex(v),
Diameter (D)
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 149 5. Hasil dan Pembahasan
Input program berupa jumlah vertex/titik. Dari jumlah vertex tersebut dibangkitkan bobot/biaya tiap edge untuk suatu graf lengkap. Kemudian data tersebut diurutkan berdasarkan bobot/biaya terkecil dan kemudian diperoleh solusi optimal MST. Sebagai contoh, akan dibangkitkan data secara
acak dengan jumlah vertex 10, dari 10 vertex tersebut dihubungkan sebagai graf lengkap sehingga mempunyai edge sebanyak 45. Untuk proses menentukan graf lengkap dapat dilihat pada gambar 2. Kemudian dari graf lengkap tersebut dibangkitkan biaya/bobot secara acak untuk masing-masing edge dengan nilai yang bervariasi. Berikut ini hasil simulasi data untuk 10 vertex.
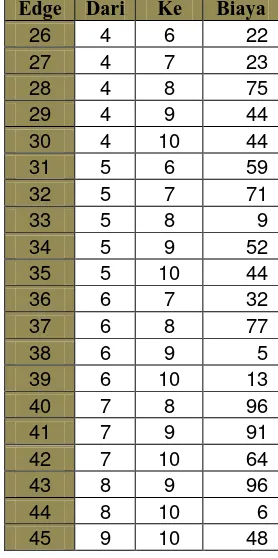
Tabel 1. Data graf lengkap dengan jumlah vertex 10.
Edge Dari Ke Biaya Edge Dari Ke Biaya
1 1 2 10 26 4 6 22 2 1 3 57 27 4 7 23 3 1 4 44 28 4 8 75 4 1 5 43 29 4 9 44 5 1 6 35 30 4 10 44 6 1 7 41 31 5 6 59 7 1 8 64 32 5 7 71 8 1 9 92 33 5 8 9 9 1 10 47 34 5 9 52 10 2 3 10 35 5 10 44 11 2 4 38 36 6 7 32 12 2 5 32 37 6 8 77 13 2 6 27 38 6 9 5 14 2 7 77 39 6 10 13 15 2 8 79 40 7 8 96 16 2 9 49 41 7 9 91 17 2 10 24 42 7 10 64 18 3 4 33 43 8 9 96 19 3 5 92 44 8 10 6 20 3 6 21 45 9 10 48 21 3 7 44
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 150 Tabel 2. Proses mengurutkan data berdasarkan bobot/biaya.
Edge Dari Ke Biaya Edge Dari Ke Biaya
Setelah proses pengurutan data, edge dipasang satu persatu ke dalam tree dimulai dari bobot biaya yang terendah sampai memenuhi MST dan proses akan berhenti jika jumlah edge = vertex -1. Adapun langkah-langkah dalam pemasangan edge ke dalam tree
dipasang karena akan membentuk sirkuit.
9. Pasang edge dari vertex 4 ke 6. 10. Pasang edge dari vertex 4 ke 7. 11. Karena jumlah edge = vertex-1,
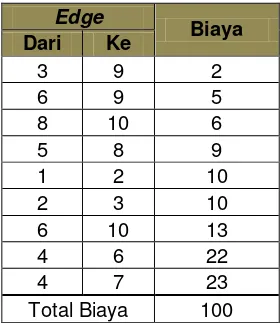
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 151 Tabel 3. Solusi optimal MST
menggunakan algoritma Kruskal. bobot/ biaya yaitu 100. Sedangkan pada Tabel 4 yaitu solusi MST tanpa menggunakan algoritma didapatkan bobot/biaya yaitu 433. Dari nilai tersebut dapat disimpulkan bahwa algoritma Kruskal dapat digunakan untuk mencari solusi optimal MST, bahkan nilai yang didapatkan jauh lebih
minimum dibandingkan dengan solusi yang tidak menggunakan algoritma.
6. Kesimpulan
Data yang digunakan untuk contoh simulasi diatas hanya data dengan jumlah vertex 10, sedangkan untuk jumlah vertex lebih dari 10 bisa menggunakan program komputasi yang disini menggunakan bahasa pemrograman C/C++ sehingga akan lebih mengefisienkan waktu perhitungan. Program komputasi ini juga nantinya dapat dikembangkan untuk MST dengan algoritma yang lain ataupun dengan memodifikasi algoritma Kruskal untuk aplikasi graf lainnya.
DAFTAR PUSTAKA
Deo, N. 1989. Graph Theory with Applications to Engineering and Computer Science. Prentice Hall, Inc. Englewood Cliffs, New Jersey. 461 hlm.
Gruber, M. and Raidl, G.R. 2005. Variable Neighborhood Search for the Bounded Diameter
ISSN 2089 – 8703 Vol.1 No.2, Oktober 2012 152 Munir, R. 2001. Matematika Diskrit.
Informatika, Bandung. Hlm 353-456.