Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA.

(1)

APLIKASINYA PADA DNA

N U R M A I L Y

SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR

(2)

Dengan ini saya menyatakan bahwa tesis dengan judul “Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA” adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

(3)

NURMAILY.

The Study of Discrete Hidden Markov Model and Its Application on

DNA Sequence. Under supervision of

BERLIAN SETIAWATY

and

N. K.

KUTHA ARDANA.

A discrete hidden Markov model is a model which consists of the cause of event and

observation process. This model assumes that the cause of event is a Markov chain,

which is not observed directly. The observation process has discrete range.

Parameters of this model are transition probability matrices. They are estimated using

the maximum likelihood method and expectation maximization algorithm. The

estimation procedure involves the change of measure. The estimation of parameters

uses Mathematica 7.0, a functional programming based on algebraic computer

systems. The model is applied to the DNA

sequence. The estimated parameters are

used to calculate the expectation of DNA sequence. The result depends on the

decision of the initial value. There should be another study for determining the initial

value which gives the optimal result.

(4)

NURMAILY.

Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA. Di

bawah bimbingan

BERLIAN SETIAWATY

dan

N.K. KUTHA ARDANA.

Setiap kejadian berkaitan erat dengan penyebab kejadian. Jika penyebab kejadian

tersebut tidak diamati secara langsung dan membentuk rantai Markov, maka

pasangan kejadian dan penyebabnya dapat dimodelkan dengan model Hidden

Markov (Hidden Markov Model, HMM).

Semua proses didefinisikan pada ruang peluang

Ω

, ,

. Misalkan

;

adalah rantai Markov dengan state berhingga yang bersifat homogen dan diasumsikan

tidak diamati secara langsung, sedangkan

;

adalah proses

observasinya. Pasangan proses stokastik

,

merupakan model Hidden

Markov.

Model

Hidden

Markov (Elliot et al. 1995) yang digunakan pada karya ilmiah ini

adalah

+

_Y _CX _W , untuk

di mana

, , … ,

,

, , ,

,

A

dan

C

merupakan

matriks peluang transisi dengan

dan

,

yang

memenuhi

∑ 1, , dan ∑ 1, .

dan

memenuhi

_| _, _|

_| _diag _diag

_diag _diag _.

Jika

, maka vektor

, , … ,

merupakan nilai harapan

dari

, yaitu

dan untuk

ergodic memenuhi

dan

∑

1

.

Parameter yang digunakan pada model di atas adalah

, 1

,

, 1

.

Akan ditentukan parameter baru dengan menggunakan algoritme EM

, 1

,

, ̂

, 1

,

(5)

∑

,

_,

∑

_,

,

.

2.

Pendugaan Banyaknya Lompatan

=

,

Penduga banyaknya lompatan adalah

_, ₁

∑

_,

,

.

Penduga smoother banyaknya lompatan adalah

_,

∑

_,

,

.

3.

Pendugaan Lamanya Waktu Kejadian

,

Penduga lamanya waktu kejadian adalah

_, ∑ _, , , _.

Penduga smoother lamanya waktu kejadian adalah

_, ∑ _, , .

4.

Pendugaan untuk Proses Observasi

∑

,

.

Penduga untuk proses observasi adala

,

∑

,

.

Penduga smoother untuk proses observasi adalah

_,

∑

_,

,

.

Dari pendugaan rekursif dapat ditentukan parameter model sebagai berikut

,

1

,

.

̂

,

1

, 1

.

Nilai Harapan

adalah

|

∑ ∑

1 1 .

Model Hidden Markov diskret di atas diaplikasikan pada perubahan urutan basa DNA

pada spesies

Aspergillus niger

, dengan

N = 2. Dalam perkembangan lebih lanjut,

dibuat suatu program komputasi yang berbasis pemprograman fungsional untuk

menyelesaikan masalah tersebut. Software yang digunakan adalah Mathematica 7.0.

Hasil yang di peroleh pada penelitian ini sangat bergantung pada penentuan nilai

awal. Sampai saat ini hasil yang diperoleh belum cukup baik, karena belum

ditemukan cara untuk menentukan nilai awal yang paling baik sehingga hasil yang

diperoleh optimal.

(6)

© Hak Cipta milik IPB, tahun 2009 Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

(7)

APLIKASINYA PADA DNA

N U R M A I L Y

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2009

(8)

(9)

Disetujui Komisi Pembimbing

Dr. Berlian Setiawaty, M.S. Ir. N. K. Kutha Ardana, M.Sc. Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof, Dr. Ir. Khairil A. Notodiputro, M.S.

(10)

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala rahmat dan karunia-Nya sehingga tugas akhir yang berjudul “Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA” ini bisa terselesaikan sebagai salah satu syarat untuk menyelesaikan pendidikan pada Program Studi Matematika, Sekolah Pascasarjana Institut Pertanian Bogor.

Terimakasih yang mendalam penulis sampaikan kepada:

1. Dr. Berlian Setiawaty, M.S. dan Ir. N. K. Kutha Ardana, M.Sc. selaku pembimbing yang telah memberikan bimbingan dan motivasinya.

2. Dr. Ir. Wayan Mangku, M.Sc. selaku penguji yang telah memberikan saran dan kritiknya.

3. Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB.

4. Seluruh keluarga atas segala dukungan, doa dan kasih sayangnya.

5. Mahasiswa S2 Matematika Terapan IPB angkatan 2007, serta semua pihak yang telah membantu penulis.

Penulis menyadari bahwa tugas akhir ini masih begitu banyak kekurangan. Dengan segala keterbatasan yang ada, semoga tugas akhir ini bermanfaat.

(11)

APLIKASINYA PADA DNA

N U R M A I L Y

SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR

(12)

Dengan ini saya menyatakan bahwa tesis dengan judul “Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA” adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

(13)

NURMAILY.

The Study of Discrete Hidden Markov Model and Its Application on

DNA Sequence. Under supervision of

BERLIAN SETIAWATY

and

N. K.

KUTHA ARDANA.

A discrete hidden Markov model is a model which consists of the cause of event and

observation process. This model assumes that the cause of event is a Markov chain,

which is not observed directly. The observation process has discrete range.

Parameters of this model are transition probability matrices. They are estimated using

the maximum likelihood method and expectation maximization algorithm. The

estimation procedure involves the change of measure. The estimation of parameters

uses Mathematica 7.0, a functional programming based on algebraic computer

systems. The model is applied to the DNA

sequence. The estimated parameters are

used to calculate the expectation of DNA sequence. The result depends on the

decision of the initial value. There should be another study for determining the initial

value which gives the optimal result.

(14)

NURMAILY.

Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA. Di

bawah bimbingan

BERLIAN SETIAWATY

dan

N.K. KUTHA ARDANA.

Setiap kejadian berkaitan erat dengan penyebab kejadian. Jika penyebab kejadian

tersebut tidak diamati secara langsung dan membentuk rantai Markov, maka

pasangan kejadian dan penyebabnya dapat dimodelkan dengan model Hidden

Markov (Hidden Markov Model, HMM).

Semua proses didefinisikan pada ruang peluang

Ω

, ,

. Misalkan

;

adalah rantai Markov dengan state berhingga yang bersifat homogen dan diasumsikan

tidak diamati secara langsung, sedangkan

;

adalah proses

observasinya. Pasangan proses stokastik

,

merupakan model Hidden

Markov.

Model

Hidden

Markov (Elliot et al. 1995) yang digunakan pada karya ilmiah ini

adalah

+

_Y _CX _W , untuk

di mana

, , … ,

,

, , ,

,

A

dan

C

merupakan

matriks peluang transisi dengan

dan

,

yang

memenuhi

∑ 1, , dan ∑ 1, .

dan

memenuhi

_| _, _|

_| _diag _diag

_diag _diag _.

Jika

, maka vektor

, , … ,

merupakan nilai harapan

dari

, yaitu

dan untuk

ergodic memenuhi

dan

∑

1

.

Parameter yang digunakan pada model di atas adalah

, 1

,

, 1

.

Akan ditentukan parameter baru dengan menggunakan algoritme EM

, 1

,

, ̂

, 1

,

(15)

∑

,

_,

∑

_,

,

.

2.

Pendugaan Banyaknya Lompatan

=

,

Penduga banyaknya lompatan adalah

_, ₁

∑

_,

,

.

Penduga smoother banyaknya lompatan adalah

_,

∑

_,

,

.

3.

Pendugaan Lamanya Waktu Kejadian

,

Penduga lamanya waktu kejadian adalah

_, ∑ _, , , _.

Penduga smoother lamanya waktu kejadian adalah

_, ∑ _, , .

4.

Pendugaan untuk Proses Observasi

∑

,

.

Penduga untuk proses observasi adala

,

∑

,

.

Penduga smoother untuk proses observasi adalah

_,

∑

_,

,

.

Dari pendugaan rekursif dapat ditentukan parameter model sebagai berikut

,

1

,

.

̂

,

1

, 1

.

Nilai Harapan

adalah

|

∑ ∑

1 1 .

Model Hidden Markov diskret di atas diaplikasikan pada perubahan urutan basa DNA

pada spesies

Aspergillus niger

, dengan

N = 2. Dalam perkembangan lebih lanjut,

dibuat suatu program komputasi yang berbasis pemprograman fungsional untuk

menyelesaikan masalah tersebut. Software yang digunakan adalah Mathematica 7.0.

Hasil yang di peroleh pada penelitian ini sangat bergantung pada penentuan nilai

awal. Sampai saat ini hasil yang diperoleh belum cukup baik, karena belum

ditemukan cara untuk menentukan nilai awal yang paling baik sehingga hasil yang

diperoleh optimal.

(16)

© Hak Cipta milik IPB, tahun 2009 Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah

b. Pengutipan tidak merugikan kepentingan yang wajar IPB

(17)

APLIKASINYA PADA DNA

N U R M A I L Y

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2009

(18)

(19)

Disetujui Komisi Pembimbing

Dr. Berlian Setiawaty, M.S. Ir. N. K. Kutha Ardana, M.Sc. Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Prof, Dr. Ir. Khairil A. Notodiputro, M.S.

(20)

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala rahmat dan karunia-Nya sehingga tugas akhir yang berjudul “Kajian Model Hidden Markov Diskret dan Aplikasinya pada DNA” ini bisa terselesaikan sebagai salah satu syarat untuk menyelesaikan pendidikan pada Program Studi Matematika, Sekolah Pascasarjana Institut Pertanian Bogor.

Terimakasih yang mendalam penulis sampaikan kepada:

1. Dr. Berlian Setiawaty, M.S. dan Ir. N. K. Kutha Ardana, M.Sc. selaku pembimbing yang telah memberikan bimbingan dan motivasinya.

2. Dr. Ir. Wayan Mangku, M.Sc. selaku penguji yang telah memberikan saran dan kritiknya.

3. Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB.

4. Seluruh keluarga atas segala dukungan, doa dan kasih sayangnya.

5. Mahasiswa S2 Matematika Terapan IPB angkatan 2007, serta semua pihak yang telah membantu penulis.

Penulis menyadari bahwa tugas akhir ini masih begitu banyak kekurangan. Dengan segala keterbatasan yang ada, semoga tugas akhir ini bermanfaat.

(21)

Penulis dilahirkan di Banda Aceh pada tanggal 21 Mei 1971 dari pasangan Bapak Rusli Tgk. Ali (Alm) dan Ibu Nurjannah. Penulis merupakan anak ketiga dari lima bersaudara.

Pendidikan sarjana ditempuh di Program Studi Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas Syiah Kuala Banda Aceh, lulus pada tahun 1996 dan pada tahun 2007 penulis diberi kesempatan melanjutkan studi di Program Studi Matematika Terapan, Sekolah Pascasarjana Institut Pertanian Bogor dengan beasiswa dari Departemen Agama Republik Indonesia.

(22)

DAFTAR ISI ……… xii

DAFTAR GAMBAR ……….. xiv

DAFTAR LAMPIRAN ………... xv

BAB 1 PENDAHULUAN

1.1 Latar Belakang ………... 1

1.2 Tujuan Penelitian ……….... 3

BAB 2 LANDASAN TEORI

2.1 Pengantar Teori Peluang ………... 4

2.2 Rantai Markov ……….... 10

2.3 Ruang Hasil Kali Dalam ………..

13

BAB 3 MODEL

HIDDEN

MARKOV

3.1

State

dan Proses Observasi dalam waktu diskret ………

15

3.2 Perubahan Ukuran ………...

21

3.3 Pendugaan Rekursif ……….

29

3.4 Pendugaan Parameter ………..

38

3.5 Nilai Harapan

……….. 47 3.6 Algoritme Pendugaan Parameter ………... 47 BAB 4 APLIKASI MODEL HIDDEN MARKOV DISKRET PADA DNA

4.1 DNA Sebagai Materi Genetik ………. 50 4.2 Data Input DNA ……….. 52 4.3 Aplikasi Model Hidden Markov Diskret pada DNA ……….. 53 4.4 Hasil Komputasi ………

54

BAB 5 KESIMPULAN DAN SARAN

5.1 Kesimpulan ………...

58

5.2 Saran ……….

58

DAFTAR PUSTAKA ………. 59

(23)

(24)

Halaman

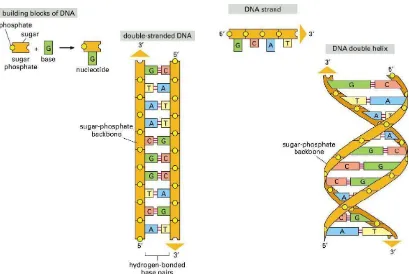
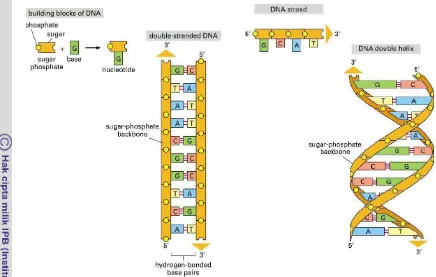
1 Pembentukan secara skematik struktur dsDNA dari gula fosfat

sebagai backbone dan basa nukleotida (A). Bentuk skematik

double-helix DNA (B)………

52

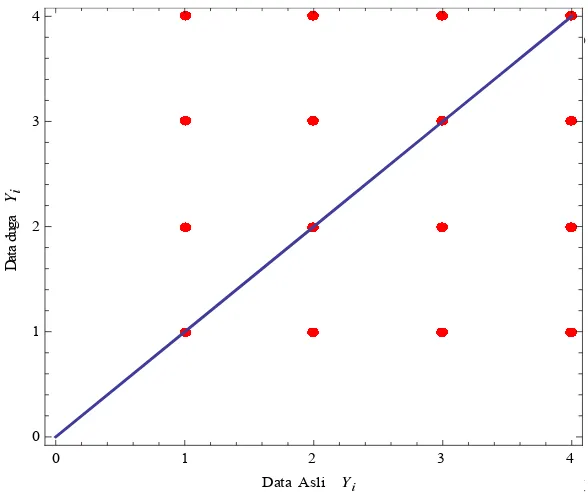
2 Grafik distribusi nilai dugaan urutan DNA menggunakan penduga

smoother

untuk 2 penyebab kejadian (

N =

2). Banyaknya data,

T

= 1000. Nilai awal

. 1

.

. 9

. 4 ,

.1

.

. 9

.

.4

.

.4

. 9

dan

.49

. 1

..………...

55

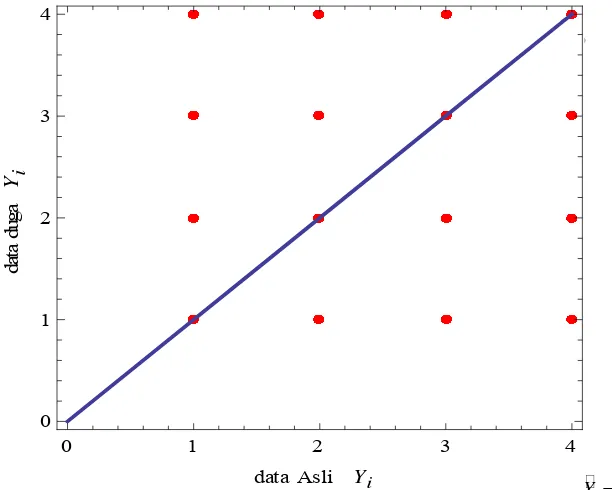
3

Grafik distribusi nilai dugaan urutan DNA menggunakan penduga

smoother

untuk 2 penyebab kejadian (

N =

2). Banyaknya data,

T

= 1000. Nilai awal

.

,

.

.1

.

.4

dan

.

(25)

DAFTAR LAMPIRAN

Halaman

1

Bukti Teorema 3.3.5 ………... 61

2

Program 1...

66

3

Program 2...

72

4

Tabel nilai harapan model dari Program 1...

78

(26)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Dalam kehidupan sehari-hari banyak fenomena yang dapat dimodelkan dengan proses

stokastik. Setiap kejadian berkaitan erat dengan penyebab kejadian tersebut. Jika

penyebab kejadian tersebut tidak diamati secara langsung dan membentuk rantai

Markov, maka pasangan kejadian dan penyebabnya dapat dimodelkan dengan model

Hidden

Markov (

Hidden

Markov

Model

, HMM).

Misalkan

;

adalah penyebab kejadian yang tidak diamati secara langsung

dan membentuk rantai Markov yang bersifat homogen, sedangkan

;

merupakan proses observasi, maka pasangan

,

merupakan

Hidden

Markov

Model

. Untuk

dan

peubah acak diskret maka pasangan

,

merupakan

Hidden

Markov

Model

diskret.

Karakteristik dari Model

Hidden

Markov dicirikan oleh parameter-parameternya,

antara lain berupa matriks peluang transisi. Parameter tersebut diduga melalui

pendugaan ulang parameter dengan menggunakan algoritme

Expectation

Maximization

(EM), sehingga diperoleh parameter model dalam bentuk pendugaan

rekursif. Pendugaan rekursif ini nantinya dapat dievaluasi kembali dengan

menggunakan parameter atau mungkin dengan data yang baru.

Aplikasi Model

Hidden

Markov diskret sudah banyak dikembangkan pada berbagai

bidang antara lain, di bidang biologi yaitu “Penerapan

Hidden

Markov Model dalam

Prediksi Gen Organisme Prokariotik” (Hermanto, 2007), di bidang kebahasaan yaitu

“Penggunaan

Hidden

Markov Model untuk Kompresi Kalimat” (Wibisono,2008),

”Sistem Pengenalan Bicara dengan Menggunakan Sistem

Hidden

Markov Model”

(Hasymi,1996), di bidang teknologi komunikasi yaitu “Algoritma Viterbi dalam

Metode HMM pada teknologi Speech Recognition” (Irfani, 2007),”Selecting

Hidden

(27)

2008), di bidang teknik yaitu “Aplikasi Pengenalan Wicara HMM untuk Kendali

Robot PDA” (Bachtiar, 2007), “Computational Issues in Parameter Estimation for

Stationary

Hidden

Markov Models” (Bulla dan Berzel, 2008), “Kajian

Hidden

Markov Diskret dan Aplikasinya pada Harga Gabah Kering Panen” (Jamal, 2008),

di bidang budaya yaitu “Pengenalan Karakter Mandarin Secara On-Line dengan

Menggunakan

Hidden

Markov Models” (Hadi, 2005).

Dalam tesis ini akan dibahas aplikasi Model

Hidden

Markov diskret Elliott

et al

.

1995 yang telah dikaji oleh Jamal (2008). Model ini diaplikasikan untuk

menggambarkan struktur urutan DNA pada spesies Aspergillus niger

.

Dengan

menggunakan data urutan DNA pada spesies Aspergillus niger

,

maka dapat diduga

parameter modelnya. Sebelum melakukan pendugaan parameter, terlebih dahulu

dilakukan perubahan ukuran peluang yang kemudian diinterpretasikan kembali

dengan menggunakan peluang asal. Perubahan ukuran peluang ini dibatasi oleh

turunan Radon-Nykodim.

Dalam ukuran peluang yang baru, dilakukan pendugaan parameter melalui pendugaan

ulang parameter. Hasilnya berupa pendugaan rekursif di antaranya penduga untuk

state

, penduga untuk banyaknya loncatan, penduga lamanya rantai Markov berada

pada suatu

state

tertentu dan penduga proses observasi. Pendugaan rekursif ini

kemudian digunakan untuk menentukan parameter dengan menggunakan algoritme

Expectation Maximization

(EM ).

Dalam perkembangan lebih lanjut, dibuat suatu program komputasi yang berbasis

pemprograman fungsional untuk menyelesaikan masalah Model

Hidden

Markov

diskret.

Software

yang digunakan adalah

Mathematica

7.0. Keuntungan

(28)

1.2 Tujuan Penelitian

Tujuan dari penelitian ini adalah

1.

Mengkaji Model

Hidden

Markov diskret (Elliot

et al

. 1995).

2.

Melakukan pendugaan parameter melalui pendugaan ulang parameter,

a.

Pendugaan untuk

state

,

b.

Pendugaan untuk banyaknya loncatan,

c.

Pendugaan lamanya rantai Markov berada pada suatu

state

,

d.

Pendugaan proses observasi.

(29)

4

2.1 Pengantar Teori Peluang

Definisi 2.1.1 Percobaan Acak (Ross 1996)

Dalam suatu percobaan seringkali dilakukan pengulangan yang biasanya dilakukan

dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat

diketahui, namun hasil pada percobaan berikutnya tidak dapat diketahui dengan tepat.

Percobaan seperti ini, yang dapat diulang dalam kondisi yang sama, disebut

percobaan acak.

Definisi 2.1.2 Ruang Contoh dan Kejadian (Ghahramani 2005)

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut

Ruang

contoh

dan dinotasikan dengan

Ω

. Suatu kejadian

A

adalah himpunan bagian dari

Ω

.

Definisi 2.1.3 Medan-

σ

(Ghahramani 2005)

Medan-

σ

adalah himpunan yang anggotanya merupakan himpunan bagian dari

Ω

yang memenuhi:

1

;

2 Jika

, ,

maka

∞

;

3 Jika

maka

.

Definisi 2.1.4 Ukuran Peluang (Ghahramani 2005)

Misalkan

adalah

medan-

σ

dari ruang contoh

Ω

.

Ukuran Peluang

adalah suatu

fungsi

:

,1

pada

Ω,

yang memenuhi:

1

,

;

(30)

3 Jika

, ,

adalah himpunan yang saling lepas yaitu

A

_i

∩

A

_j

=

φ

untuk

setiap pasangan

i≠ j

, maka

∑

∞ = ∞ =

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1 1

)

(

i i i

i

P

A

P

U

. Pasangan

Ω, ,

) disebut

ruang

peluang.

Definisi 2.1.5 Kejadian Saling Bebas (Grimmet dan Stirzaker 2001)

Kejadian

A

dan

B

dikatakan saling bebas jika

P(A∩B)=P(A)P(B).

Secara umum,

himpunan kejadian

{

A

_i

:

i

∈

I

}

dikatakan saling bebas jika

∏

∈ ∈

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

J i i J i

i

P

A

P

I

(

)

untuk setiap himpunan bagian berhingga dari

J

dari

I

.

Definisi 2.1.6 Peluang Bersyarat (Ghahramani 2005)

Misalkan

Ω, ,

) adalah ruang peluang dan

,

maka peluang

A

dengan

syarat

B

didefinisikan sebagai

|

.

Definisi 2.1.7 Peubah Acak (Grimmet dan Stirzaker 2001)

Misalkan

Ω

adalah ruang contoh dan adalah

medan-

σ

dari

Ω. Suatu peubah acak

X

adalah

fungsi

: Ω

dengan

{

ω

∈

Ω

:

X

(

ω

)

∈

A

}

∈

untuk setiap

.

Definisi 2.1.8 Peubah Acak Diskret (Grimmet dan Stirzaker 2001)

Peubah acak

X

dikatakan diskret jika nilainya hanya pada himpunan bagian tercacah

(31)

Definisi 2.1.9 Fungsi Sebaran (Grimmet dan Stirzaker 2001)

Fungsi sebaran dari suatu peubah acak

X

adalah

:

,1 ,

yang didefinisikan

oleh

.

Definisi 2.1.10 Fungsi Kerapatan Peluang (Grimmet dan Stirzaker 2001)

Misalkan

Ω, ,

adalah ruang peluang. Fungsi kerapatan peluang dari peubah acak

diskret

X

adalah suatu fungsi

p

:

S

→

[ ]

0

,

1

yang didefinisikan oleh

)

(

)

(

x

P

X

x

p

_X

=

untuk setiap

x

∈

S

.

Definisi 2.1.11 Fungsi Kerapatan Peluang Bersama Dua Peubah Acak diskret

dan Marginal (Grimmet dan Stirzaker 2001)

Misalkan

Ω, ,

adalah ruang peluang. Fungsi kerapatan peluang bersama dari

peubah acak diskret

X

dan

Y

adalah suatu fungsi

p

:

S

×

S

→

[ ]

0

,

1

yang didefinisikan

oleh

p

_XY

(

x

,

y

)

=

P

(

X

=

x

,

Y

=

y

)

untuk setiap

x,y∈S.

Fungsi kerapatan peluang marginal dari peubah acak

X

dan

Y

adalah berturut-turut

∑

,

∑

, .

Definisi 2.1.12 Fungsi Kerapatan Peluang Bersyarat (Ross 1996)

Jika

X

dan

Y

merupakan peubah acak diskret, maka fungsi kerapatan peluang

bersyarat dari

X

jika diberikan

Y=y

, terdefinisi untuk setiap

y

sedemikian sehingga

P(Y=y)

>0 adalah

(32)

Definisi 2.1.13 Bebas Stokastik Identik (Hogg

et al.

2005)

Misalkan

X

₁

,

X

₂

,...,

X

_n

adalah

n

peubah acak yang memiliki fungsi kerapatan yang

sama yaitu

sehingga

M

dan fungsi kerapatan bersamanya adalah

,

.

Peubah acak

X

₁

,

X

₂

,

K

,

X

_n

disebut bebas

stokastik identik.

Definisi 2.1.14 Nilai Harapan Peubah Acak Diskret (Ghahramani 2005)

Jika

X

adalah peubah acak diskret dengan fungsi kerapatan peluang

)

(

)

(

x

P

X

x

p

_X

=

maka nilai harapan dari

X

adalah

∑

=

x

X

x

xp

X

E

[

]

(

)

.

Definisi 2.1.15 Nilai Harapan Bersyarat (Ghahramani 2005)

Misalkan

X

dan

Y

adalah peubah acak diskret dengan fungsi kerapatan peluang

bersyarat dari

X

dengan syarat

Y=y

adalah

_|

|

, maka nilai harapan bersyarat

dari

X

dengan syarat

Y=y

adalah

|

∑

|

.

Definisi 2.1.16 Fungsi Indikator (Cassela dan Berger 1990)

Misalkan

A

adalah suatu kejadian pada ruang peluang

Ω, ,

.

Fungsi indikator dari

(33)

1, jika

, jika

.

Definisi 2.1.17 Himpunan

P-Null

(Grimmet dan Stirzaker 2001)

Misalkan

Ω

, ,

adalah ruang peluang. Himpunan

P-Null

Ω:

A,

,

.

Definisi 2.1.18 Ruang Peluang Lengkap (Billingsley 1986)

Ruang peluang

Ω, ,

disebut lengkap, jika

A⊂ B,B∈

,

dan

P(B)=0

maka

.

Definisi 2.1.19 Filtrasi (Grimmet dan Stirzaker 2001)

Misalkan adalah

medan-

σ

dan

, ,

merupakan barisan

submedan-dari

,

disebut

filtrasi

jika

untuk semua

k

∈

.

Definisi 2.1.20 Filtrasi Lengkap (Protter 1995)

Misalkan

Ω, ,

adalah ruang peluang lengkap. Misalkan =

;

adalah

sebuah filtrasi. Jika

memuat semua himpunan

P-Null

di

maka disebut filtrasi

lengkap.

Definisi 2.1.21 Terukur

(Measurable)

Misalkan

X

adalah peubah acak diskret yang terdefinisi pada ruang peluang

Ω, ,

dan

S

adalah ruang

state X

. Jika

{

ω

∈

Ω

;

X

(

ω

)

∈

A

}

∈

untuk setiap

A⊂S,

maka

X

(34)

Definisi 2.1.22

Adapted

Misalkan

Ω, ,

adalah ruang peluang. Barisan peubah acak

;

dikatakan

adapted

terhadap filtrasi {

jika

terukur-

untuk setiap

.

Definisi 2.1.23

Predictable

Misalkan

adalah

filtrasi

. Barisan peubah acak

;

dikatakan

predictable

(terduga), jika

terukur-

untuk setiap

k

.

Definisi 2.1.24 Nilai Harapan Bersyarat (Shreve 2004)

Misalkan

Ω, ,

adalah ruang peluang dan

adalah submedan-

σ

dari

.

Misalkan

X

adalah peubah acak yang terintegralkan pada

Ω, ,

. Maka

|

disebut nilai harapan bersyarat dari

X

jika diketahui , didefinisikan sebagai sebarang

peubah acak

Y

yang memenuhi:

1

Y

terukur- ;

2

∫

YdP

=

∫

XdP

∀

A

∈

A A

,

;

Persamaan

|

dapat ditulis

|

.

Teorema 2.1.25 Nilai Harapan Bersyarat (Billingsley 1986)

Misalkan

X

terintegralkan,

dan

adalah dua medan-

σ

yang memenuhi

,

maka berlaku:

|

| |

| .

Teorema 2.1.26. Sifat-sifat Nilai Harapan Bersyarat (Shreve 2004)

Misalkan

X,Y

, dan

XY

terintegralkan, maka berlaku:

1

|

;

(35)

3

|

| , , skalar

;

4 Jika

X

≥

0

, maka

|

;

5 Jika

Y

terukur- maka

|

.

Definisi 2.1.27. Kontinu Absolut (Billingsley 1986)

Jika

P

dan

_

P

adalah dua ukuran peluang pada

Ω,

. Ukuran peluang

P

dikatakan

kontinu absolut ke ukuran peluang

_

P

jika untuk setiap

A∈F,P(A)=0

mengakibatkan

_

P

(A)=0,

dinotasikan

_

P

<<

. Jika

_

P

<<

dan

P

<<

P

_

maka

kedua ukuran dikatakan ekuivalen dan dinotasikan

.

_

P

P≡

Definisi 2.1.28 Radon-Nikodym (Billingsley 1986)

Jika

P

dan

_

P

adalah dua ukuran peluang pada

Ω,

sedemikian sehingga

,

_

P

<<

maka terdapat peubah acak tak negatif

Λ

sehingga

_

P

=

∫

Λ

A

dP

A

)

(

untuk semua

dinotasikan

=

Λ

.

2.2

Rantai Markov

Definisi 2.2.1 Ruang

State

Misalkan

S

adalah himpunan nilai dari barisan peubah acak, maka

S

disebut ruang

state

.

Definisi 2.2.2 Proses Stokastik (Ross 1996)

Proses stokastik

X

=

;

terdefinisi pada ruang peluang

Ω, ,

adalah

(36)

Definisi 2.2.3 Rantai Markov dengan Waktu diskret (Grimmet dan Stirzaker

2001)

Misalkan

Ω, ,

adalah ruang peluang dan

S

adalah ruang

state.

Proses stokastik

;

dengan ruang

state S

, disebut rantai Markov dengan waktu diskret

jika untuk setiap

k

= {0,1,2,…}, berlaku:

|

,

|

untuk semua kemungkinan nilai dari

i

₀

,

i

₁

,...,

i

_k

,

i

_k₊₁

∈

S

.

Definisi 2.2.4 Matriks Peluang Transisi (Grimmet dan Stirzaker 2001)

Misalkan

X

=

;

adalah rantai Markov dengan

state S

berukuran

N.

matriks transisi

, dengan

|

untuk

S i

j, ∈

adalah matriks peluang transisi dari

X

.

Definisi 2.2.5 Rantai Markov Homogen (Grimmet dan Stirzaker 2001)

Misalkan

X

=

;

adalah rantai Markov dengan ruang

State

S,

dikatakan

homogen jika

|

untuk

j,i∈S.

Definisi 2.2.6 Peluang Transisi

n-step

(

(a(jin))

(Ross 1996)

Misalkan

X

=

adalah rantai Markov dengan ruang

state S.

Peluang transisi

n-step

dari

X

adalah peluang proses berpindah dari

state i

ke

state j

dengan

n

langkah yang didefinisikan oleh:

|

,

, ,

S

.

Definisi 2.2.7

Accessible

(Ross 1996)

Suatu

state j

disebut terakses (

accessible

) dari suatu

state i

, ditulis

i→ j,

jika ada

(37)

Definisi 2.2.8

Communicate

(Ross 1996)

Dua

state i

dan

j

disebut berkomunikasi (

communicate

), ditulis

i↔ j,

jika

state i

dapat diakses dari

state j

dan

state j

dapat diakses dari

state i.

Definisi 2.2.9 Kelas

State

(Ross 1996)

Himpunan tak kosong

S

disebut kelas

state

apabila semua pasangan

state

yang

merupakan anggota dari

S

berkomunikasi satu dengan yang lainnya, serta tidak ada

state

yang merupakan anggota

S

yang berkomunikasi dengan suatu

state

yang bukan

anggota dari

S.

Definisi 2.2.10

Irreducible

(Ross 1996)

Rantai Markov disebut tak tereduksi

(irreducible)

jika hanya terdapat satu kelas

state,

yaitu jika semua

state

-nya berkomunikasi satu dengan yang lainnya.

Definisi 2.2.11

Recurrent

(Ross 1996)

Peluang bahwa suatu proses yang dimulai dari

state i

akan bertransisi ke

state j

∑

∞

.

State i

berulang (

recurrent

) jika

1.

Teorema 2.2.12

Recurrent

(Ross 1996)

State i

berulang (

recurrent

) jika

∑

∞₌

=

∞

0

) ( n

n ii

a

.

Definisi 2.2.13 (Ross 1996)

1

Suatu

state i

disebut memiliki periode

d

jika

d

adalah persekutuan pembagi

(38)

2

Suatu

state

dengan periode = 1 disebut

aperiodic

, sedangkan

state

dengan

periode

≥

2 disebut

periodic

;

3

Suatu

state

disebut berulang positif jika

state

tersebut berulang serta berlaku: jika

proses dimulai dari

state i

, maka nilai harapan dari waktu sampai proses tersebut

kembali ke

state i

adalah bilangan berhingga;

4

Rantai Markov dengan

state

berulang positif dan

aperiodic

disebut

ergodic

.

Teorema 2.2.14 Nilai Harapan Rantai Markov Homogen (Ross 1996)

Misalkan

;

adalah rantai Markov yang

ergodic

dengan ruang

state

S

berukuran

N

dan misalkan

A

merupakan matriks peluang transisi berukuran

N

×

N

dengan

A

=

(

a

_ji

)

dan

|

maka nilai harapan dari

X

dinotasikan dengan

E[X]=

π

yang memenuhi:

π

=

A

dan

1

.

1

∑

=

N

j j

π

2.3

Ruang Hasil Kali Dalam

Definisi 2.3.1 Ruang Vektor (Anton dan Rorres 2004)

V

disebut ruang vektor, jika untuk setiap vektor

u,v,w

∈

V

dan sebarang skalar

k

dan

l

dipenuhi aksioma berikut:

1 Jika

u,v

∈

V

, maka

u+v

∈

V;

2

u+v=v+u;

3

u+

(

v

+

w

)

=(u+v)+w;

4 Ada

0

∈

V

sehingga

0+u=u+0=u

,

∀

u

∈

V

;

5 Untuk

∀

u

∈

V

, ada -

u

∈

V

sehingga

u+(-u)=(-u)+u=0;

6 Jika

k

adalah sebarang skalar dan

u

∈

V

, maka

k u

∈

V

;

(39)

8

(k+l)u=ku+lu;

9

k(lu)=(kl)u;

10

lu=u.

Definisi 2.3.2 Perkalian Dalam (Anton dan Rorres 2004)

Jika u = (

u

₁

,

u

₂

,

K

,

u

_n

) dan v = (

v

₁

,

v

₂

,

K

,

v

_n

) adalah sebarang vektor pada

,

maka

hasil kali dalam

euclied

u.v

didefinisikan oleh:

u.v=

u

1

v

1

+

u

2

v

2

+

K

+

u

_n

v

_n

.

Definisi 2.3.3 Ruang Hasil Kali Dalam (Anton dan Rorres 2004)

Sebuah hasil kali dalam pada ruang vektor real

V

adalah fungsi yang mengasosiasikan

bilangan real

u,v

dengan masing-masing pasangan

vektor

u

dan

v

pada

V

sedemikian sehingga aksioma-aksioma berikut terpenuhi untuk semua

u, v, w

∈

V

dan

skalar

k

.

1.

u,v = v,u

;

2.

u+v,w = u,w + v,w

;

3.

ku,v =k u,v

;

4.

v,v ≥0;

dan

v,v =0

jika dan hanya jika

v =

0.

(40)

BAB III

MODEL

HIDDEN

MARKOV

3.1 State dan Proses Observasi dalam waktu diskret

Semua proses didefinisikan pada ruang peluang Ω, , . Misalkan

; adalah rantai Markov dengan state berhingga yang bersifat

homogen dan diasumsikan tidak diamati secara langsung, sedangkan

; adalah proses observasinya. Pasangan proses stokastik , merupakan model Hidden Markov.

Ruang state dari X adalah , , … , dengan , … , ,1, , … , , yaitu himpunan vektor satuan di , di mana hanya elemen ke-i yang bernilai

1 dan lainnya 0.

Misalkan , , , merupakan medan-σ yang dibangkitkan oleh

, , , dan merupakan filtrasi lengkap yang dibangkitkan oleh .

Karena merupakan rantai Markov homogen, maka berdasarkan sifat rantai

Markov diperoleh

, , ,

.

Lema 3.1.1 [Elliot et al.1995]

Misalkan merupakan peluang transisi dan

merupakan matriks peluang transisi yang memenuhi ∑ 1, maka

| | .

Bukti:

(41)

, , … , .

Sehingga dapat ditulis

.

Jadi

, , … ,

. ■

Didefinisikan

_(3.1)

dengan

| |

|

| | | |

. Sehingga diperoleh persamaan state

. (3.2)

, . Bukti:

Karena , 1, untuk

, untuk ,

maka

, ∑ ,

(42)

Jika , maka vektor , , … , merupakan nilai harapan dari , yaitu dan untuk ergodic memenuhi dan

∑ 1.

Proses state tidak diamati secara langsung namun terdapat proses observasi yaitu

, , ,

di mana bersifat bebas stokastik identik, dan saling bebas. Ruang state dari adalah , , , dengan merupakan vektor satuan di .

Misalkan , , , , , , , merupakan medan-σ dari Ω yang dibangkitkan oleh , , , dan , , , dan merupakan filtrasi lengkap yang dibangkitkan oleh . Misalkan , , , merupakan medan-σ dari Ω yang dibangkitkan oleh , , , dan merupakan filtrasi lengkap yang dibangkitkan oleh , maka diperoleh

, , , , , , ,

.

Misalkan

C

=

(

c

_ji

)

_M_×_N adalah matriks peluang transisi, di mana

| dan memenuhi ∑ 1,1 , 1 ,

maka

| .

Bukti:

Misalkan

X

_k

=

e

_i, maka

| ∑ |

∑

(43)

Sehingga dapat ditulis | .

Jadi | | . ■

Didefinisikan

(3.3)

dengan

| |

| | | | | |

.

Sehingga dapat diperoleh suatu persamaan observasi

. (3.4)

Notasi 3.1.4

Misalkan , 1,

, dan , , , ,

dengan ∑ 1.

Misalkan | . Untuk

X

_k

=

e

_l, maka

| , |

∑ , |

|

,

, , ,

(44)

Sehingga dapat ditulis , | ∑ , .

Jadi , | ∑ , dan

, , , maka

| .

diag diag diag

dan

|

diag diag ,

di mana diag(z) merupakan matriks diagonal yang unsur diagonalnya adalah

vektor z.

Bukti:

dan .

Karena .

,

maka

diag

diag diag(

diag diag diag(

(45)

diag diag diag

dan

|

]

diag diag ,

di mana diag(z) merupakan matriks diagonal yang unsur diagonalnya adalah

vektor z.

Bukti:

dan .

Karena

, maka

diag

diag diag(

diag diag diag(

. ■

Sehingga didapat model hidden Markov Elliot et al. (1995) dalam waktu diskret

dengan ukuran peluang P pada ruang state S sebagai berikut:

, untuk (3.5)

di mana , , A dan C merupakan matriks peluang transisi dengan

(46)

yang memenuhi

∑ 1,

∑ 1, ,

dan memenuhi:

| , |

| diag diag

| diag diag .

3.2 Perubahan Ukuran

3.2.1 Teorema Bersyarat Bayes

Teorema 3.2.1 Teorema Bersyarat Bayes [Elliott et al.1995]

Misalkan Ω, , merupakan ruang peluang, merupakan submedan- dari dan merupakan ukuran peluang lain yang kontinu absolut terhadap P dengan

turunan Radon-Nikodym Λ. Jika adalah sebarang peubah acak terintegralkan dan terukur- , maka berlaku

[ | | |

.

Bukti:

Menurut definisi 2.1.22 harus ditunjukkan:

(i) |

|

terukur-Karena Λ| merupakan nilai harapan dari Λ dengan syarat maka

Λ| terukur- , dan Λ| yang merupakan nilai harapan dari Λ dengan syarat maka Λ| terukur- . Karena |

| merupakan pembagian

fungsi terukur- , maka |

(47)

(ii) | Λ|

Λ| ,

Definisikan

|

| , untuk Λ|

, untuk Λ| ,

maka | . Jadi terukur- .

Akan ditunjukkan

| , .

Ambil sebarang.

Misal : Λ| , sehingga . Maka dari definisi 2.1.22,

Λ| Λ dan Λ , sehingga atau Λ hampir pasti di G.

Selanjutnya : Λ| , maka dapat dituliskan di mana dan , sehingga

|

Λ

Λ Λ . (3.6)

Karena Λ hampir pasti pada , maka

Λ .

Selanjutnya

|

| | |

(48)

Λ

_||

|

Λ|

_||

Λ|

Λ

Λ ,

maka

Λ .

Sehingga persamaan (3.6) menjadi

Λ Λ

Λ

| . Jadi

|

| , . ■

Lema 3.2.2 [Elliott et al.1995]

Jika { merupakan barisan peubah acak yang bisa diintegralkan, maka

| _| |

.

(49)

3.2.2 Perubahan Ukuran

Perubahan ukuran peluang diperoleh dengan mengubah ukuran peluang asal

menjadi peluang baru yang kemudian diinterpretasikan kembali ke dalam peluang

asal. Perubahan ukuran ini dibatasi oleh turunan Radon-Nikodym.

Di bawah ukuran P pada Ω, dan adalah medan- yang dibangkitkan , berlaku:

• X merupakan rantai Markov yang homogen dan memenuhi

, dan | .

• , di mana | dan

merupakan peubah acak yang bergantung pada .

Akan dikontruksikan suatu peluang baru pada Ω, yang kontinu absolut terhadap P. Misalkan ukuran peluang baru pada Ω, yang dibatasi oleh turunan Radon-Nikodym

_Λ_k_.

(

3.7)

Definisikan

∏

, (3.8)

dan

Λ ∏ , (3.9)

di mana 1,

, . Jadi adalah fungsi tak linear dari sehingga dapat

ditulis

∑

. (3.10)

(50)

Bukti:

Berdasarkan definisi (3.8) dan (3.10), diperoleh

| ∏ 1

1 1 1

∑ 1

1 1

1

|

∑ 1

1 1

|

1

1∑ 1

1

1 1

1∑ ₁

1

1.

Di bawah , , , merupakan peubah acak yang bebas stokastik identik yang menyebar seragam dengan peluang 1 pada masing-masing , 1 . Akan dibuktikan : .

Bukti:

Dengan sifat

, | , |

| 1 ,

dan menggunakan nilai harapan di bawah ukuran peluang , Lema 3.2.2 dan Lema 3.2.3, maka

1 [ , | , Λ 1_Λ 1, |

1 |

Λ _Λ1 1, |

(51)

Λ 1 1, |

Λ ₁|

, |

| , (3.12)

berdasarkan (3.11) dan (3.12), diperoleh

1 | , |

∏

, |

∑

, |

|

₁

1

₁ .

Karena 1 , 1, maka . Sehingga

1 1. ■

Sehingga di bawah ukuran pada Ω, akan berlaku:

• merupakan rantai Markov yang homogen dan memenuhi

, dan | .

• Y merupakan barisan peubah acak diskret dengan , , ,

yang bersifat bebas stokastik identik dan menyebar seragam dengan

(52)

Lema 3.2.5 [Elliot et al. 1995]

| .

Bukti:

Berdasarkan Persamaan (3.1), diperoleh

| | ,

|

. ■

| .

Bukti:

Berdasarkan Lema 3.2.5 diperoleh,

| | , |

| |

|

. ■

Akan dikontruksi kembali ukuran peluang P pada Ω, yang kontinu absolut pada dengan turunan Radon-Nikodym Λ sehingga di bawah P, model (3.5) dipenuhi yaitu:

• merupakan rantai Markov homogen yang memenuhi

dan | .

• , di mana | dan

merupakan peubah acak yang bergantung pada . Misalkan

dan

(53)

Untuk menentukan P dari didefinisikan dan Λ yang merupakan invers dari dan Λ , yaitu

∏ , (3.14)

Λ ∏ , (3.15) dan Λ

.

, (3.16) dimana 1

1. (3.17)

Bukti:

1

|

∑ ₁ ₁

|

∑ ₁ ₁

|

∑

₁

1|

∑ ₁ 1 ∑

1. ■

Di bawah ukuran P,

|

.

Bukti:

Dengan menggunakan Lema 3.2.2

(54)

Λ 1 1, |

Λ ₁|

Λ 1 1, |

Λ ₁ |

1 1, |

1 |

,

(3.18)

berdasarkan (3.17) dan (3.18) diperoleh

1| , |

∏ , |

, |

, , |

, |

( 1|

1 .

Sehingga berdasarkan notasi 3.1.4 dapat ditulis,

|

. ■ Dengan , maka

|

.

Sehingga persamaan observasinya dapat ditulis

.

3.3 Pendugaan Rekursif

Untuk melakukan pendugaan parameter, maka dibentuk suatu pendugaan rekursif

(55)

, , , dan merupakan filtrasi yang dibangkitkan oleh , , ,

dan , , , .

Dari subbab 3.2, di bawah ukuran pada Ω, berlaku

, di mana pada ( , memenuhi | , dan { bebas stokastik identik dengan 1 1 , serta dan saling bebas.

Definisikan

Λ , | untuk 1 , , sehingga

∑ ∑ Λ , | Λ ∑ , |

Λ | . (3.19)

Untuk , , , maka Λ | , , Bukti:

Λ | , ∑ Λ | , ∑ Λ | , ∑ Λ | , Λ , |

, . ■

Notasi 3.3.2

Jika , merupakan barisan peubah acak bernilai skalar yang terintegralkan, dinotasikan

(56)

Dengan menggunakan Lema 3.2.2 dan persamaan (3.20) maka

| Λ_Λ

.

(3.21)

Sebagai nilai awal

, di mana 1.

Misalkan 1 1,1, … ,1 . Maka

, 1 ∑ , 1. Akibatnya

, 1 Λ | , 1

Λ , 1 |

, 1 )

. (3.22)

Jika 1 maka dari (3.19), (3.20) dan (3.22) diperoleh 1 , 1

Λ | , 1

Λ , 1 |

[Λ

∑ .

Misalkan proses ; bernilai skalar dan adapted terhadap serta memenuhi

, ,

∑ , , , ,

(57)

di mana , { , , adalah proses predictable terhadap , bernilai skalar, merupakan vektor berdimensi N, dan merupakan vektor

berdimensi M.

Notasi 3.3.3 Jika proses , adapted terhadap , dinotasikan _, Λ | .

Notasi 3.3.4 Untuk penyederhanaan dinotasikan

∏ .

Teorema 3.3.5 [Elliot et al. 1995]

Untuk 1 dengan , , , adalah kolom ke-j dari matriks dan , , , adalah kolom ke-j dari matriks , maka

,

∑ , , , ,

diag Λ , | .

Bukti: (Lampiran 1)

3.3.1 Penduga untuk State

Dengan menggunakan Teorema 3.3.5 dan Lema 3.2.6, ambil

1, , maka penduga untuk state didefinisikan

, 1 , 1 , , ,

(58)

∑ ,

∑ , .

Jadi

, 1

∑ , . (3.23)

Bentuk pendugaan rekursif untuk nilai harapan tak ternormalkan dari , disebut unnormalized smoother, jika diketahui , 1. Bentuk ini dapat diperoleh dengan mengambil , , 1, 1

, , maka dengan menggunakan Teorema 3.3.5 diperoleh

, ∑ , , , ,

diag Λ , | .

∑ , , .

Jadi

_, ∑ _, , . (3.24)

3.3.2 Pendugaan Banyaknya Lompatan

Banyaknya rantai Markov berpindah dari state ke state sampai waktu ke-k didefinisikan sebagai berikut:

=∑ , , .

Dengan menggunakan , maka

=∑ , ,

∑ , , , ,

, ,

, , , )

(59)

, , ,

, , , .

Dan dengan menggunakan Teorema 3.3.5 dan Lema3.2.6 dapat didefinisikan

,

∑ , , , ,

diag Λ , |

∑ , , , , ,

diag Λ , |

∑ , Λ | , , ,

diag Λ , | .

Ambil , , , , , , ,

sehingga diperoleh

,

∑ , Λ , | , , ,

diag Λ , , |

∑ , , , ,

diag Λ , , |

∑ , , ∑ , , ,

diag Λ , , |

∑ , , , , ,

diag Λ , , |

∑ , , , ,

diag Λ , , |

∑ , , , ,

diag Λ , | }

∑ , , , ,

(60)

∑ , , , ,

diag

∑ , , ,

diag

∑ , , , .

Jadi

,

∑ _, , , . (3.25)

Jika ₁ diketahui, maka bentuk unnormalized smoother untuk adalah

Λ | , .

Ambil , , maka dengan menggunakan

Teorema 3.3.5 diperoleh

, ∑ , , . (3.26)

3.3.3 Pendugaan Lamanya Waktu Kejadian

Misalkan banyaknya kejadian rantai Markov X berada pada state ,

1 , sampai waktu ke-k didefinisikan

∑ ,

∑ , ,

, .

Dengan menggunakan Teorema 3.3.5, penduga untuk waktu kejadian dapat

didefinisikan

,

∑ , , , ,

(61)

∑ , , , , ,

diag Λ , |

∑ , Λ | , , ,

diag Λ , | .

Untuk , , , , , diperoleh ,

∑ , Λ , | , , ,

diag Λ , |

∑ , , , ,

∑ , , , , ,

∑ , , ∑ , , ,

∑ , , , , ,

∑ , , , .

Jadi

, ∑ , , , . (3.27)

Bentuk unnormalized smoother untuk jika diketahui adalah .

Ambil , , , maka dengan menggunakan

Teorema 3.3.5 diperoleh

_, ∑ _, , . (3.28)

3.3.4 Pendugaan untuk Proses Observasi

Banyak kejadian berada pada state , 1 , dan berada pada state

, 1 , sampai waktu ke-k, didefinisikan

∑ , , , 1 , 1 , maka

∑ , ,

(62)

, ,

, , .

Dengan menggunakan Teorema 3.3.7 dan Lema 3.3.2, dapat didefinisikan

,

∑ , , , ,

diag Λ , |

∑ , , , , ,

diag Λ , |

∑ , , Λ , | ,

diag Λ , | .

Untuk , , , , diperoleh ,

∑ , , Λ , , | ,

diag Λ , |

∑ , Λ , , | ,

∑ , ,

∑ Λ , , | ,

∑ , ,

Λ , , | ,

∑ , , , , , ,

∑ , , ∏ , , , ,

∑ , , , , .

Jadi

,

(63)

Bentuk unnormalized smoother untuk dan memilih ,

1 , , maka dengan menggunakan Teorema 3.3.7 diperoleh

_, ∑ _, , . (3.30)

3.4 Pendugaan Parameter

Pendugaan parameter model Hidden Markov dilakukan dengan pendugaan ulang

parameter. Metode yang digunakan adalah algoritme EM dan hasilnya berupa

parameter dalam bentuk pendugaan rekursif.

3.4.1 Maksimum Likelihood

Misalkan , Θ adalah himpunan ukuran peluang yang terdefinisi pada

Ω, dan kontinu absolut terhadap . Misalkan , fungsi Likelihood yang digunakan untuk menghitung penduga parameter berdasarkan informasi

adalah

| ,

dan Maximum Likelihood Estimation (MLE) didefinisikan oleh

arg max .

3.4.2 Expectation Maximization

Langkah-langkah Excpectation Maximization (EM) adalah:

1. Set nilai awal parameter , dengan . 2. Set = dan hitung . , dengan , = log | . 3. Cari arg max , .

(64)

Parameter yang digunakan pada model (3.5) adalah

, 1 , , , 1 , 1 .

Akan ditentukan parameter baru dengan menggunakan algoritme EM

, 1 , , ̂ , 1 , 1 .

3.4.3 Pendugaan Parameter

Notasi 3.4.3.1

Untuk proses , , ditulis | . Dalam waktu diskret, kondisi ini mendefinisikan -optional projection.

Untuk menggantikan parameter dengan pada rantai Markov ,

didefinisikan oleh

∏

_, , , , Λ ∏ dan Λ .

Lema 3.4.3.2 [Elliot et al. 1995]

Di bawah ukuran peluang dan misalkan , maka , | .

Bukti:

, | _Λ1, Λ 1

1

1, Λ 1

Λ ₁

Λ ₁, ₁

Λ ₁

1, 1

1

1, ∏ 1,

, , 1

(65)

1, ∏ 1 1,

∏ ₁ 1,

1, ∑ 1 1,

∑ ₁ ₁,

1,

∑ ₁ ₁,

1,

∑ ₁ ₁,

1,

∑ ₁ ₁,

∑ ₁ ₁ ,

∑ ₁ ∑ ₁ ₁ ,

1

∑ ₁ ₁

∑ ₁

∑ ₁ ,

karena ∑ 1, maka

, | . ■

Teorema 3.4.3.3 [Elliot et al. 1995]

Penduga baru untuk parameter pada waktu pengamatan diberikan oleh

(66)

Bukti:

log Λ log ∏ ∏ , , ,

∑ , ∑ , , log log

∑ , log log

∑ , log ∑ , log

∑ , log ,

di mana bebas terhadap dengan ∑ _, log , sehingga

logΛ | ∑ , log

∑ , log |

∑ , log | |

∑ , log . (3.32)

Untuk memenuhi ∑ 1 dengan

∑ , ∑ , ∑ ∑ ∑ ,

∑ ∑

∑ 1

(3.33)

dan

∑ , . (3.34)

Akan ditentukan yang memaksimumkan persamaan (3.32) sebagai fungsi

objektif dengan persamaan (3.34) sebagai fungsi kendala. Dengan menggunakan

pengali lagrange diperoleh

, ∑ _, log ∑ _, .

Turunan pertama terhadap dan , serta dan sehingga

(67)

(3.35)

∑ _,

∑ _, . (3.36)

Dari persamaan (3.35) diperoleh

.

(3.37)

Substitusikan persamaan (3.37) ke persamaan (3.36)

∑ ,

1 _∑ _∑ _, _,

,

1 _∑ _∑ _∑ _, _,

1 _∑ _∑ _, 1 _∑ ₁ 1

1,

(68)

.

Jadi

.

3.4.4 Penduga Parameter ̂

Untuk mengganti parameter dengan ̂ pada matriks , didefinisikan

∏

̂ , , , Λ ∏ dan Λ .

Lema 3.4.4.1 [Elliott et al.1995]

Di bawah ukuran dan misalkan = , maka

, | ̂ .

Bukti:

, | ,

, |

|

, ∏ ∏ , 1,

∏ ∏ , 1,

, ∏ 1,

∏ 1,

, ∑ ₁,

(69)

1,

∑ ₁,

1,

∑ ₁,

∑ ₁ ,

∑ ∑ ₁ ,

1

∑ ₁

∑

,

karena ∑ ̂ 1, maka

, | ̂ .

Teorema 3.4.4.2 Penduga maksimum likelihood untuk parameter ̂ pada waktu pengamatan diberikan oleh

̂ .

Bukti:

log Λ log ∏ ∏ ∏ , ,

∑ ∑ ∑ , , log ̂ log

∑ ∑ log ̂ log

∑ ∑ log ̂ ∑ ∑ log

(70)

di mana bebas terhadap ̂ dengan ∑ ∑ log , sehingga

log Λ ∑ ∑1 1 log ̂

∑ ∑1 1 log ̂ |

∑ ∑ log ̂1 1 |

∑ ∑ log ̂ , (3.38)

Untuk ̂ memenuhi ∑ ̂ 1, maka

∑ ∑ ∑ , ̂ ∑ ∑ ∑ , ̂

∑ ∑ ̂

∑ 1

sehingga

∑ ∑ ̂ . (3.39)

Dengan menggunakan pengali lagrange, dapat ditentukan ̂ yang memaksimumkan persamaan (3.38) sebagai fungsi objektif dengan persamaan

(3.39) sebagai fungsi kendala, sehingga diperoleh

. ̂, ∑ ∑ log ̂ ∑ ∑ ̂ .

Dengan menggunakan turunan pertama terhadap ̂ dan , serta

̂ dan

sehingga diperoleh

̂ ̂

̂ . (3.40)

∑ ∑ ̂

(71)

Dari persamaan (3.40) diperoleh

̂

.

(3.42)

Substitusikan persamaan (3.42) ke persamaan (3.41)

∑ ∑ ̂

∑ ∑

∑ ∑ ∑

1 1 1 1, ,

∑ ∑ ∑

1 1 1 1, ,

∑ ∑

1 1 ,

1 _∑ ₁ 1

1,

sehingga ̂ , 1 , 1 optimum bila

̂ 1

̂ . Jadi

(72)

3.5 Nilai Harapan

Nilai Penduga terhadap adalah

|

∑ |

∑ ∑ , |

∑ ∑ | |

∑ ∑ |

∑ ∑ .

3.5 Algoritme Pendugaan Parameter

Diketahui parameter model berbentuk

, 1 , , , 1 , 1 .

Akan ditentukan parameter baru

, 1 , , ̂ , 1 , 1 ,

yang memaksimumkan pseudo-loglikelihood bersyaratnya. Algoritme untuk

menduga parameter tersebut diperoleh dari Setiawaty dan Kristina (2005) dengan

beberapa penambahan langkah sebagai berikut:.

Langkah 1:

Tetapkan N (banyaknya state penyebab kejadian), T (banyaknya data) dan input

data .

Langkah 2:

Untuk N = 1 sampai dengan kriteria terpenuhi, maka tentukan nilai awal untuk:

(73)

Langkah 3:

Lakukan untuk 1 sampai dengan .

1 Tetapkan nilai awal untuk proses pendugaan

: vektor unit di

.

2 Lakukan untuk sampai dengan 1 a. Hitung penduga rekursif smoother

_, ∑ _, , . _, ∑ _, , . _, ∑ _, , . _, ∑ _, , . di mana

∏ _,

, 1 dengan 1 1,1, … ,1 . b. Hitung penduga parameter

1

̂ 1 . c. Tuliskan

1 . d. Tentukan 1 dari

(74)

3. Berikan nilai

1 1

1 .

4. Ulangi 1 sampai 3 untuk l berikutnya.

Langkah 4

Hitung nilai ∑ ∑ .

Langkah 5

Hitung nilai

1

∑

.

Langkah 6

(75)

BAB IV

APLIK