i
ANALISIS KESULITAN SISWA MEMECAHKAN
MASALAH FISIKA BERBENTUK GRAFIK DENGAN
TES DIAGNOSTIK
Skripsi
disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Pendidikan
Program Studi Pendidikan Fisika
oleh Anton Setyono
4201412081
JURUSAN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI SEMARANG
iv
MOTTO
Boleh jadi kamu membenci sesuatu, padahal ia amat baik bagi kamu. Dan boleh jadi kamu mencintai sesuatu, padahal ia amat buruk bagi kamu. Allah Maha mengetahui sedangkan kamu tidak mengetahui”
(Al-Baqarah: 216)
Bermimpilah seolah - olah anda hidup selamanya. Hiduplah seakan-akan inilah hari terakhir anda.
(James Dean)
PERSEMBAHAN
Untuk Ayah, Ibu, Mbak, dan Mas yang selalu mendoakan dan mendukungku, serta memberiku semangat untuk terus belajar.
Untuk teman – teman Pendidikan Fisika angkatan 2012
v
KATA PENGANTAR
Puji syukur kehadirat Allah SWT atas limpahan rahmat dan karunia-Nya, sehingga penulisan skripsi yang berjudul “Analisis Kesulitan Siswa Dalam Memecahkan Masalah Fisika Berbentuk Grafik Dengan Tes Diagnostik” dapat selesai.
Saya menyadari bahwa skripsi ini tidak akan terselesaikan dengan baik tanpa adanya partisipasi dan bantuan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis ingin menyampaikan ucapan terima kasih kepada:
1. Prof. Dr. Fathur Rokhman, M.Hum., rektor Universitas Negeri Semarang; 2. Prof. Dr. Zaenuri, S.E. M.Si. Akt., dekan Fakultas Matematika dan Ilmu
Pengetahuan Alam, Universitas Negeri Semarang;
3. Dr. Suharto Linuwih, M.Si., ketua Jurusan Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Negeri Semarang;
4. Dr. Sunyoto Eko Nugroho, M.Si. , dosen pembimbing I yang telah membimbing, memberikan arahan, saran, motivasi, dan nasehat dalam penyusunan skripsi;
5. Dr. Ian Yulianti, S.Si. M. Eng., dosen pembimbing II yang telah membimbing, memberikan arahan, saran, motivasi, dan nasehat dalam penyusunan skripsi; 6. Dr. Achmad Sopyan, M.Pd, selaku dosen wali dan seluruh dosen Jurusan
Fisika UNNES yang telah memberikan bekal ilmu kepada penulis selama menempuh studi;
7. Hartati,M.Pd., kepala SMP N 06 Petarukan yang telah memberikan ijin penelitian kepada penulis;
8. Ima Purwo S.,S.Pd., guru kelas VIII SMP N 06 Petarukan yang telah berkenan membantu dan bekerjasama dalam penelitian;
vi
vii
ABSTRAK
Setyono, A. 2016. Analisis Kesulitan Siswa dalam Memecahkan Masalah Fisika Berbentuk Grafik. Skripsi. Jurusan Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Negeri Semarang. Pembimbing Utama: Dr. Sunyoto Eko Nugroho, M.Si. Pembimbing Pendamping: Dr. Ian Yulianti, S.Si. M. Eng.
Kata Kunci: grafik, tes diagnostik, kesulitan belajar, pemecahan masalah.
viii
DAFTAR ISI
Halaman
HALAMAN JUDUL ... i
HALAMAN PERNYATAAN... ii
HALAMAN PENGESAHAN... iii
MOTTO DAN PERSEMBAHAN... iv
KATA PENGANTAR... v
ABSTRAK... vi
DAFTAR ISI…... viii
DAFTAR TABEL... ix
DAFTAR GAMBAR... x
DAFTAR LAMPIRAN... xi
BAB 1. PENDAHULUAN... 1
1.1Latar Belakang... 1.2Rumusan Masalah……… 1.3Pembatasan Masalah... 1.4Tujuan Penelitian... 1.5Manfaat Penelitian... 1.6Penegasan Istilah... 1.6.1 Tes Dignostik..……… 1.6.2 Kemampuan Pemecahan Masalah…...………... 1.6.3 Grafik.………. 1.7Sistematika Penulisan... 1 3 4 4 4 5 5 5 6 6 2. TINJAUAN PUSTAKA... 8
ix
2.1.1 Pengertian Pemecahan Masalah ..……….. 2.1.2 Faktor- faktor Penghambat Pemecahan Masalah…………... 2.2 Kesulitan Masalah... 2.3 Evaluasi…... 2.3.1 Pengertian Evaluasi ..……….
2.3.2 Tes Diagnostik……..……….
2.4 Grafik………..………
2.4.1 Kemampuan Pemecahan Masalah Fisika Berbentuk Grafik .. 2.6 Kerangka Berfikir...
8 9 11 13 13 15 18 19 20
3. METODE PENELITIAN... 22 3.1 Lokasi dan Waktu Penelitian ... 3.2 Subjek Penelitian ... 3.3 Desain Penelitian... 3.3.1 Langkah Langkah Penelitian….……….... 3.4 Metode Pengumpulan Data...
3.4.1 Metode Tes……….
3.4.2 Metode Wawancara..……….
3.5 Analisis Tes Ujicoba... 3.5.1 Uji Validitas Butir Soal ….……… 3.5.2 Uji Realibilitas Butir Soal ……….……… 3.5.3 Uji Kesukaran Butir Soal …….……….……… 3.5.4 Uji Daya Beda Butir Soal ……….……… 3.6 Analisis Data...
3.6.1 Analisis Kemampuan Pemecahan Masalah Fisika
Berbentuk Grafik………...
3.6.2 Analisis Profil Kesulitan Siswa……….………
22 22 22 23 25 25 25 26 26 27 28 29 29 29 30
4. HASIL DAN PEMBAHASAN………..….. 4.1 Hasil Penelitian………..…...
x
4.1.2 Profil Kesulitan Siswa…..………... 4.1.2.1 Analisis Kesulitan Siswa Berdasarkan Pencapaian
KKM……….
4.1.2.2 Analisis Kesulitan Siswa Berdasarkan Penguasan Pengetahuan Prasyarat….…….……… 4.1.2.3 Analisis Kesulitan Siswa Berdasarkan Profil
Materi……… 4.1.2.4 Analisis Kesulitan Siswa Berdasarkan
Miskonsepsi……… 4.1.2.5 Analisis Kesulitan Siswa Berdasarkan Tahapan
Pemecahan Masalah……….……….
4.2 Pembahasan………...
4.2.1 Kemampuan Pemecahan Masalah Berbentuk Grafik …..….. 4.2.1.1 Interpretasi Grafik………..………. 4.2.1.2 Kemampuan Memprediksi...… ………. 4.2.1.3 Kemampuan Transformasi…...…….………. 4.2.2 Profil Kesulitan Siswa……….…………...
4.2.2.1 Profil Kesulitan Siswa Berdasarkan Pencapaian
KKM……….
4.2.2.2 Profil Kesulitan Siswa Berdasarkan Penguasan Pengetahuan Prasyarat….………….…………...… 4.2.2.3 Profil Kesulitan Siswa Berdasarkan Profil
Materi…………..……… 4.2.2.4 Profil Kesulitan Siswa Berdasarkan
Miskonsepsi………...
4.2.2.5 Profil Kesulitan Siswa Berdasarkan Tahapan Pemecahan Masalah……….. 4.3 Keterbatasan Penelitian………...
33 33 34 35 36 38 39 39 39 40 41 42 42 44 46 47 48 49
5. PENUTUP………...
5.1 Simpulan………...
xi
5.2 Saran………. 51
DAFTAR PUSTAKA... 52
xii
DAFTAR TABEL
Tabel Halaman 3.1Tabel Pelaksanaan Penelitian……..……… 3.2Kriteria Validitas Soal Ujicoba Instrumen ….………..………. 3.3Kriteria Reliabilitas Soal…..………... 3.4Kriteria Tingkat Kesukaran Butir Soal..………. 3.5Kriteria Tingkat Daya Beda Butir Soal…..………... 3.6Kriteria Kemampuan Pemecahan Masalah Berbentuk Grafik ………... 3.7Kriteria Kesulitan Siswa ……….………... .
xiii
DAFTAR GAMBAR
Gambar Halaman 2.1 Kerangka Berfikir ………... 3.1 Desain Penelitian... 4.1 Kemampuan Pemecahan Masalah Berbentuk Grafik…..……… 4.2 Profil Kesulitan Berdasarkan Pencapaian KKM ...……..…. 4.3 Profil Kesulitan Siswa Berdasarkan Penguasaan Pengetahuan
Prasyarat………. 4.4 Profil Kesulitan Siswa Terhadap Profil Materi …….……… 4.5 Grafik Hubungan Jarak Terhadap Waktu ………..… 4.6 Hasil Pekerjaan Siswa Yang Berkaitan Dengan Miskonsepsi ..……. 4.7 Profil Kesulitan Siswa Berdasarkan Tahapan Pemecahan
Masalahnya……….. 4.8 Hasil Pekerjaan Siswa Dalam Menentukan Percepatan ………. 4.9 Hasil Pekerjaan Siswa Dalam Memperkirakan Posisi Benda………. 4.10 Hasil Pekerjaan Siswa Yang Menunjukkan Kurangnya Penguasaan Konsep……….. 4.11 Hasil Pekerjaan Siswa Yang Menunjukkan Kurangnya Pengetahuan
Prasyarat………... 4.12 Hasil Pekerjaan Siswa Yang Menunjukkan Kesulitan Dalam Operasi Hitung………...
21 24 32 34
35 36 37 37
38 39 41
43
45
xiv
DAFTAR LAMPIRAN
Lampiran Halaman 1. Daftar Kode Peserta Ujicoba ……….. 2. Daftar Kode Peserta Penelitian ………..……
3. Analisis Hasil Uji Coba………..
4. Analisis Kemampuan Pemecahan Masalah berbentuk Grafik…..……. 5. Analisis Kesulitan Siswa Berdasarkan Profil Materi……….… 6. Analisis Kesulitan Siswa Berdasarkan Pencapaian ………... 7. Analisis Kesulitan Berdasarkan Pengetahuan Prasyarat dan
Miskonsepsi……….
8. Analisis Kesulitan Berdasarkan Tahapan Pemecahan Masalah…..…… 9. Kisi Kisi Tes Diagnostik Untuk Mengetahui Kesulitan Siswa Dalam
Memecahkan Masalah Fisika Berbentuk Grafik…………..………….. 10.Soal dan Kunci Jawaban Tes Diagnostik Kesulitan Dalam
Memecahkan Masalah Berbentuk Grafik………...
11.Cuplikan Wawancara…..………
12.Dokumentasi Penelitian………..
13.Surat Penetapan Dosbing………
14.Surat Keterangan Telah Melaksanakan Penelitian……….
55 56 57 60 63 65
69 72
81
1
BAB 1
PENDAHULUAN
1.1
Latar Belakang Masalah
Fisika sebagai sebuah ilmu pengetahuan yang dekat dengan fenomena alam, dapat diterjemahkan dalam berbagai bentuk representasi. Salah satunya yaitu representasi dalam bentuk grafik. Pada era informasi ini, kemampuan memahami grafik bagi siswa sangat penting. Menurut Subali (2015), grafik sering dianggap sebagai perangkat matematika, karena berkomunikasi melalui representasi grafik membutuhkan kompetensi matematika seperti persepsi visual, berpikir logis, merencanakan data, memprediksi gerakan garis dan mendeduksi hubungan antara variabel.
Salah satu alasan pentingnya pemahaman representasi grafik karena grafik mampu memberikan informasi kuantitatif yang mudah dipahami. Selain itu, data yang disajikan dengan grafik menjadi lebih mudah dipahami bila dibanding dengan data yang disajikan dalam bentuk kalimat uraian. Kemampuan menganalisis grafik dalam bentuk kalimat verbal maupun non verbal sangat diperlukan oleh siswa, khususnya pada bidang fisika. Kemampuan menganalisis data yang dimaksud mencakup kemampuan membuat grafik, mengungkapkan makna fisis pada grafik, melakukan prediksi dan interpretasi serta melakukan transformasi grafik (Nugroho & Darsono, 2007).
memadai. Hasil penelitian Bunawan et al. (2015), juga menunjukkan bahwa kemahiran dalam menganalisis grafik bergantung pada jenis grafik dan level atau tipe pertanyaan yang dikembangkan.
Grafik memiliki banyak makna yang dapat mewakili suatu fenomena. Banyak siswa dapat menggambar grafik linier, dapat menentukan gradiennya, tetapi tidak dapat menjelaskan makna dari gradient tersebut. Padahal di fisika, gradien memiliki suatu makna tertentu. Planinic et al. (2011), melakukan penelitian yang membandingkan arti/makna gradien suatu grafik pada konteks fisika dan konteks matematika. Planinic et al. (2011), mendapatkan bahwa pemahaman makna gradien grafik pada konteks fisika masih sangat lemah daripada konteks matematika.
Hasil penelitian Planinic et al. (2011), juga menunjukkan bahwa pertanyaan yang sama pada tentang konsep makna grafik pada konteks yang berbeda, yaitu fisika dan matematika didapatkan hasil yang berbeda pula. Hasil pertanyaan dari makna grafik dalam konteks fisika sebesar 42 % dan dalam konteks matematika sebesar 67 %. Data tersebut menunjukkan bahwa pemahaman siswa dalam grafik masih lebih rendah daripada dalam konteks matematika.
Dari pemaparan di atas terlihat bahwa pemahaman siswa terhadap grafik dalam konteks fisika masih kurang. Selain itu, hasil penelitian Nazam et al.
(2012), menemukan bahwa siswa mengalami kesulitan dalam membaca, menafsirkan dan memahami informasi yang tergambar dalam grafik.
dapat berhasil dengan efektif, terlebih dahulu guru harus memahami letak kesulitan yang dihadapi oleh siswa. Dorongan guru untuk memecahkan masalah kesulitan siswa merupakan salah satu unsur dalam pengembangan profesi guru. Hal ini berlandaskan pada prinsip diagnosis dalam konteks pemecahan masalah. Masalah kesulitan belajar siswa dapat ditemukan dengan memberikan tes diagnostik.
Menurut Depdiknas (2007: 1), tes diagnostik adalah tes yang digunakan untuk mengetahui kelemahan-kelemahan siswa sehingga hasil tersebut dapat digunakan sebagai dasar untuk memberikan tindak lanjut berupa perlakuan yang tepat dan sesuai dengan kelemahan yang dimiliki siswa. Tes diagnostik dapat berupa tes pilihan ganda dengan alasan yang sudah ditentukan, tes pilihan ganda dengan alasanterbuka dan tes esai tertulis.
Tes diagnostik perlu dilakukan untuk mengetahui kelemahan dan kekuatan siswa terhadap penguasaan suatu bagian atau keseluruhan materi pelajaran. Dengan tes diagnostik, kesulitan-kesulitan belajar yang muncul dapat diidentifikasi sehingga kegagalan dan keberhasilan siswa dapat diketahui. Berdasarkan uraian di atas, maka peneliti memilih judul “Analisis Kesulitan Siswa Dalam Memecahkan Masalah Fisika Berbentuk Grafik Dengan Tes Diagnostik”.
1.2
Rumusan Masalah
(1) Bagaimanakah kemampuan siswa dalam memecahkan masalah fisika berbentuk grafik?
(2) Bagaimanakah profil kesulitan siswa dalam memecahkan masalah fisika berbentuk grafik?
1.3
Pembatasan Masalah
Beberapa batasan masalah yang perlu diperhatikan dalam penelitian ini adalah: (1) Tes diagnostik dapat dikembangkan untuk setiap pokok bahasan mata
pelajaran IPA di SMP, tetapi dalam penelitian ini dibatasi pada materi gerak lurus kelas VIII semester 1 dengan soal hanya berbentuk grafik. (2) Penelitian dibatasi pada materi Gerak Lurus Beraturan (GLB) dan Gerak
Lurus Berubah Beraturan (GLBB).
1.4
Tujuan Penelitian
Sesuai dengan permasalahan, maka tujuan dari penelitian ini adalah untuk mengetahui kemampuan siswa dan profil kesulitan siswa dalam memecahkan masalah fisika yang berbentuk grafik dengan menggunakan tes diagnostik pada siswa SMP kelas VIII.
1.5
Manfaat Penelitian
Manfaat yang diharapkan dari penelitian ini adalah : (1) Bagi Guru :
memberikan penanggulangan yang sesuai dengan jenis masalah yang dihadapi siswa.
(2) Bagi Sekolah :
Meningkatkan kualitas pembelajaran fisika di sekolah. (3) Bagi Peneliti :
Menambah wawasan, pengetahuan dan keterampilan khususnya yang terkait dengan kesulitan siswa dalam memecahkan masalah fisika berbentuk grafik.
1.6
Penegasan Istilah
Untuk memperjelas penafsiran dan menghindari perbedaan pemahaman terhadap istilah-istilah yang digunakan dalam penelitian ini, maka diperlukan adanya penegasan istilah.
1.6.1 Tes Diagnostik
Menurut Depdiknas (2007: 1), tes diagnostik adalah tes yang digunakan untuk mengetahui kelemahan-kelemahan siswa sehingga hasil tersebut dapat digunakan sebagai dasar untuk memberikan tindak lanjut berupa perlakuan yang tepat dan sesuai dengan kelemahan yang dimiliki siswa.
1.6.2 Kemampuan Pemecahan Masalah
dan konsep terdefinisi. Demikian pula aturan dan konsep terdefinisi dapat dikuasai jika ditunjang oleh pemahaman konsep konkrit. Pemecahan masalah pada penelitian ini adalah kemampuan siswa dalam mengerjakan soal-soal fisika dalam bentuk grafik.
1.6.3 Grafik
Menurut Warsito yang dikutip oleh Marjani (2013), Grafik adalah suatu grafis yang menggunakan titik-titik atau garis untuk menyampaikan informasi statistik yang saling berhubungan.
1.7
Sitematika Penulisan Skripsi
Penulisan skripsi ini secara garis besar dibagi menjadi tiga bagian yaitu
bagian pendahuluan skripsi, bagian isi skripsi dan bagian akhir skripsi. Bagian
awal skripsi terdiri dari halaman judul, persetujuan pembimbing, pengesahan
kelulusan, pernyataan, motto dan persembahan, kata pengantar, sari, daftar isi,
daftar tabel dan daftar lampiran. Pada bagian isi skripsi terdiri dari hal-hal berikut
ini.
Bab 1 Pendahuluan. Bab ini berisi tentang : latar belakang masalah,
rumusan masalah, pembatasan masalah, tujuan penelitian, manfaat penelitian,
penegasan istilah dan sistematika penulisan skripsi.
Bab 2 Landasan Teori. Landasan teori berisi tentang: teori-teori yang
mendasari penelitian (pemecahan masalahi, kesulitan belajar, tes diagnostik ,
Bab 3 Metode Penelitian. Bab ini berisi tentang: objek penelitian (waktu
dan tempat penelitian; populasi; sampel), variabel penelitian, desain penelitian,
metode pengumpulan data, instrumen penelitian dan metode analisis data.
Bab 4 Hasil penelitian dan pembahasan. Bab ini berisi tentang hasil-hasil
penelitian dan pembahasannya.
Bab 5 Penutup. Bab ini berisi simpulan dan saran dari penelitian. Pada
8
BAB 2
TINJAUAN PUSTAKA
2.1
Pemecahan Masalah
2.1.1 Pengertian Pemecahan Masalah
Menurut Anderson, sebagaimana dikutip oleh Schunk (2012:416), beberapa pakar teori menganggap pemecahan masalah menjadi proses kunci dalam pembelajaran, khususnya pada ranah – ranah seperti sains dan matematika. Pemecahan masalah adalah proses menerapkan pengetahuan yang diperoleh sebelumnya kedalam situasi baru yang baru dikenal. Ciri dari soal atau tugas dalam bentuk memecahkan masalah adalah : ada tantangan dalam materi penugasan dan masalah tidak dapat diselesaikan menggunakan prosedur yang diketahui oleh penjawab atau pemecah masalah.
jika memungkinkan menurunkan penyelesaian lain yang berbeda atau menerapkan hasil penyelesaian untuk menyelesaikan masalah lain.
Dari uraian beberapa teori di atas, maka ditarik suatu kesimpulan bahwa pemecahan masalah adalah suatu tahapan yang dilakukan seseorang untuk mengatasi masalahnya. Metode pemecahan masalah memberikan kesempatan pada siswa menyelesaikan masalahnya sendiri dan mendapatkan pengalaman secara langsung.
2.1.2 Faktor- Faktor Penghambat Pemecahan Masalah
Kesalahan dan hambatan yang sering muncul dalam memecahkan masalah, sebagai berikut: (1) Ketidakcermatan dalam membaca; (2) Ketidakcermatan dalam berpikir; (3) Kelemahan dalam analisis masalah; serta (4) Kekuranggigihan.
Beberapa Indikator yang menunjukkan adanya ketidakcermatan siswa dalam membaca yaitu: (1) membaca soal tanpa perhatian yang kuat pada makna / pengertiannya; (2) mengabaikan satu atau lebih kata yang kurang familiar; (3) mengabaikan satu atau lebih fakta atau ide; (4) tidak membaca kembali bagian yang sulit; (5) memulai menyelesaikan soal sebelum membaca lengkap soal tersebut.
(3) bekerja terlalu cepat; serta (4) mengambil kesimpulan di pertengahan jalan tanpa pemikiran yang matang.
Untuk kelemahan dalam analisis masalah yang terjadi pada siswa ditandai dengan: (1) gagal membedah masalah kompleks menjadi bagian-bagian atau gagal menggunakan bagian-bagian masalah untuk memahami masalah secara keseluruhan; (2) tidak menggunakan pengetahuan atau konsep utama untuk mencoba memahami ide-ide yang kurang jelas; (3) tidak menggunakan kamus atau sumber lainnya saat diperlukan untuk mamahami masalah; serta (4) tidak secara aktif mengkonstruksi ide atau gagasan di atas kertas (bila coret-coretan di atas kertas dapat membantu memahami masalahnya).
Faktor penghambat yang terakhir dalam pemecahan masalah yaitu kekuranggigihan dan indikator – indikator yang menyertainya yaitu (1) tidak percaya diri atau menganggap enteng masalah; (2) memilih jawaban berdasarkan intuisi belaka (menggunakan perasaan dalam mencoba menebak jawaban); (3) menyelesaikan masalah hanya secara teknis belaka tanpa pemikiran; serta (4) berpikir nalar hanya pada bagian kecil masalah, menyerah, lalu melompat pada kesimpulan (Whimbey&Lochhead,1999).
2.2
Kesulitan Belajar
Suatu keadaan ketika siswa tidak dapat belajar sebagaimana mestinya, itulah yang disebut dengan “kesulitan belajar”. Berikut ini definisi kesulitan belajar menurut para ahli : Rumini et al., mengemukakan bahwa kesulitan belajar merupakan kondisi saat siswa mengalami hambatan-hambatan tertentu untuk mengikuti proses pembelajaran dan mencapai hasil belajar secara optimal (Irham dan Wiyani, 2013:254). Sejalan dengan pendapat tersebut menurut Blassic & Jones, kesulitan belajar yang dialami siswa menunjukkan adanya kesenjangan atau jarak antara prestasi akademik yang diharapkan dengan prestasi akademik yang dicapai oleh siswa pada kenyataannya (Irham & Wiyani, 2013:253).
digunakan untuk mendiagnosis ketidakmampuan siswa dalam memecahkan permasalahan yang berstruktur.
Kesulitan pengetahuan terstruktur dapat ditinjau dari kemampuan: bahasa (verbal), menggunakan skema, membuat strategi dan membuat algoritma berdasarkan ketetapan Depdiknas (2002: 33) yang dikutip oleh Rusilowati (2006). Kemampuan bahasa dapat diartikan sebagai kemampuan menerjemahkan soal. Pada kemampuan ini siswa dituntut untuk memberi makna pertanyaan yang diajukan dalam soal. Setiap siswa harus mampu memahami setiap pertanyaan dari kata kunci yang terdapat pada soal. Kemampuan menggunakan skema diartikan sebagai kemampuan memahami konsep atau prinsip yang dapat digunakan untuk menyelesaian soal. Siswa dituntut untuk menggunakan skema pengetahuan dalam mengidentifikasi permasalahan. Siswa harus mengetahui prinsip atau aturan yang diperlukan untuk menyelesaikan soal. Kemampuan membuat strategi dapat diartikan sebagai kemampuan merencanakan pemecahan masalah. Siswa harus membuat cara atau langkah-langkah yang harus digunakan untuk menyelesaikan soal. Kemampuan membuat algoritma menekankan pada penyelesaian atau pengerjaan soal. Siswa harus menggunakan kemampuan matematik (berhitung) yang tepat untuk dapat membuat kesimpulan.
belajar; (3) mewawancarai orangtua atau wali siswa untuk mengetahui hal ihwal keluarga yang mungkin menimbulkan kesulitan belajar; (4) memberikan tes diagnostik bidang kecakapan tertentu untuk mengetahui hakiki kesulitan belajar yang dialami siswa; serta (5) memberikan tes kemampuan intelegensi (IQ) khususnya kepada siswa yang diduga mengalami kesulitan belajar. Dari langkah – langkah tersebut peneliti memilih menggunakan tes diagnostik untuk mengetahui kesulitan siswa.
2.3
Evaluasi
2.3.1Pengertian Evaluasi
Arikunto (2006) mengungkapkan bahwa kita tidak dapat mengadakan penilaian sebelum kita mengadakan pengukuran. Mengukur adalah membandingkan sesuatu dengan satu ukuran. Pengukuran bersifat kuantitatif, menilai adalah mengambil suatu keputusan terhadap sesuatu dengan ukuran baik dan buruk. Penilaian bersifat kuantitatif. Mengadakan evaluasi meliputi kedua langkah diatas, yakni mengukur dan menilai. Sejalan dengan pengertian tersebut, Zainul & Nasution (2001) menyatakan bahwa evaluasi dapat dinyatakan sebagai suatu proses pengambilan keputusan dengan menggunakan informasi yang diperoleh melalui pengukuran hasil belajar, baik yang menggunakan instrumen tes maupun non tes.
Evaluasi merupakan suatu proses yang sistematis untuk menentukan atau membuat keputusan sampai sejauhmana tujuan-tujuan pengajaran telah dicapai oleh siswa (Purwanto, 2002).
Astin (1993) mengajukan tiga butir yang harus dievaluasi agar hasilnya dapat meningkatkan kualitas pendidikan. Ketiga butir tersebut adalah masukan, lingkungan sekolah dan keluarannya. Selama ini yang dievaluasi adalah prestasi belajar peserta didik, khususnya pada ranah kognitif saja. Ranah afektif jarang diperhatikan lembaga pendidikan, walau semua menganggap hal ini penting, tetapi sulit untuk mengukurnya. Secara umum, tujuan evaluasi adalah: (a) Untuk menghimpun data dan informasi yang akan dijadikan sebagai bukti mengenai taraf perkembangan atau kemajuan yang dialami peserta didik setelah mereka mengikuti proses pembelajaran dalam jangka waktu tertentu; (b) untuk mengetahui tingkat efektifitas proses pembelajaran yang telah dilakukan oleh guru dan peserta didik. Dengan kata lain, tujuan umum evaluasi adalah untuk memperoleh data pembuktian yang akan menjadi petunjuk sampai dimana tingkat pencapaian kemajuan peserta didik terhadap tujuan atau kompetensi yang telah ditetapkan setelah mereka menempuh proses pembelajaran dalam jangka waktu tertentu.
mengukur pengetahuan, keterampilan, intelegensi, bakat, atau kemampuan lain yang dimiliki oleh seseorang.
2.3.2Tes Diagnostik
Depdiknas (2007: 4) menyatakan bahwa tes diagnostik berfungsi untuk mengidentifikasi masalah atau kesulitan yang dialami siswa, serta merencanakan tindak lanjut berupa upaya-upaya pemecahan masalah atau kesulitan yang telah teridentifikasi. Menurut Arikunto (2006: 34), tes diagnostik adalah salah satu tes yang digunakan untuk mengetahui kelemahan-kelemahan siswa sehingga dari kelemahan-kelemahan tersebut dapat diberikan perlakuan yang tepat.
Secara garis besar langkah-langkah pengembangan tes diagnostik menurut Ditjen Manajemen Pendidikan Dasar dan Menengah (2007: 6) yaitu mengidentifikasi kompetensi dasar yang belum tercapai ketuntasannya, menentukan kemungkinan sumber masalah, menentukan bentuk dan jumlah soal yang sesuai, menyusun kisi – kisi soal, menulis soal, mengulas soal dan menyusun kriteria penilaian.
sejumlah indikator, karena itu bila suatu kompetensi dasar tidak tercapai, perlu didiagnosis indikator-indikator mana saja yang tidak mampu dimunculkan. Mungkin saja masalah hanya terjadi pada indikator-indikator tertentu, maka cukup pada indikator-indikator itu saja disusun tes diagnostik yang sesuai.
Setelah kompetensi dasar atau indikator yang bermasalah teridentifikasi, mulai ditemukan (dilokalisasi) kemungkinan sumber masalahnya. Dalam pembelajaran sains, terdapat tiga sumber utama yang sering menimbulkan masalah, yaitu: a) tidak terpenuhinya kemampuan prasyarat; b) terjadinya miskonsepsi; dan c) rendahnya kemampuan memecahkan masalah (problem solving). Di samping itu juga harus diperhatikan hakikat sains yang memiliki dimensi sikap, proses dan produk. Sumber masalah bisa terjadi pada masing-masing dimensi tersebut.
Sebagaimana kegiat,an seorang dokter dalam mendiagnosis suatu penyakit, maka ketika seorang guru ingin menemukan “penyakit“ (baca: masalah) yang dialami siswanya, maka perlu dipilih alat diagnosis yang tepat berupa butir-butir tes diagnostik yang sesuai. Butir tes tersebut dapat berupa tes pilihan, esai (uraian), maupun kinerja (performa) sesuai dengan sumber masalah yang diduga dan pada dimensi mana masalah tersebut terjadi.
Sesuai kisi-kisi soal yang telah disusun kemudian ditulis butir-butir soal. Soal tes diagnostik tentu memiliki karakteristik yang berbeda dengan butir soal tes yang lain. Jawaban atau respons yang diberikan oleh siswa harus memberikan informasi yang cukup untuk menduga masalah atau kesulitan yang dialaminya (memiliki fungsi diagnosis). Pada soal uraian, logika berpikir siswa dapat diketahui guru dari jawaban yang ia tulis, tetapi pada soal pilihan. Karena itu siswa perlu menyertakan alasan atau penjelasan ketika memilih alternatif jawaban tertentu.
Butir soal yang baik tentu memenuhi validitas isi, untuk itu soal yang telah ditulis harus divalidasi oleh seorang pakar di bidang tersebut. Bila soal yang telah ditulis oleh guru tidak memungkinkan untuk divalidasi oleh seorang pakar, soal tersebut dapat direvisi oleh guru-guru sejenis dalam MGMPS atau setidaknya oleh guru-guru mapel serumpun dalam satu sekolah. Jawaban atau respon yang diberikan oleh siswa terhadap soal tes diagnostik tentu bervariasi, karena itu untuk memberikan penilaian yang adil dan interpretasi diagnosis yang akurat harus disusun suatu kriteria penilaian, apalagi bila tes yang sama dilakukan oleh guru yang berbeda atau dilakukan oleh lebih dari satu orang guru.
ber”penyakit” sehingga harus diberikan perlakuan yang sesuai (Ditjen Manajemen Pendidikan Dasar dan Menengah, 2007: 6).
Menurut Depdiknas (2007: 2), tes diagnostik memiliki karakteristik: (1) dirancang untuk mendeteksi kesulitan belajar siswa, karena itu format dan respons yang dijaring harus didesain memiliki fungsi diagnostik, (2) dikembangkan berdasar analisis terhadap sumber-sumber kesalahan atau kesulitan yang mungkin menjadi penyebab munculnya masalah (penyakit) siswa, (3) serta menggunakan soal-soal bentuk supply response (bentuk uraian atau jawaban singkat), sehingga mampu menangkap informasi secara lengkap. Bila ada alasan tertentu sehingga mengunakan bentuk selected response (misalnya bentuk pilihan ganda), harus disertakan penjelasan mengapa memilih jawaban tertentu sehingga dapat meminimalisir jawaban tebakan dan dapat ditentukan tipe kesalahan atau masalahnya.
2.4
Grafik
Grafik merupakan alat bantu visual yang menyatakan hubungan dua variabel, misalnya ketika memeriksa hubungan dua variabel pada tabel akan mengalami kesulitan, akan tetapi bila disajikan dalam grafik akan dapat terlihat dengan segera hubungan antar variabel. Dan grafik dalam eksperimen untuk menentukan titik ukur mana yang masih dibutuhkan dan apakah kesalahan yang aneh tidak dilakukan selama eksperimen.
Sejalan dengan pendapat sebelumnya, menurut Beichner (1994), menyatakan kemampuan membaca grafik amat penting untuk mengembangkan konsep-konsep fisika. Hampir semua konsep fisika menjadikan grafik dalam penjelasannya, atau sebaliknya menjelaskan dengan menggunakan grafik. Glazer (2011) mengemukakan bahwa kemampuan interpretasi grafik dipengaruhi oleh aspek karakteristik grafik, misalnya format, jenis, gambar, ekspektasi pengamat, kebiasaan membaca grafik, konten grafik dan pengetahuan awal tentang grafik tersebut.
2.4.1 Kemampuan Pemecahan Masalah Fisika Berbentuk Grafik
Menurut Gok dan Silay (2010), kemampuan pemecahan masalah adalah kemampuan siswa menggunakan informasi yang ada untuk menentukan apa yang harus dikerjakan dalam suatu keadaan tertentu.
kemampuan siswa dalam menyelesaikan suatu masalah fisika khususnya yang berbentuk grafik.
Dalam tahapan tahapan pemecahan masalah fisika berbentuk grafik didalamnya akan ada kemampuan memahami grafik harus dimiliki. Adapun keterampilan memahami grafik dalam penelitian Nugroho & Darsono (2007) yaitu keterampilan membuat grafik, keterampilan membaca grafik, ketrampilan melakukan prediksi menggunakan grafik dan ketrampilan mentransformasikan grafik (Nugroho & Darsono, 2007). Beichner (1994) menemukan beberapa kesalahan yang sering terjadi dalam menginterpretasikan grafik kinematika, (1) siswa menganggap grafik sebagai gambar harafiah dari suatu keadaan, (2) siswa masih bingung dengan arti kemiringan suatu garis dalam suatu grafik dan (3) siswa masih kesulitan membedakan grafik hubungan jarak terhadap waktu dengan grafik hubungan kecepatan terhadap waktu.
2.5
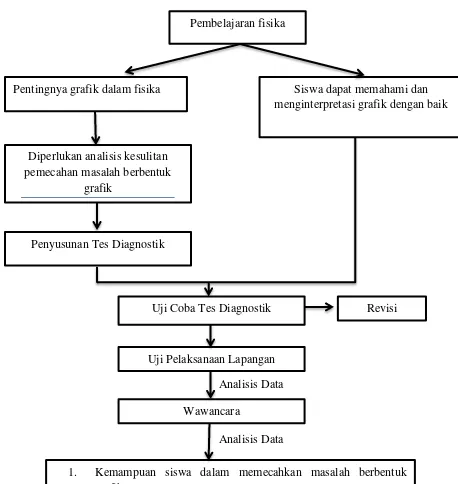
Kerangka Berpikir
Pentingnya grafik dalam fisika Siswa dapat memahami dan menginterpretasi grafik dengan baik Pembelajaran fisika
Diperlukan analisis kesulitan pemecahan masalah berbentuk
grafik
Penyusunan Tes Diagnostik
Uji Pelaksanaan Lapangan Uji Coba Tes Diagnostik
Wawancara
Revisi
1. Kemampuan siswa dalam memecahkan masalah berbentuk grafik.
[image:35.595.92.550.103.587.2]2. Profil Kesulitan siswa dalam memecahkan masalah berbentuk grafik
Analisis Data
Analisis Data
22
BAB 3
METODE PENELITIAN
3.1
Lokasi dan Waktu Penelitian
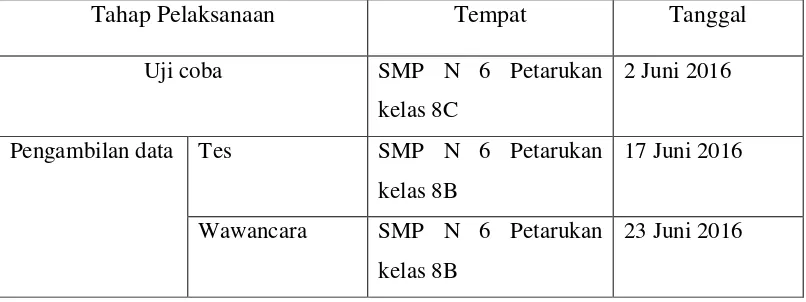
[image:36.595.114.517.355.506.2]Penelitian dilaksanakan di SMP Negeri 06 Petarukan yang berlokasi di DesaWidodaren, Kec. Petarukan, Kab. Pemalang. Penelitian ini dibagi menjadi dua tahap, yaitu tahap uji coba soal dan tahap pengambilan data. Pelaksanaan penelitian dapat dilihat dalam Tabel 3.1.
Tabel 3.1Pelaksanaan Penelitian
Tahap Pelaksanaan Tempat Tanggal
Uji coba SMP N 6 Petarukan kelas 8C
2 Juni 2016
Pengambilan data Tes SMP N 6 Petarukan kelas 8B
17 Juni 2016
Wawancara SMP N 6 Petarukan kelas 8B
23 Juni 2016
3.2
Subjek Penelitian
Subjek dalam penelitian ini adalah siswa kelas VIII SMP Negeri 6 Petarukan berjumlah 36 siswa dapat dilihat pada Lampiran 2.
3.3
Desain Penelitian
peristiwa, kejadian yang terjadi pada saat sekarang. Dengan kata lain, penelitian ini memusatkan perhatian pada masalah aktual sebagaimana adanya pada saat penelitian dilaksanakan. Langkah awal penelitian ini adalah melakukan kajian terhadap beberapa sumber penelitian berupa beberapa jurnal penelitian dan buku-buku teks yang memiliki topik sama dengan penelitian ini. Dalam penelitian kualitatif ini, peneliti menelusuri tentang kesulitan siswa dalam memecahkan masalah fisika berbentuk grafik.
3.3.1 Langkah – Langkah Penelitian
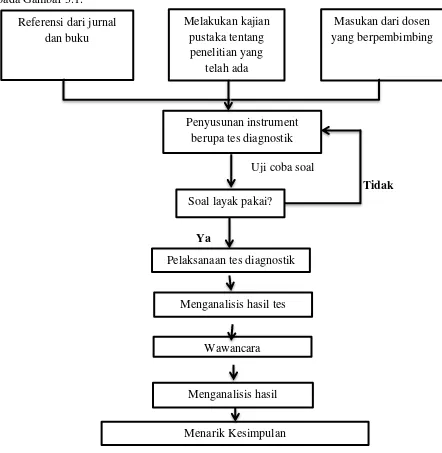
Langkah awal yang dilakukan dalam penelitian ini adalah mengkaji dan mempelajari beberapa penelitian tentang kemampuan analisis grafik yang telah ada. Langkah ini dilakukan dengan cara mencari dan membaca berbagai jurnal ataupun artikel dari internet, perpustakaan dan sumber lainnya. Setelah mempelajari jurnal dari penelitian yang telah ada, langkah selanjutnya adalah penyusunan instrumen penelitian yang dimulai dengan membuat desain tes diagnostik yang meliputi kisi – kisi tes diagnostik, penulisan soal tes diagnostik dan rubrik penilaian tes diagnostik. Dalam kisi - kisi soal terkandung indikator indikator soal yang akan ditulis. Selanjutnya tes diagnostik akan di uji cobakan.
Uji coba soal
Ya Referensi dari jurnal
dan buku
Masukan dari dosen yang berpembimbing Melakukan kajian
pustaka tentang penelitian yang
telah ada
Penyusunan instrument berupa tes diagnostik
Soal layak pakai?
Pelaksanaan tes diagnostik
Wawancara
Menarik Kesimpulan Menganalisis hasil tes
Menganalisis hasil wawancara
Tidak data. Setelah data diperoleh, dilakukan analisis karakteristik butir tes yang meliputi validitas dan reliabilitas.
[image:38.595.116.558.259.712.2]Data yang diperoleh juga dianalisis berdasarkan teknik analisis deskriptif untuk mengetahui kesulitan siswa terhadap masalah fisika berbentuk grafik pada masing-masing indikator. Untuk lebih jelasnya, desain penelitian ditunjukkan pada Gambar 3.1.
3.4
Metode Pengumpulan Data
3.4.1Metode Tes
Metode Tes yang digunakan pada penelitian ini merupakan tes diagnostik yang disusun untuk dapat mengetahui kesulitan siswa dalam memecahkan masalah fisika yang berbentuk grafik. Berdasarkan indikator pencapaian KKM dan kemampuan memahami grafik dihasilkan kisi - kisi tes yang terdapat pada Lampiran 9 dan soal yang terdapat pada lampiran 10. Indikator tes berdasarkan pencapaian KKM yang dimaksud yaitu: (1) memahami grafik GLB dan GLBB; (2) menentukan posisi dan jarak tempuh berdasarkan grafik; (3) menentukan kecepatan berdasarkan grafik; (4) menentukan kelajuan berdasarkan grafik; serta (5) menentukan percepatan berdasarkan grafik. Sementara itu, kemampuan memahami grafik yang dimaksud adalah kemampuan interpretasi, kemampuan prediksi, baik interpolasi maupun ekstrapolasi dan kemampuan transformasi. Data yang diambil dengan metode tes berupa hasil pekerjaan siswa dalam mengerjakan tes diagnostik.
3.4.2Metode Wawancara
Wawancara yang dilakukan diperlukan untuk mendapatkan informasi yang mendalam dan mendukung mengenai apa yang telah didapatkan dari tes tertulis. Wawancara yang dilakukan adalah mengenai jawaban yang dikerjakan oleh siswa. Untuk menghindari agar tidak ada data yang terlewatkan maka digunakan
3.5
Analisis Perangkat Tes Ujicoba
3.5.1 Uji Validitas Butir Soal
Menurut Arikunto (2009: 76), dalam konteks item soal, sebuah item soal dikatakan valid apabila mempunyai dukungan yang besar terhadap total skor. Validitas soal diukur dengan rumus korelasi product moment dengan angka kasar yang dikemukakan oleh Pearson :
Keterangan:
rxy : koefisien antara variabel X dan variabel Y, dua variabel yang dikorelasikan
X : skor item soal tertentu
Y : skor total
Setelah diperoleh harga rxy, kemudian harga rxy dibandingkan dengan r
[image:40.595.107.517.612.697.2]kritik product moment tabel dengan taraf α = 5%, jika rxy> rtabel, maka soal dikatakan valid, demikian sebaliknya. Validitas ini masih dikategorikan menjadi tiga kriteria, yaitu: rendah, cukup, tinggi dan sangat tinggi. Butir soal yang dipakai diambil dari soal yang memiliki validitas dengan kriteria cukup, tinggi dan sangat tinggi seperti yang disajikan dalam Tabel 3.2 (Arikunto, 2009: 75).
Tabel 3.2 Kriteria Validitas Soal Ujicoba Instrumen
Rentang Validitas Kriteria
0,8 ≤ r ≤ 1,0 Sangat Tinggi
0,6 ≤ r ≤ 0,8 Tinggi
0,4 ≤ r ≤ 0,6 Cukup
0,2 ≤ r ≤ 0,4 Rendah
Hasil perhitungan validitas ujicoba soal sidapatkan dan dibandingkan dengan rtabel korelasi product moment dengan taraf signifikansi 5%. Jika rxy >
rtabel, butir soal valid. Jumlah soal yang diujikan sebanyak 18 butir soal.
Berdasarkan hasil analisis validitas butir soal didapat semua soal dinyatakan valid.
3.5.2 Uji Reliabilitas Butir Soal
Instrumen soal yang baik memiliki kualitas valid dan reliabel. Sebuah tes dikatakan mempunyai reliabilitas yang tinggi jika tes tersebut memberikan data hasil yang ajeg (tetap) walaupun diberikan pada waktu yang berbeda kepada responden yang sama (Arikunto, 2009).
Menurut Arikunto (2006), untuk menguji reliabilitas soal uraian sebagai berikut:
Keterangan:
r11 : reliabilitas instrument
n : banyaknya butir soal ∑σi2
: jumlah varians skor tiap item σi2
: varians total
[image:41.595.120.427.647.736.2]Adapun pedoman untuk memberikan interprestasi reliabilitas menurut Sugiyono (2013) ditampilkan oleh Tabel 3.3.
Setelah r11 diketahui, kemudian dibandingkan dengan harga rtabel. Apabila
r11 > rtabel maka dikatakan instrument tersebut reliabel. Dari hasil perhitungan diperoleh rhitung soal= 0,78 dengan taraf signifikansi 5% didapatkan rtabel soal = 0,404, karena rhitung > rtabel maka soal tersebut dikatakan reliabel.
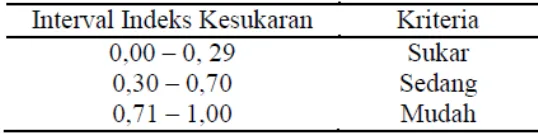
3.5.3 Uji Kesukaran Butir Soal
Sebuah soal dikatakan baik jika mengandung tingkat kesulitan yang bervariasi dan proporsional. Bilangan yang menunjukkan sukar atau mudahnya suatu soal disebut indeks kesukaran (difficulty index).
Analisis tingkat kesukaran soal ini dilakukan menggunakan data hasil uji coba soal dengan membandingkan jumlah siswa yang menjawab benar dibandingkan jumlah keseluruhan siswa (Arikunto, 2009: 208), seperti yang ditunjukkan dalam persamaan berikut:
Keterangan:
P : indeks kesukaran
B : jumlah siswa menjawab benar
JS : jumlah seluruh siswa peserta tes
[image:42.595.119.388.617.684.2]3.5.4 Uji Daya Beda Butir Soal
Daya beda (DB) soal adalah kemampuan suatu butir soal untuk membedakan siswa yang telah menguasai materi dan belum menguasai materi. Angka yang menunjukkan besarnya daya pembeda disebut indeks diskrimasi. Rumus untuk mencari besarnya daya beda suatu soal adalah sebagai berikut:
Keterangan :
DB : Daya Beda
BA : Banyaknya peserta kelompok atas yang menjawab dengan benar
BB : Banyaknya peserta kelompok bawah yang menjawab dengan benar
N : Jumlah siswa yang mengerjakan tes
[image:43.595.106.517.468.540.2]Hasil perhitungan daya beda soal dibandingkan dengan kriteria daya beda soal seperti yang tersaji dalam Tabel 3.5
Tabel 3.5 Kriteria Daya Beda Soal Ujicoba
3.6
Analisis Data
3.6.1Analisis Kemampuan Pemecahan Masalah Fisika Berbentuk Grafik Kemampuan siswa memahami grafik didapat dari hasil pekerjaan siswa dalam mengerjakan soal diagnostik. Analisis data disini menggunakan metode analisis deskriptif untuk mengetahui tingkat kemampuan siswa dalam memecahkan masalah fisika dalam bentuk grafik. Adapun rumus untuk analisis deskripsi persentase menurut Ali yang dikutip oleh Irawati ( 2014) yaitu:
Rentang Validitas Kriteria
0 < DB ≤ 0,19 Soal tidak dipakai 0,2 < DB ≤ 0,29 Soal diperbaiki
[image:44.595.105.480.238.346.2]
Menurut Walandauw sebagaimana dikutip oleh Bakri (2012) untuk kriteria kemampuan pemecahan masalah berbentuk grafik dapat dilihat pada Tabel 3.6 Tabel 3.6 Kriteria Kemampuan Pemecahan Masalah Berbentuk Grafik
Kategori Persentase
Baik Sekali 78% - 100%
Baik 66% - 79%
Sedang 56% - 65%
Kurang ≤ 55%
3.6.2Analisis Profil Kesulitan Siswa
Analisis kesulitan siswa yaitu berdasarkan KKM, profil materi, prasyarat pengetahuan, miskonsepsi dan tahapan pemecahan masalah. Untuk analisis berdasarkan KKM dan profil materi menggunakan persentase skor siswa digunakan rumus:
Ketentuan kategori kesulitan berdasarkan pencapaian KKM :
KKM ketuntasan : 65 %, siswa mengalami kesulitan jika : % skor ≤ 35% : kategori kuat
% skor > 35% : kategori lemah
menggunakan skor melainkan frekuensi. Ketentuan kategori kesulitan siswa terdapat pada Tabel 3.7 (Sudijono, 2011).
Tabel 3.7 Kriteria Kesulitan Siswa
Persentase (%) Kategori
80 – 100 Sangat Tinggi
66 – 79 Tinggi
40 – 65 Sedang
0 – 39 Rendah
32
48.3
34.36
53.01
48.61
0 10 20 30 40 50 60
Interpretasi Prediksi Interpolasi Prediksi Ekstrapolasi Transformasi
Per
sen
tase
(
%
)
Jenis Kemampuan Grafik
Kemampuan Pemecahan Masalah
Berbentuk Grafik
BAB 4
HASIL PENELITIAN DAN PEMBAHASAN
4.1
Hasil Penelitian
4.1.1Kemampuan Pemecahan Masalah Berbentuk Grafik
Kemampuan pemecahan masalah berbentuk grafik yang diukur disini yaitu kemampuan pemecahan masalah yang berkaitan dengan kemampuan interpretasi grafik, memprediksi grafik, baik interpolasi maupun ekstrapolasi dan transformasi suatu grafik (Nugroho & Darsono, 2007).
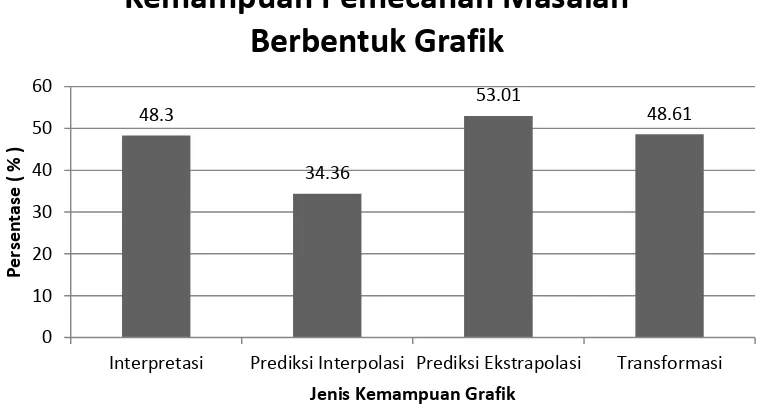
[image:46.595.125.508.479.685.2]Proses pengambilan data dilakukan dengan menggunakan tes diagnostik yang disusun untuk mengukur kemampuan siswa dalam menyelesaikan masalah berbentuk grafik seperti pada lampiran 9. Hasil pengambilan data digambarkan pada Gambar 4.1. Analisis data selengkapnya dapat dilihat pada Lampiran 4.
Gambar 4.1 menunjukan bahwa kemampuan siswa dalam pemecahan masalah berbentuk grafik yang paling tinggi adalah kemampuan siswa dalam mengekstrapolasi grafik, yaitu sebesar 53,01%. Persentase yang paling rendah adalah kemampuan siswa dalam menginterpolasi grafik, yaitu sebesar 34,36%.
4.1.2Profil Kesulitan Siswa
Selain kemampuan pemecahan masalah fisika berbentuk grafik, pada penelitian ini juga dianalisis profil kesulitan siswa. Profil kesulitan yang dianalisis disini berdasarkan: (1) pencapaian KKM; (2) pengetahuan prasyarat; (3) profil materi; (4) miskonsepsi; serta (5) tahap – tahap pemecahan masalah. Analisis data dilakukan berdasarkan hasil siswa dalam mengerjakan tes diagnostik yang telah dilaksanakan dan didukung oleh hasil wawancara.
4.1.2.1Analisis Kesulitan Siswa Berdasarkan Pencapaian KKM
50.23 54.44 49.42 55.90 61.46 0.00 10.00 20.00 30.00 40.00 50.00 60.00 70.00
Paham GLB & GLBB
Menentukan Jarak Tempuh &
Posisi Menentukan kecepatan Menentukan Kelajuan Menentukan Percepatan Per sen tase Sko r(% )
Indikator Tes Diagnostik
[image:48.595.117.540.123.358.2]Profil Kesulitan Berdasarkan Pencapaian KKM
Gambar 4.2 Profil Kesulitan Berdasarkan Pencapaian KKM
Gambar 4.2 menunjukan bahwa kesulitan siswa dalam pemecahan masalah berbentuk grafik berdasarkan pencapaian KKM mempunyai persentase yang tidak berbeda jauh antara satu indikator dengan indikator lainnya. Kesulitan siswa berdasarkan pencapaian KKM memiliki persentase kesulitan paling tinggi adalah indikator menentukan percepatan, yaitu sebesar 61,46 %. Persentase kesulitan yang paling rendah adalah indikator menentukan kecepatan, yaitu sebesar 49,42%.
4.1.2.2Analisis Kesulitan Siswa Berdasarkan Penguasaan Pengetahuan
Prasyarat
operasi hitung dan persamaan linier sederhana yang dilihat pada Lampiran 7. Profil kesulitan siswa berdasarkan penguasaan pengetahuan prasyarat dapat dilihat pada Gambar 4.3.
Gambar 4.3 Profil Kesulitan Siswa Berdasarkan Penguasaan Pengetahuan Prasyarat
Dari Gambar 4.3 dapat diketahui bahwa siswa masih mengalami kesulitan dalam operasi hitung dan persamaan linier pada pengetahuan prasyarat yang harus dimiliki. Keduanya memiliki persentase kesulitan yang sama, yaitu sebesar 52,78%. Untuk pengetahuan prasyarat siswa dalam menguasai luas bangun datar, persentase kesulitan siswa sebesar 16,67%.
4.1.2.3Analisis Kesulitan Siswa Terhadap Profil Materi
Analisis kesulitan siswa terhadap profil materi bertujuan untuk mengetahui sub – sub materi yang sudah dan belum dikuasai oleh siswa dimana data
16.67
52.78 52.78
0 10 20 30 40 50 60
Luas bangun datar Operasi hitung Persamaan linier
Per
sen
tase
(
%
)
Pengetahuan Prasyarat
59.55 57.22 61.46
35.94
53.5
0 10 20 30 40 50 60 70
Jarak dan Perpindahan
Kecepatan dan Kelajuan
Percepatan GLB GLBB
Pr
e
sesn
tase
(
%
)
Sub - Sub Materi
Profil Kesulitan Siswa Terhadap Profil
Materi
[image:50.595.127.497.209.432.2]selengkapnya dapat dilihat pada Lampiran 5. Berikut ini profil kesulitan siswa terhadap profil materi yang diperlihatkan pada Gambar 4.4.
Gambar 4.4 Profil Kesulitan Siswa Terhadap Profil Materi
Dari Gambar 4.4 dapat diketahui bahwa berdasarkan pendekatan profil materi, siswa mengalami kesulitan paling besar pada sub materi percepatan. Persentase kesulitan siswa pada sub materi percepatan sebesar 61,46 %. Persentase kesulitan terendah terletak pada sub materi gerak lurus beraturan atau GLB, yaitu sebesar 35,94 %.
4.1.2.4Analisis Kesulitan Siswa Berdasarkan Miskonsepsi
80
160 160
0 0
20 40 60 80 100 120 140 160 180
0 20 40 60 80
s
(m
)
t (s)
[image:51.595.176.476.349.488.2] [image:51.595.157.474.382.711.2]kecepatan dan kelajuan didapatkan dari jumlah siswa yang mengalami miskonsepsi dibagi dengan jumlah keseluruhan siswa. Dari hasil analisis data yang dapat dilihat pada Lampiran 7, persentase kesulitan berdasarkan miskonsepsi yaitu sebesar 63,89 %. Contoh hasil jawaban siswa yang menunjukan adanya miskonsepsi yang dialami siswa seperti soal yang menguji kemampuan siswa dalam menentukan kecepatan dan kelajuan dari detik ke 40 sampai ke 60 pada grafik yang sama yaitu pada Gambar 4.5 dan jawaban siswa disajikan pada Gambar 4.6.
Gambar 4.5 Grafik Hubungan Jarak Terhadap Waktu
25 45.83 68.65 77.18 0 10 20 30 40 50 60 70 80 90 Tahap memahami masalah Tahap membuat rencana Tahap pelaksanaan rencana Tahap Peninjauan Kembali Pr e sesn tase ( % )
Langkah Pemecahan Masalah
Profil Kesulitan Siswa Berdasarkan Tahapan
Pemecahan Masalah
4.1.2.5Analisis Kesulitan Siswa Berdasarkan Tahapan Pemecahan Masalah
[image:52.595.116.523.430.651.2]Pada penelitian ini tahapan pemecahan masalah yang dipakai yaitu tahapan pemecahan masalah menurut Polya. Tahapan pemecahan masalah polya dimulai dari pemahaman masalah. Setelah siswa dapat memahami masalahnya dilanjutkan dengan pembuatan rencana pemecahan masalah. Pembuatan rencana diteruskan dengan melaksanakan pemecahan masalah tersebut serta diakhiri dengan peninjauan kembali solusi yang telah diperoleh. Untuk perhitangan selengkapnya untuk setiap tahapan polya dilihat pada Lampiran 8. Berikut profil kesulitan siswa berdasarkan tahapan pemecahan masalahnya yang disajikan pada Gambar 4.7.
Dari Gambar 4.7 dapat diketahui bahwa berdasarkan tahapan tahapan pemecahan masalah menurut Polya, siswa mengalami kesulitan paling besar pada tahap peninjauan kembali. Persentase kesulitan siswa pada tahap meninjau kembali sebesar 77,18 %. Sementara itu, persentase kesulitan terendah pada tahap memahami masalah adalah tahapan memahami masalah yaitu sebesar 25,00 %.
4.2
Pembahasan
4.2.1Kemampuan Pemecahan Masalah Berbentuk Grafik 4.2.1.1Interpretasi Grafik
Hasil penelitian dari kemampuan ini yang disajikan pada Gambar 4.1 menunjukan bahwa kemampuan siswa pada kemampuan ini tergolong kurang sesuai kriteria yang ditunjukkan oleh Tabel 3.6. Kemampuan interpretasi grafik disini mencakup beberapa indikator, yaitu menghitung gradien dan mengetahui besaran apa yang ditunjukan gradien, serta dapat mengambil informasi dari grafik tersebut.
[image:53.595.203.431.622.730.2]Sebagian siswa dapat menghitung gradien yang ditunjukan grafik, tetapi tidak dapat mengetahui besaran apa yang dimaksud seperti jawaban siswa untuk soal yang menguji kemampuan siswa dalam menentukan percepatan berdasarkan grafik hubungan kecepatan terhadap waktu disajikan pada Gambar 4.8.
Berdasarkan jawaban di atas dapat dilihat bahwa siswa tidak mengetahui satuan yang tepat yang menunjukkan bahwa siswa tersebut hanya mengetahui perhitungan matematisnya tanpa mengetahui besaran apa yang dicari. Sejalan dengan itu, Planinic et al. (2011), melakukan penelitian yang membandingkan arti / makna gradien suatu grafik pada konteks fisika dan konteks matematika. Planinic et al. (2011), mengatakan bahwa pemahaman makna gradien grafik pada konteks fisika masih sangat lemah daripada konteks matematika.
4.2.1.2Kemampuan Memprediksi
Pada kemampuan ini indikator yang diukur yaitu memperkirakan berdasarkan grafik baik itu keadaan di dalam grafik / interpolasi maupun keadaan di luar grafik/ekstrapolasi. Kemampuan memprediksi dalam penelitian ini terbatas pada bentuk grafik linier. Sesuai dengan data yang disajikan pada Gambar 4.1, pada kemampuan memprediksi keadaan di dalam grafik / interpolasi dapat digolongkan kurang sesuai kriteria yang ditunjukkan oleh Tabel 3.6.
siswa yang disajikan pada Gambar 4.9 untuk jawaban dari soal yang membuat siswa memperkirakan posisi benda pada detik ke-7 berdasarkan grafik yang tersedia.
Gambar 4.9 Hasil Pekerjaan Siswa Dalam Memperkirakan Posisi Benda Berdasarkan wawancara dari siswa tersebut, dia hanya beranggapan setiap detik posisinya akan bertambah lima meter tanpa memikirkan konsep gerak lurus.
4.2.1.3Kemampuan transformasi
(1994) menunjukkan bahwa kemampuan dalam mengartikan grafik masih rendah. Salah satu kesalahan yang umum siswa masih kesulitan dalam membedakan arti grafik jarak terhadap waktu dengan kecepatan terhadap waktu.
Pada kemampuan transformasi pada penelitian ini, siswa diminta menjelaskan dari sebuah grafik baik termasuk gerak lurus beraturan (GLB) maupun gerak lurus berubah beraturan (GLBB). Siswa cenderung hanya bisa menjawab bahwa grafik itu termasuk gerak GLB atau GLBB tanpa menjelaskan bagaimana kecepatan dan percepatan yang terjadi dari gerak tersebut.
4.2.2Profil Kesulitan Siswa
4.2.2.1Profil Kesulitan Siswa Berdasarkan KKM
Pada profil kesulitan siswa berdasarkan KKM memiliki rata – rata persentase untuk semua indikatornya yaitu 53,01%. Nilai ini lebih besar dari batas KKM untuk siswa SMP N 6 Petarukan yaitu harus lebih rendah dari 35%. Hal ini berarti secara umum siswa masih belum tuntas dan masih mengalami kesulitan.
Selain pada indikator dapat memahami grafik GLB dan GLBB, siswa juga mengalami kesulitan pada semua indikator yang ada. Hal ini mungkin dikarenakan penguasaan konsep dari siswa tentang gerak lurus. Berikut ini disajikan hasil pengerjaan siswa yang menunjukkan adanya kurangnya penguasaan konsep.
[image:57.595.191.434.329.501.2]Siswa diminta menentukan jarak tempuh selama 4 sekon dan memprediksikan jarak pada detik ke 20 dari sebuah grafik gerak lurus beraturan dengan kecepatan 20 m/s. Jawaban siswa disajikan pada Gambar 4.10.
Gambar 4.10 Hasil Pekerjaan Siswa Yang Menunjukkan Kurangnya Penguasaan Konsep
disimpulkan bahwa siswa belum memahami konsep gerak lurus beraturan yang memiliki kecepatan yang selalu tetap.
Sejalan dengan itu Pujianto et al. (2013), melakukan penelitian tentang konsepsi siswa pada konsep gerak lurus beraturan menemukan bahwa sebagian besar responden memiliki konsepsi yang salah. Konsepsi yang salah ini dikarenakan siswa yang menjadi responden menganggap jika suatu kendaraan bergerak dengan arah dan kecepatan tetap selama 10 menit merupakan gerak lurus berubah beraturan.
4.2.2.2Profil Kesulitan Siswa Berdasarkan Pengetahuan Prasyarat
grafik gerak lurus beraturan hubungan kecepatan terhadap waktu dengan kecepatan 20 m/s. Jawaban siswa tersebut disajikan pada Gambar 4.11.
Gambar 4.11 Hasil Pekerjaan Siswa Yang Menunjukkan Kurangnya Pengetahuan Prasyarat
Dari jawaban siswa tersebut terlihat siswa salah menggunakan rumus luas, karena jawaban yang tepat menggunakan luas persegi panjang dan jawaban siswa menggunakan luas segitiga.
Persentase kesulitan pengetahuan prasyarat operasi hitung ditunjukkan oleh Gambar 4.3 dan termasuk dalam kategori kesulitan sedang. Secara umum, siswa masih mengalami kesulitan dalam operasi hitung. Hal ini juga didukung dari hasil wawancara yang dilakukan seperti pada Lampiran 11 mengatakan bahwa mengalami kesulitan dalam perhitungan. Berikut contoh hasil pengerjaan siswa yang disajikan pada Gambar 4.12 dan hasil wawancara yang menunjukan bahwa terdapat kesulitan dalam operasi hitung. Pada soal siswa diminta menentukan kelajuan berdasarkan grafik hubungan jarak terhadap waktu.
[image:59.595.185.458.596.705.2]
Kesulitan siswa dalam operasi hitung sesuai dengan hasil penelitian dari Rusilowati (2006) yang menyatakan bahwa salah satu penyebab kesulitan belajar siswa yaitu kesulitan dalam operasi hitung atau perhitungan matematisnya. Selain itu, penyebab lainnya yaitu pemahaman konsep dan mengkonversian satuan. Berdasarkan Gambar 4.3 juga, pengetahuan prasyarat siswa terhadap penguasaan persamaan linear sederhana termasuk dalam kategori sedang. Penguasaan persamaan linear sederhana digunakan untuk membantu memprediksi berdasarkan grafik baik interpolasi maupun ekstrapolasi.
4.2.2.3Profil Kesulitan Siswa Berdasarkan Profil Materi
Profil kesulitan siswa berdasarkan profil materi ini digunakan untuk mengetahui persentase kesulitan siswa dalam menguasai suatu materi untuk setiap sub materinya. Sub materi dari materi dari penelitian ini yaitu jarak dan perpindahan; kecepatan dan kelajuan; percepatan; gerak lurus beraturan (GLB); serta gerak lurus berubah beraturan (GLBB). Analisis kesulitan ini juga menggunakan KKM sebagai batas penguasaan siswa.
Dari lima sub materi pada materi gerak lurus ini, siswa masih mengalami kesulitan, terutama pada sub materi percepatan yang memiliki persentase kesulitan lebih tinggi dari dari persentase sub materi yang lainnya sesuai yang tunjukkan pada Gambar 4.4. Kesulitan pada sub materi jarak dan perpindahan umumnya dikarenakan siswa merasa kesulitan dalam memprediksi jarak tempuh berdasarkan grafik yang ada.
dengan hasil penelitian Pujianto et al. (2013), yaitu siswa memiliki pemahaman bahwa percepatan adalah kecepatan dibagi waktu. Konsepsi ini didasarkan pada rumus percepatan, tetapi belum memahami benda yang dipercepat maka jarak yang ditempuh setiap detiknya mengalami peningkatan. Persentase kesulitannya yaitu 62,50 %.
4.2.2.4Profil Kesulitan Siswa Berdasarkan Miskonsepsi
Padahal sebenarnya speedometer digunakan untuk mengukur kelajuan dari suatu benda.
Sejalan dengan itu, Pujianto et al. (2013), mengatakan siswa masih sulit membedakan antara konsep kelajuan dan kecepatan. Miskonsepsi ini diawali ketika siswa tidak mampu menentukan jarak dan perpindahannya.
4.2.2.5Profil Kesulitan Siswa Berdasarkan Tahapan Pemecahan Masalah
Tahapan pemecahan masalah yang dipakai disini berdasarkan tahapan menurut Polya. Tahapannya dimulai dari pemahaman masalah, membuat rencana, melaksanakan rencana dan memeriksa kembali. Berdasarkan hasil analisis kesulitan yang ditunjukkan pada Gambar 4.6, rata rata persentase siswa yang mengalami kesulitan pada tahap memeriksa kembali termasuk dalam kategori sangat tinggi.
Untuk persentase siswa yang masih memiliki kesulitan pada tahap melaksanakan rencana tergolong dalam kategori tinggi. Selanjutnya, untuk persentase siswa yang mengalami kesulitan pada tahap membuat rencana termasuk dalam kategori sedang. Dan terakhir, untuk persentase siswa yang mengalami kesulitan pada tahap memahami masalah termasuk kategori rendah menurut Sudijono (2011).
dilakukan oleh Andriani et al. (2016), tentang analisis kesulitan siswa dalam menyelesaikan soal gerak lurus.
Pada tahap memahami masalah, siswa tidak terlalu mendapat kesulitan. Siswa mengalami kesulitan dimulai dari tahap membuat rencana dikarenakan pada tahap membuat rencana siswa mengalami kebingungan dan tidak mengetahui rumus-rumus yang tepat yang harus digunakan dan siswa tidak dapat menerapkan konsep-konsep yang telah dipelajarinya. Pada tahap melaksanakan rencana siswa mengalami masalah, misalnya pada salah satu pengetahuan prasyaratnya yaitu pada operasi hitung. Pada tahap peninjauan kembali, siswa paling mengalami kesulitan yang dikarenakan siswa yang tidak meninjau kembali jawabannya dengan alasan kehabisan/kekurangan waktu dan merasakan kebingungan atau justru siswa merasa yakin dengan jawabannya.
4.3
Keterbatasan Masalah
BAB 5
PENUTUP
5.1
Simpulan
Berdasarkan hasil penelitian dan pembahasan maka dapat diambil simpulan sebagai berikut:
1. Kemampuan siswa dalam memecahkan masalah fisika berbentuk grafik memilik persentase tergolong rendah untuk kemampuan interpretasi grafik sebesar 48,30%; kemampuan interpolasi sebesar 34,36%; kemampuan ekstrapolasi sebesar 53,01%; dan kemampuan transformasi sebesar 48,61%.
dan persamaan linier sama yaitu 52,78 % termasuk dalam kategori sedang. Untuk profil kesulitan siswa berdasarkan profil materi, persentase kesulitan siswa dalam tiap sub - sub materi yaitu sub materi jarak dan perpindahan sebesar 59,55 %; kecepatan dan kelajuan sebesar 57,22 %; percepatan sebesar 61,46 %; GLB sebesar 35,94 %; serta GLBB sebesar 53,50 %. Untuk profil kesulitan siswa berdasarkan miskonsepsi, persentase kesulitan siswa yaitu 63,89 % dan termasuk dalam kategori tinggi. Serta yang terakhir, profil kesulitan siswa berdasarkan tahap – tahap pemecahan masalah. Persentase kesulitan siswa untuk tiap tahapan yaitu tahap memahami masalah sebesar 25,00 % termasuk kategori rendah, tahap membuat rencana sebesar 45,83 % termasuk kategori sedang, tahap melaksanakan rencana sebesar 68,63 % termasuk kategori tinggi, serta tahap peninjauan kembali sebesar 77,28 % termasuk kategori tinggi.
5.2
Saran
DAFTAR PUSTAKA
Andriani, L.N.Y., Darsikin, & A. Hatibe. 2016. Analisis Kesulitan Siswa dalam Menyelesaikan Soal Gerak Lurus. Jurnal Pendidikan Fisika Tadulako (JPFT), 4(3): 36-41.
Arikunto, S. 2006. Dasar-Dasar Evaluasi Pendidikan. Jakarta: PT Bumi Rupa Aksara.
Arikunto, S. 2009. Dasar-Dasar Evaluasi Pendidikan (Edisi Revisi). Jakarta: PT Bumi Rupa Aksara.
Astin, A. W. 1993. The Philosophy and Practice of Assessment and Evaluation in a Higher Education. New York: Maxwell Maxmillan.
Bakri, M. 2012. Kemampuan Siswa Memahami Grafik Pada Konsep Biologi : Studi Deskriptif Pada Siswa Kelas I Man Kupang. Thesis. Bandung : Universitas Pendidikan Indonesia.
Beichner, R.J. 1994. Testing Student Interpretation Of Kinetic Graph. American Journal of Physics, 62:750-762 .
Bunawan ,W., A. Setiawan, Nahadi, & A. Rusli. 2015. Penilaian Pemahaman Representasi Grafik Materi Optika Geometri Menggunakan Tes Diagnostik.
Cakrawala Pendidikan, 34(2):257-267.
Depdiknas. 2007. Pedoman Pengembangan Tes Diagnostik Mata Pelajaran IPA SMP/MTs. Jakarta: Ditjen Manajemen Pendidikan Dasar dan Menengah. Djaali & Muljono. 2008. Pengukuran Dalam Bidang Pendidikan. Jakarta:
PT.Grasindo.
Gagne, L.J. Briggs, & W.W. Wager. 1992. Principles of Instructional Design. New York: Holt Rinehart & Winston.
Glazer, N. 2011. Challenges with Graph Interpretation : A Review of the Literature. Studies in Science Education, 47(2): 183-210.
Irawati, D.R. 2014. Analisis Penguasaan Konsep Fisika Pada Pokok Bahasan Besaran Dan Satuan Kelas X Sma Negeri 1 Sale Rembang. Skripsi. Semarang: FMIPA UNNES.
Irham, M. & Wiyani. 2013. Psikologi Pendidikan. Yogyakarta: Ar-Ruzz Media. Kemdikbud. 2015. Kamus Besar Bahasa Indonesia Online. Online Tersedia di
http://kbbi.co.id [diakses 12-02-2016].
Marjani. 2013. Makalah Media Pembelajaran Grafik. Tersedia di
http://documents.tips/documents/makalah-media-grafis.html[diakses 20-03-2016].
McDermot, L.C., M.L. Rosenquist, & E.H. Vanzee . 1987. Student Difficulties In Connecting From Kinematic. American Journal of Physics, 55:503-513. Nazam S, Meltem S., & Ali B. 2012. Investigating students’ abilities related to
graphing skill. Procedia - Social and Behavioral Sciences, 46: 2942 – 2946. Nugroho, S.E., & Darsono. 2007. Model Pembelajaran Dengan Peningkatan Guided Inquiry Untuk Meningkatkan Kemampuan Interpretasi Grafik Pada
Mahasiswa Fisika. Laporan Penelitian. Semarang : FMIPA UNNES.
Planinic, M., Z.M. Sipus, H. Katic, A. Susan, & L. Ivanjek. 2011. Comparison of Students Understanding of Line Graph Slope in Physics and Mathematics.
International Journal of Science and Mathematics Education, 10:1393-1414.
Pujianto, A., Nurjannah, & I.W.Darmadi. 2013. Analisis Konsepsi Siswa Pada Konsep Kinematika Gerak Lurus. Jurnal Pendidikan Fisika Tadulako (JPFT), 1(1): 16-21.
Purwanto, M.N. 2002. Prinsip-Prinsip dan Teknik Evaluasi Pembelajaran. Bandung : Remaja Rosdakarya .
Rusilowati, A. 2006. Profil Kesulitan Belajar Fisika Pokok Bahasan Kelistrikan Siswa SMA di Kota Semarang. Jurnal Pendidikan Fisika Indonesia, 10(2): 100-106.
Subali, B., D. Rusdiana, H. Firman, & I. Kaniawati. 2015. Analisis Kemampuan Interpretasi Grafik Kinematika pada Mahasiswa Calon Guru Fisika.
Prosiding Simposium Nasional Inovasi dan Pembelajaran Sains 2015
(SNIPS 2015), Bandung, 8 dan 9 Juni.
Sudijono, Anas. 2011. Pengantar Statistik Pendidikan. Jakarta: Rajawali Pers. Sugiyono. 2013. Metode Penelitian Pendidikan Pendekatan Kualitatif,
Kuantitatif,dan RnD. Bandung : Alfabeta.
Wardani. 1991. Diagnosis Kesulitan Belajar dan Perbaikan Belajar. Jakarta: Ditjen Binbaga Islam dan Universitas Terbuka.
Lampiran 1.
Daftar Kode Siswa Ujicoba
No Simbol
1 UC-1
2 UC-2
3 UC-3
4 UC-4
5 UC-5
6 UC-6
7 UC-7
8 UC-8
9 UC-9
10 UC-10
11 UC-11
12 UC-12
13 UC-13
14 UC-14
15 UC-15
16 UC-16
17 UC-17
18 UC-18
19 UC-19
20 UC-20
21 UC-21
22 UC-22
23 UC-23
24 UC-24
25 UC-25
26 UC-26
27 UC-27
28 UC-28
29 UC-29
30 UC-30
31 UC-31
32 UC-32
33 UC-33
34 UC-34
35 UC-35
36 UC-36
Lampiran 2.
Daftar Simbol Siswa Penelitian
No Simbol
1 S-1
2 S-2
3 S-3
4 S-4
5 S-5
6 S-6
7 S-7
8 S-8
9 S-9
10 S-10
11 S-11
12 S-12
13 S-13
14 S-14
15 S-15
16 S-16
17 S-17
18 S-18
19 S-19
20 S-20
21 S-21
22 S-22
23 S-23
24 S-24
25 S-25
26 S-26
27 S-27
28 S-28
29 S-29
30 S-30
31 S-31
32 S-32
33 S-33
34 S-34
35 S-35
Lampiran 3.
Analisis Hasil Uji Coba
No Kode Nomor Soal ∑Y ∑Y2
1a 1b 1c 2a 2b 3a 3b 3c 4a 4b 5a 5b 6a 6b 6c 7 8a 8b
1 UC-3 4 4 3 4 3 2 4 4 4 3 2 2 4 3 4 1 2 2 55 3025
2 UC-23 4 2 4 2 4 4 2 2 0 4 4 3 4 4 4 4 1 2 54 2916
3 UC-15 4 4 2 3 2 2 4 4 2 1 4 2 4 2 2 4 4 2 52 2704
4 UC-1 2 4 4 4 2 2 0 4 3 3 4 4 2 3 1 4 1 4 51 2601
5 UC-5 2 4 4 2 4 2 2 2 4 2 4 1 4 4 1 4 2 2 50 2500
6 UC-33 2 4 4 3 4 2 2 0 2 3 4 1 4 4 4 3 0 0 46 2116
7 UC-14 1 4 4 4 4 1 1 3 2 3 4 2 1 4 1 4 1 2 46 2116
8 UC-30 2 0 4 4 4 1 2 2 4 2 4 2 1 4 2 4 2 1 45 2025
9 UC-29 4 2 2 3 2 2 2 2 2 3 4 4 1 4 2 3 1 1 44 1936
10 UC-26 4 2 2 3 2 2 2 2 2 3 4 4 1 4 2 3 0 1 43 1849
11 UC-36 4 2 3 0 4 0 1 0 0 2 4 0 4 3 2 4 4 2 39 1521
12 UC-24 4 1 3 0 3 0 1 0 0 2 3 0 3 3 2 4 2 2 33 1089
13 UC-31 2 2 3 0 2 3 0 1 0 0 3 0 1 4 4 4 0 1 30 900
14 UC-16 3 1 3 3 3 0 0 2 1 2 3 0 2 4 0 1 2 1 31 961
15 UC-28 4 4 4 2 4 1 0 1 0 1 4 0 0 1 0 2 0 0 28 784