A graph theoretic condition for irreduci

arXiv:1112.1653v1 [math.CO] 7 Dec 2011

A graph-theoretic condition for irreducibility of a set of

cone preserving matrices

Murad Banajia,∗_{, Andrew Burbanks}a

a

Department of Mathematics, University of Portsmouth, Lion Gate Building, Lion Terrace, Portsmouth, Hampshire PO1 3HF, UK.

Abstract

Given a closed, convex and pointed coneK in Rn, we present a result which infersK-irreducibility of sets ofK-quasipositive matrices from strong connect-edness of certain bipartite digraphs. The matrix-sets are defined via products, and the main result is relevant to applications in biology and chemistry. Several examples are presented.

Keywords: partial order, convex cone, irreducibility, strong monotonicity 2000 MSC:15B48, 15B35

1. Introduction

A digraph G is strongly connected, or irreducible, if given any vertices u

andv, there exists a (directed) path fromutov in G. It is well known that a digraph is strongly connected if and only if its adjacency matrix is irreducible [1]. Here, given a coneK, we present a result which infersK-irreducibility of sets of K-quasipositive matrices from strong connectedness of associated bipartite digraphs. Graph-theoretic approaches toK-irreducibility of sets ofK-positive matrices have been described in earlier work [2, 3, 4]. These approaches are somewhat different in structure and philosophy to that described here. We will comment further on this in the concluding section.

We will be interested in closed, convex cones in Rn _{which are additionally}

pointed (i.e., ify ∈K andy 6= 0, then −y 6∈K). Closed, convex and pointed cones will be abbreviated asCCPcones. We do not assume the cones are solid (i.e., have nonempty interior inRn) – however if a CCP cone is, additionally, solid, then it will be termed aproper cone. For basic definitions and results on cones inRn the reader is referred to [1, 5].

Let K ⊂ Rn be a CCP cone. Consider an n×n matrix M. Recall that

M is K-positive if M K ⊆ K. Defining Rn≥0 to be the (closed) nonnegative orthant in Rn, a nonnegative matrix is thenRn≥0-positive. We will refer toM asK-quasipositiveif there exists an α∈R such thatM +αI is K-positive.

Rn≥0-quasipositive matrices – generally referred to simply as quasipositive, or Metzler – are just those with nonnegative off-diagonal entries. We define M

to beK-reducible if there exists a nontrivial faceF ofK such thatM leaves spanF invariant. This is a slight generalisation of the original definition of K -reducibility forK-positive matrices [6] in order to allow us to apply the term to matrices which are not necessarilyK-positive. A matrix which is not K -reducible isK-irreducible. Note that an irreducible matrix could be termed Rn

≥0-irreducible in this terminology. Alternatively any other orthant inRncould be chosen asK.

Remark 1. Given a CCP coneK⊂Rn_{, ann×nmatrixM isK-irreducible if}

and only ifM+αI isK-irreducible for eachα∈R. In one direction we choose

α= 0. The other direction follows because given any face F of K,spanF is a vector subspace ofRn.

Motivation from dynamical systems. Motivation for examining K -irreducibility of a set of K-quasipositive matrices comes from the theory of monotone dynamical systems [7, 8]. Convex, pointed cones define partial orders in a natural way. Given a proper coneK and aC1 _{vector fieldf :R}n_→Rn_{, if}

the Jacobian matrixDf(x) isK-quasipositive andK-irreducible at eachx∈Rn, then the associated local flow is strongly monotone with respect to the partial order defined byK. This result and a variety of technical modifications provide useful conditions which can be used to deduce the asymptotic behaviour of dynamical systems.

Remark 2. Although the main results on monotone dynamical systems require the order cone to be solid, a CCP coneK which fails to be solid is as useful as a proper one when the local flow or semiflow leaves cosets ofspanK invariant. Trivially, K has nonempty relative interior in spanK, and attention can be restricted to cosets ofspanK. This situation arises frequently in applications to biology and chemistry.

2. Some background material

Sets of matrices. It is convenient to use some notions from qualitative matrix theory. LetM be a real matrix.

1. Q(M), the qualitative class of M [9] is the set of all matrices with the same dimensions and sign pattern as M, namely if N ∈ Q(M), then

Mij>0⇒Nij>0,Mij <0⇒Nij <0 andMij = 0⇒Nij = 0.

2. Q0(M) will stand for the closure ofQ(M), namely if N ∈ Q0(M), then

Mij>0⇒Nij≥0,Mij <0⇒Nij ≤0 andMij = 0⇒Nij = 0.

3. Q1(M) will be the set of all matricesN with the same dimensions asM

and satisfyingMijNij≥0.

Remark 3. SupposeK is an orthant inRn andM is ann×n K-quasipositive matrix. It can easily be shown that each matrix inQ0(M) is K-quasipositive. Since in this caseK-irreducibility is simply irreducibility, if M isK-irreducible then each matrix inQ(M)isK-irreducible. However, the same is not true for

Q0(M)which, after all, contains the zero matrix.

Notation for matrices. Given any matrixM, we refer to thekth column ofM as Mk and thekth row ofM asMk. We define the new matrixM(k)by

M_ij(k)=Mij ifi=k andMij(k)= 0 otherwise: i.e., M(k) is derived fromM by

replacing all entries not in thekth row with zeros. We define a set of matrices

Mto berow-completeifM ∈M⇒M(k)_{∈Mfor eachk. Clearly, given any} matrixM,Q0(M) is row-complete; but much smaller sets can be row-complete. For example, given some fixedm×nmatrixN,

M={DN : D is a nonnegativem×m diagonal matrix}

is row-complete.

Digraphs associated with square matrices. Given ann×nmatrixM, letGM be the associated digraph onn verticesu1, . . . , un defined in the usual

way: the arcuiuj exists inGM iffMij6= 0.

Remark 4. Following on from Remark 3, if K is an orthant in Rn, then K -irreducibility of an n×n matrix M is equivalent to strong connectedness of

GM.

Bipartite digraphs associated with matrix-pairs. Given an n×m

matrixA and an m×n matrixB, define a bipartite digraph GA,B on n+m

vertices as follows: associate a set ofnverticesu1, . . . , unwith the rows ofA(we

will refer to these as the “row vertices” ofGA,B); associate another mvertices

v1, . . . , vmwith the columns ofA(we will refer to these as the “column vertices”

ofGA,B); add the arcuivj iffAij 6= 0; add the arcvjui iffBji6= 0.

Remark 5. This is a specialisation of the general construction of block-circulant digraphs from sets of appropriately dimensioned matrices in [10]. If A and B

are binary matrices (with AB a square matrix), then the adjacency matrix of

GA,B is simply

0 A

B 0

.

The context of the main result. Fundamental early results on con-vergence in monotone dynamical systems [11] apply to systems with Jaco-bian matrices which are quasipositive and irreducible (in our terminologyRn

≥0 -quasipositive and Rn

≥0-irreducible). Generalising from Rn≥0 to all orthants is straightforward: whereK is an orthant, there is a simple graph-theoretic test [7] to decideK-quasipositivity of a givenn×nmatrixM. By Remarks 3 and 4,

K-quasipositivity extends to all ofQ0(M), andK-irreducibility of someM′ _∈

We are interested in how this situation generalises whenKis not necessarily an orthant. In general, given aK-quasipositive matrixM, we can rarely expect all matrices in Q0(M) to be K-quasipositive. However the following situation is not uncommon: there are matricesAand ˜B such thatAB isK-quasipositive for eachB ∈ Q0( ˜B). The practical relevance is to applications in biology and chemistry where Jacobian matrices often have a constant initial factor, but a second factor with variable entries whose signs are, however, known. A number of particular examples were presented in [12]. More generally it may also happen thatABisK-quasipositive for eachBin some setB, whereBis a proper subset of the closure of some qualitative class.

Given a set of K-quasipositive matrices of the form {AB : B ∈ B}, we would hope that there is a natural graph-theoretic test to decide which mem-bers of this set are also K-irreducible. Theorem 1 provides precisely such a condition: providedBis row-complete and the initial factorA satisfies a mild genericity condition,K-irreducibility of AB follows from strong connectedness of the bipartite digraphGA,B. In the special case where K is the nonnegative

orthant,Ais the identity matrix, andBis the set of nonnegative matrices, the results reduce to well known ones.

Remark 6. Our motivation for considering row-complete sets of matrices is as follows: consider a set ofK-quasipositive matrices of the form{AB : B∈B}, whereBis row-complete. Clearly

AB =AX

k

B(k)=X

k

AB(k)=X

k

AkBk.

So any matrix in the set can be written as a sum of rank 1 K-quasipositive matrices.

3. The main result

From now onK⊂Rn will be a CCP cone inRn,Aann×mmatrix andB

a row-complete set ofm×nmatrices. For anyB ∈B,AB is ann×n matrix. The main result of this paper is:

Theorem 1. Assume thatImA6⊆spanF for any nontrivial faceF ofK. Sup-pose that for each B ∈ B, AB is K-quasipositive. Then whenever GA,B is

strongly connected,AB is also K-irreducible.

An immediate corollary of Theorem 1 is:

Corollary 2. Assume that ImA 6⊆ spanF for any nontrivial face F of K. Suppose that for eachB∈B,ABisK-positive. Then wheneverGA,Bis strongly

connected,AB is alsoK-irreducible.

Proof. _{K-positivity of AB impliesK-quasipositivity of AB. The result now}

Remark 7. Note that ifImA⊆spanF for some nontrivial faceF of K, then trivially AB isK-reducible. To see that the assumption that ImA6⊆spanF is in general necessary in Theorem 1, consider the matrices

Λ =

1 2 2 1

, A=

1 1 2 2

, B=

a b

c d

wherea, b, c, d≥0. LetK={Λz : z∈R2≥0}. Then

ABΛ1= (a+c+ 2(b+d))Λ1, ABΛ2= (2(a+c) +b+d)Λ1

which are both clearly inK for any a, b, c, d≥0. SoAB isK-positive. On the other hand F ={rΛ1 : r ≥0} satisfies (AB)F ⊆ F for all B, so AB is K -reducible for all nonnegative values ofa, b, c, d. However, fora, b, c, d >0,GA,B

is the complete bipartite digraphK2,2, which is obviously strongly connected.

4. Proofs

We need some preliminary lemmas in order to prove Theorem 1. The fol-lowing is proved as Lemma 4.4 in [12]:

Lemma 3. Let F be a face of K, v1, v2 ∈ F, and w ∈ Rn. If there exist

α, β >0 such thatv1+αw∈K andv2−βw∈K, thenw∈span(F).

Proof. _{Define y1 ≡v1+αw and y2 ≡v2−βw. Theny3 ≡y1+ (α/β)y2 =}

v1+ (α/β)v2 ∈F. Sincey3 ∈F, y3−y1 = (α/β)y2 ∈K, andy1 ∈K, by the definition of a face,y1∈F. Sow= (y1−v1)/α∈span(F).

Extremals. A one dimensional face of K will be termed an extremal ray or an extremal for short, and any nonzero vector in an extremal ray will be an extremal vector ofK.

Lemma 4. Suppose that for each B ∈B,AB is K-quasipositive. Let E be an extremal vector of K. Then for each (fixed) j either Aj = rE for some real

numberror Bj_{E ≥0 for allB ∈BorB}j_{E ≤0 for allB∈B.}

Proof. _{Suppose there exist j and B, B ∈ B such that p1 ≡ B}j_{E > 0 and}

p2 ≡ −BjE > 0. Note that AB (j)

= AjB j

and AB(j) = AjBj. Since B is

row-complete,B(j), B(j)∈B and soAB(j),AB(j)areK-quasipositive. Letα1 andα2 be such that AB

(j)

E+α1E ∈K and AB(j)E+α2E ∈K respectively. We can assume (w.l.o.g.) thatα1, α2>0. Then:

AB(j)E+α1E=AjB j

E+α1E=α1E+p1Aj ∈K

and

AB(j)E+α2E =AjBjE+α2E =α2E −p2Aj ∈K.

Remark 8. An alternative phrasing of Lemma 4 is that ifAj is not collinear

withE then eitherBj_{∈ Q1(E}T_{)for allB ∈BorB}j_{∈ Q1(−E}T_{)for allB∈B.}

Lemma 5. Let F be a nontrivial face of K, {J(k)} be a finite set of n×n K-quasipositive matrices and J = P

J(k). If there exists x ∈ F such that

Jx∈spanF, then J(k)x∈spanF for each k.

Proof. _{ByK-quasipositivity of eachJ(k) we can write}

J(k)x=pk+qk

Lemma 6. LetAB beK-quasipositive for eachB∈Band letF be a nontrivial face ofK spanned by (pairwise independent) extremal vectors{Λi}i∈I. Choose

and fix someB ∈B. Then given any nonempty setR ⊆ {1, . . . , m}, either (i)

Suppose (iii) does not hold, i.e., P

k∈RAkBkΛi ∈ spanF for each Λi ∈ F.

Applying Lemma 5 withJ(k) =AkBk, we get for eachk∈ Rand each Λi∈F

thatAkBkΛi∈spanF. So for each fixedk∈ R, eitherAk∈spanForBkΛi= 0

for alli∈ I.

Proof of Theorem 1. _{We show that if AB is K-reducible for some B ∈} B, then GA,B cannot be strongly connected. Let {Λi} be a set of pairwise

independent extremal vectors ofK. LetF be a nontrivial face ofK such that spanF is left invariant byAB, and letI be the indices of vectors Λi inF, i.e.,

out, and (ii) must hold. ConsequentlyBk_Λ

i= 0 impliesBklΛli= 0 for eachl.

1. Suppose thatRis empty. Then, for each i∈ I, and all k, l,BklΛli = 0.

Fix somei∈ I and somel such that Λli 6= 0; thenBkl= 0 for allk (the

lth column ofBis zero). By the definition ofGA,B, this means that there

are no arcs incident into the row vertex ul. Thus GA,B is not strongly

connected.

2. Suppose thatRis nonempty. Givenk′ _{∈ Rwe can writeA}

k′ =P_i∈IqiΛi

for some constantsqi, so for anyk∈ Rc,

Bk_A k′ =

X

i∈I

qiBkΛi= 0.

Moreover, since for eachi∈ I and eachl,BklΛli= 0, we getBklAlk′ = 0.

In terms ofGA,B, this means that there is no directed path of length 2 from

any column vertexvk with k∈ Rc to a column vertex vk′ with k′ ∈ R.

Thus there is no directed path (of any length) of the formvk· · ·vk′ with k∈ Rc_{, k}′_{∈ R, andG}

A,Bis not strongly connected.

5. Examples

The examples below illustrate application of Theorem 1 and Corollary 2.

Example 1. Consider the special case where Corollary 2 is applied with

A =I, B the nonnegative matrices and K =Rn≥0. Since ImI = Rn, clearly ImI 6⊆spanF for any nontrivial faceF ofRn

≥0. It is also immediate that for eachB∈B, the n×nmatrixIB is K-positive. Now we show that that GI,B

is strongly connected if and only ifGB is strongly connected. (i) SupposeGB

is strongly connected. An arc from vertex i to vertex j in GB implies that

Bij 6= 0. But Bij =IiiBij, and since Iii = 1 this implies that there exists a

path uiviuj in GI,B. Thus a path from vertex i to vertex j in GB implies a

path from vertex ui to vertex uj in GI,B. Thus strong connectedness of GB

implies a path between any two row verticesui anduj ofGI,B. On the other

hand since all arcsuivi exist inGI,B, the pathui· · ·uj implies the existence of

pathsui· · ·vj, vi· · ·uj and vi· · ·vj. (ii) Suppose GI,B is strongly connected.

The pathvi· · ·vj inGI,B immediately implies a path from vertexito vertexj

inGB. Thus we recover from Corollary 2 the fact that for a nonnegative matrix

B, strong connectedness ofGB implies irreducibility ofB.

Example 2. Let

A= Λ =

 

1 0 −1 1 −2 0

−1 1 0



 and B˜=

 

−1 0 1

0 1 0 1 0 0

 

LetB=Q0( ˜B) and define

Kis a CCP cone in R3. (It is easy to show that any nonsingularn×nmatrix defines a proper simplicial cone inRn in this way.) SinceA= Λ it is immediate that ImA does not lie in the span of any nontrivial face of K. Consider any

B∈B, i.e., any matrix of the form

B=

 

−a 0 b

0 c 0

d 0 0

 

wherea, b, c, d≥0. Since A= Λ,

ABΛ + (a+b+ 2c+d)Λ = Λ(BΛ + (a+b+ 2c+d)I)

and it can be checked that BΛ + (a+b+ 2c+d)I is nonnegative. Thus AB

is K-quasipositive for all B ∈ B. On the other hand GA,B is illustrated in

Figure 1 for anyB∈relintBand can be seen to be strongly connected. SoAB

isK-irreducible for anyB ∈relintB.

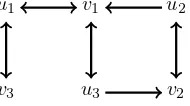
u1 v1 u2

v3 u3 v2

Figure 1:G_A,B for the system in Example 2 withB∈relintB. By inspection the digraph is strongly connected.

Example 3. We consider cases where B is not the closure of a qualitative class, but is a smaller set. Suppose Λ is ann×mmatrix,A= Λ andK={Λz :

z ∈ Rm≥0} is a CCP cone in Rn. As in the previous example, it is immediate that ImAdoes not lie in the span of any nontrivial face of K. For somem×n

matrix ˜B, define

B={DB˜ : Dis a nonnegative diagonal matrix}.

Clearly B is row-complete. Suppose, further, that ˜BΛ is nonnegative, and consequentlyDB˜Λ is nonnegative for any nonnegative diagonal matrixD. Then given anyB=DB˜∈B,ABΛ = Λ(DB˜Λ), and soABisK-positive. Corollary 2 applies and can be used to deduceK-irreducibility ofAB. For example, choose

A= Λ =

 

1 1 −1 0 2 4 1 2 −3



 and ˜B =  

3 0 −1 1 3 0

−2 1 2



.

As in Example 2, Since Λ is nonsingular, the coneKgenerated by Λ is a proper cone in R3. It can be checked that ˜BΛ is a nonnegative matrix, so AB is

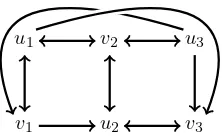
u1 v2 u3

v1 u2 v3

Figure 2: G_{A,B for the system in Example 3 with}B ∈relintB. The digraph contains the Hamiltonian cycle (u1v3u2v2u3v1) and so is strongly connected.

any B =DB˜ where D has positive diagonal entries). The digraph is strongly connected and so, by Corollary 2,AB isK-irreducible.

Example 4. The following is an example with a cone which is not solid. Let

A= any nontrivial face (i.e., any extremal) ofK. Defining

T =

is illustrated in Figure 3 for any B ∈ relintB and can be seen to be strongly connected. SoAB isK-irreducible for anyB∈relintB.

Example 5. As a final, nontrivial, example, let

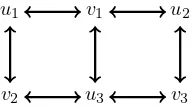
v2 u3 v3

u1 v1 u2

Figure 3:G_A,B for the system in Example 4 withB∈relintB. By inspection the digraph is strongly connected.

andB=Q0(−AT). Define

K={Λz : z∈R8≥0}.

Various facts can be confirmed either theoretically or via computation: 1. K is a proper cone inR4.

2. ImA6⊆spanF for any nontrivial faceF ofK. 3. For eachB ∈B,AB isK-quasipositive.

Some insight into the structure ofK and the proof of these facts is provided in the Appendix. It now follows from Theorem 1 that wheneverGA,B is strongly

connected,AB (and hence AB+αI for eachα∈R) is also K-irreducible. For example, it can easily be checked that forB∈relintB(namelyB∈ Q(−AT_)),

GA,B is strongly connected and so AB is K-irreducible. The condition that

B ∈ relintB can be relaxed while maintainingK-irreducibility. The digraphs

GA,B for two choices ofB∈Bare illustrated in Figure 4.

u4

u2

u3

v3 v2

v1

u1

u4

u2

u3

v3 v2

v1

u1

Figure 4:Left.The digraphG_A,BwhereA_{is as shown in (2) and}B_{is any matrix in}Q(−AT ). u_{i is the row vertex corresponding to row}i_inA_{, while}v_{i corresponds to column}i_. Right. SettingB22=B13=B34= 0 removes the arcsv2u2,v1u3,v3u4 fromGA,B, but still gives a strongly connected digraph.

Confirming K-irreducibility for choices ofB without the aid of Theorem 1 is possible but tedious, requiring computation of the action ofAB on each of the 26 nontrivial faces ofK.

6. Concluding remarks

Rather different graph-theoretic approaches to questions of irreducibility of matrices are taken in [2, 3, 4]. In [4], for example, polyhedral cones with nK

were presented derivingK-irreducibility of matrices fromK-quasipositivity of these matrices and strong connectedness of the digraphs. The construction relies, however on knowledge of the matrix action on each extremal ofK.

In our approach described here, K is not necessarily polyhedral and no knowledge of the facial structure or particular action of matrices on extremals ofK is required. In compensation, however, we assume that a set of matrices with a particular structure (row-completeness) areallK-quasipositive, and K -quasipositivity of this entire set is essential for the proofs. This stronger assump-tion aboutK-quasipositivity allows weaker assumptions about the structure of

Kand the action of the matrices on faces ofK. Thus both the construction of the digraph here and the assumptions are somewhat different from earlier work in this area.

Appendix A. Some details connected with Example 5

That K is closed and convex is immediate from the definition. Note that ΛP =Iwhere P is the nonnegative matrix

P = is strictly positive, so pT_{Λz > 0 for any nonnegative and nonzero z. Thus}

p∈intK∗_{, whereK}∗_{is the dual cone toK. SinceK}∗_{has nonempty interior this}

implies thatKis pointed (ifKcontains a nonzeroy∈R4such thaty,−y∈K, we get the contradiction pT_{y > 0 and p}T_{(−y) > 0). Putting together these} observations,K is a proper cone inR4.

It can be checked that each Λi spans a different extremal ofK, namely, no

Λican be constructed as a nonnegative combination of others. Further, the two

dimensional faces ofK are spanned by pairs of Λi foribelonging to:

{1,2},{1,3},{2,4},{3,4},{1,5},{2,6},{3,7},{4,8},{5,6},{5,7},{6,8},{7,8}.

while the three dimensional faces of K are spanned by sets of four Λi for i

belonging to:

{1,2,3,4},{1,2,5,6},{3,4,7,8},{1,3,5,7},{2,4,6,8} and {5,6,7,8}.

That ImAdoes not lie in spanF for any nontrivial faceF can be confirmed theoretically, or checked by demonstrating for each three dimensional face F

That AB is K-quasipositive for all B ∈ Q0(−AT_{) can easily be checked.}

In other wordsAB isK-quasipositive.

References

[1] A. Berman and R. Plemmons. Nonnegative matrices in the mathematical sciences. Academic Press, New York, 1979.

[2] G. Barker and B. Tam. Graphs for cone preserving maps. Linear Algebra Appl., 37:199–204, 1981.

[3] G. Barker and B. Tam. Graphs and irreducible cone preserving maps. Linear and Multilinear Algebra, 31:19–25, 1992.

[4] H. Kunze and D. Siegel. A graph theoretic approach to strong monotonicity with respect to polyhedral cones. Positivity, 6:95–113, 2002.

[5] G. Barker. The lattices of faces of a finite dimensional cone.Linear Algebra Appl., 7:71–82, 1973.

[6] J. S. Vandergraft. Spectral properties of matrices which have invariant cones. SIAM J. Appl. Math., 16(6):1208–1222, 1968.

[8] M.W. Hirsch and H. Smith. Handbook of Differential Equations: Ordi-nary Differential Equations, Vol II, chapter Monotone Dynamical Systems, pages 239–357. Elsevier B. V., Amsterdam, 2005.

[9] R. A. Brualdi and B. L. Shader. Matrices of sign-solvable linear systems. Number 116 in Cambridge tracts in mathematics. Cambridge University Press, 1995.

[10] M. Banaji and C. Rutherford. P-matrices and signed digraphs. Discrete Math., 311(4):295–301, 2011.

[11] M.W. Hirsch. Systems of differential equations that are competitive or cooperative II: convergence almost everywhere. SIAM J. Math. Anal., 16(3):423–439, 1985.

[12] M. Banaji. Monotonicity in chemical reaction systems. Dyn Syst, 24(1):1– 30, 2009.