Penyelesaian Pemrograman Separabel Menggunakan Fungsi Linier Piecewise Dengan Formulasi Delta

PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN FUNGSI LINIERPIECEWISE DENGAN FORMULASI DELTA

SKRIPSI

RINI ANDRIA NINGSIH

060803004

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

LINIERPIECEWISE DENGAN FORMULASI DELTA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

RINI ANDRIA NINGSIH 060803004

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

i

PERSETUJUAN

Judul : PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN

FUNGSI LINIERPIECEWISE DENGAN FORMULASI DELTA

Kategori : SKRIPSI

Nama : RINI ANDRIA NINGSIH

Nomor Induk Mahasiswa : 060803004

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Januari 2011

Komisi Pembimbing:

Pembimbing 2 Pembimbing 1

Drs. Suwarno Ariswoyo, M.Si Drs.Faigiziduhu Bu’ulolo, M.Si NIP.19500321 198003 1 001 NIP. 19531218 198003 1 003

Diketahui/ Disetujui oleh:

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

PERNYATAAN

PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN FUNGSI LINIERPIECEWISE DENGAN FORMULASI DELTA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Januari 2011

iii

PENGHARGAAN

Puji dan Syukur penulis panjatkan kepada Tuhan Yang Maha Pengasih dan Maha Penyayang, dengan limpah karunia-Nya kepada penulis selama dalam proses penyelesaian skripsi ini.

Skripsi ini disusun sebagai salah satu syarat untuk memperoleh gelar sarjana Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara. Skripsi ini merupakan hasil dari studi literatur yang telah dikerjakan penulis, dengan judul ” PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN FUNGSI LINIERPIECEWISE _{DENGAN FORMULASI DELTA”.}

Penulis menyadari selama pengerjaan penulisan ini masih menemukan banyak kesulitan yang disebabkan oleh terbatasnya ilmu yang penulis miliki. Karena itu penulis menyadari tanpa bantuan dari berbagai pihak tidaklah mungkin skripsi ini dapat diselesaiakan dengan baik.

Pada kesempatan ini, penulis ingin menyampaikan ucapan syukur dan terima kasih kepada:

1. Bapak Drs. Faigiziduhu Bu’ulolo, M.Si selaku dosen pembimbing I yang telah memberikan banyak bimbingan dan arahan dalam penulisan skripsi ini.

2. Bapak Drs. Suwarno Ariswoyo, M.Si selaku dosen pembimbing II atas bantuan dan penjelasan yang diberikan demi selesainya skripsi ini.

3. Bapak Drs. H. Haludin Panjaitan dan Ibu Dra. Elly Rosmaini, M.Si selaku komisi penguji atas masukan dan saran yang telah diberikan demi perbaikan skripsi ini.

4. Bapak Prof. Dr. Tulus, M.Si selaku ketua jurusan departemen matematika FMIPA USU. 5. Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU.

6. Semua Dosen Departemen Matematika FMIPA USU dan Pegawai FMIPA USU yang tidak bisa disebutkan satu persatu.

disebutkan satu persatu, spesial buat Muhammad Yudha Azlan, yang sangat banyak membantu, selalu menyemangati, dan mendukung selama proses pengerjaan skripsi ini.

9. Buat keluarga terkasih Ibu Suriyana, Bapak Supriadi, sepupu-sepupu penulis Sari, Didiek, Dinna, Teguh, Tiwi, Reza, dan seluruh keluarga besar lainnya yang namanya tidak bisa disebutkan satu persatu, atas motivasi serta doa yang sangat berarti dalam hidup penulis.

Penulis menyadari bahwa masih banyak kekurangan dalam menyelesaikan skripsi ini. Oleh karena itu penulis mengharapkan masukan dan kritikan yang bersifat membangun demi kesempurnaan skripsi ini.

Medan, Januari 2011

v

PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN FUNGSI LINIERPIECEWISE DENGAN FORMULASI DELTA

ABSTRAK

SOLUTION OF SEPARABLE PROGRAMMING USE PIECEWISE LINEAR FUNCTION WITH DELTA FORMULATION

ABSTRACT

vii

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Gambar ix

Daftar Tabel x

Bab 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 4

1.3 Pembatasan Masalah 4

1.4 Tujuan Penelitian 4

1.5 Manfaat Penelitian 4

1.6 Metodologi Penelitian 5

1.7 Tinjauan Pustaka 5

Bab 2 LANDASAN TEORI 8

2.1 Teori-Teori Pendukung 8

2.1.1 Ruas Garis 8

2.1.2 Pemrograman tak linier 9

2.1.3 Fungsi Kontinu 9

2.1.4 Solusi Fisibel dan Solusi Optimal 9

2.1.5 Himpunan Buka 10

2.1.6 Global Optimal 10

2.1.8 Fungsi Konveks 10

2.1.9 Fungsi Konkaf 11

2.1.10 Teknik Batas Atas 12

2.2 Metode Simpleks dan Metode Simpleks untuk Variabel Terbatas 13

2.2.1 Metode Simpleks 13

2.2.2 Metode Simpleks untuk Variabel Terbatas 14

Bab 3 PEMBAHASAN 15

3.1 Pemrograman Separabel 15

3.2 Pemrograman Separabel dengan Menggunakan Hampiran Fungsi Linier Piecewise 16

3.3 Formulasi Lambda dan Formulasi Delta 17

3.3.1 Formulasi Lambda 17

3.3.2 Formulasi Delta 20

3.4 Menyelesaikan Persoalan Pemrograman Separabel dengan Menggunakan Fungsi Linier Piecewise dengan Formulasi Delta 23

Bab 4 KESIMPULAN DAN SARAN 28

4.1 Kesimpulan 28

4.2 Saran 29

ix

DAFTAR GAMBAR

Halaman

Gambar 2.1 Fungsi konveks dan fungsi konkaf pada pemrograman separabel 12

Gambar 3.1 Fungsi perkiraan linear putus-bersambung 16

Gambar 3.2 Memperkirakan f x₁( )₁ pada panel A, dan f x₂( )₂ pada panel B dengan fungsi linear

putus-bersambung 20

Gambar 3.3 Fungsi Linear putus bersambung sebagai hampiran fungsi nonlinear dengan formulasi delta 22

DAFTAR TABEL

v

PENYELESAIAN PEMROGRAMAN SEPARABEL MENGGUNAKAN FUNGSI LINIERPIECEWISE DENGAN FORMULASI DELTA

ABSTRAK

SOLUTION OF SEPARABLE PROGRAMMING USE PIECEWISE LINEAR FUNCTION WITH DELTA FORMULATION

ABSTRACT

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Dalam keadaan dimana menghadapi persoalan program linier yang besar, maka akan berusaha untuk mencari penyelesaian optimal dengan menggunakan algoritma komputasi, seperti algoritma simpleks dengan biaya sekecil mungkin. Salah satu variasi model program linier adalah pemrograman separabel.

Pemrograman separabel adalah pemrograman tak linear yang fungsi objektif dan fungsi kendalanya dapat diekspresikan sebagai penjumlahan fungsi dan setiap fungsinya hanya terdiri atas satu variabel.

Secara umum model dasar dari suatu pemrograman separabel adalah sebagai berikut:

Optimumkan



_{1 2}



 

1

, ,...,

n

n j j

j

Z f x x x f x



 



Fungsi kendala :



1 2



 

1

, ,...,

n

i n ij j i

j

g x x x g x atau b







 

0 j x  Untuk i = 1,2,..,m

j = 1,2,..,n

Pemrograman separabel hanya digunakan untuk menganalisis persoalan-persoalan yang memiliki fungsi-fungsi kontinu dengan perubahan gradien yang kecil. Jika fungsi kontinu mengalami perubahan besar pada gradiennya, maka dapat menerapkan program integer tercampur. Sifat lainnya adalah pemrograman separabel memberikan optimum pada fungsi nonlinear, sedangkan program integer dapat memberikan global optimum.

Pada umumnya masalah pemrograman separabel dapat diselesaikan dengan menggunakan kondisi Karush-Kuhn-Tucker. Selain itu dapat juga diselesaikan dengan menggunakan hampiran fungsi linier piecewise, atau dengan metode lain seperti metode cutting plane, program dinamik, dan lain-lain.

Pada tulisan ini akan membahas masalah pengoptimuman yang menghampiri masalah pemrograman separabel. Hampiran dilakukan dengan mengganti setiap fungsi nonlinier dengan fungsi linierpiecewise.

Suatu fungsi tujuan f x_j( _j) dalam pemrograman separabel dikatakan putus-bersambung (piece-wise) karena segmen-segmen dari fungsi f x_j( _j) tersebut secara sendiri-sendiri (terputus-putus) dipisah-pisahkan dan membentuk fungsi yang linier sehingga diperoleh f x₁( ),₁ f x₂( ),₂ f x₃( )₃ , dan seterusnya. Jika fungsi yang diputus-putus tersebut disambung, maka hasilnya diperkirakan akan mendekati fungsi nonlinier.

Pada pemrograman separabel, ada tiga kondisi yaitu fungsi tujuannya nonlinier, fungsi kendalanya linier, atau fungsi tujuan dan kendalanya nonlinier. Sehingga pada ketiga kondisi tersebut dapat diganti dengan fungsi linier yang dianggap sama atau mendekati keadaan nonlinier, yaitu dengan cara membagi suatu bidang fungsi nonlinier menjadi beberapa sub bidang atau segmen.

3

Penyelesaian masalah hampiran fungsi linier piecewise dapat juga diselesaikan metode simpleks dengan restricted basis entry rule (variabel terbatas). Jika fungsi objektifnya merupakan fungsi konveks sempurna dan fungsi kendalanya merupakan konveks, maka aturan variabel terbatas pada metode simpleks dapat dihilangkan dan bisa digunakan hanya dengan metode simpleks biasa.

Keakuratan dari hampiran fungsi linier piecewise dipengaruhi oleh banyaknya titik kisi. Jika titik kisi bertambah, maka variabel pada masalah hampiran pemrograman linier akan bertambah. Untuk mengatasi hal tersebut, dapat digunakan modifikasi metode hampiran yang menggunakan sedikit titik kisi diawal perhitungan.

Misalkan f x( ) dan g x( ) memenuhi semua asumsi dari pemrograman separabel dan fungsi linier bagian demi bagian yang diperoleh, dapat dituliskan kembali sebagai fungsi linier dengan menghapus indeks khusus pada suatu model pemrograman linier, maka penyelesaian optimalnya secara otomatis memenuhi suatu batasan yang diberikan.

Cara efisien dan cepat untuk menyelesaikan model tersebut adalah dengan menggunakan jenis tertentu dari metode simpleks yang berhubungan dengan batas atas kendala. Kemudian setelah memperoleh suatu penyelesaian optimal dari model tersebut, maka hitunglah secara berurutan

1

nj

j jk

k

x x







, dengan j=1,2,...,n untuk

melihat penyelesaian yang optimal dari pemrograman separabel sebelumnya (yang didekati secara bagian demi bagian).

Dari uraian di atas, maka penulis memilih judul ” Penyelesaian

Pemrograman Separabel Menggunakan fungsi linier Piecewise dengan

1.2. Perumusan Masalah

Permasalahan yang akan diuraikan dalam tulisan ini adalah bagaimana cara mengoptimumkan masalah pada pemrograman separabel. Di mana pada pemrograman ini, fungsi yang nonlinier dapat diselesaikan dengan hampiran fungsi linier piecewise

dengan menggunakan formulasi delta.

1.3. Pembatasan Masalah

Ada dua cara untuk memformulasikan fungsi linier piecewise, yaitu dengan formulasi lambda dan formulasi delta. Pada formulasi lambda, variabel  didefinisikan untuk setiap titik kisi, sedangkan formulasi delta, variabel  didefinisikan untuk setiap interval diantara titik kisi.

Akan tetapi pada tulisan ini untuk membatasi persoalan, maka hanya akan membahas fungsi linier piecewise dengan formulasi delta. Karena, untuk formulasi lambda telah dibahas pada tulisan sebelumnya.

1.4. Tujuan Penelitian

Tujuan penelitian dari penulisan ini adalah menyelesaikan permasalahan pemrograman separabel dengan hampiran fungsi linier piecewise dengan menggunakan formulasi delta tanpa harus mengabaikan kendala yang ada, kemudian mengoptimalkan fungsi tujuan dari pemrograman separabel.

1.5. Manfaat Penelitian

5

yang dimaksud adalah memaksimumkan atau meminimumkan fungsi tujuan dari pemrograman separabel.

1.6. Metode Penelitian

Untuk melancarkan penelitian ini, maka metode yang dilakukan adalah dengan studi literatur. Oleh karena itu, ada beberapa tahap yang dilakukan dalam pemecahan masalah yang dihadapi, yaitu:

1. Menjelaskan pengertian dasar pemrograman separabel,

2. Menjelaskan pemrograman separabel dengan menggunakan hampiran fungsi linier piecewise,

3. Menjelaskan pengertian formulasi lambda dan formulasi delta,

4. Menyelesaikan suatu masalah sebagai aplikasi dari hampiran fungsi linier

piecewise dengan formulasi delta.

1.7. Tinjauan Pustaka

Hiller dan Liberman (1990) mengatakan pemrograman separabel dapat diasumsikan bahwa fungsi objektif f x( ) disebut konkaf, dan fungsi konstrain g x_i( ) disebut konfek merupakan fungsi-fungsi dari pemrograman separabel. Model dasar program separabel adalah sebagai berikut:

Optimumkan ( maksimumkan atau minimumkan ):



1 2



 

1

, ,...,

n

n j j

j

Z f x x x f x



 



Fungsi kendala :



1 2



 

1

, ,...,

n

i n ij j i

j

g x x x g x atau b







 

0 j x 

Contoh :

Min Z 30x135x2 212 3x22

Kendala 2 2

1 2 2 250

x  x 

1 2 20

x  x

1, 2 0

x x 

Untuk persoalan pengoptimuman contoh tersebut yang merupakan sebuah persoalan pemrograman separabel dengan :

2

1 1 1 1

2

11 1 1

21 1 1

1

( ) 30 2 ( )

( ) 250

f x x x

g x x g x x b      2

2 2 2 2

2

12 2 2

22 2 2

2

( ) 35 3 ( ) 2 ( )

20

f x x x

g x x g x x b

 

  

B.D. Nasendi dan Affendi Anwar (1984) menjelaskan jenis-jenis variasi model program linier, menjelaskan pengertian program separabel dan model dasar dari suatu pemrograman separabel. Fungsi f(x) dikatakan dapat dipisahkan (separabel) jika dapat menuliskan fungsi tersebut sebagai jumlah dari n buah fungsi yang terpisah-pisah. Secara sistematis, pernyataan tersebut adalah sebagai berikut:

1 2

( ) ( , ,..., _n)

Z  f x  f x x x adalah separabel, Jika f x x( ,_{1 2},...,x_n) f x₁( )₁  f x₂( ) ...₂   f x_n( _n)

Suatu fungsi tujuan f x_j( _j) dalam program separabel disebut putus-bersambung (piece-wise) karena segmen-segmen dari fungsi f x_j( _j) tersebut secara sendiri-sendiri, dipisah-pisahkan dan membentuk fungsi yang linier sehingga dapat

1( ),1 2( ),2 3( )3

f x f x f x , dan seterusnya. Jika fungsi yang diputus-putus tadi disambung, maka hasilnya diperkirakan akan mendekati fungsi nonlinier.

7

nonlinier ke dalam beberapa sub-bidang, ada dua cara untuk memformulasikan fungsi linier putus-bersambung, yaitu dengan formulasi lambda dan formulasi delta.

Buku lain karangan Winston (1995) menjelaskan bahwa fungsi yang didefinisikan oleh rumus yang berlainan dibagian yang berbeda dari daerah asalnya dinamakan fungsi putus-bersambung.

LANDASAN TEORI

Untuk mempermudah dalam menyelesaikan pembahasan pada bab ini, maka akan diberikan beberapa definisi dan beberapa teori dasar yang mendukung.

2.1. Teori – Teori Pendukung

2.1.1. Ruas Garis

Definisi 1. Ruas Garis

Jika ada di R2 atau R3, maka sebuah garis pada Rn dibentuk dari dua titik. Pada R2

garis yang menghubungkan dua buah titik yakni x₁ dan x₂ dapat diekspresikan sebagai himpunan dari semua titik x, yang memenuhi:

2 ( 1 2) 1 (1 ) 2

x x  x x x   x

Jika x₁ dan x₂ merupakan titik-titik yang berada di n

R , maka garis yang menghubungkan x₁ dan x₂ adalah himpunan dari semua titik yang terdapat pada himpunan

1 { 1 (1 ) ,2

L  x xx   x dengan 0}

dengan catatan untuk 0, xx₂ dan untuk 1, xx₁. Sehingga untuk 0  1, didapat x merupakan titik yang terdapat pada garis L₁ yang mana berada diantara x₁ dan x₂. Sehingga dapat didefinisikan bahwa ruas garis yang berada diantara x₁ dan x₂adalah himpunan titik pada

2 { 1 (1 ) 2

9

2.1.1. Pemrograman Tak Linier

Secara umum, masalah pemrograman tak linear adalah menentukan g x_i( ) sehingga ( )

f x maksimum/minimum, dengan kendala g x_i( )b_i untuk setiap i1, 2,...,m dan 0

x , di mana fungsi f x( ) dan fungsi g x_i( ) merupakan fungsi-fungsi dengan n

peubah.

2.1.2. Fungsi Kontinu

Jika f didefinisikan pada himpunan bagian D dari Rn, maka

lim

( ) x a

f x L

 

bermakna bahwa untuk setiap bilangan  0 terdapat sebuah bilangan terkait  0 sedemikian rupa sehingga f x( ) L  bilamana xD dan 0  x a  .S

[James Stewart, 2008]

2.1.3. Solusi Fisibel dan Solusi Optimal

Definisi 2. Solusi Fisibel

Misalkan diberikan masalah pengoptimuman Min (Maks) f x( ), terhadap ( )

g x  p; x0, dengan xRn. Maka solusi fisibel dari masalah pengoptimuman tersebut adalah nilai yang memenuhi kendala g x( ) p x; 0.

[Rao, 1985]

Definisi 3. Solusi Optimal

Solusi optimal adalah solusi fisibel yang mengoptimumkan fungsi objektif (tujuan).

2.1.4. Himpunan Buka

Himpunan GRn dikatakan terbuka di Rn jika  x G terdapat bilangan real r0 sehingga  y Rn yang memenuhi x y r adalah anggota G.

Catatan:

Di , ( ,1 2,...,

n

n

R x x x didefinisikan sebagai x12  x22 ... xn2 .

[Bartle, 1976]

2.1.5. Global Optimal

Jika f merupakan suatu fungsi konveks yang selalu berbeda, kemudian kondisinya penting dan cukup untuk x* menjadi suatu global optimal atas f pada Rn adalah

*

( ) 0

f x

  .

2.1.6. Gradien

Jika f adalah fungsi dua variabel x dan y, maka gradien f adalah fungsi vektor f yang didefinisikan oleh f x y( , ) f x y_x( , ), f x y_y( , ) f i f j

x y

 

   

 

[James Stewart, 2008]

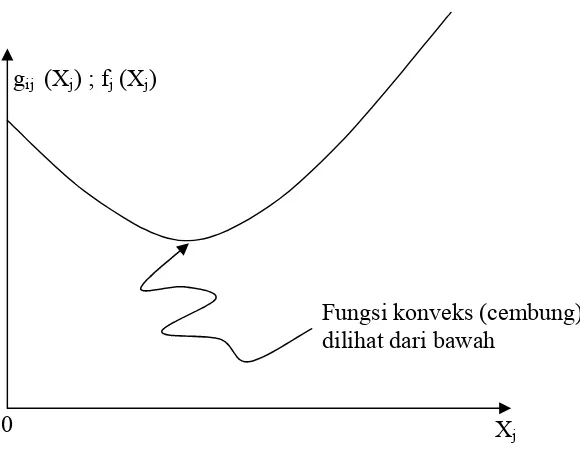
2.1.7. Fungsi Konveks

1 2

( , ,..., _n)

f x x x adalah fungsi konveks jika, untuk setiap pasangan titik pada grafik

1 2

( , ,..., _n)

11

Disebut fungsi konveks sempurna jika segmen garis berada seluruhnya di atas grafik kecuali pada titik akhir (endpoint) segmen garis.

Ada dua sifat penting fungsi konveks, yaitu:

 Jika f x x( ,1 2,...,xn) adalah fungsi konveks, maka

1 2 1 2

( , ,..., _n) ( , ,..., _n)

g x x x  f x x x adalah fungsi konkaf, dan sebaliknya.  Penjumlahan fungsi – fungsi konveks adalah fungsi konveks.

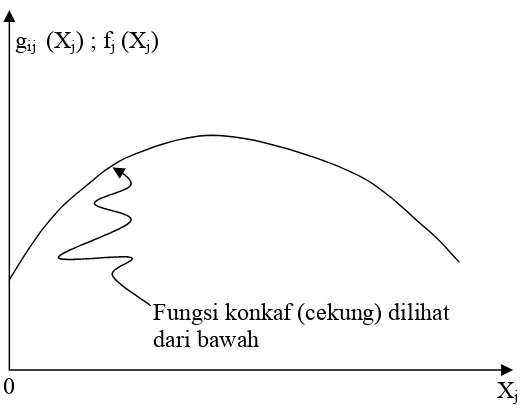
2.1.8. Fungsi Konkaf

1 2

( , ,..., _n)

f x x x adalah fungsi konkaf jika untuk setiap pasangan titik pada grafik

1 2

( , ,..., _n)

f x x x , segmen garis yang menggabungkan kedua titik tersebut berada di bawah atau pada grafik f x x( ,_{1 2},...,x_n).(lihat gambar 2.2).

Disebut fungsi konkaf sempurna jika segmen garis berada seluruhnya di bawah grafik kecuali pada titik akhir (endpoint) segmen garis.

Gambar 2.1. fungsi konkaf pada pemrograman separabel Fungsi konkaf (cekung) dilihat

dari bawah

0 _Xj

Gambar 2.2. fungsi konveks pada pemrograman separabel

2.1.9. Teknik Batas Atas

Teknik batas atas memberikan suatu cara untuk menyempurnakan metode simpleks untuk situasi yang lazim di mana banyak atau semua variabel mempunyai batas-batas atas secara eksplisit. Teknik ini memberikan kemudahan untuk menyelesaikan masalah-masalah besar. Pada umumnya kendala batas atas yaitu:

1 2

1 2 1

...

( ... )

j j jk i

j j jk

j i

x x x b

atau x x x b atau

x b

       



Fungsi konveks (cembung) dilihat dari bawah

0 _Xj

13

2.2. Metode Simpleks dan Metode Simpleks untuk Variabel Terbatas

2.2.1. Metode Simpleks

Metode sinpleks merupakan algoritma yang efisien untuk menyelesaikan persoalan-persoalan pemrograman linier.

Diberikan pemrograman linier dalam bentuk standart: Min Z C xT

Terhadap Axb 0 x

Langkah-langkah iterasi formal dari metode simpleks adalah sebagai berikut:  Langkah 1 : Dengan menggunakan bentuk standar (dengan sisi kanan semua

nonnegatif), tentukan pemecahan dasar awal yang layak.

 Langkah 2 : Pilih variabel masuk dari antara variabel nondasar dengan menggunakan kondisi optimalitas.

 Langkah 3 : Pilih variabel keluar dari variabel dasar saat ini dengan menggunakan kondisi kefisibelan.

 Langkah 4 : Tentukan nilai variabel yang baru dengan membuat variabel masuk tersebut dengan variabel dasar dan variabel keluar sebagai variabel nondasar, kemudian kembali ke langkah 2.

Catatan:

Kondisi Optimalitas : Variabel masuk dalam maksimisasi (minimisasi) adalah variabel nondasar dengan koefisien yang paling positif (negatif) dalam persamaan tujuan. Koefisien dengan nilai yang sama dapat diplih secara sembarang. Nilai optimum dicapai ketika semua koefisien nondasar dalam persamaan tujuan adalah nonpositif (nonnegatif).

2.2.2. Metode Simpleks Untuk Variabel Terbatas

Diberikan pemrograman linier dalam bentuk standart: Min Z C xT

Terhadap Axb 0 x 1

Berikut adalah langkah-langkah iterasi formal dari metode simpleks untuk variabel terbatas:

Langkah 1: Pemrograman linier dalam bentuk kanonik

Langkah 2: pilih kolom pivot, koefisien objektif paling positif (sebagai calon variabel basis), misalkan x_s

1. Jika Us  t1 t2: maka rasio test 1 min , 0

i is is b t a a      _  _    

2. Jika a_is 0 : maka rasio batas atas ₂ min k i, 0 is is U b t a a       _  _   

  dengan Uk adalah batas atas variabel basis x_k pada kendala ke-i.

Langkah 3: x_s min



U t t_k, ,_{1 2}



dengan U_s adalah batas atas variabel x_s. Langkah 4: Jika minimumnya:

i. U_s, substitusikan batas atas untuk x_s(atau x_s) dan x_s tetap variabel nonbasis.

Catatan : substitusikan batas atas x_j x_j U_j  x_j U_j x_j ii.t₁, pivot seperti biasa dan x_s variabel basis, x_s variabel nonbasis.

iii. t₂, substitusikan batas atas untuk variabel basis x_k (atau x_k) dan x_s masuk sebagai basis.

BAB 3

PEMBAHASAN

3.1. Pemrograman Separabel

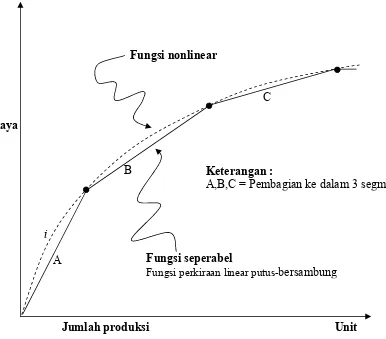
Pemrograman separabel merupakan bentuk atau variasi khusus dari pemrograman nonlinier di mana pada fungsi objektif dan funsi kendalanya dapat dinyatakan sebagai penjumlahan n-fungsi dan pada setiap fungsinya terdiri dari satu variabel. Dalam pemrograman ini, pada fungsi nonlinier dapat digantikan oleh sebuah fungsi linier yang diperkirakan mendekati keadaan fungsi nonlinier semula. (Lihat gambar 3.1).

Gambar 3.1. fungsi perkiraan linear putus-bersambung

Fungsi nonlinear

A

B

C

Fungsi seperabel

Fungsi perkiraan linear putus-bersambung

Jumlah produksi Unit

Biaya

Keterangan :

A,B,C = Pembagian ke dalam 3 segmen

Bentuk umum pemrograman separabel adalah: Optimumkan ( maksimumkan atau minimumkan ):



1 2



 

1

, ,...,

n

n j j

j

Z f x x x f x



 



Fungsi kendala :



1 2



 

1

, ,...,

n

i n ij j i

j

g x x x g x atau b







 

0 j x  Untuk i = 1,2,..,m

j = 1,2,..,n

3.2. Pemrograman Separabel dengan Menggunakan Hampiran Fungsi Linier

Piecewise

Suatu fungsi tujuan f x_j( _j) dalam program separabel disebut putus-bersambung (piece-wise) karena segmen-segmen dari fungsi f x_j( _j) tersebut secara sendiri-sendiri, dipisah-pisahkan dan membentuk fungsi yang linier sehingga dapat

1( ),1 2( ),2 3( )3

f x f x f x , dan seterusnya. Jika fungsi yang diputus-putus tadi disambung, maka hasilnya diperkirakan akan mendekati fungsi nonlinier.

Contoh :

Maksimumkan Z= ₁2 6 _{1 2}2 8 ₂ 1 ₃ 2 x  x  x x  x

Kendala

1 2 3

2

1 2

1 2 3

5 3 , , 0

x x x

x x

x x x

    



Masalah tersebut adalah merupakan persoalan separabel, yaitu:

2

1 1 1 1

11 1 1

2

( ) 6

( ) ( )

f x x x

g x x

g x x

   

2

2 2 2 2

12 2 2

( ) 8

( ) ( )

f x x x g x x

g x x

    

3 3 3

13 3 3

1 ( )

2 ( ) ( ) 0

f x x

g x x g x

17

Untuk persoalan tersebut pada fungsi nonlinier dapat dihampiri oleh fungsi linier piecewise. Bila dimisalkan  merupakan fungsi kontinu dengan variabel  pada interval [a,b], akan didefinisikan fungsi linier piecewise  merupakan hampiran dari fungsi  pada [a,b].

Pada pemrograman separabel, ada tiga kondisi yaitu fungsi tujuannya nonlinier, fungsi kendalanya linier, atau fungsi tujuan dan kendalanya nonlinier. Sehingga pada ketiga kondisi tersebut dapat diganti dengan fungsi linier yang dianggap sama atau mendekati keadaan nonlinier, yaitu dengan cara membagi suatu bidang fungsi nonlinier menjadi beberapa sub bidang. Setelah itu, ada dua cara untuk memformulasikan fungsi linier piecewise, yaitu dengan formulasi lambda dan formulasi delta.

3.3. Formulasi Lambda dan Formulasi Delta

3.3.1. Formulasi Lambda

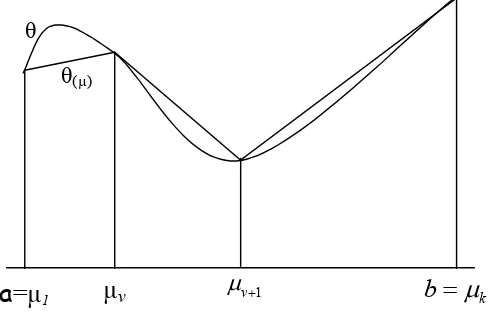
Misalkan  merupakan fungsi kontinu dengan variabel  pada interval [a,b]. Apabila interval [a,b] dipartisi menjadi interval-interval yang lebih kecil, dengan titik partisi (grid point) a ₁, ₂,...,_k b seperti pada gambar 3.3.1.a. pada pengambilan titik-titik kisi ini tidak harus berjarak sama.

Perhatikan fungsi nonlinier  pada interval



 _v, _v1



akan dihampiri dengan cara sebagai berikut: misalkan   _v (1  ) _v1 untuk  

 

0,1 . Dari definisi 1,

 adalah titik kisi pada ruas garis yang menghubungkan _v dan _v1, maka:

^

1

( ) ( _v) (1 ) ( _v )        

[image:32.595.162.384.91.234.2] [image:32.595.198.442.344.500.2]

Gambar 3.3.1.a. Fungsi linier piecewise sebagai hampiran nonlinier.

Hampiran suatu fungsi nonlinier dengan fungsi linier piecewise dipengaruhi oleh banyaknya titik kisi. Perhatikan gambar berikut:

Gambar 3.3.1.b. Fungsi linier piecewise sebagai hampiran fungsi nonlinier dengan titik kisi

Dari gambar tersebut terlihat bahwa, jika semakin banyak titik kisi yang diambil maka diperoleh hampiran yang lebih baik.

Perhatikan contoh ilustrasi berikut:

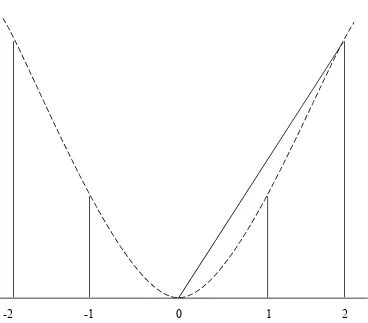
Diberikan fungsi   ( ) 2. Grafik dari fungsi  pada interval [-2,2]. Perhatikan gambar 3.3.1.c berikut.

θ

a =µ1 µv µ µv+1 b =µk

^

( )  

k b



1

v  

θ

µv

θ(µ)

19

-2 -1 0 1 1,5 2

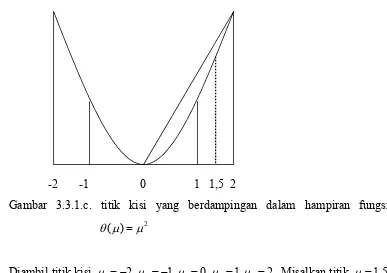
Gambar 3.3.1.c. titik kisi yang berdampingan dalam hampiran fungsi

2

( )   

Diambil titik kisi ₁ 2,₂  1,₃ 0,₄ 1,₅ 2. Misalkan titik  1,5 dituliskan kombinasi konveks 1(1) 1(2)

2 2 dengan titik kisi 4 1,5 2, maka terdapat dua _v positif dan berdampingan, sehingga (1,5)2, 25 dan

1 1

(1,5) (1) (2) 2,5

2 2

      .

Misalkan titik  1,5 dituliskan kombinasi konveks 1(0) 3(2)

4 4 dengan titik kisi ₃ 0,₅ 2, maka terdapat dua _v positif dan berdampingan, sehingga

(1,5) 2, 25

  dan (1,5) 1 (0) 3 (2) 3

4 4

      .

Misalkan titik  1,5 dituliskan kombinasi konveks 1(0) 1(1) 4(2) 6 6 6

dengan titik kisi ₃ 0,₄ 1 dan  ₅ 2. Pada kasus ini terdapat tiga _v positif dan ketiga titik kisinya saling berdampingan, maka (1,5)2, 25 dan

1 1 4

(1,5) (0) (1) (2) 2,83

6 6 6

[image:33.595.135.522.94.367.2]

Misalkan titik  1,5 dituliskan kombinasi konveks 1( 1) 1(1) 6(2) 8  8 8

dengan titik kisi ₂  1,₄ 1 dan  ₅ 2. Pada kasus ini terdapat tiga _v positif dimana ada dua titik kisinya berdampingan dan lainnya tidak, maka (1,5)2, 25 dan

^ _{1 1 6}

(1,5) ( 1) (1) (2) 3,125

8 8 8

         .

Hasil dari ilustrasi tersebut dapat dilihat bahwa jika titik  tidak merupakan kombinasi konveks dari yang paling banyak dua titik kisi dengan  _v 0 yang berdampingan, maka hampiran yang diperoleh tidak lebih baik dibandingkan dengan bila titik  merupakan kombinasi konveks dari dua titik kisi dengan  _v 0 yang berdampingan.

Pada umumnya fungsi nonlinier  pada interval [a,b] dapat dihampiri pleh fungsi linier piecewise  dengan titik kisi  ₁, ₂,...,_k yang didefinisikan sebagai:

1 ( ) ( ), k v v v       



1 1, k v v   



 _v 0 dengan

1 k v v v    





untuk v1, 2,...,k, dan

paling banyak dua _v bernilai positif dan jika ada dua  _v 0 maka kedua titik kisi yang berpadanan dengan _v tersebut harus berdampingan.

3.3.2. Formulasi Delta

21

Perhatikan fungsi nonlinear f pada interval [a,b]. Pada formulasi delta akan dihampiri dengan cara sebagai berikut:

1

v v v

   

   ,

1

( ) ( )

v v v

f f  f  _

   .

Misalkan ₀

1 ( ) p v v v     

 



 , maka:

0 1 ( ) ( ) ( ) p v v v

f  f  f  

 





0 v 1 untuk v1, 2,...,p

Perhatikan ilustrasi berikut;

Misalkan didefinisikanL{j f_j dan g_ij adalah fungsi linier untuk 1, 2,..., }

i m . Didefinisikan titik-titik kisi x_vj untuk v1, 2,...,k_j. Pada interval ,

j j a b  

  dengan a b_j, _j 0 untuk setiap jL. Diberikan fungsi f yang didefinisikan sebagai f( )  2. Grafik fungsi f pada intrval [-2,2] diperlihatkan pada gambar 3.3.2.b.

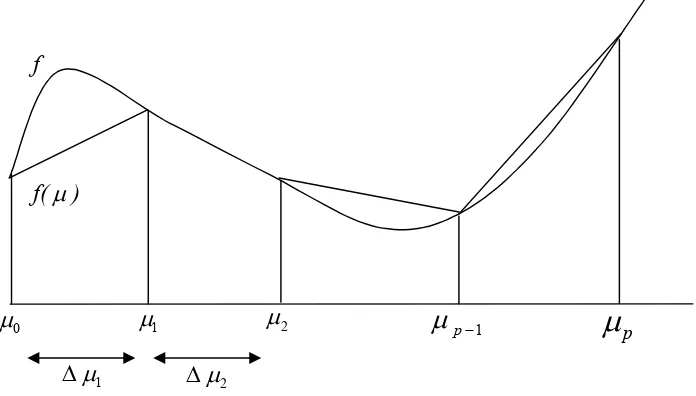
Gambar 3.3.2.a. Fungsi Linear Piecewise sebagai hampiran fungsi nonlinear dengan formulasi delta.

f

f()

0

 1 2

∆1 ∆2

p



1 p

[image:35.595.166.514.469.667.2]

[image:36.595.145.513.85.408.2]

Gambar 3.3.2.b. Pentingnya paling banyak satu _v yang nilainya 0 _ 1

Misalkan titik kisi yang digunakan adalah

0 2, 1 1, 2 0, 3 1, 4 2

            dan        ₁ 1, ₂ 1, ₃ 1, ₄ 1. Maka titik 1

4

 dituliskan sebagai 2 (1)1 1(1) (1)1 (1)0 4

       , dengan

1 2 3 4

1

1, 1, , 0

4

        . Pada kasus ini terdapat suatu _v yang nilainya 0 _v 1.

Maka 1 1

4 16 f   _{ }

  dan nilai hampirannya adalah

1 1 1

4 ( 3)1 ( 1)1 (1) (3)0

4 4 4

f        _{ }  

  .

23

3.4. Menyelesaikan Persoalan Pemrograman Separabel dengan Menggunakan

Fungsi Linier Piecewise_{dengan Formulasi Delta}

Diberikan masalah pemrograman separabel sebagai berikut: Maks ₁2 6 _{1 2}2 8 ₂ 1 ₃

2 Z  x x  x x  x

Terhadap

1 2 3

2

1 2

1 2 3

5 3 , , 0

x x x

x x

x x x

    



Perhatikan bahwa L={3}, oleh karena itu titik kisi tidak digunakan untuk x₃. Dari kendala–kendala dapat diketahui bahwa x x₁, ₂, dan x₃ terletak pada interval [0,5]. Maka titik–titik kisi yang digunakan adalah 0,2,4,5. sehingga :

11 0

x  ,x₂₁ 2,x₃₁ 4,x₄₁5

1 01 11 21 31

11 01 1.11 1.21 1.31

( ) 0, 8, 0, 3,

( ) 0, 2, 2, 1

f x f f f

g x g g g

       

      

12 0

x  ,x₂₂ 2,x₃₂ 4,x₄₂ 5

2 02 12 22 32

22 02 2.12 2.22 2.32

( ) 0, 12, 4, 1,

( ) 0, 4, 12, 9

f x f f f

g x g g g

        

      

1 11 21 31

2 12 22 32

0 [2 2 1 ]

0 [2 2 1 ]

x x               Dari rumus

2 11 21 31 12 22 32

g ( )x  (0 4 12 9 ) (0 2   2 1 )3

0 1

( ) ( ) ( ) ( )

j

P

j j j vj vj

j L j L v

f x f x f x f 

  

 

  _   _

 

diperoleh

11 21 31 12 22 32 3

1

( ) (0 8 0 3 ) (0 12 4 1 )

2 f x                x

Dari rumus

1 1 0 1, 1

( ) ( ) ( ) ( )

i j j j j vj vj

j L j L

g x g x g x g  P

   









_ 



 _

diperoleh

1( ) (0 2 11 2 21 1 31) (0 2 12 2 22 1 32) 3 5

g x                x

2 11 21 31 12 22 32

g ( )x  (0 4 12 9 ) (0 2   2 1 )3 Jadi, diperoleh pemrograman linear;

Min f(2,3, 0) 22

11 21 31 12 22 32 3

1

( ) (0 8 0 3 ) (0 12 4 1 )

2 f x                x

Terhadap

1 11 21 31 12 22 32 3

2 11 21 31 12 22 32

( ) (2 2 1 ) (2 2 1 ) 5

( ) (4 12 9 ) (2 2 1 ) 3

g x x

g x

     

     

       

      

dengan 0vj 1 untuk v=1,2,3 dan j=1,2,3.

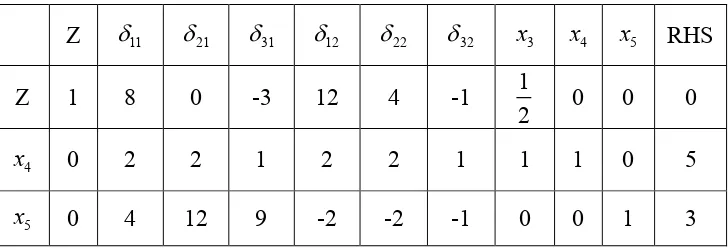
Masalah ini diselesaikan dengan menggunakan metode simpleks untuk variabel terbatas untuk pemilihan variabel tak dasar yang masuk basis, sehingga diperoleh tabel simpleks di bawah ini.



Z 11 21 31 12 22 32 x3 x4 x5 RHS

Z 1 8 0 -3 12 4 -1 1

2 0 0 0

4

x 0 2 2 1 2 2 1 1 1 0 5

5

[image:38.595.128.492.591.716.2]

x 0 4 12 9 -2 -2 -1 0 0 1 3

25

1

5 5

min

2 2

t      

2 t  

12 1

U 



1 2 12



5

min , , min , ,1 1

2

t t U    

 

Substitusikan batas atas untuk ₁₂, dan ₁₂ tetap variabel nonbasis

12 12 1 12 1 12

     



Z 11 21 31 12 22 32 x3 x4 x5 RHS

Z 1 8 0 -3 -12 4 -1 1

2 0 0 -12

4

x 0 2 2 1 -2 2 1 1 1 0 5

5

[image:39.595.111.513.73.408.2]

x 0 4 12 9 2 -2 -1 0 0 1 3

Tabel 2. Penyelesaian kedua dari tabel simpleks untuk variabel terbatas

1

3 5 5

min ,

2 4 4

t     

2

t tidakada

11 1

U 



1 2 11



5

min , , min ,1 1

4 t t U   

 

Sehingga substitusi batas atas untuk ₁₁, dan ₁₁ tetap variabel nonbasis

11 11 1 11 1 11

      .

= 

Z 11 21 31 12 22 32 x3 x4 x5 RHS

Z 1 -8 0 -3 -12 4 -1 1

2 0 0 -20

4 x

0 -2 2 1 -2 2 1 1 1 0 5

5

x 0 -4 12 9 2 -2 -1 0 0 1 3

4

[image:39.595.113.536.440.734.2]

1

1 1

min

2 2

t      

2 t  

12 1

U 



1 2 12



1 1

min , , min , ,1

2 2

t t U    

 

Jadi, ₂₂ masuk ke dalam basis menggantikan x₄.

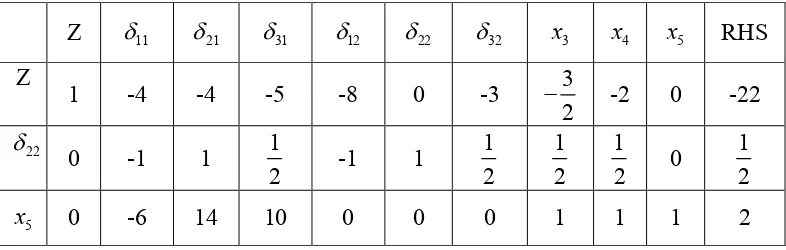
Z 11 21 31 12 22 32 x3 x4 x5 RHS

Z

1 -4 -4 -5 -8 0 -3 3

2

 -2 0 -22

22

 _{0 -1 1} 1

2 -1 1

1 2 1 2 1 2 0 1 2 5

[image:40.595.144.537.261.386.2]

x 0 -6 14 10 0 0 0 1 1 1 2

Tabel 4. Penyelesaian keempat dari tabel simpleks untuk variabel terbatas Sehingga, solusi optimalnya:

11 21 31 12 22 32

11 21 31 12 22 32

0 0 0 0 1 2 0 1

1, 0, 0, 1, , 0

2                         

Jadi, diperoleh hasil optimal:

1 2 3

( , , )

x x x x dengan :

1 11 21 31

2 12 22 32

3

0 (2 2 1 ) 2 0 (2 2 1 ) 3 0 x x x                 

27

KESIMPULAN DAN SARAN

4.1. KESIMPULAN

Fungsi nonlinier dapat dihampiri oleh funsi linier putus-bersambung (piecewise linear function). Hampiran suatu fungsi nonlinier dengan fungsi linier piecewise dipengaruhi oleh banyaknya titik kisi. Jika titik kisi bertambah, maka variabel pada masalah hampiran pemrograman linier akan bertambah. Untuk mengatasi hal tersebut, dapat digunakan modifikasi metode hampiran yang menggunakan sedikit titik kisi diawal perhitungan.

Ada dua cara untuk memformulasikan fungsi linear putus-bersambung yaitu dengan formulasi lambda dan formulasi delta. Dalam formulasai lambda, variabel  didefinisikan untuk setiap titik kisi. Sedangkan, dalam formulasi delta, variabel  didefinisikan untuk setiap interval diantara titik kisi.

Masalah pemrograman separabel P dihampiri dengan mengganti setiap fungsi objektif dan fungsi kendalanya yang nonlinear dengan fungsi linear putus-bersambung (piecewise linear function) yang didefinisikan sebagai masalah AP. Dengan menggantikan fungsi objektif dan fungsi kendalanya yang nonlinier oleh hampiran-hampiran liniernya, maka Masalah AP dapat dituliskan sebagai Masalah LAP

29

4.2. SARAN

DAFTAR PUSTAKA

Nasendi, B.D., ” Program Linear dan Variasinya”, PT Gramedia, Jakarta, 1985.

Hiller, Frederick.S. dan Liberman, Gerald.L., “ Introduction to Operation Research ”, McGraw-Hill.Inc, USA, 1990.

M. Minoux.,” Mathematical Programming Theory and Algorithms ”, Bordas Dunod Gauthier-Villars, Paris, 1983

Bazaraa M.S., H.D. Sherali & C.M. Shetty, “Nonlinear Programming: Theory and

Algorithms”, 2nd

ed . John Wiley, New York, 1993.

Bartle R.G., “The Element of Real Analysis”, 2nded. John Willey, New York, 1976..

S.S. Rao., “Optimization: Theory and Applications”, 2nded. Wiley Eastern Limited, New Delhi, 1984.

Ben-Israel A, Ben-Tal, & S. Zlobec.,”Optimality in Nonlinear Programming: A Feasible Directions Approach”, John Wiley & Sons, New York, 1981.

Gunawan Ellen & Ardi Wirda Mulia,”Pengantar Riset Operasi”, 5th

ed. Gelora Aksara Pratama, Jakarta, 1994.