ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b] (STUDI KASUS : FUNGSI IRASIONAL)

ABSTRACT

ANALYSIS OF APPROXIMATION FUNCTIONS BY MINIMUM NORM METHOD IN HILBERT SPACE C[a, b]

(CASE STUDIES : IRATIONAL FUNCTIONS)

By

M. ASRI MULATSIH

Usually, approximation of functions used in numerical analysis. Two main reasons for application of approximation of functions are : to give efective approximation of functions, and to simplified complex function. Given a function f , with some or all point are given, we wish to get approximation of spesific function f that can be easier to be analyzed.For example, we wish to compute �+ ��

1 8

0 . Then we approximate its integran by series Maclaurin. Optimization problems, espesially good aprroximation of function that can’t get the best solution (for large errors) in real space , it can be solved by mathematics system simplier, by carryng out the problem to abstract space or vector space, espesially in Hilbert space C[a,b]. The problem known as minimum norm problem in Hilbert Space C[a,b]. By minimum norm method we have minimum approximation errors.

ABSTRAK

ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[a, b]

(STUDI KASUS : FUNGSI IRASIONAL)

Oleh

M. ASRI MULATSIH

Aproksimasi fungsi dalam proses komputasi sering digunakan hampir di semua bidang analisis numerik. Dua alasan utama penggunaan aproksimasi fungsi adalah untuk memberikan fungsi pendekatan yang efektif dan mendekati suatu fungsi yang rumit dengan fungsi yang lebih sederhana. Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapa nilai di titik-titik tertentu saja, kita ingin memperoleh aproksimasi untuk f yang mempunyai bentuk tertentu dengan kesalahan yang dapat kita kontrol.

Misalnya kita hendak menghitung �+ �� 1

8

0 , kita hampiri integrannya dengan deret Maclaurin. Masalah optimisasi khususnya aproksmasi fungsi terbaik yang tidak medapatkan solusi terbaik (ralat yang besar) dalam ruang fisis atau yang dikenal sebagai ruang real , dapat dipecahkan dengan sistem matematis yang sederhana, dengan membawa masalah aproksimasi tersebut ke ruang abstrak (berisi aksioma-aksioma) atau ruang vekor, khususnya pada ruang Hilbert C[a,b]. Masalah tersebut dikenal sebagai masalah minimum norm dalam ruang Hilbert C[a,b]. Dengan menggunakan konsep minimum norm akan diperoleh kesalahan optimal (galat) yang minimum.

ANALISIS APROKSIMASI FUNGSI DENGAN METODE MINIMUM NORM PADA RUANG HILBERT C[ a, b]

( STUDI KASUS: FUNGSI IRASIONAL )

Oleh

M. Asri Mulatsih

Skripsi

Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

RIWAYAT HIDUP

Penulis dilahirkan di Pringsewu Timur, Kabupaten Pringsewu pada tanggal 7 Oktober 1992, sebagai anak keempat dari empat bersaudara dari bapak F. X. Harsono dan Ibu L. Suwarni. Penulis telah mengawali Pendidikan Taman Kanak-kanak Fransiskus di Pringsewu Timur Kabupaten Pringsewu pada tahun 1998, Sekolah Dasar Fransiskus Pringsewu pada tahun 2004, Sekolah Menengah Pertama Xaverius Pringsewu pada tahun 2007, Sekolah Menengah Atas Xaverius Pringsewu pada tahun 2010.

MOTO

Dan apa saja yang kamu minta dalam doa dengan penuh

kepercayaan, kamu akan menerimanya

( Matius 21:22 )

Dibalik suatu keberhasilan ada doa dan usaha

(M. Asri Mulatsih)

Maka berdoalah agar Tuhan mentenagai ketegasan anda

untuk melakukan yang anda ketahui sebagai cara

mendekatkan anda kepada cita-cita dan impian anda

PERSEMBAHAN

Dengan segala cinta dan kasih sayang kupersembahkan karya kecilku ini untuk orang-orang yang akan selalu berharga dalam hidupku.

Tuhan Yesus Kristus

Yang menjadi kekuatanku ketika putus asa

Bapak, ibu, Mas Ari , Mas Virri, Mas Aris, semua teman, dan keluarga besarku

Yang selalu memberikan canda dan tawa, selalu berdoauntuk keberhasilanku, dan selalu memberikan kasih sayang yang tidak ternilai.

Para pendidikku

Dosen Pembimbing dan Penguji yang sangat berjasa, atas bimbingan dan ajarannya.

SANWACANA

Puji syukur penulis panjatkan kepada Allah Bapa di Surga, yang telah memberikan kasih karunia, anugerah, dan Berkat-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi dengan baik.

Skripsi dengan judul “Analisis Aproksimasi Fungsi Dengan Metode Minimum Norm Pada Ruang Hilbert C[a,b] ( Studi Kasus: Fungsi Irasional)” disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains (S.Si.) di Universitas Lampung.

Skripsi ini dapat diselesaikan berkat bantuan sdan bimbingan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin mengucapkan terima kasih banyak kepada:

1. Bapak Prof. Suharso, Ph.D., selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

2. Bapak Amanto, S. Si., M. Si., selaku dosen pembimbing utama yang telah membimbing dan mengarahkan penulis dari awal hingga akhir.

Pengetahuan Alam Universitas Lampung yang telah banyak membantu dan memberikan banyak pengarahan dalam proses penyusunan skripsi ini.

4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku dosen penguji dan juga Ketua Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung, atas kesediaannya untuk menguji, memberikan saran, dan kritik yang membangun dalam proses penyelesaian skripsi ini.

5. Bapak Ahmad Faisol, S. Si., M. Sc., selaku dosen pembimbing akademik yang membimbing dan mengarahkan penulis selama kuliah.

6. Dosen, staf dan karyawan Jurusan Matematika FMIPA UNILA yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.

7. Untuk Bapak, Ibu, Mas Ari, Mas Virri, dan Mas Aris yang selalu memberikan semangat, doa, serta canda tawa dalam menyelesaikan skripsi ini.

8. Sahabat-sahabatku Duma, Fransiska, Rara, Eka, Apit, Dita, Encis, dan MATH 2010 yang selalu memberikan dukungan serta canda tawa.

9. Almamaterku tercinta Universitas Lampung.

Penulis menyadari bahwa masih banyak kelemahan dan kekurangan dari skripsi ini. Oleh karena itu, segala kritik dan saran yang bersifat membangun sangat penulis harapkan. Akhir kata penulis berharap agar skripsi ini dapat bermanfaat bagi penulis maupun pembaca.

Bandar Lampung, Juli 2014 Penulis

i

DAFTAR ISI

Halaman

DAFTAR ISI ... xiv

DAFTAR GAMBAR ... xv

I. PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Rumusan Masalah ... 3

1.3 Batasan Masalah ... 3

1.4 Tujuan Penelitian ... 4

1.5 Manfaat Penelitian ... 4

II. TINJAUAN PUSTAKA ... 5

2.1 Aproksimasi Fungsi ... 5

2.2 Kesalahan Aproksimasi Fungsi ... 6

2.3 Teorema Proyeksi ... 7

2.4 Deret Maclaurin ... 16

2.5 Fungsi Irasional ... 17

III. METODE PENELITIAN ... 18

3.1 Waktu dan Tempat Penelitian ... 18

3.2 Metodologi Penelitian ... 18

IV. HASIL DAN PEMBAHASAN ... 20

4.1 Masalah Aproksimasi Terbaik Fungsi Irasional Dengan Metode Minimum Norm Pada Ruang Hilbert C[a,b]... 20

4.2 Masalah Aproksimasi Terbaik Fungsi Irasional Dengan Deret Maclaurin ... 53

V. KESIMPULAN ... 54

DAFTAR GAMBAR

Gambar Halaman

I. PENDAHULUAN

1.1. Latar Belakang dan Masalah

2

Cara mencari aproksimasi fungsi tersebut adalah dengan optimisasi. Optimisasi adalah suatu proses memaksimumkan atau meminimumkan suatu fungsi objektif yang memenuhi kendala tertentu. Suatu masalah optimisasi yang tidak mendapatkan solusi terbaik dalam ruang fisis atau ruang real, dapat dipecahkan dengan suatu sistem matematis, yaitu dengan membawa masalah tersebut ke ruang abstrak (berisi aksioma-aksioma) atau ruang vektor (Kreyzig, 1978). Masalah aproksimasi fungsi di tersebut dapat diselesaikan pada ruang vektor, yaitu dengan metode optimisasi ruang vektor. Ruang vektor yang digunakan adalah ruang Hilbert. Ruang Hilbert merupakan ruang abstrak yang di dalamnya memuat perpaduan tiga konsep, yaitu Aljabar, Analisis dan Geometri. Konsep geometri yang digunakan adalah mengenai proyeksi, sebab ruang Hilbert dibangun oleh konsep inner product (Berberian, 1961). Penelitian tentang masalah tersebut, diantaranya adalah penyelesaian masalah minimum norm pada ruang Hilbert L2[a,b] (Amanto dkk, 2003). Selanjutnya penelitian yang sama juga dilakukan pada ruang Hilbert yang lain, yaitu ruang Hilbert C[a,b] (Joko Waluyo, 2003). Dalam hal ini konsep yang digunakan yaitu minimum norm pada ruang Hilbert C[a,b]. Fungsi yang akan dicari aproksimasinya adalah fungsi-fungsi kontinu bernilai real yang terdefinisi pada [a,b]. Pada penelitian tersebut baru sampai pada tahap mencari solusinya, belum pada tahap evaluasi atau analisis hasil terkait dengan galat yang dihasilkannya.

3

Proyeksi [Adkinson (2001) & Luenberger (2001)]. Dalam pemecahan masalah ini, langkah penting yang harus diperhatikan adalah pemilihan basis yang bebas linear yang membangun ruang fungsi yang akan diaproksimasi dan penentuan kesalahan optimal atau ralat optimal dari aproksimasi yang diambil. Basis ini tidak tunggal. Pemilihan basis yang berbeda akan menghasilkan aproksimasi fungsi yang sama dan juga kesalahan optimal yang sama pula. Oleh karena itu, berdasarkan latar belakang masalah tersebut penulis ingin mengangkat judul " Analisis Aproksimasi Fungsi Dengan Metode Minimum Norm Pada Ruang Hilbert C[a,b] ( Studi Kasus : Fungsi Irasional) ".

1.2. Rumusan Masalah

Berdasarkan latar belakang masalah tersebut di atas, maka yang menjadi permasalahan dalam penelitian ini adalah:

“Bagaimana analisis aproksimasi fungsi irasional dengan metode minimum norm pada ruang Hilbert C[a,b]?”

1.3. Batasan Masalah

4

1.4. Tujuan Penelitian

Adapun tujuan penelitian ini adalah Tujuan penelitian ini adalah menganalisa galat yang terjadi pada aproksimasi fungsi irasional dengan metode optimasi ruang vektor, yaitu minimum norm pada ruang Hilbert C[a,b] untuk mendapatkan aproksimasi fungsi irasional yang terbaik.

1.5. Manfaat Penelitian

Manfaat penelitian ini adalah :

1. Memberikan konsep analisa terhadap analisis galat atas pemilihan basis yang dilakukan pada aproksimasi fungsi irasional dengan metode minimum norm pada ruang Hilbert C[a,b] sehingga akan diperoleh aproksimasi fungsi irasional terbaik dengan galat (kesalahan) yang paling kecil.

2. Memberikan kontribusi bagi peneliti tentang metode minimum norm pada ruang Hilbert C[a,b].

II. TINJAUAN PUSTAKA

Dalam proses penelitian untuk menganalisis aproksimasi fungsi dengan metode minimum norm pada ruang hilbert C[a,b] (Studi kasus: fungsi irasional), penulis menggunakan definisi, teorema dan konsep dasar sebagai berikut:

2.1.Aproksimasi Fungsi

6

Ada dua jenis penggunaan aproksimasi pada suatu fungsi, yaitu:

1. Menggantikan fungsi-fungsi yang rumit dengan fungsi yang lebih sederhana sehingga banyak operasi umum, seperti fungsi irasional dan fungsi integral, atau bahkan mengevaluasi fungsi tersebut dapat dilakukan dengan mudah. 2. Untuk memperoleh kembali suatu fungsi dari informasi sebagian mengenai

fungsi itu, misalnya dari suatu tabel nilai ( Santoso, 2003 ).

2.2.Kesalahan Aproksimasi Fungsi

Dalam perhitungan dengan aproksimasi mungkin akan terjadi suatu kesalahan terhadap nilai eksaknya. Menurut Triatmodjo (2002), terdapat tiga jenis kesalahan yang mungkin terjadi dalam perhitungan dengan aproksimasi yaitu kesalahan bawaan, kesalahan pembulatan (round-off error), dan kesalahan pemotongan (truncation error).

Definisi 2.2.1. Kesalahan Bawaan

Kesalahan bawaan adalah kesalahan dari nilai data yang terjadi karena kekeliruan dalam menyalin data, salah membaca skala atau kesalahan karena kurangnya pengertian mengenai hukum-hukum fisik dari data yang diukur (Triatmodjo, 2002).

7

Definisi 2.2.2. Kesalahan Pembulatan (round-off error).

Kesalahan pembulatan adalah kesalahan yang terjadi karena tidak diperhitungkannya beberapa angka terakhir dari suatu bilangan (Triatmodjo, 2002). Kesalahan pembulatan misalnya 3,1415926 dapat dibulatkan menjadi 3,14.

Definisi 2.2.3. Kesalahan Pemotongan (truncation error).

Kesalahan pemotongan adalah kesalahan yang terjadi karena hanya diperhitungkannya beberapa suku pertama dari suatu deret tak hingga (Triatmodjo, 2002). Selain definisi di atas, kesalahan pemotongan (truncation error) juga didefinisikan sebagai kesalahan yang timbul dari penggunaan suatu aproksimasi pengganti prosedur matematika yang eksak (Chapra, 2002). Kesalahan pemotongan terjadi misalnya pada penggunaan aproksimasi dengan deret Taylor. Kesalahan (error) yang muncul dalam penggunaan aproksimasi diharapkan bernilai sangat kecil sehingga nilai yang diperoleh mendekati atau hampir sama dengan nilai eksaknya. Oleh karena itu, dalam menghampiri suatu fungsi deret pangkat tak hingga nilai kesalahannya akan bernilai semakin kecil jika suku-suku deret yang digunakan untuk menghampiri fungsi tersebut semakin banyak.

2.3.Teorema Proyeksi

8

Definisi 2.3.1 (Luenberger, 1969)

Dalam suatu ruang pre-Hilbert X, vektor x,y  X dikatakan ortogonal jika <x, y>= 0, dinotasikan dengan x  y. Suatu vektor x dikatakan ortogonal dengan himpunan S, dinotasikan x  S jika x  s untuk setiap s  S.

Lemma berikut menunjukkan bahwa Teorema Phytagorean dalam geometri bidang merupakan akibat dari konsep ortogonalitas.

Lemma 2.3.1

Misalkan X suatu ruang Hilbert dan x, y  X. Jika x  y, maka

2 2 2

y x y

x  

Bukti :

y y x y y x x x y x y x y

x 2   ,   ,  ,  ,  ,

= x 2 00 y 2 = x 2 y 2. 

Selanjutnya akan dibahas suatu masalah optimisasi yang berhubungan dengan Teorema proyeksi. Misalkan X suatu ruang Pre-Hilbert, diberikan suatu vektor x X dan M ruang bagian dari X, maka akan ditentukan vektor m M yang terdekat ke x, yaitu vektor yang meminimalkan xm .

Jika x berada di M maka penyelesaiannya trivial, yaitu vektor x sendiri. Secara umum ada empat pernyataan penting dalam penyelesaian masalah tersebut yaitu :

1. Adakah vektor m  M yang meminimalkan xm ? 2. Apakah penyelesaiannya tunggal ?

9

4. Bagaimana menentukan penyelesaian optimal ?

Pernyataan nomor 1, 2 dan 3 akan dijawab dengan Teorema proyeksi. Ada dua versi Teorema proyeksi, satu versi pada ruang Pre-Hilbert dan satu versi yang lain pada ruang Hilbert dengan hipotesis dan kesimpulan yang lebih kuat.

Teorema 2.3.2 (Teorema Proyeksi di Ruang pre-Hilbert)

Misalkan X suatu ruang Pre-Hilbert, M suatu ruang bagian dari X dan x sebarang vektor di X. Jika ada vektor m₀M , sedemikian sehingga xm_o  xm,mM , maka m0 tunggal. Syarat perlu dan cukup m₀M , suatu vektor minimal tunggal di M adalah vektor selisih x – m0 ortogonal terhadap M.

Bukti :

Akan di tunjukkan jika m0 adalah vektor minimal, maka x – m0 ortogonal terhadap M. Andaikan kondisi sebaliknya, terdapat m M yang tidak ortogonal terhadap x

10

Ini berarti  m1 dengan m1 = m0 + m sehingga

2 0 2

1 x m

m

x   , ini berarti m1 bukan vektor minimal. Jadi m0 vektor minimal maka x – m0 ortogonal terhadap M atau (x – m0)  m, mM. Dengan demikian jika x – m0 tidak ortogonal terhadap M maka m0 bukan vektor minimal.

Selanjutnya akan ditunjukkan jika vektor x – m0 ortogonal terhadap M, diambil sebarang mM, berdasarkan Teorema Phytagorea :

2

0 2

0 2

0 0 2

m m m

x m m m x m

x        

sehingga xm2  xm₀ 2 untuk m m0 . 

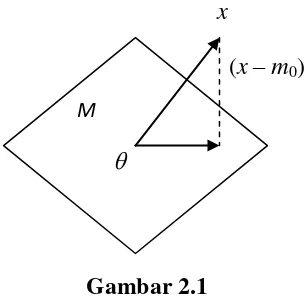
Dalam dimensi tiga, teorema proyeksi ini dapat dinyatakan sebagai berikut : Ruang bagian M adalah bidang yang melalui titik asal dan x di ruang dimensi tiga X. Jika ada vektor minimal m0 M maka m0 tunggal dan vektor selisih x – m0 tegak lurus terhadap bidang M, seperti digambarkan dalam gambar di bawah ini :

x

(x – m0)

Gambar 2.1

Teorema di atas belum menjamin keberadaan vektor minimal, tetapi jika ada vektor minimal m0 , maka m0 tunggal dan vektor selisih x – m0 ortogonal terhadap ruang bagian M. Dengan hipotesis yang lebih kuat didapatkan kesimpulan yang

11

lebih kuat, yaitu terjaminnya keberadaan vektor minimal. Hal ini dinyatakan dalam teorema berikut.

Teorema 2.3.3 Teorema Proyeksi Klasik

Misalkan H ruang Hilbert dan M ruang bagian tertutup dari H, maka untuk minimal tunggal adalah vektor selisih x – m0 ortogonal terhadap ruang bagian M. Bukti :

Ketunggalan dan ortogonalitasnya telah dibuktikan pada Teorema 2.3.2, sehingga tinggal membuktikan keberadaan vektor minimal. Jika xM dan m0 = x maka bukti selesai.

Misalkan xM dan didefinisikan x m M Menurut hukum jajaran genjang (parallelogram),

2 dengan menyusun kembali persamaan di atas didapatkan :

2

Karena M ruang bagian linier sehingga dari definisi ,

12

2 2 2

2

4 2

2     



 _{i j i}

j m m x x m

m

karena



 2



2

x

mi , i

Maka



mj mi 2



0 , i, j .

Dengan demikian {mi} adalah barisan Cauchy dan karena M ruang bagian tertutup dari ruang lengkap, maka barisan {mi} mempunyai limit m₀ di dalam M.

Dengan kekontinuan norm maka xm₀ . 

Jadi dalam penulisan ini, Teorema proyeksi klasik menjamin keberadaan dan ketunggalan penyelesaian optimal serta kondisi yang harus dipenuhi agar keberadaan vektor minimal ada penyelesaian optimalnya, penyelesaian optimalnya sendiri belum dapat ditentukan.

Selanjutnya teorema proyeksi di atas akan ditetapkan untuk membangun sifat struktural tambahan dari suatu ruang Hilbert, antara lain adalah dalam sebarang ruang bagian tertutup dari ruang Hilbert, sebarang vektor dapat ditulis sebagai jumlahan dua vektor, satu vektor di ruang bagian tertutup dan vektor yang lain ortogonal terhadapnya.

Definisi 2.3.2 (Luenberger, 1969)

13

Menurut Teorema proyeksi, vektor minimal tunggal m0 adalah proyeksi ortogonal x pada M, atau vektor selisih x – m0 ortogonal terhadap setiap vektor yi .

Dengan demikian :  x₁y₁₂y₂..._ny_n,y_i 0 untuk i = 1, 2, ...., n. normal untuk masalah minimalisasi.

Matriks n x n yang berhubungan dengan vektor y1, y2,...,yn yaitu :

14

disebut matriks Gram dari y1, y2, y3, ..., yn. Matriks ini adalah tranpose dari matriks koefisien normal.

Teorema 2.3.4

sedemikian sehingga





 . Karena barisan-barisan pada determinan Gram

bergantung pada yi, maka determinannya nol.

Misalkan g = g(y1, y2,…., yn) = 0. Maka ada kebergantungan linier di antara barisan-barisannya sehingga terdapat konstanta I yang tidak semuanya nol

sedemikian hingga





y2,…., yn bergantung linier. 

15

maka selalu dihasilkan penyelesaian yang tidak tunggal, bukan penyelesaian yang tidak konsisten.

Teorema berikut menyatakan jarak minimum suatu vektor ke ruang bagian dapat dicari dengan determinan matriks Gram.

Teorema 2.3.5

Misalkan y1,….., yn bebas linear dan  jarak minimum vektor x ke ruang bagian M yang dibangun oleh yi, yaitu :



16

2.4.Deret Maclaurin

17

Sehingga diperoleh deret Maclaurin dari fungsi � = �₀18 + 1 �

�+ 1 = 1 +

1 2

1!�+⋯ = 1 +1

2�

2.5.Fungsi Irasional

Fungsi Irasional adalah akar dari fungsi polinom. Bentuk umumnya :

= ₀ + ₁ + ₂ 2₊⋯_{+ , tidak bulat, ,} � _R

III. METODOLOGI PENELITIAN

3.1.Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester genap tahun akademik 2014/2015, bertempat di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

3.2.Metode Penelitian

Penelitian ini menggunakan metode yang bersifat studi pustaka, yaitu dengan mempelajari, menganalisis masalah dengan definisi-definisi, dan definisi tersebut menjadi acuan berfikir untuk mengemukakan teori yang sesuai dengan masalah yang bersangkutan, dan kemudian membuat kesimpulan.

Adapun langkah-langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:

19

2. Membawa masalah aproksimasi fungsi ke ruang Hilbert C[a,b] dengan cara terlebih dahulu menentukan produk skalar terhadap ruang Hilbert C[a,b] yang sesuai untuk digunakan.

3. Menentukan basis-basis yang akan digunakan Mencari penyelesaian optimal (aproksimasi fungsi terbaik) dengan persamaan normal.

4. Menentukan kesalahan optimal dari pengambialan basis yang berbeda-beda pada langkah (2) dan melakukan analisis serta evaluasi terhadap galat dan fungsi yang dihasilkan.

5. Melakukan langkah (1) s.d. (4) untuk kasus fungsi yang lain.

V. KESIMPULAN

Masalah optimisasi khususnya aproksimasi fungsi irasional terbaik yang tidak mendapatkan solusi terbaik dalam ruang real, dapat dipecahkan dengan membawa masalah aproksimasi tersebut ke ruang vektor, khususnya pada ruang Hilbert C[a,b]. Masalah tersebut dikenal sebagai masalah minimum norm dalam ruang Hilbert C[a,b] dengan studi kasus fungsi irasional. Dengan menggunakan konsep minimum norm akan diperoleh kesalahan optimal (galat) yang minimum. Dibandingkan dengan menggunakan metode deret Maclaurin yang menghasilkan galat berdasarkan pada panjang suku pada deret.

DAFTAR PUSTAKA

Albari. 2001. Matematika Untuk Ekonomi dan Bisnis. Yogyakarta: Ekonisia. Amanto, Suharsono, dan Waluyo, J.,2003. Penyelesaian Masalah Minimum Norm

dalam Ruang Hilbert L2[a,b]. Jurnal Matematika, Aplikasi dan Pembelajarannya (JMAP), Vol 2, hal. 124 – 131.

Atkinson, K. And Han, W., 2001. Theoretical Numerical Analysis : A Functional Analysis Framework. Springer Verlag, New York.

Berberian, SK., 1961. Introduction to Hilbert Space, Academic Press, Inc., New York.

Joko Waluyo, 2003. Penyelesaian Masalah Minimum Norm Dalam Ruang Hilbert C[a,b]. Skripsi, Jurusan Matematika FMIPA Unila.

Kreyzig, Erwin. 1978. Introductory Functional Analysis with Applications. New York : John Willey.

Luenberger, D.G., 1969. Optimization by Vector Space Methods John Wiley and Sons, New York.

Munir, Rinaldi. 2006. Metode Numerik. Bandung: Informatika Bandung. Purcell, Edwin J. 2004. Kalkulus. Jilid Dua. Jakarta: Erlangga.

Santoso, Gatot Iman. 2003. Aproksimasi Polinomial sebagai Metode Hampiran untuk Fungsi Turunan ke-n yang Kontinu. Madiun: Universitas Katolik Widya Mandala.

Soemantri, R. 1994. Fungsi Variabel Kompleks. Yogyakarta: Universitas Gadjah Mada.