Analisis kestabilan model SIR, SIR vaksinasi, SEIR dan MSEIR sebagai model-model penyebaran penyakit Campak (Measles)

(1)

ABSTRACT

ACE SUHENDAR. Stability analysis of mathematical models: SIR , SIR with vaccination, SEIR

and MSEIR of the outbreak of measles diseases. Supervised by ALI KUSNANTO and PAIAN SIANTURI.

Measles disease is an extremely dangerous disease. It caused by virus that spreads through direct to the contact with victims or air. Measles disease can cause complication, mustle disfunction and organ, physical defect, paralysis and death.

A vaccination program is a powerful method to control the measles disease outbreak. The

measles disease outbreak can be studied using mathematical model. The model is known as SIR, SIR of vaccination, SEIR and MSEIR epidemic model. In this research, the SIR of epidemic model, SIR of vaccination, SEIR and MSEIR is derived by including the factors of birth, death, vaccination, body profection and immunity. The vaccination is held to prevent the measles disease outbreak.

Based on stability analysis conducted, the SIR model, SIR of vaccination, SEIR and

(2)

ABSTRAK

ACE SUHENDAR. Analisis Kestabilan Model SIR, SIR vaksinasi, SEIR dan MSEIR Sebagai Model-model Penyebaran Penyakit Campak (Measles). Dibimbing oleh ALI KUSNANTO dan PAIAN SIANTURI.

Penyakit campak (measles) merupakan penyakit yang sangat berbahaya, penyakit ini disebabkan oleh virus yang dapat menyebar melalui kontak langsung dengan penderita dan udara. Penyakit campak (measles) dapat menyebabkan komplikasi, kerusakan otak dan organ tubuh yang lainnya, cacat seumur hidup, kelumpuhan dan bahkan kematian.

Program vaksinasi merupakan metode yang baik untuk mencegah penyebarannya. Penyebaran penyakit ini dapat dipelajari dengan mengunakan model matematika. Model tersebut dikenal sebagai model endemik SIR, SIR vaksinasi, SEIR dan MSEIR. Pada penelitian ini, model

SIR, SIR vaksinasi, SEIR dan MSEIR diturunkan ulang dengan memperhatikan faktor kelahiran, kematian, vaksinasi dan kekebalan tubuh.

(3)

I PENDAHULUAN

1.1 Latar Belakang

Salah satu ancaman terhadap manusia adalah penyakit, terutama penyakit menular yang dibawa oleh berbagai macam mikroba seperti bakteri, jamur, parasit dan virus. Penyakit campak (measles) merupakan penyakit yang sangat berbahaya, penyakit tersebut disebabkan oleh virus yang dapat menyebar melalui kontak langsung dengan penderita, udara dan batuk. Tubuh mempunyai kemampuan untuk mengatasi sampai batas tertentu. Dalam hal ini, dikatakan bahwa sistem pertahanan tubuh (sistem imun) orang tersebut cukup baik untuk mengatasi dan mengalahkan kuman-kuman penyakit tersebut. Tetapi bila kuman penyakit tesebut ganas, sistem pertahanan tubuh yang lemah tidak mampu mencegah kuman atau virus itu berkembangbiak, sehingga dapat mengakibatkan penyakit berat yang membawa kepada cacat atau kematian.

Kinbaby (2008) menyatakan bahwa penyakit campak (measles) tersebut dinilai berbahaya karena dapat menyebabkan komplikasi, kerusakan otak dan organ tubuh lainnya, cacat seumur hidup, kelumpuhan dan bahkan kematian.

Vaksinasi telah menjadi salah satu strategi yang cukup berhasil dalam mencegah penyakit campak (measles) (Sleeman, 1983), namun tidak sepenuhnya dapat melindungi penerima vaksin secara merata. Perlindungan yang diberikan vaksin tergantung pada kekebalan tubuh penerima vaksin (Hethcote, 2000). Kegagalan vaksin untuk melindungi penerima vaksin secara merata dan menentukan kondisi apa yang diperlukan untuk mengurangi bahkan membasmi infeksi penyakit campak (measles) pada suatu populasi.

Perkembangan ilmu pengetahuan di bidang matematika juga turut mememberikan peranan penting dalam mencegah meluasnya penyebaran penyakit campak (measles) (Castellli dan Romanelli, 2009). Peranan tersebut berupa model matematika yang mempelajari penyebaran penyakit. Matematika memberikan salah satu solusi penyelesaian penyebaran penyakit campak (measles). Pertama, pola endemik bisa digambaran secara matematis dengan mendekati keadaan sebenarnya melalui suatu model matematika. Kedua, dengan matematika akan dianalisis pola endemik melalui model yang telah dirumuskan berdasarkan suatu asumsi.

Model matematika yang dimaksud adalah model epidemik SIR, SIR vaksinasi, SEIR dan

MSEIR. Model SIR, SIR vaksinasi, SEIR dan

MSEIR ini dikenalkan oleh Kermack dan McKendrik pada tahun 1929. Model SIR, SIR vaksinasi, SEIR dan MSEIR pada awalnya dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam populasi tertutup dan bersifat epidemik. Model endemik SIR

menggambarkan penyebaran suatu penyakit, dimana total populasi pada model ini diasumsikan konstan karena pengaruh kelahiran, kematian maupun migrasi diperhatikan. Laju kelahiran pada model SIR

diasumsikan sama dengan laju kematian. Menurut Grassly dan Frasher (2006), tidak semua sistem persamaan differensial dapat ditentukan penyelesaian eksaknya. Oleh karena itu, diperlukan informasi lain untuk mengamati prilaku sistem. Prilaku sistem dapat diamati pada titik-titik dimana sistem berada pada keadaan stasioner atau kesetimbangan. Titik tersebut selanjutnya disebut titik keseimbangan. Konsep perilaku sistem pada titik keseimbangan dikenal dengan kestabilan. Kestabilan tersebut merupakan informasi untuk menyebarkan perilaku sistem. Oleh karena itu, dalam model emdemi SIR, SIR vaksinasi, SEIR dan MSEIR

dengan memperhatikan faktor vaksinasi perlu ditentukan kestabilan di titik keseimbangan untuk mengetahui dan menginterpretasikan perilaku sistem.

Hethcote (2000) menyebutkan bahwa pada model SIR, SIR vaksinasi, SEIR dan

MSEIR populasi dibagi menjadi tiga kelompok yaitu kelompok individu yang rentan penyakit (S), kelompok individu yang terinfeksi (I), dan kelompok individu yang telah sembuh dan kebal dari penyakit (R). Secara garis besar, model epidemik SIR, SIR vaksinasi, SEIR dan

(4)

1.2 Tujuan

Tujuan utama penulisan karya ilmiah ini adalah:

1. Memeriksa kestabilan model SIR, SIR vaksinasi, SEIR dan MSEIR pada masing-masing titik tetapnya dan menentukan perbedaan dari keempat model tersebut,

2. Dengan dinamika perubahan populasi pada model SIR, SIR vaksinasi, SEIR dan

MSEIR didapat orbit kestabilannya, 3. Mendapatkan dan menginterpretasikan

bilangan reproduksi dasar dari model

SIR, SIR vaksinasi, SEIR dan MSEIR,

1.3 Metode

Metode tersebut dianalisis melalui dua cara yaitu secara matematis dan secara numerik. Secara matematis, dengan menganalisis kestabilan melalui penentuan titik tetap, orbit kestabilan, dinamika populasi dan kondisi yang memenuhi kestabilannya. Secara numerik menggunakan Software Maple 12 dengan diberikan parameter-parameter berbeda.

II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial

Definisi 1 Sistem Persamaan Diferensial Linear (SPDL)

Misalkan suatu persamaan differensial linear orde 1 dinyatakan sebagai berikut: ̇ = g(t) dengan dan g(t) adalah fungsi dari waktu t. Bila adalah suatu matriks berukuran n x n dengan koefisien konstan dan g(t) dinyatakan sebagai vektor konstan b maka diperoleh sebagai berikut;

= ̇ = Ax + b, x(0) = x0

(Farlow 1994)

Definisi 2 Titik Tetap

Misalkan diberikan sistem persamaan differensial (SPD) sebagai berikut:

= ̇ = f(x), x ϵ

Suatu titik yang memenuhi f( = 0 disebut titik keseimbangan atau titik tetap dari sistem.

(Tu 1994) Definisi 3 Titik Tetap Stabil

Titik adalah titik tetap sebuah SPD dan

x(t) adalah solusi yang memenuhi kondisi awal x(0)=x0 dan x0 . Titik dikatakan titik tetap stabil jika terdapat ɛ0 > 0, yang memenuhi sifat berikut; untuk setiap ɛ1, 0 < ɛ1< ɛ0, terdapat ɛ0 > 0 sedemikian sehingga jika || - x0 || < ɛ maka || - x(t)|| < ɛ1, untuk setiap t > t0.

(Szidarovszky & Bahill 1998)

Definisi 4 Titik Tetap Takstabil

Misalkan adalah titik tetap sebuah SPD mandiri dan x(t) adalah sebuah solusi SPD mandiri dengan nilai awal x(0)= x0 dengan

x0 Titik dikatakan titik tetap tak stabil

jika terdapat radius ρ > 0 dengan ciri sebagai berikut: untuk sembarang r > 0 terdapat posisi awal x0 memenuhi || - x0 || < r, berakibat solusi x(t) memenuhi || - x(t)|| ρ, untuk paling sedikit satu t > 0.

(Anton 1995)

Definisi 5 Titik Tetap Stabil Asimtotik Lokal

Titik dikatakan titik tetap asimtotik lokal jika titik dan terdapat ɛ > 0 sedemikian sehingga jika || - x0 || < 0 maka

Definisi 6 Titik Tetap Stabil Asimtotik Global

Titik dikatakan titik tetap asismtot global jika titik stabil dan x0 ϵ (Szidarovszky & Bahill 1998) Definisi titik tetap stabil menyatakan bahwa titik stabil jika seluruh orbit (lintasan kurva dan yang menggambarkan solusi x(t) berada pada radius ε1, jika nilai awal (x0) yang terpilih cukup dekat dengan Titik tetap stabil asimtotik global, dipilih nilai awal (x0) di luar radius ε0 sehingga solusi x(t) adalah untuk t → .

Definisi 7 Nilai Eigen dan Vektor Eigen Misalkan A adalah matriks n x n ,maka suatu matrik taknol x di dalam disebut vektor eigen dari A, jika untuk suatu skalar , yang disebut nilai eigen dari A diperoleh;

Ax = x

(5)

1.2 Tujuan

Tujuan utama penulisan karya ilmiah ini adalah:

1. Memeriksa kestabilan model SIR, SIR vaksinasi, SEIR dan MSEIR pada masing-masing titik tetapnya dan menentukan perbedaan dari keempat model tersebut,

2. Dengan dinamika perubahan populasi pada model SIR, SIR vaksinasi, SEIR dan

MSEIR didapat orbit kestabilannya, 3. Mendapatkan dan menginterpretasikan

bilangan reproduksi dasar dari model

SIR, SIR vaksinasi, SEIR dan MSEIR,

1.3 Metode

Metode tersebut dianalisis melalui dua cara yaitu secara matematis dan secara numerik. Secara matematis, dengan menganalisis kestabilan melalui penentuan titik tetap, orbit kestabilan, dinamika populasi dan kondisi yang memenuhi kestabilannya. Secara numerik menggunakan Software Maple 12 dengan diberikan parameter-parameter berbeda.

II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial

Definisi 1 Sistem Persamaan Diferensial Linear (SPDL)

Misalkan suatu persamaan differensial linear orde 1 dinyatakan sebagai berikut: ̇ = g(t) dengan dan g(t) adalah fungsi dari waktu t. Bila adalah suatu matriks berukuran n x n dengan koefisien konstan dan g(t) dinyatakan sebagai vektor konstan b maka diperoleh sebagai berikut;

= ̇ = Ax + b, x(0) = x0

(Farlow 1994)

Definisi 2 Titik Tetap

Misalkan diberikan sistem persamaan differensial (SPD) sebagai berikut:

= ̇ = f(x), x ϵ

Suatu titik yang memenuhi f( = 0 disebut titik keseimbangan atau titik tetap dari sistem.

(Tu 1994) Definisi 3 Titik Tetap Stabil

Titik adalah titik tetap sebuah SPD dan

x(t) adalah solusi yang memenuhi kondisi awal x(0)=x0 dan x0 . Titik dikatakan titik tetap stabil jika terdapat ɛ0 > 0, yang memenuhi sifat berikut; untuk setiap ɛ1, 0 < ɛ1< ɛ0, terdapat ɛ0 > 0 sedemikian sehingga jika || - x0 || < ɛ maka || - x(t)|| < ɛ1, untuk setiap t > t0.

Definisi 4 Titik Tetap Takstabil

Misalkan adalah titik tetap sebuah SPD mandiri dan x(t) adalah sebuah solusi SPD mandiri dengan nilai awal x(0)= x0 dengan

x0 Titik dikatakan titik tetap tak stabil

jika terdapat radius ρ > 0 dengan ciri sebagai berikut: untuk sembarang r > 0 terdapat posisi awal x0 memenuhi || - x0 || < r, berakibat solusi x(t) memenuhi || - x(t)|| ρ, untuk paling sedikit satu t > 0.

(Anton 1995)

Definisi 5 Titik Tetap Stabil Asimtotik Lokal

Titik dikatakan titik tetap asimtotik lokal jika titik dan terdapat ɛ > 0 sedemikian sehingga jika || - x0 || < 0 maka

Definisi 6 Titik Tetap Stabil Asimtotik Global

Titik dikatakan titik tetap asismtot global jika titik stabil dan x0 ϵ (Szidarovszky & Bahill 1998) Definisi titik tetap stabil menyatakan bahwa titik stabil jika seluruh orbit (lintasan kurva dan yang menggambarkan solusi x(t) berada pada radius ε1, jika nilai awal (x0) yang terpilih cukup dekat dengan Titik tetap stabil asimtotik global, dipilih nilai awal (x0) di luar radius ε0 sehingga solusi x(t) adalah untuk t → .

Definisi 7 Nilai Eigen dan Vektor Eigen Misalkan A adalah matriks n x n ,maka suatu matrik taknol x di dalam disebut vektor eigen dari A, jika untuk suatu skalar , yang disebut nilai eigen dari A diperoleh;

Ax = x

(6)

dapat dituliskan sebagai berikut: (c)x = 0, dengan I matriks identitas persamaan Ax = x mempunyai solusi tak nol jika dan hanya jika det (A - I) = 0, persamaan ini dinamakan persamaan karakteristik.

(Anton 1995)

Definisi 8 Analisis Kestabilan Titik Tetap Misalkan diberikan matriks A yang berukuran 2 x 2 sebagai berikut:

A =

Dengan persamaan karakteristik det(A – I) = 0, dan I adalah matriks identitas, maka persamaan karakteristiknya menjadi: det

= 0, sedemikian sehingga diperoleh persamaan , dengan τ = trace(A) = a+d dan = det(A) = ad-bc. Dengan demikian diperoleh nilai eigen dari A adalah j,k = √ .

Analisis kestabilan titik tetap dilakukan untuk setiap nilai eigen yang diperoleh. Secara umum kestabilan suatu titik tetap didasarkan pada kriteria berikut:

Stabil jika

a. Setiap nilai eigen real adalah negatif ( j < 0) untuk setiap j) b. Setiap komponen nilai eigen

kompleks lebih kecil atau sama dengan nol, (Re( j 0) untuk setiap j).

Tak Stabil jika

a. Setiap nilai eigen real adalah positif ( j > 0) untuk setiap j) b. Setiap komponen nilai eigen

kompleks lebih besar dari nol, (Re( j 0) untuk setiap j).

Sadel jika

Perkalian dua buah nilai eigen real sembarang adalah negatif ( j, k< 0 untuk j dan k sembarang).

(Tu, 1994) Definisi 9 Pelinearan

Untuk suatu SPD taklinear, analisis kestabilan dilakukan melalui pelinearan. Misalkan diberikan SPD taklinear sebagai berikut:

̇ = f(x)

Dengan menggunakan ekspansi Taylor untuk suatu titik tetap , maka persamaan diatas dapat ditulis sebagai berikut:

̇= Ax + Ҩ(x)

Persamaan tersebut SPD taklinear dengan A adalah matriks Jakobi,

A = Df( ) = Df(x) x =x* = [ ] =[ ] Dan Ҩ(x) suku berorde tinggi yang bersifat ) = 0. Selanjutnya Ax pada

persamaan diatas disebut pelinearan dari sistem tak linear persamaan (1.8) yang didapatkan dalam bentuk ̇ = Ax. Untuk sistem yang berada dalam bidang (n=2) akan diperoleh;

̇ = f(x) = Ax + Ҩ(x) dengan ̇ = f1(x) = + Ҩ1(x1,x2) ̇ = f2(x) = + Ҩ2(x1,x2) dengan = ,

=

= ,

=

dan = = 0 dengan r = √ Nilai Ҩ1 dan Ҩ2 kecil sekali, sehingga dapat diabaikan.

(Tu 1994)

Definisi 10 Kriteria Kestabilan

Teorema 1: (Rout-Hurwitz Criterion)

Misalkan , …, bilangan real. Semua nilai eigen dari persamaan karakteristik

Mempunyai bagian real yang negatif jika dan hanya jika determinan dari matriks untuk setiap j= 1, 2, 3,…, n

[

] adalah positif dengan jika k > n

Berdasarkan kriteria Routh-Hurwitz, untuk suatu nilai n = 2 maka titik stabil jika dan hanya jika dan disajikan pada teorema berikut.

(Fisher 1990) Teorema 2

Misalkan A, B bilangan-bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik

adalah negatif jika dan hanya jika A dan B

(7)

2.2 Bilangan Reproduksi Dasar

Bilangan reproduksi dasar adalah potensi penularan penyakit pada populasi rentan, merupakan rata-rata jumlah individu yang terinfeksi secara langsung oleh seorang penderita selama masa penularannya bila termasuk dalam populasi yang seluruhnya masih rentan.

Untuk mengetahui tingkat penyebaran suatu penyakit diperlukan suatu parameter tertentu. Parameter yang biasa digunakan dalam masalah penyebaran penyakit adalah bilangan reproduksi dasar. Hethcote (2000) menyatakan bahwa bilangan reproduksi dasar merupakan rasio yang menunjukkan jumlah

individu rentan yang dapat menderita penyakit yang disebabkan oleh satu individu infeksi.

Kondisi yang akan timbul adalah satu diantara tiga kemungkinan ini;

a. Jika , maka penyakit akan menghilang,

b. Jika , maka penyakit akan menetap (endemis),

c. Jika , maka penyakit akan meningkat menjadi wabah.

(Giesecke 1994)

III PEMODELAN

3.1 Model SIR

Model SIR pada awalnya dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam poulasi tertutup dan bersifat epidemik. Hethcote (2000) menyatakan bahwa pada model epidemi SIR klasik, populasi dibagi menjadi tiga kelompok yaitu, kelompok individu yang sehat tetapi dapat terinfeksi penyakit (rentan), kelompok individu yang terinfeksi dan dapat sembuh dari penyakit

(infeksi) dan kelompok individu yang telah sembuh dan kebal dari penyakit (pulih). Dalam kasus yang paling dasar kita membuat asumsi bahwa sekali seorang individu telah terinfeksi dan kemudian telah pulih, maka individu tersebut tidak akan terjangkit kembali dikarenakan adanya kekebalan tubuh yang kuat. Dengan menganggap bahwa tingkat penularan penyakit sebanding dengan jumlah pertemuan antara individu rentan dan individu yang terinfeksi.

Gambar 1. Dinamika populasi dalam model SIR

Dari gambar 1 model SIR dapat dituliskan sebagai berikut:

= -β S

= β S –ξI (1)

= ξI – R

Keterangan:

: populasi individu

: kelompok individu yang rentan terinfeksi penyakit,

I : kelompok individu yang terinfeksi

penyakit dan dapat sembuh dari penyakit,

R : kelompok individu yang telah sembuh dan kebal dari penyakit, β : laju penularan penyakit,

ξ : laju kesembuhan,

µ : laju kelahiran dan laju kematian

Dengan β, µ dan ξ adalah parameter positif yang merupakan tingkat transmisi. Sebagaimana ditetapkan, bahwa nilai dari (S

+ I + R) = N, sehingga S + I + R adalah konstan. Dalam populasi individu bahwa laju kelahiran sama dengan laju kematian. Populasi S akan meningkat seiring dengan bertambahnya individu kedalam suatu

Rentan (S) Infeksi (I) Pulih (R)

β

ξ

μ

µ

(8)

2.2 Bilangan Reproduksi Dasar

Bilangan reproduksi dasar adalah potensi penularan penyakit pada populasi rentan, merupakan rata-rata jumlah individu yang terinfeksi secara langsung oleh seorang penderita selama masa penularannya bila termasuk dalam populasi yang seluruhnya masih rentan.

Untuk mengetahui tingkat penyebaran suatu penyakit diperlukan suatu parameter tertentu. Parameter yang biasa digunakan dalam masalah penyebaran penyakit adalah bilangan reproduksi dasar. Hethcote (2000) menyatakan bahwa bilangan reproduksi dasar merupakan rasio yang menunjukkan jumlah

individu rentan yang dapat menderita penyakit yang disebabkan oleh satu individu infeksi.

Kondisi yang akan timbul adalah satu diantara tiga kemungkinan ini;

a. Jika , maka penyakit akan menghilang,

b. Jika , maka penyakit akan menetap (endemis),

c. Jika , maka penyakit akan meningkat menjadi wabah.

(Giesecke 1994)

III PEMODELAN

3.1 Model SIR

Model SIR pada awalnya dikembangkan untuk mengetahui laju penyebaran dan kepunahan suatu wabah penyakit dalam poulasi tertutup dan bersifat epidemik. Hethcote (2000) menyatakan bahwa pada model epidemi SIR klasik, populasi dibagi menjadi tiga kelompok yaitu, kelompok individu yang sehat tetapi dapat terinfeksi penyakit (rentan), kelompok individu yang terinfeksi dan dapat sembuh dari penyakit

(infeksi) dan kelompok individu yang telah sembuh dan kebal dari penyakit (pulih). Dalam kasus yang paling dasar kita membuat asumsi bahwa sekali seorang individu telah terinfeksi dan kemudian telah pulih, maka individu tersebut tidak akan terjangkit kembali dikarenakan adanya kekebalan tubuh yang kuat. Dengan menganggap bahwa tingkat penularan penyakit sebanding dengan jumlah pertemuan antara individu rentan dan individu yang terinfeksi.

Gambar 1. Dinamika populasi dalam model SIR

Dari gambar 1 model SIR dapat dituliskan sebagai berikut:

= -β S

= β S –ξI (1)

= ξI – R

Keterangan:

: populasi individu

: kelompok individu yang rentan terinfeksi penyakit,

I : kelompok individu yang terinfeksi

penyakit dan dapat sembuh dari penyakit,

R : kelompok individu yang telah sembuh dan kebal dari penyakit, β : laju penularan penyakit,

ξ : laju kesembuhan,

µ : laju kelahiran dan laju kematian

Dengan β, µ dan ξ adalah parameter positif yang merupakan tingkat transmisi. Sebagaimana ditetapkan, bahwa nilai dari (S

+ I + R) = N, sehingga S + I + R adalah konstan. Dalam populasi individu bahwa laju kelahiran sama dengan laju kematian. Populasi S akan meningkat seiring dengan bertambahnya individu kedalam suatu

Rentan (S) Infeksi (I) Pulih (R)

β

ξ

μ

µ

(9)

populasi dan berkurangnya kekebalan tubuh yang disebabkan oleh infeksi alam yang menyerang tubuh. Populasi I akan meningkat dengan bertambahnya individu yang terinfeksi dari kelas S.

Kekebalan tubuh yang terinfeksi akan berubah seiring dengan berjalannya waktu, maka individu yang terinfeksi akan pulih memasuki individu R. Jadi, populasi R akan meningkat sesuai dengan meningkatnya individu yang pulih dari infeksi dan akan bekurang seiring dengan perubahan kekebalan. Penyebaran penyakit campak (measles) diasumsikan muncul pada saat individu kehilangan kekebalan tubuh dan hilang kendali ketika virus itu datang. Hal ini mengarah pada model endemik SIR. Proporsi banyaknya individu pada masing-masing kelompok dapat dinyatakan sebagai berikut;

s = , i = , dan r =

diperoleh persamaan sebagai berikut;

= ₍ βsi + – s

(

= βsi –(ξ+ )i

(2)

=

= ξi – r

3.2 Model SIR dengan vaksinasi

Model endemik SIR dengan memeperhatikan faktor vaksinasi diturunkan ulang dari model endemi SIR klasik. Model penyebaran penyakit diturunkan menggunkan

asumsi atau batasan tertentu. Hethcote (2000) menyebutkan bahwa asumsi-asumsi yang digunakan dalam model penyebaran penyakit sebagai berikut;

 Jumlah populasi diasumsikan cukup besar,

 Populasi diasumsikan tertutup, oleh karena itu tidak ada populasi yang masuk ke dalam populasi atau keluar dari populasi tersebut,

 Pada model SIR, faktor kelahiran dan kematian diperhatikan, jumlah kelahiran dan kematian dalam tiap satuan waktu diasumsikan sama,  Populasi diasumsikan bercampur

secara homogen yang berarti setiap individu mempunyai kemungkinan yang sama dalam melakukan kontak dengan individu lainya,

 Individu yang terinfeksi penyakit dapat sembuh dari penyakit dan dapat pula menimbulkan kematian akibat penyakit tersebut.

Selanjutnya, program vaksinasi diperhatikan dalam model. Asumsi yang digunakan terhadap vaksinasi tersebut adalah sebagai berikut;

 Vaksinasi hanya diberikan pada individu yang baru lahir atau yang masih dalam usia anak- anak ( < 12 tahun ),

 Keampuhan vaksinasi adalah 100%, hal ini berarti setiap individu yang telah mendapatkan vaksinasi akan kebal dari penyakit. Kekebalan yang terjadi karena vaksinasi bersifat permanen.

(10)

Gambar 2. Dinamika populasi dalam model SIR dengan pengaruh vaksinasi Gambar 2 di atas populasi yang lahir akan

memasuki dua individu yaitu; pertama masuk ke individu rentan dan yang kedua populasi bisa langsung memasuki individu pulih. Individu yang tidak memperoleh vaksinasi akan memasuki kelompok individu rentan dan berpotensi untuk terinfeksi penyakit campak (measles) maka individu rentan akan memasuki individu pulih.

Dengan N = S + I + R. Untuk proses tranmisi vaksinasi dengan menggunakan asumsi yaitu:

 Terjadi penularan dari individu ke individu yang lain,

 Semua parameter dan variabel yang digunakan tidak negatif,

 Tidak ada individu yang sudah terinfeksi masuk ke dalam individu baru.

Model endemik SIR dengan mempertimbangkan pengaruh vaksinasi selengkapnya dapat diekpresikan sebagai berikut (lihat gambar 2);

= (3)

=

S(0) > 0, I(0) > 0 dan R(0) ,

Persamaan (3) dapat diskala dengan total populasi N untuk menyerderhanakan persamaan (3) dan memudahkan analisis yang dilakukan. Proporsi banyaknya individu pada masing-masing kelompok dapat dinyatakan sebagai berikut;

s = , i = , dan r =

=

= si( + )s (4)

=

+ i - r

3.3 Model SEIR

Pada model SEIR bahwa laju kelahiran yang terjadi dalam populasi diasumsikan sama dengan laju kematian, dimana tingkat kelahiran dan tingkat kematian ditandai dengan . Dalam keberadaan penyakit menular, salah satu tugas utamanya adalah pemberantasan melalui langkah-langkah pencegahan dan jika mungkin, melalui pembentukan program vaksinasi massal.

β

ξ

Pulih (R) Infeksi (I)

Rentan (S)

(1-

�

)

�

Type equat on here

(Vaksin)

(11)

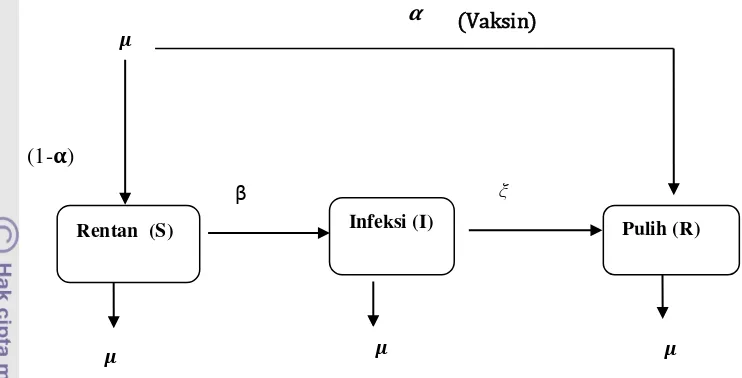
Gambar 3. Dinamika populasi dalam model SEIR . Sebuah penyakit dimana bayi yang baru

lahir divaksinasi (dengan vaksin memberikan kekebalan seumur hidup) dengan nilai ϵ (0,1) maka akan diperoleh model sebagai berikut (lihat gambar 3);

=

= E

=

= ξI - R (5)

dengan S(0) > 0, I(0) > 0, E(0) > 0 dan R(0) .

Keterangan:

N : populasi individu

S : kelompok individu yang rentan terinfeksi penyakit,

E : kelompok individu laten,

I : kelompok individu yang terinfeksi penyakit dan dapat sembuh dari penyakit,

R : kelompok individu yang telah sembuh dan kebal dari penyakit,

: laju penularan penyakit, � : laju kesembuhan,

µ : laju kelahiran dan laju kematian, : laju vaksinasi,

: laju kekebalan tubuh.

Dimana β, τ, , ρ, � dan ξ adalah parameter positif. Sistem dapat skala total populasi N untuk menyerderhanakan sistem (5) dan memudahkan analisis yang dilakukan,

sehingga akan diperoleh model sebagai berikut;

=

= (6)

= ξi - r

Rentan (S) Laten (E) Infeksi (I) Pulih (R)

μ

ρ

(1-

α �

ξ

µ

μ

µ

μ

(12)

3.4 Model MSEIR

Model endemik MSEIR dengan mempertimbangkan imunisasi dan laju

kelahiran tidak sama dengan laju kematian dapat diekspresikan sebagai berikut (lihat gambar 4);

Gambar 4. Dinamika populasi dalam model MSEIR Diperoleh persamaan sebagai berikut;

�

(7)

Dengan daerah asal sebagai berikut;

� ={(M, S, E, I, R) : M E , S

, M + S + E + I + R .

Keterangan:

N : populasi individu,

M : kelompok individu yang telah mendapat imunitas,

S : kelompok individu yang rentan terinfeksi penyakit,

E : kelompok individu laten,

I : kelompok individu yang terinfeksi penyakit dan dapat sembuh dari penyakit,

R : kelompok individu yang telah

sembuh dan kebal dari penyakit, : laju penularan penyakit,

� : laju kesembuhan,

µ : laju kelahiran dan laju kematian : laju vaksinasi,

: laju perubahan imunitas,

Proporsi banyaknya individu pada masing-masing kelompok dapat dinyatakan sebagai berikut;

m =

,

s = , e =

,

i = , dan r = dimana, m + s + e + i + r = 1

,

�

(8)

� ={(m,s,e,i,r) : m e , s

, m + s + e + i+ r

M

S

E

I

R

ɓ

µ

(13)

IV PEMBAHASAN

4.1 Model SIR

4.1.1 Titik Tetap

Untuk mendapatkan titik tetap diperoleh dari dua persamaan singular (

an

sehingga dari persamaan (2) diperoleh :

- si + – s = 0 (9)

si –( + )i = 0

didapat titik tetap yaitu E0 = (1, 0) dan

E1 =

=

Dengan menggunkan Software Maple 12

dan parameter yang digunakan , , dan diperoleh nilai titik tetap yaitu E0 = (1, 0) dan E1= (0.5, 0.4). E0 merupakan titik tetap tanpa penyakit dan E1 merupakan titik tetap endemik.

4.1.2 Konstruksi Matriks Jacobi untuk Model SIR

Dari Persamaan (2) akan diperoleh matriks jacobi sebagai berikut;

[ ] [ _] (10)

4.1.3 Analisis Kestabilan Titik Tetap Model

SIR

Titik tetap E0 = (1, 0) disubstitusikan ke dalam persamaan (10) sehingga akan diperoleh sebagai berikut;

[ _]

Untuk memperoleh nilai eigen dari matrik jacobi di atas maka |J – I| = 0, sehingga diperoleh nilai eigen, yaitu;

 (- - ) ( ) = 0 Didapat nilai eigen sebagai berikut;

1 = - < 0

2 =

untuk dan j < 0 (j =1, 2), nilai 1 = - < 0 dan 2 < 0 maka < 0. Jika 1 = - < 0 dan 2 < 0 maka titik bersifat stabil dan

jika 1 < 0 dan 2 > 0, maka titik bersifat sadel. Nilai mengakibatkan

Oleh karena itu, titik akan stabil asimptotik untuk . Namun, jika nilai maka titik akan tidak stabil. Dengan nilai dan diperoleh maka dapat disimpulkan bahwa titik E0 = (1, 0) tidak stabil asimptotik.

Kestabilan sistem di titik tetap E1

Tititk tetap E1=

disubstitusikan pada

persamaan (10), maka akan diperoleh matriks jacobinya sebagai berikut ini;

[ ]

Untuk memperoleh nilai eigen dari matriks jacobi di atas maka |J – I| = 0, sehingga diperoleh nilai eigen yaitu;

=

+

Jika nilai

maka titik E1

bersifat stabil asimtotik, jika nilai

maka E1 bersifat sadel. Nilai

maka titik E1 =

adalah titik

stabil asimptotik.

4.1.4 Bilangan Reproduksi untuk model

SIR

R0 dari model SIR diperoleh sebagai berikut;

persamaan di atas setelah dilinearisasi diperoleh sebagai berikut;

(14)

R0 =

4.1.5 Orbit dan Kestabilan Sistem Model

SIR

Orbit kestabilan diperoleh dengan menggunakan Software Maple 12 sehingga diperoleh bentuk orbit seperti di bawah ini. Dengan memilih nilai-nilai parameter sebagai berikut: = 0.5, β = 0.8, = 0.4dan ξ = 0.03. Hal ini berimplikasi . Titik tetap yang diperoleh adalah yang bersifat tak stabil dan yang bersifat stabil. Orbit disajikan sebagai berikut.

Gambar 5. Orbit kstabilan model SIR

dibidang SI

Pada gambar 5 di atas terlihat bahwa orbitnya menuju titik E1. Oleh karena itu, titik tetap endemik bersifat stabil asimptotik. Hal tersebut menunjukkan bahwa ada individu I

yang dapat menyebarluaskan penyakit campak (measles) sehingga kelompok individu S terinfeksi penyakit.

Gambar 6. Dinamika populasi S, I, dan R

menurut waktu (tahun)

Gambar 6 merupakan bidang solusi untuk

S, I dan R yang menuju titik tetap stabil bila dimasukkan nilai awal S = 0.8, I = 0.2 dan R = 0 sehingga menuju titik E1 (s, i) = (0.54, 0.43). Seiring berjalannya waktu proporsi kelompok individu S akan semakin berkurang. Hal ini terjadi karena kelompok individu S terinfeksi oleh penyakit campak (measles) dan memasuki kelompok individu I. Pada waktu tertentu proporsi individu pada kelompok S

tidak mengalami perubahan dan mencapai kondisi setimbang.

Pada proporsi kelompok individu I

mengalami kenaikkan dari keadaan awal, Kenaikkan jumlah individu I terjadi karena adanya tambahan individu dari individu S

yang terinfeksi virus. Proporsi individu R

mengalami kenaikkan, hal ini disebabkan oleh adanya kelompok individu I yang sembuh dari penyakit sehingga akan memasuki kelompok individu R.

4.2 Model SIR vaksinasi

an

, sehingga dari persamaan (4) diperoleh :

- – s = 0

si – i = 0 (12)

Di dapat nilai titik tetap yaitu E0(s, i) = , 0) dan E1(s, i)

=

. Dengan menggunakan

Software Maple 12 dan parameter yang digunakan , , , dan = 0.4 diperoleh nilai titik tetap yaitu E0(s, i) = (0.5, 0) dan E1(s, i) = (0.54, -0.03). E0 merupakan titik tetap tanpa penyakit dan E1 merupakan titik tetap endemik.

.4.2.2 Konstruksi Matriks Jacobi untuk Model SIR vaksinasi

Dari Persamaan (4) akan diperoleh matriks jacobi sebagai berikut;

[

] [ _]

(15)

(13) 4.2.3 Analisis Kestabilan Titik Tetap Model

SIRvaksinasi

Titik tetap E0 = , 0) disubstitusikan ke dalam persamaan (13) sehingga akan diperoleh;

[ _]

Untuk memperoleh nilai eigen dari matriks jacobi di atas maka |J – I| = 0, sehingga diperoleh nilai eigen yaitu;

 (- - )( ) = 0

1 = - < 0

2 =

Jika i < 0 untuk i = 1,2. Nilai > 0 mengakibatkan 1 = - < 0, jika 2< 0 maka < . Jika 1 < 0 dan 2 < 0, maka titik tetap bersifat stabil dan jika 1< 0 dan 2 > 0, maka titik tetap bersifat sadel. Nilai < mengakibatkan

= < 1. Jika < 1

maka merupakan titik tetap stabil asimtotik. Dengan kata lain, syarat terjadinya bebas penyakit adalah bilangan reproduksi dasar harus kurang dari satu. Jika > 1 maka

akan tidak stabil. Dengan mengambil

parameter positif diperoleh < 1, sehingga

merupakan titik tetap stabil asimtotik.

Tititk tetap =

disubstitusikan pada persamaan (13), maka akan diperoleh matriks jacobinya sebagai berikut ini;

[ _]

Dari persamaan diatas diperoleh nilai eigen dari matriks jacobi yaitu;

√

Dari persamaan di atas, titik tetap endemik hanya akan muncul ketika , sedangkan nilai merupakan bilangan real negatif atau berupa bilangan kompleks. Dengan bilangan real bernilai negatif untuk 1<

sehingga menyebabkan titik akan stabil asimtotik.

4.2.4 Bilangan Reproduksi Dasar untuk model SIR vaksinasi

R0 dari model SIR diperoleh sebagai berikut;

Persamaan di atas setelah dilinearisasi diperoleh sebagai berikut;

(14)

R0 =

4.2.5 Orbit dan Kestabilan Sistem Model

SIR vaksinasi

Orbit kestabilan diperoleh dengan menggunakan software Maple 12 sehingga diperoleh bentuk orbit seperti dibawah ini. Dengan memilih nilai-nilai parameter sebagai berikut: = 0.5, β = 0.8, = 0.4dan ξ = 0.03, hal ini berimplikasi pada < 1 maka akan diperoleh yang bersifat stabil dan yang bersifat tak stabil. Orbit disajikan sebagai berikut;

(16)

Gambar 8. Dinamika populasi S, I dan R

Pada gambar 8 di atas kita dapat melihat bagaimana hubungan individu rentan, infeksi dan pulih. Seiring berjalannya waktu poroporsi individu rentan akan semakin berkurang. Hal ini, disebabkan oleh kelompok individu rentan terjangkit penyakit dan memasuki kelompok individu infeksi. Pada waktu tertentu, proporsi individu pada kelompok rentan tidak mengalami perubahan lagi. Pada keadaan tersebut, sistem berada pada titik kesetimbangan.

Kelompok individu infeksi mengalami penurunan. Hal ini disebabkan oleh karena kelompok individu rentan tidak terjangkit penyakit setelah adanya penerimaan vaksin. Sehingga pada waktu tertentu kelompok individu rentan tidak memasuki individu I, semakin besar individu rentan yang tidak terjangkit penyakit maka kelompok individu infeksi akan semakin berkurang dan akan mencapai titik stabilan.

Program vaksinasi dilakukan untuk mencegah meluasnya penyebaran penyakit campak (measles). Vaksinasi diasumsikan berhasil jika pada waktu tertentu penyakit akan menghilang dari populasi I. Bilangan reproduksi dasar dapat juga digunakan untuk menentukan apakah penyakit campak (measles) tersebut akan menghilang dari populasi I pada waktu tertentu jika nilai dan jika Penyakit campak (measles) akan ada sampai batas waktu yang tak terbatas.

Upaya pencegahan penyebaran penyakit campak (measles) dapat dilakukan dengan program vaksinasi pada tingkat �. Pengaruh vaksinasi dapat dilihat dari prilaku proposi individu I yang bersifat endemik. Berdasarkan persamaan (4) tingkat vaksinasi minimum yang diperlukan dalam pencegahan penyebaran penyakit campak (measles) ialah = 0.4625. Menganalisis bagaimana

pengaruh vaksinasi jika tingkat vaksinasi lebih kecil dari vaksinasi minimum.

Gambar 9. Proporsi individu I pada saat nilai = 0.4625, = 0.3 , = 0.1, dan = 0

Dari gambar 9 menunjukan bahwa semua vaksinasi yang diberikan bahwa penyakit akan selalu ada dalam jangka waktu yang tak terbatas. Oleh karena itu, penyakit campak (measles) bersifat endemik. Dengan demikian vaksinasi yang dilakukan tidak berhasil membuat penyakit campak (measles) menghilang dari populasi individu I.

Dengan demikian jika < = 0.4625, maka penyakit campak (measles) tidak akan menghilang dari populasi individu I dalam jangka waktu yang tak terbatas. Kondisi kesetimbangan yang dicapai dalam individu I

merupakan titik kesetimbangan endemik.

Tabel 1. Titik Tetap, Bilangan Reproduksi Dasar dan Kestabilan.

Titik Tetap Kestabilan 0

(1, 0)

1.86 -Stabil asimtotik - Takstabil 0.1

(1, 0)

1.67 -Stabil asimtotik -Takstabil 0.3

(0.7, 0)

1.3 -Stabil asimtotik -Takstabil

Dari Tabel 1 dapat di lihat bahwa jika semakin tinggi tingkat vaksinasi yang diberikan maka nilai bilangan reproduksi dasar akan semakin menurun. Namun demikian < c= 0.4625, nilai

sehingga penyakit campak (measles) akan selalu ada dalam jangka waktu yang tak batas.

(17)

diberikan agar penyebaran campak (measles) dapat dicegah dengan sangat baik. Oleh karena itu, selanjutnya akan dilakukan simulasi nilai

yang lebih besar dari

Selajutnya akan menganalisis bagaimana pengaruh vaksinasi jika tingkat vaksinasi yang diberikan lebih besar dari tingkat vaksinasi minimum.

Gambar 10. Proporsi individu I pada saat nilai = 0.4625, = 0.6, = 0.9 , dan =1

Dalam waktu kurang lebih 15 tahun maka sistem akan mencapai stabil dan mencapai titik stabi di = (0.5, 0). merupakan titik tetap bebas penyakit dikarenakan proporsi individu I = 0. Besarnya bilangan reproduksi dasar ialah = 0.74. Titik tetap bebas penyakit tersebut bersifat stabil asimtotis karena nilai .

Jika setiap kelahiran memperoleh vaksin sebesar = 1. Diberikan vaksinasi pada tingkat = 1, maka proporsi individu I ditunjukan oleh warna biru. Untuk = 1, penyakit akan menghilang dari populasi dalam jangka waktu kurang lebih 15 tahun. Dalam waktu kurang lebih 15 tahun maka sistem akan mencapai stabil dan mencapai titik stabil di = (0.5, 0).

Dengan demikian Penyakit campak (measles) akan menghilang dari populasi untuk nilai tingkat vaksinasi lebih besar dari tingkat vaksinasi minimum Semakin besar tingkat vaksinasi maka semakin cepat penyakit menghilang dari populasi.

Tabel 2. Titik Tetap, Bilangan Reproduksi Dasar dan Kestabilan

� Titik tetap Kestabilan

0.6

(0.5, -0.2)

0.9

(0.5, -0.4)

1

(50, -16)

0 -Stabil

asimtotik -Takstabil

Dari Tabel 2 dapat di lihat bahwa jika semakin tinggi tingkat vaksinasi yang diberikan maka bilangan reproduksi dasar akan semakin menurun. Namun demikian <

c = 0.4625, nilai

sehingga penyakit campak (measles

akan selalu ada dalam jangka waktu yang tak batas. Tabel 2 juga menunjukkan bahwa untuk < c = 0.4625, kenaikan tingkat vaksinasi dapat menyebabkan semakin menurunnya bilangan reproduksi dasar ( Untuk = 1, titik stabil pada proporsi kelompok individu rentan bernilai nol. Hal tersebut menunjukkan bahwa semua individu rentan kebal dari penyebaran penyakit campak (measles) dan akan memasuki kelompok individu pulih. Titik stabil yang dicapai ialah titik tetap stabil bebas penyakit dikarenakan proporsi kelompok individu infeksi bernilai nol.

4.3 Model SEIR

an , sehingga dari persamaan (4) diperoleh :

= 0 (15)

= 0

didapat nilai titik tetap yaitu E0 (s, e, i)= (1, 0, 0) dan E1(s, e, i)=

(

(18)

, dan diperoleh nilai titik tetap yaitu E0 = (1, 0, 0) dan E1= (0.29, 0.22, 0.45)

.

E0 merupakan titik tetap tanpa penyakit dan E1 merupakan titik tetap endemik.

4.3.2 Konstruksi Matriks Jacobi Untuk Model SEIR

Misalkan sistem persamaan (6) dituliskan sebagai berikut: [ ] [ ] (15) dengan � � (16)

SEIR

Kestabilan sistem di titik tetap E0(s, e, i) = (1, 0, 0). Titik tetap E0disubstitusikan pada persamaan (16), maka akan diperoleh

�

Dari matriks di atas diperoleh nilai-nilai eigen sebagai berikut;

1=

2 = �

3 =

Jika 1 < 0, 2 < 0 dan 3 < 0, maka E0 bersifat stabil dan jika 1 < 0, 2 < 0 dan 3 > 0, maka E0 bersifat sadel.

Kestabilan sistem di titik tetap E1(s, e, i)

= (

Titik tetap E1 disubstitusikan pada persamaan (16), maka akan diperoleh

J= �

�

Dari matriks di atas diperoleh nilai-nilai eigen sebagai berikut:

1=

2 = �

3 =

Jika 1 < 0, 2 < 0 dan 3 < 0, maka E1 bersifat stabil dan jika 1 < 0, 2 < 0 dan 3 > 0, maka bersifat sadel.

Teorema 1.

a. Jika < c, maka sebuah titik tetap endemik yang tunggal dari model merupakan tititk tetap stabil asimtotik global.

b. Misalakan > c , titik tetap tanpa penyakit merupakan titik tetap stabil asimtotik global didalam Ὠ.

Berdasarkan model SEIR yang digunakan maka diperoleh dua titik tetap endemik ( c< < *). Dari dua titk tetap endemik yang diperoleh dari model di atas tidak dapat menjadi stabil secara bersamaan di dalam Ὠ.

4.3.4 Bilangan Reproduksi untuk model

SEIR

R0 dari model SIR diperoleh sebagai berikut

�

(17) Sehingga akan diperoleh

R0

4.3.5 Orbit dan Kestabilan Sistem Model

SEIR

(19)

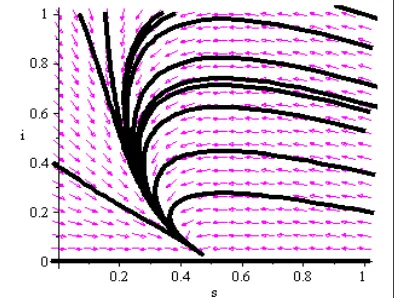
Gambar 11. Orbit kestabilan model SEIR di bidang SI.

Pada gambar 11 terlihat bahwa orbitnya menuju titik . Oleh karena itu titik tetap endemik bersifat titik tetap stabil. Hal tersebut menunjukkan bahwa ada kelompok individu I yang dapat menyebarluaskan penyakit sehingga kelompok individu S terinfeksi penyakit campak (measles) dan memasuki kelompok individu R.

Pada saat keadaan stabil, penyakit akan tetap ada sampai waktu tak terbatas. Oleh karena itu, penyakit campak (measles) bersifat endemik. Berdasarkan persamaan (10), model

SEIR akan mencapai stabil pada saat =( ( ). Titik merupakan titik stabil endemik karena .

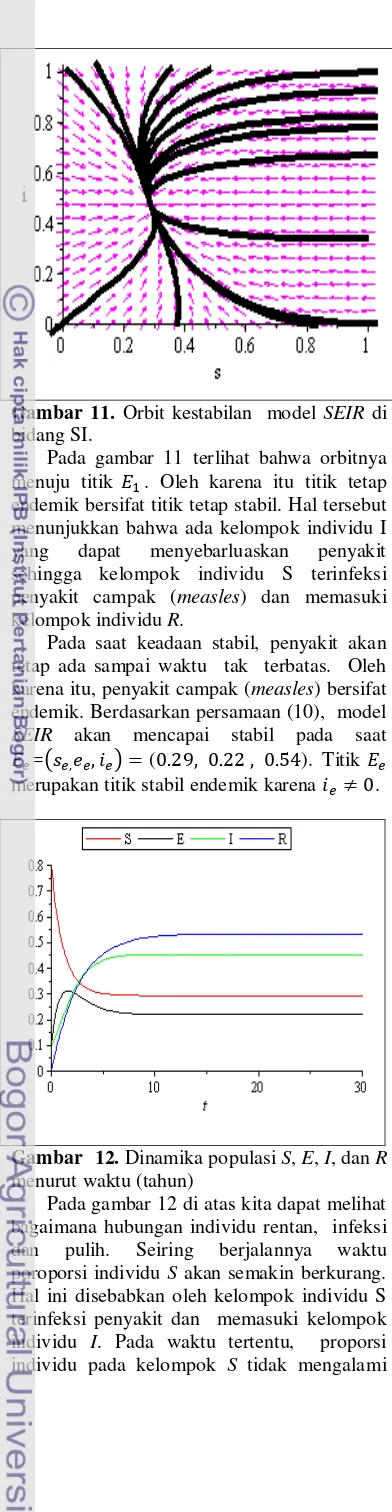
Gambar 12. Dinamika populasi S, E, I, dan R

Pada gambar 12 di atas kita dapat melihat bagaimana hubungan individu rentan, infeksi dan pulih. Seiring berjalannya waktu poroporsi individu S akan semakin berkurang. Hal ini disebabkan oleh kelompok individu S terinfeksi penyakit dan memasuki kelompok individu I. Pada waktu tertentu, proporsi individu pada kelompok S tidak mengalami

perubahan lagi. Pada keadaan tersebut, sistem berada pada titik stabil.

Kelompok individu I mengalami kenaikan. Hal ini disebabkan oleh karena kelompok individu S terjangkit penyakit campak (measles). Sehingga pada waktu tertentu kelompok individu S tidak memasuki individu I, semakin besar individu S yang tidak terjangkit penyakit maka kelompok individu I akan semakin berkurang dan akan mencapai titik stabilannya.

Besarnya bilangan reproduksi dasar ketika = 0 ialah = 3.72. Nilai mengakibatkan kedua nilai eigen matriks jacobi pada model SEIR ini berupa bilangan real positif. Hal tersebut menunjukkan titik stabil endemik bersifat stabil asimtotik.

Upaya pencegahan penyebaran penyakit campak (measles) dapat dilakukan dengan program vaksinasi pada tingkat . Pengaruh vaksinasi dapat dilihat dari prilaku proposi individu I yang bersifat endemik. Berdasarkan persamaan (6) tingkat vaksinasi minimun yang diperlukan dalam pencegahan penyebaran penyakit campak (measles)ialah = 0.4625. Selanjutnya akan menganalisis bagaimana pengaruh vaksin jika tingkat vaksinasi lebih kecil dari vaksinasi minimum.

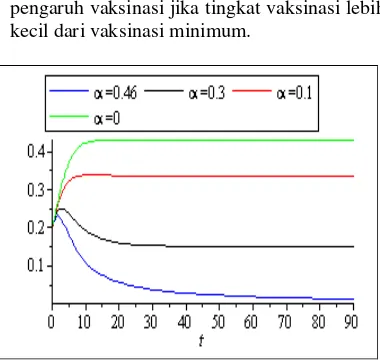
Gambar 13. Proporsi individu Infeksi pada sataun waktu (tahun)

Dari gambar 13 warna biru menunjukkan proporsi individu untuk tingkat vaksinasi minimum = 0.4625. Warna hitam menunjukkan proporsi individu I untuk vaksiansi = 0.3, warna merah menunjukkan proporsi individu I untuk vaksinasi = 0.1 dan warna hijau menunjukkan proporsi individu I untuk vaksinasi = 0.

(20)

yang diberikan bahwa penyakit akan selalu ada dalam jangka waktu yang tak terbatas. Oleh karena itu, penyakit campak (measles) bersifat endemik. Dengan demikian vaksinasi yang dilakukan tidak berhasil membuat penyakit campak (measles) menghilang dari populasi individu I.

Dengan demikian jika < c = 0.4625, maka penyakit campak (measles) tidak akan menghilang dari populasi individu I dalam jangka waktu yang tak terbatas. Titik stabil yang dicapai dalam individu I merupakan titik stabil endemik.

Tabel 3. Titik Tetap, Bilangan Reproduksi Dasar dan Kestabilan

� Titik stabil kestabilan

0 3.72 Stabil asimtotik 0.1 3.35 Stabil

asimtotik 0.3 2.66 Stabil

asimtotik

Dari Tabel 3 dapat dilihat bahwa dengan meningkatkan vaksinasi yang diberikan pada model SEIR ternyata bilangan reproduksi dasar mengalami penurunan. Namun demikian < c = 0.4625, nilai sehingga penyakit campak (measles) tidak akan menghilang dari populasi.

Selajutnya akan menganalisis bagaimana pengaruh vaksinasi jika tingkat vaksinasi yang diberikan lebih besar dari tingakat vaksinasi minimum.

Gambar 14. Proporsi individu I

Jika diberikan vaksinasi pada tingkat = 0.6, maka proporsi individu I ditunjukan oleh warna hijau. Untuk = 0.6, penyakit akan menghilang dari populasi dalam jangka waktu kurang lebih 4 tahun dan mencapai titik stabil di = (0.29, 0.22, 0.54). merupakan titik tetap endemik dikarenakan proporsi individu I

0. Besarnya bilangan reproduksi dasar adalah = 3.72. Titik tetap bebas penyakit tersebut bersifat stabil asimtotik karena nilai

.

Jika, setiap kelahiran memperoleh vaksin sebesar = 1. Jika diberikan vaksinasi pada tingkat = 1, maka proporsi individu I

ditunjukan oleh warna biru . Untuk = 1, penyakit akan menghilang dari populasi dalam jangka waktu kurang lebih 5 tahun. Dalam waktu kurang lebih 5 tahun maka sistem akan mencapai stabil dan mencapai titik stabi di = (0.29, 0.22, 0.54).

Dengan demikian penyakit campak (measles) akan menghilang dari populasi untuk nilai tingkat vaksinasi lebih besar dari tingkat vaksinasi minimum Semakin besar tingkat vaksinasi maka semakin cepat penyakit menghilang dari populasi.

Tabel 4. Titik Tetap, Bilangan Reproduksi Dasar dan Kestabilan

� Titik stabil Kestabilan

0.6 1.49 Stabil asimtotik 0.9 1.27 Stabil

asimtotik 1 1.04 Stabil

asimtotik

Dari Tabel 4 dapat dilihat bahwa jika semakin tinggi tingkat vaksinasi yang diberikan pada model SEIR maka nilai rasio reproduksi dasar mengalami penurunan. Dengan demikian, untuk tingkat vaksinasi yang lebih besar dari tingkat vaksinasi minimum, bilangan reproduksi dasar mengalami penurunan. Namun demikian sehingga penyakit campak (measles ) akan selalu ada dalam jangka waktu yang tidak terbatas.

4.4 Model MSEIR

an

, sehingga dari persamaan

(7) diperoleh :

(18)

(21)

Titik tetap . Jika , maka akan memperoleh titik kestabilan endemik di � sebagai berikut;

( ( ( dimana

Jika < 1, maka

< 0 untuk t > 0, hal

ini menunjukkan bahwa jumlah penderita penyakit campak (measles) berangsur - angsur semakin berkurang sedemikian hingga penyakit akan menghilang dari populasi dan tidak terjadi endemik pada populasi tersebut. Jika > 1, maka

> 0 untuk t > 0, artinya

jumlah penderita akan bertambah sehingga penyakit akan menyebarluas dan menjadi endemik. Titik tetap endemik pada model

MSEIR juga menunjukkan bahwa terdapat individu pada kelompok I yang dapat menyebarkan penyakit kepada individu S

4.4.2 Konstruksi Matriks Jacobi untuk Model MSEIR

Misalkan sistem persamaan (10) dituliskan sebagai berikut;

[ ] (19) Kestabilan persamaan (5) , (6) , (9) , dan (10) akan diperoleh dengan menganalisis nilai eigen matriks Jacobi pada titik tetap yang didapat.

MSEIR

Matriks jacobi di titik E1= adalah

Dengan menggunakan persamaan di atas di peroleh nilai eigen sebagai berikut;

=

Sehingga ada nilai positif, jika maka merupakan stabil asimtotik. Jika

merupakan titik tetap stabil hiperbolik yang tidak stabil dengan mainfold dan terjadi persinggungan dengan daerah D, sehingga

merupakan stabil global asimtotik.

4.4.4 Bilangan Reproduksi Dasar Model

MSEIR

R0 dari model MSEIR diperoleh sebagai berikut;

Sehingga akan diperoleh

4.4.5 Orbit dan Kestabilan Sistem Model

MSEIR

Orbit kestabilan diperoleh dengan menggunakan software Maple 12 sehingga diperoleh bentuk orbit seperti dibawah. Dengan memilih nilai-nilai parameter sebagai berikut; = 0.5, β = 0.8, = 0.4 , dan ξ = 0.03, maka akan diperoleh

(22)

Gambar 15. Orbit kestabilan model MSEIR

di bidang SI.

Dari gambar 15 terlihat bahwa orbitnya menuju titik tetap . Oleh karena itu, titik tetap bersifat titik tetap stabil. Hal tersebut menunjukkan bahwa ada kelompok individu infeksi yang dapat menyebarluaskan virus sihingga kelompok individu rentan terinfeksi penyakit dan individu rentan akan memasuki individu infeksi.

Gambar 16. Proporsi individu S, I, E dan R

dalam satuan waktu (tahun)

Dari gambar 16 di atas kita dapat melihat bagaimana hubungan ketiga individu tersebut. Seiring dengan berjalannya waktu proporsi individu rentan akan semakin berkurang. Hal ini disebabkan individu rentan telah terinfeksi oleh virus dan individu rentan memasuki individu infeksi. Pada waktu tertentu, proporsi individu pada kelompok individu rentan tidak mengalami perubahan lagi dan sistem berada pada titik stabil. Dengan meningkatnya individu rentan menyebabkan kelompok individu infeksi mengalami penurunan.

Semakin besar individu rentan terjangkit virus maka kelompok individu infeksi akan semakin berkurang dan akan mencapai titik stabilannya.

Berdasarkan definisi titik kestabilan, nilai

S pada persamaan (2) dan (4) didekati dengan titik kestabilan bebas penyakit yaitu , sehingga akan diperoleh nilai dapat disederhanakan sebagai berikut;

=

dan

(21)

Dari ketiga persamaan di atas dapat didefinisiskan tingkat vaksinasi minimum yang diperlukan untuk mencegah penyebaran penyakit. Tingkat vaksinasi yang diperlukan untuk mencegah penyebaran penyakit, dengan penyakit akan berangsur-angsur menghilang dari populasi I dan akan memasuki klompok individu R untuk Dengan demikian, untuk diperoleh tingkat vaksinasi minimum untuk model SIR

sebagai berikut;

(22)

Dan tingkat vaksinasi minimum untuk model

SEIR sebagai berikut;

(23)

Menurut Makinde (2007) menyatakan bahwa tingkat vaksinasi yang diberikan harus lebih besar daripada supaya penyakit dapat dicegah penyebarannya. Jika tingkat vaksinasi yang diberikan lebih besar dari tingkat vaksinasi minimum maka pa a model SIR dan model SEIR masing-masing diberikan sebagai berikut;

<

= 1

<

(23)

Dan (24)

= 1

Dari persamaan (24) mengakibatkan bahwa jumlah individu pada kelompok I secara berangsur-angsur akan semakin berkurang dan penyakit akan menghilang dan akan memasuki ke dalam kelompok R dalam waktu tertentu. Jika vaksinasi maka

>

= 1

>

= 1

Dan

= 1

Hal ini menunjukkan bahwa jumlah individu pada kelompok I dalam jangka waktu yang berangsur- angsur akan semakin meningkat dan penyakit akan menjadi endemik.

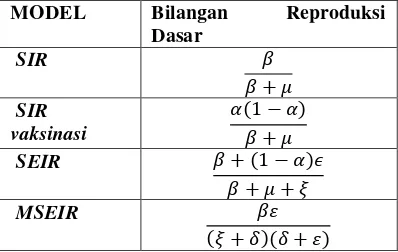
Tabel 5. Perbandingan Bilangan Reproduksi Dasar antara model SIR, SIR vaksinasi,SEIR dan MSEIR

MODEL Bilangan Reproduksi

Dasar

SIR

SIR vaksinasi

SEIR �

MSEIR

Dari Tabel 5 terlihat bahwa adanya perbedaan bilangan reproduksi dasar antara model SIR, SIR vaksinasi, SEIR dan MSEIR. Dengan mengambil parameter β, , , �, ξ dan bilangan positif, bilangan reproduksi dasar pada model MSEIR lebih kecil dari model

SEIR, SIR vaksinasi dan SIR. Hal ini menunjukkan bahwa kondisi bebas penyakit pada model MSEIR lebih cepat tercapai titik kestabilan daripada model SEIR,SIR vaksinasi

dan SIR sehingga kelompok individu infeksi akan memasuki kelompok individu pulih. Begitu juga hal sebaliknya, kondisi penyakit campak (measles) akan lebih cepat tercapai pada model SEIR, SIR vaksinasi dan SIR jika dibandingkan dengan model MSEIR.

Kriteria kestabilan titik tetap yang dilihat dari nilai bilangan reproduksi dasar antara model SIR, SIR vaksinasi, SEIR dan MSEIR

disajikan sebagai berikut;

Tabel 6. Kriteria Kestabilan Titik Tetap model SIR, SIR vaksinasi, SEIR dan MSEIR

Kriteria Kestabilan Titik Tetap

Model SIR Model SIR vaksinasi

Model SEIR Model MSEIR

Bebas penyakit

stabil (

�

Tetap endemik

stabil

( �

(24)

Tabel 7. Perbandingan Titik Tetap antara model SIR, SIR vaksinasi, SEIR dan MSEIR

Tititk Tetap Bebas Penyakit

Titik Tetap Endemik

Model SIR (1, 0)

Model SIR

vaksinasi

(1-α, 0)

Model SEIR (1, 0, 0)

�

(

Model

MSEIR

(1, 0, 0)

(

Dari Table 7 di atas, diketahui bahwa model SIR, SIR vaksinasi, SEIR dan

MSEIR memilki titik tetap bebas penyakit yang sama yaitu populasi total hanya terdiri dari kelompok individu rentan, sedangkan kelompok individu kelas populasi lainnya tidak ada. Hal ini berarti bahwa populasi beresiko tinggi mencapai kapasitas maksimum.

Dari Table 7 juga terlihat adanya perbedaan titik tetap endemik antara model

SIR, SIR vaksinasi, SEIR dan MSEIR. Perbedaan tersebut terjadi karena pada

model SIR dan SIR vaksinasi kelompok individu rentan tidak memasuki individu laten, individu rentan tersebut langsung memasuki kelompok individu infeksi. Pada model SEIR dan MSEIR individu rentan masuk terlebih dahulu ke individu laten kemudian dilanjutkan ke individu infeksi. Akibatnya ketika penyakit campak (measles) terjadi, jumlah setiap kelas populasi pada model SIR, SIR vaksiansi berbeda dengan jumlah setiap kelas populasi pada model

(25)

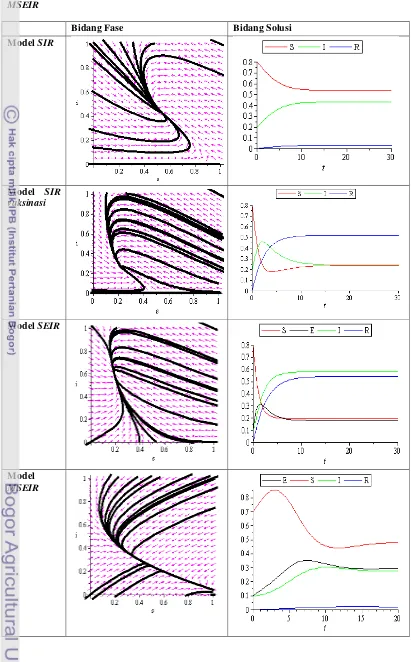
Tabel 8. Plot Bidang Fase dan Bidang Solusi untuk model SIR,SIR vaksinasi, SEIR dan

MSEIR

Bidang Fase Bidang Solusi

Model SIR

Model SIR vaksinasi

Model SEIR

Model

(26)

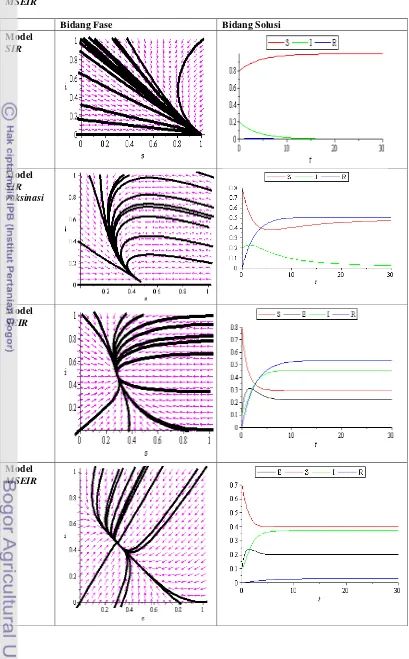
Tabel 9. Plot Bidang Fase dan Bidang Solusi untuk model SIR, SIR vaksinasi, SEIR dan

MSEIR

Bidang Fase Bidang Solusi

Model

SIR

Model

SIR vaksinasi

Model

SEIR

Model

(27)

Dari Tabel di atas dapat dilihat bahwa dengan menggunakan parameter positif yang sama pada setiap masing-masing model, diperoleh plot bidang fase dan bidang solusi yang berbeda dari setiap masing- masing model. Titik tetap endemik model SIR, SIR vaksinasi dan SEIR merupakan titik tetap yang bersifat stabil, seperti pada tabel 9, semua orbit yang berada di sekitar titik tetap bergerak mendekati titik tersebut. Sedangkan pada titik tetap model MSEIR

merupakan titik tetap yang bersifat tak stabil, dimana semua orbit yang berada di sekitar titik tetap bergerak menjauhi titik tersebut. Titik tetap bebas penyakit model

SIR dan SIR vaksinasi bersifat stabil dan titik tetap bebas penyakit model SEIR dan MSEIR

bersifat tak stabil, dengan menggunakan parameter yang sama diperoleh titik endemik model MSEIR bersifat stabil. Hal ini disebabkan adanya perbedaan kriteria kstabilan model SIR, SIR vaksinasi, SEIR

(28)

V SIMPULAN

Model penyebaran penyakit campak (measles) pada populasi dapat digambarkan dalam empat model yaitu SIR, SIR vaksinasi,

SEIR dan MSEIR. Semua model ini mempunyai dua titik tetap; yaitu titik tetap tanpa penyakit ( dan titik tetap endemik.( ). Analisis model dilakukan dengan mencari kestabilan di sekitar titik tetap ke empat model tersebut.

Dari analisis yang dilakukan didapatkan bahwa kestabilan kedua titik tetap tidak terjadi secara bersamaan. Jika stabil maka tidak stabil demikian pula sebaliknya. Analisis yang dilakukan menghasilkan bilangan reproduksi dasar dan tingkat vaksinasi minimum yang dibutuhkan agar berhasil dalam mencegah penyebaran penyakit campak (measles). Untuk nilai tingkat vaksinasi di bawah tingkat vaksinasi minimum, penyakit akan bersifat endemik dan untuk nilai vaksinasi di atas nilai tingkat vaksinasi minimum, penyakit akan menghilang dari populasi individu. Ketika titik tetap tanpa penyakit bersifat simpul stabil, dan titik tetap endemik bersifat spiral takstabil sehingga virus akan hilang dari populasi. Ketika titik tetap tanpa penyakit bersifat sadel, dan titik tetap endemik akan bersifat spiral stabil sehingga virus akan bertahan dalam populasi. Dari ke empat model tersebut diperoleh bahwa bilangan reproduksi dasar pada model MSEIR lebih kecil daripada

model SIR, SIR vaksinasi dan SEIR, hal ini menunjukkan bahwa model MSEIR akan lebih cepat mencapai kondisi stabil.

Kondisi bebas penyakit pada model

MSEIR lebih cepat tercapai daripada model

SIR, dan model SEIR. Begitu juga sebaliknya, kondisi virus yang masuk akan lebih cepat tercapai pada model SIR dan model SEIR jika dibandingkan dengan model MSEIR. Hal ini disebabkan adanya perbedaan kriteria kstabilan model SIR, SIR vaksinasi, SEIR dan MSEIR, baik kriteria kestabilan titik tetap bebas penyakit maupun kriteria kestabilan titik tetap endemik. Model SIR, SIR vaksinasi, SEIR dan

(29)

PENYAKIT CAMPAK (

MEASLES

)

ACE SUHENDAR

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(30)

DAFTAR PUSTAKA

Anton H. 1995. Aljabar Linier Elementer.

Edisi ke-5. Terjemahan Pantur Silaban dan I Nyoman Susila. Jakarta: Erlangga.

Castellini H & Romanelli L. On the Propagation of Social Epidemic in Sosial. Networks under SIR Model. 70: 40-53.

Farlow SJ. 1994 . An Introduction to Differential Equations and Their Applications. Mc Graw-Hill, New York.

Gieseacke J. 1994. Modern Infectious Disease Epidemiology. Oxford University Press, New York.

Grassly NC & Frasher C. 2006. Seasoanal Infectious Disease Epidemiology.

Proceedings of the Royal Society B. Departement of Infectious Epidermiology. Imperial College, London

Hethcote H W. 2000. The Mathematic of Infectious Diseases. SIAM Review 42. No.4 5599-653.

Jones DS & Sleeman BD. 1983. Differential Equations and Mathematical Biology. Allen and Unwin, Boston.

Kinbaby.