F
IMPL
Diajukan u
FAKULTA
PLEMENTA
BERKA
n untuk mele
PROGR
DE
AS ILMU K
UNIV
TASI KRIPTO
AS-BERKA
D
elengkapi tug
Sarj
YOGI A
0
GRAM STU
EPARTEM
KOMPUTE
IVERSITA
TOGRAFI A
AS TEKS, G
DAN VIDEO
SKRIPSI
tugas dan me
rjana Komp
I ADITIA P
0 7 1 4 0 1 0 8
UDI S1 ILM
MEN ILMU
TER DAN T
AS SUMAT
MEDAN
2014
ALGORITM
GAMBAR, S
EO
memenuhi sy
puter
PUTRA.
8 3
LMU KOMP
U KOMPUT
TEKNOLO
TERA UTA
PERSETUJUAN
Judul : IMPLEMENTASI KRIPTOGRAFI ALGORITMA
RSA PADA BERKAS-BERKAS TEKS, GAMBAR, AUDIO, DAN VIDEO
Kategori : SKRIPSI
Nama : YOGI ADITIA PUTRA
Nomor Induk Mahasiswa : 071401083
Program Studi : SARJANA (S1) ILMU KOMPUTER
Departemen : ILMU KOMPUTER
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI
INFORMASI (FASILKOM-TI) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, 27 Maret 2014 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Amer Sharif,S.Si,M.Kom Dian Rachmawati,S.Si,M.Kom
NIP : - NIP. 198307232009122004
Diketahui/Disetujui oleh
Program Studi Ilmu Komputer FASILKOM-TI USU Ketua,
PERNYATAAN
IMPLEMENTASI KRIPTOGRAFI ALGORITMA RSA PADA
BERKAS-BERKAS TEKS, GAMBAR, SUARA DAN VIDEO
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Maret 2014
PENGHARGAAN
Puji dan syukur yang tiada henti penulis ucapkan kehadirat Allah SWT yang telah memberikan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan tugas akhir ini.
Dengan sepenuh ketulusan hati, pada kesempatan ini penulis menyampaikan terima kasih kepada semua pihak yang telah membantu penyelesaian skripsi ini. Penulis mengucapkan terima kasih teristimewa kepada:
1. Bapak Dr. Poltak Sihombing, M.Kom sebagai Ketua Program Studi Ilmu Komputer sekaligus sebagai dosen pembanding yang telah memberikan saran, masukan dan kritikan yang sangat berguna bagi penulis sehingga skripsi ini dapat selesai dengan baik.
2. Ibu Maya Silvi Lydia, BSc. MSc sebagai Sekretaris Program Studi Ilmu Komputer.
3. Bapak Prof. Dr. Muhammad Zarlis sebagai Dekan Fakultas Ilmu Komputer dan Teknologi Informasi .
4. Para Pembantu Dekan Fakultas Ilmu Komputer dan Teknologi Informasi . 5. Ibu Dian Rachmawati, S.Si, M.Kom sebagai dosen pembimbing yang telah
banyak memberikan saran dan masukan yang sangat berguna bagi penulis sehingga skripsi ini dapat selesai dengan baik
6. Bapak Amer Sharif,S.Si,M.Kom sebagai dosen pembimbing yang telah banyak meluangkan waktunya dalam memberikan bimbingan, kritik dan masukan kepada penulis.
7. Bapak M. Andri Budiman,S.T,M.Comp.Sc sebagai dosen pembanding yang telah banyak meluangkan waktu untuk memberikan bimbingan kritik dan masukan pada penulis.
8. Seluruh dosen serta pegawai di Program Studi S1 Ilmu Komputer Departemen Ilmu Komputer FMIPA USU.
9. Ayahanda dan Ibunda Joni Indra,S.T,M.T dan Erita Rustam,S.pd yang selalu memberikan cinta kasih dan semangat serta kepercayaan selama masa kuliah baik dalam bentuk maetriil serta moril dalam menyelesaikan skripsi ini.
10. Kakanda dan adinda tercinta Aulia Khairina dan Fauzan Ramadhana yang telah banyak membantu dan member semangat kepada penulis.
11. Dan juga kepada teman-teman seperjuangan stambuk 2007, khususnya Subardi Wansyah, Indra Gunawan, Kalsum Mustika, Reza Affandy, Berki Rahmat, dan Isnan Nisa Nasution yang telah memberikan semangat dan motivasi kepada saya.
Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan. Oleh karena itu penulis mengharapkan kritik dan saran dari semua pihak yang bersifat membangun demi kesempurnaan dan pengembangan skripsi ini. Penulis berharap semoga skripsi ini bermanfaat bagi penulis sendiri pada khususnya dan pembaca pada umumnya.
IMPLEMENTASI KRIPTOGRAFI ALGORITMA RSA PADA
BERKAS-BERKAS TEKS, GAMBAR, SUARA
DAN VIDEO
ABSTRAK
Data komputer sekarang ini telah menjadi hal yang penting dalam kehidupan manusia. Segala informasi dulunya dicitrakan pada sebuah kertas, rekaman, atau perangkat sedangkan sekarang hanya cukup membutuhkan suatu perangkat berbasis komputer untuk menghasilkan informasi yang tidak terbatas jumlahnya dalam sebuah data digital. Keamanan sebuah data belum menjadi perhatian oleh masyarakat saat ini. Mudahnya akses terhadap data-data digital berbanding dengan tingginya kriminal dalam dunia komputer seperti pembajakan, manipulasi, dan Spekulasi terhadap data sangat kerap terjadi. Teknik kriptografi menjadi salah satu pilihan bagus untuk meningkatkan keamanan data. Kriptogafi merupakan suatu teknik manipulasi sebuah data sehingga orang lain hanya mengetahui data tersebut berbentuk sebuah kode yg tidak dikenalinya. Algoritma RSA merupakan bagian dari algoritma dengan kunci asimetri, yaitu kunci yang digunakan dalam proses pengkodean (enkripsi) berbeda dengan kunci pada proses pengekstrakan (dekripsi). Parameter dari kehandalan algoritma kriptografi ini terletak dari nilai-nilai prima yang digunakan dalam proses pembangkitan kedua pasangan kunci, yaitu kunci publik dan kunci privat. Semakin besar nilai prima maka semakit kuat kunci yang digunakan sehingga kesulitan para pemecah kode juga semakin tinggi. Proses pembangkitan kunci juga tidak terlepas dari algoritma pendukung yang digunakan yaitu algoritma Monte-Carlo sebagai pembangkit bilangan acak, dan algoritma Miller-Rabin sebagai algoritma pengecekan keprimaan suatu bilangan. Penggabungan dua algoritma dalam pembangkitan kunci tentu juga meningkatkan tingkat keberhasilan menghasilkan Kunci yang handal. Algoritma ini mampu memanipulasi berkas dengan format apapun dengan estimasi waktu yang relatif cepat. Hasil Enkripsi ini dapat dikembalikan melalui proses dekripsi ke berkas orisinil dengan persentase keberhasilan recovery sebesar 100 persen.
Kata Kunci : Kriptografi, Algoritma RSA, Monte Carlo, Miller Rabin, Semua berkas
THE IMPLEMENTATION OF RSA CRYPTOGRAPHY ALGORITHM ON THE TEXT, IMAGE, SOUND, AND VIDEO FILES
ABSTRACT
Presently, computer Data had being an important thing on human life. Before, all of information was put on a paper, in recording, and or other device whereas now we only need the computer to produce unlimited information on a digital data. Data security is not the main attention today. The digital data that people can access easily are proportional with Cyber Crime increase such as Piracy, data manipulation, and speculation happening today. Cryptography Technic is one of the best choice to improve data security. Cryptography is data manipulation technic so peoples can only see the data in the form of unknown codes. RSA algorithm is one of the asymmetric key algorithm, so the key used in ecnryption is different with key used for Decryption. Realibility parameters of this cryptography algorithm is the prime values used so the large the keys is more difficult to solve. Key Generation process is also part of algorithm used. This research uses Monte Carlo Algorithm for Random Numbers Generation, and Miller Rabin Algorithm as Primality Test Algorithm of the numbers. Combining these algorithms in Keys Generation surely improve the Large Prime Number Generation Success rate thus improving data security. The algorithm is applied to files with different formats and sizes. The result of encryption from this application maybe restored to its original form by using the decryption process with successful recovery percentage of 100 percent.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii Penghargaan iv Abstrak v Abstract vi Daftar Isi vii Daftar Tabel x Daftar Gambar xi Bab 1 Pendahuluan 1.1 Latar Belakang 1
1.2 Rumusan Masalah 2
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 4
1.6 Metodologi Penelitian 4
1.7 Sistematika Penulisan 5
Bab 2 Landasan Teori 2.1 kriptografi 7
2.1.1 pengertian Kriptografi 7
2.1.2 Komponen Kriptografi 7
2.1.3 Tujuan Kriptografi 8
2.1.4 Terminologi dan Konsep Dasar kriptografi 9
2.1.5 Jenis kriptografi 11
2.1.6 Algoritma Kriptografi Rivest Shamir Adleman (RSA) 13
2.1.6.1 Proses Pembangkitan Kunci 14
2.1.6.2 Pembangkitan dan Pengecekan Bilangan Prima 15
2.1.6.3 Algoritma Enkripsi 17
2.1.6.4 Algoritma Dekripsi 17
Bab 3 Analisis dan Perancangan Sistem 3.1 Analisis Permasalahan 19
3.2 Analisis Persyaratan (Requirment Analysis) 20
3.2.1 Persyaratan Fungsional (Functional Requirment) 21
3.2.2 Persyaratan Nonfungsional (Nonfunctional Requirment) 21
3.3 Permodelan Sistem dengan Use Case dan Activity Diagram 22
3.3.1 Use Case Key Generation 24
3.3.2 Use Case Enkripsi 25
3.4.1 Analisis Sistem utama 28
3.4.2 Analisis Sistem Algoritma RSA 30
3.4.3 Pembangkitan (Generate) Kunci Publik dan Kunci Privat 30
3.4.4 Sistem Enkripsi Sebuah Berkas 35
3.4.5 Sistem Enkripsi Sebuah Berkas 37
3.5 Perancangan Antarmuka (Interface) 39
3.5.1 Rancangan Halaman Utama 28
3.5.2 Rancangan Halaman Menu Enkripsi Kriptografi RSA 40
3.5.3 Rancangan Halaman Menu Enkripsi Kriptografi RSA 48
3.5.4 Rancangan Halaman Help 51
Bab 4 Implementasi dan Pengujian Sistem 53
4.1 Implementasi 53
4.1.1 Sistem Algoritma Kriptografi RSA 53
4.1.2 Sistem Antarmuka (Interface) 66 4.2 Pengujian Sistem 70
4.2.1 Pengujian Proses Enkripsi dan Dekripsi Algoritma RSA 70
4.2.2 Pengujian Proses Enkripsi dan Dekripsi Algoritma RSA Terhadap Berkas 74
Bab 5 Kesimpulan dan Saran 80
5.1 Kesimpulan 80
5.2. Saran 81
Daftar Pustaka 82
Lampiran A : Tabel ASCII A-1
DAFTAR TABEL
Halaman
Tabel 3.1 Spesifikasi Use Case Keys generatton 24
Tabel 3.2 Spesifikasi Use Case Enkripsi 25
Tabel 3.3 Spesifikasi Use Case Dekripsi 27
Tabel 3.4 Rincian Rancangan Halaman Utama Kriptografi RSA 40 Tabel 3.5 Rincian Rancangan Halaman Menu Enkripsi Kriptografi RSA 41 Tabel 3.6 Rincian Rancangan Halaman Initial Key Kriptografi RSA 42 Tabel 3.7 Rincian Rancangan Halaman Pembangkit Kunci Kriptografi RSA 44 Tabel 3.8 Rincian Rancangan Halaman Input Plaintext dan Ciphertext
Kriptografi RSA 46 Tabel 3.9 Rincian Rancangan Halaman Data Information Kriptografi RSA 47 Tabel 3.10 Rincian Rancangan Halaman Menu Enkripsi Kriptografi RSA 48 Tabel 3.11 Rincian Rancangan Halaman Insert Ciphertext Kriptografi RSA 50
Tabel 3.12 Rincian Rancangan Halaman Help 51
Tabel 4.1 Percobaan Pembangkitan Kunci-Kunci RSA 71
Tabel 4.2 Percobaan Enkripsi RSA terhadap beberapa berkas dengan format
tertentu 71
DAFTAR GAMBAR
Halaman Gambar 2.1 Perbandingan bentuk plainteks dan cipherteks 9
Gambar 2.2 Skema proses kriptografi simetri 11
Gambar 2.3 Skema kriptografi asimetri 12
Gambar 2.4 Skema kriptografi asimetri 12
Gambar 3.1 Diagram Ishikawa untuk Analisa Masalah 20 Gambar 3.2 Use Case Diagram yang akan dikembangkan 23 Gambar 3.3 Activity Diagram proses Keys Generation 25
Gambar 3.4 Activity Diagram proses Enkripsi 26
Gambar 3.5 Activity Diagram proses Dekripsi 28
Gambar 3.6 Skema Global Diagram Alir Proses Enkripsi dan Dekripsi 29 Gambar 3.7 Skema Global Diagram Alir Proses Pembangkitan Kunci RSA 32 Gambar 3.8 Skema Global Diagram Alir Algoritma Pembangkit Bilangan Acak
monte Carlo 33
Gambar 3.9 Skema Global Diagram Alir Algoritma Miller Rabin 34 Gambar 3.10 Skema Global Diagram Alir Proses Enkripsi RSA 36 Gambar 3.11 Skema Global Diagram Alir Proses Dekripsi RSA 38 Gambar 3.12 Rancangan halaman Utama antarmuka Sistem 39
Gambar 3.13 Tampilan Halaman Menu RSA 41
Gambar 3.14 Tampilan Halaman Menu Initial Key RSA 42
Gambar 3.15 Tampilan Pembangkitan Kunci 43
Gambar 3.16 Tampilan Halaman Menu Input Plaintext dan Ciphertext RSA 45 Gambar 3.17 Tampilan Halaman Data Information enkripsi RSA 47
Gambar 3.18 Tampilan Halaman Menu Dekripsi RSA 48
Gambar 3.19 Tampilan Halaman Insert Cipherteks RSA 50
Gambar 3.20 Tampilan Halaman Help 51
Gambar 4.1 Prosedur Generate Kunci 66
Gambar 4.2 inisialisasi kunci 67
Gambar 4.3 Prosedur insert plaintext 67
Gambar 4.4 Data Information 68
Gambar 4.5 Berkas SecretKey.ini 68
Gambar 4.6 Prosedur Inisialisasi kunci Dekripsi 69
Gambar 4.7 Prosedur Insert Ciphertext 70
Gambar 4.8 Isi Berkas Plainteks Berkas 2coba.Txt 74
Gambar 4.9 Informasi Parameter Proses Enkripsi Pada Berkas Text 75
Gambar 4.10 Hasil Enkripsi Berkas Text 75
Gambar 4.11 Hasil Dekripsi Berkas Text yang telah Dienkripsi 75
Gambar 4.12 Penampakan Berkas Gambar (Kunka1.Png) 76
Gambar 4.13 Informasi Parameter Proses Enkripsi pada Berkas Gambar 76
Gambar 4.14 Hasil Enkripsi Berkas Gambar 77
Gambar 4.15 Hasil Dekripsi Berkas Gambar yang telah Dienkripsi 77 Gambar 4.16 Informasi Parameter Proses Enkripsi Pada Berkas Suara 78
IMPLEMENTASI KRIPTOGRAFI ALGORITMA RSA PADA
BERKAS-BERKAS TEKS, GAMBAR, SUARA
DAN VIDEO
ABSTRAK
Data komputer sekarang ini telah menjadi hal yang penting dalam kehidupan manusia. Segala informasi dulunya dicitrakan pada sebuah kertas, rekaman, atau perangkat sedangkan sekarang hanya cukup membutuhkan suatu perangkat berbasis komputer untuk menghasilkan informasi yang tidak terbatas jumlahnya dalam sebuah data digital. Keamanan sebuah data belum menjadi perhatian oleh masyarakat saat ini. Mudahnya akses terhadap data-data digital berbanding dengan tingginya kriminal dalam dunia komputer seperti pembajakan, manipulasi, dan Spekulasi terhadap data sangat kerap terjadi. Teknik kriptografi menjadi salah satu pilihan bagus untuk meningkatkan keamanan data. Kriptogafi merupakan suatu teknik manipulasi sebuah data sehingga orang lain hanya mengetahui data tersebut berbentuk sebuah kode yg tidak dikenalinya. Algoritma RSA merupakan bagian dari algoritma dengan kunci asimetri, yaitu kunci yang digunakan dalam proses pengkodean (enkripsi) berbeda dengan kunci pada proses pengekstrakan (dekripsi). Parameter dari kehandalan algoritma kriptografi ini terletak dari nilai-nilai prima yang digunakan dalam proses pembangkitan kedua pasangan kunci, yaitu kunci publik dan kunci privat. Semakin besar nilai prima maka semakit kuat kunci yang digunakan sehingga kesulitan para pemecah kode juga semakin tinggi. Proses pembangkitan kunci juga tidak terlepas dari algoritma pendukung yang digunakan yaitu algoritma Monte-Carlo sebagai pembangkit bilangan acak, dan algoritma Miller-Rabin sebagai algoritma pengecekan keprimaan suatu bilangan. Penggabungan dua algoritma dalam pembangkitan kunci tentu juga meningkatkan tingkat keberhasilan menghasilkan Kunci yang handal. Algoritma ini mampu memanipulasi berkas dengan format apapun dengan estimasi waktu yang relatif cepat. Hasil Enkripsi ini dapat dikembalikan melalui proses dekripsi ke berkas orisinil dengan persentase keberhasilan recovery sebesar 100 persen.
Kata Kunci : Kriptografi, Algoritma RSA, Monte Carlo, Miller Rabin, Semua berkas
THE IMPLEMENTATION OF RSA CRYPTOGRAPHY ALGORITHM ON THE TEXT, IMAGE, SOUND, AND VIDEO FILES
ABSTRACT
Presently, computer Data had being an important thing on human life. Before, all of information was put on a paper, in recording, and or other device whereas now we only need the computer to produce unlimited information on a digital data. Data security is not the main attention today. The digital data that people can access easily are proportional with Cyber Crime increase such as Piracy, data manipulation, and speculation happening today. Cryptography Technic is one of the best choice to improve data security. Cryptography is data manipulation technic so peoples can only see the data in the form of unknown codes. RSA algorithm is one of the asymmetric key algorithm, so the key used in ecnryption is different with key used for Decryption. Realibility parameters of this cryptography algorithm is the prime values used so the large the keys is more difficult to solve. Key Generation process is also part of algorithm used. This research uses Monte Carlo Algorithm for Random Numbers Generation, and Miller Rabin Algorithm as Primality Test Algorithm of the numbers. Combining these algorithms in Keys Generation surely improve the Large Prime Number Generation Success rate thus improving data security. The algorithm is applied to files with different formats and sizes. The result of encryption from this application maybe restored to its original form by using the decryption process with successful recovery percentage of 100 percent.
BAB I
PENDAHULUAN
1.1 Latar Belakang
Perkembangan dunia komputer dan multimedia pada saat ini memberikan dampak yang besar terhadap pola hidup masyarakat terutama dalam proses penyampaian informasi. Informasi menentukan hampir setiap elemen dari kehidupan manusia. Tanpa adanya suatu informasi hampir semuanya tidak dapat dilakukan dengan baik. Keamanan suatu informasi pada zaman global ini juga telah menjadi sebuah kebutuhan vital dalam beberapa aspek kehidupan. Akan tetapi dalam pesatnya perkembangan teknologi informasi sampai saat ini memberikan dampak positif dan negatif dimana menjadi suatu kemudahan kepada setiap orang untuk mendapatkan suatu informasi ataupun sebuah data tanpa harus membutuhkan proses yang lama. Berbagai cara dilakukan banyak orang untuk mendapatkannya.
Dari permasalahan tersebut tersebut menjadi keharusan kepada pemilik data atau informasi merancang suatu sistem keamanan terhadap data dan informasinya. Masalah keamanan tentunya menjadi salah satu aspek terpenting dari sebuah sistem multimedia. Akan tetapi masalah keamanan seringkali kurang mendapatkan perhatian dari para perancang dan pengelola sistem informasi. Jika tidak mengganggu performa sistem, maka masalah keamanan seringkali tidak begitu dipedulikan, bahkan ditiadakan.
permutasi (transposisi). Sedangkan kriptografi modern adalah algoritma yang lebih kompleks daripada algoritma kriptografi klasik, hal ini disebabkan algoritma sekarang ini harus menggunakan komputer. Dalam hal ini algoritma yang akan penulis pergunakan adalah algoritma kriptografi modern.
Sedangkan Steganografi adalah seni dan ilmu menulis pesan tersembunyi atau menyembunyikan pesan dengan suatu cara sehingga selain si pengirim dan si penerima. Tidak ada seorangpun yang mengetahui atau menyadari bahwa ada suatu pesan rahasia. Teknik steganografi meliputi banyak sekali metode komunikasi untuk menyembunyikan pesan rahasia (teks atau gambar) di dalam berkas-berkas lain yang mengandung teks, image, bahkan audio tanpa menunjukkan ciri-ciri perubahan yang nyata atau terlihat dalam kualitas dan struktur dari berkas semula. Oleh karena itu, steganografi semakin dibutuhkan guna memberikan keamanan yang maksimal dalam proses pengiriman informasi. Teknik steganografi umum digunakan bersamaan dengan menggunakan dua media yang berbeda dimana salah satunya berfungsi sebagai media yang berisikan informasi dan yang lain berfungsi sebagai media pembawa informasi tersebut.
Terdapat beberapa algoritma yang dapat digunakan orang untuk melakukan proses pengamanan data tersebut. Diantaranya adalah algoritma Rivest Shamir Adleman (RSA) yang penulis gunakan dalam skripsi ini. Oleh karena itu dari permasalahan tersebut penulis berencana meimplementasikan sistem kriptogafi berbasis komputer dengan membuat suatu aplikasi yang dapat menyembunyikan sebuah data dalam suatu berkas multimedia dimana dilakukan proses enkripsi terlebih dahulu sehingga dalam proses pengiriman data, orang-orang yang berhasil memperoleh data dari berkas pembawa tidak dapat mengetahui berkas sebenarnya meskipun berkas tersebut berhasil diekstrak.
1.2 Rumusan Masalah
a. Bagaimana cara merancang suatu aplikasi untuk mengimplementasikan sistem kriptografi terhadap berkas-berkas dengan format apapun baik berkas teks, gambar, suara maupun berkas video.
b. Apakah seluruh berkas tersebut dapat dienkripsi menggunakan Algoritma RSA ini sehingga orang lain tidak mengetahui dengan baik bentuk dan isi berkas tersebut.
c. Apakah pasangan kunci yang digunakan (dalam hal ini kunci publik dan kunci private) memiliki tingkat keamanan yang sangat baik.
d. Apakah berkas yang telah dienkripsi dapat dikembali menjadi bentuk berkas orisinil yang utuh seperti sebelum dilakukannya proses enkripsi tanpa ada cacat sedikitpun.
1.3 Batasan Masalah
Untuk menghindari penyimpangan pembahasan dari tujuan awal maka diperlukan batasan masalah skripsi ini adalah sebagai berikut:
a. Aplikasi dapat mengubah sebuah berkas yang memiliki format tertentu menjadi sebuah berkas baru yang tidak dapat dikenali berkas sebenarnya. b. Dalam batasan ini berkas tersebut adalah berkas teks, gambar, suara, dan
video.
c. Algoritma enkripsi dan dekripsi data yang digunakan adalah algoritma RSA (Rivest Shamir Adleman).
d. Proses pembangkitan kunci publik dan kunci privat pada proses enkripsi RSA dilakukan secara acak (random) menggunakan algoritma Monte-Carlo dan dimana kedua nilai acak hanya dilakukan pengecekan apakah bilangan tersebut merupakan bilangan prima apa tidak menggunakan algoritma Miller-Rabin. e. Panjang kunci publik dan kunci privat yang akan dibangkitkan yaitu maksimal
sebesar 64 bit.
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah
1. Bagaimana cara pengimplementasikan algoritma kriptografi yaitu algoritma RSA dalam proses enkripsi sebuah data dan selanjutnya dilakukan dekripsi terhadap data tersebut kembali.
2. Menganalisa proses dekripsi data menjadi sebuah data utuh seperti sebelum mengalami proses enkripsi.
3. Menganalisa perbandingan data yang telah dienkripsi dan didekripsi dengan data yang orisinil (recovery).
1.5 Manfaat Penelitian
Manfaat yang dapat diperoleh dari penulisan skripsi ini adalah sebagai berikut:
Meningkatkan keamanan terhadap data dimana pengguna dapat menyembunyikan sebuah data pada sebuah media pembawa terutama dalam proses pengiriman sebuah data.
1.6 Metodologi Penelitian
Metodologi penelitian yang akan digunakan adalah: 1. Studi Literatur
Pada tahap ini dilakukan pencarian sumber pengetahuan dan informasi dari jurnal, buku-buku, paper dan e-book yang terkait dengan pokok bahasan penelitian.
2. Analisis dan Perancangan Sistem
3. Implementasi Sistem
Pada tahap ini dilakukan proses pengkodean (coding) berdasarkan analisis kebutuhan yang telah dilakukan sebelumnya kedalam bahasa pemrograman.
Dalam hal ini bahasa pemrograman yang digunakan yaitu Borland Delphi 7. 4. Pengujian dan Analisa Sistem
Pada tahap ini dilakukan pengujian dari aplikasi yang dibangun terhadap beberapa data yang akan dienkripsi dan dilakukan analisis terhadap data-data tersebut.
5. Penyusunan Laporan dan Dokumentasi Sistem
Pembuatan report terhadap analisis yang dilakukan serta penjelasan sistem secara keseluruhan.
1.7 Sistematika Penulisan
Agar penulisan menjadi lebih terstruktur, maka penulisan ini dibagi menjadi lima bab, antara lain sebagai berikut:
BAB 1 : Pendahuluan
Bab ini berisi mengenai latar belakang masalah, perumusan masalah, batasan masalah, tujuan penulisan dan sistematika penulisan.
BAB 2 : Tinjauan Teoritis
Bab ini dibahas mengenai teori-teori apa saja yang menjadi tinjauan penulis dalam menyelesaikan penelitian ini diantaranya teori algoritma kriptografi RSA, dan algoritma pembangkitan bilangan acak Monte Carlo, dan algoritma pengecekan bilangan prima Miller-Rabin.
BAB 3: Analisis danPerancangan Sistem
BAB 4: Implementasi dan Pengujian Sistem
Bab ini berisi mengenai implementasi sistem berdasarkan tahapan perancangan dengan menggunakan bahasa pemrograman Borland Delphi 7 serta tahapan pengujian sistem untuk melihat apakah sistem sudah berjalan sesuai perancangan atau tidak.
BAB 5: Kesimpulan dan Saran
BAB 2
LANDASAN TEORI
2.1 Kriptografi
2.1.1 Pengertian kriptografi
Kriptografi (Cryptography) berasal dari Bahasa Yunani. Menurut bahasanya, istilah tersebut terdiri dari kata kripto dan graphia. Kripto berarti secret (rahasia) dan
graphia berarti writing (tulisan). Menurut terminologinya, kriprografi adalah ilmu dan seni untuk menjaga keamanan pesan ketika pesan dikirim dari suatu tempat ke tempat yang lain. Dalam kamus bahasa Inggris Oxford, pengertian kriptografi adalah ”Sebuah teknik rahasia dalam penulisan, dengan karakter khusus, dengan menggunakan huruf dan karakter di luar bentuk aslinya, atau dengan metode-metode lain yang hanya dapat dipahami oleh pihak-pihak yang memproses kunci, juga semua hal yang ditulis dengan cara seperti ini ”(Dony ariyus, ”Keamanan Multimedia”, 2007, hal : 19).
2.1.2 Komponen kriptografi
Pada dasarnya, kriptografi terdiri dari beberapa komponen penting seperti (Dony Aryus, ”keamanan Multimedia”, 2007, hal :19-20) :
b. Dekripsi, merupakan kebalikan dari enkirpsi yakni pesan yang telah dienkripsi dikembalikan ke bentuk asalnya (plaintext), yang disebut dekripsi pesan. Algoritma yang digunakan untuk dekripsi berbeda dengan yang digunakan untuk enkripsi.
c. Key (kunci), kunci yang dimaksud disini adalah kunci yang dipakai untuk melakukan proses enkripsi dan dekripsi. Kunci terbagi menjadi dua bagian, yakni kunci pribadi (private key) dan kunci umum (public key).
d. Ciphertext, merupakan suaut pesan yang sudah melalui proses enkripsi. Pesan yang ada pada ciphertext tidak bisa dibaca karena berisi karakter-karakter yang tidak memiliki makna (arti).
e. Plaintext (atau cleartext) merupakan suatu pesan bermakna yang ditulis atau diketik dan plaintext itulah yang akan diproses menggunakan algoritma kriptografi agar menjadi chipertext.
f. Pesan, dapat berupa data atau informasi yang dikirim (melalui media tertentu) atau disimpan dalam media perekaman.
g. Kriptanalisis, bisa diartikan sebagai analisis sandi atau suatu ilmu untuk mendapatkan plaintext tanpa harus mengetahui kunci secara wajar.
2.1.3 Tujuan kriptografi
Kriptografi memiliki tujuan untuk memberi layanan keamanan yakni sebagai berikut (Munir, 2006, hal : 9) :
a. Kerahasiaan (confidentiality), adalah layanan yang ditujukan untuk menjaga agar pesan tidak dapat dibaca oleh pihak-pihak yang tidak berhak.
b. Integritas Data (data integrity), adalah layanan yang menjamin bahwa pesan masih asli/utuh atau belum pernah dimanipulasi selama pengiriminan.
c. Otentikasi (authentication), adalah layanan yang berhubungan dengan identifikasi, baik mengidentifikasi kebenaran pihak-pihak yang berkomunikasi maupun mengidentifikasi kebenaran sumber pesan.
menyangkal melakukan pengiriman atau penerima pesan menyangkal telah menerima pesan.
2.1.4 Terminologi dan Konsep Dasar Kriptografi
Dalam bidang kriptografi akan ditemukan beberapa istilah atau teminologi. Istilah-istilah tersebut sangat penting untuk diketahui dalam memahami ilmu kriptografi. Oleh karena itu penulis akan menjelaskan beberapa istilah penting dalam bidang kriptografi yang akan sering penulis gunakan dalam tulisan ini. Berikut merupakan istilah-istilah tersebut.
a. Plainteks dan Cipherteks
Pesan merupakan data atau informasi yang dimengerti maknanya secara langsung. Nama latin dari pesan adalah plainteks (plaintext). Pesan tersebut dapat dikirim (melalui kurir, saluran telekomunikasi, dan lain-lain) dan dapat juga disimpan dalam media penyimpanan (kertas, perangkat storage, dan lain-lain). Pesan dapat berupa teks, video, gambar, dan lain-lain. Agar pesan tersebut tidak dapat dimengerti makanya bagi pihak lain, maka pesan perlu disandikan ke bentuk lain yang tidak dipahami. Bentuk pesan yang telah tersandikan tersebut dinamakan dengan cipherteks. Perbandingan antara plainteks dan cipherteks dapat kita lihat pada gambar 2.1 berikut.
b. Peserta Komunikasi
Komunikasi data melibatkan pertukaran pesan antara dua entitas. Entitas yang pertama adalah pengirim, yang berfungsi mengirim pesan kepada entitas lain. Entitas kedua ada penerima, yang berfungsi menerima pesan yang dikirimkan. Entitas-entitas ini dapat berupa orang, mesin komputer, sebuah kartu kredit, dan sebagainya. Pengirim ingin mengirimkan pesan dengan aman sampai ke penerima. Jadi solusinya adalah dilakukan penyandian terhadap pesan tersebut agar tidak diketahui pihak-pihak yagn tidak berkepentingan terhadap pesan tersebut.
c. Enkripsi dan Dekripsi
Proses penyandian pesan, dari plainteks ke cipherteks dinamakan dengan enkripsi (encryption) dan enchipering (standar nama menurut ISO 7498-2). Sedangkan proses mengembalikan pesan dari cipherteks ke plainteks dinamakan dengan dekripsi (decryption) dan dechipering (standar nama menurut ISO 7498-2). Proses enkripsi dan dekripsi dapat diterapkan pada pesan yagn dikirim ataupun pesan yang disimpan. (M Yuli Andri, 2009, hal 13)
d. Kriptanalis dan Kriptologi
2.1.5 Jenis kriptografi
Kriptografi dibagi menjadi dua bagian berdasarkan kunci yang dipakai dalam proses enkripsi dan dekripsi, yaitu (M Yuli Andri, 2009, hal 14) :
a. Kriptografi simetri, algoritma ini disebut juga algoritma klasik karena memakai kunci yang sama untuk proses enkripsi dan dekripsi. Istilah lain dari kriptografi ini adalah kriptografi kunci privat (privat-key cryptography), kriptografi kunci rahasia (secret-key cryptography), atau kriptografi konvensional (conventional cryptography). Dalam kriptografi kunci simetri dapat diasumsikan bahwa si penerima dan pengirim pesan telah terlebih dahulu berbagi kunci sebelum pesan dikirimkan. Keamanan dari sistem ini terletak pada kerahasiaan kuncinya.
Skema dari proses kriptografi simetri ini dapat dilihat pada gambar 2.2 berikut.
Private Key, K
Plaintext,P Ciphertext, C Plaintext, P Gambar 2.2 Skema proses kriptografi simetri
Terdapat dua teknik dasar yang biasa diguna kan pada kriptografi simetri yaitu teknik subsitusi dimana pergantian setiap karakter plaintext
dengan karakter lain dan teknik transposisi (permutasi) dimana teknik ini menggunakan permutasi karakter.
Beberapa algoritma yang menggunakan kunci yang sama (simetri) antara lain :
o Data encryption Standard (DES)
o International Data Encryption Algorithm (IDEA) o Advanced Encryption Standard (AES)
Enkripsi Dk(C) = P Enkripsi
b. Kriptografi Asimetri, Berbeda dengan kripfotgrafi kunci simetri, kriptografi kunci publik memiliki dua buah kunci yang berbeda pada proses enkripsi dan deskripsinya. Nama lain dari kunci asimetris ini adalah kriptografi kunci-publik (public-key cryptography). Kunci untuk enkripsi pada kriptografi asimetri ini tidak rahasia (diketahui oleh publik), sedangkan kunci untuk dekripsi bersifat rahasia (kunci privat). Enititas pengirim akan mengenkripsi dengan menggunakan kunci publik, sedangkan entitas penerima mendekripsi menggunakan kunci privat. Skema dari proses kriptografi asimetri ini dapat dilihat pada gambar 2.3 berikut.
Kunci Publik, K1 Kunci Privat, K2
Plaintext,P Ciphertext, C Plaintext, P
Gambar 2.3 Skema kriptografi asimetri
Kriptografi asimetri ini dapat dianalogikan seperti kotak surat yang terkunci dan memiliki lubang untuk memasukkan surat. Setiap orang dapat memasukkan surat ke dalam kotak surat tersebut, tetapi hanya pemilik surat yang memiliki kunci dan yang dapat membuka kotak surat. Kunci publik dapat dikirim ke penerima melalui saluran yang sama dengan saluran yang digunakan untuk mengirim pesan, tidak perlu takut karena pihak yang tidak berkepentingan tidak akan dapat mendekripsi pesan tersebut, karena tidak memiliki kunci privat, atau penerima dapat memberikan kunci publik yang diinginkan kepada pengirim.
Beberapa algoritma yang menggunakan kunci yang berbeda (asimetri) antara lain :
o Digital Signature Algorithm (DSA) o Rivest Shamir Adleman (RSA) o Diffie-Helman (DH)
Enkripsi Ek(P) = C
2.1.6 Algoritma Kriptografi Rivest Shamir Adleman (RSA)
Dari sekian banyak algoritma kriptografi kunci publik yang pernah dibuat, algoritma RSA merupakan algoritma yang paling populer dan cukup aman dikarena algoritma RSA melakukan menfaktoran bilangan yang cukup besar. Algoritma RSA sendiri dibuat oleh tiga orang peneliti dari MIT (Massachussets Institute of Technology) pada tahun 1976. Mereka adalah Ron Rivest, Adi Shamir, Leonard Adleman. RSA diambil dari tiap nama belakang mereka. (Dony Ariyus,”keamanan Multimedia”, 2007, hal 80).
Keamanan algoritma RSA terletak pada sulitnya memfaktorkan bilangan yang besar menjadi faktor-faktor prima. Pemfaktoran dilakukan untuk memperoleh kunci pribadi. Selama pemfaktoran bilangan besar menjadi faktor-faktor prima belum ditemukan algoritma yang mangkus, maka selama itu pula keamanan algoritma RSA tetap terjamin. Dikarenakan makin besar ukuran kunci, maka makin besar juga kemungkinan kombinasi kunci yang bisa dijebol dengan metode memeriksa kombinasi satu persatu kunci atau lebih dikenal dengan istilah brute force attack
sehingga tidak ekonomis dan sulit untuk memecahkan sandi tersebut.
Terdapat beberapa besaran yang digunakan pada algoritma RSA, yakni: 1. p dan q bilangan prima (rahasia)
2. N = p⋅q (tidak rahasia)
3. φ(N) = (p – 1)(q – 1) (rahasia) 4. e (kunci enkripsi) (tidak rahasia) 5. d (kunci dekripsi) (rahasia)
6. X (plainteks) (rahasia)
7. Y (cipherteks) (tidak rahasia)
2.1.6.1 Proses Pembangkitan Kunci
a. Pilih dua bilangan (integer) prima p dan q secara acak, dimana p q. Bilangan ini harus cukup besar untuk memperoleh tingkat keamanan yang tinggi.
b. Hitung N = p.q, (p q, karena jika p=q maka nilai N= p2 dan akan mudah mendapatkan nilai N),bilangan N disebut parameter sekuriti.
c. Hitung φ(N)= (p-1)(q-1). φ(N) merupakan nilai totient euler dari suatu bilangan N dimana menyatakan jumlah bilangan bulat positif yang lebih kecil dari N dan prima terhadap N.
d. Pilih bilangan bulat (integer) sebagai kunci publik antara satu dan φ(N) (1< e <
φ(N)) yang tidak mempunyai faktor pembagi dari φ(N). sehingga gcd(e. φ(N)) = 1. Dapat dikatakan bahwa e relatif prima terhadap φ(N).
e. Greatest Common Divisor (gcd) dari dua buah bilangan tidak lain adalah irisan dari himpunan faktor bilangan prima dari kedua bilangan tersebut. Contohnya,
gcd (a,b) gcd(10,15) = 5
gcd((2 x 5),(3 x 5)) = 5
ketika kedua bilangan tidak memiliki faktor bersama, maka gcdnya menjadi 1
f. Menghitung bilangan bulat d dimana 1 < d < φ(N), sehingga e.d 1 (mod
φ(N)). Menurut persamaan Chinese Remainder Theorem (CRT) yang menyatakan bahwa a b (mod m) ekivalen dengan a = b+ k.m, atau dapat dinyatakan dengan persamaan :
e.d 1 (mod φ(N)) atau e.d (mod φ(N)) = 1
Dengan mencoba nilai d = 0,1,2,3, .. sehingga memenuhi persamaan tersebut. hasil dari algoritma tersebut adalah :
2.1.6.2 Pembangkit dan Pengecekan Bilangan Prima
Dalam proses pembangkitan kunci publik dan privat pada algoritma kriptografi RSA, dibutuhkan dua bilangan p dan q yang merupakan bilangan prima dan merupakan bilangan yang dapat dikatakan sangat besar. Hal ini dapat diantisipasi dengan menggunakan suatu algoritma pembangkit bilangan acak serta dilakukan pengecekan bilangan tersebut merupakan bilangan Prima atau bukan.
Terdapat banyak algoritma pembangkit bilangan acak yang digunakan pada dunia komputer. Akan tetapi algoritma yang digunakan adalah algoritma pembangkit bilangan acak Monte Carlo. Dikarenakan pada hal ini sistem hanya akan
meng-generate suatu angka dari suara batasan kumpulan angka yang nantinya akan digunakan pada proses pembangkitan kunci pada RSA. Akan tetapi sebelum digunakan dilakukan kembali pengecekan apakah nilai tersebut merupakan bilangan prima atau tidak. Algoritma pengecekan bilangan prima penulis menggunakan algoritma Miller Rabin.
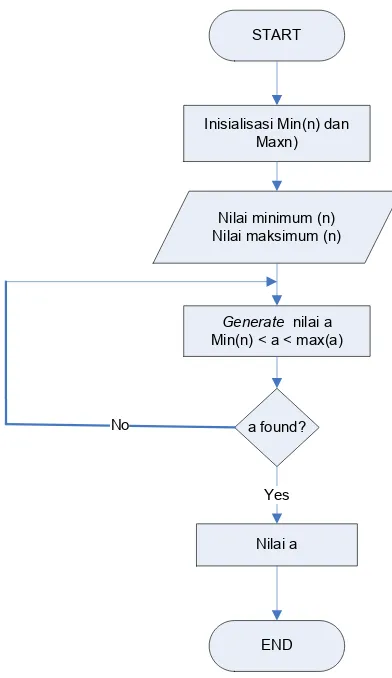
• Algoritma pembangkit bilangan acak Monte Carlo
Metode Monte Carlo merupakan dasar untuk semua algoritma dari metode simulasi yang didasari pada pemikiran penyelesaian suatu masalah untuk mendapatkan hasil yang lebih baik dengan cara memberi nilai sebanyak-banyaknya (generated Random Number) untuk mendapatkan ketelitian yang lebih tinggi. Metode ini menganut sistem pemrograman yang bebas tanpa terlalu banyak diikat oleh aturan tertentu. Secara umum algoritma ini dapat diperlihatkan pada pseudocode sederhana seperti berikut.
Input : n,k , dimana n < a < k; Output : a
MonteCRandom (a,n,k) I <- 0
Repeat until a found or i=k Random(a), n < a < k I = i +1
pada bahasa pemgrograman Borland Delphi 7 khususnya telah tersedia suatu fungsi yang langsung menggunakan algoritma ini dalam proses pembangkit bilangan acak yaitu random().
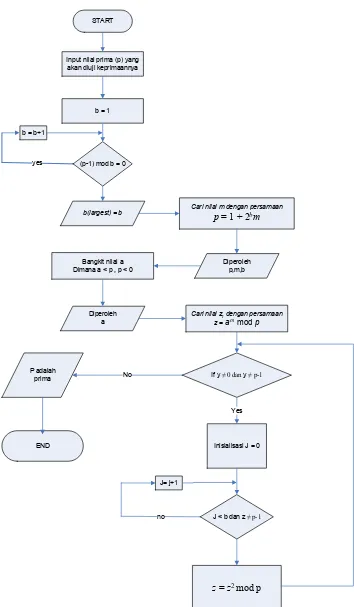
• Algoritma Pengecekan Bilangan Prima Miller Rabin
Pengecekan bilangan prima Miller Rabin merupakan salah satu metode atau algoritma pengetesan keprimaan suatu bilangan hasil generate sebelumnya. Algoritma ini awalnya diciptakan oleh Gary L. Miller, akan tetapi telah dimodifikasi oleh Michael O. Rabin. Secara garis besar langkah-langkah dari algoritma ini adalah sebagai berikut. Persamaan dari Algoritma ini adalah
x2 1 (mod p) (x-1 )(x+1) 0 (mod p)
Secara garis besar proses dari pengecekan bilangan bilangan prima Miller Rabin dapat dijelaskan sebagai berikut.
1) Input bilangan p yang akan diuji keprimaannya.
2) Hitung b, yang dalam hal ini 2b adalah nilai pangkat 2 terbesar yang habis membagi p – 1.
3) Hitung m sedemikian sehingga p = 1 + 2bm.maka diperoleh : p, m, dan b
4) Bangkitkan bilangan acak a yang lebih kecil dari p. 5) Nyatakan j = 0 dan hitung z = am mod p.
6) Jika z = 1 atau z = p – 1, maka p lolos dari pengujian dan mungkin prima. 7) Jika z > 0 dan z = 1, maka p bukan prima.
8) Nyatakan j = j + 1. Jika j < b dan z≠p – 1, nyatakan z = z2 mod p dan kembali ke langkah (6). Jika z = p – 1, maka p lolos pengujian dan mungkin prima.
9) Jika j = b dan z≠p – 1, maka p tidak prima.
2.1.6.3 Algoritma Enkripsi
Proses enkripsi dilakukan dengan menggunakan kunci publik. Prosedurnya antara lain:
1) Ambil kunci publik penerima pesan (e), dan modulus N.
2) Plainteks dinyatakan dengan blok-blok m1,m2,...,mn sedemikian sehingga setiap blok mempresentasikan nilai di dalam selang [0,N-1].
3) Setiap blok mi dienkripsikan menjadi blok ci dengan rumus ci = miemod N
2.2.6.4 Algoritma dekripsi
Proses dekripsi dilakukan dengan menggunakan kunci privat (d,N) dimana setiap blok chiperteks ci didekripsikan kembali menjadi blok mi dengan rumus :
mi = cid mod N
Penggunaan algoritma tersebut diatas dapat dicontohkan sebagai berikut :
Misalkan p = 47 dan q = 71 (keduanya prima). Selanjutnya menghitung nilai
N = p⋅q = 3337 dan φ(N)= (p – 1)(q – 1) = 3220
Pilih kunci publik e = 79, karena 79 relatif prima dengan 3220. e dan N dapat dipublikasikan ke umum.
Selanjutnya akan dihitung kunci dekripsi d menggunakan : e.d 1 (mod φ(N)) atau ed mod φ
Dengan mencoba nilai-nilai d = 1, 2, 3, …, diperoleh nilai SK yang bulat adalah 1019. Ini adalah kunci dekripsi yang harus dirahasiakan.
Selanjutnya pesan yang akan dikirim adalah m = SKRIPSIKU Atau dalam desimal (kode ASCII) adalah : 837582738083737585
Kemudian nilai tersebut akan dipecah menjadi blok-blok m. Nilai-nilai m harus masih dalam selang [0, 3337-1]. Maka blok yang akan terbentuk adalah :
m1 = 837 ; m2 = 582 ; m3 = 738 ; m4 = 083 ; m5 = 737 ; m6 = 585
Sebelumnya telah diketahui kunci publik adalah e = 79 dan N = 3337. Maka pesan m dapat dienkripsikan, yakni :
c1 = 83779 mod 3337 = 792 ; c2 = 58279 mod 3337 = 776 ; c3 = 73879 mod 3337 = 2623 ; c4 = 08379 mod 3337 = 2251; c5 = 73779 mod 3337 = 2037 ; c6 = 58579 mod 3337 = 685 ;
Sehingga chiperteks yang dihasilkan adalah : 792 776 2623 2251 2037 685
Selanjutnya pesan yang telah terenkripsi tersebut dikirimkan kepada penerima pesan, yang mana telah memiliki kunci privat (d,N) = (1019,3337) sehingga :
m1 = 7921019 mod 3337 = 837 ; m2 = 7761019 mod 3337 = 582 ; m3 = 26231019 mod 3337 = 738 ; m4 = 22511019 mod 3337 =083 ; m5 = 20371019 mod 3337 = 737 ; m2 = 6851019 mod 3337 =585 ;
maka akan dihasilkan kembali m = 837 582 738 083 737 585
BAB 3
ANALISIS DAN PERANCANGAN SISTEM
3.1 Analisis Permasalahan
Penggunaan algoritma kriptografi dalam aktivitas teknologi informasi pada saat ini sudah sering digunakan. Begitu juga halnya steganografi dalam proses penyembunyian data dalam jenis data lainnya.
Dalam merancang suatu sistem diperlukan analisis terhadap sistem yang akan dirancang terlebih dahulu. Tujuan dari analisis itu sendiri adalah agar sistem yang dirancang menjadi tepat guna dan ketahanan dari sistem tersebut akan lebih baik. Disamping itu dengan melakukan sebuah analisis kita akan dapat mempermudah kerja kita dalam membuat sistem, dan jika suatu saat nanti ada perbaikan atau penambahan dalam sistem tersebut, maka akan mudah diselesaikan.
Dalam hal ini penulis menggunakan algoritma Rivest Shamir Adleman (RSA) sebagai algoritma kriptografi dan berkas yang menjadi objek kriptografi adalah seluruh berkas berformat apapun baik berkas teks, gambar, suara, ataupun video. Masalah autentikasi data pada proses kriptografi ini menjadi perhatian utama. Dimana keberhasilan proses kriptografi sangat dipengaruhi oleh bilangan prima pada pembangkitan kedua kunci RSA. Apabila ada ketidaksesuaian dari parameter-parameter yang dibutuhkan maka proses pengembalian berkas kode menjadi berkas orisinil tidak akan berhasil.
membantu mempermudah dalam membangun sebuah sistem. Bagian kepala atau kotak yang berada di sisi kanan merupakan masalah utamanya, sedangkan di bagian tulangnya merupakan penyebab.
Gambar 3.1 : Diagram Ishikawa untuk Analisa Masalah
3.2 Analisis Persyaratan (Requirment Analysis)
Analisa ini bertujuan untuk mengidentifikasikan dan menyatakan persyaratan apa saja yang dibutuhkan oleh sistem agar dapat berjalan sesuai dengan yang diharapkan. Analisis persyaratan ini terdiri atas dua bagian yaitu analisis fungsional (functional requirement) dan analisis nonfungsional (nonfunctional requirement). Dimana persyaratan fungsional adalah aktifitas dan layanan yang harus diberikan/disediakan oleh sebuah sistem, dan persyaratan nonfungsional berkaitan dengan fitur, karakteristik, dan batasan lainnya yang menentukan apakah sistem memuaskan atau tidak. Kedua analisis ini merupakan hal yang penting untuk menentukan hal-hal yang harus dimiliki sistem.
3.2.1 Persyaratan Fungsional (Functional Requirment)
Analisis fungsional dibutuhkan untuk mengetahui hal-hal yang bisa dikerjakan oleh sistem. Berikut akan dijabarkan fungsi-fungsi yang dapat dikerjakan oleh sistem.
1. Kunci publik dan kunci privat yang akan dipakai dapat dilakukan secara manual ataupun otomatis (dengan menggunakan sebuah modul pembangkit kunci RSA).
2. Pembangkitan bilangan prima yang akan digunakan dalam mendapatkan kunci asimetri RSA juga dilakukan secara acak.
3. Sistem akan melakukan proses enkripsi terhadap seluruh berkas dengan format apapun dan dekripsi terhadap berkas enkripsi dengan tingkat keberhasilan sempurna (menghasilkan berkas plainteks orisinil).
3.2.2 Persyaratan Nonfungsional (Nonfunctional Requirment)
Analisis nonfungsional berhubungan dengan hal-hal berikut ini :
1. Performa
Perangkat lunak yang akan dibangun dapat menunjukkan hasil dari proses pembangkitan kunci dan dapat memilih apakah kunci akan digunakan apa tidak serta proses enkripsi dan dekripsi dilakukan secara bertahap atau terstruktur.
2. Mudah dipelajari dan digunakan
Perangkat lunak yang akan dibangun memiliki tampilan yang user friendly
3. Keamanan
Parameter yang digunakan pada pembangkitan kunci menggunakan nilai yang cukup besar sehingga sangat sulit yang dilakukan pemecahan kunci. Hasil generate akan disimpan pada sebuah berkas lain yang hanya dimiliki oleh pengguna aplikasi.
4. Efisien
Setiap proses pada perangkat lunak tidak membutuhkan waktu yang cukup lama tergantung dari ukuran berkas yang akan diolah.
5. Dokumentasi
Perangkat lunak yang akan dibangun menyimpan semua paramater yang telah digunakan dan menampilkan kembali kepada user sebelum melakukan eksekusi.
6. Kontrol
Perangkat lunak yang akan dibangun akan menampilkan pesan error
untuk setiap kesalahan atau parameter yang tidak sesuai
3.3 Permodelan Sistem dengan Use Case dan Activity Diagram
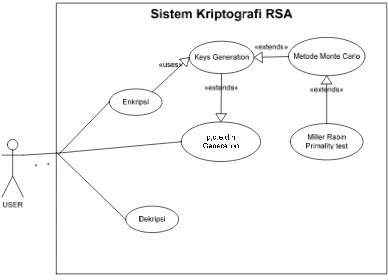
Permodelan sistem dilakukan untuk memperoleh gambaran yang lebih jelas tentang objek-objek yang berinteraksi antara user dan sistem. Use case adalah salah satu permodelan yang digunakan dalam memodelkan persyaratan sistem. Dengan use case digambarkan siapa saja yang berinteraksi dengan sistem dan apa saja dilakukan oleh sistem.
Berikut ini adalah diagram use case yang dirancang sebagai permodelan persyaratan sistem.
Gambar 3.2 : Use Case Diagram yang akan dikembangkan
Diagram pada gambar 3.2 menjelaskan segala aktivitas yang dilakukan user terhadap sistem. User pertama memilih menu yang akan digunakan (enkripsi/dekripsi), selanjutnya untuk enkripsi user harus menginput plainteks,
meng-generate parameter (yang nantinya menghasilkan dua kunci yaitu kunci publik dan kunci privat). Sedangkan untuk dekripsi user harus menginputkan cipherteks dan kunci privat untuk melanjutkan ke proses dekripsi berkas.
3.3.1 Use Case Key Generation
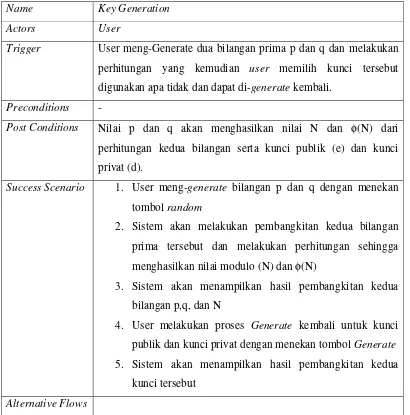
Name Key Generation Actors User
Trigger User meng-Generate dua bilangan prima p dan q dan melakukan perhitungan yang kemudian user memilih kunci tersebut digunakan apa tidak dan dapat di-generate kembali.
Preconditions -
Post Conditions Nilai p dan q akan menghasilkan nilai N dan φ(N) dari perhitungan kedua bilangan serta kunci publik (e) dan kunci privat (d).
Success Scenario 1. User meng-generate bilangan p dan q dengan menekan tombol random
2. Sistem akan melakukan pembangkitan kedua bilangan prima tersebut dan melakukan perhitungan sehingga menghasilkan nilai modulo (N) dan φ(N)
3. Sistem akan menampilkan hasil pembangkitan kedua bilangan p,q, dan N
4. User melakukan proses Generate kembali untuk kunci publik dan kunci privat dengan menekan tombol Generate
5. Sistem akan menampilkan hasil pembangkitan kedua kunci tersebut
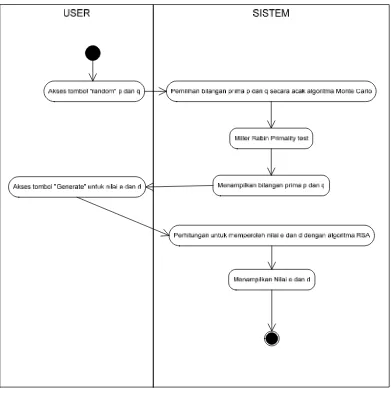
[image:36.612.121.531.98.513.2]Alternative Flows
Gambar 3.3 : Activity Diagram proses Keys Generation
3.3.2 Use Case Enkripsi
Berikut merupakan spesifikasi use case Enkripsi beserta tabel activity Diagram
seperti yang digambarkan pada tabel 3.2 dan gambar 3.4.
Name Enkripsi
Actors User
dilakukan setelah pross input parameter dilakukan.
Preconditions Nilai N, φ(N), dan kunci publik (e) telah diperoleh dan ditampilkan serta telah menginput plainteks yang akan dienkripsi
Post Conditions Proses enkripsi terhadapt berkas asli dengan menggunakan Algoritma RSA akan menghasilkan berkas baru dengan format .enc
Success Scenario 1. User memulai proses enkripsi dengan menekan tombol enkripsi
2. Plainteks dienkripsi sesuai dengan prosedur enkripsi algoritma RSA dengan menggunakan parameter dan kunci yang telah diperoleh.
3. Sistem akan menampilkan bahwa proses enkripsi sudah berhasil dilakukan.
4. Output menghasilkan berkas baru yang merupakan berkas enkripsi
[image:38.612.119.521.83.421.2]Alternative Flows
Gambar 3.4 : Activity Diagram proses Enkripsi
3.3.3 Use Case Dekripsi
Berikut merupakan spesifikasi use case Enkripsi beserta tabel activity Diagram
seperti yang digambarkan pada tabel 3.3 dan gambar 3.5.
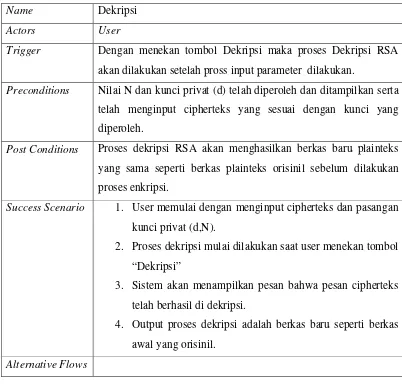
Name Dekripsi
Actors User
Trigger Dengan menekan tombol Dekripsi maka proses Dekripsi RSA akan dilakukan setelah pross input parameter dilakukan.
Preconditions Nilai N dan kunci privat (d) telah diperoleh dan ditampilkan serta telah menginput cipherteks yang sesuai dengan kunci yang diperoleh.
Post Conditions Proses dekripsi RSA akan menghasilkan berkas baru plainteks yang sama seperti berkas plainteks orisinil sebelum dilakukan proses enkripsi.
Success Scenario 1. User memulai dengan menginput cipherteks dan pasangan kunci privat (d,N).
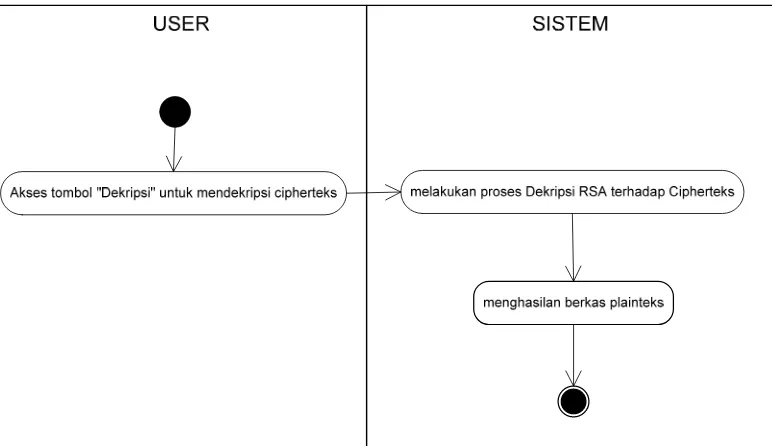
2. Proses dekripsi mulai dilakukan saat user menekan tombol “Dekripsi”
3. Sistem akan menampilkan pesan bahwa pesan cipherteks telah berhasil di dekripsi.
4. Output proses dekripsi adalah berkas baru seperti berkas awal yang orisinil.
[image:39.612.121.523.213.597.2]Alternative Flows
Gambar 3.5 : Activity Diagram proses Dekripsi
3.4 Analisis Sistem
Analisis sistem dalam penelitian ini akan dibagi menjadi tiga bagian sistem yakni sistem utama aplikasi, sistem algoritma, dan sistem antarmuka (interface). Pada sistem utama aplikasi akan dibahas mengenai proses utama program ini yakni proses penyembunyian data dan pengekstrakan data. Dalam sistem algoritma akan dibahas tentang algoritma-algoritma yang digunakan pada sistem dan desain algoritma tersebut. Dan dalam sistem antarmuka akan dibahas tentang desain tampilan pada aplikasi tersebut.
3.4.1 Analisis Sistem Utama
isinya (chipertext) dimana disebut proses enkripsi dan Sedangkan sistem yang kedua yaitu sistem dekripsi yang merupakan sebuah proses mengekstrak data acak (chipertext) dan mengolahnya kembali menjadi data utuh (plaintext).
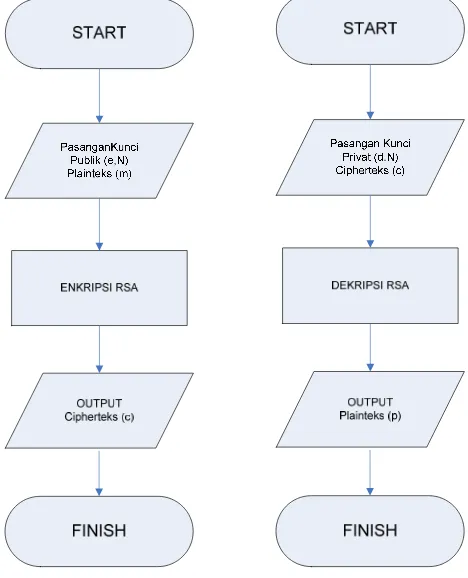
Sistem utama aplikasi yakni proses enkripsi dan proses dekripsi tersebut dapat dilihat pada gambar 3.6 berikut.
[image:41.612.206.440.201.490.2]
Gambar 3.6 : Skema Global Diagram Alir Proses Enkripsi dan Dekripsi
3.4.2 Analisis Sistem Algoritma RSA
Dalam sistem algoritma Kriptografi RSA ini terdapat tiga proses utama, yaitu proses generate kunci Publik dan kunci Privat dimana masing-masing akan digunakan dalam proses enkripsi dan dekripsi, proses enkripsi mengubah plainteks menjadi cipherteks dan proses dekripsi mengubah cipherteks menjadi plainteks.
Prinsip kerja algoritma RSA terletak pada sulitnya memfaktorkan bilangan yang besar bahkan sangat besar menjadi faktor-faktor prima. Pemfaktoran dilakukan untuk mendapatkan kunci privat. Selama bilangan tersebut tidak dapat difaktorkan, selama itu pula keamanan algoritma RSA akan sangat tinggi. Dalam algoritma RSA terdapat beberapa besaran-besaran yang penting, yaitu sebagai berikut:
a. Nilai p dan q yaitu bilangan prima yang diambil secara acak, atau untuk lebih baiknya langsung dipilih oleh orang yang akan menerima pesan. Sifat dari kedua bilangan ini adalah rahasia, dimana hanya pengirim pesan dan penerima pesan yang mengetahuinya.
b. N=p.q, sifat dari N adalah tidak rahasia, yang bearti bisa diketahui oleh publik. c. φ(N) = (p-1)(q-1), Sifat dari bilangan ini adalah rahasia
d. e (kunci enkripsi), kunci enkripsi bersifat tidak rahasia. e. d (kunci dekripsi), dekripsi bersifat rahasia.
f. m (plainteks), plainteks merupakan informasi awal yang bersifat rahasia. g. c (Cipherteks), cipherteks merupakan infromasi yang telah dienkripsi yang
bersifat tidak rahasia. (Dony Artyus,2006)
3.4.3 Pembangkitan (Generate) Kunci Publik dan Kunci Privat
dilakukan pada awal sebelum melakukan proses enkripsi dimana membutuhkan dua bilangan (integer) prima secara acak, dalam hal ini diharuskan menggunakan sebuah pembangkit yang secara otomatis generasi bilangan tersebut dikarenakan angka-angka tersebut cukup besar dan banyak untuk memperoleh keamanan yang lebih tinggi dan lebih baik. Selanjutnya terdapat juga proses pengecekan apakah bilangan tersebut merupakan bilangan prima apa tidak sehingga akan terjadi looping yang cukup lama sampai menemukan nilai prima yang sesuai dengan syarat.
Sehingga dalam keseluruhan proses pembangkitan kunci publik dan kunci privat diperoleh paramater-paramater yang dibutuhkan dalam proses selanjutnya yaitu proses enkripsi data ( plainteks). Paramater-parameter itu yakni nilai dari kunci publik (e), kunci privat (d), serta nilai modulo (N). Nilai modulo akan selalu digunakan dalam proses enkripsi maupun dekripsi. Berikut adalah langkah-langkah dalam pembangkitan pasangan kunci :
a. Proses pertama proses pembangkitan atau generate dua buah bilangan prima secara acak (dalam hal ini menggunakan algoritma pembangkit bilangan acak). Besaran itu adalah nilai q dan q.
b. Hitung nilai n=p.q dan φ(N) = (p-1)(q-1)
c. Pilih satu kunci publik (e) dimana 1 < e < φ(N), yang disimbolkan dengan e. syarat dari pemilihan kunci ini adalah e harus relatif prima terhadap φ(N). d. Membangkitkan kunci privat (d) dengan persamaan e.d mod φ(N) = 1
Hasil dari algoritma di atas adalah :
1. Kunci publik adalah pasangan (e,N) 2. Kunci privat adalah pasangan (d,N)
Pada proses pembangkitan dua pasangan kunci publik dan kunci privat, terdapat dua algoritma algoritma lain yang akan digunakan yakni pembangkit bilangan acak Monte-Carlo dan algoritma penguji keprimaan suatu bilangan yaitu menggunakan algoritma Miller-Rabin. Untuk penjelasan tentang algoritma-algoritma tersebut telah dijelaskan pada Bab 2 Subbab 2.1.4.2 Pembangkit dan Pengecekan Bilangan Prima. Secara global kedua proses tersebut dapat digambarkan seperti pada gambar 3.8 dan gambar 3.9 berikut.
! "
# !
$ %
& ' (
)( & ' %
* $ $&
' *
+ *
, ' %
, & -& ' -&.(
[image:46.612.147.501.71.678.2],' ".(
3.4.4 Sistem Enkripsi Sebuah Berkas
Proses enkripsi dalam algoritma kriptografi RSA memiliki dua variabel inputan, yaitu kunci publik (dalam hal ini kunci yang diperoleh dari proses pembangkitan kunci) dan data yang akan dienkripsi (plainteks). Sebelum proses enkripsi dilakukan terhadap plainteks, seperti yang telah dijelaskan sebelumnya bahwa dilakukan pembangkitan dua buah kunci yaitu kunci publik dan kunci privat yang akan digunakan dalam proses enkripsi dan dekripsi akan tetapi user juga dapat menggunakan kunci publik dan kunci privat yang telah dimiliki.
Setelah memperoleh kunci publik selanjutnya dilakukan proses enkripsi yang terlebih dahulu palinteks dibagi menjadi blok-blok yang kemudian akan diakukan enkripsi. Langkah-langkah dari proses enkripsi adalah sebagai berikut :
a. Langkah pertama adalah mengambil nilai kunci publik (e) dan modulo (N) dari proses pembangkitan kunci.
b. Input berkas yang akan dienkripsi (plainteks) yaitu berkas-berkas yang memiliki format apapun.
c. Berkas yang akan dienkripsi kemudian diubah kedalam bentuk ASCII sesuai dengan tabel ASCII.
d. Membagi berkas tersebut menjadi beberapa blok (mi) dengan syarat mi < n dengan length(mi) = length(mi+1).
e. Setelah itu setiap blok dari berkas yang telah diubah dienkripsikan menggunakan pasangan kunci publik.
3.4.5 Sistem Dekripsi Sebuah Berkas
Proses dekripsi dalam algoritma kriptografi RSA memiliki tiga parameter inputan, yaitu kunci privat (d), dan nilai modulo (N) yang diperoleh dari dari proses enkripsi yang telah dilakukan sebelumnya terhadap berkas palinteks.
3.5 Perancangan Antarmuka (Interface)
Perancangan antarmuka (interface) merupakan tampilan program aplikasi yang akan digunakan oleh pemakai (user) untuk dapat berkomunikasi dengan komputer. Tahapan ini sangat penting karena antarmuka yang baik akan membuat user
merasakan kenyamanan dalam menggunakan sebuah aplikassi komputer.
Untuk lebih memudahkan pembuatan antarmuka suatu sistem, perlu dilakukan terlebih dahulu perancangan struktur menu program dari sistem yang akan dibangun, hal ini sangat berguna untuk mengetahui urutan menu yang akan digunakan oleh user. Berikut struktur menu-menu yang akan dirancang pada aplikasi sistem pakar ini. Hal ini telah dijelaskan pada sub bab sebelumnya tentang analsis sistem antarmuka.
3.5.1 Rancangan Halaman Utama
[image:51.612.167.487.450.672.2]Halaman ini merupakan halaman yang akan muncul pertama kali saat program dijalankan. Gambar 3.12 berikut adalah rancangan halaman utama sistem kriptografi RSA ini.
Gambar 3.12 : Rancangan halaman Utama antarmuka Sistem
2
3
1
4
Komponen yang dipakai untuk membangun antarmuka halaman menu enkripsi kriptografi RSA seperti pada gambar 3.12 dapat dilihat pada tabel 3.4 berikut.
No Tipe Nama Label Keterangan
1 Label Label22 RSA Cryptography Judul Utama Aplikasi 2 Panel PanelEnkripsi Enkripsi Tombol menampilkan modul
Menu Enkripsi
3 Panel PanelDekripsi Dekripsi Tombol menampilkan modul menu Dekripsi
4 Shape Shape14 - Back seluruh modul dan
dokumentasi tentang penulis
5 Button btnHelp Help Tombol menampilkan Help
Tabel 3.4 : Rincian Rancangan Halaman Utama Kriptografi RSA
Pada halaman utama diatas terdapat menu yang dapat dipiih oleh user pada sebuah menu proses yaitu enkripsi dan dekripsi sesuai kebutuhan user dalam proses kriptografi ini.
3.5.2 Rancangan Halaman Menu Enkripsi Kriptografi RSA
Gambar 3.13 : Tampilan Halaman Menu RSA
Komponen yang dipakai untuk membangun antarmuka halaman menu enkripsi kriptografi RSA seperti pada gambar 3.13 dapat dilihat pada tabel 3.5 berikut.
No Tipe Nama Label Keterangan
1 Panel PanelEStep1 Initial Key
Menampilkan PnlEStep1 yaitu panel inisial kunci
2 Panel PanelEStep2 Plaintext Menampilkan pnlEStep2 yaitu panel input plaintext dan lokasi ciphertext
3 Panel PanelEStep3 Push to
encrypt
Tombol yang berfungsi untuk memulai proses enkripsi (menampilkan data information sebelum proses enkripsi)
4 Panel PnlEnkripsi Panel
Enkripsi Panel utama menu enkripsi
Tabel 3.5 : Rincian Rancangan Halaman Menu Enkripsi Kriptografi RSA
3
6
4
Gambar 3.14 : Tampilan Halaman Menu Initial Key RSA
Komponen yang dipakai untuk membangun antarmuka halaman menu intial Key kriptografi RSA seperti pada gambar 3.14 dapat dilihat pada tabel 3.6 berikut.
No Tipe Nama Label Keterangan
1 Label Label2 Data Ecnryption Judul Menu Enkripsi
2 Label Label3 Key Initialitation Judul SubMenu Inisialisasi Kunci 3 Label Label4 Public Key Label Kunci Publik
4 Label Label8 Please Insert .. Label Instruksi 5 Label Label5 Private Key Label Kunci Privat
6 Label Label24 Modulo Label Modulo
7 Edit PuKUtama - Kotak edit tempat informasi nilai Kunci Publik
8 Edit PrKUtama - Kotak edit tempat informasi nilai kunci privat
9 Edit NUtama - Kotak edit tempat informasi nilai modulo
10 Button Button1 Generate ! Tombol untuk menampilkan modul
[image:54.612.174.475.78.285.2]generate key
Tabel 3.6 : Rincian Rancangan Halaman Initial Key Kriptografi RSA
1
2
4
3
5
6
7
8 9
Pada proses enkripsi terdapat tiga tahap proses yang dalam hal ini divisualisasikan ke dalam tombol-tombol, yaitu key initialitation, Plaintext dan
[image:55.612.187.463.273.539.2]Chipertext dan ”push to encrypt”. Pada key initialitation berfungsi sebagai pembangkit dua bilangan yang akan menjadi kunci publik dan privat. User dapat memilih apakah kunci dibangkit secara acak atau memilih mengikuti proses pembangkitan (dalam hal ini submenu diberikan agar user lebih mudah melakukan pembangkitan kunci) dimana angka dibangkit melalui angka-angka prima yang dapat dipilih sndiri oleh user. Tampilan pembangkitan kunci dapat dilihat pada gambar 3.15 dibawah.
Gambar 3.15 : Tampilan Pembangkitan Kunci
Komponen yang dipakai untuk membangun antarmuka halaman menu enkripsi kriptografi RSA seperti pada gambar 3.15 dapat dilihat pada tabel 3.7 berikut.
1
2
3
4
5
7
6
8
9
10
11
12
13
14
15
16
No Tipe Nama Label Keterangan
1 label Label1 - Judul Form generate Kunci
2 label Label3 Primes
Generate Judul
3 Label Label4 Prime 1 (p) Label judul prima 1 4 Label Label5 Prime 2(q) Label judul prima 2
5 Label p - Label nilai prima p
6 Label q - Label nilai prima
7 checkbox Chexkbox 2 Random Tombol untuk random prima p 8 checkbox Checkbox 1 Random Tombol untuk random prima q
9 Button btnGenerate Generate!
Tombol untuk memulai proses generate nilai kunci publik (e) dan kunci privat (d)
10 label Label6 Modulo (N) Label judul modulo (n) 11 Label Label7 Public Key (e) Label judul public key
12 Label Label8 Private Key (d) Label judul private key
13 Label edN - Label informasi nilai modulo
14 Label PuK2 - Label informasi nilai kunci
Publik (e)
15 Label PrK2 - Label informasi nilai kunci
Privat (d)
16 Button Button2 Finish
Mengakhiri proses pembangkitan kunci dan menyimpan nilai yang telah dibangkitkan
17 Progressbar PB1 - Komponen yang digunakan
sebagai indikator proses
Tabel 3.7 : Rincian Rancangan Halaman Pembangkit Kunci Kriptografi RSA
diperoleh nilai p dan q). Setelah proses pambangkitan selesai dilakukan, dengan mengklik tombol Finish maka nilai kunci publik dan kunci privat akan ter-generate ke modul utama sehingga tahap selanjutnya dapat dilakukan.
Tahap selanjutnya adalah memasukkan plaintext yang akan dienkripsi dan nama dan lokasi file ouput ciphertext yang akan dihasilkan setalah dilakukanya proses enkripsi. Output dari proses ini adalah sebuah berkas dengan format encrypted file
[image:57.612.171.477.358.568.2](.enc). Setelah itu maka akan dilanjutkan ke proses berikutnya yaitu proses enkripsi. Saat user mengklik tombol ”push to encrypt” maka akan menampilkan data informasi tentang seluruh parameter yang telah diperoleh. Sehingga dapat menjadi pertinggalan kriptografer apabila ada kesalahan. proses enkripsi dilakukan dengan tahap-tahap enkripsi yang sudah dijelaskan sebelumnya. Tampilan menu enkripsi dapat digambarkan pada gambar 3.16 berikut.
Gambar 3.16 : Tampilan Halaman Menu Input Plaintext dan Ciphertext RSA
Komponen yang dipakai untuk membangun antarmuka halaman menu Input
Plaintext dan Ciphertext kriptografi RSA seperti pada gambar 3.16 dapat dilihat pada tabel 3.8 berikut.
1
2
3
4
9 5
7 6
8
No Tipe Nama Label Keterangan 1 label Label9 Plaintext dan
Ciphertext
Judul
2
Label Label6 Searching
Plaintext and ciphertext location
Label instruksi menu dekripsi
3 Label Label10 Plaintext Label judul plainteks 4 label Label7 Ciphertext Label judul cipherteks
5 edit Plaintext1 - Komponen edit informasi tentang plainteks
6 Label Label11 Filename Label informasi nama berkas pada kotak plaintext
7 edit Ciphertext1 - Komponen edit untuk informasi tentang ciphertext
8 Label Label12 Filename Label informasi nama berkas pada kotak ciphertext
9 Label S1 Search Label yang berfungsi sebagai
tombol untuk searching Plaintext
10 label S2 search Label yang berfungsi sebagai
[image:58.612.122.527.77.476.2]tombol untuk searching ciphertext
Gambar 3.17 : Tampilan Halaman Data Information enkripsi RSA
Komponen yang dipakai untuk membangun antarmuka Data Information
kriptografi RSA seperti pada gambar 3.17 dapat dilihat pada tabel 3.9 berikut.
No Tipe Nama Label Keterangan
1 Label Label2 Ecnryption Data
Information Judul Form Data Information
2 Label Label4 Modulo (n) Label judul modulo 3 Label Label3 Public key (e) Label judul kunci publik 4 Label Label5 Private key (d) Label judul kunci privat 5 Label Label6 Plaintext filename Label judul nama plainteks
6 Label Im - Label informasi modulo
7 Label IPuK - Label informasi kunci publik
8 Label IPrK - Label informasi kunci privat
9 Label Iplaintext - Label informasi nama plainteks 10 Label ICiphertext - Label informasi nama cipherteks
11 Button Button2 x Tombol untuk membatalkan dan
kembali ke menu sebelumnya 12 Button enkripsi Save dan encrypt
now
Tombol untuk memulai proses enkripsi dan menyimpan data 13 label Label7 Ciphertext filename Label judul nama cipherteks
Tabel 3.9 : Rincian Rancangan Halaman D