Implementasi Contra Harmonic Mean Filter Untuk Mereduksi Noise Pada Citra Digital

(1)

LISTING PROGRAM

1. Menu

function varargout = MENU(varargin) % MENU M-file for MENU.fig

% MENU, by itself, creates a new MENU or raises the existing

% MENU('CALLBACK',hObject,eventData,handles,...) calls the local

% applied to the GUI before MENU_OpeningFunction gets called. An

% unrecognized property name or invalid value makes property application

% See also: GUIDE, GUIDATA, GUIHANDLES

% Edit the above text to modify the response to help MENU

% Last Modified by GUIDE v2.5 13-Mar-2014 07:15:03

% Begin initialization code - DO NOT EDIT gui_Singleton = 1; if nargin && ischar(varargin{1})

gui_State.gui_Callback = str2func(varargin{1}); end

if nargout

[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); else

gui_mainfcn(gui_State, varargin{:}); end

% End initialization code - DO NOT EDIT

% --- Executes just before MENU is made visible.

(2)

% hObject handle to figure

% eventdata reserved - to be defined in a future version of MATLAB

% handles structure with handles and user data (see GUIDATA) % varargin command line arguments to MENU (see VARARGIN)

% Choose default command line output for MENU handles.output = hObject;

% Update handles structure guidata(hObject, handles);

% UIWAIT makes MENU wait for user response (see UIRESUME) % uiwait(handles.figure1);

% --- Outputs from this function are returned to the command line.

function varargout = MENU_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see

VARARGOUT);

% handles structure with handles and user data (see GUIDATA)

% Get default command line output from handles structure varargout{1} = handles.output;

function mnuKomp_Callback(hObject, eventdata, handles) % hObject handle to mnuKomp (see GCBO)

% handles structure with handles and user data (see GUIDATA) NoiseRemove

% ---

function Untitled_1_Callback(hObject, eventdata, handles) % hObject handle to Untitled_1 (see GCBO)

% ---

function mnuKeluar_Callback(hObject, eventdata, handles) % hObject handle to mnuKeluar (see GCBO)

% handles structure with handles and user data (see GUIDATA) close

(3)

function figure1_CreateFcn(hObject, eventdata, handles) % hObject handle to figure1 (see GCBO)

% handles empty - handles not created until after all CreateFcns called

% --- Executes during object creation, after setting all properties.

function axes1_CreateFcn(hObject, eventdata, handles) % hObject handle to axes1 (see GCBO)

% ---

function Abt_Callback(hObject, eventdata, handles) % hObject handle to Abt (see GCBO)

function mnuHelp_Callback(hObject, eventdata, handles) % hObject handle to mnuHelp (see GCBO)

% handles structure with handles and user data (see GUIDATA) Help

2. Reduksi Noise

function varargout = NoiseRemove(varargin) % NOISEREMOVE M-file for NoiseRemove.fig

% NOISEREMOVE, by itself, creates a new NOISEREMOVE or raises the existing

% NOISEREMOVE('CALLBACK',hObject,eventData,handles,...) calls the local

% function named CALLBACK in NOISEREMOVE.M with the given input arguments.

%

% NOISEREMOVE('Property','Value',...) creates a new NOISEREMOVE or raises the

% existing singleton*. Starting from the left, property value pairs are

(4)

% stop. All inputs are passed to NoiseRemove_OpeningFcn via varargin.

% Edit the above text to modify the response to help NoiseRemove

if nargout

% --- Executes just before NoiseRemove is made visible. function NoiseRemove_OpeningFcn(hObject, eventdata, handles, varargin)

% This function has no output args, see OutputFcn. % hObject handle to figure

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to NoiseRemove (see VARARGIN)

% Choose default command line output for NoiseRemove handles.output = hObject;

% UIWAIT makes NoiseRemove wait for user response (see UIRESUME) % uiwait(handles.figure1);

% --- Outputs from this function are returned to the command line. function varargout = NoiseRemove_OutputFcn(hObject, eventdata, handles)

% varargout cell array for returning output args (see VARARGOUT); % hObject handle to figure

(5)

% --- Executes on button press in cmdLoad.

function cmdLoad_Callback(hObject, eventdata, handles) % hObject handle to cmdLoad (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) global S;

%proyek=guidata(gcbo);

[FileName,PathName]=uigetfile({'*.bmp;*.jpg'},' Pilih file citra'); if isequal (FileName,0)

%errordlg('Error ..!','Tidak ada image yang dipilih'); return;

else

S=imread([PathName,FileName]); lebar=size(S,2);

tinggi=size(S,1);

set (handles.txtNmFile,'string',fullfile(PathName,FileName)); set (handles.txtLebar,'string',num2str(lebar));

set (handles.txtTinggi,'string',num2str(tinggi)); axes(handles.axes1);

imshow(S), title('Citra Asli'); end

% --- Executes on button press in cmdProses.

function cmdProses_Callback(hObject, eventdata, handles) % hObject handle to cmdProses (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) global F;

global G;

%global PNoise;

%if isequal (PNoise,0)

% errordlg('Error ..!','Probabilitas noise belum diinput'); % return;

%else

% disp PNoise;

% errordlg('Ok ..!','Probabilitas noise ok'); [m n]=size(F);

(6)

% --- Executes on button press in cmdClear.

function cmdClear_Callback(hObject, eventdata, handles) % hObject handle to cmdClear (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)

% --- Executes on button press in cmdQuit.

function cmdQuit_Callback(hObject, eventdata, handles) % hObject handle to cmdQuit (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) close

% --- Executes on button press in pushbutton5.

function pushbutton5_Callback(hObject, eventdata, handles) % hObject handle to pushbutton5 (see GCBO)

% --- Executes on button press in cmdSave.

function cmdSave_Callback(hObject, eventdata, handles) % hObject handle to cmdSave (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) global G;

global mmed;

proyek=guidata(gcbo);

[namafile,direktori]=uiputfile({'*.jpg';'*.*'},' Save citra hasil'); if isequal (namafile,0)

(7)

else

set (handles.axes3); %H = uint8(G);

H = uint8(mmed);

%imwrite(G,strcat(direktori,namafile)); imwrite(H,strcat(direktori,namafile)); end

function txtLebar_Callback(hObject, eventdata, handles) % hObject handle to txtLebar (see GCBO)

% Hints: get(hObject,'String') returns contents of txtLebar as text % str2double(get(hObject,'String')) returns contents of txtLebar as a double

% --- Executes during object creation, after setting all properties. function txtLebar_CreateFcn(hObject, eventdata, handles)

% hObject handle to txtLebar (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles empty - handles not created until after all CreateFcns called

% Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER.

if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))

set(hObject,'BackgroundColor','white'); end

function txtTinggi_Callback(hObject, eventdata, handles) % hObject handle to txtTinggi (see GCBO)

% Hints: get(hObject,'String') returns contents of txtTinggi as text % str2double(get(hObject,'String')) returns contents of

txtTinggi as a double

% --- Executes during object creation, after setting all properties. function txtTinggi_CreateFcn(hObject, eventdata, handles)

% hObject handle to txtTinggi (see GCBO)

% --- Executes on button press in cmdNoise.

function cmdNoise_Callback(hObject, eventdata, handles) % hObject handle to cmdNoise (see GCBO)

(8)

% handles structure with handles and user data (see GUIDATA) %F = imnoise(S,'salt & pepper',0.1);

F = imnoise(S,'salt & pepper',PNoise); F = im2double(F);

axes(handles.axes2);

imshow(F), title('Citra Noise');

function txtPNoise_Callback(hObject, eventdata, handles) % hObject handle to txtPNoise (see GCBO)

% Hints: get(hObject,'String') returns contents of txtPNoise as text % str2double(get(hObject,'String')) returns contents of

txtPNoise as a double

% --- Executes during object creation, after setting all properties. function txtPNoise_CreateFcn(hObject, eventdata, handles)

% hObject handle to txtPNoise (see GCBO)

% --- Executes on button press in cmdProses1.

function cmdProses1_Callback(hObject, eventdata, handles) % hObject handle to cmdProses1 (see GCBO)

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) global S;

global F; global mmed;

(9)

% matriks akhir setelah di filter

% menampilkan citra grayscale dengan range 0-255

%figure, imshow(mmed,[0 255]); title('Citra Hasil Filter'); %warning on;

%imshow(mmed), title('Citra Hasil Noise Remover'); imshow(mmed,[0 255]); title('Citra Hasil Filter');

function varargout = Help(varargin) % HELP M-file for Help.fig

(10)

% HELP('CALLBACK',hObject,eventData,handles,...) calls the % existing singleton*. Starting from the left, property value pairs are

% applied to the GUI before Help_OpeningFunction gets called. An

% Edit the above text to modify the response to help Help

if nargout

% --- Executes just before Help is made visible.

function Help_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to Help (see VARARGIN)

% Choose default command line output for Help handles.output = hObject;

(11)

% --- Outputs from this function are returned to the command line. function varargout = Help_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hObject handle to figure

% --- Executes during object creation, after setting all properties. function figure1_CreateFcn(hObject, eventdata, handles)

% hObject handle to figure1 (see GCBO)

4. About

function varargout = About(varargin) % ABOUT M-file for About.fig

% ABOUT, by itself, creates a new ABOUT or raises the existing

% ABOUT('CALLBACK',hObject,eventData,handles,...) calls the local

% function named CALLBACK in ABOUT.M with the given input arguments.

%

% ABOUT('Property','Value',...) creates a new ABOUT or raises the

% existing singleton*. Starting from the left, property value pairs are

% applied to the GUI before About_OpeningFunction gets called. An

% Edit the above text to modify the response to help About

% Begin initialization code - DO NOT EDIT gui_Singleton = 1;

(12)

'gui_LayoutFcn', [] , ... 'gui_Callback', []); if nargin && ischar(varargin{1})

if nargout

% --- Executes just before About is made visible.

function About_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.

% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to About (see VARARGIN)

% Choose default command line output for About handles.output = hObject;

function varargout = About_OutputFcn(hObject, eventdata, handles) varargout{1} = handles.output;

imshow('D:\TA-USU-2014\NITIKA\Program\logoUSU.jpg');

% --- Executes during object creation, after setting all properties. function figure1_CreateFcn(hObject, eventdata, handles)

% hObject handle to figure1 (see GCBO)

(13)

Basuki, A. 2005. Pengolahan Citra Digital Menggunakan Visual Basic. Jakarta: Penerbit Graha Ilmu.

Firdausy, K., Sutikno, T. & Ary, O.P. 2007, Analisis Unjuk Kerja Metode Smoothing Image dengan Tapis Mean, Median, Modus, dan Gaussian.

Gunara, A., Tritoasomoro, I.I & Raharjo, J. 2007. Analisa Perbandingan Reduksi Noise Pada Citra Antara Discrete Wavelet Transform (DWT) Dengan Dual-Tree Complex Wavelet Transform (DTCWT). Seminar Nasional Sistem dan Informatika 2007: Bali, 16 November 2007. Departemen Teknik Elektro Sekolah Tinggi Teknologi Telkom Bandung–Bandung.

Jannah, A.2008. Analisis Perbandingan Metode Filter Gaussian, Mean dan Median terhadap Reduksi Noise Salt dan Peppers.

Munir, R. 2004. Pengolahan Citra Digital dengan Pendekatan Algoritmik, Bandung: Penerbit Informatika.

Murinto, Aribowo, E & Syazali, R. 2007. Analisis Perbandingan Metode Intensity Filtering Dengan Metode Frequency Filtering Sebagai Reduksi Noise Pada Citra Digital. Seminar Nasional Aplikasi Teknologi Informasi 2007 (SNATI 2007) ISSN: 1907-5022 Yogyakarta, 16 Juni 2007.

Murni, A. 2002. Pengantar Pengolahan Citra, Elex Media Komputindo.

Prasetyo, E. 2011. Pengolahan Citra Digital dan Aplikasinya menggunakan

MATLAB.Yogyakarta. Penerbit: ANDI.

Putra, D. 2010. Pengolahan Citra Digital. Yogyakarta. Penerbit: ANDI.

Somasundaram & Pritha N.A. 2010. Performance Evaluation of Arithmetic, Geomatric and Contra Harmonic Mean Filter for Image Denoising. UGC Sponsered National Conference of Emerging Computing Paradigms Departement Computer Science Dindigul India.

Sulistyo, W., Bech, Y.R. & Frans, F.Y. 2009. Analisis Penerapan Metode Median Filter Untuk Mengurangi Noise Pada Citra Digital. Konferensi Nasional Sistem dan Informatika 2009; Bali, November 14, 2009.

(14)

BAB 3

ANALISIS DAN PERANCANGAN

3.1 Analisis

Reduksi noise menggunakan algoritma Contra Harmonic Mean Filter adalah proses

filtering untuk mengurangi noise dari citra dengan tahap-tahap sebagai berikut: a. Membaca nilai piksel.

b. Menghitung nilai RGB piksel. c. Menghitung nilai grayscale piksel. d. Penambahan noise pada citra grayscale.

e. Perhitungan Nilai piksel pada blok 3 x 3 piksel dengan filter Contra Harmonic Mean.

f. Pemetaan hasil perhitungan piksel ke citra hasil g. Perhitungan nilai MSE.

Proses pertama adalah membaca nilai piksel citra untuk mendapatkan data

bitmap untuk menghitung nilai RGB dan pembentukan citra grayscale. Pada proses penambahan noise, dihasilkan satu data citra ber-noise yang digunakan sebagai data

input untuk proses pemilihan matriks input. Pada proses ini matriks citra noise yang awalnya berukuran 2 dimensi (memiliki baris dan kolom) akan dipecah dan diambil per kolom. Sehingga proses ini akan menghasilkan data berupa matriks yang berukuran 1 kolom dan n baris.

Data ini akan digunakan sebagai input untuk proses selanjutnya yaitu perhitungan dengan filter yang digunakan. Hal ini dilakukan hingga semua piksel habis diproses untuk pembentukan citra output. Data pada setiap proses akan berukuran 1 dimensi, sehingga setiap kolom disimpan pada suatu matriks temporary

(15)

3.1.1 Membaca Nilai Piksel

Pada citra digital 24-bit tidak terdapat palet RGB, karena nilai RGB langsung diuraikan dalam data bitmap. Setiap elemen data bitmap panjangnya 3 byte, masing-masing byte menyatakan komponen R, G, dan B. Data bitmap pada citra dapat dilihat pada Gambar 3.1.

Gambar 3.1 Data Bitmap pada Citra

Pada citra bitmap 24-bit, tiap pikselnya mengandung 24-bit kandungan warna atau 8-bit untuk masing-masing warna dasar (R, G, dan B), dengan kisaran nilai kandungan antara 0 (00000000) sampai 255 (11111111) untuk tiap warna. Pada contoh format citra 24-bit di atas data pertama adalah header yang berisi informasi nama file, jenis format dan dimensi citra. Di bawah data bitmap terdapat piksel pertama mempunyai R = 10010000 (biner), G = 01011010 (biner), B = 011110001 (biner).

Bagian terkecil sebuah citra adalah piksel yang memiliki nilai intensitas hasil kuantisasi peralatan digital. Citra warna memiliki tiga komponen warna yang setiap komponen warna menggunakan penyimpanan 8 bit atau 1 byte. Berarti jumlah bit dalam 1 piksel adalah sebanyak 3 x 8 bit = 24 bit. Jadi untuk menghitung jumlah piksel sebuah citra dilakukan dengan membagi nilai intensitas citra dengan 24 bit. Representasi nilai piksel pada citra warna dapat dilihat pada Gambar 3.2.

Gambar 3.2 Representasi Piksel pada Citra <Header>

(16)

Nilai intensitas citra disimpan dalam data bitmap dalam bentuk nilai biner dengan nilai antara 0 dan 1. Jadi jumlah pikselnya adalah jumlah kelipatan 24 bit. Misalnya sebuah citra dengan nilai intensitas di atas adalah:

111100001111000011111110001100001111000011111111111100001111000011111 000111100001111000011111001111100001111000011111010101100001111000011 111111111100001111000011111111111100001111000011010111111110000111100 001100000111110000111100001111011000111100001111000011111111111100001 111000011111000011100001111000011110101011110000111100001111000110111 111000011110000111111111111000011110000111010111111110000111100001111 1111 dan seterusnya.

Nilai 111100001111000011111111 = 24 bit mewakili 1 piksel dari citra.

Jika jumlah bit citra di atas adalah 1.800.000 bit, maka jumlah piksel-nya adalah 1.800.000/24 bit = 75.000 piksel. Pada reduksi noise ini dilakukan per blok citra dengan ukuran per bloknya adalah 3 x 3 piksel atau 9 piksel, maka jumlah blok adalah 75.000/9 = 8.333 blok atau digenapkan menjadi 8.000 blok.

3.1.2 Menghitung Nilai RGB

Proses reduksi noise dilakukan per blok citra yang terdiri dari 9 piksel (3x3), maka citra pada Gambar 3.2 di atas dilakukan pembagian piksel dalam ukuran 3 x 3, di mana piksel yang berada di posisi tengah merupakan pikselyang akan diuji. Maka penghitungan nilai komponen warna RGB-nya dilakukan dalam 9 piksel seperti pada Gambar 3.3.

1 2 3

4 5 6

7 8 9

(17)

Misalnya nilai piksel 1 dalam biner 24 bit adalah: Piksel 1 f(0,0) = 111100001111000011111111 Piksel 2 f(0,1) = 100000011110000111110000 Piksel 3 f(0,2) = 110000001111000011111111 Piksel 4 f(1,0) = 101110011110000111110000 Piksel 5 f(1,1) = 111100001111110011110011 Piksel 6 f(1,2) = 110110011110000101110010 Piksel 7 f(2,0) = 010100001111000011100111 Piksel 8 f(2,1) = 100000011110000111110111 Piksel 9 f(2,2) = 101110111111000010011100

Untuk mendapatkan masing-masing nilai Red, Green dan Blue (RGB) dihitung dengan rumus sebagai berikut:

Nilai Red = c and 255 ……….. (3.1) Nilai Green = (c and 65280) / 256 ……….. (3.2) Nilai Blue = ((c and 16711680) / 256)/256 ……….. (3.3)

Dimana c adalah nilai piksel citra Perhitungan Nilai Red, Green, Blue:

1. Nilai piksel(0,0) adalah 111100001111000011111111 Nilai Red = 111100001111000011111111 and 11111111

= 11111111 dalam biner = 255 (desimal)

Nilai Green = (111100001111000011111111 and 1111111100000000)/ 100000000 = 11110000 (biner) = 240 (desimal)

Nilai Blue = ((111100001111000011111111 and 111111110000000000000000)/ 100000000)/100000000 = 11110000 = 240 (desimal)

Sehingga diperoleh nilai Red, Green, Blue piksel (0,0):

Red = 11110001 = 255 (desimal)

Green = 10110100 = 240 (desimal)

(18)

2. Nilai piksel (0,1) adalah 100000011110000111110000 (24 bit). Nilai Red = 100000011110000111110000 and 11111111

Nilai Green = (100000011110000111110000 and 1111111100000000)/ 100000000 = 11100001 (biner) = 225 (desimal)

Nilai Blue = ((100000011110000111110000 and 111111110000000000000000)/ 100000000)/100000000 = 10000001 = 129 (desimal)

Red = 11110001 = 240 (desimal)

Green = 10110100 = 225 (desimal)

Blue = 10010000 = 129 (desimal)

Nilai Green = (110000001111000011111111 and 1111111100000000)/ 100000000

= 11110000 (biner) = 240 (desimal) Nilai Blue = ((110000001111000011111111 and

111111110000000000000000)/100000000)/100000000 = 11000000 = 192 (desimal)

Red = 11110001 = 255 (desimal)

Green = 10110100 = 240 (desimal)

Blue = 10010000 = 192 (desimal)

(19)

= 11100001 (biner) = 225 (desimal) Nilai Blue = ((101110011110000111110000 and 111111110000000000000000)/

100000000)/100000000 = 10111001 = 185 (desimal) Sehingga diperoleh nilai Red, Green, Blue piksel (1,0):

Red = 11110001 = 240 (desimal)

Green = 10110100 = 225 (desimal)

Blue = 10010000 = 185 (desimal)

5. Nilai piksel (1,1) adalah 111100001111110011110011

Nilai Red = 111100001111110011110011 and 11111111 = 11110011 dalam biner = 243 (desimal)

Nilai Green = (111100001111110011110011 and 1111111100000000)/

100000000

= 11111100 (biner) = 252 (desimal) Nilai Blue = ((111100001111110011110011 and 111111110000000000000000)/

Red = 11110001 = 243 (desimal)

Green = 10110100 = 252 (desimal)

Blue = 10010000 = 249 (desimal)

Nilai Green = (110110011110000101110010 and 1111111100000000) / 100000000

111111110000000000000000)/

(20)

Red = 11110001 = 114 (desimal)

Green = 10110100 = 225 (desimal)

Blue = 10010000 = 217 (desimal)

Nilai Green = (010100001111000011100111 and 1111111100000000)/

100000000

111111110000000000000000)/

Red = 11110001 = 231 (desimal)

Green = 10110100 = 240 (desimal)

Blue = 10010000 = 80 (desimal)

Nilai Green = (101110110011000011111100 and 1111111100000000)/

100000000

111111110000000000000000)/ 100000000)/100000000

= 10111011 = 187 (desimal)

Red = 11110001 = 252 (desimal)

Green = 10110100 = 48 (desimal)

(21)

Nilai Green = (101110111111000010011100 and 1111111100000000)/ 100000000

111111110000000000000000)/

100000000)/100000000 = 10111011= 187 (desimal) Sehingga diperoleh nilai Red, Green, Blue piksel (2,2):

Red = 11110001 = 156 (desimal)

Green = 10110100 = 240 (desimal)

Blue = 10010000 = 187 (desimal)

Selanjutnya nilai Red, Green, Blue semua piksel pada citra noise blok 1 dimasukkan ke dalam matriks seperti pada Gambar 3.4.

255,240,240 240,225,129 255,240,192 240,225,185 243,252,249 114,225,217 231,240,80 252,48,187 156,240,187

Gambar 3.4 Matriks Nilai Red, Green, Blue Citra Noise Blok 1

Matriks citra pada Gambar 3.4 adalah hasil dari perhitungan semua nilai red, green dan blue citra Noise pada Gambar 3.3.

3.1.3 Menghitung Nilai Grayscale

Nilai Red, Green, Blue per piksel pada Gambar 3.4 di atas, selanjutnya dikonversi ke nilai grayscale dengan cara mencari nilai rata-rata per piksel.

f₀ (x,y) = �fR(x,y)+fG(x,y)+fB(x,y)

(22)

dimana

fR adalah nilai komponen red

fG adalah nilai komponen green

fB adalah nilai komponen blue

Nilai grayscale dihitung dengan menggunakan persamaan (3.4) sebagai berikut: Piksel (0,0) = (255,240,240) = (255+240+240)/3 = 198

Piksel (0,1) = (240,225,129) = (240+225+129)/3 = 245 Piksel (0,2) = (255,240,192) = (255+240+192)/3 = 229 Piksel (1,0) = (240,225,185) = (240+225+185)/3 = 217 Piksel (1,1) = (243,252,249) = (243+252+249)/3 = 248 Piksel (1,2) = (114,225,217) = (114+225+217)/3 = 185 Piksel (2,0) = (231,240,80) = (231+240+80)/3 = 184 Piksel (2,1) = (252,48,187) = (252+48+187)/3 = 162 Piksel (2,2) = (156,240,187) = (156+240+187)/3 = 194

Nilai grayscale semua piksel pada citra noise blok 1 selanjutnya dimasukkan ke dalam matriks nilai grayscale seperti pada Gambar 3.5.

198 245 229 217 248 185 184 162 194

Gambar 3.5 Matriks Nilai Grayscale Citra Noise Blok 1

Matriks citra pada Gambar 3.5 adalah hasil dari perhitungan grayscale semua nilai

red, green dan blue citra Noise pada Gambar 3.4.

3.1.4 Penambahan Noise

(23)

penambahan noise pada citra pada Gambar 3.5 dengan mengganti nilai piksel secara acak dengan nilai 0 dan 255 seperti pada Gambar 3.6.

198 245 229 198 245 229 217 248 185 217 248 0 184 162 194 0 162 194

Gambar 3.6 Matriks Citra Hasil Penambahan Noise

3.1.5 Contra Harmonic MeanFilter

Contra Harmonic Mean Filter bekerja dengan baik pada tipe salt noise, tetapi tidak untuk pepper noise. Filter ini juga bekerja dengan baik pada jenis noise yang lain seperti noise Gaussian (Prasetyo, 2011). Filter ini dirumuskan dengan:

F(x,y)

=

∑(�,�)∈��

(�,�) �+1

∑(�,�)∈�_��(�,�)�

... (3.5)

dimana:

(s,t) = kordinat windowsub-image

Sxy = region citra

g(s,t) = nilai citra terkorupsi pada kordinat sub-image

Q = order filter

Citra yang akan diolah adalah seperti pada citra Gambar 3.5 diatas dengan menggunakan persamaan 3.5.

Bila Q=1, maka:

F (x,y) = 1982+2452+2292+2172+2482+02+02+1622+1942

198+245+229+217+248+0+0+162+194 ≈ 217.10 = 217

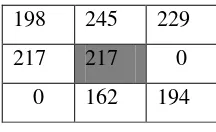
Sehingga bagian dari citra ini berubah menjadi matriks seperti pada Gambar 3.7.

198 245 229

217 217 0

0 162 194

Gambar 3.7 Matriks Citra Hasil Penambahan Noise 0

(24)

Proses perhitungan nilai piksel untuk blok citra ke n dilakukan sama dengan perhitungan di atas sehingga diperoleh citra yang lebih baik hasil reduksi noise.

3.1.6 Perhitungan Nilai Mean Squared Error (MSE)

MSE citra hasil reduksi noise adalah rata-rata kuadrat nilai kesalahan antara citra asli dengan citra hasil reduksi noise dengan rumus sebagai berikut:

MSE = 1

�� ∑ ∑� �[�(�,�)− �′(�,�)] 2

Dimana:

X = lebar citra dalam piksel

Y = tinggi citra dalam piksel

I = nilai piksel citra sebelum reduksi noise I’ = nilai piksel citra sesudah reduksi noise

Perhitungan nilai MSE menggunakan matriks citra Gambar 3.8 dan 3.9.

198 245 229 xx

217 248 0 xx

0 162 194 xx

Gambar 3.8 Matriks Citra Sebelum Reduksi Noise

198 245 229 xx

217 217 0 xx

0 162 194 xx

(25)

MSE = 1

�� ∑ ∑� �[�(�,�)− �′(�,�)] 2

MSE = 1

3�3 ∑ ∑3 3[�(�,�)− �′(�,�)] 2

MSE (0.0) = 1/9 (198 -198)2 = 1/9 (0)2 MSE (0.0) = 0

MSE (0.1) = 1/9 (217 -217)2 = 1/9 (0)2 MSE (0.1) = 0

MSE (0.2) = 1/9 (184 -0)2 = 1/9 (184)2 MSE (0.2) = 3762

MSE (1.0) = 1/9 (245 -245)2 = 1/9 (0)2 MSE (1.0) = 0

MSE (1.1) = 1/9 (248 -217)2 = 1/9 (961)2 MSE (1.1) = 106.77

MSE (1.2) = 1/9 (162 -160)2 = 1/9 (0)2 MSE (1.2) = 0

MSE (2.0) = 1/9 (229 -229)2 = 1/9 (0)2 MSE (2.0) = 0

MSE (2.1) = 1/9 (185 -0)2 = 1/9 (0)2 MSE (2.1) = 3803

MSE (2.2) = 1/9 (194 -194)2 = 1/9 (0)2 MSE (2.2) = 0

MSE Total = 3762+106+3803= 7.671 3.2 Perancangan Sistem

Berdasarkan analisa yang penulis lakukan terhadap algoritma Contra HarmonicMean Filter untuk mereduksi noise pada sebuah citra digital, penulis melakukan perancangan terhadap perangkat lunak yaitu:

1. Perancangan Flow Chart Reduksi NoiseContra Harmonic Mean Filter

2. Perancangan Data Flow Diagram Reduksi Noise Contra Harmonic Mean Filter

(26)

3.2.1 Flow Chart Reduksi NoiseContra HarmonicMean Filter

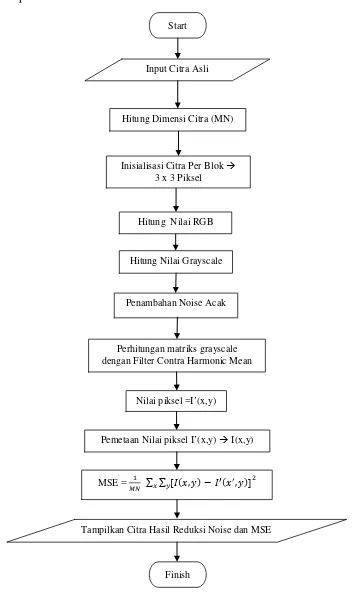
Flow Chart Reduksi noise dengan algoritma Contra Harmonic Mean Filter dapat dilihat pada Gambar 3.10.

Gambar 3.10 Flowchart Proses Reduksi Noise Contra Harmonic Mean Filter

Start

Input Citra Asli

Hitung Nilai Grayscale

Perhitungan matriks grayscale dengan Filter Contra Harmonic Mean

MSE = 1

�� ∑ ∑� �[�(�,�)− �′(�′,�)] 2

Penambahan Noise Acak

Tampilkan Citra Hasil Reduksi Noise dan MSE

Finish Hitung Nilai RGB Inisialisasi Citra Per Blok 

3 x 3 Piksel

Nilai piksel =I’(x,y)

(27)

3.2.2 Data Flow Diagram (DFD)

DFD merupakan suatu model logika aliran data atau proses yang dibuat untuk menggambarkan hubungan antara sistem dengan entitas luar dalam pengolahan data pada sistem. Pada sistem ini akan digunakan DFD Level 0 dan Level 1.

3.2.2.1 Data Flow Diagram Level 0 Reduksi Noise

DFD Level 0 Reduksi Noise merupakan diagram konteks yang menggambarkan seluruh input ke sistem atau output dari sistem. Data Flow Diagram Reduksi Noise

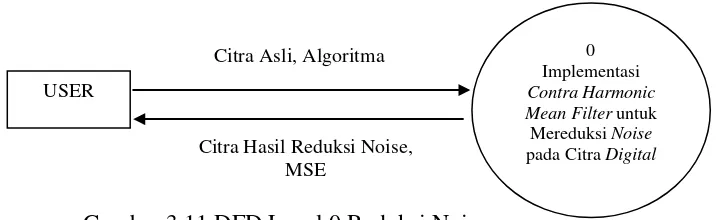
untuk level 0 dapat dilihat pada Gambar 3.11.

Gambar 3.11 DFD Level 0 Reduksi Noise

Pada diagram konteks atau DFD level 0 hanya terdiri dari satu proses yaitu Implementasi Contra Harmonic Mean Filter untuk Mereduksi Noise pada Citra

Digital. User menginputkan file citra asli bernoise ke dalam sistem dan diolah menghasilkan output citra yang tereduksi noise yang diberikan kepada user.

3.2.2.2 Data Flow Diagram Level 1 Reduksi Noise Contra Harmonic Mean Filter

Pada level ini, proses tunggal dari DFD Level 0 dipecah menjadi 9 proses yaitu proses Pembacaan Nilai Piksel Citra, Perhitungan nilai RGB, Perhitungan nilai

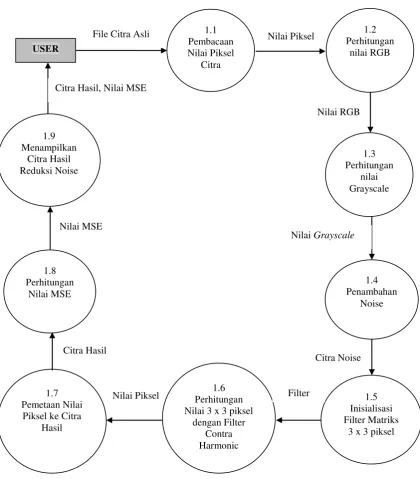
Grayscale, Penambahan Noise, Inisialisasi Filter Matriks 3 x 3 piksel, Perhitungan Nilai 3 x 3 piksel dengan Filter Contra Harmonic Mean, Pemetaan Nilai Piksel Ke Citra Hasil, Perhitungan MSE serta Menampilkan Citra Hasil Reduksi Noise. DFD Level 1 Reduksi Noise Contra Harmonic Mean Filter dapat dilihat pada Gambar 3.12.

USER

0 Implementasi

Contra Harmonic MeanFilter untuk

Mereduksi Noise

pada Citra Digital

Citra Asli, Algoritma

(28)

Gambar 3.12 DFD Level 1 Reduksi Noise Arithmetic Mean Filter

Pada Gambar 3.12, User menginputkan file citra dalam Proses Pembacaan Nilai Piksel, Perhitungan Nilai RGB, Perhitungan Nilai Grayscale. Setelah Perhitungan Nilai Grayscale dilakukan proses Penambahan Noise pada citra grayscale, Inisialisasi filter yang berisi matriks 3 x 3 piksel dengan nilai 1/9. Selanjutnya pemetaan nilai piksel tersebut ke citra ber-noise, perhitungan nilai MSE dan menampilkan citra hasil reduksi. Citra Hasil, Nilai MSE

(29)

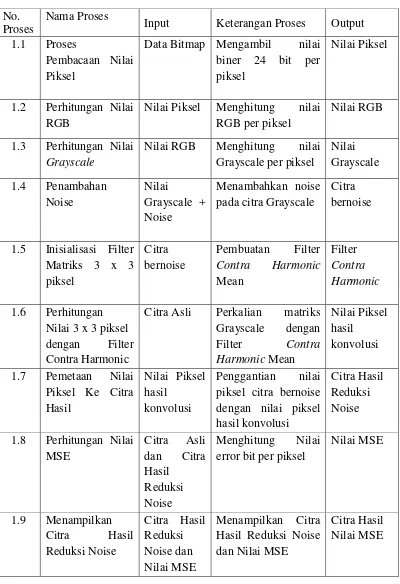
Proses-proses yang terjadi pada DFD level 1 dapat diuraikan dengan menggunakan spesifikasi proses pada Tabel 3.1.

Tabel 3.1 Spesifikasi Proses DFD Level 1 Reduksi Noise e Contra Harmonic Mean Filter

No. Proses

Nama Proses

Input Keterangan Proses Output 1.1 Proses

Pembacaan Nilai Piksel

Data Bitmap Mengambil nilai biner 24 bit per piksel

Nilai Piksel

1.2 Perhitungan Nilai RGB

Nilai Piksel Menghitung nilai RGB per piksel

Nilai RGB

1.3 Perhitungan Nilai

Grayscale

Nilai RGB Menghitung nilai Grayscale per piksel

1.5 Inisialisasi Filter Matriks 3 x 3

Citra Asli Perkalian matriks Grayscale dengan 1.7 Pemetaan Nilai

Piksel Ke Citra dengan nilai piksel hasil konvolusi

Citra Hasil Reduksi Noise 1.8 Perhitungan Nilai

MSE error bit per piksel

(30)

Tabel 3.2 Kamus Data Pada DFD Level 1 Reduksi Noise Contra HarmonicMean Filter

Nama Tipe Data Keterangan

Nilai piksel Long Nilai intensitas citra per piksel Nilai RGB Integer Nilai Warna citra per piksel Nilai Grayscale Integer Nilai keabu-abuan citra per piksel Nilai MSE Integer Jumlah error bit pada citra

3.2.3 Perancangan Antar Muka Program

Setelah melakukan analisa terhadap proses kerja dari reduksi noise, selanjutnya dilakukan perancangan terhadap antar muka yang akan digunakan sebagai media interaksi antara pengguna dan sistem yang dirancang. Perancangan antar muka perangkat lunak ini terdiri dari:

3.2.3.1 Rancangan Menu Utama

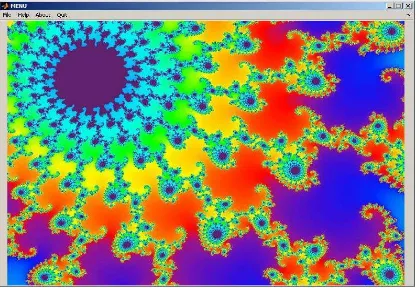
Rancangan Menu utama berfungsi untuk menampilkan judul skripsi serta menu pendukung perangkat lunak Reduksi Noise, Help serta About. Rancangan Menu Utama dapat dilihat pada Gambar 3.13.

Gambar 3.13 Menu Utama

(31)

3.2.3.2 Rancangan Reduksi Noise

Rancangan Reduksi Noise berfungsi untuk melakukan proses penghapusan noise pada citra digital yang di-input. Adapun bentuk rancangan dari Reduksi Noise ini seperti terlihat pada Gambar 3.14.

Gambar 3.14 Rancangan Reduksi Noise

3.2.3.3 Perancangan Pengujian

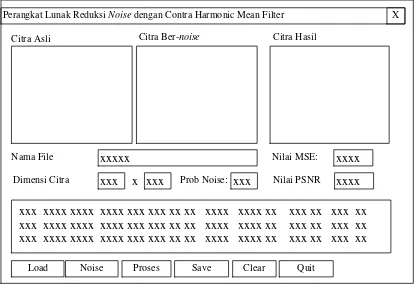
Perancangan Pengujian adalah rancangan yang menampilkan informasi hasil pengujian perangkat lunak reduksi noise yang dilakukan pada citra yang ber-noise. Rancangan Pengujian seperti paga Gambar 3.15.

Perangkat Lunak Reduksi Noise dengan Contra Harmonic Mean Filter X

Citra Asli Citra Ber-noise Citra Hasil

Dimensi Citra _xxx Prob Noise:

xxxxx Nilai MSE: _xxxx

Nama File

xxx xxxx xxxx xxxx xxx xxx xx xx xxxx xxxx xx xxx xx xxx xx xxx xxxx xxxx xxxx xxx xxx xx xx xxxx xxxx xx xxx xx xxx xx xxx xxxx xxxx xxxx xxx xxx xx xx xxxx xxxx xx xxx xx xxx xx

Load Proses Save Clear Quit

x xxx xxx Nilai PSNR _xxxx

(32)

HASIL PENGUJIAN No Nama Citra

Asli

Size Citra Nama Citra

Hasil

Size Citra MSE

Xx Xxxxxxxxxxxx Xxx Xxxxxxxxxxxxx Xxx Xxx

Gambar 3.15 Rancangan Pengujian

3.2.3.4 Rancangan About

Rancangan About berfungsi untuk menampilkan informasi mengenai profil penulis skripsi. Rancangan About seperti pada Gambar 3.16.

Gambar 3.16 Rancangan About

3.2.3.5 Rancangan Help

Rancangan Help berfungsi untuk menampilkan sekilas informasi mengenai tata cara penggunaan perangkat lunak reduksi noise. Rancangan Help seperti pada Gambar 3.17.

About X

IMPLEMENTASI CONTRA HARMONIC MEAN FILTER UNTUK MEREDUKSI NOISE PADA

CITRA DIGITAL

NITIKA

101421045

FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA

MEDAN 2014

(33)

Gambar 3.17 Rancangan Help

Help X

Tata Cara Pengoperasian Program Reduksi Noise

(34)

4.1 Implementasi

Implementasi Contra Harmonic Mean Filter untuk Mereduksi Noise pada Citra

Digital adalah tampilan hasil rancangan dari penulisan kode program dimulai dari program Menu Utama, File, Help dan About.

4.1.1 Tampilan Menu Utama

Tampilan Menu Utama merupakan tampilan yang muncul setelah menjalankan program Utama. Tampilan ini berisi judul skripsi, gambar latar serta tampilan menu. Tampilan Menu terdiri dari File, Help, About serta Quit. Pada menu File terdapat program reduksi noise dengan algoritma Contra Harmonic Mean Filter. Tampilan Menu Utama dapat dilihat pada Gambar 4.1.

(35)

4.1.2 Tampilan Reduksi Contra HarmonicMeanFilter

Tampilan Reduksi Contra Harmonic Mean Filter merupakan tampilan berguna untuk melakukan proses mereduksi noise dengan algoritma Contra Harmonic Mean Filter. Tampilan Reduksi Contra HarmonicMeanFilter dapat dilihat pada Gambar 4.2.

Gambar 4.2 Tampilan Reduksi Noise Contra HarmonicMeanFilter

(36)

4.1.3 Tampilan Help

Tampilan Help berfungsi untuk menampilkan penjelasan proses-proses yang terjadi pada proses reduksi noise. Tampilan Help dapat dilihat pada Gambar 4.3.

Gambar 4.3 Tampilan Help

4.1.4 Tampilan About

Tampilan About berfungsi untuk menampilkan keterangan tentang skripsi perbndingan reduksi noise dengan algoritma Contra Harmonic MeanFilter. Tampilan About dapat dilihat pada Gambar 4.4.

(37)

4.2 Hasil Pengujian

Pengujian reduksi noise dengan menggunakan algoritma Contra Harmonic Mean Filter dilakukan dengan variasi nilai probabilitas noise yaitu 0.01 %, 0.1 % dan 0.2 %.

4.2.1 Probabilitas Noise 0.01 %

Hasil pengujian kompresi citra untuk probabilitas noise 0.01 % dapat dilihat pada Gambar 4.5.

Gambar 4.5 Tampilan Hasil Pengujian dengan Probabilitas Noise 0.01 %

Keterangan: citra yang akan direduksi noisenya berdimensi 220 x 294 piksel dengan probabilitas noise 0.01 %. Hasil reduksi noise menghasilkan 3 citra hasil dengan nilai MSE adalah 1219.95, 1219.94 dan 1219.96 dengan nilai PSNR adalah 6.798, 6.798 dan 6.798.

(38)

Gambar 4.6 Tampilan Hasil Pengujian dengan Probabilitas Noise 0.1 %

Hasil pengujian kompresi citra untuk probabilitas noise 0.2 % dapat dilihat pada Gambar 4.7.

(39)

4.2.4 Daftar Hasil Pengujian Reduksi Noise

Daftar hasil pengujian reduksi noise adalah informasi yang menampilkan hasil reduksi noise antara lain adalah nama file citra yang akan direduksi noisenya, size, nama file citra hasil reduksi serta nilai PSNR. Daftar hasil pengujian reduksi noise dapat dilihat seperti pada Tabel 4.1.

Tabel 4.1 Tampilan Daftar Hasil Pengujian Reduksi Noise No Nama Citra Size

(Kb)

Nama Citra Hasil

Size (Kb)

PSNR

1 Gentong_1.jpg 79.2 GentongRed_1.jpg 31.5 6.798 2 Image3.jpg 5.20 Image3Red.jpg 10.9 7.632 3 LenaNoise.bmp 481 LenaRed.bmp 482 10.04 4 Paprica.jpg 12 PapricaRed.jpg 22.6 9.16 5 Doggy5.jpg 123 DoggyRed.jpg 26.6 9.01

Dari Tabel 4.1 citra hasil reduksi noise dapat dilihat sebagai berikut:

(40)

Image3.jpg Image3Red.jpg

LenaNoise.bmp LenaRed.bmp

Paprica.jpg PapricaRed.jpg

(41)

5.1 Kesimpulan

Setelah mengaplikasikan perangkat lunak Implementasi Contra Harmonic Mean Filter untuk mereduksi noise pada citra digital maka dapat disimpulkan bahwa perangkat lunak dapat melakukan reduksi noise pada citra digital dengan menampilkan tiga citra hasil reduksi noise dan nilai PSNR yang bervariasi rata-rata adalah 8.528.

5.2 Saran

(42)

BAB 2

LANDASAN TEORI

2.1 Definisi Pengolahan Citra

Pengolahan citra adalah pemrosesan citra, khususnya menggunakan komputer, menjadi citra yang kualitasnya lebih baik dan sesuai dengan keinginan pemakai. Pengolahan citra bertujuan memperbaiki kualitas citra agar mudah diinterpretasi oleh manusia atau mesin komputer (Munir, 2004).

Pengolahan citra adalah sebuah merupakan disiplin ilmu yang memplajari hal-hal yang berkaitan dengan perbaikan kualitas gambar (peningkatan kontras, transformasi warna, restorasi citra), transformasi gambar (rotasi, translasi, skala, transformasi geometrik), melakukan pemilihan citra cirri (feature images) yang optimal untuk tujuan analisis, melakukan proses penarikan informasi atau deskripsi objek atau pengenalan objek yang terkandung pada citra, melakukan kompresi atau reduksi data untuk tujuan penyimpanan data, transmisi data, dan waktu proses data. Input dari pengolahan citra adalah citra, sedangkan output-nya adalah citra hasil pengolahan (Sutoyo, 2009).

Sutoyo (2009) memaparkan bahwa teknik-teknik pengolahan citra mentransformasikan citra ke citra yang lain. Jadi masukannya adalah citra dan keluarannya juga citra, namun citra keluaran atau hasil mempunyai kualitas lebih baik dari pada citra masukan. Alur proses pengolahan citra dapat dilihat pada Gambar 2.1.

Gambar 2.1 Alur Proses pengolahan citra Citra Asli

Proses Pengolahan

Citra

(43)

2.1.1 Klasifikasi Pengolahan Citra

Menurut Sutoyo (2009), terdapat beberapa operasi di dalam pengolahan citra yang dapat diklasifikasi dalam beberapa jenis, antara lain:

1. Perbaikan Kualitas Citra (Image Enhancement)

Jenis operasi ini bertujuan untuk memperbaiki citra dengan cara memanipulasi parameter parameter citra. Dengan operasi ini, ciri-ciri khusus yang terdapat di dalam citra lebih ditonjolkan. Contoh-contoh perbaikan citra adalah:

a. Perbaikan kontras gelap atau terang.

b. Perbaikan tepian obyek (edge enchancement)

c. Penajaman citra (sharpening).

d. Pemberian warna semu (peseudocoloring). e. Penipisan derau (noise filtering).

2. Pemugaran Citra (Image restoration)

Operasi ini bertujuan untuk menghilangkan atau meminimumkan cacat pada citra. Tujuannya hmpir sama dengan operasi perbaikan citra, bedanya pada pemugaran citra penyebab degradasi gambar diketahui. Contoh operasinya adalah:

a. Penghilangan kesamaran (deblurring)

b. Penghilangan derau (noise)

3. Pemampatan Citra (Image Compression)

(44)

4. Segmentasi Citra (Image Segmentation)

Jenis operasi ini bertujuan untuk memecahkan suatu citra ke dalam beberapa segmen dengan suatu kriteria tertentu. Jenis operasi ini berkaitan erat dengan pengenalan pola.

5. Analisa Citra (Image Analysis)

Jenis operasi ini bertujuan menghitung besaran kuantitatif dari citra untuk menghasilkan deskripsinya. Teknik analisa citra mengekstraksi ciri-ciri tertentu membantu dalam identifikasi obyek. Proses segmentasi terkadang diperlukan untuk mengalokasi obyek yang diinginkan dari sekelilingnya. Contoh-contoh analisa citra antara lain:

a. Pendeteksi tepi obyek (edge detection) b. Ekstraksi batas (boundary)

c. Representasi daerah (region)

6. Rekonstruksi Citra (Image Reconstruction)

Jenis operasi ini bertujuan untuk membentuk ulang obyek dari beberapa citra hasil proyeksi. Opersi rekonstruksi citra banyak digunakan dalam dunia medis. Misalnya beberapa foto rontgen dengan sinar X digunakan untuk membentuk ulang gambar organ tubuh.

2.2 Citra Digital

Citra merupakan suatu signal digital yang dapat di observasi oleh sistem visual manusia. Ditinjau dari sudut pandang matematis, citra merupakan fungsi

(45)

2.2.1 Definisi Citra Digital

Beberapa definisi citra digital menurut para ahli dipaparkan sebagai berikut:

Menurut Sachs (2000), citra digital merupakan suatu gambar yang tersusun dari piksel, dimana tiap pixel merepresentasikan warna (tingkat keabuan untuk gambar hitam putih) pada suatu titik gambar.

Sedangkan menurut Fahmi (2007), citra digital adalah gambar dua dimensi yang dapat ditampilkan pada layar monitor komputer sebagai himpunan berhingga (diskrit) nilai

digital yang disebut dengan piksel (picture elements).

Fahmi (2007) menyatakan bahwa citra digital (diskrit) dihasilkan dari citra analog (kontinu) melalui digitalisasi. Digitalisasi citra analog terdiri atas penerokan (sampling) dan kuantisasi (quantization). Penerokan (sampling) adalah pembagian citra ke dalam elemen-elemen diskrit (piksel), sedangkan kuantisasi (quantization)

adalah pemberian nilai intensitas warna pada setiap piksel dengan nilai yang berupa bilangan bulat.

Gambar 2.2 Citra Digital

(46)

lebar atu lebar dikalikan dengan panjang. Salah satu contoh citra digital dapat dilihat pada Gambar2.2.

Citra digital yang berukuran N x M lazim dinyatakan dengan matriks yang berukuran N baris dan M kolom seperti pada Gambar 2.3

f(x,y)=

Gambar 2.3 Representasi citra digital dalam matriks N x M

Warna digital adalah kombinasi dari tiga warna primer yaitu (red), hijau (green), dan biru (blue) (RGB). Setiap warna dapat dispesifikasikan sebagai triplet nilai intensitas RGB, dengan setiap intensitas berkisar antara 0 sampai 255, yaitu:

Red : RGB (255, 0, 0) ……….………….………..………(2.2)

Green : RGB (0, 255, 0) .……….……….……… (2.3)

Blue : RGB (0, 0, 255) …..………. (2.4)

Dari nilai triplet RGB persamaan (2) sampai (4) di atas dapat dikonversikan ke dalam nilai desimal seperti dibawah ini:

Red : 255*2560 + 0*2561 + 0*2562 = 255 + 0 + 0 = 255 ………..………...…(2.5)

Green : 0*2560 + 255*2561 + 0*2562 = 0 + 65,280 + 0 = 65,280 ………(2.6)

Blue : 0*2560 + 0*2561 + 255*2562 = 0 + 0 + 16,711,680 = 16,711,680 ….…(2.7)

Rumus dasar mencari nilai RGB citra adalah:

R = COLOR And RGB(255, 0, 0) ….……….……….…. (2.8)

G = (COLOR And RGB(0, 255, 0)) / 256 .…….….………...… (2.9)

(47)

Dari persamaan (2.5) sampai (2.7) diatas, rumus RGB pada persamaan (2.8) sampai (2.10) menjadi:

Nilai R = c and 255 ………...………... (2.11) Nilai G = (c and 65,280)/256 ..………...……….……..…..….. (2.12) Nilai B = ((c and 16,711,680)/256)/256 ………...………... (2.13) Dimana c adalah nilai intensitas piksel citra.

Ada beberapa format citra digital yang dijumpai, antara lain :

1. Bitmap (BMP)

Format citra ini adalah yang paling umum dan merupakan format standard windows. Ukuran file-nya besar karena bisa mencapai ukuran megabyte. File ini merupakan format yang belum terkompresi dan menggunakan sistem warna RGB (Red, Green, Blue) di mana masing-masing warna pixel-nya terdiri dari 3 komponen R, G, dan B yang dicampur menjadi satu. File BMP dapat dibuka dengan berbagai macam software pembuka gambar seperti ACDSee, Paint, Irvan

View dan lain-lain. File BMP tidak bisa (sangat jarang) digunakan di web (internet)

karena ukurannya yang besar. Detail gambar BMP dapat dilihat pada Tabel 2.1 dan Tabel 2.1.

Tabel 2.1 Bitmap Info Header

Nama Field Ukuran (Byte) Keterangan

beSize 4 Memori Header

beWidth 2 Lebar Gambar

beHeight 2 Tinggi Gambar

bePlanes 2 Harus 1

(48)

Tabel 2.2 Bitmap Core Header

Nama Field Ukuran (Byte) Keterangan

bfType 2 Mengandung karakter “BM” yang

mengidentifikasikan tipe file

bfSize 4 Memori file

bfReserved1 2 Tidak dipergunakan

bfReserved2 2 Tidak dipergunakan

bfOffBits 4 Offset untuk memulai data pixel

2. Joint Photographic Expert Group (JPEG/JPG)

Citra dengan format JPEG adalah yang paling terkenal sampai sekarang ini, karena berukuran kecil (hanya puluhan/ratusan KB saja) dan bersifat portable. Citraini sering digunakan pada bidang fotografi untuk menyimpan file foto hasil perekaman analog to digital converter (ADC). Karena ukurannya kecil maka file

ini banyak digunakan di Web (internet).

Format citra JPEG adalah suatu desain untuk mengkompresi citra baik gray-level maupun citra full-color. JPEG tidak hanya menangani data dalam bentuk citra, tetapi juga dapat berhubungan dengan gambar yang disebut dengan motion picture (MPEG). JPEG merupakan singkatan dari Joint Photographic Experts Group, merupakan suatu komite yang menyusun standar citra pada akhir tahun 80-an dan awal tahun 90-an. Kata “Joint” pada JPEG melambangkan status data di dalam kerja sama panitia ISO dan ITU_T. Format yang dihasilkan merupakan standar ISO IS-10918. Format file ini dikembangkan oleh C-Cube Micro systems untuk memberikan sebuah metode yang efisien untuk menyimpan citra dengan jumlah warna yang sangat banyak seperti foto kamera.

(49)

dengan citra aslinya, tetapi perbedaan ini sangat sulit dideteksi oleh mata manusia (Putra, 2010).

2.2.2 Jenis – jenis Citra Digital

Ada banyak cara untuk menyimpan citra digital di dalam memori. Cara penyimpanan menentukan jenis citra digital yang terbentuk. Beberapa jenis citra

digital yang sering digunakan adalah citra biner, citra grayscale dan citra warna.

1. Citra Biner (Monokrom)

Citra biner (monokrom) hanya memiliki 2 warna yaitu hitam dan putih. Dibutuhkan 1 bit di memori untuk menyimpan kedua warna ini.

Gradasi warna :

0 1

Bit 0 = warna hitam Bit 1 = warna putih

2. Citra Grayscale (skala keabuan)

Banyaknya warna tergantung pada jumlah bit yang disediakan di memori untuk menampung kebutuhan warna ini. Citra 2 bit mewakili 4 warna dengan gradasi warna berikut:

0 1 2 3

Citra 3 bit mewakili 8 warna dengan gradasi warna berikut :

0 1 2 3 4 5 6 7

(50)

3. Citra Warna (True Color)

Setiap piksel pada citra warna mewakili warna yang merupakan kombinasi dari tiga warna dasar (RGB = Red Green Blue). Setiap warna dasar menggunakan penyimpanan 8 bit = 1 byte, yang berarti setiap warna mempunyai gradasi sebanyak 255 warna. Berarti setiap piksel mempunyai kombinasi warna sebanyak 28 .28 .28 = 224 = 16 juta warna lebih. Itulah sebabnya format ini dinamakan true color karena mempunyai jumlah warna yang cukup besar sehingga bisa dikatakan hampir mencakup semua warna di alam.

Penyimpanan citra true color di dalam memori berbeda dengan citra

grayscale. Setiap piksel dari citra grayscale 256 gradasi warna diwakili oleh 1 byte.

Sedangkan 1 piksel citra true color diwakili oleh 3 byte, dimana masing – masing byte

merepresentasikan warna merah (red), hijau (green) dan biru (blue). Gambar 2.3 adalah contoh citra warna.

Gambar 2.3 Contoh citra warna

2.3 Format File Citra Bitmap

(51)

untuk memanipulasi warna, tetapi untuk mengubah objek lebih sulit. Tampilan bitmap mampu menunjukkan kehalusan gradasi bayangan dan warna dari sebuah gambar. Oleh karena itu, bitmap merupakan media elektronik yang paling tepat untk gambar – gambar dengan perpaduan gradasi warna yang rumit, seperti foto dan lukisan digital. Citra bitmap biasanya diperoleh dengan scanner, camera digital, video capture dan lain – lain.

Terjemahan bebas bitmap adalah pemetaan bit. Artinya nilai intensitas piksel di dalam citra dipetakan ke sejumlah bit tertentu. Peta bit umumnya adalah 8, yang berarti setiap piksel panjangnya 8 bit. Delapan bit ini mempresentasikan nilai intensitas piksel. Dengan demikian ada sebanyak 28 =256 derajat keabuan, mulai dari 0 (00000000) sampai 255 (11111111). Setiap berkas bitmap terdiri atas header berkas, header bitmap, informasi palet dan data bitmap. Header adalah data yang terdapat pada awal bagian berkas citra.

Terdapat tiga macam citra dalam format BMP, yaitu citra biner, citra berwarna dan citra hitam-puth (grayscale). Citra biner hanya memiliki dua nilai keabuan 0 dan 1. Oleh kerena itu 1 bit telah cukup untuk mempresentasikan nilai piksel. Citra berwarna adalah citra yang lebih umum. Warna yang terlihat di dalam citra bitmap merupakan kombinasi dari tiga komponen warna, yaitu : R (Red), G (Green) dan B (Blue). Kombinasi dari tiga warna RGB tersebut menghasilkan warna yang khas untuk piksel yang bersangkutan. Pada citra 256 warna, setiap piksel memiliki panjang 8-bit, akan tetapi komponen RGBnya disimpan dalam tabel RGB yang disebut palet.

2.4 Noise

Noise adalah bintik-bintik atau kotoran yang sering timbul pada citra (image).

(52)

noise, untuk menghasilkan noise digunakan bilangan acak sebagai pengganti bilangan

noise yang dihasilkan. Berdasarkan bentuk dan karakteristiknya, noise pada citra dibedakan menjadi beberapa jenis, yaitu :Gaussian Noise, SpeckleNoise dan Salt And Paper Noise seperti terlihat pada Gambar 2.4.

(a) (b) (c)

Gambar 2.4 Jenis-jenis Noise: (a) Gaussian, (b) Salt (c) Pepper

Noise Gaussian merupakan model noise yang mengikuti distribusi normal standar dengan rata-rata 0 dan standar deviasi 1. Efek Gaussian noise adalah munculnya titik-titik berwarna yang jumlahnya sama dengan persentase noise. Noise Speckle merupakan model noise yang memberikan warna hitam pada titik yang terkena noise, sedangkan noise salt and paper tampak seperti taburan garam karena memberikan warna putih pada titik yang terkena noise (Murinto, et al. 2007).

2.5 Membangkitkan Noise Gaussian

Noise Gaussian dapat dibangkitkan dengan cara membangkitkan bilangan acak [0,1] dengan distribusi Gaussian. Kemudian untuk titik-titik yang terkena noise, nilai fungsi citra ditambahkan dengan nilai noise yang ada, atau dirumuskan dengan:

y(i,j) = x(i,j)+ p.a ... (2.14) dimana:

a = nilai bilangan acak berdistribusi Gaussian

p = prosentase noise

y(i,j) = nilai citra terkena noise.

(53)

Untuk membangkitkan bilangan acak berdistribusi Gaussian, tidak dapat langsung menggunakan fungsi rnd, tetapi diperlukan suatu metode yang digunakan untuk mengubah distribusi bilangan acak ke dalam fungsi f tertentu. Dalam buku ini digunakan metode rejection untuk memudahkan dalam alur pembuatan programnya. Metode rejection dikembangkan dengan cara membangkitkan dua bilangan acak (x,y) dan ditolak bila y > f(x). Contoh noise Gausian dengan tingkat persentase noisenya dapat dilihat seperti pada Gambar 2.5.

Gambar 2.5 Beberapa Contoh Noise Gaussian Dengan Persentase 10%, 20%, 30%, 50%, 75% dan 90%.

2.6 Filter Domain Spasial

Istilah filter di sini sebenarnya mengacu kepada proses domain frekuensi, yaitu meloloskan (menerima) komponen frekuensi tertentu dan menghilangkan (menolak) frekuensi yang lain. Sebagai contoh, filter lolos rendah (Low Pass Filter/LPF) berarti meloloskan komponen frekuensi yang rendah. Low Pass Filter menghasilkan citra

(54)

banyak bidang untuk berbagai aplikasi, khususnya bagian ini untuk peningkatan kualitas citra dan perbaikan citra (Sulistyo, et al. 2009).

2.6.1 Mean Filter (Filter Rata-rata)

Pada filter rata-rata, nilai intensitas setiap piksel diganti dengan rata-rata dari nilai intensitas piksel tersebut dengan piksel-piksel tetangganya. Filter rata-rata merupakan filter h dalam bentuk matriks berukuran mxn (biasanya m=n) dan nilainya sama untuk setiap elemen (Gunara et al, 2007). Ukuran mxn ini yang menentukan jumlah tetangga yang harus dilibatkan dalam perhitungan. Karena bersifat LPF maka jumlah seluruh elemen adalah satu. Secara matematis filter rata-rata dapat dituliskan sebagai berikut:

h(x,y) = 1

��, 1 ≤ x≤ m, 1 ≤ y≤ n ... (2.15)

Keterangan:

h(x,y) = filter h (filter rata-rata)

n = jumlah baris pada filter h (filter rata-rata)

m = jumlah kolom pada filter h (filter rata-rata)

x = koordinat letak citra pada titik x

y = koordinat letak citra pada titik y Contoh filter rata-rata berukuran 3 x 3 adalah:

h(x,y) = �

1/9 1/9 1/9

� ... (2.16)

angka 1/9 diperoleh dari persamaan h(x,y) = 1

�� dimana m dan n adalah contoh

dimensi citra 3x3 piksel dan diperoleh nilai h(x,y) = 1

3�3 = 1/9

Operasi rata-rata dapat dipandang sebagai konvolusi yaitu perkalian fungsi diskrit antara citra f(x,y) dan filter g(x,y) (pada bagian ini filter h(x,y) dimisalkan sebagai

g(x,y)).

(55)

Dalam hal ini, h(x,y) disebut sebagai konvolusi dari f(x,y) dengan respon

g(x,y). Apabila g(x,y) adalah matriks berukuran 3x3 seperti diperlihatkan pada Gambar 2.4, f(x,y) adalah piksel yang dikenai operasi beserta tetangganya, maka h(x,y)

adalah hasil dari perhitungan dari persamaan berikut:

h (x,y) = AP1 + BP2 + CP3 + DP4 + EP5 + FP6 + GP7 + HP8 + IP9 ... (2.18)

Dari persamaan tersebut terlihat bahwa titik pusat jendela konvolusi yang merupakan piksel yang akan dimodifikasi nilainya bersesuaian dengan titik E dan faktor pemberat A, B, C, D, E, …, I pada matriks konvolusi adalah nilai dari g[-k,-l], dengan k,l = -1, 0, +1. Dalam manipulasi citra untuk menghasilkan citra yang baru, konvolusi berarti komputasi dari jumlah pembobotan terhadap piksel-piksel pada citra. Maka respon g[x,y] dapat disebut juga cetakan konvolusi, karena hasil dari operasi konvolusi sangat tergantung pada g[x,y]. Setiap nilai piksel pada citra nilai h[i,j] dihitung dengan memetakan cetakan konvolusi ke piksel [i,j] dalam citra asal, kemudian ditambahkan kepada jumlah pembobotan piksel-piksel tetangganya dimana nilai pembobotan bersesuaian dengan cetakan konvolusi. Operasi ini diilustrasikan dalam Gambar 2.6 menggunakan cetakan konvolusi 3x3. Untuk menjaga agar hasil perhitungan nilai intensitas yang baru tidak melebihi nilai maksimum yang dapat ditampung, maka faktor pembobot dari cetakan konvolusi (A, B, C, …, I) merupakan bilangan-bilangan pecahan yang jumlahnya satu. Konvolusi bersifat invariant (lokasi piksel tidak mempengaruhi hasil operasi), karena filter pembobotan yang digunakan sama pada seluruh bagian citra (Syarifuddin, 2003).

Gambar 2.6 Contoh matriks 3x3 untuk konvolusi

(56)

... (2.19) Pilih f(x,y) ukuran 3x3, dimulai dari pojok kiri atas. Kemudian, hitung konvolusinya dengan filter h(x,y).

Tabel 2.3 Nilai konfolusi dengan filter h(x,y).

Hasil konvolusi g(x,y) adalah:

1

9[(1x5) + (2x3)+ (1x4)+ (1x2) + (1x1) + (1x6) + (1x3) + (1x0)] = 3

Jadi nilai piksel 2 diganti oleh 3, tempatkan pada matriks yang baru, hasilnya adalah: Tabel 2.4 Hasil konfolusi dengan filter h(x,y).

(57)

Tabel 2.5 Nilai pergeseran dengan filter h(x,y).

Hasil konvolusinya adalah:

1

9[(1x3) + (1x3)+ (1x0)+ (1x2) + (1x1) + (1x3) + (1x3) + (1x0)] = 2

Jadi nilai piksel 1 diganti dengan 2, kemudian tempatkan pada matriks yang baru.

Tabel 2.6 Matriks hasil konfolusi

Proses perhitungan kemudian dilakukan terus hingga f(x,y) ukuran 3x3 sampai pada ujung kanan bawah hasilnya adalah:

(58)

Apabila digambarkan maka akan tampak sebagai berikut:

Dengan menggunakan filter rata-rata 3x3, maka proses filter dilakukan dengan cara menghitung konvolusi dari kernel filter rata-rata 3x3 dan H, maka diperoleh:

Y = H Xor F

Bila digambarkan maka hasil filter rata-rata dapat dilihat seperti Gambar 2.7 sebagai berikut:

Gambar 2.7 Hasil Filter Rata-rata

Hasilnya terdapat titik-titik yang berbeda (dianggap sebagai noise) akan dikurangi hingga mendekati nilai dominan. Salah satu efek dari hasil filter ini adalah efek blur.

2.6.2 Contra Harmonic Mean Filter

Contra Harmonic Mean Filter bekerja dengan baik pada tipe salt noise, tetapi tidak untuk pepper noise. Filter ini juga bekerja dengan baik pada jenis noise yang lain seperti noise Gaussian (Prasetyo, 2011). Contra Harmonic Mean Filter

merupakan solusi untuk menyelesaikan kasus bila derau additive berupa derau salt & pepper. Filter ini dirumuskan dengan:

... (2.20) dimana:

(s,t) = kordinat windowsub-image Sxy = region citra