Pengaruh Faktor Proporsional Pada Jaringan Saraf Propagasi Balik Untuk Pengenalan Wajah Berbasis Eigenfaces

(1)

WAJAH BERBASIS

EIGENFACES

SKRIPSI

QUARTHANO REAVINDO

040803037

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

PENGARUH FAKTOR PROPORSIONAL PADA JARINGAN SARAF PROPAGASI BALIK UNTUK PENGENALAN

WAJAH BERBASIS EIGENFACES

SKRIPSI

Diajukan untuk melengkapi dan memenuhi syarat mencapai gelar Sarjana Sains

QUARTHANO REAVINDO 040803037

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : PENGARUH FAKTOR PROPORSIONAL PADA JARINGAN SARAF PROPAGASI BALIK UNTUK PENGENALAN WAJAH BERBASIS EIGENFACES

Kategori : SKRIPSI

Nama : QUARTHANO REAVINDO

Nomor Induk Mahasiswa : 040803037

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Juni 2009

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Syahriol Sitorus, S.Si, M.IT Drs. Suyanto, M.Kom

NIP. 132174687 NIP. 131572440

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

(4)

PERNYATAAN

PENGARUH FAKTOR PROPORSIONAL PADA JARINGAN SARAF PROPAGASI BALIK UNTUK PENGENALAN

WAJAH BERBASIS EIGENFACES

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2009

(5)

PENGHARGAAN

Alhamdulillah, puji dan syukur penulis panjatkan kepada Allah Ta’ala, karena dengan limpahan karunia-Nya skripsi ini berhasil diselesaikan.

Ucapan terima kasih saya sampaikan kepada Drs. Suyanto, M.Kom dan Syahriol Sitorus, S.Si, M.IT selaku pembimbing pada penyelesaian skripsi ini yang telah memberikan panduan dan penuh kepercayaan kepada saya untuk menyempurnakan kajian ini. Panduan ringkas dan padat serta profesional telah diberikan kepada saya agar dapat menyelesaikam tugas ini. Ucapan terima kasih juga ditujukan kepada Ketua dan Sekretaris Departemen Matematika, Dr. Saib Suwilo, M.Sc dan Drs. Henri Rani Sitepu, M.Si. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, semua dosen pada Departemen Matematika FMIPA USU, dan para pegawai di FMIPA USU. Tidak terlupakan kepada bapak dan ibu tercinta yang selalu memberikan doa dan dorongan untuk menyelesaikan tugas ini secepatnya.

(6)

ABSTRAK

(7)

THE INFLUENCE OF PROPORTIONAL FACTOR AT BACKPROPAGATION FOR THE RECOGNITION

OF THE FACE THAT BASED ON EIGENFACES

ABSTRACT

At this time the standard backpropagation has been developed by 2 learning factors,

that are learning rate (α) and momentum (β). The third factor that is called

(8)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar isi vii

Daftar Tabel ix

Daftar Gambar x

Bab 1 Pendahuluan 1

1.1 Latar Belakang 1

1.2 Identifikasi Masalah 4

1.3 Batasan Masalah 4

1.4 Tujuan Penelitian 5

1.5 Kerangka Penelitian 5

1.6 Tinjauan Pustaka 8

Bab 2 Landasan Teori 10

2.1 Jaringan Saraf Propagasi Balik 10 2.2 Transformasi Data Dengan Menggunakan Metode

Principal Component Analysis (PCA) 23

Bab 3 Metodologi 27

3.1 Metode Pengumpulan Data 27

3.2 Metode Normalisasi Data 29

3.3 Metode Penentuan Arsitektur Jaringan 31 3.4 Metode Inisialisasi Bobot-Bobot Awal 33

3.5 Metode Pelatihan 34

3.6 Metode Pengujian 38

Bab 4 Hasil dan Pembahasan 41

4.1 Hasil dan Pembahasan Penelitian Jaringan

Saraf Propagasi Balik dengan 2 Faktor 41 4.2 Hasil dan Pembahasan Penelitian Jaringan

(9)

Bab 5 Penutup 56

5.1 Kesimpulan 56

5.2 Saran 57

Daftar Pustaka 58

Lampiran A 60

Lampiran B 61

(10)

DAFTAR TABEL

Halaman Tabel 3.1 Tabel Pelabelan Data Diskrit Dari Setiap Citra Wajah 28 Tabel 3.2 Tabel Pelabelan Data Normal Dari Setiap Citra Wajah 30 Tabel 3.3 Tabel Pendefinisian Target Keluaran 31 Tabel 3.4 Tabel Susunan Data Pelatihan 34

Tabel 3.5 Tabel Data Pengujian 39

Tabel 4.1 Tabel Hasil Penelitian Kelompok Penelitian I 41 Tabel 4.2 Tabel Hasil Penelitian Kelompok Penelitian II 42 Tabel 4.3 Tabel Hasil Penelitian Implementasi Menaik Tahap 1

Pada Kelompok Penelitian I 44

Tabel 4.4 Tabel Hasil Penelitian Implementasi Menurun Tahap 1

Tabel 4.5 Tabel Hasil Penelitian Implementasi Menaik Tahap 1

Pada Kelompok Penelitian II 46

(11)

DAFTAR GAMBAR

Halaman

Gambar 1.1 Proses Pada Suatu Neuron 1

Gambar 1.2 Kerangka Penelitian 6

Gambar 2.1 Arsitektur Jaringan Saraf Propagasi Balik 11 Gambar 3.1 Arsitektur Jaringan Saraf Pada Penelitian 32 Gambar 4.1 Grafik Pelatihan Kelompok Penelitian I 42 Gambar 4.2 Grafik Pelatihan Kelompok Penelitian II 43 Gambar 4.3 Grafik Pelatihan Dengan Implementasi Faktor Proporsional

Tahap 1 Pada Kelompok Penelitian I 45 Gambar 4.4 Grafik Pelatihan Dengan Implementasi Faktor Proporsional

Tahap 1 Pada Kelompok Penelitian II 47 Gambar 4.5 Grafik Pelatihan Dengan Implementasi Faktor Proporsional

Tahap 2 Pada Kelompok Penelitian II 51 Gambar 4.7 Grafik Pelatihan Dengan Implementasi Faktor Proporsional

(12)

ABSTRAK

(13)

THE INFLUENCE OF PROPORTIONAL FACTOR AT BACKPROPAGATION FOR THE RECOGNITION

OF THE FACE THAT BASED ON EIGENFACES

ABSTRACT

At this time the standard backpropagation has been developed by 2 learning factors,

that are learning rate (α) and momentum (β). The third factor that is called

(14)

BAB 1

PENDAHULUAN

1. 1 Latar Belakang

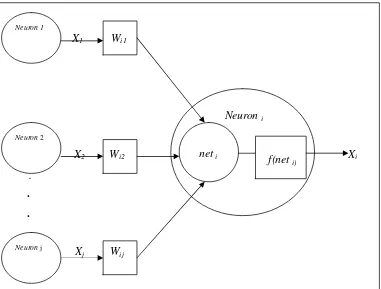
Jaringan saraf buatan merupakan kumpulan dari elemen-elemen pemrosesan buatan yang disebut neuron. Sebuah neuron akan mempunyai banyak nilai masukan yang berasal dari neuron-neuron lain yang berhubungan dengan neuron tersebut dan akan menghasilkan sebuah nilai keluaran. Neuron tersebut akan berhubungan dengan neuron-neuron yang lain jika ada bobot-bobot yang menghubungkannya. Hal tersebut dapat digambarkan sebagai berikut:

X1 Wi1

Neuron i

X2 Wi2 Xi

.

. .

Xj

Gambar 1. 1 Proses pada suatu neuron

Neuron 1

Neuron 2

Neuron j

Wij

(15)

Pandang neuron ipada gambar di atas. Dari gambar tersebut dapat kita lihat bahwa neuron i menerima nilai-nilai masukan dari neuron-neuron j (xj), nilai-nilai

masukan tersebut dapat diterima karena adanya bobot-bobot yang menghubungkan antara neuron-neuron j dengan neuron i tersebut. Bobot-bobot tersebut adalah wij

yaitu bobot-bobot yang menghubungkan neuron-neuron j dengan neuron i. Sebelum neuron i mengeluarkan nilai keluarannya, maka neuron i terlebih dahulu akan menghitung nilai “net input”nya (neti). Persamaan matematis untuk menghitung nilai

tersebut adalah

dimana fungsi tersebut merupakan fungsi aktivasi, yaitu fungsi yang digunakan untuk mengaktifkan suatu neuron sehingga menghasilkan nilai keluaran yang diinginkan.

Nilai keluaran dari neuron i tersebut dapat diteruskan ke neuron yang lain atau akan dapat menjadi nilai keluaran aktual, hal ini tergantung pada letak dari neuron i tersebut. Jika neuron i tersebut menghasilkan nilai keluaran aktual, maka nilai tersebut akan dibandingkan dengan suatu nilai yang disebut target. Perbandingan kedua nilai tersebut yang akan memunculkan suatu error.

Pelatihan pada jaringan saraf dilakukan untuk meminimalkan error yang terjadi, yang pada intinya adalah dengan mencari bobot-bobot terbaik(Freeman et al, 1992). Salah satu aturan yang dapat digunakan untuk mencari bobot terbaik adalah aturan delta, secara matematis aturan tersebut dapat dirumuskan sebagai berikut:

(16)

Salah satu metode pelatihan yang menggunakan aturan delta adalah metode pelatihan propagasi balik, namun karena jaringan saraf propagasi balik menggunakan konsep jaringan saraf berlapis banyak maka akan ada lapisan tersembunyi pada jaringan saraf propagasi balik. Dengan adanya lapisan tersembunyi yang terletak diantara lapisan masukan dan lapisan keluaran maka aturan delta akan mengalami perluasan sehingga disebut aturan delta yang digeneralisasi(Schalkoff, 1992).Pada jaringan saraf propagasi balik agar perubahan yang besar bisa terjadi, maka w_ij dapat dikalikan dengan suatu variabel yang disebut juga laju pembelajaran ( ) (Freeman et al, 1992). Hal ini dapat mempercepat untuk mendapatkan bobot-bobot yang diinginkan, sehingga persamaan (1.4)dapat dituliskan menjadi

( )

Faktor lain yang selama ini telah banyak digunakan untuk mengontrol penyesuaian bobot adalah momentum ( ) . Hal ini menyebabkan pada persamaan (1.5) akan bertambah satu suku lagi, sehingga dituliskan menjadi

( )

Disamping kedua faktor tersebut, faktor ketiga yang selanjutnya dimunculkan adalah faktor proporsional ( ) (Zweiri et al, 2003). Penambahan faktor ketiga tersebut akan

(17)

1. 2 Identifikasi Masalah

Suku ketiga yang menyertai faktor proporsional adalah e w t( ( )), dimana ( ( ))

e w t merupakan jumlah dari selisih antara target dengan nilai keluaran aktual setiap neuron di lapisan keluaran. Sehingga masalah pada penelitian ini adalah :

1. Bagaimana suku ketiga tersebut diimplementasikan untuk melakukan penyesuaian bobot pada lapisan tersembunyi?

2. Bagaimana kinerja dari jaringan saraf propagasi balik yang telah memanfaatkan faktor ketiga tersebut dalam pengenalan pola khususnya pola eigenfaces wajah seseorang?

1. 3 Batasan Masalah

Agar penelitian ini tidak mengambang dan fokus pada hal-hal yang diinginkan, maka perlu adanya beberapa batasan yaitu :

1. Pola wajah yang digunakan adalah pola wajah manusia yang bersifat statis pada posisi frontal

2. Format wajah yang digunakan adalah PCX model grey level 8 bit 3. Fungsi aktivasi yang digunakan adalah fungsi sigmoid

4. Bobot awal hanya diinisialisasi dengan metode nguyen widrow 5. Lapisan tersembunyi yang digunakan hanya satu lapisan

6. Fungsi erorr yang digunakan adalah fungsi Mean Square Error (MSE) 7. Kesalahan pelatihan dihitung dengan Sum Square Error(SSE)

8. Kesalahan pelatihan yang diinginkan adalah 0. 01 9. Epoch maksimum adalah 1000

(18)

1. 4 Tujuan Penelitian

Penelitian ini bertujuan untuk memberikan teori baru mengenai jaringan saraf propagasi balik, yaitu dengan menambahkan faktor ketiga yang disebut faktor proporsional. Disamping itu penelitian ini juga bertujuan untuk membandingkan kinerja dari jaringan saraf propagasi balik tiga faktor tersebut dengan jaringan saraf propagasi balik yang standard (dua faktor) pada pengenalan wajah berbasis eigenfaces.

1. 5 Kerangka Penelitian

(19)

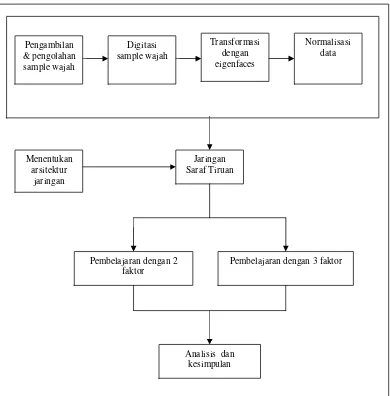
Gambar 1. 2 Kerangka Penelitian

Penjelasan dari bagan diatas adalah sebagai berikut:

1. Pengambilan sampel wajah dilakukan dengan kamera digital sebanyak lima orang dalam enam konfigurasi yaitu netral, tertawa, senyum, sedih, marah, dan kaget.

2. Setiap sampel diroping dengan sebuah windows berukuran 33 x 33. Kroping tersebut meliputi bagian mata, hidung, dan mulut

3. Hasil kroping diubah dari keadaan kontinu ke keadaan diskrit

4. Transformasikan pola diskrit tersebut dengan menggunakan eigenfaces 5. Normalisasi data hasil transformasi

Jaringan Saraf Tiruan Menentukan

arsitektur jaringan

Pembelajaran dengan 2 faktor

Pembelajaran dengan 3 faktor

Analisis dan kesimpulan Pengambilan

& pengolahan sample wajah

Digitasi sample wajah

Transformasi dengan eigenfaces

(20)

6. Bagi data hasil transformasi menjadi dua kelompok yaitu data untuk pelatihan dan data untuk pengujian

7. Tetapkan pola target yang diinginkan

8. Tetapkan arsitektur jaringan saraf propagasi balik yang diinginkan seperti: a. Banyaknya neuron pada lapisan masukan

b. Banyaknya neuron pada lapisan keluaran c. Banyaknya neuron pada lapisan tersembunyi

9. Buat dua kelompok penelitian dimana setiap kelompok memiliki 9 percobaan yang berbeda berdasarkan nilai laju pembelajaran ( ) , dan momentum( ) . Kelompok tersebut adalah sebagai berikut :

a. Kelompok I nilai dan  yang digunakan sama dan akan meningkat dari 0. 1 sampai dengan 0. 9

b. Kelompok II nilaiakan meningkat dari 0. 1 sampai dengan 0.9 sedangkan nilai akan menurun dari nilai 0. 9 sampai dengan 0. 1

10.Dari setiap kelompok tersebut diadakan simulasi terhadap data pelatihan untuk melihat kecepatan konvergensinya

11.Hasil dari pelatihan tersebut selanjutnya diuji untuk mengamati kemamapuan memorisasi dan generalisasi jaringan.

12.Selanjutnya faktor proporsional diimplementasikan kedalam setiap kelompok melalui 3 tahap. Implementasi tahap 1 dilakukan dengan nilai faktor proporsional pada interval [ 0.1 , 0.9 ] sedangkan implementasi tahap 2 dilakukan dengan nilai faktor proporsional pada interval [ 0.01 , 0.09 ], dan implementasi tahap 3 dilakukan dengan nilai faktor proporsional pada interval [ 0.001 , 0.009 ].

13.Untuk setiap implementasi lakukan kembali simulasi seperti pada langkah 10 dan 11

(21)

1. 6 Tinjauan Pustaka

Berikut ini akan diberikan beberapa tinjauan pustaka mengenai eigenfaces dan jaringan saraf propagasi balik

1.6.1 Jaringan saraf propagasi balik

Jaringan saraf propagasi balik menggunakan metode pelatihan yang terawasi. Metode pelatihan yang terawasi adalah metode pelatihan yang memiliki target. Pelatihan pada jaringan saraf propagasi balik merupakan pencarian terhadap bobot-bobot yang sesuai untuk menghasilkan error yang diinginkan. Error pada setiap iterasi pelatihan dapat dicari dengan suatu fungsi yang disebut fungsi error.

Jaringan saraf propagasi balik yang menggunakan konsep jaringan berlapis banyak akan mencari bobot-bobot yang sesuai melalui atuiran delta yang digeneralisasi. Aturan delta yang digeneralisasi merupakan perluasan dari aturan delta yang akan memunculkan faktor kesalahan pada lapisan tersembunyi dan faktor kesalahan pada lapisan keluaran. Faktor kesalahan tersebut muncul karena dalam mencari bobot yang diinginkan, aturan delta menggunakan metode gradient descent. Metode gradient descent memandang bahwa kesalahan merupakan fungsi bobot (Setawan, 1999). Bobot senantiasa di ubah setiap kali pembelajaran sehingga menyebabkan kesalahan semakin kecil. Perubahan bobot melalui metode gradient descent dapat dirumuskan sesuai dengan persamaan (1. 4).

(22)

Faktor proporsional mampu meningkatkan kecepatan konvergensi jaringan pada permasalahan XOR(Zweiri et al, 2003). Pada permasalahan pengklasifikasian data, faktor proporsional mampu meningkatkan kinerja pada pengklasifikasian data kecil yaitu data yang mempunyai jumlah instans sebanyak 16(Saman, 2006).

Untuk pengklasifikasian data berukuran sedang dengan jumlah instans sebanyak 150, faktor proporsional menyebabkan kinerja jaringan menjadi buruk(Saman, 2006). Hal yang sama juga terjadi pada pengklasifikasian data yang berukuran besar yaitu data yang menggunakan jumlah instans sebanyak 600 (Saman, 2006).

1.6.2 Eigenfaces

Eigenfaces merupakan suatu metode yang digunakan untuk mentransformasikan dan mereduksi dimensi dari suatu citra (Setawan, 1999). Eigenfaces menggunakan metode Principal Component Analysis (PCA) yaitu suatu metode matematika untuk merepresentasikan sebuah objek, mengekstraksi ciri-ciri sebuah objek dan mereduksi sebuah objek dengan cara mentransformasikannya menggunakan eigenvalue dan eigenvector secara linier(Harahap, 2007).

Eigenfaces dapat diperoleh dengan terlebih dahulu merepresentasikan setiap matriks wajah menjadi matriks linier, yang kemudian akan ditentukan vektor wajah rata-ratanya. Dari vektor wajah rata-rata tersebut akan dicari matriks covariancenya yang selanjutnya akan diperoleh eigenvalue dan eigenvectornya. Melalui eigenvector matriks covariance inilah akan kita peroleh eigenfaces yang selanjutnya akan digunakan untuk mendapatkan objek pada penelitian ini. Namun data tersebut harus dinormalisasikan terlebih dahulu untuk dapat menjadi pola masukan yang baik pada jaringan saraf propagasi balik.

(23)

BAB 2

LANDASAN TEORI

2.1Jaringan Saraf Propagasi Balik

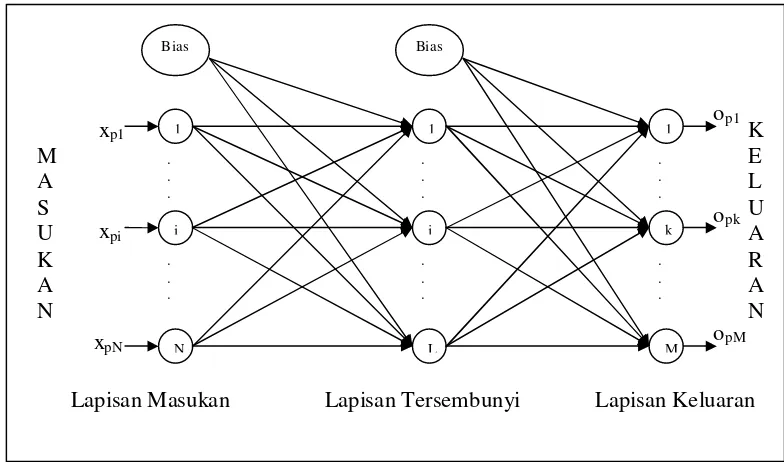
Jaringan saraf propagasi balik merupakan jaringan saraf yang menggunakan konsep jaringan berlapis jamak. Lapisan pertama adalah lapisan masukan (input) dan yang terakhir adalah lapisan keluaran (output). Lapisan diantara lapisan masukan dan lapisan keluaran disebut dengan lapisan tersembunyi (hidden) (Hermawan, 2006).

Jaringan saraf propagasi balik menerapkan metode pelatihan yang terawasi yaitu metode pelatihan yang memberikan nilai target yang diinginkan dari setiap neuron pada lapisan keluaran. Puspitaningrum (2006, hal:125) menyatakan bahwa istilah “propagasi balik” atau “penyiaran kembali”diambil dari cara kerja jaringan ini, yaitu bahwa gradien error neuron-neuron lapisan tersembunyi diturunkan dari penyiaran kembali error-error yang diasosiasikan dengan neuron-neuron lapisan keluaran. Hal ini karena nilai target untuk neuron-neuron tersembunyi tidak diberikan.

2.1.1 Arsitektur jaringan saraf propagasi balik

Pada jaringan saraf propagasi balik setiap lapisan akan memiliki jumlah

(24)

Gambar 2. 1 Arsitktur Jaringan Saraf Propagasi Balik

2.1.2 Proses komputasi jaringan

Proses komputasi pada jaringan saraf propagasi balik dapat dibagi menjadi dua tahap yaitu komputasi maju (pass forward) dan komputasi mundur (pass backward) (Setawan, 1999). Komputasi maju bertujuan untuk menghasilkan nilai keluaran aktual, sedangkan komputasi mundur bertujuan untuk melakukan perubahan nilai bobot pada setiap lapisan.

2.1.2.1 Komputasi maju

Komputasi maju pada jaringan saraf propagasi balik dimulai dari lapisan masukan tetapi neuron-neuron yang melakukan proses komputasi adalah neuron-neuron pada lapisan tersembunyi. Hal ini disebabkan karena neuron-neuron pada lapisan masukan hanya berfungsi meneruskan nilai masukan untuk neuron-neuron pada lapisan tersembunyi.

(25)

Proses komputasi maju pada jaringan saraf propagasi balik yang memiliki satu lapisan tersembunyi dapat dijabarkan sebagai berikut. Misalkan Xp = (xp1, xp2, . . . ,

xpN ) merupakan vektor masukan untuk pola ke p dari setiap neuron pada lapisan

masukan yang akan diteruskan ke setiap neuron j pada lapisan tersembunyi. Setiap neuron j pada lapisan tersembunyi untuk selanjutnya akan melakukan proses komputasi seperti yang telah diterangkan pada bab 1 yaitu dengan terlebih dahulu setiap neuron pada lapisan tersembunyi akan diaktifkan oleh fungsi aktifasinya sehingga akan menghasilkan suatu nilai, nilai tersebut adalah

(26)

Nilai-nilai tersebut yang selanjutnya akan di teruskan sebagai nilai masukan untuk setiap neuron k pada lapisan berikutnya (lapisan keluaran). Pada lapisan keluaran proses komputasi yang sama seperti pada lapisan tersembunyi juga terjadi, yaitu dengan menghitung nilai net input dari setiap neuron k pada lapisan keluaran yang di rumuskan sebagai berikut :

Dengan menggunakan nilai net input pada lapisan keluaran ( o pk

net ) ini, maka setiap neuron pada lapisan keluaran akan diaktifkan oleh fungsi aktifasinya sehingga akan menghasilkan nilai keluaran aktual, nilai keluaran aktual tersebut adalah

o_pk  f_ko(neto_pk) (2.4)

(27)

2.1.2.2 Komputasi mundur

Komputasi mundur bertujuan untuk melakukan perubahan terhadap bobot jaringan. Salah satu aturan pada jaringan saraf yang digunakan untuk melakukan perubahan bobot adalah aturan delta, yang dapat dituliskan dalam persamaan matematika sebagai berikut

w t(  1) w t( ) w t( ) (2.5) dimana

w t( 1) = bobot pada iterasi ke t+1 w t( ) = bobot pada iterasi ke t

w t( ) = perubahan bobot pada iterasi ke t

Aturan delta melakukan perubahan bobot dengan tujuan untuk meminimalkan error yang terjadi (Fausett, 1994). Perubahan bobot yang meminimalkan error dapat ditentukan dengan menggunakan metode steepest descent yaitu dengan menghitung negatif gradien dari error (Freeman et al, 1992). Error secara eksplisit dapat dipandang sebagai fungsi dari bobot, sehingga untuk menentukan gradien dari error dapat dilakukan dengan menurunkannya secara parsial terhadap bobot (Fausett, 1994).

Aturan delta pada jaringan saraf propagasi balik merupakan aturan delta yang digeneralisasi, karena fungsi aktifasi yang digunakannya adalah fungsi yang dapat diturunkan(Fausett, 1994).

(28)

2.1.2.2.1 Komputasi mundur tahap I

Komputasi mundur tahap I adalah komputasi mundur dari lapisan keluaran ke lapisan tersembunyi yang bertujuan untuk melakukan perubahan terhadap bobot- bobot antar kedua lapisan tersebut.

(29)

Pada persamaan (2.9) diatas f_ko'(neto_pk)adalah turunan pertama dari fungsi aktifasi neuron keluaran. Penelitian ini menggunakan fungsi aktifasi sigmoid untuk mengaktifkan neuron-neuron pada lapisan keluaran, yang bentuknya adalah sebagai berikut neuron lapisan keluaran yang disimbolkan dengan o

pk

(30)

2.1.2.2.2 Komputasi mundur tahap II

Komputasi mundur tahap II adalah komputasi mundur dari lapisan tersembunyi ke lapisan masukan yang bertujuan untuk melakukan perubahan terhadap bobot- bobot antar kedua lapisan tersebut.

Komputasi mundur tahap II memerlukan analisis matematika yang lebih cermat karena setiap neuron pada lapisan tersembunyi tidak memiliki target yang harus dipenuhi oleh nilai keluarannya, sehingga error pada lapisan tersembunyi tidak dapat ditentukan rumusannya. Namun hal tersebut tidak menjadi masalah ketika kita akan melakukan perubahan bobot pada lapisan tersembunyi karena secara intuisi nilai error pada persamaan (2. 6) dapat kita hubungkan dengan bobot-bobot pada lapisan tersembunyi (wh_ji) (Freeman et al, 1992). Secara matematis hal tersebut dapat dijabarkan sebagai berikut, dari persamaan (2. 6) kita ketahui bahwa

2 juga tergantung pada i_pj. Sedangkan dari persamaan (2. 1) dan persamaan (2. 2) kita ketahui bahwa nilai i_pj merupakan nilai keluaran dari neuron lapisan tersembunyi yang berhubungan dengan bobot-bobot pada lapisan tersembunyi (wh_ji). Hal ini menyebabkan gradien dari E_p pada lapisan tersembunyi dapat diperoleh dengan menurunkannya secara parsial terhadap bobot-bobot pada lapisan tersembunyi ( h)

(31)

maka persamaan (2. 17) dapat ditulis menjadi

(32)

1

neuron lapisan tersembunyi yang disimbolkan dengan h pj

Dengan aturan delta, maka perubahan bobot-bobot antara lapisan masukan dengan lapisan tersembunyi adalah

Setiap iterasi t pada komputasi maju dan komputasi mundur dilakukan untuk setiap pola pelatihan p. Satu siklus pelatihan (epoch) adalah suatu keaadaan ketika seluruh pola telah melalui proses komputasi maju dan proses komputasi mundur.

2.1.3 Komputasi pelatihan

(33)

Pada penelitian ini kesalahan pelatihan dihitung dengan Sum Squere Error (SSE). Jika pelatihan pada jaringan saraf propagasi balik akan melibatkan P buah pola, maka kesalahan pelatihan yang dihitung pada setiap epoch untuk penelitian ini di rumuskan sebagai berikut

1 e

P p p

E SSE

E





(2.28)

dimana

Ee = kesalahan pelatihan untuk setiap epoch

SSE = Sum Squere Error

Ep = kesalahan jaringan untuk pola ke p

Pelatihan pada jaringan saraf propagasi balik dilakukan sampai tercapainya kesalahan pelatihan yang diinginkan atau sampai batas epoch maksimum.

2.1.4 Faktor-faktor pada jaringan saraf propagasi balik

Jaringan saraf yang baik adalah jaringan saraf yang mampu mempelajari pola yang ada dengan cepat, sehingga proses pelatihan tidak membutuhkan waktu yang lama dan mempunyai tingkat akurasi yang baik. Pada jaringan saraf propagasi balik ada beberapa faktor yang dapat diteliti untuk melakukan hal tersebut yaitu:

2.1.4.1 Laju pembelajaran ()

(34)

Hubungan laju pembelajaran dengan perubahan bobot pada lapisan keluaran dapat

Hal tersebut juga dilakukan terhadap penyesuaian bobot pada lapisan tersembunyi, sehingga perubahan bobot pada lapisan tersembunyi menjadi

h( ) p

Momentum merupakan parameter yang berfungsi terutama untuk

meningkatkan kecepatan pembelajaran (Setawan, 1999). Penyesuaian bobot dengan momentum akan mempertimbangkan penyesuaian bobot pada langkah sebelumnya. Hal ini menyebabkan perubahan bobot pada lapisan keluaran menjadi

( ) p ( 1)

Hal yang sama juga terjadi pada perubahan bobot pada lapisan tersembunyi, sehingga perubahan bobot pada lapisan tersembunyi akan menjadi

( ) p ( 1)

(35)

Pada penelitian ini digunakan faktor ketiga yang disebut sebagai faktor proporsional (). Faktor proporsional ini pertama sekali diperkenalkan dan digunakan pada permasalahan XOR (Zweiri et al, 2003). Modifikasi terhadap jaringan saraf propagasi balik dengan menambahkan faktor ketiga yang disebut faktor proporsional akan menyebabkan bertambahnya satu konstanta baru yang menyertainya, konstanta tersebut adalah e(w(t)) (Zweiri et al, 2003). Untuk mendapatkan nilai e(w(t)) maka dapat digunakan rumus berikut ini (Zweiri et al, 2003):

( ( )) _k

Faktor ketiga tersebut menyebabkan perubahan bobot pada lapisan keluaran akan menjadi

Sedangkan perubahan bobot pada lapisan tersembunyi akan menjadi

(36)

2.2 Transformasi data dengan menggunakan metode Principal Component Analysis (PCA)

Metode Principal Component Analysis (PCA) merupakan suatu metode matematika untuk merepresentasikan data, mengekstraksi ciri-ciri data tersebut dan mereduksinya dengan cara mentransformasikannya menggunakan eigenvalue dan eigenvektor secara linier(Harahap, 2007).

Suwandi et al (2006 : hal 8 ) menyatakan bahwa kegunaan utama dari Principal Component Analysis (PCA) adalah untuk mengurangi variasi yang ada dengan tetap menjaga informasi yang diperlukan, supaya variasi yang tersisa memang variasi yang paling menonjol dan paling mencerminkan feature yang ada. Sisa variasi yang tersisa ini disebut sebagai Principal Component. Pada proses pengurangan variasi ini dilakukan dengan mereduksi daerah matriks yang mempunyai nilai ciri mulai dari yang paling lemah. Kegunaan lain dari Principal Component Analysis (PCA) adalah akan membuat aplikasi yang menggunakannya akan lebih cepat, karena data yang digunakan sudah direduksi.

Eigenvektor-eigenvektor yang diperoleh pada metode Principal Component Analysis (PCA) merupakan eigenvektor-eigenvektor dari matriks covariance. Untuk memperoleh matriks covariance, terlebih dahulu harus dihitung perbedaan antara data-data tersebut dengan rata-ratanya. Andaikan terdapat M data, maka untuk menghitung rata-ratanya dapat dilakukan dengan menggunakan rumus:

1 M

i i

M





 



(2.37)

dimana

 = rata-rata

i

(37)

Pengurangan setiap data dengan rata-ratanya tersebut dapat dilakukan dengan menggunakan rumus berikut ini

1, 2,3, ,

i i i M

       (2. 38) dimana

i

 = selisih data ke-i dengan rata-rata

i

 = data ke-i

 = rata-rata

Selisih tersebut yang selanjutnya akan digunakan untuk menghitung matriks covariance dengan menggunakan rumus:

C  A AT (2. 39) dimana

C = matriks covariance



1 2 3 M



A      

AT = transpose matriks A

Dari persamaan 2. 39 dapat disimpulkan bahwa matriks covariance ( C ) tersebut merupakan matriks persegi. Dengan demikian untuk mendapatkan eigenvektor-eigenvektor dari suatu matriks persegi, terlebih dahulu harus dihitung eigenvalue-eigenvalue dari matriks persegi tersebut (Spence et al, 2000).

Untuk hal tersebut kita harus memahami beberapa teori pada aljabar linier mengenai eigenvalue dan eigenvektor. Misalkan B merupakan sebuah matriks persegi berukuran n x n maka sebuah vektor tak nol v disebut eigenvektor dari B, jika

Bv = λv (2.40)

(38)

Eigenvalue-eigenvalue dari sebuah matriks persegi B yang berukuran n x n merupakan nilai dari λ yang memenuhi

det (BI_n)  0 (2.41) dimana

n

I = matriks identitas berukuran n x n

Persamaan (2.41) diatas merupakan persamaan karekteristik dari B sedangkan det (BI_n)disebut polynomial karekteristik dari B. Dari persamaan tersebut dapat diketahui bahwa eigenvalue-eigenvalue dari matriks B merupakan akar-akar dari polinomial karekteristik B (Spence et al, 2000). Sehingga Eigenvektor-eigenvektor yang berkorespondensi dengan eigenvalue-eigenvalue dari matriks B tersebut merupakan solusi tak nol dari

(BI_n)x  0 (2.42)

Untuk matriks covariance ( C ) yang berukuran sangat besar maka dapat dilakukan suatu modifikasi matematis untuk mendapatkan eigenvektor-eigenvektor dari matriks covariance tersebut sehingga lebih efisien dalam penerapannya. Modifikasi matematis tersebut dilakukan dengan membentuk sebuah matriks baru, misalkan matriks baru tersebut adalah matriks L. Matriks L merupakan matriks yang dibentuk dari perkalian antara matriks AT dengan matriks A, dengan kata lain L = AT A. Misalkan eigenvektor-eigenvektor dari matriks L adalah viuntuk setiap

eigenvalue-eigenvalue_i, maka akan berlaku

L v_i  _iv_i T

i i i

A A v   v (2.43)

Pada persamaan (2.43) tersebut jika kedua ruas dikalikan dengan A maka akan berlaku

A A A vT _i  _iAv_i (2.44) karena

AAT = C maka

(39)

Dari persamaan (2.45) dapat disimpulkan bahwa Avi merupakan eigenvektor dari

matriks covariance ( C ) untuk eigenvalue yang bersesuaian ( µi ).

Transformasi data dengan menggunakan metode Principal Component Analysis (PCA) dilakukan untuk mentransformasikan data tersebut ke ruang dimensi yang lebih kecil. Ruang dimensi yang lebih kecil dan merupakan ruang dimensi yang terbaik dapat ditentukan melalui eigenvektor-eigenvektor terbaik, yaitu eigenvektor-eigenvektor yang berkorespondensi dengan eigenvalue-eigenvalue terbesar dari matriks covariance ( C ) (Asmat, 2008). Eigenvektor-eigenvektor yang diperoleh melalui modifikasi matematis yang dilakukan untuk mendapatkan eigenvektor-eigenvektor pada matriks covariance ( C ) yang berukuran sangat besar juga merupakan eigenvektor-eigenvektor yang terbaik (Asmat, 2008).

Misalkan eigenvektor-eigenvektor terbaik dari matriks covariance ( C ) adalah u1 , u2 , u3 , . . . , uk maka

 _i UT _i , i = 1, 2, 3, . . . , M (2.46) dimana

_i = hasil transformasi data ke-i UT =[ u1 u2 u3 . . . uk ]T

(40)

BAB III

METODOLOGI

3.1 Metode Pengumpulan Data

Data yang digunakan pada penelitian ini merupakan data diskrit berbasis eigenfaces dari citra wajah . Untuk hal tersebut maka terlebih dahulu dilakukan pengolahan terhadap citra wajah agar memenuhi karekteristik yang diinginkan untuk penelitian ini, sehingga untuk selanjutnya dapat diproyeksikan menggunakan eigenfaces.

3.1.1 Pengambilan dan pengolahan citra wajah

Pengambilan citra wajah dilakukan dengan kamera digital terhadap lima orang dalam enam konfigurasi dasar wajah manusia secara psikologi, yaitu : netral, tertawa, senyum, sedih, marah, dan kaget (Setawan, 1999). Citra wajah yang dihasilkan dari kamera digital tersebut adalah dalam format JPG, mode RGB, dan beresolusi 640 x 640. Citra Wajah tersebut dapat dilihat pada Lampiran A.

(41)

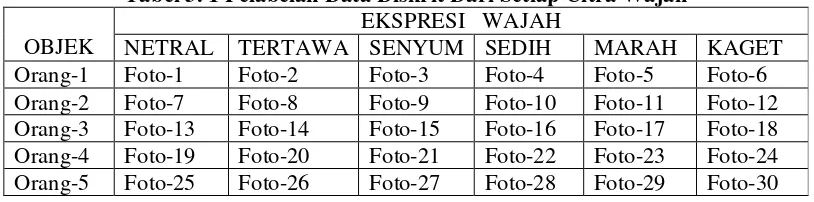
Penelitian ini menggunakan data dalam bentuk pola-pola diskrit dari citra wajah, sehingga setiap citra wajah harus diubah representasinya dari keadaan kontinu ke dalam bentuk pola-pola diskrit melalui informasi gray level. Perubahan representasi citra wajah tersebut dapat dilakukan dengan perangkat lunak bacaimage. Perangkat lunak bacaimage yang dibuat oleh Drs. Suyanto M.Kom dan kawan-kawan, merupakan perangkat lunak yang mampu merubah representasi suatu citra wajah yang berformat PCX dengan mode gray level 8 bit dari keadaan kontinu ke keadaan diskrit. Hasil perubahan terhadap setiap citra wajah yang digunakan pada penelitian ini adalah sebuah matriks berukuran 33 x 33 yang berisi nilai-nilai diskrit dari setiap citra wajah. Untuk memudahkan dalam penggunaan data-data tersebut, maka dilakukanlah pelabelan terhadap data diskrit dari setiap citra wajah tersebut dengan cara sebagai berikut :

Tabel 3. 1 Pelabelan Data Diskrit Dari Setiap Citra Wajah EKSPRESI WAJAH

OBJEK NETRAL TERTAWA SENYUM SEDIH MARAH KAGET Orang-1 Foto-1 Foto-2 Foto-3 Foto-4 Foto-5 Foto-6 Orang-2 Foto-7 Foto-8 Foto-9 Foto-10 Foto-11 Foto-12 Orang-3 Foto-13 Foto-14 Foto-15 Foto-16 Foto-17 Foto-18 Orang-4 Foto-19 Foto-20 Foto-21 Foto-22 Foto-23 Foto-24 Orang-5 Foto-25 Foto-26 Foto-27 Foto-28 Foto-29 Foto-30

3.1.2 Proyeksi data diskrit citra wajah dengan eigenfaces

Proyeksi data diskrit citra wajah dengan eigenfaces merupakan penerapan metode Principal Component Analysis (PCA) pada data yang berbentuk citra wajah. Hal tersebut dapat dilakukan karena suatu citra wajah dapat dipandang sebagai suatu vektor (Setawan, 1999). Jika citra tersebut memiliki lebar dan tinggi masing-masing adalah w dan h piksel, jumlah komponen vektor tersebut adalah w x h piksel. Berdasarkan tingkat keabuan, setiap piksel dikodekan dengan nilai 0 – 255 (Setawan, 1999).

(42)

tentunya dimensi tersebut tidak optimal, maka perlu dilakukan reduksi, namun perlu dipertimbangkan pula bahwa setiap piksel saling bergantung terhadap piksel tetangganya. Dengan demikian perlu suatu metode untuk mendapatkan dimensi yang optimal. Metode eigenfaces dapat digunakan untuk mentransformasi dan reduksi dimensi tanpa kehilangan ciri yang ada.”(Setawan, 1999, hal: 7).

Algoritma untuk memproyeksikan setiap data diskrit citra wajah yang berukuran N x N ke dalam face space dengan dimensi yang lebih kecil adalah sebagai berikut

Step 1: for i= 1 to banyak data

Step 1a: representasikan setiap matriks citra yang berukuran

N x N ke dalam vektor wajah(Γi )yang berukuran N2 x 1

Step 2: end for

Step 3: hitung vektor citra rata-rata ( Ψ )

Step 4: hitung mean subtracted images ( Φi )

Step 5: Bentuk matriks covariance ( C )

Step 6: Hitung eigenvalue-eigenvalue dari matriks covariance

Step 7: Tentukan eigenvektor-eigenvektor terbaik yang bersesuaian

dari eigenvalue-eigenvalue terbesar. Eigenvektor-eigenvektor

tersebut merupakan eigenfaces

Step 8: Bentuk face space ( U )

Step 9: Proyeksikan setiap vektor image kedalam face space (_i )

Step10: Selesai

Proses transformasi dengan menggunakan metode eigenfaces berdasarkan algoritma tersebut akan menghasilkan 30 vektor hasil transformasi yang berdimensi 30 x 1.

3.2 Metode Normalisasi Data

(43)

Data yang sesuai untuk menjadi nilai masukan pada jaringan saraf propagasi balik adalah data yang terletak pada range -1 dan 1 atau pada range 0 dan 1,sehingga kuadrat dari data masukan berada pada range 0 dan 1(Halim et al, 2000). Hal ini dilakukan agar nilai keluaran yang dihasilkan dapat terletak pada range 0 dan 1.

Proses normalisasi data pada penelitian ini akan menggunakan rumusan matematis sebagai berikut (Gazali, 2003) :





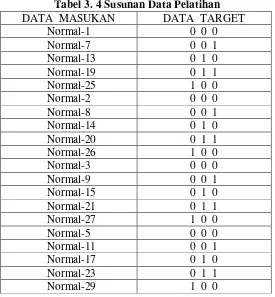
Setiap kolom pada matriks normal tersebut adalah data hasil normalisasi dari setiap citra wajah yang akan digunakan sebagai data masukan pada penelitian ini. Untuk memudahkan dalam penggunaan data-data tersebut, maka dilakukanlah pelabelan terhadap data normal dari setiap citra wajah tersebut dengan cara sebagai berikut :

Tabel 3. 2 Pelabelan Data Normal Dari Setiap Citra Wajah EKSPRESI WAJAH

OBJEK NETRAL TERTAWA SENYUM SEDIH MARAH KAGET Orang-1 Normal-1 Normal-2 Normal-3 Normal-4 Normal-5 Normal-6 Orang-2 Normal -7 Normal -8 Normal -9 Normal -10 Normal -11 Normal -12 Orang-3 Normal -13 Normal -14 Normal -15 Normal -16 Normal -17 Normal -18 Orang-4 Normal -19 Normal -20 Normal -21 Normal -22 Normal -23 Normal -24 Orang-5 Normal -25 Normal -26 Normal -27 Normal -28 Normal -29 Normal -30

(44)

3.3 Metode Penentuan arsitektur jaringan

Jaringan saraf propagasi balik yang digunakan pada penelitian ini merupakan jaringan saraf propagasi balik dengan 1 lapisan tersembunyi (hidden layer). Dengan demikian penelitian ini akan menggunakan 3 lapisan yaitu lapisan masukan (input layer ), lapisan tersembunyi (hidden layer) dan lapisan keluaran (output layer). Setiap lapisan akan memiliki neuron-neuron yang jumlahnya tergantung dari permasalahan yang akan diselesaikan.

Data masukan pada penelitian ini adalah data hasil proyeksi ke dalam face space yang telah mengalami proses normalisasi dengan dimensi 30 x 1. Hal ini menyebabkan lapisan masukan pada penelitian ini akan memiliki neuron sebanyak 30 buah neuron.

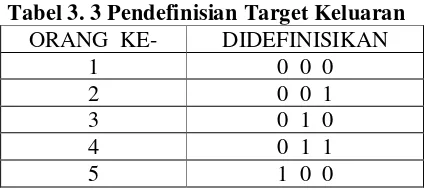
Untuk menentukan jumlah neuron pada lapisan keluaran, maka yang menjadi acuan adalah bagaimana cara mendefinisikan target keluaran dari suatu penelitian. Target keluaran dapat didefinisikan sesuai kebutuhan, dengan ketetapan yang harus dipegang adalah pola keluaran harus unik (Setawan, 1999). Dalam penelitian ini terdapat 5 orang yang digunakan sebagai objek, maka harus terdapat 5 pola target keluaran yang unik. Dengan demikian maka pendefinisian pola target keluaran pada penelitian ini adalah sebagai berikut :

Tabel 3. 3 Pendefinisian Target Keluaran ORANG KE- DIDEFINISIKAN

1 0 0 0

2 0 0 1

3 0 1 0

4 0 1 1

5 1 0 0

(45)

Untuk menentukan jumlah neuron pada lapisan tersembunyi banyak cara yang dapat digunakan. Salah satu cara yang digunakan pada penelitian ini adalah (Saman, 2006)

*

L  N M ( 3. 2 )

dimana

L = jumlah neuron pada lapisan tersembunyi N = jumlah neuron pada lapisan masukan M = jumlah neuron pada lapisan keluaran

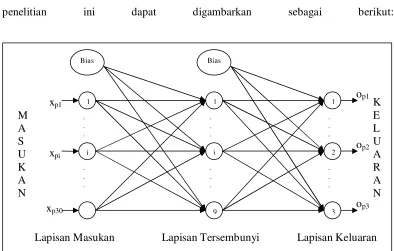
Dengan demikian maka pada penelitian ini jumlah neuron pada lapisan tersembunyi ada sebanyak 9 buah neuron. Sehingga arsitektur jaringan saraf yang digunakan pada penelitian ini dapat digambarkan sebagai berikut:

Gambar 3. 1 Arsitektur jaringan saraf pada penelitian

Bias

(46)

3.4 Metode Inisialisasi Bobot-Bobot Awal

Bobot-bobot awal pada penelitian ini ditentukan menggunakan metode Nguyen-Widrow. Metode tersebut dikembangkan oleh Nguyen dan Widrow pada tahun 1990. Metode tersebut menggunakan faktor skala (µ) yang didefinisikan sebagai berikut (Fausett, 1994):

µ = 0.7 * ( L )1/N (3.3) dimana

N = jumlah neuron pada lapisan masukan L = jumlah neuron pada lapisan tersembunyi Metode ini hanya digunakan untuk menginisialisasi bobot awal dari neuron-neuron lapisan masukan ke neuron-neuron lapisan tersembunyi, sedangkan bobot awal dari neuron-neuron lapisan tersembunyi ke neuron-neuron lapisan keluaran diinisialisasi dengan inisialisasi acak(puspitaningrum, 2006). Sehingga algoritma untuk melakukan inisialisasi bobot awal dengan metode Nguyen-Widrow adalah sebagai berikut:

step 1 : Inisialisasi setiap bobot dari neuron-neuron lapisan

masukan ke neuron-neuron lapisan tersembunyi (wh_ji) dalam

interval [-0.5 , 0.5 ] step 2 : Hitung faktor skala (µ)

step 3 : Hitung wh_j  (w_jh₁)2(wh_j₂)2(wh_j₃)2  (wh_jN)2

step 4 : Hitung ( )( ) ( )( )

h ji h

ji h

j w lama w baru

w





(47)

3.5 Metode Pelatihan

Pada saat pelatihan jaringan saraf dapat dipandang sebagai suatu sistem yang belajar(Puspitaningrum, 2006). Belajar pada jaringan saraf propagasi balik adalah belajar yang terawasi, dimana terdapat pasangan masukan dan target yang harus dipenuhi sehingga dibutuhkan data masukan dan target untuk suatu pelatihan.

Untuk hal tersebut maka pelatihan pada penelitian ini menggunakan data diskrit citra wajah dalam ekspresi netral, tertawa, senyum, dan marah yang telah mengalami proses normalisasi sebagai data masukan. Sedangkan data keluaran yang telah didefinisikan pada bagian 3. 3 digunakan sebagai data target. Data tersebut disusun berurutan dari orang pertama sampai orang ke lima dalam ekspresi netral, kemudian kembali lagi dari orang pertama sampai orang ke lima dalam ekspresi tertawa, dan seterusnya sampai orang ke lima dalam ekspresi marah. Pasangan data masukan dan target pelatihan pada penelitian ini adalah sebagai berikut

(48)

Pada penelitian ini, pelatihan dilakukan melalui 2 tahap yaitu dengan jaringan saraf propagasi balik 2 faktor dan dengan jaringan saraf propagasi balik 3 faktor. Kedua jenis pelatihan tersebut dilakukan dengan menggunakan data pelatihan yang sama.

3.5.1 Metode pelatihan dengan jaringan saraf propagasi balik 2 faktor

Pelatihan dengan jaringan saraf propagasi balik yang menggunakan 2 faktor, yaitu laju pembelajaran (α) dan momentum (β) dilakukan berdasarkan algoritma berikut ini: Step 1: Inisialisasi bobot-bobot awal dari setiap lapisan

Step 2: Set epoch maksimum = 1000,

Kesalahan pelatihan maksimum = 0.01, epoch = 0 Step 3: Epoch = epoch + 1

Step 4: For p =1 to banyak data pelatihan do

Step4a: setiap neuron i pada lapisan masukan meneruskan

nilai-nilai masukan dari setiap pola masukan (xpi)

Step4b: Hitung net input dari setiap neuron j pada lapisan

tersembunyi (neth_pj)

Step4c: Hitung nilai keluaran dari setiap neuron j pada lapisan

tersembunyi (ipj)

Step4f: Hitung nilai keluaran aktual dari setiap neuron k pada

lapisan keluaran (opk)

Step4g: Hitung kesalahan dari setiap neuron k pada lapisan

keluaran(_pko ) o pk

(49)

Step4h: Hitung kesalahan dari setiap neuron j pada lapisan

Step4i: Hitung perubahan bobot-bobot lapisan tersembunyi

( ) ( 1)

h h h

ji pj pi ji

w p   x  w p

    

Step4j: Hitung perubahan bobot-bobot lapisan keluaran

( ) ( 1)

o o o

kj pk pj kj

w p   i  w p

    

Step4k: Hitung bobot-bobot lapisan tersembunyi yang baru h

ji

w baru = wh_ji lama +  wh_ji( )p

Step4l: Hitung bobot-bobot lapisan keluaran yang baru

w_kjo baru = w_kjo lama +  w_kjo( )p Step5: End for

Step6: Hitung kesalahan pelatihan

Step7: Kerjakan step 3 sampai step 6 jika kesalahan pelatihan > kesalahan pelatihan maksimum atau epoch pelatihan < epoch pelatihan maksimum

Step8: Selesai

Pelatihan dengan jaringan saraf propagasi balik yang menggunakan 2 faktor dilakukan dalam 2 kelompok pelatihan, setiap kelompok terdiri atas 9 percobaan yang berbeda berdasarkan nilai laju pembelajaran (α) dan momentum (β) yang digunakan. Setiap percobaan pada kelompok I menggunakan nilai yang sama dan meningkat dalam interval [0.1 , 0.9] untuk laju pembelajaran (α) dan momentum (β). Sedangkan kelompok II menggunakan nilai laju pembelajaran (α) yang meningkat dari 0.1 sampai 0.9 sedangkan nilai momentum (β) yang digunakan akan menurun dari 0.9 sampai 0.1.

3.5.2 Metode pelatihan dengan jaringan saraf propagasi balik 3 faktor

Pelatihan dengan jaringan saraf propagasi balik dengan 3 faktor, yaitu laju pembelajaran (α), momentum (β) dan faktor proporsional (γ) dilakukan berdasarkan algoritma berikut ini:

Step 1: Inisialisasi bobot-bobot awal dari setiap lapisan Step 2: Set epoch maksimum = 1000,

Kesalahan pelatihan maksimum = 0.01, epoch = 0 Step 3: Epoch = epoch + 1

Step 4: For p =1 to banyak data pelatihan do

(50)

tersembunyi (ipj)

Step4d: Hitung net input dari setiap neuron k pada lapisan

keluaran(neto_pk)

Step4f: Hitung nilai keluaran aktual dari setiap neuron k pada

lapisan keluaran (opk)

Step4g: Hitung kesalahan dari setiap neuron k pada lapisan

keluaran(_pko ) o pk

 = (y_pk o_pk) o_pk (1o_pk)

Step4h: Hitung kesalahan dari setiap neuron j pada lapisan

tersembunyi(_pjo )

Step4j: Hitung perubahan bobot-bobot lapisan tersembunyi

( ) ( 1)

h h h

ji pj pi ji

w p   x  w p

     +  ek

Step4k: Hitung perubahan bobot-bobot lapisan keluaran

( ) ( 1)

o o o

kj pk pj kj

w p   i  w p

     +  ek

Step4l: Hitung bobot-bobot lapisan tersembunyi yang baru h

ji

w baru = wh_ji lama +  wh_ji( )p

Step4m: Hitung bobot-bobot lapisan keluaran yang baru

w_kjo baru = w_kjo lama +  w_kjo( )p Step5: End for

Step6: Hitung kesalahan pelatihan

Step7: Kerjakan step 3 sampai step 6 jika kesalahan pelatihan > kesalahan pelatihan maksimum atau epoch pelatihan < epoch pelatihan maksimum

(51)

Untuk mengamati pengaruh faktor proporsional pada penelitian ini, maka pelatihan dilakukan dengan mengimplementasikan faktor proporsional tersebut kedalam setiap kelompok pelatihan jaringan saraf propagasi balik 2 faktor dalam 3 tahap. Implementasi tahap 1 dilakukan dengan nilai faktor proporsional (γ) pada interval [0.1 , 0.9], tahap 2 pada interval [0.01 , 0.09] dan tahap 3 pada interval [0.001 , 0.009]. Setiap tahap implementasi dilakukan secara menaik dan menurun.

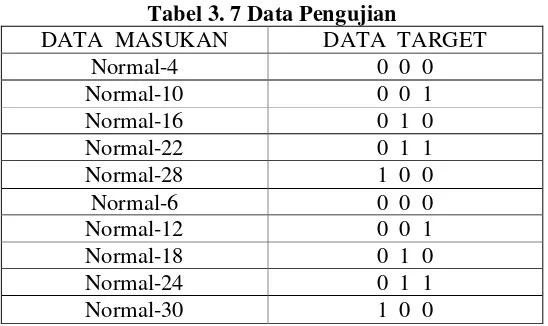
3.6 Metode Pengujian

Hasil pelatihan pada jaringan saraf adalah bobot-bobot yang telah mengalami modifikasi selama pelatihan berlangsung. Hermawan (2006, hal:102) menyatakan bahwa tujuan akhir dari seluruh proses dengan menggunakan pendekatan jaringan saraf tiruan adalah menguji seberapa besar pola atau data dikenali oleh jaringan. Dengan demikian setelah pelatihan berakhir maka selanjutnya hasil pelatihan harus diuji untuk mengetahui tingkat keberhasilan pelatihan dalam waktu pelatihan yang telah ditetapkan.

(52)

Tabel 3. 7 Data Pengujian

Proses pengujian pada penelitian ini menggunakan algoritma berikut ini Step 1: Inisialisasi bobot-bobot dari setiap lapisan dengan bobot-

bobot hasil pelatihan

Step 2: For p =1 to banyak data yang diujikan do

nilai-nilai masukan dari setiap pola masukan (xpi)

tersembunyi (neth_pj)

tersembunyi (ipj)

Step3d: Hitung net input dari setiap neuron k pada lapisan

keluaran(neto_pk)

Step3e: Hitung nilai keluaran aktual dari setiap neuron k pada

(53)

Hasil dari algoritma pengujian tersebut adalah vektor-vektor yang bernilai 0 atau 1. Dari setiap vektor keluaran yang dihasilkan tersebut maka akan dibandingkan dengan vektor-vektor target yang bersesuaian dengan data yang digunakan pada pengujian. Dengan demikian dapat diketahui kemampuan memorisasi atau kemampuan generalisasi dari jaringan saraf tersebut. Namun perlu diingat bahwa tujuan lain dari pelatihan jaringan adalah keseimbangan antara kemampuan memorisasi dan kemampuan generalisasi jaringan (Puspitaningrum, 2006).

Kemampuan memorisasi dan kemampuan generalisasi jaringan diukur dari berapa banyak pola yang dikenali, hal tersebut diketahui melalui nilai keluaran yang dihasilkan oleh jaringan saraf tersebut pada saat proses pengujian berlangsung. Kemampuan memorisasi jaringan dapat dihitung dengan rumus berikut ini:

memorisasi jumlah data yang dikenali 100 % jumlah data pelatihan

  (3. 4)

Sedangkan kemampuan generalisasi jaringan dihitung dengan rumus:

generalisasi jumlah data yang dikenali 100 % jumlah data pengujian

  (3. 5)

(54)

BAB 4

HASIL DAN PEMBAHASAN

4.1 Hasil dan Pembahasan Penelitian Jaringan Saraf Propagasi Balik dengan 2 Faktor

Penelitian pada jaringan saraf propagasi balik yang menggunakan 2 faktor dilakukan melalui 2 kelompok penelitian yang berbeda berdasarkan penggunaan nilai laju pembelajaran dan momentum. Hasil dari kelompok penelitian I adalah sebagai berikut

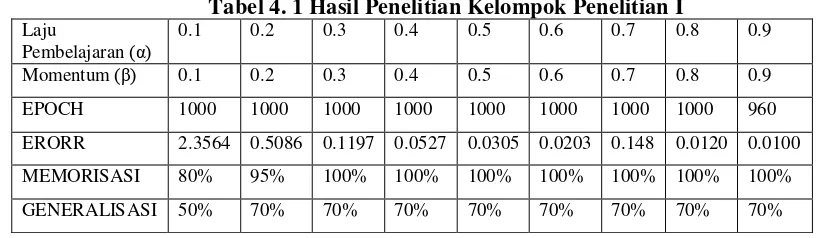
Tabel 4. 1 Hasil Penelitian Kelompok Penelitian I Laju

Pembelajaran (α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum (β) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 960

ERORR 2.3564 0.5086 0.1197 0.0527 0.0305 0.0203 0.148 0.0120 0.0100

MEMORISASI 80% 95% 100% 100% 100% 100% 100% 100% 100%

GENERALISASI 50% 70% 70% 70% 70% 70% 70% 70% 70%

Hasil diatas menunjukkan bahwa nilai kesalahan pelatihan yang dihasilkan dari setiap percobaan terus menurun dan pada akhir percobaan (percobaan 9) kesalahan pelatihan yang dihasilkan bisa mencapai kesalahan pelatihan yang diinginkan dalam 960 epoch. Kemampuan memorisasi jaringan juga terus meningkat sampai 100 %. Kemampuan generalisasi juga terus meningkat sampai 70 %. Untuk melakukan pengamatan terhadap konvergensi jaringan dapat dilakukan melalui pengamatan terhadap grafik selama pelatihan berikut ini

(55)

0 100 200 300 400 500 600 700 800 900 1000

Gambar 4. 1 Grafik Pelatihan Kelompok Penelitian I

Dari gambar tersebut dapat dilihat bahwa tingkat konvergensi jaringan selama pelatihan sangat baik karena setiap percobaan terus mengalami konvergensi ke arah yang diinginkan. Dari grafik-grafik tersebut dapat juga diketahui bahwa kesalahan pelatihan yang dihasilkan pada setiap epoch pelatihan mengalami penurunan. Kesalahan pelatihan dari percobaan 1 sampai percobaan 9 juga mengalami penurunan.

Hasil dari kelompok penelitian II juga tidak jauh berbeda dari hasil penelitian kelompok sebelumnya, hal ini dapat dilihat pada tabel berikut

Tabel 4.2 Hasil Penelitian Kelompok Penelitian II Laju

(56)

EPOCH PELATIHAN

S

E

0 100 200 300 400 500 600 700 800 900 1000 1

2 3 4 5 6

percobaan1 percobaan2 percobaan3 percobaan4 percobaan5 percobaan6 percobaan7 percobaan8 percobaan9

Gambar4. 2 Grafik Pelatihan Kelompok Penelitian II

(57)

4.2 Hasil dan Pembahasan Penelitian Jaringan Saraf Propagasi Balik dengan 3 Faktor

Untuk mengamati pengaruh faktor proporsional (γ) pada jaringan saraf propagasi balik untuk pengenalan wajah berbasis eigenfaces maka faktor proporsional (γ) diimplementasikan melalui 3 tahap. Hal tersebut dilakukan untuk mengetahui bagaimana ukuran faktor proporsional dalam mempengaruhi kinerja jaringan saraf.

4.2.1 Hasil dan pembahasan implementasi tahap 1

Implementasi tahap 1 dilakukan dengan menggunakan nilai faktor proporsional (γ) pada interval [0.1 , 0.9]. Hasil implementasi pada kelompok penelitian I adalah sebagai berikut

Tabel 4.3 Hasil Penelitian Implementasi Menaik Tahap 1 Pada Kelompok Penelitian I

(58)

Dari hasil tersebut dapat dilihat bahwa kesalahan pelatihan yang dihasilkan pada setiap percobaan tidak mengalami penurunan. Kesalahan pelatihan yang dihasilkan juga tidak stabil. Kesalahan pelatihan terkecil hanya bisa mencapai 6.4025. Kemampuan memorisasi terbaik sangat rendah, hanya mencapai 35 % pada percobaan 6 dari implementasi menurun . Kemampuan generalisasi terbaik juga hanya mencapai 40 %, yaitu pada percobaan 6 dari implementasi menaik . Grafik selama pelatihan dari penelitian diatas adalah sebagai berikut

0 100 200 300 400 500 600 700 800 900 1000

(59)

Kedua grafik tersebut menggambarkan tingkat konvergensi dari implementasi faktor proporsional tahap 1 pada kelompok pelatihan I. Kedua grafik tersebut menunjukkan bahwa selama pelatihan berlangsung kesalahan pelatihan yang dihasilkan tidak konvergen kearah yang diinginkan. Dengan demikian implementasi tahap 1 pada kelompok pelatihan I telah membuat ketidakstabilan konvergensi.

Tabel 4.5 Hasil Penelitian Implementasi Menaik Tahap 1 Pada Kelompok Penelitian II

Tabel 4.6 Hasil Penelitian Implementasi Menurun Tahap 1 Pada Kelompok Penelitian II

(60)

sangat rendah, hanya mencapai 35 % dan 40 % untuk kemampuan memorisasi dan

Gambar 4.4 Grafik Pelatihan Dengan Implementasi Faktor Proporsional Tahap 1 Pada Kelompok Penelitian II

(61)

Implementasi tahap 2 dilakukan dengan menggunakan nilai faktor proporsional (γ) pada interval [ 0.01 , 0.09 ]. Implementasi tersebut dilakukan secara menaik dan menurun terhadap setiap kelompok penelitian.

Tabel 4.7 Hasil Penelitian Implementasi Menaik Tahap 2 Pada Kelompok Penelitian I

Tabel 4.8 Hasil Penelitian Implementasi Menurun Tahap 2 Pada Kelompok Penelitian I

Dari tabel-tabel diatas dapat kita lihat bahwa pada percobaan-percobaan awal implementasi yang dilakukan secara menaik, kesalahan pelatihan yang dihasilkan dapat mengalami penurunan sampai mencapai 2.4545 pada percobaan 3. Pada percobaan-percobaan berikutnya kesalahan pelatihan yang dihasilkan terus mengalami peningkatan seiring dengan meningkatnya nilai faktor proporsional yang digunakan. Hal yang sama juga terjadi pada kemampuan memorisasi dan generalisasi jaringan. Pada implementasi menurun kesalahan pelatihan yang dihasilkan dapat mencapai 0.0112 pada percobaan 9, dengan kemampuan memorisasi 100% dan kemampuan generalisasi 70%.

(62)

0 100 200 300 400 500 600 700 800 900 1000

Gambar 4.5 Grafik Pelatihan Dengan Implementasi Faktor Proporsional Tahap 2 Pada Kelompok Penelitian I

(63)

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

Faktor Proporsional(γ)

0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 2.4752 1.8734 2.2410 2.2113 6.6815 6.8198 7.2399 8.6536 8.9999

MEMORISASI 55% 75% 75% 70% 20% 20% 20% 20% 20%

GENERALISASI 30% 50% 30% 30% 20% 20% 20% 20% 20%

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 6.6821 6.7418 6.7544 6.7341 6.6815 6.6077 6.5453 5.1910 4.5944

MEMORISASI 20% 20% 20% 20% 20% 20% 20% 35% 50%

GENERALISASI 20% 20% 20% 20% 20% 20% 20% 40% 30%

(64)

0 100 200 300 400 500 600 700 800 900 1000

Gambar 4.6 Grafik Pelatihan Dengan implementasi Faktor Proporsional Tahap 2 Pada Kelompok Penelitian II

(65)

Implementasi tahap 3 dilakukan dengan menggunakan nilai faktor proporsional (γ) pada interval [ 0.001 , 0.009 ]. Implementasi tersebut dilakukan secara menaik dan menurun terhadap setiap kelompok penelitian.

Tabel 4.11 Hasil Penelitian Implementasi Menaik Tahap 3 Pada Kelompok Penelitian I

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 2.5138 0.6405 0.1480 0.0619 0.0368 0.0243 0.0219 0.0143 0.0109

MEMORISASI 70% 95% 100% 100% 100% 100% 100% 100% 100%

GENERALISASI 50% 70% 70% 70% 70% 70% 80% 80% 80%

Tabel 4.12 Hasil Penelitian Implementasi Menurun Tahap 3 Pada Kelompok Penelitian I

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

0.009 0.008 0.007 0.006 0.005 0.004 0.003 0.002 0.001

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 4.3215 1.4221 0.3599 0.0711 0.0368 0.0223 0.0164 0.0117 0.0102

MEMORISASI 40% 95% 95% 100% 100% 100% 100% 100% 100%

GENERALISASI 20% 50% 70% 80% 70% 70% 70% 70% 70%

(66)

0 100 200 300 400 500 600 700 800 900 1000

Gambar 4.7 Grafik Pelatihan Dengan Implementasi Faktor Proporsional Tahap 3 Pada Kelompok Penelitian I

(67)

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 0.9707 0.1795 0.0678 0.0488 0.0368 0.0294 0.0252 0.0224 0.0204

MEMORISASI 95% 100% 100% 100% 100% 100% 100% 100% 100%

GENERALISASI 70% 70% 70% 80% 70% 70% 70% 70% 70%

Laju

Pembelajaran(α)

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Momentum(β) 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1

0.009 0.008 0.007 0.006 0.005 0.004 0.003 0.002 0.001

EPOCH 1000 1000 1000 1000 1000 1000 1000 1000 1000

ERORR 2.4227 0.4345 0.1333 0.0564 0.0368 0.0279 0.0247 0.0210 0.0201

MEMORISASI 70% 95% 100% 100% 100% 100% 100% 100% 100%

GENERALISASI 50% 70% 80% 80% 70% 70% 70% 70% 70%

(68)

0 100 200 300 400 500 600 700 800 900 1000

Gambar 4.8 Grafik Pelatihan Dengan Implementasi Faktor Proporsional Tahap 3 Pada Kelompok Penelitian II.

(69)

BAB 5

PENUTUP

Setelah melakukan evaluasi terhadap kinerja dari jaringan saraf propagasi balik dengan 2 faktor dan jaringan saraf propagasi balik dengan 3 faktor, maka pada bab ini akan disimpulkan mengenai pengaruh faktor proporsional pada jaringan saraf propagasi balik untuk pengenalan wajah berbasis eigenfaces. Pada bab ini penulis juga menyarankan hal-hal yang berkaitan dengan pengembangan penelitian selanjutnya mengenai implementasi faktor proporsional pada jaringan saraf propagasi balik.

5.1 Kesimpulan

Dari hasil evaluasi terhadap kinerja jaringan saraf propagasi balik dengan 2 faktor dan 3 faktor maka dapat disimpulkan bahwa:

1. Penggunaan faktor proporsional (γ) dalam interval [ 0.1 , 0.9 ] mengakibatkan: jaringan tidak konvergen dan tingkat konvergensinya juga tidak stabil. Hal ini berarti bahwa kesalahan-kesalahan pelatihan yang dihasilkan pada setiap epoch pelatihan tidak mengalami penurunan menuju nilai kesalahan pelatihan yang diinginkan.