YUYUN KHAIRUNISA
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2015
PEMODELAN SUPPORT VECTOR MACHINE QUANTILE REGRESSION
UNTUK PREDIKSI CURAH HUJAN BULANAN PADA MUSIM KEMARAU
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
*Dengan ini saya menyatakan bahwa tesis Pemodelan Support Vector Machine Quantile Regression untuk prediksi total curah hujan bulanan pada musim kemarau studi kasus Kabupaten Indramayu adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Agustus 2015 Yuyun Khairunisa NIM G651130261
*
RINGKASAN
YUYUN KHAIRUNISA. Pemodelan Support Vector Machine Quantile Regression untuk Prediksi Curah Hujan Bulanan pada Musim Kemarau Studi Kasus Kabupaten Indramayu. Komisi Pembimbing AGUS BUONO dan AJI HAMIM WIGENA.
Curah hujan adalah salah satu unsur cuaca yang memiliki besar pengaruhnya terhadap sektor pertanian di Indonesia. Sejak tahun 1990, banyak daerah di Indonesia sering dilanda kekeringan dan kebanjiran sebagai dampak dari iklim yang ekstrim. Akibatnya, kegagalan panen atau puso melanda ratusan hektar sawah di Jawa (Iskandar, 2007). General Circulation Model (GCM) merupakan alat utama yang dikembangkan oleh para peneliti untuk mempelajari dan memprediksi perubahan iklim. Prediksi iklim menggunakan mesin pembelajaran dapat diterapkan untuk membantu membuat keputusan di masa depan. Salah satu aplikasi dari mesin pembelajaran yang paling maju adalah Support Vector Machine yang dapat digunakan dalam kasus-kasus klasifikasi dan regresi. Tujuan dari penelitian ini adalah mengembangkan model Statistical Downscaling menggunakan SVMQR dalam memprediksi curah hujan di musim kemarau serta merekomendasikan model GCM dengan kinerja paling baik yang dapat digunakan untuk melakukan prediksi curah hujan bulanan pada musim kemarau di Kabupaten Indramayu.
Penelitian ini mengembangkan metode Support Vector Machine Quantile Regression (SVMQR) dalam memprediksi total curah hujan selama musim kemarau di Kabupaten Indramayu. Fungsi regresi SVMQR didekati menggunakan
hyperplane Quantile Regression (QR). QR teknik memiliki kemampuan prediksi dari nilai ekstrim berdasarkan fungsi kuantil yang ditentukan (Koenker 2005).
Radial Basis Function (RBF) digunakan sebagai kernel SVMQR. Pencarian parameter yang optimal dilakukan dengan menggunakan metode grid search. Curah hujan bulanan pada musim kemarau yaitu bulan Mei, Juni, Juli dan Agustus diprediksi berdasarkan nilai kuantil yang diperoleh dari posisi distribusi data. Model dengan kinerja paling baik adalah model yang memiliki nilai korelasi terbesar dan nilai Root Mean Square Error (RMSE) terkecil.
Model yang paling direkomendasikan untuk digunakan dalam memprediksi curah hujan bulan Mei, Juni, Juli dan Agustus adalah model GCM CMC1-CanCM3. Korelasi yang dihasilkan model GCM CMC1-CanCM3 untuk prediksi bulan Agustus adalah 99% dengan nilai RMSEP 0.01. Prediksi model GCM CMC1-CanCM3 untuk bulan Mei, Juni dan Juli adalah 99%, 82% dan 95% dengan nilai RMSEP 0.05, 22 dan 8.9. Secara umum, hasil prediksi yang dihasilkan dengan metode SVMQR untuk menduga curah hujan bulan Mei Juni Juli dan Agustus cukup akurat dengan nilai korelasi yang hampir mendekati satu dan nilai RMSE yang kecil.
SUMMARY
YUYUN KHAIRUNISA. Support Vector Machine Quantile Regression Modelling for Monthly Rainfall Prediction in The Dry Season in Indramayu District. Supervised by AGUS BUONO and AJI HAMIM WIGENA.
Rainfall is one of the elements of weather that has great affects to the agricultural sector in Indonesia. Since 1990, many regions in Indonesia is often hit by drought and flooding as the effect of extreme climate. As a result, hundreds of hectares of rice fields in Java sweep over by crop failures or called puso (Iskandar, 2007). Today GCM is the main tool to study and predict climate change. Climate prediction using machine learning can be applied to help make decisions in the future. One of the most advanced machine learning application is the Support Vector Machine that can be used in cases of classification and regression.
This study developed Support Vector Machine Regression quantile (SVMQR) method in predicting total rainfall during the dry season in Indramayu. Regression function on SVMQR was approximated by Quantile Regression (QR) hyperplane. QR technique has the predictive ability of the extreme value based on a specified quantile function (Koenker 2005). Radial Basis Function (RBF) was used as SVMQR kernel. The searching of the optimal parameters was conducted using a grid search algorithm. In this study, dry season rainfall on May, June, July and August predicted monthly based on the value obtained quantile in the every position of data distribution. The recommended model was the model which had the biggest correlation value and smallest Root Mean Square Error (RMSE) value.
The Most recommended model for predicting rainfall in May, June, July and August is CanCM3 GCM model. The correlation value of CMC1-value near to one and RMSE CMC1-values was small.
© Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Ilmu Komputer
PEMODELAN SUPPORT VECTOR MACHINE QUANTILE REGRESSION
UNTUK PREDIKSI TOTAL CURAH HUJAN BULANAN PADA MUSIM KEMARAU
STUDI KASUS KABUPATEN INDRAMAYU
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2015
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah Subhanahu Wa Ta’ala atas segala karunia-Nya sehingga tesis berjudul Pemodelan Support Vector Machine Quantile Regression untuk Prediksi Total Curah Hujan Bulanan Pada Musim Kemarau Di Kabupaten Indramayu berhasil diselesaikan.
Terima kasih penulis ucapkan kepada Bapak Dr Ir Agus Buono, MSi MKom dan Bapak Dr. Ir. Aji Hamim Wigena, MSc atas ilmu, saran dan bimbingannya serta kepada Bapak Irman Hermadi, SSi MS PhD sebagai penguji tugas akhir. Terima kasih penulis ucapkan kepada Dr. Insuk Sohn yang telah memberikan masukan mengenai algoritme SVMQR yang lebih efisien pada penelitian ini.
Terima kasih penulis ucapkan kepada Suami (Dedek Hendrianto) yang telah mendukung penyelesaian studi, juga kepada Ayah (Suwarto), Ibu (Khairul Maliyah) dan Ananda (Khanza Zhafira M) yang telah menjadi inspirasi hidup, sumber kekuatan, motivasi dan doa. Terima Kasih kepada adik-adik (Irfan, Beryl, Sirly) serta seluruh keluarga, atas segala doa, dukungan dan kasih sayangnya. Ucapan terima kasih juga untuk teman-teman satu kos (Mulyati, Fuzy Yustika, Melly Br Bangun) dan satu lab Computational Intelligence (Mustakim, Abdul Basith Hermanianto, Fildza Novadiwanti), yang telah membantu dan banyak memberi masukan dalam penyelesaian tugas akhir. Penulis mengucapkan terima kasih kepada rekan-rekan Pascasarjana Ilmu Komputer 2013 yang telah memberi dukungan dan semangat.
Terima kasih penulis ucapkan kepada seluruh dosen Ilmu Komputer atas ilmu dan bimbingannya semoga menjadi ilmu yang berkah. Dinas Pendidikan Perguruan Tinggi (DIKTI) atas bantuan Beasiswa Pendidikan Pascasarjana Dalam Negeri (BPPDN) untuk penyelesain penelitian.
Semoga karya ilmiah ini bermanfaat.
DAFTAR TABEL
1 Hasil luaran PCA data GCM 11
2 Ringkasan nilai RMSE dan Korelasi (R) pada masing-masing kuantil 15
DAFTAR GAMBAR 1 Ilustrasi GCM (NOAA 2012) ... 4
2 Metode penelitian... 5
3 Ilustrasi Downscaling (JAMSTEC 2015) ... 6
4 Ilustrasi algoritme grid search (Agmalaro 2011) ... 11
5 Ilustrasi diagram taylor (Taylor 2001) ... 12
6 Histogram karakteristik data curah hujan pada Kabupaten Indramayu ... 14
7 Boxplot karakteristik data curah hujan pada Kabupaten Indramayu ... 14
8 Plot data observasi dan hasil prediksi keseluruhan model SVMQR pada kuantil ke-3 ... 15
9 Plot data observasi dan hasil prediksi keseluruhan model SVMQR pada kuantil ke-18 ... 15
10 Plot data observasi dan hasil prediksi keseluruhan model SVMQR pada kuantil ke-28 ... 16
11 Plot data observasi dan hasil prediksi keseluruhan model SVMQR pada kuantil ke-45 ... 17
12 Diagram Taylor hasil pemodelan SVMQR pada bulan Mei ... 18
13 Diagram Taylor hasil pemodelan SVMQR pada bulan Juni ... 19
14 Diagram Taylor hasil pemodelan SVMQR pada bulan Juli ... 20
15 Diagram Taylor hasil pemodelan SVMQR pada bulan Agustus ... 20
15 Contoh garis pemodelan QR (Koenker 2005) 26
DAFTAR LAMPIRAN 1 Ilustrasi Quantile Regression (QR) 26
2 Algoritme SupportVector Machine Quantile Regression (SVMQR) 30
3 Hasil prediksi SVMQR pada kuantil ke-3 31
4 Hasil prediksi SVMQR pada kuantil ke-18 33
5 Hasil prediksi SVMQR pada kuantil ke-28 35
1 PENDAHULUAN
Latar Belakang
Curah hujan merupakan salah satu unsur cuaca yang sangat berpengaruh terhadap sektor pertanian. Keteraturan pola dan distribusi curah hujan disuatu wilayah merupakan jaminan berlangsungnya aktifitas pertanian (Estiningtyas et al. 2007). Sejak tahun 1990-an, berbagai kawasan di Indonesia sering dilanda kekeringan dan kebanjiran. Akibatnya, tiap terjadi kekeringan ratusan hektar sawah di Pulau Jawa mengalami gagal panen atau puso (Iskandar 2007). Kabupaten Indramayu merupakan salah satu sentra produksi pertanian di Indonesia dengan produk utama berupa padi. Kekeringan pada musim kemarau merupakan faktor utama penyebab gagal panen di Kabupaten Indramayu (79.8 %) setelah serangan hama (15,6%) dan bencana banjir (5,6%) (Estiningtyas 2012). Oleh karena itu, prediksi curah hujan musim kemarau perlu dilakukan sebagai langkah antisipasi atau mitigasi oleh pihak terkait terhadap bencana kekeringan di Kabupaten Indramayu.
Keteraturan pola curah hujan erat kaitannya dengan keteraturan iklim. Salah satu pendekatan untuk memodelkan iklim adalah dengan mengaplikasikan model komputer digital yang disebut General Circulation Model (GCM). GCM dibuat berdasarkan kaidah-kaidah fisika atmosfer untuk memodelkan sistem iklim bumi. Namun skala spasial yang digunakan dalam GCM masih bersifat kasar atau global. Hasil ini tentu saja tidak dapat menjelaskan variabilitas dalam skala lokal yang lebih detail, sehingga untuk memenuhi kebutuhan informasi dalam sektor pertanian GCM tidak mempunyai arti yang nyata. Salah satu cara untuk menurunkan ukuran skala spasialnya digunakan metode Downscaling (Haryoko 2004).
Prediksi iklim menggunakan machine learning dapat diaplikasikan untuk membantu pengambilan keputusan di masa depan. Salah satu penerapan machine learning yang paling mutakhir adalah Support Vector Machine yang dapat digunakan pada kasus klasifikasi maupun regresi. Metode Support Vector Regression (SVR) merupakan perluasan dari Support Vector Machine untuk kasus regresi dengan output bilangan riil atau kontinyu. SVR digunakan dalam prediksi cuaca dan iklim didasarkan performa teknik ini dalam prediksi data time series serta model yang dihasilkan dapat mengatasi overfitting (Smola dan Schölkopf 2003). Hyperplane (garis pemisah) pada SVR menggunakan hyperplane regresi linear. Dalam penelitian ini metode Support Vector Machine Quantile Regression (SVMQR) diaplikasikan dalam memprediksi total curah hujan pada musim kemarau di Kabupaten Indramayu. Fungsi regresi pada SVMQR menggunakan hyperplane Quantile Regression (QR). Teknik Quantile Regression memiliki kemampuan prediksi pada nilai ekstrim berdasarkan nilai quantile yang ditentukan (Koenker 2005).
Perumusan Masalah
2
1. Bagaimana pengembangan metode SVMQR dalam prediksi curah hujan pada kondisi ekstrim kering atau musim kemarau?
2. Diantara kelima model GCM yaitu model CMC1-CanCM3, CMC2-CanCM4, NCEP-CFSv1, NASA-GMAO-062012 dan GFDL-CM2p1 manakah yang memiliki kinerja paling baik dalam memprediksi total curah hujan pada musim kemarau di Kabupaten Indramayu?
Tujuan Penelitian
Tujuan dari penelitian ini adalah :
1. Mengembangkan model statistical downscaling menggunakan SVMQR dalam memprediksi curah hujan di musim kemarau di Kabupaten Indramayu.
2. Merekomendasikan model GCM dengan kinerja paling baik yang dapat digunakan untuk melakukan prediksi curah hujan bulanan pada musim kemarau di Kabupaten Indramayu.
Manfaat Penelitian
Manfaat yang diharapkan melalui penelitian ini adalah dihasilkan suatu model SVMQR dari Statistical Downscaling luaran GCM untuk prediksi total curah hujan di musim kemarau di Kabupaten Indramayu. Sehingga dapat dijadikan referensi melakukan pendugaan curah hujan pada musim kemarau dengan lebih baik.
Ruang Lingkup Penelitian
Beberapa ruang lingkup yang digunakan pada penelitian ini diantaranya :
1. Data curah hujan yang digunakan berasal dari 15 stasiun hujan di Kabupaten Indramayu tahun 1980 sampai dengan 2008.
2. Total curah hujan yang akan diprediksi adalah total curah hujan musim kemarau yaitu bulan Mei, Juni, Juli dan Agustus.
Penelitian Terkait
ekstrim di Kabupaten Indramayu, hasil penelitian menunjukkan bahwa peluang kejadian curah hujan ekstrim di quantile 90 dan 95 cukup efektif untuk menduga nilai ekstrim basah. Menurut Djuraidah dan Wigena (2011) yang telah menggunakan QR untuk mengeksplorasi curah hujan di kabupaten Indramayu, regresi quantile dapat digunakan untuk mendeteksi kondisi-kondisi ekstrim, baik ekstrim kering (quantile ke-5) maupun ekstrim basah (quantile ke-95).
Hwang et al. (2008) menggabungkan metode Support Vector Machine dan Quantile Regression (SVMQR) untuk kasus linear dan nonlinear, yang dilakukan dengan membangkitkan 100 dataset secara acak. Penelitian tersebut juga membandingkan akurasi metode SVMQR dengan QR konvensional dan hasilnya adalah SVMQR memiliki nilai akurasi yang lebih tinggi dibandingkan QR dibuktikan dengan nilai standar eror SVMQR yang lebih kecil untuk fungsi quantile = 0.1, = 0.5 dan = 0.9. Metode SVMQR pada kasus nonlinear pernah diterapkan oleh Sohn et al. (2008) menggunakan Iterative Reweighted Least Square (IRWLS) berdasarkan metode newton. Metode SVMQR memiliki performa yang lebih baik pada situasi dimana variabilitas error pada setiap data bersifat heterogen dalam jangkauan intensitas tertentu.
2 TINJAUAN PUSTAKA
Curah hujan musim kemarau
Curah hujan merupakan ketinggian air hujan yang terkumpul dalam tempat yang datar, tidak menguap, tidak meresap, dan tidak mengalir. Curah hujan 1 (satu) millimeter, artinya dalam luasan satu meter persegi pada tempat yang datar tertampung air setinggi satu millimeter atau tertampung air sebanyak satu liter (BMKG 2012).
4
General Circulation Model (GCM)
Para peneliti membangun sebuah model untuk memahami perubahan iklim yang kompleks dengan beberapa pendekatan, salah satunya adalah dengan membangun model yang mengaplikasikan komputer digital yang disebut Global Circulation Model (GCM). GCM adalah model dinamik yang didasarkan pemahaman yang mendalam mengenai sistem iklim saat ini untuk mensimulasi proses-proses fisik atmosfer dan lautan, yang dapat mengesimasi iklim global. Model ini telah dikembangkan dua dekade terakhir dan membutuhkan komputasi yang ekstensif untuk menjalankannya. Tujuan utama model iklim khususnya GCM adalah untuk menggambarkan secara kuantitatif terjadinya perubahan iklim seperti curah hujan, suhu, tekanan udara, dan radiasi akibat terjadinya perubahan konsentrasi CO2 di atmosfer. Ilustrasi GCM tertera pada Gambar 1.
Gambar 1 Ilustrasi GCM (NOAA 2012)
3 METODE PENELITIAN
Identifikasi dan Perumusan Masalah
Penelitian ini dilatarbelakangi oleh perlunya pengembangan metode prediksi total curah hujan di musim kemarau yang lebih akurat dan mampu menjangkau kondisi ekstrim. Sehingga penelitian ini bertujuan untuk mengembangkan model Support Vector Machine Quantile Regression (SVMQR) untuk prediksi total curah hujan musim kemarau di Kabupaten Indramayu. Penelusuran literatur yang berasal dari buku, jurnal ilmiah maupun situs badan resmi milik pemerintah diperlukan untuk mencapai tujuan penelitian. Penelusuran literatur yang diperlukan terkait dengan GCM, Downscaling, curah hujan musim kemarau, PCA dan SVMQR.
6
Penentuan variabel respon dan prediktor
Data yang digunakan sebagai prediktor adalah data luaran GCM dengan peubah presipitasi. Sedangkan data curah hujan pada musim kemarau yaitu pada bulan Mei, Juni, Juli dan Agustus digunakan sebagai data yang akan diprediksi.
Pengumpulan data
Terdapat dua jenis data yang digunakan dalam penelitian ini, yaitu data curah hujan sebagai peubah respon dan data luaran GCM sebagai prediktor. Data curah hujan yang dimaksud adalah curah hujan pada musim kemarau di Kabupaten Indramayu yaitu curah hujan pada bulan Mei, Juni, Juli dan Agustus periode tahun 1981 sampai dengan tahun 2008. Data curah hujan merupakan data sekunder yang diambil dari 15 stasiun hujan di Kabupaten Indramayu yaitu Stasiun Bangkir, Bulak, Bondan, Cidempet, Cikedung, Juntinyuat, Kedokan Bunder, Krangkeng, Losarang, Lohbener, Sukadana, Sumurwatu, Sudimampir, Tugu dan Ujung Garis. Data curah hujan berasal dari Badan Meteorologi Klimatologi dan Geofisika (BMKG).
Peubah prediktor GCM yang digunakan adalah luaran presipitasi hindcast dari lima model yaitu CMC1-CanCM3, CMC2-CanCM4, NCEP-CFSv1, NASA-GMAO-062012 dan GFDL-CM2p5-FLOR-A06 yang diperoleh dari Internasional Research Institute Data Library (IRIDL) dan dapat diunduh pada situs web www.iridl.ldeo.columbia.edu. Downscaling luaran GCM dalam penelitian ini menggunakan grid berukuran persegi berukuran 5 × 5 dengan resolusi 1° × 1° untuk setiap grid pada 106°- 110° BT dan 59°- 63° LS di atas sekitar wilayah Indramayu.
Teknik downscaling dapat didefinisikan sebagai suatu proses transformasi data dari suatu grid dengan unit skala besar menjadi data pada grid-grid dengan unit yang lebih kecil (Wigena, 2006). Ilustrasi proses downscaling tertera pada Gambar 3.
Statistical Downscaling (SD) menggunakan fungsi transfer yang menggambarkan hubungan fungsional sirkulasi atmosfer global dengan unsur-unsur iklim lokal, secara umum persamaan SD adalah sebagai berikut (Buono et al. 2010):
= ) (1)
Dimana :
Y = peubah iklim lokal (variabel respon iklim) X = peubah luaran GCM
PCA adalah sebuah teknik untuk membangun variabel-variabel baru yang merupakan kombinasi linear dari variabel-variabel asli. Jumlah maksimum dari variabel baru ini akan sama dengan jumlah dari variabel lama, dan variabel-variabel baru ini tidak saling berkorelasi satu sama lain. Variabel-variabel-variabel baru disebut juga sebagai principle component. PCA merupakan metode yang banyak digunakan untuk mereduksi sejumlah dimensi, misalkan p, dari sebuah dataset (variabel) menjadi q variabel baru, dengan q p. Setiap q variabel baru hasil reduksi merupakan kombinasi linear dari p variabel asal, dengan variansi yang dimiliki oleh p variabel asal, sebagian besar dapat diterangkan oleh q variabel baru. (Djakaria et al. 2010). PCA akan cukup efektif jika antar p peubah asal memiliki korelasi yang cukup tinggi.
Objek pengamatan pada penelitian ini adalah vektor grid dengan dimensi p peubah. Grid= [grid1 grid2 grid3… gridp] yang akan direduksi menjadi vektor Y = [y1
y2 y3 … yq], dimana q < p. Dalam bentuk matematis, vektor Y merupakan kombinasi
linear dari variabel-variabel grid1, grid2 ,grid3,… gridp yang dapat dinyatakan sebagai:
Y = w1grid1 + w2grid2+…. + wpgridp (2)
dengan
wi adalah bobot atau koefisien untuk variabel ke-i
gridi adalah nilai peubah grid ke-i
Y adalah kombinasi linear dari peubah grid
PCA menentukan suatu metode untuk mendapatkan nilai-nilai koefisien atau bobot dari kombinasi linier variabel-variabel pembentuknya dengan ketentuan sebagai berikut:
8
c. Komponen utama dibentuk berdasarkan urutan varians dari yang terbesar hingga yang terkecil, dalam arti sebagai berikut :
• Principal Component pertama (PC1) merupakan kombinasi linier dari seluruh variabel yang diamati dan memiliki varians terbesar
• Principal Component kedua (PC2) merupakan kombinasi linier dari seluruh variabel yang diamati yang bersifat ortogonal terhadap PC1 dan memiliki varians kedua terbesar
• Principal Component ke p (PCp) merupakan kombinasi linier dari seluruh variabel yang diamati yang bersifat ortogonal terhadap PC1, PC2, … , PC(p -1) dan memiliki varians yang terkecil.
Permasalahan yang ada adalah bagaimana menentukan vektor koefisien w
sebagai peubah baru yang dapat menangkap keragaman dari peubah asal (vektor grid). Dengan kata lain vektor w harus mampu memaksimumkan varians dari Yp,p = 1,2,3,..,n , yang diformulasikan sebagai (Johnson 1998) :
Var(yi)= = ∑ (3)
dimana Σ adalah matriks kovarians dari vektor Grid.
Proses reduksi dimensi harus menentukan berapa banyak komponen utama yang mesti diambil. Ada beberapa cara untuk menentukan berapa banyak komponen utama yang harus diambil diantaranya adalah menggunakan proporsi kumulatif varians terhadap total varians.
Data observasi yang dipilih terdiri dari 28 periode yaitu tahun 1981-2008, sehingga data GCM yang digunakan juga memiliki periode yang sama yakni tahun 1981-2008. Grid yang digunakan adalah 5 × 5. Jumlah keseluruhan untuk data input menjadi cukup besar yaitu 336 (28 × 12) data dengan atribut data GCM sebanyak 25 (5 × 5) buah. Sehingga total data yang digunakan sebelum proses PCA adalah 8400 data. Data tersebut cukup besar sehingga diperlukan metode PCA untuk membentuk variabel baru dengan dimensi yang lebih kecil. Principle Component yang diambil dalam penelitian ini adalah 2 (dua) principle component. Sehingga total data yang digunakan setelah dilakukan proses PCA adalah 672 (28 × 12 × 2) data.
Pembagian data
Metode pembagian data latih dan data uji yang digunakan dalam penelitian ini adalah K-fold Cross Validation dengan K sebanyak 10. Algoritme dari K-fold Cross Validation dapat dijelaskan dengan langkah-langkah berikut:
1. Kelompokkan data ke sejumlah 10 bagian yang sama besar.
2. Pada bagian ke-K, bagian K-1 data lainnya digunakan sebagai data latih, model prediksi yang dihasilkan kemudian dicobakan pada bagian ke-K untuk mendapatkan nilai prediksi error.
Pembagian data pada langkah 1 dilakukan tanpa pengacakan data terlebih dahulu dikarenakan penelitian ini menggunakan data deret waktu. Keuntungan dari menggunakan metode K-fold Cross Validation adalah semua data digunakan baik sebagai data latih maupun data uji.
Pemodelan Support Vector Machine Quantile Regression
Diberikan data training (xi,yi) Rd × R, i=1,2,…..,n. Model Quantile
Regression (QR) diperkenalkan oleh Koenker dan Basset (1978) sebagai berikut :
) = untuk (0,1) (4)
dimana adalah penduga parameter QR yang merupakan solusi dari
∑ ) untuk θ (0,1) (5) merupakan fungsi cek yang didefinisikan sebagai
(r)= θrI(r≥0)+ (θ-1)rI(r<0)untuk θ (0,1) (6)
dimana I(.) adalah fungsi identitas.
SVR menggunakan hyperplane regresi linear dalam mengaproksimasi fungsi dari data, sedangkan SVMQR menggunakan QR sebagai fungsi yang mengaproksimasi data. Ilustrasi sederhana dari QR tertera pada lampiran 2. QR dapat bekerja dengan kernel SVR dengan mengganti parameter loss function. Parameter loss function pada SVR disebut dengan ε-insensitive, Sedangkan dalam SVMQR parameter loss function (ψ(ξ) yang digunakan adalah pinball loss function (Hwang, 2005) dimana ψ(ξ) = (1- ) ψ jika ψ < 0 dan ψ(ξ) = jika ψ > 0. Sehingga implementasi regresi kuantil pada SVR dengan formulasi sebagai berikut:
Minimasi ½||w||2 + C ∑ untuk (0,1) (7) batas atas error pada pelatihan sedangkan merupakan batas bawah error pelatihan. Konstanta C merupakan nilai tawar menawar ketipisan fungsi f dan jumlah deviasi yang ditolerir. Persamaan (7) lebih mudah diselesaikan dengan membangun fungsi Lagrange sebagai berikut:
∑ + (1- - ∑ + + wt ) - ∑ + -
wt ) - ∑ + ) (8)
Setelah persamaan (8) diturunkan parsial terhadap w, kemudian disubstitusikan kembali pada persamaan (8) didapatkan masalah optimisasi sebagai berikut :
∑ ∑ (9)
10
̂ = ∑ ̂ - ̂ ) dan ̂ ∑ ̂ - ̂ ) x (10) QR nonlinear menggunakan fungsi kuantil dari peubah respon untuk prediktor yang diasumsikan berhubungan secara nonlinear terhadap vektor input
Rd. QR nonlinear membutuhkan transformasi vektor input kedalam ruang fitur berdimensi tinggi Rf dengan menggunakan fungsi pemetaan ). Seringkali ϕ(x)
tidak tersedia atau tidak bisa dihitung, namun terdapat suatu fungsi kernel, K(x, x’)
yang dapat untuk menggantikan perkalian titik (ϕ(x), ϕ(x)‘ ) untuk memetakan vector
input kedalam ruang fitur berdimensi tinggi. Fungsi kuantil dari peubah respon
untuk prediktor diformulasikan sebagai berikut:
) = ) untuk (0,1) (11)
Dimana adalah QR ke- . Dengan membangun fungsi lagrange menggunakan kernel K(.,.),didapatkan masalah pengoptimasian sebagai berikut :
∑ ∑ (12)
dengan konstrain dan . Dengan menyelesaikan persamaan optimisasi (9) didapatkan multiplier lagrange yang optimal yaitu dan
didapatkan fungsi kuantil ke-θ pada vektor input sebagai berikut :
̂ ∑ ̂ - ̂ ) , (13)
Kernel yang digunakan adalah kernel Radial Basis Function (RBF) yang umum digunakan dan didefinisikan sebagai :
‖ ‖ (14)
Proses SVMQR dengan kernel RBF membutuhkan dua nilai parameter yang
harus ditentukan terlebih dahulu, nilai tersebut adalah γ sebagai parameter kernel dan
nilai C (cost) atau nilai pinalti untuk error yang lebih besar dari ε. Nilai parameter sangat berpengaruh terhadap model SVMQR yang dihasilkan. Tahapan komputasi SVMQR dalam bentuk pseudocode tertera pada lampiran 2.
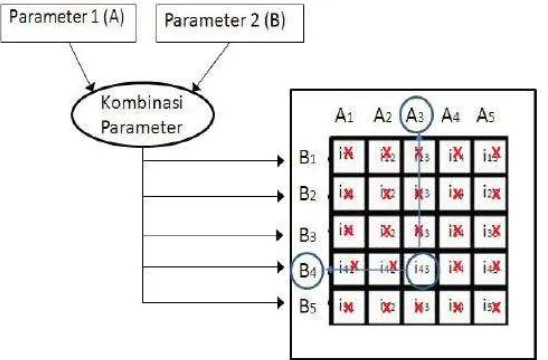
Metode grid search
Gambar 4 Ilustrasi metode grid search (Agmalaro 2011)
Pengujian
Pengujian dilakukan dengan memasukkan data uji pada model SVMQR untuk mendapatkan keluaran berupa nilai hasil prediksi. Nilai hasil prediksi didapatkan dengan menggunakan metode prediksi satu langkah kedepan (One ahead prediction) dengan jangka waktu 10 tahun kedepan.
Evaluasi dan Analisis
Diagram Taylor (Taylor 2001) menyediakan cara untuk merangkum seberapa dekat kesesuaian satu atau lebih pola model terhadap pola data observasi. Kesamaan pola data model dan pola observasi dihitung dengan korelasi, perbedaan Centered Root-Mean-Square (CRMS) dan standar deviasinya. Diagram ini sangat berguna dalam mengevaluasi beberapa aspek model kompleks atau dalam mengukur keterampilan relatif beberapa model . Ilustrasi diagram taylor tertera pada gambar 5. Kecocokan model dikatakan semakin baik jika R mendekati 1 dan NRMSE mendekati 0. Koefisien korelasi menunjukkan kekuatan hubungan antara dua peubah. Koefisien korelasi dihitung berdasarkan formula berikut :
R= ∑ ∑ ∑
√ ∑ ∑ ∑ ∑
(15) dengan
= nilai aktual/observasi
12
Gambar 5 Ilustrasi diagram Taylor (Taylor 2001)
Nilai kesalahan (error) digunakan untuk mengetahui besarnya simpangan nilai dugaan terhadap nilai aktual. Perhitungan error menggunakan Root Mean Square Error Prediction (RMSEP) adalah sebagai berikut :
RMSEP = √∑ (16)
dengan
= nilai aktual/observasi
= nilai prediksi = jumlah data
4 HASIL DAN PEMBAHASAN
Hasil reduksi dimensi data luaran GCM dengan PCA
Tabel 1 Hasil luaran PCA data GCM 4.3216 . Komponen pertama ini (PC1) ini dapat menjelaskan 95.7 persen keragaman data. Komponen kedua (PC2) memiliki eigenvalue 0.1470 dan dapat menjelaskan 3.3 persen keragaman. Bersama dengan komponen pertama (PC1), keduanya merepresentasikan 99 persen dari keragaman total. Kedua komponen PC1 dan PC2 yang merepresentasikan 99 persen keragaman total bisa dinilai telah cukup menangkap struktur data. Komponen-komponen lainnya memiliki proporsi keragaman yang kecil bisa dianggap tidak penting. Komponen pertama dan kedua dari model GCM CMC2-CanCM4 sudah cukup mewakili 98.5% dari total keragaman 25 variabel. Demikian pula untuk model NCEP-CFSv1, NASA-GMAO-062012 dan GFDL-CM2p1, yang juga mengambil komponen pertama dan kedua yang mampu menjelaskan sebanyak 98.4%, 97.9% dan 98.7% dari keragaman total.
Karakteristik pola curah hujan musim kemarau pada Kabupaten Indramayu
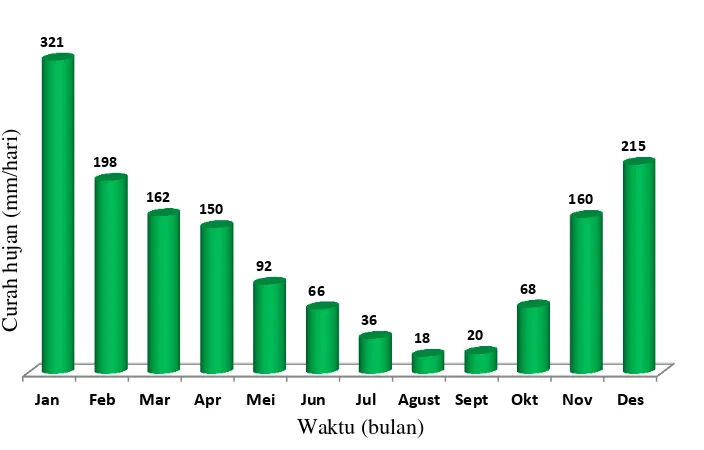
Karakteristik data curah hujan pada Kabupaten Indramayu dapat dilihat pada gambar 6 dan gambar 7. Data curah hujan bulanan yang diplotkan adalah rata-rata curah hujan bulanan dari 15 stasiun hujan selama periode 28 tahun (1981-2008). Berdasarkan karakteristik data hujan bulanan diatas, terlihat bahwa curah hujan bulan Mei yaitu sebesar 92 terletak pada kuantil (persentil) 45, curah hujan bulan Juni yaitu sebesar 66 terletak pada kuantil 28. Sedangkan curah hujan bulan Juli yaitu sebesar 36 terletak pada kuantil 18 dan curah hujan bulan Agustus yaitu sebesar 18 terletak pada kuantil 3.
14
Gambar 6 Histogram karakteristik data curah hujan pada Kabupaten Indramayu
Gambar 7 Boxplot karakteristik data curah hujan pada Kabupaten Indramayu
Jan Feb Mar Apr Mei Jun Jul Agust Sept Okt Nov Des
Pemodelan Statistical Downscaling luaran GCM menggunakan SVMQR
Pemodelan SVMQR pada kuantil ke-45
Prediksi curah hujan bulan Mei dilakukan dengan metode SVMQR pada kuantil ke 45. Pola data observasi dan hasil estimasi keseluruhan model SVMQR pada kuantil ke-45 tertera pada gambar 8.
Gambar 8 Plot data observasi dan hasil estimasi keseluruhan model SVMQR pada kuantil ke-45
Diantara kelima model GCM, hanya dua model GCM yaitu CMC1-CanCM3 dan CMC2-CanCM4 yang dapat mengikuti pola data observasi. Model GCM yang dapat direkomendasikan untuk memodelkan curah hujan bulan Mei adalah model GCM CMC1-CanCM3 dengan nilai korelasi paling besar yaitu 95% dan error prediksi (RMSEP) terkecil yaitu 8.9. Secara umum nilai error prediksi (RMSEP) bulan Mei dan bulan Juni yang dihasilkan kelima model GCM lebih besar dibandingkan nilai RMSEP pada bulan Juli dan Agustus. Hal ini dikarenakan pada bulan Mei dan Juni masih dalam masa pancaroba sehingga nilai curah hujan masih sulit diprediksi (Loetan 2011).
Pemodelan SVMQR pada kuantil ke-28
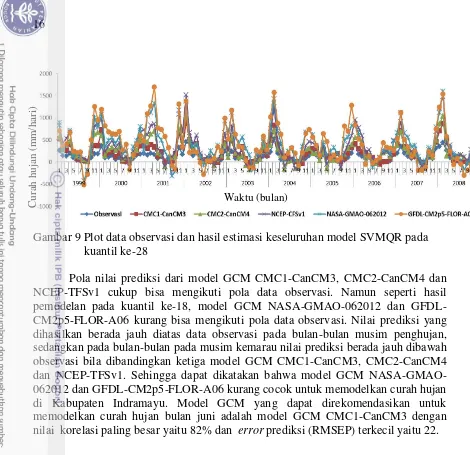
Prediksi curah hujan bulan Juni dilakukan dengan metode SVMQR pada kuantil ke 28. Pola data observasi dan hasil estimasi keseluruhan model SVMQR pada kuantil ke-18 tertera pada gambar 9.
Waktu (bulan)
C
ur
ah hu
jan
(m
m
/har
16
Gambar 9 Plot data observasi dan hasil estimasi keseluruhan model SVMQR pada kuantil ke-28
Pola nilai prediksi dari model GCM CMC1-CanCM3, CMC2-CanCM4 dan NCEP-TFSv1 cukup bisa mengikuti pola data observasi. Namun seperti hasil pemodelan pada kuantil ke-18, model GCM NASA-GMAO-062012 dan GFDL-CM2p5-FLOR-A06 kurang bisa mengikuti pola data observasi. Nilai prediksi yang dihasilkan berada jauh diatas data observasi pada bulan-bulan musim penghujan, sedangkan pada bulan-bulan pada musim kemarau nilai prediksi berada jauh dibawah observasi bila dibandingkan ketiga model GCM CMC1-CanCM3, CMC2-CanCM4 dan NCEP-TFSv1. Sehingga dapat dikatakan bahwa model GCM NASA-GMAO-062012 dan GFDL-CM2p5-FLOR-A06 kurang cocok untuk memodelkan curah hujan di Kabupaten Indramayu. Model GCM yang dapat direkomendasikan untuk memodelkan curah hujan bulan juni adalah model GCM CMC1-CanCM3 dengan nilai korelasi paling besar yaitu 82% dan error prediksi (RMSEP) terkecil yaitu 22.
Pemodelan SVMQR pada kuantil ke-18
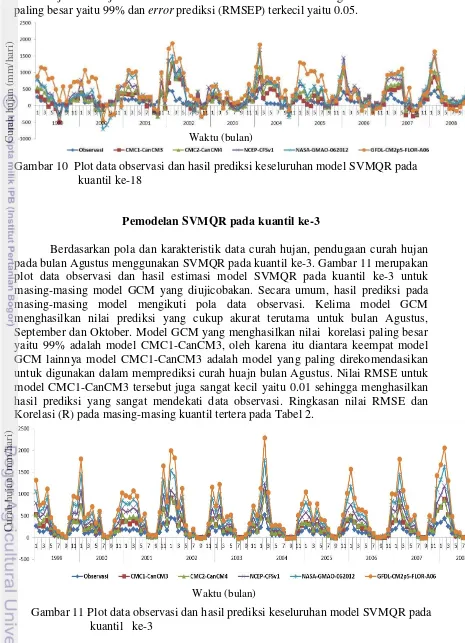
Prediksi curah hujan bulan Juli dilakukan dengan metode SVMQR pada kuantil ke 18. Hasil prediksi yang didapatkan oleh kelima model secara umum mengikuti pola data observasi yang ada. Model yang paling direkomendasikan untuk memprediksi curah hujan bulan Juli adalah model GCM CMC1-CanCM3 dengan nilai RMSE paling kecil yaitu 0.05. Pola data observasi dan hasil estimasi keseluruhan model SVMQR pada kuantil ke-18 tertera pada gambar 10.
Dilihat dari hasil plot data observasi dan nilai hasil prediksi kelima model GCM pada kuantil ke-18, pola hasil prediksi model CMC1-CanCM3, CMC2-CanCM4 dan NCEP-TFSv1 mengikuti pola data observasi. Namun, kedua model GCM lainnya yaitu NASA-GMAO-062012 dan GFDL-CM2p5-FLOR-A06 kurang bisa mengikuti pola data observasi karena nilai prediksi yang dihasilkan jauh diatas data observasi. Oleh karena itu dapat disimpulkan bahwa kedua model GCM NASA-GMAO-062012 dan GFDL-CM2p5-FLOR-A06 kurang bisa memodelkan curah hujan bulan Juli. Model GCM yang dapat direkomendasikan untuk memodelkan
curah hujan bulan juli adalah model GCM CMC1-CanCM3 dengan nilai korelasi paling besar yaitu 99% dan error prediksi (RMSEP) terkecil yaitu 0.05.
Gambar 10 Plot data observasi dan hasil prediksi keseluruhan model SVMQR pada kuantil ke-18
Pemodelan SVMQR pada kuantil ke-3
Berdasarkan pola dan karakteristik data curah hujan, pendugaan curah hujan pada bulan Agustus menggunakan SVMQR pada kuantil ke-3. Gambar 11 merupakan plot data observasi dan hasil estimasi model SVMQR pada kuantil ke-3 untuk masing-masing model GCM yang diujicobakan. Secara umum, hasil prediksi pada masing-masing model mengikuti pola data observasi. Kelima model GCM menghasilkan nilai prediksi yang cukup akurat terutama untuk bulan Agustus, September dan Oktober. Model GCM yang menghasilkan nilai korelasi paling besar yaitu 99% adalah model CMC1-CanCM3, oleh karena itu diantara keempat model GCM lainnya model CMC1-CanCM3 adalah model yang paling direkomendasikan untuk digunakan dalam memprediksi curah huajn bulan Agustus. Nilai RMSE untuk model CMC1-CanCM3 tersebut juga sangat kecil yaitu 0.01 sehingga menghasilkan hasil prediksi yang sangat mendekati data observasi. Ringkasan nilai RMSE dan Korelasi (R) pada masing-masing kuantil tertera pada Tabel 2.
Waktu (bulan)
18
Tabel 2 Ringkasan nilai RMSE dan Korelasi (R) pada masing-masing kuantil
Model GCM Q3 Q18 Q28 Q45
RMSE R RMSE R RMSE R RMSE R
CMC1-CanCM3 0.01 0.99 0.05 0.99 22 0.82 8.9 0.95 CMC2-CanCM4 14.36 0.09 36 -0.3 48.4 0.55 74 -0.08
NCEP-CFSv1 2.5 89 3.9 0.98 31.4 0.66 23 -0.63
NASA-GMAO-062012
53 -0.26 215 0.1 149 0.43 168.2 0.53 GFDL CM2P1 3238 -0.2 235 0.68 260 -0.08 100.2 -0.38
Validasi Model
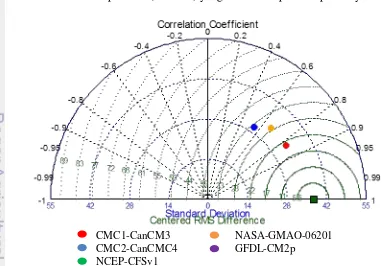
Validasi untuk keakuratan model GCM pada tiap-tiap kuantil dapat digambarkan dengan diagram taylor. Diagram taylor dapat memvisualisasikan seberapa dekat pola dari data model yang dihasilkan dengan pola data observasi. Similaritas antara kedua pola diukur dengan nilai korelasinya (Taylor 2011). Gambar 12, 13, 14 dan 15 menunjukkan performa kelima model GCM dalam memprediksi pola curah hujan pada bulan Mei, Juni, Juli dan Agustus. . Performa kelima model GCM dievaluasi berdasarkan nilai korelasi (R) dan Root Mean Square Error Prediction (RMSEP) .
Gambar 12 Diagram Taylor hasil pemodelan SVMQR pada bulan Mei Hasil pemodelan SVMQR bulan Mei menunjukkan bahwa model GCM CMC1-CAnCM3 memiliki akurasi paling tinggi dengan nilai korelasi 95%, artinya sebesar 95% nilai prediksi dapat dijalaskan oleh hubungan linearnya dengan nilai observasi. Nilai error prediksi (RMSEP) yang dihasilkan puncukup kecil yaitu 8.9.
Gambar 13 Diagram Taylor hasil pemodelan SVMQR pada bulan Juli CMC1-CanCM3 NASA-GMAO-06201
CMC2-CanCMC4 GFDL-CM2p NCEP-CFSv1
CMC1-CanCM3 NASA-GMAO-06201 CMC2-CanCMC4 GFDL-CM2p
20
CMC1-CanCM3 NASA-GMAO-06201 CMC2-CanCMC4 GFDL-CM2p
NCEP-CFSv1
CMC1-CanCM3 NASA-GMAO-06201
CMC2-CanCMC4 GFDL-CM2p NCEP-CFSv1
Gambar 14 Diagram Taylor model GCM pada bulan Juni
Model GCM CMC1-CanCM3 juga menunjukkan akurasi paling tinggi diantara keempat model GCM lainnya untuk prediksi bulan Juni, Juli dan Agustus. Nilai korelasi yang dihasilkan oleh model GCM CMC1-CanCM3 untuk bulan Juni adalah 82%, sedangkan untuk bulan Juli dan Agustus nilai korelasi yang didapatkan adalah 99%. Nilai error prediksi (RMSEP) yang dihasilkan oleh model GCM CMC1-CanCM3 pada bulan Juni, Juli dan Agustus juga cukup kecil yaitu 22, 0.05 dan 0.01.
5 KESIMPULAN DAN SARAN
Kesimpulan
Penelitian ini berhasil melakukan prediksi total curah hujan musim kemarau di Kabupaten Indramayu dengan metode Support Vector Machine Quantile Regression (SVMQR). Secara keseluruhan model yang dihasilkan untuk prediksi curah hujan dimusim kemarau cukup baik bila dilihat dari hasil rataan prediksi maupun rataan RMSE. Pada penelitian ini curah hujan bulan kemarau yaitu bulan Mei, Juni, Juli dan Agustus diprediksi setiap bulannya berdasarkan nilai kuantil yang diperoleh dari posisi sebaran data observasi. Sehingga estimasi curah hujan bulan Agustus diprediksi dengan SVMQR pada kuantil ke-3, sedangkan estimasi curah hujan bulan Juli, Juni dan Mei diprediksi dengan SVMQR pada kuantil ke-18, 28 dan 45. Model yang paling direkomendasikan untuk digunakan dalam memprediksi curah hujan bulan Mei, Juni, Juli dan Agustus adalah model GCM CMC1-CanCM3. Semakin kecil nilai RMSE maka hasil prediksi akan semakin mendekati nilai observasi. Karena nilai RMSEP yang dihasilkan cukup besar, dapat disimpulkan model GCM NASA-GMAO-062012 dan GFDL-CM2p1 kurang cocok untuk memodelkan curah hujan di Kabupaten Indramayu. Dibandingkan dengan bulan Juli dan Agustus, akurasi prediksi curah hujan bulan Mei dan Juni lebih kecil, hal ini dikarenakan pada bulan Mei dan Juni masih dalam masa pancaroba sehingga nilai curah hujan masih sulit diprediksi. Secara umum, hasil prediksi yang dihasilkan dengan metode SVMQR untuk menduga curah hujan bulan Mei Juni Juli dan Agustus cukup akurat dengan nilai korelasi yang hampir mendekati satu dan nilai RMSE yang didapat pun kecil.
Saran
1. Penelitian ini belum mengakomodir pencarian parameter terbaik dengan menggunakan metode optimasi. Penelitian selanjutnya dapat menerapkan algoritme particle swarm optimization (PSO), ant colony optimization (ACO) maupun algoritme optimasi lainnya untuk mendapatkan parameter yang optimal. 2. Prediktor yang digunakan untuk pembentukan model SVMQR pada penelitian ini
22
DAFTAR PUSTAKA
Agmalaro, MA. 2011. Pemodelan Statistical Downscaling Data GCM Menggunakan Support Vector Regression untuk Memprediksi Curah Hujan Bulanan Indramayu [tesis]. Bogor (ID): Institut Pertanian Bogor.
Barrodale I, Roberts F. 1974. Solution of an overdetermined system of equations in the l1 norm. J Communications of the ACM. 17:319-320.
[BMKG] Badan Meteorologi, Klimatologi, dan Geofisika. 2012. Buletin Analisis Hujan dan Indeks Kekeringan Bulan November 2012 dan Prakiraan Hujan Bulan Januari, Februari dan Maret 2013. Bogor (ID) : BMKG.
[BMKG] Badan Meteorologi, Klimatologi, dan Geofisika. 2015. Informasi trend curah hujan. [diunduh pada 30 Agust 2015]. Tersedia pada : http://www.bmkg.go.id/BMKG_Pusat/Informasi_Iklim/Informasi_Perubahan_Ik lim/Informasi_Trend_Curah_Hujan.bmkg
Buono A, Faqih A, Rakhman A, Santikayasa IP, Ramadhan A, Muttaqien MR, Agmalaro MA, Boer R. 2010. A Principle Component Analysis Cascade With Multivariate Regression For Statistical Downscaling Technique : A Case Study in Indramayu District. International Conference on Advanced Computer Science and Information Systems; 2010 Nov 20-23; Bali, Indonesia. Depok (ID) : Universitas Indonesia. Hlmn 321-327.
Djakaria I, Guritno S, Kartiko SH. 2010. Visualization of Iris Data Using Principal Component Analysis and Kernel Principal Component Analysis. Jurnal Ilmu Dasar. 11(1) :31-38.
Djuraidah A, Wigena AH. 2011. Regresi Kuantil Untuk Eksplorasi Pola Curah Hujan di Kabupaten Indramayu. Jurnal Ilmu Dasar 12(1): 50-56.
Estiningtyas W, Ramadhani F, Aldrian E. 2007. Analisis Korelasi Curah Hujan dan Suhu Permukaan Laut Wilayah Indonesia, Serta Implikasinya Untuk Prakiraan Curah Hujan (Studi Kasus Kabupaten Cilacap). Jurnal Agromet Indonesia. 21(2):46-60.
Haryoko I, Sugiarto Y, Syaukat Y.2008. Keterkaitan Perubahan Iklim dan Produksi Pangan Strategis: Telaah kebijakan independen dalam bidang perdagangan dan pembangunan. SEAMEO BIOTROP for Kemitraan partnership.
Haryoko U, Pawitan H, Aldrian E, Wigena AH. 2013. Penentuan Domain Spasial NWP Dalam Pembangunan Model Output Statistics. Jurnal Meteorologi dan Geofisika. 14(3):117-126.
24
[JAMSTEC] Japan Agency for Marine-Earth Science and Technology. 2007. Downscaling [diunduh 30 Agus 15]. Tersedia pada: https://www.jamstec.go.jp/sousei/eng/research/ theme_c.html.
Johnson RA, Wichern DW. 1998. Applied Multivariate Statistical Analysis. Fifth Edition. New Jersey (US) : Prentice-Hall Inc.
Koenker, R. 2005. Quantile Regression. New York (US) : Cambridge University Press.
Koenker R, Hallock KF. 2001. American Economic Association : Quantile Regression. Journal of Economic Perspective. 15(4):143-156.
Koenker R, P Ng, Portnoy S. 1994. Quantile smoothing splines. J Biometrics. 81:673-80.
Koenker R, D’Orey V. 1987. Computing Regression Quantiles.J Applied Statistics. 36:383-393.
Loetan S. 2011. Stabilkan Harga Pangan Kala Musim Berubah. Jurnal Komunika 7(1): 1-2.
Mondiana, YQ. 2012. Pemodelan Statistical Downscaling dengan Regresi Quantile untuk Pendugaan Curah Hujan Ekstrim (Studi Kasus Stasiun Bangkir Kabupaten Indramayu) [tesis]. Bogor (ID): Institut Pertanian Bogor.
[NOAA] National Oceanic And Atmospheric Administration. 2012. Climate Modelling [diunduh 30 Agus 2015]. Tersedia pada: http://celebrating200years.noaa.gov/
breakthroughs/climate_model/modeling_schematic.html.
Sanusi 2014. Optimasi SVR Dengan PSO Pada Pemodelan Statistical Downscaling Untuk Prediksi Curah Hujan Di Musim Kemarau [tesis]. Bogor (ID): Institut Pertanian Bogor.
Schölkopf B, Smola AJ, Williamson RC dan Bartlett PI. 2000. New Support Vector Algorithms. J Neural Comput. 12:1207-1245.
Sohn I, Kim S, Hwang C, Lee JW, Shin J. 2008. Support Vector Machine Quantile Regression for Detecting Differentially Expressed Genes In Microarray Analysis. Computational Statistics and Data Analysis 52:4104-4115.
Sutikno, Bekti RD, Susanti P, Istriana. 2010. Prakiraan Cuaca dengan Metode Autoregressive Integrated Moving Average, Neural Network, dan Adaptive Splines Treshold Autoregression di Stasiun Juanda Surabaya. Jurnal Sains Dirgantara. 8(1):43-61.
Taylor, KE. 2001. Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysics Resources. 106:7183-7192.
Vapnik V, Golowitch S, Smola A. 1997. Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. Cambride (US) : MIT Press.
Wigena, AH. 2006. Pemodelan Statistical Downscaling dengan Regresi Projection Persuit untuk Peramalan Curah Hujan. [disertasi]. Bogor (ID): Institut Pertanian Bogor.
26
Lampiran 1 Ilustrasi Quantile Regression (QR)
Quantile Regression (QR) diperkenalkan oleh Koenker dan Basset (2005) yang merupakan metode statistika praktis untuk memperkirakan dan membangun inferensia model pada fungsi quantile bersyarat tertentu. Metode ini tidak terpengaruh oleh adanya pencilan dan memberikan hasil yang stabil jika terdapat data pencilan. Contoh garis pemodelan QRtertera pada gambar 16.
Gambar 16 Contoh garis pemodelan QR (Koenker 2005)
Bentuk quantile sinonim dengan persentil, median merupakan salah satu ukuran statistik yang paling terbaik dari quantile. Diketahui bahwa median sampel dapat didefinisikan sebagai nilai tengah (atau separuh nilai diantara dua nilai tengah) dari himpunan data yang terurut. Lebih umumnya, 25% dan 75% quantile sampel dapat didefinisikan sebagai nilai yang membagi data dalam proporsi seperempat dan tigaperempat.
QR dapat digunakan untuk mengatasi keterbatasan regresi linear jika data tidak simetris, persamaan regresi :
= + + ... + + εi,τ (15) Dimana:
= nilai pegamatan ke-i pada quantile ke-τ = nilai pengamatan ke-i peubah prediktor ke-p
= penduga parameter pada quantile ke-τ
εi,τ = sisaan ke-i dan quantile ke-τ i = 1,...,n j= 1, ... , p
jika dituliskan dalam bentuk matriks adalah sebagai berikut :
[ ]
Atau secara umum, bentuk model regresi kuantil adalah
y = X’ + ε (16)
dengan
X = (x1,...,xn) adalah vektor respon berukuran n x p,
= ( p)’ adalah vektor parameter berukuran p x 1, Dan ε= (ε1,..., εn)’ adalah vektor galat berukuran (n x 1).
Dalam regresi median, penduga koefisien model regresi adalah solusi dari minimasi fungsi (Barrodale dan Roberts, 1974):
∑ (17)
Dalam regresi kuantil terdapat pembobotan menggunakan linear loss function, sehingga pendugaan parameter model regresi kuantil merupakan solusi dari fungsi
(Koenker dan D’Orey, 1985): diselesaikan dengan pemrograman linear dalam dua tahap :
1. Menemukan solusi pada setiap iterasi atau dalam istilah pemrograman linear disebut basic solution (b) dengan formulasi
(19)
Dimana h adalah himpunan bagian berukuran-p dari n subset integer pertama, xh adalah submatrix dari X berukuran h, dan yh adalah subvektor dari Y.
2. Setelah mendapatkan nilai b dilakukan iterasi sampai nilai optimum dari persamaan berikut didapatkan :
̂ ∑ { ∑ { (20)
.
Contoh ilustrasi pendugaan parameter pada QR
Misalkan Y adalah peubah respon berdimensi 1 x 5 dimana y=
( )
dan X adalah
prediktor dengan dua variabel berdimensi 2 x 5 dimana X =
28
Sehingga didapatkan tiga basic solution karena basic solution kedua dan ketiga sama, b= {
( ) ( ) }
dari ketiga nilai b diatas dilakukan iterasi untuk mendapatkan nilai yang optimum.
= 21.6 + 16.473 = 38.073
Berdasarkan ketiga iterasi diatas persamaan QR akan mencapai nilai minimum pada b = (
30
Lampiran 2 Algoritme SVMQR
Tahapan komputasi pada metode Support Vector Machine Quantile Regression (SVMQR) dapat dijabarkan dalam pseudocode berikut:
1. Inisialisasi fungsi dan parameter
2. Menghitung nilai kernel (dengan fungsi RBF kernel) H=zeros(n,n); O=zeros(n,n);
4. Menghitung penduga parameter beta dengan Quadratic programming vlb = zeros(2*n,1);
vub = C*ones(2*n,1); x0 = zeros(2*n,1); A =[]; b =[];
[alpha2 lambda2 how2] = qp(Q2, L2, A, b, vlb, vub, x0,1); alp21 = alpha2(1:n); alp22 = alpha2(n+1:2*n);
beta2 = qt2*alp21-(1-qt2)*alp22; 5. Menghitung nilai prediksi (FY2)
32
Model GCM Tahun Observasi Prediksi RMSEP Korelasi
GFDL Flor 1999 14 -16484.6 32381 -0.26
CM2P1 2000 3 35144.52
2001 8 34974.58
2002 2 30318.1
2003 0 -6118
2004 0 46598.78
2005 12 21718.91
2006 0 -11420.3
2007 1 58053.04
34
Model GCM Tahun Observasi Prediksi RMSEP Korelasi
2008 0 -125.287
GFDL Flor 1999 27 432.9358 235.17 0.68
CM2P1 2000 11 251.1564
2001 12 16.5572
2002 38 271.0367
2003 0 -2.7401
2004 45 208.1893
2005 44 371.7791
2006 13 -93.28
2007 18 337.0323
36
Model GCM Tahun Observasi Prediksi RMSEP Korelasi
GFDL Flor 1999 40 32.3565 260.29 -0.08
CM2P1 2000 101 126.9191
2001 123 238.9717
2002 11 -206.44
2003 36 -270.92
2004 48 -38.3031
2005 71 -170.294
2006 44 94.5043
2007 112 -129.776
Model GCM Tahun Observasi Prediksi RMSEP Korelasi
38
Model GCM Tahun Observasi Prediksi RMSEP Korelasi
GFDL Flor 1999 97 74.1576 100.2 -0.38
CM2P1 2000 59 -31.3071
2001 80 92.2889
2002 56 143.418
2003 105 9.328
2004 63 112.2275
2005 95 8.5701
2006 113 -124.179
2007 78 -48.0392
RIWAYAT HIDUP