1
ANALISIS KESTABILAN MODEL MANGSA-PEMANGSA
DENGAN INTERFERENSI ANTARPEMANGSA
FIKRI AZHARI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
2
ABSTRAK
FIKRI AZHARI. Analisis Kestabilan Model Mangsa-Pemangsa dengan Interferensi Antarpemangsa. Dibimbing oleh ALI KUSNANTO dan TONI BAKHTIAR.
Dalam karya ilmiah ini direkonstruksi model mangsa-pemangsa dari tiga spesies hewan dalam suatu rantai makanan, dengan dua spesies pemangsa dan satu spesies mangsa yang disusun oleh Feng et al. (2010). Dari model tersebut diteliti pengaruh dari interferensi antarpemangsa berdasarkan tingkat kejenuhan dan persaingannya. Hasil analisis diperoleh lima titik tetap, dimana dua diantaranya bersifat sadel. Pengaruh tingkat kejenuhan dan persaingan terhadap dinamika populasi ditunjukkan dengan pendekatan numerik, dari empat kondisi. Kondisi pertama, tingkat kejenuhan kedua spesies pemangsa lebih besar dibandingkan dengan persaingannya, sedangkan kondisi kedua tingkat persaingan pemangsa kedua spesies pemangsa lebih besar dibandingkan dengan tingkat kejenuhannya. Kondisi ketiga tingkat kejenuhan pemangsa I lebih besar dibandingkan dengan tingkat persaingannya, tetapi tingkat kejenuhan pemangsa II lebih kecil dibandingkan tingkat persaingannya. Kondisi keempat tingkat kejenuhan pemangsa I lebih kecil dibandingkan dengan tingkat persaingannya, tetapi tingkat kejenuhan pemangsa II lebih besar dibandingkan tingkat persaingannya. Secara umum, melalui simulasi, disimpulkan bahwa tingkat kejenuhan pemangsa I dan tingkat persaingan pemangsa II memengaruhi kestabilan populasi, sedangkan tingkat kejenuhan pemangsa II dan tingkat persaingan pemangsa I tidak memengaruhi kestabilan populasi.
3
ABSTRACT
FIKRI AZHARI. Stability Analysis of Predator-Prey Model with Interference between Predators. Supervised by ALI KUSNANTO and TONI BAKHTIAR.
In this study we reconstructed a predator-prey model of three animal species in a food chain, which consist of two species of predator and one species of prey (Feng et al. (2010)). From this model we investigated the effects of interference between predators based on the saturation and competition levels. In the stability analysis five equilibrium points obtained, in which two of them are unstable saddles. The effects of saturation and competition levels to population dynamics is shown by using numerical approach, where four conditions are considered. In the first condition, the saturation level of two predators is bigger than the competition level. In the second condition, the saturation level of two predators is lower than the competition level. In the third condition, the saturation level of predator I is bigger than its competition level, but saturation level of predator II is lower than its competition level. The fourth condition, the saturation level of predator I is lower than its competition level, but saturation level of predator II is bigger than its competition level. In general, the simulation results of the four conditions above, concluded that the saturation level of predator I and competition level of predator II effects the stability of populations, whereas saturation level of predator II and competition level of predator I did not effects the stability of populations.
4
ANALISIS KESTABILAN MODEL MANGSA-PEMANGSA
DENGAN INTERFERENSI ANTARPEMANGSA
FIKRI AZHARI
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
5
Judul
: Analisis Kestabilan Model Mangsa-Pemangsa dengan Interferensi
Antarpemangsa
Nama
: Fikri Azhari
NRP
: G54080072
Menyetujui,
Pembimbing I
Drs. Ali Kusnanto, M.Si.
NIP. 19650820 199003 1 001
Pembimbing II
Dr. Toni Bakhtiar, M.Sc.
NIP. 19720627 199702 1 002
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP. 19650505 198903 2 004
v
PRAKATA
Syukur Alhamdulillah penulis mengucapkan puji syukur kehadirat Allah SWT yang senantiasa memberikan nikmat iman serta nikmat islam. Limpahan rahmat dan hidayah-Nya yang besar, sehingga penulis dapat menyelesaikan karya ilmiah ini. Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari berbagai pihak, baik secara langsung maupun tidak langsung. Oleh karena itu penulis ingin mengucapkan rasa terima kasih yang sebesar-besarnya kepada:
1. Mama dan Ayah yang telah memberikan didikan, kasih sayang, dukungan secara moril, materi, nasihat dan motivasi, serta doa yang tiada henti-hentinya. Untuk kakak dan adik-adikku, Nisa El Islami, Mohammad Haviz, Aulia Miftah El Karimi, dan Lutfiah Fazra El Ghifari, terima kasih atas doa dan dukungannya,
2. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing I dan Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing II. Terima kasih atas waktu, ilmu yang diberikan dan kesabaran dalam membimbing penulis,
3. Dr. Paian Sianturi selaku dosen penguji. Terima kasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis,
4. Semua dosen Departemen Matematika, terima kasih atas ilmu yang telah diberikan,
5. Bu Susi, Pak Yono, Bu Ade, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terima kasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis,
6. Surya Pratiwi atas doa, motivasi dan dukungannya, serta teman-teman mahasiswa Matematika angkatan 44, 45, dan 46,
7. Teman-teman satu bimbingan: Dewi, Ade, dan Irma. Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
8. Teman-teman satu kostan Alma: Bambang, Issanto, Wahyu, Lodian, Aldi, Afnan, Whendy, Annas, dan Agus. Terima kasih atas doa, bantuan, dukungan semangat dan nasihatnya,
9. Teman-teman lainnya yang telah mendukung selama ini, yang tidak dapat disebutkan satu per satu.
Penulis menyadari bahwa dalam karya ilmiah ini masih terdapat kekurangan, oleh karena itu penulis mengharapkan saran dan kritik dari semua pihak. Semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang memerlukan.
Bogor, Januari 2013
vi
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 19 Februari 1991 sebagai anak kedua dari empat bersaudara, anak dari pasangan Bustanul Arifin dan Hanik Qomariyah. Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 2002 di SD Negeri 04 Pagi Jakarta, Sekolah Menengah Pertama Negeri 234 Jakarta tahun 2005, Sekolah Menengah Atas Negeri 89 Jakarta tahun 2008, kemudian pada tahun yang sama penulis masuk Institut Pertanian Bogor melalui jalur Seleksi Nasional Masuk Perguruan Tinggi Negeri, jurusan Matematika, FMIPA.
vii
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR TABEL ... viii
DAFTAR LAMPIRAN ... ix
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan Penulisan ... 1
1.3 Sistematika Penulisan ... 1
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial ... 2
2.2 Titik Tetap ... 2
2.3 Titik Tetap Stabil ... 2
2.4 Titik Tetap Takstabil ... 2
2.5 Pelinearan ... 2
2.6 Nilai Eigen dan Vektor Eigen ... 2
2.7 Analisis Kestabilan Titik Tetap ... 2
2.8 Penondimensionalan ... 3
III PEMBAHASAN 3.1 Perumusan Model ... 4
3.2 Analisis Kestabilan Titik Tetap ... 5
IV SIMULASI 4.1 Pengaruh Tingkat Kejenuhan Pemangsa I ( ) ... 7
4.2 Pengaruh Tingkat Kejenuhan Pemangsa II ( ) ... 9
4.3 Pengaruh Tingkat Persaingan Pemangsa I ( ) ... 10
4.4 Pengaruh Tingkat Persaingan Pemangsa II ( ) ... 12
V SIMPULAN ... 14
VI DAFTAR PUSTAKA ... 15
viii
DAFTAR GAMBAR
Halaman
1 Pengaruh pada kondisi dan ... 7
2 Dinamika populasi pada kondisi dan ... 8
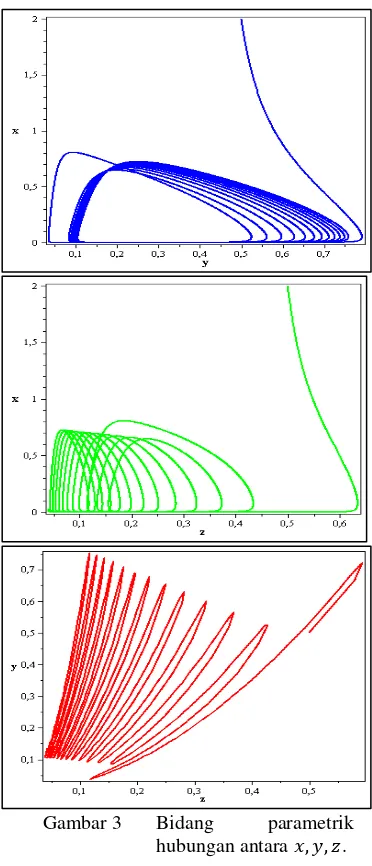
3 Bidang parametrik hubungan antara (kondisi ke-1) ... 8
4 Dinamika populasi ketika ... 9
5 Bidang parametrik hubungan antara ketika ... 9
6 Pengaruh pada kondisi dan ... 9
7 Dinamika populasi pada kondisi dan ... 10
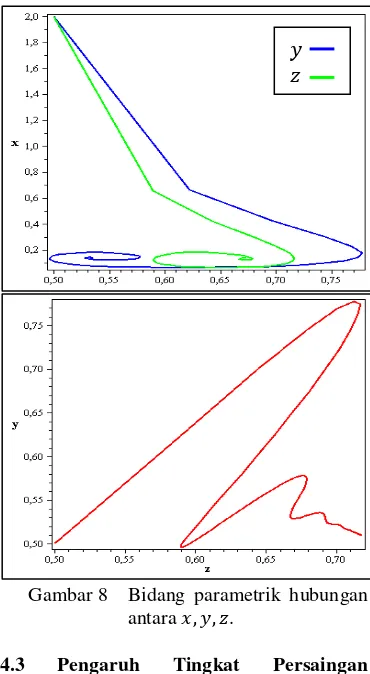
8 Bidang parametrik hubungan antara (kondisi ke-2) ... 10
9 Pengaruh pada kondisi dan ... 11
10 Dinamika populasi pada kondisi dan ... 11
11 Bidang parametrik hubungan antara (kondisi ke-3) ... 11
12 Dinamika populasi ketika ... 12
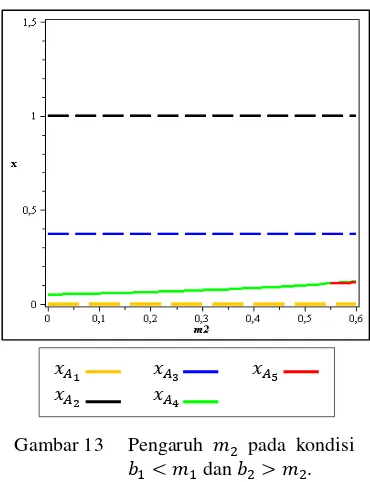
13 Pengaruh pada kondisi dan ... 12
14 Dinamika populasi pada kondisi dan ... 12
15 Dinamika populasi ketika ... 13
DAFTAR TABEL
Halaman 1 Kasus kestabilan titik tetap dan ... 7ix
DAFTAR LAMPIRAN
Halaman
1 Penondimensionalan model mangsa-pemangsa ... 17
2 Penentuan titik tetap ... 20
3 Penentuan nilai eigen ... 24
4 Kode program untuk Gambar 1 ... 28
5 Kode program untuk Gambar 2 ... 29
6 Kode program untuk Gambar 3 ... 30
7 Kode program untuk Gambar 4 ... 31
8 Kode program untuk Gambar 5 ... 31
9 Kode program untuk Gambar 6 ... 32
10 Kode program untuk Gambar 7 ... 33
11 Kode program untuk Gambar 8 ... 33
12 Kode program untuk Gambar 9 ... 34
13 Kode program untuk Gambar 10 ... 35
14 Kode program untuk Gambar 11 ... 36
15 Kode program untuk Gambar 12 ... 37
16 Kode program untuk Gambar 13 ... 37
17 Kode program untuk Gambar 14 ... 38
I PENDAHULUAN
1.1 Latar Belakang
Makhluk hidup terdiri atas bermacam-macam spesies yang membentuk komunitas dan hidup bersama. Makhluk hidup selalu bergantung kepada makhluk hidup lain. Ada beberapa jenis hubungan yang dapat terjadi antarspesies. Salah satu interaksi tersebut adalah predasi, yaitu hubungan antara mangsa (prey) dan pemangsa (predator). Tiap pemangsa akan bersaing dengan individu lain yang sejenis untuk memperoleh mangsanya guna mempertahankan hidup. Di dalam hubungan tersebut pemangsa juga berperan sebagai pengontrol populasi mangsa.
Awalnya model mangsa-pemangsa berfokus hanya pada peran predasi, dengan interferensi antarpemangsa diabaikan. Di tahun 1975, Beddington-DeAngelis mem-perkenalkan suatu model mangsa-pemangsa dengan ditambahkan adanya interferensi antarapemangsa dengan jenis yang berbeda. (Feng et al. 2010)
Dalam sistem mangsa-pemangsa interferensi dapat diartikan sebagai adanya persaingan dalam memangsa. Manfaat persaingan antarpemangsa ialah untuk mengatur besarnya populasi dan memastikan ketersediaan makanan, ruang, dan sumber daya lain yang diperlukan untuk eksistensi dan reproduksi. Jadi, adanya persaingan di dalam sistem mangsa-pemangsa dapat memengaruhi kestabilan dinamika populasi. Selain itu, persaingan dapat berdampak positif pada kestabilan dan daya tahan jika tingkat persaingan antarpemangsa rendah, dan sebaliknya jika tingkat persaingan antarpemangsa tinggi maka populasi pemangsa semakin berkurang.
Selain tingkat persaingan antarpemangsa, tingkat kejenuhan memangsa juga memengaruhi kestabilan sistem. Semakin besar tingkat kejenuhan pemangsa maka populasi pemangsa semakin berkurang.
Dalam karya ilmiah ini, direkonstruksi model mangsa-pemangsa yang melibatkan tiga spesies hewan yang membentuk suatu rantai makanan, dengan dua spesies pemangsa dan satu spesies mangsa yang disusun oleh Feng et al. (2010). Dari model tersebut akan diteliti efek dari interferensi pemangsa dalam tingkatan yang berbeda berdasarkan tingkat kejenuhan dan tingkat persaingan antarpemangsa.
1.2 Tujuan Penulisan
Tujuan dari penulisan karya ilmiah ini ialah:
1. Memelajari model mangsa-pemangsa Feng et al. (2010) dengan adanya interferensi antarpemangsa.
2. Melihat pengaruh tingkat kejenuhan dan persaingan antarpemangsa terhadap kestabilan sistem.
1.3 Sistematika Penulisan
II LANDASAN TEORI
2.1 Sistem Persamaan Diferensial
Sistem persamaan diferensial orde satu dengan persamaan dan buah fungsi yang tak diketahui dapat ditulis sebagai berikut:
̇
dengan
( ) ( ).
Jika linear maka sistem persamaan diferensial di atas disebut linear, sebaliknya jika tidak linear maka sistem persamaan diferensial di atas disebut taklinear. Jika tidak bergantung secara eksplisit pada , yaitu
( ), maka disebut sistem persamaan diferensial mandiri.
Sistem persamaan diferensial linear mandiri dapat ditulis sebagai berikut:
̇ ,
dengan adalah matriks koefisien berukuran
dan adalah vektor koefisien berukuran . Jika maka sistem persamaan diferensial di atas disebut homogen.
Solusi dari sistem persamaan diferensial linear mandiri homogen sebagai berikut:
, disebut dengan solusi trivial. Jika tidak demikian disebut solusi nontrivial.
2.2 Titik Tetap
Misalkan diberikan sistem persamaan diferensial sebagai berikut:
̇ .
Titik disebut titik tetap jika memenuhi
. Titik tetap disebut juga titik kritis atau titik keseimbangan.
(Tu 1994) 2.3 Titik Tetap Stabil
Misalkan titik adalah titik tetap sebuah sistem persamaan diferensial mandiri dan adalah solusi yang memenuhi kondisi awal
dengan . Titik dikatakan titik tetap stabil jika dengan
| | , maka | | . (Verhulst 1990) 2.4 Titik Tetap Takstabil
Misalkan titik adalah titik tetap sebuah sistem persamaan diferensial mandiri dan adalah solusi yang memenuhi kondisi awal
dengan . Titik dikatakan titik tetap takstabil jika
dengan | | , maka | |
.
(Verhulst 1990) 2.5 Pelinearan
Untuk suatu sistem persamaan diferensial taklinear, analisis kestabilannya dilakukan melalui pelinearan. Misalkan diberikan sistem persamaan diferensial taklinear sebagai berikut:
̇ . (2.1) Dengan menggunakan ekspansi Taylor di sekitar titik tetap , maka persamaan (2.1) dapat ditulis sebagai berikut:
̇ . (2.2) Persamaan tersebut merupakan sistem persamaan diferensial taklinear dengan matriks Jacobi, [ ]
dan suku berorde tinggi yang bersifat
. Selanjutnya pada persamaan (2.2) disebut pelinearan dari sistem taklinear persamaan (2.2) yang dituliskan dalam bentuk
̇ .
(Tu 1994) 2.6 Nilai Eigen dan Vektor Eigen
Misalkan matriks berukuran . Suatu vektor taknol di disebut vektor eigen dari , jika untuk suatu skalar berlaku:
. (2.3) Vektor disebut vektor eigen yang bersesuaian dengan nilai eigen . Untuk mencari nilai eigen dari matriks , maka persamaan (2.3) dapat ditulis sebagai berikut:
, (2.4) dengan matriks identitas. Persamaan (2.4) memunyai solusi taknol jika dan hanya jika:
. (2.5) Persamaan (2.5) disebut persamaan karakteristik dari matriks .
(Anton 1995) 2.7 Analisis Kestabilan Titik Tetap
Misalkan diberikan matriks berukuran
sebagai berikut:
,
, sedemikian sehingga diperoleh persamaan:
, dengan
,
. Dengan demikian diperoleh nilai eigen dari matriks sebagai berikut:
√ Ada tiga kasus untuk nilai : Kasus I
Jika maka kedua nilai eigen bernilai real dan berbeda tanda, sehingga titik tetap bersifat sadel.
Kasus II
i Jika dan maka kedua nilai eigen bernilai real dan positif, sehingga titik tetap bersifat simpul tak stabil. Jika maka kedua nilai eigen bernilai real dan negatif, sehingga titik tetap bersifat simpul stabil.
ii Jika dan maka kedua nilai eigen bernilai kompleks (
dengan , √ ), sehingga titik tetap bersifat spiral tak stabil. Jika
maka kedua nilai eigen bernilai kompleks , sehingga titik tetap bersifat spiral stabil. Jika maka kedua nilai eigen imajiner murni
, sehingga titik tetap bersifat center. iii maka kedua nilai eigen
bernilai sama, sehingga pada kasus ini titik tetap bersifat simpul sejati.
Kasus III
Jika maka salah satu nilai eigen bernilai nol, titik tetap bersifat degenerate.
(Strogatz 1994) Analisis kestabilan titik tetap dapat juga dikaji berdasarkan kondisi Routh-Hurwitz. Misalkan a a a1, 2, 3, ,ak adalah
bilangan-bilangan real dengan aj 0 jika jk.
Semua nilai eigen dari persamaan karakteristik
1 2 1
1 2 1
( ) k k k k k 0
p a a a a memunyai bagian real yang negatif jika dan hanya jika determinan dari matriks Mj untuk setiap j1, 2,3, ,k adalah positif.
1 3 5 2 1
2 4 2 2
1 3 2 3
1 0
0 0 0 0 0
j
j
j j
a a a a
a a a
M a a a
Menurut kondisi Routh-Hurwitz, untuk
2,3k berlaku bahwa titik tetap x* stabil jika dan hanya jika
.
(Keshet 1988) 2.8 Penondimensionalan
Penondimensionalan adalah suatu metode untuk menyederhanakan suatu persamaan banyak parameter menjadi persamaan dengan lebih sedikit parameter. Biasanya penondimensionalan mengelompokkan beberapa parameter dengan sebuah parameter tunggal.
(Strogatz 1994) Contoh:
Diberikan model mangsa pemangsa berikut:
̇
(2.7)
̇
Persamaan (2.7) memiliki empat parameter, yaitu , , , dan . Dengan memisalkan
, , ,
maka diperoleh model dengan satu parameter yaitu,
̇ ,
4
III PEMBAHASAN
3.1 Perumusan Model
Dalam karya ilmiah ini dibahas model mangsa-pemangsa yang menggambarkan suatu rantai makanan antara dua spesies pemangsa dan satu spesies mangsa dengan adanya faktor kejenuhan memangsa dan persaingan antarpemangsa. Berikut ini adalah sistem persamaan modelnya:
( ) di mana dengan
: banyaknya populasi mangsa ( ; ekor),
: banyaknya populasi pemangsa I ( ; ekor),
: banyaknya populasi pemangsa II ( ; ekor),
: laju pertumbuhan intrinsik mangsa (per hari),
: daya dukung lingkungan bagi mangsa, : kemampuan maksimum pemangsa I
dalam mencari mangsa (per hari), : kemampuan maksimum pemangsa II
dalam mencari mangsa (per hari), : tingkat kejenuhan pemangsa I (ekor),
: tingkat kejenuhan pemangsa II (ekor), : tingkat persaingan pemangsa I, : tingkat persaingan pemangsa II,
: koefisien interaksi antara mangsa dan pemangsa I,
: koefisien interaksi antara mangsa dan pemangsa II,
: laju kematian pemangsa I (per hari), : laju kematian pemangsa II (per hari).
Besaran dan merupakan suatu interaksi (respon fungsional) yang
menggambarkan laju pemangsaan dan ketersediaan makanan (mangsa).
Laju pertumbuhan intirinsik mangsa dipengaruhi oleh laju pertumbuhan pemangsa
dan , di mana tumbuh secara logistik. Laju pertumbuhan populasi pemangsa dipengaruhi oleh interferensi antarpemangsa yaitu tingkat persaingan dan kejenuhan yang dikurangi oleh laju kematian populasi pemangsa ( ), untuk . Kedua faktor tersebut akan dianalisis untuk melihat pengaruh kestabilan sistem.
Untuk menyederhanakan model (3.1) maka dilakukan penondimensionalan, sehingga skala parameter yang digunakan, yaitu:
1 2
, , ,
X AY A Z
y z
K RK RK
x
dengan , , dan . Sistem persamaan yang baru menjadi:
1 1 2 2
1 1
1 1
2 2
2 2
(1
)
xy
xz
dx
x
x
b
x m y
b
x m z
dt
dy
xy
a
d y
dt
b
x m y
dz
xz
a
d z
dt
b
x m z
(bukti lihat Lampiran 1)
Titik tetap pada persamaan (3.2) dapat dinyatakan ke dalam bentuk dan juga dapat diperoleh dengan menentukan
,
, dan
, sehingga persamaannya:
1 1 2 2
1 1
1 1
2 2
2 2
(1
)
0
0
0
xy
xz
x
x
b
x m y
b
x m z
xy
a
d y
b
x m y
xz
a
d z
b
x m z
Dengan menyelesaikan sistem persamaan (3.3) diperoleh lima titik tetap yaitu , , ̅ ̅ , ̃ ̃ , dan .
(bukti lihat Lampiran 2)
(3.2)
(3.3)
3.2 Analisis Kestabilan Titik Tetap Misalkan dari persamaan (3.3) dituliskan sebagai berikut:
1
1 1 2 2
2 1 1
1 1
3 2 2
2 2
( , , ) 1
( , , )
( , , )
y z
g x y z x x x
b x m y b x m z
x
g x y z y a d y
b x m y
x
g x y z z a d z
b x m z
Dengan melakukan pelinearan pada persamaan (3.4) maka diperoleh matriks Jacobi sebagai berikut:
1 1 1
1
2 2 2
2
3 3 3
3
g g g
x g x x
x y z
g g g
J y y g y
x y z
g g g
z z z g
x y z
Analisis Kestabilan Titik Tetap
Matriks Jacobi yang berpadanan dengan titik tetap A1(0, 0, 0) ialah:
1 1
2
1 0 0
0 0 0 0 J d d .
Nilai eigen diperoleh dengan menyelesaikan persamaan karakteristik
1
det(
J
I
)
0,
yaitu: 1 1 , 2 d1, 3 d2. Karena parameter diasumsikan taknegatif, maka 1 0 dan 2, 3 0, sehingga kestabilan titik tetapnya selalu bersifat sadel.
Analisis Kestabilan Titik Tetap
Matriks Jacobi yang berpadanan dengan titik tetap A2(1, 0, 0) ialah:
1 2
1 1 1 2
1
2 2 2
2 1 1 1 1 1 ( 1) 0 0 1 ( 1) 0 0 1 b b
a d b J
b
a d b b .
Persamaan karakteristik titik tetap
2
det(
J
I
) 0
, sehingga diperoleh nilai eigennya:1 1
, 1 1 1 2
1
( 1) 1
a d b
b
,
2 2 2 3
2
( 1) 1
a d b
b
.
Jika kestabilan titik tetap bersifat stabil, tetapi jika sedikitnya ada satu nilai eigen real atau yang positif maka titik tetap bersifat sadel. Agar titik tetap bersifat stabil maka dan
, selain itu akan bersifat sadel.
Analisis Kestabilan Titik Tetap Diberikan titik tetap ̅ ̅ :
2
1 1 1 1 1 1
1 1 4 2
w w a b d m x
a m
,
1 1 1 1
1 1
(a d x) b d y
d m
,
dengan
1 1 1 1 1 .
w a m a d
Di bawah ini merupakan matriks Jacobi yang berpadanan dengan titik tetap
̅ ̅ :
1
2 2
1 1 1 1 1 1 1 1 2
1 1 1 1 1
3 2 2 1
1 1 1 1 1 1 1 1
2 2 2 1 2 ( ) ( ) 0 ( ) ( ) 0 0 xym
y xy x x
x
b x m y b x m y b x m y b x m y b x
a y a xy a x a xym
J d
b x m y b x m y b x m y b x m y
6
Matriks J3 dimisalkan sebagai berikut:
( ),
dari setiap elemen matriks J3 diperoleh nilai eigennya: 2 1,2 4 2 , 2 3 2 2 a x d b x , dengan , .
Jika dan kedua nilai eigen berbeda tanda, maka titik tetap bersifat sadel, sedangkan jika , dan kondisi akan bersifat spiral stabil.
Analisis Kestabilan Titik Tetap Titik tetap ̃ ̃ :
2
2 2 2 2 2 2
2 2
4
, 2
w w a b d m
x
a m
2 2 2 2
2 2
( )
,
a d x b d
z
d m
dengan
2 2 2 2 2.
w a m a d
Matriks Jacobi yang berpadanan dengan titik tetap ̃ ̃ :
2
2 2
2 2 2 2 2 2 2 2 1
2 2 2 2 2
4 2 2 2
2 2 2 2 2 2 2 2
1 1 1 1 2 ( ) ( ) 0 ( ) ( ) 0 0 xzm
z xz x x
x
b x m z b x m z b x m z b x m z b x
a z a xz a x a xzm
J d
b x m z b x m z b x m z b x m z
a x d b x
Jika matriks J4 dimisalkan sebagai berikut:
(
),
diperoleh nilai eigen dari matriks J4, yaitu: 2 1,2 4 2 , 1 3 1 1 a x d b x , dengan , .
Jika dan kedua nilai eigen berbeda tanda, maka titik tetap bersifat sadel. Jika , dan , maka titik tetap bersifat stabil atau spiral stabil.
Analisis Kestabilan Titik Tetap
Matriks Jacobi dari titik tetap
* * *
5
( ,
,
)
A
x y z
diberikan sebagai berikut: (
),
dengan Vij merupakan elemen dari matriks 5
J , persamaan karakteristiknya menjadi:
3 2
1 2 3 0,
di mana
1 (V11 V22 V33),
2 V V11 22 V V11 33 V V22 33 V V12 21 V V13 31 ,
3 V V V11 22 33 V V V12 21 33 V V V13 31 22 .
(bukti lihat Lampiran 3)
Berdasarkan kriteria Routh-Hurwitz, titik tetap
A
5
( ,
x y z
* *,
*)
stabil jika dan hanya jika:*
* 1 1 1 1
1 1
( )
0, x a d b d y
d m
*
* 2 2 2 2
2 2
( )
0, x a d b d z
d m
1 0,
3 0, 1 2 3.
Dari kelima titik tetap yang diperoleh, kestabilan titik tetap dan , dapat dilihat pada Tabel 1.
7
Tabel 1 Kasus kestabilan titik tetap dan .
Kasus Titik Tetap
dan Sadel Sadel
dan Sadel Sadel
dan Sadel Sadel
dan Sadel Stabil
IV SIMULASI
Pengaruh persaingan antarpemangsa dan tingkat kejenuhan pemangsa diamati dengan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu . Solusi numerik dilakukan dengan menyubstitusikan nilai parameter pada persamaan (3.2). Kasus kestabilan titik tetap yang digunakan dalam simulasi ini yaitu dan di mana kestabilan kedua titik tetapnya bersifat sadel, dengan nilai parameter , , , dan tetap. Kasus tersebut merepresentasikan peristiwa mangsa-pemangsa di dalam kehidupan nyata, di mana kemampuan maksimum pemangsa dalam mencari mangsa ( ) lebih besar dibandingkan laju kematian ( ) yang dipengaruhi oleh kejenuhan pemangsa ( ), untuk . Dalam simulasi diberikan empat kondisi, dengan setiap kondisi akan diamati pengaruh persaingan dan kejenuhan pemangsa terhadap dinamika populasi.
4.1 Pengaruh Tingkat Kejenuhan Pemangsa I ( )
Untuk mengetahui pengaruh tingkat kejenuhan pemangsa I diberikan kondisi ke-1 di mana kejenuhan pemangsa I ( ) dan II ( ) lebih besar dibandingkan dengan tingkat persaingan pemangsa I ( ) dan II ( ). Nilai parameter yang digunakan ialah ,
, , , , , dan . Pada Gambar 1 ditunjukkan hubungan populasi mangsa dari kelima titik tetap terhadap ,
� , � ,
� √ , � ,
� √ .
Garis � dan � menunjukkan kondisi sadel, sedangkan garis � menunjukkan kondisi stabil. Untuk nilai , garis � menunjukkan kondisi takstabil, sedangkan untuk nilai menunjukkan kondisi stabil.
Gambar 1 Pengaruh saat kondisi dan . Dinamika Populasi pada Kondisi ke-1
Tingkat kejenuhan pemangsa I yang diberikan ialah dengan nilai awal , , . Diperoleh empat titik tetap taknegatif, dan kestabilan titik tetapnya bersifat sadel, sedangkan bersifat spiral takstabil dengan nilai eigen yang diperoleh yaitu .
� � �
8
Gambar 2 Dinamika populasi pada kondisi dan .
Gambar 2 menunjukkan populasi spesies mangsa dan kedua spesies pemangsa bersifat spiral takstabil. Awalnya populasi mangsa mengalami penurunan jumlah populasi yang sangat cepat. Hal tersebut menyebabkan jumlah spesies pemangsa I dan II juga
mengalami penurunan jumlah populasi, kemudian spesies mangsa mengalami kenaikan jumlah populasi yang menyebabkan populasi pemangsa I dan II pun juga bertambah. Kejadian tersebut berosilasi secara terus menerus.
Hasil simulasi yang ditunjukkan oleh Gambar 3 merupakan hubungan populasi spesies mangsa dengan populasi spesies pemangsa I dan II dan hubungan pemangsa I dengan pemangsa II. Hubungan populasi tersebut tidak menuju ke suatu titik tertentu pada waktu , sehingga terbentuk limit cycle.
yaitu . Dapat dilihat pada Gambar 4.
Gambar 4 Dinamika populasi ketika .
Gambar 5 Bidang parametrik hubungan antara ketika .
Hubungan populasi spesies mangsa terhadap spesies pemangsa I dan II ketika menunjukkan kestabilan yang bersifat spiral stabil. Gambar 5 terlihat hubungan tersebut menuju ke titik tetap yang menggambarkan populasi pemangsa I mengalami kepunahan dan populasi pemangsa II stabil dalam rentang waktu tertentu. 4.2 Pengaruh Tingkat Kejenuhan
Pemangsa II ( )
Untuk mengetahui pengaruh tingkat kejenuhan pemangsa II diberikan kondisi ke-2 di mana tingkat kejenuhan pemangsa I ( ) dan II ( ) lebih kecil daripada tingkat persaingan pemangsa I ( ) dan II ( ). Nilai parameter yang digunakan ialah ,
, , , , , dan . Gambar 6 menunjukkan hubungan populasi mangsa dari kelima titik tetap terhadap ,
� , � , � ,
� √ , � √ .
Gambar 6 Pengaruh pada kondisi dan . Garis putus-putus � , � , � , dan � menunjukkan kondisi bersifat sadel, sedangkan garis � menunjukkan kondisi stabil. Garis � dan � berpotongan di titik , hal tersebut tidak memengaruhi perubahan kestabilan sistem.
� � �
10
Dinamika Populasi pada Kondisi ke-2 Tingkat kejenuhan pemangsa II yang diberikan ialah dengan nilai awal , , . Jumlah populasi spesies pemangsa I dan II meningkat dengan cepat, namun ketika ketersediaan makanan berkurang, kedua spesies pemangsa mengalami penurunan jumlah populasi. Dalam rentang waktu tertentu populasi ketiga spesies mengalami kestabilan di titik tetap dengan nilai eigen . Dalam kondisi ini tingkat kejenuhan pemangsa II ( ) tidak berpengaruh terhadap kestabilan sistem, sehingga sistem akan tetap stabil walaupun nilai parameter dinaikkan ataupun. Hasil simulasi dapat dilihat pada Gambar 7.
Gambar 7 Dinamika populasi pada kondisi dan .
Gambar 8 menunjukkan hubungan populasi spesies mangsa terhadap spesies pemangsa I dan II pada kondisi dan . Dari kurva tersebut terlihat kestabilan sistem bersifat spiral stabil dalam rentang waktu tertentu.
Gambar 8 Bidang parametrik hubungan antara .
4.3 Pengaruh Tingkat Persaingan Pemangsa I ( )
Untuk mengetahui pengaruh tingkat persaingan pemangsa I diberikan kondisi ke-3 di mana tingkat kejenuhan pemangsa I ( ) lebih besar daripada tingkat persaingan I ( ) dan tingkat kejenuhan pemangsa II ( ) lebih kecil daripada tingkat persaingan pemangsa II ( ). Nilai parameter yang digunakan ialah , , , , , , dan . Gambar 9 menunjukkan hubungan populasi mangsa terhadap kelima titik tetap terhadap
,
� , � ,
3
2
1 1 1
1 1.66
0.3 0.27 (0.3 0.3) 0.03 ,
A
x m m m
m
� ,
� √ . Garis putus-putus � , � , dan � menunjukkan kondisi sadel, serta garis � menunjukkan kondisi stabil. Untuk nilai
Gambar 9 Pengaruh pada kondisi dan . Dinamika Populasi pada Kondisi ke-3
Tingkat persaingan pemangsa I yang diberikan ialah dengan nilai awal , , . Hasil simulasi dapat dilihat pada Gambar 10.
Gambar 10 Dinamika populasi pada kondisi dan .
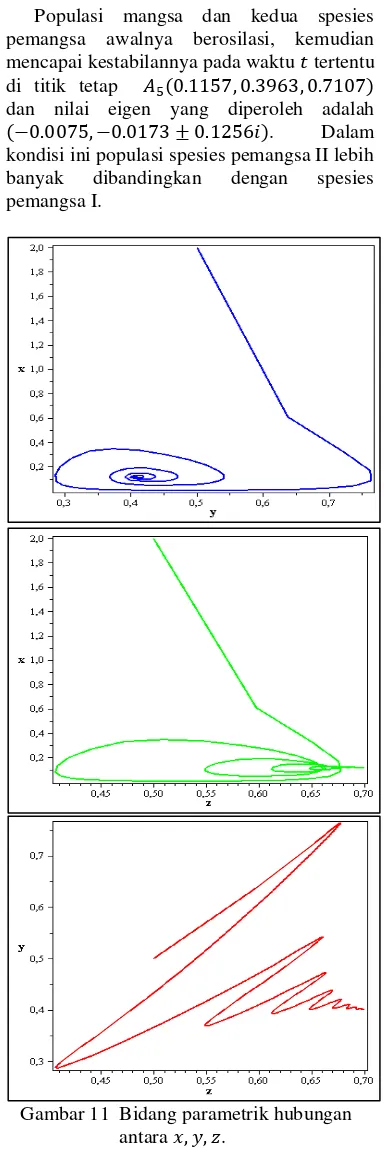
Populasi mangsa dan kedua spesies pemangsa awalnya berosilasi, kemudian mencapai kestabilannya pada waktu tertentu di titik tetap dan nilai eigen yang diperoleh adalah
. Dalam kondisi ini populasi spesies pemangsa II lebih banyak dibandingkan dengan spesies pemangsa I.
Gambar 11 Bidang parametrik hubungan antara .
Gambar 11 menunjukkan kurva bidang parametrik hubungan spesies mangsa dan kedua pemangsa bersifat spiral stabil. Untuk melihat pengaruh tingkat persaingan pemangsa I ( ), maka dinaikkan menjadi . Gambar 12 menunjukkan ketika nilai parameter dinaikkan, maka terjadi
� � �
12
perubahan kestabilan sistem dalam waktu yang singkat menuju ke titik tetap
.
Gambar 12 Dinamika populasi ketika .
4.4 Pengaruh Tingkat Persaingan Pemangsa II ( )
Untuk mengetahui pengaruh tingkat persaingan pemangsa II diberikan kondisi ke-4 di mana tingkat kejenuhan pemangsa I ( ) lebih kecil daripada tingkat persaingan I ( ) dan tingkat kejenuhan pemangsa II ( ) lebih besar daripada tingkat persaingan pemangsa II ( ). Nilai parameter yang digunakan adalah , , , , , , dan
. Gambar 13 menunjukkan hubungan populasi mangsa terhadap kelima titik tetap terhadap ,
� , � , � ,
� ( √ ), �
√ . Garis � , � , dan � menunjukkan kondisi sadel sedangkan garis � menunjukkan kondisi stabil. Garis � pada selang menunjukkan kondisi stabil.
Gambar 13 Pengaruh pada kondisi dan . Dinamika Populasi pada Kondisi ke-4
Tingkat persaingan pemangsa II yang diberikan ialah dengan nilai awal , , .
Gambar 14 Dinamika populasi pada kondisi dan .
� � �
Pada Gambar 14 populasi spesies mangsa dan spesies pemangsa II terjadi spiral takstabil, sedangkan populasi pemangsa I mengalami kepunahan. Populasi spesies mangsa dan pemangsa II yang takstabil diakibatkan tingkat persaingan kecil, sehingga proses mangsa-memangsa menjadi tidak teratur. Ketika ketersediaan makanan melimpah, jumlah populasi spesies pemangsa II bertambah banyak. Dalam waktu yang cepat populasi mangsa akan berkurang, sehingga populasi spesies pemangsa II juga berkurang. Kondisi seperti ini berosilasi secara terus-menerus.
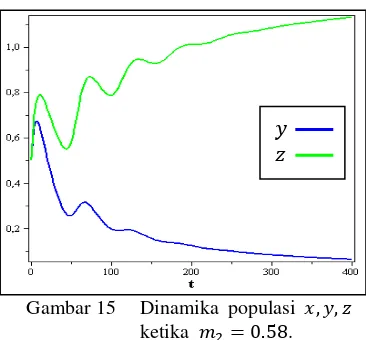
Jika nilai parameter persaingan pemangsa II ( ) dinaikkan menjadi maka akan terjadi perubahan kestabilan. Populasi pemangsa I mengalami kepunahan dalam rentang waktu tertentu sedangkan populasi pemangsa II mengalami penjumlahan populasi kemudian stabil pada titik tetap
. Kurva bidang solusinya dapat dilihat pada Gambar 15.
Gambar 15 Dinamika populasi ketika .
Ketika nilai parameter yang memengaruhi kestabilan setimbang, maka dinamika populasi mangsa dan kedua pemangsa akan stabil. Sebaliknya, ketika salah satu nilai parameter tidak setimbang maka dinamika populasi menjadi tidak stabil.
Dari empat kondisi yang diteliti, titik tetap dan selalu bersifat sadel. Pada kondisi pertama, titik tetap memiliki nilai eigen , dan bilangan-bilangan kompleks dengan bagian real positif, sehingga kestabilan bersifat spiral takstabil. Untuk kondisi kedua dan ketiga, dinamika populasinya bersifat spiral stabil menuju titik tetap , nilai eigen yang diperoleh yaitu
3 0
,
1 dan 2 adalah bilangan-bilangan kompleks dengan bagian real negatif. Sistem mengalami spiral takstabil pada kondisi keempat. Nilai eigen yang diperoleh adalah , dan bilangan-bilangan kompleks dengan bagian real positif. Berikut adalah tabel kondisi kestabilan dari hasil simulasi, dapat dilihat pada Tabel 2.Tabel 2 Kondisi kestabilan titik tetap.
Kondisi Titik Tetap
1 1
b m dan 2 2
b m Sadel Sadel Spiral takstabil
takstabil; spiral stabil - 1 1
b m dan 2 2
b m Sadel Sadel Sadel Sadel
Spiral stabil
1 1
b m dan 2 2
b m Sadel Sadel
takstabil; spiral
stabil
Sadel Spiral stabil 1 1
b m dan 2 2
b m Sadel Sadel Sadel
Spiral
8
V SIMPULAN
Dari analisis model mangsa-pemangsa dengan interferensi antarpemangsa yang terdiri dari tiga spesies diperoleh lima titik tetap. Kondisi kestabilan dari titik tetap yang diperoleh tidak mungkin stabil secara bersamaan. Dari kasus titik tetap yang digunakan, kondisi kestabilan titik tetap dan selalu bersifat sadel.
Pada dinamika populasi spesies pemangsa I dan II, faktor persaingan dan kejenuhan berpengaruh besar terhadap kestabilan sistem rantai makanan. Tingkat persaingan dan kejenuhan yang tidak seimbang akan menyebabkan jumlah populasi spesies pemangsa ataupun spesies mangsa tidak stabil. Semakin besar tingkat persaingan pemangsa ( , jumlah populasi pemangsa semakin berkurang, sedangkan semakin besar kejenuhan pemangsa , faktor kematian semakin kecil.
Dari empat kondisi yang diberikan, pada kondisi pertama hanya diperoleh empat titik tetap positif. Faktor tingkat kejenuhan
VI DAFTAR PUSTAKA
Anton H. 1995. Aljabar Linear Elementer. Ed ke-5. Terjemahan Pantur Silaban dan I Nyoman Susila. Jakarta: Erlangga. Keshet LE. 1988. Mathematical Models in
Biology. New York: The Random House.
Feng J, Zhu L & Wang H. 2010. Stability of Ecosystem Induced by Mutual Interference between Predators. China: Tianjin University.
Strogatz SH. 1994. Nonlinear Dynamics and Chaos with Applications to Physics,
Biology, Chemistry, and Engineering. New York: Perseus Books.
Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Second Revised and Enlarged Edition. Germany: Springer Verlag.
Lampiran 1 Penondimensionalan model mangsa-pemangsa
Diberikan sistem persamaan mangsa pemangsa: (3.1) , dengan:
Dilakukan penondimensionalan untuk mendapatkan sistem persamaan dengan parameter yang lebih sederhana:
dimisalkan
dX X dT
, dY Y
dT
, dZ Z
dT
̇ (1)
̇ (2)
̇ (3)
ˆ
X xx, Yyyˆ,
Z
zz
ˆ
, T t* Dari persamaan (1) diperoleh fungsi sebagai berikut:
1 2
1 1 2 2
1 X A X A X
X RX Y Z
K B X M Y B X M Z
2 1 2
1 1 2 2
A XY A XZ
RX
X RX
K B X M Y B X M Z
2 1 2
*
1 1 2 2
ˆ ˆ ˆ ˆ
ˆ ˆ ˆ
( ) ( )
ˆ ˆ ˆ ˆ
A xxyy A xxzz
dxx R
R xx xx
K B xx M yy B xx M zz
dt
2 2 1 2
*
1 1 2 2
ˆ ˆ ˆ ˆ
ˆ ˆ ˆ
ˆ ˆ ˆ ˆ
A xxyy A xxzz
x dx R
Rxx x x
K B xx M yy B xx M zz
dt
2 1 2
*
1 1 2 2
ˆ ˆ
ˆ
ˆ ˆ ˆ ˆ
A xyy A xzz
dx R
R x x x
K B xx M yy B xx M zz
dt pilih: ˆ K x R
, 1 1 ˆ y A , 2 1 ˆ z A , R 1
2
*
1 1 2 2
1 2
dx xy xz
x x
R R
dt
B xK M y B xK M z
A A
pilih:
18
2
*
1 1 2 2
dx xy xz
x x
B xK M y B xK M z
dt
pilih: K1, B1b1, B2b2, M1m1, M2m2
2
*
1 1 2 2
dx xy xz
x x
b x m y b x m z
dt
1 1 2 2
(1 )
dx xy xz
x x
dt b x m yb x m z (4)
Dari persamaan (2) diperoleh fungsi sebagai berikut: 1
1 1
1 1
A X
Y C Y D Y
B X M Y
1 1
1
1 1
C A XY
Y D Y
B X M Y
1 1
1 * 1 1 ˆ ˆ ˆ ˆ ˆ ˆ
C A xxyy dyy
D yy
B xx M yy
dt
1 1
1 * 1 1 ˆ ˆ ˆ ˆ ˆ ˆ
C A xxyy y dy
D yy
B xx M yy
dt pilih: 1 1 ˆ y A
, 1
1
A R
1 1
1 *
1 1
ˆ
ˆ ˆ
C A xxy dy
D y
B xx M yy
dt pilih: ˆ K x R
* 1 1 1
1 1
1
1
K C A xy
dy R
D y K
dt
B x M y
R A
1 1 * 1 1 C xy dy D yB x M y
dt
pilih: B1b1, C1a1, M1m1, 1 1 d D
1 1 1 1 dy xya d y
dt b x m y (5)
Dari persamaan (3) diperoleh fungsi sebagai berikut: 2
2 2
2 2
A X
Z C Z D Z
B X M Z
2 2
2
2 2
C A XZ
Z D Z
B X M Z
2 2
2 * 2 2 ˆ ˆ ˆ ˆ ˆ ˆ
C A xxzz dzz
D zz
B xx M zz
dt
2 2
2 * 2 2 ˆ ˆ ˆ ˆ ˆ ˆ
C A xxzz z dz
D zz
B xx M zz
2
1
ˆ
z A
, A2 R 1
2 2
2 *
2 2
ˆ
ˆ ˆ
C A xxz dz
D z
B xx M zz
dt pilih: ˆ K x R
* 2 2 2
2 2
2
1
K
C A xz
dz R
D z K
dt B x M z
R A
2 2 * 2 2 C xz dz D zB x M z
dt
pilih: B2b2, C2a2, M2m2, 2 2 d D
2 2 2 2 dz xza d z
dt b x m z (6)
Kemudian dari sistem persamaan (4), (5), dan (6) didapat skala baru yaitu:
X xxˆ
ˆ X x x
dengan: xˆ K R
, 1
1
R A
x X
K
Yyyˆ
ˆ Y y y dengan: 1 1 ˆ y A
, K1, R 1
maka menjadi 1
ˆ RK
y A
y A Y1
RK
Z
zz
ˆ
ˆ Z z z dengan: 2 1 ˆ z A
, K1, R 1
maka menjadi 2
ˆ RK
z A
A Z2
z RK
*
Tt
* T
t
* 1
t T
20
Lampiran 2 Penentuan titik tetap
Titik tetap akan diperoleh dengan menetapkan
1 1 2 2
(1 ) xy xz 0
x x
b x m y b x m z
(i)
1 1
1 1
0
xy
a d y
b x m y (ii)
2 2
2 2
0
xz
a d z
b x m z (iii)
Dari persamaan (i) akan diperoleh nilai sebagai berikut:
1 1 2 2
(1 ) xy xz 0
x x
b x m y b x m z
1 1 2 2
(1 ) y z 0
x x
b x m y b x m z
x
0
atau1 1 2 2
(1 x) y z 0
b x m y b x m z
x
0
atau1 1 2 2
1 x y z
b x m y b x m z
x
0
atau1 1 2 2
1 y z
x
b x m y b x m z
Dari persamaan (ii) akan diperoleh nilai sebagai berikut:
1 1
1 1
0
xy
a d y
b x m y
1 1 1 1 0 a x y d
b x m y
y0 atau 1
1
1 1
a x
d b x m y
y0 atau a x1 d b1 1d x1 d m y1 1
y0 atau 1 1 1 1
1 1
(a d x) d b y
d m
Dari persamaan (iii) akan diperoleh nilai sebagai berikut:
2 2
2 2
0
xz
a d z
b x m z
2 2 2 2 0 a x z d
b x m z
z
0
atau 22
2 2
a x d b x m z
z
0
atau a x2 d b2 2d x d m z2 2 2
z
0
atau 2 2 2 22 2
(a d x) d b z
d m
Sehingga diperoleh titik tetap
Untuk memperoleh titik tetap substitusi dan
1 1 2 2
1 y z
x
b x m y b x m z
, karena dan
1 2 0 0 1 0 0 x
b x b x
x
1
Sehingga diperoleh titik tetap
Untuk memperoleh titik tetap substitusikan dan 1 1 1 1 1 1
(a d x) d b y
d m
1 1 2 2
1 y z
x
b x m y b x m z
, karena
1 1
1 y
x
b x m y
1 1
1 x y
b x m y
1x
b1 x m y1
y 2
1 1 1 1
b x m y b x x m xyy
2
1 1 1 1 0
x x b x b y m y m xy
2
1 1 1 1 0
x x b x b y m y m xy
2
1 1 1 1 1 0
x x b x b m m x y , karena 1 1 1 1
1 1
(a d x) d b y
d m
2
1 1 1 11 1 1 1
1 1
( )
1 a d x d b 0
x x b x b m m x
d m
2
1 1 1 1 1 1 1 1 1 1 1 1 1 ( 1 1) 1 1 0 d m x d m xb d m xb d m m m x a d xd b
2
1 1 ( 1 1 1 1) 1 1 0
a m x a m a d x b d
dengan menggunakan rumus ABC didapatkan 2
1 1 1 1 1 1 1 1 1 1 1 1
1 1
( ) ( ) 4
2
a m a d a m a d a b d m x
a m
2
1 1 1 1 1 1
1 1 4 2
w w a b d m x
a m
dengan
w1a m1 1 a1 d1 substitusi ̅ ke persamaan
1 1 1 1
1 1
(a d x) d b y
d m
22
2
1 1 1 1 1 1
1 1 1 1
1 1
1 1
4
( )
2
w w a b d m
a d d b
a m y d m
Sehingga diperoleh titik tetap ̅ ̅
2
1 1 1 1 1 1
1 1 1 1
2
1 1 1 1 1 1 1 1
3
1 1 1 1
4
( )
2 4
, , 0
2
w w a b d m
a d d b
a m w w a b d m
A
a m d m
Untuk memperoleh titik tetap substitusikan dan 2 2 2 2 2 2
(a d x) d b z
d m
1 1 2 2
1 y z
x
b x m y b x m z
, karena
2 2
1 z
x
b x m z
2 2
1 x z
b x m z
1x
b2 x m z2
z 2
2 2 2 2
b x m z b x x m xzz
2
2 2 2 2 0
x x b x b z m z m xz
2
2 2 2 2 0
x x b x b z m zm xz
2
2 2 1 2 2 0
x x b x b m m x z , karena 2 2 2 2
2 2
(a d x) d b z
d m
2
2 2 2 22 2 2 2
2 2
( )
1 a d x d b 0
x x b x b m m x
d m
2
2 2 2 2 2 2 2 2 2 2 1 2 2 ( 2 2) 2 2 0 d m x d m xb d m xb d m m m x a d xd b
2
2 2 ( 2 2 2 2) 2 2 0 a m x a m a d x b d
dengan menggunakan rumus ABC didapatkan 2
2 2 2 2 2 2 2 2 2 2 2 2
2 2
( ) ( ) 4
2
a m a d a m a d a b d m x
a m
2
2 2 2 2 2 2
2 2 4 2
w w a b d m x
a m
dengan
w2a m2 2a2d2 substitusi ̃ ke persamaan
2 2 2 2
2 2
(a d x) d b z
d m
2
2 2 2 2 2 2
2 2 2 2
2 2
2 2
4
( )
2
w w a b d m
a d d b
a m z
d m
Sehingga diperoleh titik tetap ̃ ̃
2
2 2 2 2 2 2
2 2 2 2
2
2 2 2 2 2 2 2 2
4
2 2 2 2
4
( )
2 4
, 0, 2
w w a b d m
a d d b
a m w w a b d m
A
a m d m
Untuk memperoleh titik tetap substitusikan 1 1 1 1
1 1
(a d x) d b y
d m
2 2 2 2
2 2
(a d x) d b z
d m
Karena perhitungannya sulit dilakukan secara manual, maka dilakukan perhitungan menggunakan perangkat lunak matematikadengan kode sebagai berikut:
with(DEtools) :
Akan didapatkan persamaan , sehingga diperoleh titik tetap dengan *
* 1 1 1 1
1 1
(a d x) d b y
d m
*
* 2 2 2 2
2 2
(a d x) d b z
d m
24
Lampiran 3 Penentuan nilai eigen dari persamaan
Misalkan persamaan (3.3) dituliskan sebagai berikut:
1
1 1 2 2
2 1 1
1 1
3 2 2
2 2
( , , ) 1
( , , )
( , , )
y z
g x y z x x x
b x m y b x m z
x
g x y z y a d y
b x m y
x
g x y z z a d z
b x m z
Dengan melakukan pelinearan didapat matriks Jacobi sebagai berikut:
1 1 1
1
2 2 2
2
3 3 3
3
g g g
x g x x
x y z
g g g
J y y g y
x y z
g g g
z z z g
x y z
dengan
dideferensialkan terhadap
1
2 2
1 1 2 2
1 1
2
1 1 1 1
1 2
2
2 2 2 2
1 ( ) ( ) 1 ( ) ( ) 1 ( ) ( ) y z g
b x m y b x m z x
g m y
y b x m y b x m y
g m z
z b x m z b x m z
dideferensialkan terhadap
2
1 1 1 1
2 1 1
2 1 1 2 ( ) ( ) 0 g
a b x m y a x x
g a m x
y b x m y
g z
dideferensialkan terhadap
3
2 2 2 2
3
3 2 2
2 2 2 ( ) 0 ( ) g
a b x m z a x
x g
y
g a m x
z b x m z
Pelinearan titik tetap akan diperoleh matriks Jacobi sebagai berikut:
1 1
2
1 0 0
0 0 0 0 J d d
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik 1
det(J I)0
sehingga diperoleh
1
2
1 0 0
0 0 0
0 0 d d 2 1
(1)(d )( d )0
Jadi nilai eigennya adalah sebagai berikut: 1 1
2 d1
3 d2
Pelinearan titik tetap akan diperoleh matriks Jacobi sebagai berikut:
1 2
1 1 1 2
1
2 2 2
2 1 1 1 1 1 ( 1) 0 0 1 ( 1) 0 0 1 b b
a d b J
b
a d b b
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik 2
det(J I)0
sehingga diperoleh
1 2
1 1 1
1
2 2 2
2
1 1
1
1 1
( 1)
0 0 0
1
( 1)
0 0
1
b b
a d b b
26
Jadi nilai eigennya adalah sebagai berikut:
1 1
1 1 1 2
1
( 1) 1
a d b
b
2 2 2 3
2
( 1) 1
a d b
b
Pelinearan titik tetap ̅ ̅ akan diperoleh matriks Jacobi sebagai berikut:
1
2 2
1 1 1 1 1 1 1 1 2
1 1 1 1 1
3 2 2 1
1 1 1 1 1 1 1 1
2 2 2 1 2 ( ) ( ) 0 ( ) ( ) 0 0 xym
y xy x x
x
b x m y b x m y b x m y b x m y b x
a y a xy a x a xym
J d
b x m y b x m y b x m y b x m y
a x d b x
Diperoleh nilai eigen dari matriks J3:
2 1,2 4 2 di mana 11 22 G G
1 1 1
1
2 2
1 1 1 1 1 1 1 1
1 2
( ) ( )
a x a xym
y xy
x d
b x m y b x m y b x m y b x m y
1 1 1
1 2
1 1 1 1
1 2
( )
a x y xy a xym
x d
b x m y b x m y
11 22 12 21
G G G G
2 1 1 1 2 1
1 1 1 1 1 1 1 1
1 2
( ) ( )
a x a xym
y xy
x d
b x m y b x m y b x m y b x m y
1 1 1
2 2
1 1 ( 1 1 ) 1 1 ( 1 1 )
xym a y a xy
x