Analisis regresi pada data outlier dengan menggunakan least trimmed square (LTS) dan MM-Estimasi

ANALISIS REGRESI PADA DATA OUTLIER

DENGAN MENGGUNAKAN LEAST TRIMMED SQUARE

(LTS) DAN MM-ESTIMASI

Heru Nurcahyadi

PROGRAM STUDI MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI

SYARIF HIDAYATULLAH

ii

PENGESAHAN UJIAN

Skripsi berjudul “Analisis Regresi pada Data Outlier dengan Menggunkan Least Trimmed Square (LTS) dan MM-Estimasi” yang ditulis oleh Heru Nurcahyadi, NIM 105094003092 telah diuji dan dinyatakan lulus dalam sidang Munaqosyah Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta pada tanggal 19 Mei 2009. Skripsi ini telah diterima sebagai salah satu satu syarat untuk memperoleh gelar sarjana strata satu (S1) Program Studi Matematika.

Menyetujui :

Penguji 1, Penguji 2,

Yanne Irene, M.Si Gustina Elfiyanti, M.Si NIP. 19741231 2005012 018 NIP. 19820820 200901 2006

Pembimbing 1, Pembimbing 2,

Summa’inna, M.Si Bambang Ruswandi, M.Stat NIP. 150 408 699 NIP. 0305 108 301

Mengetahui :

Dekan Fakultas Sains dan Teknologi Ketua Program Studi Matematika,

PERSEMBAHAN

Skripsi ini aku persembahkan untuk kedua orang tuaku,

keluarga besarku, dan keluarga besar Prodi Matematika

MOTTO

‘

Karena sesungguhnya sesudah kesulitan itu ada kemudahan, dan

sesungguhnya sesudah kesulitan itu ada kemudahan. Maka apabila kamu telah

selesai (dari sesuatu urusan), kerjakanlah dengan sungguh-sungguh (urusan) yang

lain, dan hanya kepada Tuhanmulah kamu be

rharap.’

(QS. Alam Nasyrah ayat 5-8)

“

pelajarilah ilmu

Barang siapa mempelajarinya karena

ALLAH

, itu Taqwa.

Menuntutnya, itu Ibadah.

Mengulang-ngulangnya, itu Tasbih.

Membahasnya, itu Jihad.

Mengajarkannya kepada orang yang tidak tahu, itu Sedekah.

Memberikannya kepada ahlinya, itu mendekatkan diri kepada

ALLAH

.”

iii

PERNYATAAN

DENGAN INI SAYA MENYATAKAN BAHWA SKRIPSI INI BENAR-BENAR HASIL KARYA SENDIRI YANG BELUM PERNAH DIAJUKAN SEBAGAI SKRIPSI ATAU KARYA ILMIAH PADA PERGURUAN TINGGI ATAU LEMBAGA MANAPUN.

Jakarta, 15 Desember 2010

Heru Nurcahyadi 105094003092

vi ABSTRACT

Regression analysis is a statistical methodology that describes the relationship of independent variables and the dependent variable. From the relationship it established a model that can be used to predict the value of the dependent variable using the dependent variable. The resulting model is derived from the method of least square (LS), which must satisfy some assumptions. With the existence of a data which is not similar to most other data, called outliers, then the LS method using the resulting regression model did not meet the assumptions and regression models did not fit with the data.

Outlier on the x-direction is called leverage can be detected by using the h-hat matrix, while the y-direction is called discrepancies can be detected by using the externally studentized residual, and the influence can be detected by using DFFITS and COOK'SD.

method of least trimmed square (LTS) to produce regression models that fit to the data even though half of the data is outlier data, because it has a high value of breakdown point that is 50%. Other robust methods that have a breakdown point of 50% is MM-Estimate that use the S-Estimated initial iteration. LTS model is very good at simple regression analysis compared with MM-estimation seen from the estimated residual scale. While the multiple regression analysis of MM-Estimation is better when compared with the LTS seen from the estimated residual scale.

v

ABSTRAK

Analisis regresi adalah metodologi statistika yang menggambarkan hubungan atau pengaruh dari varibel independen dan variable dependen. Dari hubungan itu dibentuk suatu model yang bisa digunakan untuk memprediksikan nilai variable dependen dengan menggunakan variable dependen. Model yang dihasilkan diturunkan dari metode least square (LS), yang harus memenuhi beberapa asumsi. Dengan adanya suatu data yang tidak sejenis dengan sebagian data yang lain, yang disebut outlier, maka penggunaan metode LS model regresi yang dihasilkan tidak memenuhi asumsinya dan model regresinya tidak fit dengan data.

Outlier pada arah-x disebut leverage dapat dideteksi dengan menggunakan h-hat matrik, sedangkan pada arah-y disebut discrepancy dapat dideteksi dengan menggunakan externally studentized residual, dan nilai influence dapat dideteksi dengan menggunakan DFFITS dan COOK’SD.

metode least trimmed square (LTS) dapat menghasilkan model regresi yang fit terhadap data walaupun setengah dari datanya merupakan data outlier, karena mempunyai nilai breakdown point yang tinggi yaitu 50%. Metode robust yang lain yang mempunyai breakdown point 50% adalah MM-Estimasi yang menggunkan iterasi awal S-Estimasi. Model LTS sangat baik pada analisi regresi sederhana dibandingkan MM-estimasi dilihat dari estimasi skala residualnya. Sedangkan pada analisis regresi berganda MM-estimasi lebih baik jika dibandingkan dengan LTS dilihat dari estimasi skala residualnya.

vii

KATA PENGANTAR

ميح راا نمح راا ه مسب

Assalamu’alaikum Wr. Wb.

Puji syukur kehadirat Allah SWT yang telah memberi rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini. Shalawat serta salam tak lupa disampaikan kepada Nabi Muhammad SAW. Skripsi ini adalah syarat kelulusan yang harus ditempuh dalam menyelesaikan pendidikan sarjana strata satu Program Studi Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta.

Kami mengucapkan terima kasih kepada para pihak yang telah banyak membantu dalam penyelesaian skripsi ini, di antaranya :

1. Dr. Syopiansyah Jaya Putra, M.Sis, Dekan Fakultas Sains dan Teknologi . 2. Yanne Irene, M.Si, sebagai Ketua Program Studi Matematika dan dosen

penguji I.

3. Suma’inna, M.Si, Sekretaris Program Studi Matematika dan dosen Pembimbing I.

4. Bambang Ruswandi, M.Stat, dosen pembimbing II

5. Seluruh dosen Prodi Matematika yang telah memberikan ilmu-ilmu yang sangat bermanfaat bagi penulis.

viii

7. Kedua orang tuaku: H. Ahyad dan Hj. Nurhayati, adikku: Herwin Adriyan, dan keluargaku yang senantiasa mendoakan dan memberikan semangat selalu pada penulis dalam penyelesaian skripsi ini.

8. Pamanku, Sersan Satu Unang Sunarya dan keluarganya yang telah banyak mendorong dan membantu dalam penyelesaian skripsi ini.

9. Mukhlis, Dede Kurniawan, Syakur, dan Perdy atas persahabatannya selama ini, semoga selalu kekal hingga akhir waktu.

10.Seluruh teman-teman angkatan 2004, 2005, 2006, 2007, dan 2008 semoga Allah tetap mengekalkan ukhuwah kita.

Kritik dan saran sangat kami harapkan demi penyempurnaan skripsi. Mohon maaf bila ada kekurangan. Semoga skripsi ini dapat bermanfaat bagi para pembaca, khususnya bagi penulis pribadi.

Wassalamu’alaikum Wr.Wb.

Jakarta, 15 Desember 2010

ix

DAFTAR ISI

HALAMAN JUDUL ... i

PENGESAHAN UJIAN ... . ii

PERNYATAAN ... . iii

PERSEMBAHAN DAN MOTTO ... iv

ABSTRAK ... v

ABSTRACT ... vi

KATA PENGANTAR ... vii

DAFTAR ISI ... ix

DAFTAR TABEL ... xi

DAFTAR GAMBAR ... xiii

DAFTAR LAMPIRAN ... . xiv

BAB I. PENDAHULUAN ... 1

1.1. Latar Belakang ... 1

1.2. Permasalahan... 4

1.3. Pembatasan Masalah ... 4

1.4. Tujuan Penulisan ... 5

1.5. Manfaat Penulisan ... 5

BAB II. LANDASAN TEORI ... 6

2.1. Model Persamaan Regresi Linear……… 6

2.2. Outlier Dalam Regresi: Sumber, Jenis danDeteksi Outlier… 11

x

BAB III. ROBUST ESTIMASI PADA REGRESI ... 37

3.1. Least Trimmed Square ... 37

3.2. MM-Estimasi ... 45

BAB IV. APLIKASI MODEL ... 52

4.1. Aplikasi pada Regresi Sederhana ... 52

4.2. Aplikasi pada Regresi Berganda ... 60

BAB V. KESIMPULAN DAN SARAN ... 65

5.1. Kesimpulan ... 65

5.2. Saran ... 61

REFERENSI ... 67

xiii

DAFTAR GAMBAR

Gambar 2.1 : Model Regresi Linear Sederhana ... 7

Gambar 2.2 : Garis Least Square ... 9

Gambar 2.3 : Outlier pada Arah-y ... 14

Gambar 2.4 : Outlier pada Arah-x ... 15

Gambar 2.5 : Outlier pada (xk,yk) ….. ... 16

Gambar 2.6 : Fungsi Huber ... 25

Gambar 2.7 : Fungsi Bisquare ... 31

Gambar 4.1 : Plot Leverage ... ... 53

Gambar 4.2 : Scatterplot dan Garis Least Square ... 56

Gambar 4.3 : Distribusi Normal Residual Data Pensiunan ... 56

Gambar 4.4 : Garis Least Trimmed Square Data Pensiunan ... 57

Gambar 4.5 : GarisMM-EstimasiData Pensiunan ... 59

xi

[image:12.595.118.524.80.473.2]

DAFTAR TABEL

Tabel 3.3.1: Efisiensi Asimptotik S-Estimator ... 51

Tabel 4.1 : dana pensiunan ... 52

Tabel 4.2 : pemeriksaan data outlier pada arah-x dana pensiunan ... 53

Tabel 4.3 : pemeriksaan data outlier pada arah-y dana pensiunan ... 54

Tabel 4.4 : Perbandingan LS, LTS, MM-Estimasi Dana Pensiunan ... 59

Tabel 4.5 : Data Survival Time ... 60

Tabel 4.6 : pemeriksaan data outlier pada data table 4.5 . ... 62

xiv

DAFTAR LAMPIRAN

Lampiran 1 : Data Dana Pensiunan ... 68

Lampiran 2 : Pemeriksaan Data Outlier pada Arah-x Dana Pensiunan ... 68

Lampiran 3 : Pemeriksaan Data Outlier pada Arah-y Dana Pensiunan ... 69

Lampiran 4 : Data Survival Time ... 70

Lampiran 5 : Pemeriksaan Leverage Data Survival Time….. ... 71

Lampiran 6 : Pemeriksaan Discrepancy Data Survival Time…... 72

1 BAB I PENDAHULUAN

1.1 Latar Belakang

Model matematik dalam statistika merupakan penyederhanaan dari realitas atau permasalahan yang diteliti oleh statistikawan. Oleh karena itu, diperlukan asumsi-asumsi agar model tersebut dapat menggambarkan permasalahannya. Selain itu, asumsi diperlukan agar dapat merumuskan apa yang statistikawan ketahui atau terka (conjectures) mengenai penganalisisan data atau masalah permodelan statistik yang dihadapinya, dan pada saat yang bersamaan asumsi diperlukan agar model yang dihasilkan dapat memudahkan (manageable) dalam sudut pandang teoritik dan komputasinya. Salah satu asumsi yang paling banyak ditemukan dalam satatistik adalah asumsi kenormalan, yang telah ada selama 2 abad, asumsi kenormalan menjadi kerangka berpikir dalam semua metode statistik inferensi, yaitu: Regresi, analisis variansi, analisis multivarit, model runtun waktu dan lain-lain. Bahkan terdapat justifikasi untuk asumsi kenormalan dengan argumen teori yaitu teorema limit pusat.

Sering kali dalam prakteknya asumsi kenormalan terpenuhi secara aproksimasi pada sebagian besar data observasi. Bahkan, beberapa observasi berbeda pola atau bahkan tidak berpola mengikuti distribusi normal. Hal ini

dikarenakan observasi yang “tidak normal”, observasi yang terpisah dari obsevasi

2 Sehingga statistikawan kemungkinan melakukan kesalahan dalam memodelkan suatu fenomena dengan adanya kehadiran data outlier. Oleh karena itu, diperlukan metode yang bisa mengatasi masalah tersebut.

Dalam mengatasi data outlier harus dilihat dari sumber munculnya data yang menjadi outlier tersebut. Outlier mungkin ada karena adanya data terkontaminasi, yaitu adanya kesalahan pada saat melakukan pengambilan sampel pada populasi. Outlier yang disebabkan oleh data terkontaminasi dapat dihapuskan dari data penelitian atau jika memungkinkan dilakukan sampling ulang. Akan tetapi, jika setelah melakukan beberapa kali sampling ulang namun data outlier tetap muncul maka data tersebut jangan dihapuskan dari data penelitian, karena analisis data yang dihasilkan akan tidak mencerminkan populasi yang diteliti. Outlier pada kasus tersebut digolongkan pada kasus yang jarang. Untuk mengatasinya diperlukan metode lain supaya analisis data dengan hadirnya data outlier tetap tahan (robust) terhadap asumsi yang diterapkan pada penganalisisan datanya. Metode tersebut dikenal dengan Metode Robust. Metode inilah yang akan jadi penelitain penulis pada tugas akhir ini.

3 outlier pada data regresi mengakibatkan model regresi tidak memenuhi asumsinya dan model regresi tidak cocok (fit) terhadap data yang akan dimodelkan, karena nilai koefisien dari model regresi tersebut sangat dipengaruhi oleh adanya outlier. Oleh karena itu, model yang dihasilkan tidak dapat digunakan untuk memprediksikan. Sehingga, outlier pada regresi harus diatasi.

Salah satu metode guna mengatasi outlier pada regresi adalah metode robust. Metode robust yang akan dipakai pada tugas akhir ini adalah MM-Estimasi dan least trimmed square (LTS) merupakan dua metode yang mempunyai nilai breakdown point yang tinggi yaitu hampir 50%. MM-estimasi merupakan metode robust dengan iterasi point estimasi dari model regresi. Dalam MM-estimasi dibutuhkan iterasi awal (initial) dan iterasi akhir (final). LTS merupakan metode dengan pertama-tama menghitung h, banyak data yang menjdikan estimasi Robust, dengan sebelumnya menyusun residual kuadrat dari yang terkecil sampai dengan yang terbesar.

Disamping penanganan outlier pada regresi, yang lebih penting adalah pengidentifikasian data yang menjadi outlier. Metode pengidentifikasian yang digunakan pada tugas akhir ini adalah dengan melihat leverage, nilai discrepancy, dan nilai influence-nya. leverage hanya menggambarkan kasus yang terjadi pada variabel independen. Untuk tiap kasus, leverage menginformasikan seberapa jauh kasus tesebut dari nilai mean himpunan data variabel independen. Sedangkan discrepancy merupakan jarak antara nilai prediksi dengan nilai observasi dari

4 besar dan tidak jatuh pada garis regresi. dan yang terakhir nilai influence merupakan kombinasi dari ukuran leverage dan discrepancy yang menginformasikan mengenai bagaimana perubahan dari persamaan regresi jika kasus ke-i dihilangkan dari himpunan data.

1.2 Permasalahan

1. Bagaimana pengidentifikasian outlier dengan menggunakan leverage, nilai discrepancy, dan nilai influence dari data regresi.

2. Bagaimana cara mengestimasi nilai-nilai parameter model regresi dengan adanya data outlier dengan menggunakan Least trimmed square (LTS) dan MM-Estimasi pada data regresi tersebut.

3. Bagaimana perbandingan model regresi yang dihasilkan dengan menggunakan Least trimmed square (LTS) dan MM-Estimasi.

1.3 Pembatasan Masalah

Pada skripsi ini, permasalahan akan dibatasi, yaitu sebagai berikut:

1. Data outlier diasumsikan bukan berasal dari sumber kesalahan sampling, akan tetapi data outlier tersebut merupakan kejadian yang khusus atau jarang.

2. Pengidentifikasian outlier menggunakan metode h-matriks untuk mengidentifikasi nilai leverage, metode externally studentized residual untuk mengidentifikasi nilai discrepancy, dan metode

5 3. Penanganan data outlier pada regresi akan digunakan metode

MM-Estimasi dan Least Trimmed Square, kemudian perbandingannya hanya dengan melihat estimasi skala residualnya.

4. Asumsi regresi yang dipakai hanya asumsi kenormalan.

1.4 Tujuan Penulisan

1. Mengidentifikasikan data outlier dengan menggunakan leverage, nilai discrepancy, dan nilai influence dari data regresi, sehingga diketahui data yang menjadi outlier dari sekumpulan data regresi.

2. Mengetahui cara mengestimasi nilai-nilai model parameter regresi dengan adanya data outlier dengan menggunakan Least trimmed square (LTS) dan MM-Estimasi pada data regresi.

3. Membandingkan model regresi yang dihasilkan dengan menggunakan Least trimmed square (LTS) dan MM-Estimasi.

1.5 Manfaat Penulisan

1. Dapat mengetahui cara pengidentifikasian outlier dengan menggunakan leverage, nilai discrepancy, dan nilai influence dari data regresi.

2. Dapat mengetahui pengestimasian nilai-nilai model parameter regresi dengan adanya data outlier dengan menggunakan Least trimmed square (LTS) dan MM-Estimasi pada data regresi.

6 BAB II

LANDASAN TEORI

2.1 Model Persamaan Regresi Linear

Analisis regresi merupakan suatu proses pencarian model matematika terbaik yang cocok dengan data yang menghubungkan variabel dependen (juga biasa disebut respon) dengan variabel independen (prediktor). Bentuk umum model regresi linear adalah:

 



E y

y 2.1

Dengan,

y = variabel dependen

E

 

y = ekspektasi dari y.

 = random error.

Model regresi di atas tidak mempertimbangkan sejumlah variabel independen (x) yang berkorelasi sangat kuat dengan variabel dependen (y), dengan menggunakan variabel independen maka keakuratan dalam mengestiamsi

 

y

E dapat diperoleh. Sehingga E

 

y dapat diestimasi dengan bentuk persamaan

linear, yaitu:

 

y x

E ₀ ₁ 2.2

7

 

  

 x

y _{0 1} 2.3

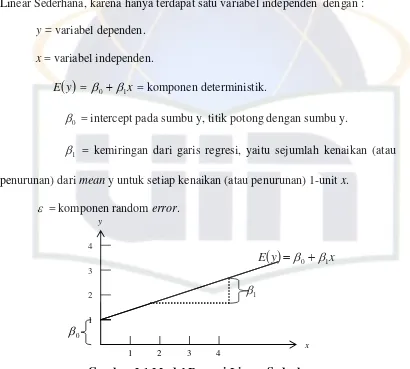
Persamaan 2.3 di atas disebut Model Linear Orde-Pertama atau Model Linear Sederhana, karena hanya terdapat satu variabel independen dengan :

y = variabel dependen. x = variabel independen.

E

 

y = ₀ ₁x = komponen deterministik.

₀ = intercept pada sumbu y, titik potong dengan sumbu y.

₁ = kemiringan dari garis regresi, yaitu sejumlah kenaikan (atau

penurunan) dari mean y untuk setiap kenaikan (atau penurunan) 1-unit x.

 = komponen random error.

Jika terdapat variabel independen lebih dari satu, maka modelnya disebut Model Regresi Linear Berganda atau Model Regresi Linear Umum dengan persamaan modelnya sebagai berikut :

  



     

 x x _kx_k

y _{0 1 2 2} ... 2.4

Pada Persamaan-persamaan di atas (2.3 dan 2.4) terdapat komponen random error (). Distribusi darimenentukan seberapa ”bagusnya” model yang

1 2 3 4 1

2 3 4

0 

1 

 

y x

E ₀ ₁

[image:20.595.114.524.177.546.2]

x y

8 menggambarkan hubungan sebenarnya antara variabel dependen y dan variabel independen x. Ada empat asumsi yang menyangkut distribusi dari , yaitu [1] :

1.Mean distribusi probabilitas dari  adalah 0. Artinya rata-rata error pada percobaan yang dilakukan secara tak hingga adalah 0 untuk setiap pengambilan variabel independen. Asusmsi ini mengakibatkan nilai mean dari y,

untuk setiap nilai x yang diberikan adalah E

 

y ₀ ₁x.

2.Variansi distribusi probabilitas dari  adalah konstan untuk setiap pengambilan variabel independen.

3.Distribusi probabilitas dari  berdistribusi normal.

4.Error dari setiap dua observasi adalah independen. Artinya error dari salah satu nilai y tidak memberikan pengaruh terhadap error dari nilai y yang lain.

Dari persamaan-persamaan di atas nilai koefisien yaitu ₀ dan _i (untuk i = 1 sampai dengan k) tidak diketahui karena merupakan nilai parameter. Oleh karena itu, dibutuhkan data sampel untuk mengestimasi koefisien-koefisien tersebut.

Misalkan Y₁,Y₂,....,Y_k merupakan variabel random berdistribusi normal dengan mean masing-masing E

 

y ₀ x_i, dengan i = 1, 2, ....,k, dan variansi yang tidak diketahui 2 Misalkan akan dicari model regresi linear sederhana.

Fungsi likelihood dari variabel random Y₁,Y₂,....,Y_k adalah:

9 Untuk memaksimumkan fungsi L



0,1,2



, atau ekuivalen dengan

meminimumkan:











2



1 2 1 0 2 2 1 0 2 2 ln 2 , , ln       



      k i i i x y k L ,

harus dipilih ₀ dan ₁dengan meminimumkan:











    k i i i x y H 1 2 1 0 1

0,  



Karena y_i ₀₁x_i  y_iE

 

y merupakan jarak vertikal dari titik



xi,yi



terhadap garis y E

 

y . Oleh karena itu, H



0,1



merepresentasikan

jumlah kuadrat tersebut. Dengan memilih ₀ dan ₁ sedemikian hingga jumlah

kuadrat dari jarak tersebut minimum dengan seperti itu artinya garis lurus

 

y E

y mem-fitting data. Oleh karena itu, metode ini disebut Metode Least square [1].

Untuk meminimumkan H



₀,₁



, harus dicari



,



0

0 1 0      

H _dan





0 , 1 1 0       H ,

 

y _{0 1}x₁

E  



xi,yi



[image:22.595.113.526.82.436.2]

 y E yi

10









 

x y k x y x k y x y H k i i k i i k i i k i i k i i i 1 1 1 0 1 1 0 1 1 1 0 0 1 0 ˆ 0 0 1 2 ,                        











   

Jadi dari penurunan diatas di dapat ˆ₀  yˆ₁x, notasi ˆ merupakan

notasi estimator untuk nilai parameter , sedangkan untuk nilai ˆ₁ adalah

sebagai berikut:









 











































                            _                                                   k i i k i i i k i i i k i i k i i k i i k i i i k i i k i i k i k i i i i k i i k i i k i k i i i i k i i i i i k i i i i x k x y x k y x y x k y x x k x k x x karena x x k x y k x y x k x k x k x k y x y x x x x y x y x y karena x x x y x y x x y H 1 2 2 1 1 1 2 1 2 1 1 1 2 1 2 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 0 1 2 1 1 1 1 0 1 1 0 ˆ 0 0 0 0 0 2 ,                 

Jadi dari penurunan di atas nilai dari ˆ₁ yang merupakan estimator dari ₁

adalah





     _k i i k i i i x k x y x k y x 1 2 2 1 1 ˆ

11 2.2 Outlier Dalam Regresi: Sumber, Jenis dan Deteksi Outlier

2.2.1 Sumber Outlier

Outlier adalah satu atau lebih data yang tidak biasa, yang tidak cocok dari sebagian data lainnya (one or more atypical data points that do not fit with the rest of the data). Outlier mungkin disebabkan karena dalam melakukan observasi melakukan beberapa kesalahan, hal ini yang biasa disebut observasi terkontaminasi, juga bisa outlier merepresentasikan observasi yang akurat dari kasus yang jarang. Apapun sumber outlier, dalam beberapa kasus menyebabkan dampak yang sangat besar dalam mengestimasi koefisien regresi , standar error,

dan estimasi keseluruhan variabel prediktor, R2.[2]

Outlier muncul karena data terkontaminasi dalam beberapa cara. Observasi yang terkontaminasi dapat dan harus diminimalisir dengan prosedur penelitian dan pengolahan data yang hati-hati. Observasi yang terkontaminasi disebabkan [2]:

1. Kesalahan pelaksanaan prosedur penelitian; misalnya: interviewer salah baca dalam beberapa pertanyaan, atau eksperimenter melakukan yang salah atau perlakuan yang kurang sempurna.

2. Ketidakakuratan dalam pengukuran variabel dependen; misalnya peralatan mengalami kerusakan sehingga pengukuran variabel dependen tidak akurat. 3. Kesalahan penulisan atau pengetikan data.

12 5. Partisipan yang kurang perhatian. Misal dala kasus tertentu, partisipan sedang dalam keadaan lelah, sakit atau mabuk, dan tidak mampu merespon dengan baik terhadap materi percobaan.

Tiap statistik diagnostik yang akan dibahas nanti, secara potensial dapat menolong dalam pendeketsian data yang terkontaminasi. Ketika peneliti mendeteksi outlier, perlakuan pertamanya adalah melihat kemungkinan bahwa outlier merupakan data yang terkontaminasi. Data dan perhitungan harus diperiksa keakurasiannya. Jika dapat diverifikasi bahwa outlier merupakan data yang terkontaminasi, maka data tersebut tidak harus dimasukkan dalam penganalisisan data. Jika memungkinkan, peneliti bisa mengganti data yang terkontaminasi ini dengan data yang benar dari kasus yang ditelitinya, atau menghapusnya dari himpunan data yang diteliti.

13 2.2.2 Jenis Outlier

Analisis regresi memberikan suatu model yang menggambarkan

hubungan dari beberapa variabel independen (X_i, i = 1,2,…n) dengan variabel dependen ( ,Y ii 1, 2,....,n). Model regresi tersebut didapatkan dengan menggunkan metode estimasi kuadrat terkecil (least square estimate). Metode LS didasarkan pada asumsi bahwa error dari model yang dihasilkan harus berdistribusi normal. Karena dengan error berdistribusi normal metode LS memberikan estimasi parameter yang optimal bagi model regresi tersebut [3].

Akan tetapi, dengan adanya data outlier asumsi kenormalan model regresi tersebut akan tidak terpenuhi [5]. Seperti diketahui pada analisis regresi, terdapat satu variabel dependen yang digambarkan pada scatterplot sebagai arah y, dan beberapa variabel independen pada scatterplot digambarkan sebagai arah x. Oleh karena itu, keberadaan data outlier mungkin teredapat pada arah-y atau pada arah-x atau di keduanya.

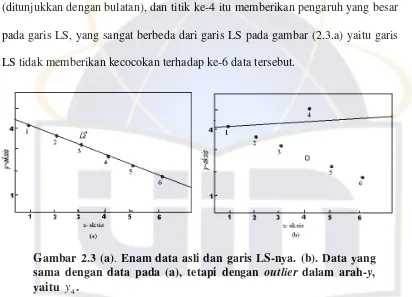
Data outlier pada arah-y akan memberikan nilai residual r yang sangat besar (positif atau negatif). Hal ini disebabkan karena data yang menjadi outlier mempunyai jarak yang sangat besar terhadap garis LS. Seperti yang ditunjukkan gambar (2.3.a) yang merupakan scatterplot dan garis LS dari enam titik,



x y1, 1



,....,



x y6, 6



, yang hampir terletak pada suatu garis lurus (garis LS). Oleh

karena itu, penyelesaian LS kecocokannya sangat bagus untuk ke-6 data tersebut. Akan tetapi, andaikan dengan data yang sama, tetapi data ke-4 merupakan data

outlier, yaitu y₄ yang disebabkan karena ada suatu kesalahan, maka titik



x y₄, ₄



[image:26.595.108.528.79.468.2]

14 Gambar 2.3 (a). Enam data asli dan garis LS-nya. (b). Data yang sama dengan data pada (a), tetapi dengan outlier dalam arah-y, yaitu y₄.

(2.3.b). titk data yang ke-4 bergeser ke atas dan jauh dari posisi asalnya (ditunjukkan dengan bulatan), dan titik ke-4 itu memberikan pengaruh yang besar pada garis LS, yang sangat berbeda dari garis LS pada gambar (2.3.a) yaitu garis LS tidak memberikan kecocokan terhadap ke-6 data tersebut.

Sedangkan data outlier pada arah-x, memberikan pengaruh yang sangat besar pada estimator metode LS karena outlier pada arah-x akan membalikkan garis LS. oleh karena itu, outlier pada arah-x disebut sebagai titik leverage [3]. Seperti ditunjukkan pada gambar (2.4.a) yang merupakan scatterplot dan garis LS

dari lima titik data



x y₁, ₁

 

,..., x y₅, ₅



yang hampir terletak pada suatu garis lurus

(garis LS). Misalkan dengan data yang sama akan tetapi titik x₁adalah outlier

yang disebabkan karena suatu kesalahan. Maka, garis LS akan berbalik dari keadaan yang digambarkan pada gambar (2.4.a), seperti yang ditunjukkan pada

gambar( 2.4.b). Hal ini dapat dijelaskan sebagai berikut: karena x1terletak jauh,

[image:27.595.112.524.141.438.2]

15 menjadi sangat besar (negatif), berkontribusi terhadap besarnya jumlah



5_i1r_i2 untuk garis tersebut. Oleh karena itu, garis asal tidak dapat dipilih dari prespektif

LS, dan tentunya garis pada gambar (2.4.b) mempunyai nilai 5 2 1 i

i r



yang

terkecil, karena itu garis asal dibalikkan menjadi garis pada gambar (2.4.b) untuk

mengurangi besarnya nilai r₁2, bahkan jika keempat bentuk lainnya, r r r r₂2, ₃2, ₄2, ₅2,

sedikit dinaikkan [3].

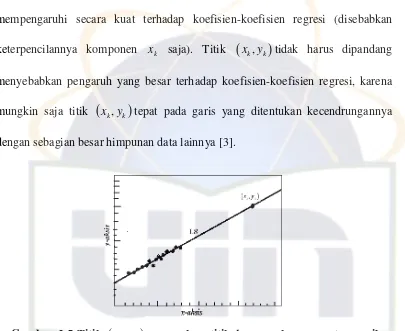
Secara umum, suatu observasi



x y_k, _k



dikatakan suatu titik leverage ketika x_kterletak jauh dari sebagian besar data observasix_idalam sampel. Sebagai catatan, bahwa suatu titik leverage tidak memasukkan nilai y_kke dalam perhitungan, jadi titik



x y_k, _k



tidak harus perlu menjadi outlier pada regresi.

Ketika



x y_k, _k



dekat terhadap garis regresi yang ditentukan dengan sebagian besar data, maka hal itu dapat diperkirakan sebagai titik leverage yang bagus seperti ditunjukkan pada gambar (2.5). Oleh karena itu, untuk mengatakan bahwa [image:28.595.111.527.87.455.2]

16 mempengaruhi secara kuat terhadap koefisien-koefisien regresi (disebabkan

keterpencilannya komponen x_k saja). Titik



x y_k, _k



tidak harus dipandang menyebabkan pengaruh yang besar terhadap koefisien-koefisien regresi, karena

mungkin saja titik



x y_k, _k



tepat pada garis yang ditentukan kecendrungannya dengan sebagian besar himpunan data lainnya [3].

Dalam regresi berganda,



x_i1,...,x_ip



terletak pada suatu ruang berdimensi p.

Suatu titik leverage tetap didefinisikan sebagai suatu titik



x_k1,...,x_kp,y_k



di mana



xk1,...,xkp



merupakan titik-titik yang terpisah dari himpunan data



xi1,...,xip



.

Seperti sebelumnya, suatu titik leverage yang berpotensial berpengaruh besar

pada koefisien regresi LS, bergantung pada nilai aktual dari y_k. akan tetapi pada situasi ini, akan sangat susah mengidentifikasi titik-titik leverage, karena dimensinya yang tinggi [3].

[image:29.595.118.523.101.432.2]

17 2.2.3 Deteksi outlier

18 1. Leverage

Leverage hanya menggambarkan kasus yang terjadi pada variabel independen. Untuk tiap kasus, leverage menginformasikan seberapa jauh kasus tesebut dari nilai mean himpunan data variabel independen. Jika hanya terdapat satu variabel independen, leverage dapat ditentukan sebagai [2]:





2

ii 2

1

leverage = h Xi MX

n x

  



2.5

dengan hii adalah leverage kasus ke-i, n banyaknya data, Xi adalah nilai untuk

kasus ke-i, MX adalah mean dari X, dan



x2merupakan jumlah kuadrat n kasus

dari simpangan Xi dari meannya. Jika kasus ke-i bernilai MX, maka bentuk kedua dari persamaan di atas akan 0 dan hii akan memiliki nilai kemungkinan yang

minimum, 1

n . Misalkan kasus ke-i skor pada X menjadi jauh dan jauh dari MX, maka akan menaikkan hii. Nilai maksimum dari hii adalah 1 nilai mean dari

leverage untuk n-kasus dalam suatu sampel adalah



1



ii

h

M  k  n, dengan k

merupakan jumlah variabel independen.

Perhitungan leverage di atas untuk kasus dengan satu variabel independen, dapat digeneralisasi untuk kasus dengan variabel independen lebih dari satu. Untuk kasus dengan banyak variabel independen, yang menjadi menarik adalah

seberapa jauh nilai-nilai untuk tiap k variabel untuk kasus ke-i, X_i1,X_i3,...,X_ik, dari centroid variabel independen, centroid merupakan mean dari data,

1, 2,..., k

M M M . Penghitungan nilai hii untuk kasus ini dengan menggunakan

19

 

1

'  '



H X X X X 2.6

dengan H merupakan matrik n n dan X merupakan matrik n



k 1



. Dengan n

merupakan banyaknya data, dan k merupakan jumlah koefisein

 

_k variabel

independen ditambah 1 sebagai nilai konstanta

 

₀ . Diagonal dari H berisi

nilai-nilai leverage. Jadi, leverage untuk kasus ke-i, hii, merupakan nilai dari baris ke-i

dan kolom ke-i darai H.

Penentuan nilai yang memiliki leverage yang besar didasarkan pada nilai cutoff. Nilai hii yang melebihi nilai cutoff dideteksi sebagai outlier. Adapun nilai

cutoff yang telah ditentukan dari [2], adalah 2



k 1



nuntuk data yang banyak



n 15



, sedangkan untuk data yang sedikit



n 15



digunakan cutoff





3 k 1 n. n



k 1



. Dengan n merupakan banyaknya data, dan k merupakan

jumlah koefisein

 

_k variabel independen ditambah 1 sebagai nilai konstanta

 

0 .

2. Discrepancy

Diagnostik statistik untuk data outlier yang kedua adalah discrepancy atau jarak antara nilai prediksi dengan nilai observasi dari variabel dependen (Y), yaitu

ˆ

i i

20 Internally studentized residuals menunjukkan satu dari dua hal yang menyangkut residual mentah (raw). Ekspektasi dari variansi residual untuk kasus ke-i diekspresikan sebagai [2]:

 

i residual





variansi e MS 1h_ii 2.7

Dengan MS_residual merupakan estimasi dari keseluruhan variansi dari residual

sekitar garis regresi =



1R2





y2





n k 1 .



hii merupakan leverage dari

kasus ke-i. standar deviasi dari residualdari kasus ke-i adalah



1



i

e residual ii

sd  MS h 2.8

Internally studentized residuals merupakan rasio dari besaran nilai residual dari kasus ke-i dengan standar deviasi dari residual kasus ke-i [2], yaitu:

i

Internally studentized residuals i

i e

e sd

 2.9

Besar dari Internally studentized residuals berjarak antara 0 dan

1

n k . Sungguh tidak menguntungkan, Internally studentized residuals tidak mengikuti distribusi standar statistk, karena persamaan (2.9) penyebut dan pembilangnya tidak saling bebas. Jadi Internally studentized residuals tidak bisa diinterpretasi menggunakan kurva normal atau t tabel. Dengan demikian, kebanyakan yang lebih disukai dalam menghitung discrepancy adalah dengan menggunakan Externally Studentized Residuals.

21 dianggap outlier dihapuskan dari himpunan data. Misalkan Y_{i i }nilai perediksi kasus ke-i, tetapi kasus ke-i dihapuskan dari himpunan data. Outlier berkontribusi secara substansial terhadap estimasi variansi residual sekitar garis regresi,

.

residual

MS Sedangkan MS_{residual i }untuk variansi residual dengan kasus ke-i yang

merupakan outlier dihapuskan dari data. Misalkan d_isebagai perbedaan antara data asli observasi, Y, dengan nilai prediksi untuk kasus ke-i yang berasal dari

himpunan data dengan kasus ke-i dihapuskan, yaitu:d_i Y_i Yˆ_{i i }. Externally

studentized residuals untuk kasus ke-i, t_i, dihitung sebagai berikut [2]:

i

i i

d

d t

SE

 2.10

Paralel dengan Persamaan (2.9), pembilang dari persamaan (2.10) merupakan residual yang mana untuk kasus ke-i dihapuskan dan penyebut merupakan standar error dengan kasus ke-i diahapuskan. Residual yang

dihapuskan, d_i, dapat dihitung dengan menggunakan residual awal, e_i, yaitu dengan

1

i i

ii

e d

h 

 2.11

dan nilai standar residual juga dapat dihitung dengan:

 

1 i

residual i d

ii

MS SE

h



 2.12

22

 



1



i

i

ii residual i

e t

MS h



 2.13

Penentuan nilai outlier berdasarkan nilai Externally studentized residuals lebih banyak digunakan. Karena jika model regresi cocok dengan data, maka Externally studentized residuals akan mengikuti distribusi t dengan df   n k 1

[2]. Penentuan nilai cutoff –nya berdasrkan distribusi t, jika nilai t_ilebih besar dari nilai t_tabel dengan derajat kepercayaan  , maka data tersebut memiliki nilai discrepancy yang besar dan dikategorikan sebagai outlier.

3. Nilai Influence

Metode yang ketiga dalam diagnostik statistik untuk mendeteksi adanya outlier adalah dengan penentuan nilai influence. Ukuran dari influence merupakan kombinasi dari ukuran leverage dan discrepancy yang menginformasikan mengenai bagaimana perubahan dari persamaan regresi jika kasus ke-i dihilangkan dari himpunan data. Dua jenis pengukuran influnece yang biasa digunakan, pertama adalah ukuran ke-influence-an global, yaitu DFFITS dan

Cook’sD, yang memberikan informasi mengenai bagaimana kasus ke-i

mempengaruhi keseluruhan krarkteristik dari persamaan regresi. jenis yang kedua adalah ukuran ke-influnece-an khusus, yaitu DFBETAS, yang menginformasikan mengenai bagaimana kasus ke-i mempengaruhi tiap-tiap koefisien regresi. umumnya, keduanya dalam pengukuran ke-influence-an harus diperiksa.

23 persamaan regresi ketika kasus ke-i dimasukkan dan tidak dimasukkan dalam perhitungan himpunan data.

Ukuran pertama dalam mengukur ke-influence-an adalah DFFITS, yang didefinisikan sebagai berikut [2]:

   

ˆ ˆ

i i i i

ii residual i

Y Y DFFITS

MS h



 2.14

dengan Yˆ_imerupakan nilai prediksi ketika kasus ke-i dimasukkan ke dalam

himpunan data, Yˆ_{i i } merupakan nilai prediksi ketika kasus ke-i dihapuskan dari

himpunan data, MS_{residual i } merupakan nilai variansi dari residual ketika kasus

ke-i dihapuskan dari himpunan data dan h_iimerupakan nilai leverage seperti yang didefinisikan pada (2.5 dan 2.6). Pembilang pada (2.14) disebut DFFIT, yang menginformasikan seberapa besar nilai prediksi kasus ke-i akan berubah dalam unit data observasi Y jika kasus ke-i dihapuskan dari data. Penyebut pada (2.14) memberikan standardisasi DFFIT sehingga DFFITSi mengestimasi nilai dari

standar deviasi di mana Yˆ_i, nilai prediksi untuk kasus ke-i, akan berubah jika kasus ke-i dihapuskan dari data.

Seperti telah disebutkan di atas ukuran ke-influence-an merupakan perkalian dari leverage dan discrepancy. Oleh karena itu, DFFITS dapat diekspresikan dengan [2]:

1

ii i i

ii

h DFFITS t

h



24 secara aljabar ekuivalen dengan (2.14). Dengan t_i merupakan externally studentized residuals yang didefinisikan pada (2.13) dan h_iimerupakan leverage yang didefinisikan pada (2.5 dan 2.6). Jika nilai t_idan h_iikeduanya naik, maka besar dari DFFITS juga akan ikut naik hal ini menunjukkan kasus tersebut mempunyai pengaruh yang besar pada hasil analisis redresi. DFFITS = 0 ketika

kasus ke-i persis terletak pada garis regresi sehingga Yˆ_itidak mengalami perubahan ketika kasus i dihapuskan. Jika terletak pada centroid data sampel masih tetap memberikan beberapa pengaruh (influence), karena nilia minimum

dari h_iiadalah 1

n. Tanda dari DFFITS akan positif jika Yˆi Yˆi i dan negatif

ketika Yˆ_i Yˆ_{i i }.

Ukuran kedua untuk mengukur ke-influence-an global pada hasil model regresi karena kasus ke-i adalah Cook’sD, yang didefinisikan sebagai dengan [2]:

 









2

ˆ ˆ

'

1

i i i i

residual

Y Y Cook sD

k MS

 





2.16

dengan Yˆ_imerupakan nilai prediksi ketika kasus ke-i dimasukkan ke dalam

himpunan data, Yˆ_{i i } merupakan nilai prediksi ketika kasus ke-i dihapuskan dari

25 pada persamaan (2.16) di atas memberikan nilai yang distandardisasi. Tidak seperti DFFITS,Cook’sD akan selalu 0, tidak bisa negatif.

DFFITS dan Cook’sD dua ukuran yang berhubugan. Oleh karena itu, DFFITS dan Cook’sD mempunyai persamaan matematik sebagai berikut [2]:





_{ }





2

'

1

residual i i

i

residual

DFFITS MS Cook sD

k MS



 2.17

DFFITS dan Cook’sD merupakan statisitk dapat saling dipertukarkan, keduanya dapat digunakan untuk memberikan informasi mengenai ke-influence -an dari kasus i yang merupakan outlier. Penentuan kasus i sebagai outlier berdasarkan cutoff masing-masing. Untuk DFFITS, nilai DFFITS (dengan

mengabaikan tandanya) yang besarnya 1untuk data ukuran kecil



n 15



dan

sedang dideteksi sebagai outlier. Sedangkan untuk data yang ukuran besar, nilai

DFFITS 2



k 1



n



 merupakan data outlier. Untuk Cook’sD digunakan nilai

cutoff 1.0 atau dengan nilai kritik dari distribusi F dengan 0.50dan



1, 1



df  k  n k , jika nilai Cook’sD melebihi nilai kritik dari distribusi F

dideteksi sebagai outlier [2].

BFBETASij merupakan jenis kedua dari ke-influence-an statistik yang

penting jika peneliti ingin memfokuskan pada koefisien regresi tertentu dalam persamaannya. BFBETASij merupakan perbandingan koefisien-koefisien regresi

26

 

 

j i

j j i ij

DFBETAS

SE_

 

 2.18

pada persamaan di atas, pembilang merupakan perbedaan dari koefisien

dengan seluruh data dimasukkan,_j , dengan koefisien jika kasus ke-i dihilangkan, _{j i }. Penyebut,

 

j i

SE_ , merupakan standar error dari _{j i } setelah

data ke-i dihapuskan. Pembagian dengan

 

j i

SE_ memberikan nilai yang telah

distandardisasi, gunanya untuk mengintrepretasi secara umum pengaruh dari kasus ke-i untuk semua koefisien regresi. Tiap kasus data akan memiliki (k + 1) BFBETASij yang berkorepodensi dengan tiap koefisien regresi dalam

persamaannya termasuk intercept

 

₀ .

Penentuan kasus yang memiliki ke-influence-an yang merupakan outlier

berdasarkan BFBETASij adalah kasus yang memiliki DFBETASij  1 untuk

ukuran sampel yang kecil dan sedang, sedangkan untuk ukuran sampel yang besar

ditentukan dengan cutoff DFBETAS_ij 2 n

  [2].

2.3 Robust Estimasi 2.3.1 M-Estimasi

Suatu estimator yang hampir baik (variansi kecil) untuk berbagai jenis distribusi, tidak perlu yang terbaik untuk sebarang dari salah satunya., disebut suatu Robust Estimator. yaitu suatu estimator yang dihubungkan dengan solusi dari persamaan:





1

0

n i i

x 



  

27

 

1

w x jika x k

k

jika k x x

 

 

Persamaan (2.19) di atas sering disebut robust M-estimator (dinotasikan

dengan ˆ) karena persamaan (2.19) tersebut dapat dianggap sebagai maksimum likelihood estimator. Jadi dalam menemukan suatu robust M-estimator harus dipilih suatu fungsi yang akan memberikan suatu estimator yang baik untuk tiap distribusi pada himpunan ruang lingkupnya.

Fungsi yang telah dikenal adalah fungsi Huber yang merupakan kombinasi yang dihubungkan dengan distribusi normal dan distribusi eksponensial ganda, yaitu [5]:

 

,

, ,

, ,

x k x k

x k x k

k k x

    

   

 

2.20

yang diturunkan dari fungsi 

 

x , dengan fungsi 

 

x adalah sebagai berikut

[5]:

 

2 ₂

2

x

x jika x k x

k x k jika x k

 _{ } 

 

 2.21

Fungsi 

 

x berbentuk quadratik pada pusatnya, tetapi naik secara linear

28 Dengan fungsi Huber masalah lain muncul, yaitu jika digandakan tiap

1, 2,..., n,

X X X estimator seperti X dan median juga akan ganda. Salah satu cara

dalam mengatasi kesulitan ini adalah dengan pemecahan yang lain, tetapi sama hasilnya, yaiut dengan memecahkan persamaan:

1

0

n i i

x d

 



 

_{ }

 



2.22

dengan d merupakan suatu estimasi skala yang robust. Nilai d yang sering digunakan adalah [6]:

 

0.6745

i i

median x median x

d   2.23

[image:41.595.118.528.78.487.2]

pembagi 0.675 dimasukkan ke dalam definisi Persamaan (2.23) adalah karena d merupakan suatu estimasi yang konsisten dari  jika data sampel munsul dari distribusi normal [6]. Jadi,  dapat di aproksimasi dengan d di bawah asumsi distribusi normal.

29 Skema pemilihan d juga memberikan suatu petunjuk dalam pemilihan nilai k. karena jika data sampel muncul dari distribusi normal, maka dapat diharapkan

kebanyakan nilai-nilai x x₁, ₂,...,x_nmemenuhi pertidaksamaan [6]:

i

x

k d



 _

2.24

kemudian [6]:

i i

x x

d d

 

 

 

_{ }

  2.25

Sebagai ilustrasi, jika seluruh nilai-nilai yang memenuhi pertidaksamaan (2.24), maka Persamaan (2.22) menjadi:

1 1

0

n n

i i

i i

x x

d d

 

 

 

 

_{ } 

 





2.26

Persamaan (2.2.6) mempunyai pemecahan x,yang tentu saja yang lebih

diinginkan karena bersesuaian dengan distribusi normal. Karena d mengaproksimasi  , nilai-nilai popular dari k yang digunakan adalah 1.5 dan 2.0 [6], karena dengan pemilihan tersebut kebanyakan variable biasanya akan memenuhi Pertidaksamaan (2.24).

Selain hal di atas, suatu proses iterasi harus selalu digunakan untuk memecahkan Persamaan (2.22). salah satu skema yang akan digambarkan adalah

Metode Newton. Misal ˆ₀ merupakan estimasi awal dari , seperti

 

0

ˆ

i

median x

  . Aproksimasi bagian sebelah kiri persamaan (2.22) dengan

30





'

0 0

0

1 1

ˆ _ˆ ˆ ₁

0,

n n

i i

i i

x x

d d d

 _{ }     _   _ _{ } _ _   _ _      





2.27 hasil dari (2.24) memberikan estimasi yag kedua dari ,

0 1 1 0 ' 0 1 ˆ ˆ ˆ , ˆ n i i n i i x d d x d                        





2.28

Persamaan (2.28) disebut langkah pertama dari M-estimasi dari , jika

digunakan ˆ1 pada tempat ˆ0, didapatkan ˆ2, langkah kedua M-estiamsi dari .

Proses ini dapat berlangsun sampai mendapatkan sebarang tingkat akurasi yang diinginkan. Dengan fungsi , penyebut pada bentuk kedua Persamaan (2.28), yaitu: ' 0 1 ˆ , n i i x d    _   _ _  



khususnya secara mudah dihitung karena '

 

x    1, k x k,dan nol

jika lainnya. Jadi penyebut tersebut merupakan penjumlahan sedehana

bilangan-bilangan x x1, 2,...,xnsedemikian hingga xiˆ0 d k.

Selain fungsi  dan Huber, suatu fungsi lain yang sering digunakan

juga adalah fungsi dan Bisquare, yang didefinisikan sebagai [5]:

 

 

3 2

1 1

1

x k jika x k

x

jika x k

 _{ }     

 



2.29

31

 

3 5

6 12 6

1

x x x

jika x k

x k k k k k k

jika x k   _   _   _       

       

 _



2.30

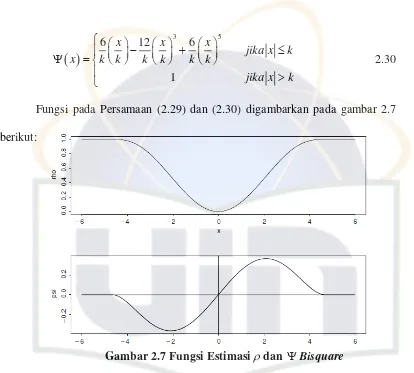
Fungsi pada Persamaan (2.29) dan (2.30) digambarkan pada gambar 2.7 berikut:

Disamping fungsi estimasi Bisquare yang telah didefinisikan pada Persamaan (2.29) dan (2.30) di atas, salah satu fungsi yang serimg digunakan juga adalah fungsi optimal, yang didefinisikan [5]:

[image:44.595.114.528.83.456.2]

Dan fungsi optimal didefinisikan dengan:

Gambar 2.7 Fungsi Estimasidan Bisquare

2.31

 

2

2 4 6 8

2

1 2 3 4

2

3.25 3

1.792 2 3

2 2

x

k jika

k

x x x x x

x k h h h h jika

k k k k k

x x

jika k





 



  

        

    _{ }   _{ }   _{ }   _{ }   

 

  



 _

32

 

1 2 3 3 5 4 7

0 3 2 3 2 x jika k

x x x x x

x k g g g g jika

k k k k k

x x jika k  _                  _{ }   _{ }   _{ }           _  Dengan 1 1 1 2 2 2 3 3 3 4 4 2 1.944, 2 1.728, 4 0.312, 6 0.016, 8 g g h g g h g g h g g h          

2.3.2 Trimmed Mean

Pendekatan lain selain M-estimasi dalam mengestimasi lokasi pada data yang mengandung outlier adalah Trimmed Mean. Dengan Trimmed Mean dalam data yang mengandung outlier seolah-olah membuang bagain data yang terbesar

dan terkecilnya. Secara jelasnya, misalkan 



0,1 2



dan m_



n1



_

dengan [.] menunujukkan bagian bulatnya, dan -Trimmed Mean didefinisikan sebagai [5]: ( ) 1 1 2 n m i i m x x n m     





2.33

dengan x_{ i} merupakan statistik terurut.

33 Trimmed Mean secara sepintas seperti menekan atau memadatkan data observasi. akan tetapi, tidak demikian. Karena hasilnya pada akhirnya merupakan fungsi untuk seluruh data observasi. Kasus khusus untuk  0 dan 0.5 merupakan mean sampel dan median sampel.

2.3.3 Ukuran ke-Robust-an

Tujuan dari metode robust secara kasar dapat dikatakan adalah untuk

mengembangkan estimasi yang mempunyai suatu kelakuan yang “baik” dalam

suatu “lingkungan” model.

Diantara ukuran yang mengukur ke-robust-an adalah: 1. Influence Function (IF)

Sebelum mendefinisikan IF terlebih dahulu akan didefinisikan dulu kurva

sensitive (sensitive curve (SC)), yaitu: misal x0suatu outlier yang ditambahkan

kedalam himpunan data, maka SC dari suatu estimasi ˆuntuk titik sampel

1,...., n

x x adalah perbedaan dari



1 0





1



ˆ x,...,x x_n, ˆ x,...,x_n

  ,

yang merupakan fungsi lokasi outlier x₀

Fungsi influence dari suatu estimator merupakan suatu jenis asimptotik

dari SC yang mengaproksimasi kelakuan dari ˆ_ketika data sampel yang terdapat

bagian kecil dari outlier, yang secara matematik didefinisikan sebagai [5]:











0



 

ˆ 0

0

ˆ 1 ˆ

IF_ x , F lim F x F



   



 



  

34







0



0

ˆ _{1 F}

            . dengan 0 x

 merupakan titik massa pada x₀, yaitu distribusi yang sedemikian

hingga P x



x0



1dan “” merupakan tanda yang menyatakan limit dari

kanan. Jika terdiri dari p parameter-parameter yang tak diketahui, maka ˆ_

merupakan vektor p-dimensi dan begitu halnya dengan IF-nya.

Kuantitas









0

ˆ 1 F _x

_   adalah nilai asimptotik dari estimasi ketika

distribusi yang membangunnya adalah F dan bagian dari outlier sama dengan

0

x . Jadi jika  kecil kuantitas tersebut dapat diaproksimasi dengan [5]:







0



 

ˆ



0



ˆ ₁ ˆ _{IF ,}

x

F F _ x F

_   _  2.35

dan bias









 

0

ˆ ₁ F _x ˆ F

_   _ diaproksimasi dengan IF_ˆ



x F0,



IF dapat dianggap sebagai kasus khusus dari kurva sensitif, dalam

pengertian berikut: ketika ditambahkan observasi yang baru x₀terhadap sampel

1, , n

x  x bagian yang terkontaminasi adalah 1



n1



, dan juga didefinisikan SC

yang distandardisasi, yaitu sebagai berikut:

 





























1 1 0 1

n 0

1 1 0 1

ˆ _{, , ,} ˆ _{, ,}

SC ,

1 1

ˆ ˆ

1 , , , , ,

n n n n

n n n n

x x x x x

x

n

n x x x x x

                2.36

yang serupa dengan Persamaan (2.34) dengan  1



n1



yang

diharapkan adalah jika x_inya i.i.d dengan distribusi F, maka

 

0



0



35

 

0

SC x merupakan variabel random, dan jika ˆ merupakan M-estimasi lokasi

dengan mempunyai batas dan fungsi- yang kontinu, atau merupakan trimmed

mean, maka untuk tiap x₀[5]

 

0 . . ˆ



0



SCn x a s IF_ x F, 2.36

dengan “a.s.”merupakan kekonvergenan dengan probabilitas 1 (“almost

sure” convergen). Hasil ini diperluas untuk M-estiamasi lokasi ˆ yaitu:









0





ˆ 0 '

ˆ

IF ,

ˆ

x x F

E x



 

 _

 

 , 2.37

dan untuk M-estimasi skala ˆadalah:









0

 





ˆ 0 '

ˆ ˆ

IF ,

ˆ ˆ

x x F

E x x



  



  



 



 . 2.38

2. Breakdown point (BP)

Breakdown point suatu titik estimasi ˆdari parameter  adalah kuantitas terbesar dari keterkontaminasian (proporsi dari outlier) yang terdapat dalam data

sedemikian hingga ˆ tetap memberikan informasi mengenai , mengenai distribusi dari titik-titik yang bukan outlier dalam himpunan data tersebut.

36

 

0, ,

   dan estimasi harus tetap terbatas, dan juga terbatas jauh dari 0, dalam

pengertian bahwa jarak antara ˆ dan 0 harus lebih besar dari suatu nilai positif.

Menurut [5] suatu asimptotik kontaminasi BP dari suatu estimasi ˆ pada F,

dinotasikan  *

 

ˆ,F ,adalah nilai *

 

0,1 sedemikian hingga untuk   *,









ˆ _{1 F G}

_   sebagai suatu fungsi dari G yang tetap terbatas, dan juga

terbatas dari batas . Definisi tersebut bermaksud bahwa terdapat suatu batas dan himpunan yang tertutup K  sedemikian hingga K   (dengan  

merupakan batas dari ) sedemikian hingga









*

ˆ _{1 F G K dan G.}

37 BAB III

ROBUST ESTIMASI PADA REGRESI

3.1 Least trimmed square (LTS)

Sebelum membahas mengenai least trimmed square (LTS), akan diketengahkan dahulu sifat-sifat ke-equivariant- an yang harus dimiliki oleh suatu

estimator ( penggunaan kata “equivariant” dalam statistic merujuk pada

transformasi sebagaimana mestinya, dan kata lawannya yaitu invariant merujuk pada kuantitas yang tetap tidak berubah), yaitu: regresi equivariant, skala equivariant, dan affine equivariant.

Suatu estimator T disebut sebagai regresi equivariant jika memenuhi:











_i, _{i i} ; 1,....,









_i, _i



; 1,....,





,

T x y x v i n T x y i n v 3.1 dengan vmerupakan sebarang vektor kolom. Suatu estimator T disebut sebagai skala equivariant jika memenuhi:











_i, _i ; 1,....,









_i, _i



; 1,....,





,

T x cy i n cT x y i n 3.2 untuk sebarang konstanta c. skala equivariant menyebabkan bahwa kecocokan secara esensial independen dari pemilihan satuan pengukuran pada variabel respons y. Sedangakan, suatu estimator T adalah affine equivariant jika memenuhi:













1













, ; 1,...., , ; 1,...., ,

i i i i

T x A y i n AT x y i n 3.3 untuk sebarang matrik persegi A y