SISTEM BONUS MALUS DENGAN FREKUENSI KLAIM
BERDISTRIBUSI GEOMETRIK DAN UKURAN KLAIM
BERDISTRIBUSI WEIBULL
LILYANI SUSANTI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Sistem Bonus-Malus dengan Frekuensi Klaim Berdistribusi Geometrik dan Ukuran Klaim Berdistribusi Weibull adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
LILYANI SUSANTI. Sistem Bonus-Malus dengan Frekuensi Klaim Berdistribusi Geometrik dan Ukuran Klaim Berdistribusi Weibull. Dibimbing oleh I GUSTI PUTU PURNABA dan I WAYAN MANGKU.
Sistem Bonus-Malus adalah salah satu sistem yang ditawarkan oleh suatu perusahaan asuransi, dalam perhitungan premi risiko berdasarkan sejarah klaim dari setiap pemegang polis. Pada karya tulis ini dijelaskan dua jenis sistem Bonus-Malus yang berbeda, yaitu sistem Bonus-Malus klasik dan sistem Bonus-Malus optimal. Sistem Bonus-Malus klasik menetapkan perhitungan premi risiko bagi setiap pemegang polis hanya berdasarkan frekuensi klaim yang diajukan. Sedangkan sistem Bonus-Malus optimal menetapkan perhitungan premi risiko bagi setiap pemegang polis berdasarkan frekuensi klaim dan ukuran klaim.
Kedua sistem Bonus-Malus tersebut dibandingkan, dengan frekuensi klaim dan ukuran klaim diasumsikan masing-masing memiliki sebaran geometrik dan Weibull. Risiko yang dihadapi oleh setiap pemegang polis berbeda-beda sehingga banyaknya klaim dan ukuran klaim yang akan diajukan setiap pemegang polis pun berbeda-beda. Dicari sebaran posterior dari parameter frekuensi dan ukuran klaim, kemudian parameter tersebut diduga menggunakan metode Bayes, sehingga diperoleh solusi kedua sistem tersebut. Solusi tersebut berupa premi yang akan datang berdasarkan sejarah klaim dari setiap pemegang polis.
Kata kunci : Sistem Bonus-Malus, sebaran geometrik, sebaran Weibull.
ABSTRACT
LILYANI SUSANTI. Bonus-Malus Systems with Geometric Distributed Claim Frequency and Weibull Distributed Claim Severity. Under supervision by I GUSTI PUTU PURNABA and I WAYAN MANGKU.
Bonus-Malus system is one of systems implemented by an insurance in calculating the risk premium based on claim history from each policyholder. In this work we discussed two different types of Bonus-Malus system namely the classical Bonus-Malus system and the optimal Bonus-Malus systems. The classical Bonus-Malus system sets the risk premium by taking into account only the number of accidents of each policyholder. While the optimal Bonus-Malus and frequency claim parameters is estimated by using Bayes method. Subsequently, solutions of both systems are obtained in term of future premium based on claim history from each policyholder.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
SISTEM BONUS MALUS DENGAN FREKUENSI KLAIM
BERDISTRIBUSI GEOMETRIK DAN UKURAN KLAIM
BERDISTRIBUSI WEIBULL
LILYANI SUSANTI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Sistem Bonus-Malus dengan Frekuensi Klaim Berdistribusi Geometrik dan Ukuran Klaim Berdistribusi Weibull
Nama : Lilyani Susanti NIM : G54110034
Disetujui oleh
Dr Ir I Gusti Putu Purnaba, DEA Pembimbing I
Prof Dr Ir I Wayan Mangku, MSc Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2014 ini ialah asuransi, dengan judul Sistem Bonus-Malus dengan Frekuensi Klaim Berdistribusi Geometrik dan Ukuran Klaim Berdistribusi Weibull.
Terima kasih penulis ucapkan kepada:
1. bapak Tri Susanto, ibu Tuti Gartini selaku orangtua yang sudah membesarkan, menyayangi, mendidik dan selalu mendoakan penulis,
2. bapak Dr Ir I Gusti Putu Purnaba, DEA selaku pembimbing I, bapak Prof Dr Ir I Wayan Mangku, MSc selaku pembimbing II dan ibu Dr Berlian Setiawaty, MS selaku penguji,
3. seluruh dosen Departemen Matematika IPB yang telah banyak membagi ilmu dan pengalamannya,
4. seluruh staf Departemen Matematika IPB yang telah memberikan semangat dan doanya,
5. Abi, Sinta teman satu bimbingan yang telah memberikan masukan untuk karya ilmiah ini,
6. Resty, Widya, Firi yang telah menjadi pembahas pada seminar tugas akhir ini, 7. sahabat belajar bareng Dinita, Ari, Arli, Widya, Dyah yang telah
memberikan doa, motivasi dan keceriaan selama masa kuliah dan penyusunan karya ilmiah ini,
8. teman-teman Matematika 48 terimakasih atas kebersamaannya selama ini, 9. kak Risma yang telah memberikan masukan selama bimbingan berlangsung, 10. kakak-kakak S2 Matematika 51 yang telah memberikan motivasi,
11. semua pihak yang terlibat dalam penyusunan karya ilmiah ini.
Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan kghususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 2
Tujuan Penelitian 2
TINJAUAN PUSTAKA 3
HASIL DAN PEMBAHASAN 8
Penentuan Premi Risiko pada Sistem Bonus-Malus 8
Penerapan Formula Premi Risiko pada Sistem Bonus-Malus 13
SIMPULAN DAN SARAN 16
Simpulan 16
Saran 16
DAFTAR PUSTAKA 17
LAMPIRAN 18
DAFTAR TABEL
1 Sistem Bonus-Malus berdasarkan komponen frekuensi klaim 13 2 Sistem Bonus-Malus berdasarkan komponen frekuensi dan ukuran
klaim (Total ukuran klaim 7500) 14
3 Sistem Bonus-Malus berdasarkan komponen frekuensi dan ukuran
klaim (Total ukuran klaim 10000) 15
DAFTAR LAMPIRAN
1 Sebaran frekuensi klaim 18
2 Sebaran posterior dari parameter frekuensi klaim 20 3 Nilai ̅ diperoleh dengan Maximum Likelihood Estimation 22
4 Nilai harapan dari sebaran gamma 23
5 Perolehan ̂ dengan solusi Bayes 25
6 Fungsi sebaran eksponensial 26
7 Fungsi sebaran tak bersyarat dari yang merupakan sebaran Weibull 27 8 Representasi alternatif dari fungsi Bessel termodifikasi 29 9 Nilai harapan dari sebaran posterior parameter ukuran klaim 30
10 Nilai harapan ukuran klaim 31
11 Fungsi rekursif dari 33
12 Premi risiko pada kasus 34
PENDAHULUAN
Latar Belakang Masalah
Asuransi adalah istilah yang digunakan untuk menggambarkan sebuah sistem atau bisnis yang merupakan tindakan perlindungan secara finansial untuk properti dari kejadian-kejadian yang tidak dapat diduga, yang melibatkan pembayaran premi secara teratur sebagai ganti polis yang menjamin perlindungan tersebut. Berbagai macam sistem digunakan oleh perusahaan asuransi untuk menarik minat masyarakat, salah satunya adalah sistem Bonus-Malus.
Sistem Bonus-Malus adalah penentuan harga premi dalam asuransi yang didasarkan pada riwayat klaim pemegang polis. Dalam sistem ini bonus akan diberikan dalam bentuk pemotongan biaya premi yang harus dibayar apabila tidak ada klaim yang diajukan pada tahun sebelumnya. Sedangkan malus diberikan dalam bentuk penambahan biaya premi apabila ada klaim yang diajukan pada tahun sebelumnya. Menurut Leimare (1998), setiap pemegang polis dari sebuah risk cell akan dibagi berdasarkan kelas Bonus-Malus dan riwayat klaim mereka, yang kemudian akan memodifikasi kelas tersebut ketika perpanjangan polis.
Sistem Bonus-Malus yang digunakan biasanya adalah sistem Bonus-Malus klasik, sistem tersebut hanya mempertimbangkan berdasarkan frekuensi klaim tanpa memperhitungkan besar atau kecil klaim tersebut. Dalam sistem ini pemegang polis yang mendapatkan kerugian kecil atau besar mendapatkan premi yang sama. Sistem ini sudah digunakan di beberapa negara dan beberapa diantaranya sudah dimodifikasi agar dapat disesuaikan dengan kebutuhan penggunaan, seperti yang sudah diteliti oleh Lemaire dan Zi (1994) di dalam jurnalnya yang menggunakan data dari 30 perusahaan yang memberikan jasa asuransi dari berbagai negara yang berbeda.
Salah satu kesalahan yang dilakukan perusahaan asuransi dalam sistem ini adalah bila pemberian bonus yang besar tidak diseimbangkan dengan pemberian malus yang sama besar. Hal ini dapat menyebabkan kerugian tidak hanya pada pemegang polis tetapi juga kepada pihak asuransi seperti yang diteliti oleh Ibiwoye et al. (2011). Kesalahan tersebut juga dapat mengakibatkan angka kecelakaan kendaraan tidak menyusut dikarenakan pemegang polis menganggap mendapatkan malus tidak memberikan dampak yang merugikan bagi mereka, seperti yang dikemukakan oleh Mamoudvand et al. (2013).
Frangos dan Vrontos (2001) membuat sistem Bonus-Malus optimal, yaitu sistem yang sudah dimodifikasi sehingga bukan hanya frekuensi klaim saja yang digunakan, tetapi besar klaim dimasukkan juga ke dalam perhitungan. Mahmoudvand dan Hassani (2009) melanjutkan penelitian tersebut dengan membuat sistem Bonus-Malus optimal diperumum.
2
Perumusan Masalah
Salah satu hal penting bagi sistem Bonus-Malus pada suatu perusahaan asuransi adalah penentuan premi risiko yang berdasarkan pada riwayat klaim pemegang polis tersebut. Terdapat dua sistem Bonus-Malus yang bisa digunakan, yaitu sistem Bonus-Malus klasik dan sistem Bonus-Malus optimal.
Pada sistem Bonus-Malus klasik, perhitungan premi risiko hanya didasarkan pada frekuensi klaim tanpa memperhitungkan besar atau kecil klaim tersebut. Sedangkan pada sistem Bonus-Malus optimal, perhitungan premi risiko didasarkan pada frekuensi dan ukuran klaim pemegang polis tersebut.
Dari beberapa uraian diatas, dapat dirumuskan beberapa masalah sebagai berikut:
1. Bagaimana menentukan premi pada sistem Bonus-Malus klasik dan sistem Bonus-Malus optimal dengan frekuensi klaim memiliki sebaran geometrik dan ukuran klaim memiliki sebaran Weibull.
2. Bagaimana perbandingan premi risiko dari kedua sistem tersebut.
Tujuan Penelitian
3
TINJAUAN PUSTAKA
Definisi 1 (Percobaan Acak)
Dalam suatu percobaan seringkali diperlukan pengulangan yang dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul adalah diketahui, tetapi hasil pada percobaan berikutnya tidak dapat diduga dengan tepat. Percobaan semacam ini disebut percobaan acak (Hogg et al. 2014).
Definisi 2 (Ruang Contoh dan Kejadian)
Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian adalah himpunan bagian dari Ω (Grimmett dan Stirzaker 1992).
Definisi 3 (Medan-σ)
Medan-σ adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian dari ruang contoh Ω yang memenuhi kondisi berikut:
Peubah acak dikatakan diskret jika nilainya hanya pada himpunan bagian yang terhitung dari (Grimmet dan Stirzaker 1992).
Catatan:
4 dan dapat direpresentasikan sebagai berikut:
5 Definisi 13 (Sebaran Eksponensial)
Suatu peubah acak dikatakan menyebar eksponensial dengan parameter , jika memiliki fungsi kepekatan peluang:
Definisi 15 (Sebaran Invers Gauss yang Diperumum (Generalized Inverse Gaussian Distribution))
Suatu peubah acak dikatakan menyebar invers gauss yang diperumum, jika memiliki fungsi kepekatan peluang:
Suatu peubah acak dikatakan menyebar Levy yang juga disebut sebagai sebaran stabil dengan parameter jika memiliki fungsi kepekatan peluang:
Suatu peubah acak dikatakan menyebar Weibull dengan parameter dan jika memiliki fungsi kepekatan peluang:
(Gray dan Pitts 2012).
Definisi 18 (Fungsi Sebaran Bersama Dua Peubah Acak)
Fungsi sebaran bersama dua peubah acak dan merupakan suatu fungsi [ ] yang didefinisikan oleh:
6
Definisi 19 (Fungsi Kepekatan Peluang Bersama dan Marginal)
Misalkan dan adalah peubah acak kontinu, maka fungsi kepekatan peluang bersama dari dan adalah
dan fungsi kepekatan peluang marginal dari peubah acak adalah ∫
7
Misalkan peubah acak memiliki sebaran prior dengan fungsi kepekatan peluang bersama yang dilambangkan dengan dan memiliki fungsi kepekatan peluang marginal . Fungsi kepekatan peluang gabungan dari dilambangkan dengan dinamakan fungsi kepekatan peluang dari sebaran posterior, dan dinyatakan dengan
fungsi kerugian kuadratik merupakan fungsi kerugian dengan kesalahan kuadrat dari parameter tersebut dinyatakan dengan:
(Bain dan Engelhardt 1993).
Definisi 28 (Fungsi Risiko)
Fungsi risiko adalah nilai harapan dari fungsi kerugian, yang dinyatakan sebagai berikut: solusi Bayes jika penduga parameter ̂ meminimumkan
[ ( ̂ ] ∫ ( ̂
8
Seseorang yang menjadi pemegang polis suatu perusahaan asuransi diharuskan membayar premi risiko atas klaim yang dibuat, penetapan besarnya premi risiko dihitung berdasarkan sistem yang ada pada perusahaan asuransi tersebut. Salah satu sistem yang digunakan oleh suatu perusahaan asuransi adalah sistem Bonus-Malus.
Terdapat dua jenis sistem Bonus-Malus yaitu sistem Bonus-Malus klasik dan sistem Bonus-Malus optimal. Kedua sistem tersebut berbeda, karena hal yang akan mempengaruhi perhitungan premi risiko setiap pemegang polis berbeda pula. Sistem Bonus-Malus klasik
Dalam sistem Bonus-Malus klasik, perhitungan premi risiko yang harus dibayarkan oleh pemegang polis asuransi hanya bergantung pada frekuensi klaim.Frekuensi klaim yang diajukan oleh setiap pemegang polis berbeda-beda sehingga nilai harapan dari banyaknya klaim yang diajukan pun berbeda-beda.
Misalkan pada asuransi mobil yang memiliki portofolio yang berbeda (heterogen), setiap pemegang polis memiliki risiko dasar yang tidak sama atas kejadian yang dialaminya. Willmot (1993) menyebutkan bahwa sebaran Poisson campuran memberikan hasil yang baik untuk data frekuensi klaim yang heterogen. Maka pada karya tulis ini digunakan sebaran Poisson campuran sebagai sebaran dari frekuensi klaim yang diajukan oleh setiap pemegang polis tersebut yaitu sebaran geometrik.
Parameter dari frekuensi klaim dilambangkan dengan yang menyebar eksponensial, sehingga frekuensi klaim untuk setiap pemegang polis merupakan sebaran geometrik. Diasumsikan banyaknya klaim yang diajukan dinyatakan dengan yang menyebar Poisson dengan parameter .
(1) Dengan menyatakan perbedaan risiko yang mendasari atas klaim dari setiap pemegang polis tersebut. Asumsikan menyebar eksponensial dengan parameter
, maka fungsi kepekatan peluangnya adalah:
9 Kemudian sebaran tak bersyarat dari yang merupakan sebaran geometrik dengan parameter
Misalkan menyatakan banyaknya klaim dari setiap pemegang polis dalamtahun , dengan . Jika total banyaknya klaim yang terjadi dalam tahun adalah ∑ maka total banyaknya klaim dalam tahun menyebar Poisson dengan parameter .
∏
(4) Untuk menduga parameter dari frekuensi klaim tersebut, digunakan pendekatan Bayes dengan fungsi kerugian kuadratik (quadratic loss function). Dengan fungsi kepekatan peluang bersama dari kumpulan klaim pemegang polis dalam tahun, dan fungsi kepekatan peluang dari maka diperoleh sebaran posterior dari parameter frekuensi klaim tersebut , karena proporsional dengan sehingga sebaran posterior dari parameter frekuensi klaim dapat ditulis sebagai:
10
Nilai harapan dari sebaran gamma dibuktikan pada Lampiran 4. Nilai ̅ diperoleh dengan Maximum Likelihood Estimation (dijelaskan pada Lampiran 3).
Jika diasumsikan premi risiko awal pada saat dinyatakan dengan , maka premi risiko yang harus dibayarkan oleh setiap pemegang polis pada tahun , adalah:
Dalam sistem Bonus-Malus optimal, perhitungan premi risiko yang harus dibayarkan oleh setiap pemegang polis asuransi selain berdasarkan frekuensi klaimtetapi juga berdasarkan ukuran klaim.
Ukuran klaim dilambangkan dengan diasumsikan memiliki sebaran eksponensial dan parameter tersebut merupakan nilai dari peubah acak yang memiliki sebaran Levy, maka ukuran klaim memiliki sebaran Weibull dengan parameter . Diasumsikan ukuran klaim dinyatakan dengan . Untuk setiap pemegang polis, menyebar eksponensial dengan parameter , fungsi kepekatan peluangnya adalah:
(8) dan fungsi sebarannya adalah (dibuktikan pada Lampiran 6):
. (9) Sebaran dari adalah Levy yang juga disebut sebagai sebaran stabil dengan parameter yang memiliki fungsi kepekatan peluang:
(10) Misalkan dinotasikan sebagai ukuran dari klaim setiap pemegang polis pada frekuensi klaim , . Total ukuran klaim yang terjadi untuk setiap pemegang polis dalam tahun adalah ∑ . Fungsi kemungkinannya menyebar eksponensial dengan parameter ,
11 Untuk menghitung atau mengukur kerugian dari aset yang diasuransikan menggunakan fungsi kerugian kuadratik. Untuk menduga parameter dari ukuran klaim tersebut digunakan pendekatan Bayes dengan fungsi kerugian kuadratik (quadratic loss function). Dengan fungsi kepekatan peluang bersama dari total ukuran klaim dari setiap polis dengan klaim sampai tahun, , dan fungsi kepekatan peluang dari maka diperoleh sebaran posterior dari parameter ukuran klaim tersebut:
(13)
∫
(
∫ (
atau dapat ditulis sebagai berikut:
(
dengan , , . Persamaan tersebut adalah bentuk dari sebaran Invers Gauss yang diperumum. Dengan mengembalikan ke persamaan (13) didapat:
√
∫ ( √ √ √
√ ( √
. (14)
Integral pada bagian penyebut dapat diubah ke fungsi Bessel yang representasinya adalah sebagai berikut:
∫ , (15) atau representasi alternatif dari fungsi Bessel termodifikasi (dibuktikan pada Lampiran 8):
12
Nilai harapan dari sebaran posterior yang merupakan sebaran Invers Gauss yang diperumum (Gaussian Inverse Generalized) adalah (diuraikan pada Lampiran 9): [ ] √ √
√ . (18)
Karena pada model awal diasumsikan menyebar eksponensial dengan parameter , maka nilai harapan yang diberikan . Dengan mengintegralkan
Jika premi risiko ditetapkan tidak hanya bergantung pada banyaknya klaim , tetapi juga bergantung pada ukuran klaim , maka premi risiko yang harus dibayarkan oleh setiap pemegang polis adalah:
√ ( ( √
( √
. (20)
Jika kita misalkan rasio dari dua fungsi Bessel adalah:
√
√ √
√ √
(21) maka fungsi rekursif dari adalah (diuraikan pada Lampiran 11):
√
13 Dari persamaan (21) dan (22) dapat dilihat bahwa premi tidak terdefinisi pada saat ukuran klaim atau pada saat tidak ada klaim yang diajukan ( )
Misalkan pada suatu perusahaan asuransi, banyaknya klaim diasumsikan menyebar geometrik dengan parameter sebesar 1,25. Dalam perhitungan premi risiko ini digunakan Prinsip Premi Bersih (Net Premium Principle).
Asumsikan premi risiko yang harus dibayarkan setiap pemegang polis setara dengan tahun pertama. Misalkan premi risiko pada tahun adalah 100. Jika mendapatkan bonus yang cukup tinggi. Sedangkan jika pemegang polis mengajukan banyak klaim pada tahun pertama maka ia akan mendapatkan malus yang cukup tinggi.
Pada tabel berikut dapat dilihat perhitungan premi risiko dalam 7 tahun dengan variasi klaim menggunakan persamaan (7) dengan perangkat lunak Microsoft Excel.
Tabel 1 Sistem Bonus-Malus berdasarkan komponen frekuensi klaim
14
Sedangkan jika pemegang polis mengajukan satu klaim pada tahun pertama maka pemegang polis tersebut harus membayar malus sebesar 11% dari premi risiko awal.
Sistem Bonus-Malus optimal
Misalkan pada perusahaan asuransi seperti di aplikasi sebelumnya, kita gunakan sistem Bonus-Malus yang dalam perhitungan premi risikonya berdasarkan dua komponen yaitu komponen frekuensi dan ukuran klaim. Premi risiko yang harus dibayarkan oleh setiap pemegang polis dengan sistem Bonus-Malus optimal dihitung dengan menggunakan persamaan (20), dan apabila tidak ada klaim yang diajukan ( ) atau ukuran klaim premi risiko dihitung dengan menggunakan persamaan (23).
Seperti pada aplikasi sebelumnya, frekuensi klaim menyebar geometrik dengan parameter sebesar 1,25. Total ukuran klaim diasumsikan menyebar Weibull dengan fungsi sebaran pada persamaan (11) dan dipilih parameter sebesar 0,05. Total ukuran klaim dipilih sebesar 7500 dan 10000, diambil dua total ukuran klaim yang berbeda untuk membandingkan efek dari total ukuran klim terhadap premi risiko.
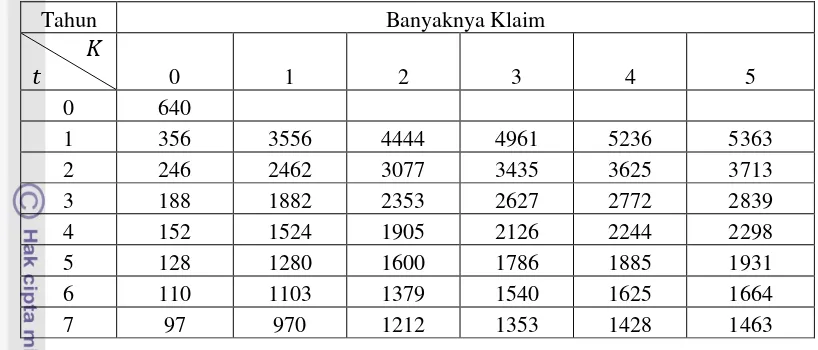
Dengan ukuran klaim 7500, jika pemegang polis mengajukan satu klaim di tahun pertama, maka ia harus membayar premi risiko sebesar 3079 (lihat Tabel 2), jadi ia mendapatkan malus dari perusahaan asuransi tersebut. Sedangkan jika total ukuran klaim 10000, seorang pemegang polis mengajukan satu klaim pada tahun pertama, ia harus membayar premi risiko sebesar 3556 (lihat Tabel 3), ia
15 Tabel 3 Sistem Bonus Malus berdasarkan komponen frekuensi dan ukuran klaim
(Total ukuran klaim sebesar 10000)
Tahun Banyaknya Klaim
0 1 2 3 4 5
0 640
1 356 3556 4444 4961 5236 5363
2 246 2462 3077 3435 3625 3713
3 188 1882 2353 2627 2772 2839
4 152 1524 1905 2126 2244 2298
5 128 1280 1600 1786 1885 1931
6 110 1103 1379 1540 1625 1664
7 97 970 1212 1353 1428 1463
Dari kedua tabel di atas dapat dilihat bahwa bagi seorang pemegang polis yang memiliki total ukuran klaim 7500, jika mengajukan satu klaim pada tahun pertama maka ia akan membayar premi risiko yang lebih tinggi dari premi risiko awal. Sedangkan bagi seorang pemegang polis yang memiliki total ukuran klaim sebesar 10000, jika ia mengajukan satu klaim pada tahun pertama maka ia harus membayar premi risiko yang jauh lebih tinggi dari premi risiko awal.
16
SIMPULAN DAN SARAN
Simpulan
Karya tulis ini telah membandingkan sistem Bonus-Malus klasik dan sistem Bonus-Malus optimal, yang biasa digunakan beberapa perusahaan asuransi seperti perusahaan asuransi mobil. Kedua sistem Bonus-Malus ini memiliki dasar perhitungan premi yang berbeda.
Dapat dilihat dari aplikasinya, sistem Bonus-Malus klasik ini bisa dikatakan tidak adil karena perhitungan premi risiko dari setiap pemegang polis tidak bergantung pada ukuran klaim setiap pemegang polis. Sedangkan perusahaan asuransi dengan sistem Bonus-Malus optimal cukup adil karena premi risiko yang harus dibayarkan oleh pemegang polis asuransi proporsional dengan risiko yang dihadapi. Premi risiko yang harus dibayarkan oleh setiap pemegang polis dengan kerugian kecil dan besar adalah berbeda. Sistem Bonus-Malus ini bergantung pada frekuensi dan ukuran klaim dari setiap pemegang polis.
Oleh karena itu, beban premi yang harus dibayarkan pada sistem Bonus-Malus optimal jauh lebih adil dibandingkan dengan sistem Bonus-Malus klasik
Saran
17
DAFTAR PUSTAKA
Abramowitz M, Stegun IA. 1964. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. New York: Dover.
Albrecher H, Constantinescu C, Loisel S. 2011. Explicit ruin formulas for models with dependence among risks. Insurance: Mathematics andEconomics 48(2):265-270.
Arnold SF. 1990. Mathematical Statistics. Prentice Hall, Inc. New Jersey.
Bain LJ, Engelhardt M. 1992. Introduction to Probability andMathematical Statistics. Ed ke-2. PWS-KENT publishing Company.Boston.
Frangos NE, Vrontos SD.2001. Design of an optimal bonus–malus systems with a frequency and a severity component on an individual basis in automobile
Hogg RV, McKean J, Craig AT. 2014. Introduction to Mathematical Statistics. Ed ke-7. Prentice Hall, Inc. New Jersey.
Ibiwoye A, Adeleke IA, Aduloju S. 2011. Quest for optimal bonus-malus in automobile insurance in developing economies: an actuarial prespective. International Business Research Vol.4 No. 4.
Lemaire J, Zi H. 1994. A comparative analysis of 30 bonus-malus systems. Astin Bulletin Vol.24No. 2.
Mahmoudvand R, Hassani H. 2009. Generalized bonus-malus systems with a frequency and a severity component on an individual basis in automobile insurance. ASTIN Bulletin 39, 307-315.
Mahmoudvand R, Edalati A, Shokoohi F. 2013. Bonus-malus system in Iran: an empirical evaluation. Journal of Data Science 11, 29-41.
Ni W, Constantinescu C, Pantelous AA. 2014. Bonus-malus systems with weibull distributed claim severities. Annals of Actuarial Science 8(2): 217-233. Tremblay L. 1992. Using the poisson inverse gaussian in bonus-malussystems.
ASTIN Bulletin 22(1): 97-106.
18
LAMPIRAN
Lampiran 1 Sebaran frekuensi klaim
Sebaran tak bersyarat dari (banyaknya klaim) adalah dengan mengintegralkan persamaan (1) dan (2), sehingga diperoleh:
∫
∫
∫
Dengan memisalkan
dan
maka: ∫
Dengan memisalkan kembali
Kita gunakan pengintegralan parsial untuk persamaan ini sehingga diperoleh: [ ⏞
∫ ]
[ ∫ ]
Dilakukan pengintegralan parsial dan dimisalkan kembali sehingga diperoleh:
[ ⏞
∫ ]
19 Kemudian dilakukan pengintegralan parsial berulang sampai diperoleh
[ ⏞
∫ ]
[ ]
, dengan dan .
Maka yang dinyatakan sebagai frekuensi klaim dalam sistem Bonus-Malus ini memiliki sebaran geometrik dengan parameter
20
Lampiran 2 Sebaran posterior dari parameter frekuensi klaim
Kita gunakan pendekatan Bayes untuk menduga parameter dari sistem Bonus-Malus klasik yaitu , dengan fungsi struktur posterior dari kumpulan frekuensi klaim pemegang polis dalam tahun, , maka diperoleh sebaran posterior dari parameter frekuensi klaim tersebut :
Sebaran awal (prior distribution):
Fungsi kepekatan peluang bersama dari total frekuensi klaim adalah ∏
dan fungsi kepekatan peluang dari :
Sebaran akhir (posterior distribution) :
. Jika
∫
∫
∫
Dengan memisalkan
dan maka:
∫
Dengan memisalkan kembali
Kita gunakan pengintegralan parsial untuk persamaan ini, maka: [ ⏞
∫ ]
21
Dilakukan pengintegralan parsial dan dimisalkan kembali, maka:
[ ⏞
∫ ]
[ ∫ ]
Kemudian dilakukan pengintegralan parsial berulang dari persamaan di atas, maka :
[ ⏞
∫ ]
[ ]
Sehingga diperoleh,
yang merupakan sebaran gamma .
Dengan menggunakan fungsi kerugian kuadratik yaitu ( ̂ ̂ , diperoleh solusi Bayes:
̂ (̅
̅ ̅ ̅ Sehingga
̂ ̅
22
Lampiran 3 Nilai ̅ diperoleh dengan Maximum Likelihood Estimation
Pada karya tulis ini digunakan Maximum Likelihood Estimation (MLE) untuk menduga parameter terhadap . Sehingga penduga parameter terhadap adalah :
∏
∑
( ( ∑ (
( ∑
Dengan MLE maka (
( ∑
(∑ ∑
̅
Penduga ̅ memaksimumkan fungsi likelihood. Bukti:
(
̅
23 Lampiran 4 Nilai harapan dari sebaran gamma
Jika suatu peubah acak memiliki sebaran gamma dengan parameter dan dengan dan , maka nilai harapan dari peubah acak tersebut adalah .
Bukti :
(
Fungsi kepekatan peluang dari sebaran tersebut adalah :
Maka,
∫
∫
∫
Dimisalkan ;
∫ (
∫
Dengan memisalkan kembali :
Gunakan pengintegralan parsial untuk persamaan tersebut: [ ⏞
∫ ]
24
Dilakukan pengintegralan parsial dan dimisalkan kembali sehingga diperoleh : [ ⏞
∫ ]
[∫ ]
Kemudian dilakukan pengintegralan parsial berulang sampai diperoleh : [ ⏞
∫ ]
[ ]
25 Lampiran 5 Perolehan ̂ dengan solusi Bayes
Jika kita menggunakan fungsi kerugian kuadratik (quadratic loss function), penduga parameter akan meminimumkan nilai harapan dari fungsi kerugian tersebut. Maka dengan solusi Bayes, penduga parameternya sama dengan nilai harapan dari sebaran posterior parameter tersebut.
Bukti:
Misalkan suatu peubah acak merupakan sebaran posterior dengan parameter dan nilai penduga parameter adalah .
Jika fungsi kerugian kuadratik dinyatakan :
[ ] [ ] maka nilai harapan dari fungsi kerugian kuadratik adalah:
{ [ ] {[ ]
{ [ ] {[ ]
{
[ ] [ ]
Karena yang akan meminimumkan nilai harapan dari fungsi kerugian kuadratik maka dengan turunan fungsi: [ [ ]]
[ ] ,
{ [ ] [ ]
[ ]
[ ] [ ]
Terbukti.
26
Lampiran 6 Fungsi sebaran eksponensial
Jika suatu peubah acak memiliki sebaran eksponensial dengan parameter , maka fungsi sebaran dari peubah acak adalah :
Bukti :
Fungsi kepekatan peluang dari sebaran tersebut adalah :
Sehingga fungsi sebaran dari peubah acak adalah :
∫
∫
28
Misalkan juga : √ , √ ∫ ( √ √ ∫
√
∫ ( √ ∫ ( √ √
Sehingga
√ √ ∫ ( √
√ √
29 Lampiran 8 Representasi alternatif dari fungsi Bessel termodifikasi
Representasi integral alternatif dari fungsi Bessel termodifikasi adalah : ∫
Bukti :
∫
∫ (
Misal ∫
∫
Misalkan ∫
∫ (
∫
30
Lampiran 9 Nilai harapan dari sebaran posterior parameter ukuran klaim
Nilai harapan dari sebaran posterior yang merupakan sebaran Invers Gauss diperumum (Generalized Inverse Gaussian) adalah:
[ ] √ √ √ . [ ] ∫
(
(√
∫
( (√
Misal √ , √
√
( ∫
√
(√
)
31 Lampiran 10 Nilai harapan dari ukuran klaim
Jika misalkan model awal diasumsikan menyebar eksponensial dengan parameter maka nilai harapan yang diberikan . Dengan mengintegralkan dengan sebaran posterior didapatkan:
[ ] √ ( √ ( √
Diasumsikan ukuran klaim dinyatakan dengan . Untuk setiap pemegang polis, menyebar eksponensial dengan parameter , fungsi kepekatan peluangnya adalah:
∫
Misalkan ( ∫
∫
Untuk menghitung atau mengukur kerugian dari aset yang diasuransikan menggunakan fungsi kerugian kuadratik. Digunakan pendekatan Bayes dengan fungsi kerugian kuadratik (quadratic loss function) untuk menduga parameter dari ukuran klaim tersebut. Dengan fungsi kepekatan peluang bersama dari total ukuran klaim dari setiap polis dengan klaim sampai tahun, , dan fungsi kepekatan peluang dari maka diperoleh sebaran posterior dari parameter ukuran klaim tersebut:
√
( ( √
atau
(
32
[ ] ∫
∫
(
(√
∫
(
(√
∫ √ (
(√
Misal √ , √
∫ √
√
√
(√
∫
√ √
(√
√ (√ (√
33 Lampiran 11 Fungsi rekursif dari
Jika kita misalkan rasio dari dua fungsi Bessel termodifikasi adalah:
√ √
√
√
√
maka fungsi rekursif dari adalah : ( √
√
√ karena
( √ ( √
√ ( √ √
√ √
√ ( √ √
( √
√
√
√
√
√
34
Lampiran 12 Premi pada kasus
Jika premi risiko ditetapkan tidak hanya bergantung pada banyaknya klaim , tetapi juga bergantung pada ukuran klaim , maka premi risiko yang harus dibayarkan oleh setiap pemegang polis adalah:
√ ( ( √
( √
. (20)
Jika kita misalkan rasio dari dua fungsi Bessel adalah:
(21)
maka fungsi rekursif dari adalah (diuraikan pada Lampiran 11):
(22) √
√ ( √
35
√ √ √
√ √ ( √
36
Lampiran 13 Bukti sifat fungsi Bessel termodifikasi
Misalkan fungsi Bessel termodifikasi maka untuk setiap , berlaku dua sifat yaitu :
1. ,
2. Bukti:
1.
∫
Misalkan ∫
∫
2. ∫
Misalkan
[ ⏞
∫
( ]
∫ (
[∫ ∫ ]
[ ] [ ]
37
RIWAYAT HIDUP
Penulis dilahirkan di Tangerang, Banten, pada tanggal 27 Agustus 1994. Penulis merupakan putri tunggal dari Bapak Tri Susanto, Ibu Tuti gartini. Tahun 2011, penulis lulus dari SMA Negeri 1 Bawang Banjarnegara dan diterima di Institut Pertanian Bogor (IPB) melalui jalur Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) Undangan. Penulis tercatat sebagai mahasiswa Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA).
Semasa menjadi mahasiswa, penulis aktif pada berbagai kegiatan. Penulis tergabung dalam Biro Kewirausahaan Gugus Mahasiswa Matematika (GUMATIKA) pada tahun 2013. Penulis juga terlibat aktif dalam kepanitiaan Pesta Sains Nasional pada tahun 2012, Matematika Ria pada tahun 2013 dan 2014 dan IPB Mathematics Challenge pada tahun 2013. Selain itu, penulis pernah menjadi asisten mata kuliah Persamaan Differensial Parsial pada tahun 2014 dan Persamaan Differensial Biasa pada tahun 2015.