Aplikasi Rantai Markov Multivariat Pada Network Genetik

APLIKASI RANTAI MARKOV MULTIVARIAT PADA

NETWORK GENETIK

SKRIPSI

NORA ANGGRIYA

070823008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

APLIKASI RANTAI MARKOV MULTIVARIAT PADA NETWORK GENETIK

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

NORA ANGGRIYA 070823008

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : APLIKASI RANTAI MARKOV MULTIVARIAT

PADA NETWORK GENETIK

Kategori : SKRIPSI

Nama : NORA ANGGRIYA

Nomor Induk Mahasiswa : 070823008

Program Studi : STATISTIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM ( FMIPA ) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, 16 Juli 2009

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Marwan Harahap, M.Eng. Dr. Sutarman, M.Sc.

NIP. 130 422 443 NIP. 131 945 359

Diketahui / Disetujui oleh

Departemen Matematika FMIPA USU Ketua

PERNYATAAN

APLIKASI RANTAI MARKOV MULTIVARIAT PADA NETWORK GENETIK

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa

kutipan dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, 16 Juli 2009

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala berkah, rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan Skripsi ini. Skripsi ini disusun sebagai salah satu syarat dalam menyelesaikan Program Studi S1 Statistika Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Ucapan terima kasih saya sampaikan kepada Dr. Sutarman, M.Sc selaku pembimbing 1 dan Drs. Marwan Harahap, M.Eng selaku pembimbing 2 pada penyelesaian Skripsi ini yang telah memberikan panduan dan penuh kepercayaan kepada saya untuk menyempurnakan kajian ini. Panduan ringkas dan padat serta profesional telah diberikan kepada saya agar penulis dapat menyelesaikan skripsi ini. Serta Drs. H. Haluddin Panjaitan dan Drs Pengarapen Bangun, M.Si yang telah bersedia menjadi dosen penguji skripsi ini. Terimakasi atas saran dan masukannya. Ucapan terima kasih juga ditujukan kepada Ketua dan Sekretaris Departemen Dr. Saib Suwilo, M.Sc dan Drs. Hendri Rani Sitepu, M.Si. Dekan dan Pembantu Dekan Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, semua dosen pada Departemen Matematika FMIPA USU, Pegawai di FMIPA USU, dan

rekan – rekan kuliah. Akhirnya, tidak terlupakan kepada kedua orang tua saya

ABSTRAK

Metode pengambilan keputusan markov merupakan suatu metode yang telah dikenal luas untuk pengambilan keputusan dalam model-model stokastik. Dalam tulisan ini dibahas penggunaan salah satu metode pengambilan keputusan markov, yaitu aplikasi network genetik.

APPLICATIONS OF MULTIVARIATE MARKOV CHAIN TO GENETIC NETWORKS

ABSTRACT

Markov Decision process is one of the well-known metodes to solve optimisation problem in stochastic modelling theory. In this paper, we show one simple example of applications to genetic networks.

The Probabilistict Boolean Networks (PBN) is a discrete-time process, the probability

distribution of gene expression at time t + 1 of the ith gene can be estimated by the

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel viii

BAB 1 PENDAHULUAN 1

1.1Latar Belakang 1

1.2Perumusan Masalah 3

1.3Tujuan Penelitian 3

1.4Kontribusi Penelitian 4

1.5Tinjauan Pustaka 4

1.6Metode Penelitian 5

1.7Sistematika Penulisan 5

BAB 2 TINJAUAN TEORITIS 7

2.1 Rantai Markov 7

2.2 Model Rantai Markov Multivariat 8

2.3 Estimasi Pada Model Parameter 11

2.4 Aplikasi Rantai Markov Multivariat Pada Network Genetik 13

BAB 3 PEMODELAN RANTAI MARKOV UNTUK NETWORK

GENETIK 17

BAB 4 KESIMPULAN DAN SARAN 32

4.1 Kesimpulan 32

4.2 Saran 32

DAFTAR TABEL

Halaman

Tabel 3.1 Hasil Deret yang Pertama 22

BAB 1

PENDAHULUAN

1.1Latar Belakang

Dengan berkembangnya ilmu pengetahuan dan teknologi yang sangat cepat dan pesat

ilmu statistik memegang peranan penting dalam kehidupan. Ilmu ini mampu

membantu meningkatkan kreatifitas dan produktifitas manusia. Pada era globalisasi

ini ilmu ini perlu diterapkan dengan cara yang lebih sederhana sehingga mudah

digunakan dalam pengambilan keputusan.

Salah satu bagian dari statistika adalah rantai markov (markov chain). Rantai

markov merupakan suatu proses stokastik yang digunakan untuk pembuatan model

dengan bermacam-macam sistem. Rantai markov ini, salah satunya digunakan untuk

membantu meramalkan kejadian-kejadian pada masa yang akan datang dengan

pengambilan keputusan.

Rantai markov (Markov Chain) adalah suatu teknik matematika yang biasa

digunakan untuk pembuatan model (modeling) bermacam-macam sistem dan proses

bisnis. Teknik ini dapat memperkirakan perubahan-perubahan pada waktu yang akan

datang dalam variabel-variabel dinamis pada waktu yang lalu. Teknik ini dapat juga

digunakan untuk menganalisis kejadian-kejadian pada waktu mendatang secara

matematis.

Penerapan rantai markov mula-mula digunakan untuk menganalisis dan

memperkirakan perilaku partikel-partikel gas dalam suatu wadah tertutup serta

meramalkan keadaan cuaca. Sebagai suatu peralatan riset operasi dalam pengambilan

keputusan manajerial. Proses markov telah banyak diterapkan untuk menganalisis

rekening, jasa persewaan mobil, perencanaan penjualan, masalah-masalah persediaan,

pemeliharaan mesin, antrian, perubahan harga pasar saham, dan administrasi rumah

sakit.

Analisis rantai markov adalah suatu teknik probabilitas yang menganalisis

pergerakan probabilitas dari satu kondisi ke kondisi yang lainnya. Rantai markov ini

dikenalkan oleh Andrei A. Markov, ahli matematika dari rusia yang lahir tahun 1856

(Ching dan Ng, 2006). Analisis markov hampir sama dengan decision analysis,

bedanya adalah analisis rantai markov tidak memberikan keputusan rekomendasi,

melainkan hanya informasi probabilitas mengenai situasi keputusan yang dapat

membantu pengambilan keputusan. Dengan demikian, analisis rantai markov

bukanlah teknik optimisasi, tetapi adalah teknik deskriptif yang menghasilkan

informasi probabilitas dimasa mendatang.

Matriks adalah suatu susunan bilangan berbentuk segiempat.

Bilangan-bilangan dalam susunan itu disebut anggota matriks tersebut.(Anton Howord,

2000:45). Ordo suatu matriks dinyatakan dengan jumlah baris dan kolom yang

terkandung dalam matriks tersebut. Matriks yang berorde (m*n), dengan m

menyatakan jumlah baris dan n menyatakan jumlah kolom. Di mana baris dalam

matriks merupakan unit pengamatan atau subyek sedangkan kolom merupakan

variabel yang diukur untuk setiap unit. Multivariat untuk menyelesaikan masalah atau

problema yang berkaitan tiga variable atau lebih. Teknik analisis statistik yang

melakukan sekelompok variabel kriteria yang saling berkorelasi sebagai satu sistem

yang memperhitungkan korelasi antar variabel–variabel tersebut.

Analisis multivariat merupakan salah satu jenis analisis statistik yang

digunakan untuk menganalisis data yang terdiri dari banyak peubah bebas

(independent variabel) dan juga banyak peubah tak bebas (dependent variabel). Data

multivariat adalah data yang dikumpulkan dari dua atau lebih observasi dengan

mengukur observasi tersebut dengan beberapa karakteristik.

1. Univariat meliputi satu variabel kriteria yang tergolong dalam himpunan data

2. Bivariat (pasangan variabel acak) dua variabel saling berkaitan

3. Multivariat terdiri dari beberapa variabel kriteria.

Jaringan kerja (model network) adalah suatu diagram yang digunakan untuk

membantu menyelesaikan masalah matematika yang cukup rumit agar menjadi lebih

sederhana dan mudah diamati. Masalah-masalah yang dapat diatasi dengan network

antara lain masalah penjadwalan (network planing), masalah transportasi, masalah

penggantian peralatan, dan masalah lintasan terpendek.

Genetik merupakan ilmu tentang pewarisan sifat individu kepada keturunannya,

berkaitan dengan gen atau faktor keturunannya. Jadi network genetik merupakan

tingkat hubungan fungsional untuk setiap kejadian pada waktu tertentu. Untuk

menyelesaikan suatu persoalan dalam pengambilan keputusan ada tidaknya

hubungan antara kondisi satu dengan kondisi lain dengan menggunakan aplikasi rantai

markov multivariat pada network genetik.

1.2Perumusan Masalah

Masalah yang dibahas dalam penelitian ini adalah memodelkan rantai markov

mutivariat pada network genetik dan memaparkan kaidah yang berhubungan

dengannya.

1.3Tujuan Penelitian

Menguraikan cara menentukan ada tidaknya hubungan tingkat sensivitas dari gene

satu ke gene yang lain dengan menggunakan aplikasi rantai markov multivariate pada

1.4Kontribusi penelitian

Menambah wawasan dan memperkaya literatur dalam bidang statistika yang

berhubungan dengan model rantai markov multivariat.

1.5Tinjauan Pustaka

Rantai markov multivariat telah digunakan diberbagai bidang. Pada bidang

matematika keuangan Artzner dan Delbaen (1997) menggunakan rantai markov untuk

menentukan risiko kegagalan hadiah dan pemasaran tidak lengkap. Sementara itu

bidang biologi Mendoza, Thieffry dan Alvarez (1999) menggunakan genetik kontrol

dari bunga morphogenesis pada Arabidopsis Thaliana. Rantai markov multivariat

digunakan pada model network genetik oleh Ching, Fung dan Ng (2004) membangun

network genetik pada contoh gene ekspresi. Salah satu penelitian gen yang penting

adalah dapat memahami mekanisme cara menjalankan sel-sel dan pengendalian nomor

besar pada operasi untuk fungsi normal, dan juga sistem sel-sel dalam penyakit.

Model dasar seperti pada network neural, non-linier sederhana, Petri nets, persamaan

differensial ditujukan untuk berbagai masalah, lihat pada Smoelen, Baxter dan Byrne

(2000) menggunakan model matematik pada network gene, neuron, oleh Bower

(2001) menggunakan model komputasi pada genetik dan network biokimia, oleh De

Jong (2002) mengunakan model dan simulasi pada sistem regulatori genetik.(Ching

dan Ng (2006)).

Pada model network ini, setiap gene adalah verteks pada network dan

jumlahnya hanya dua tingkat (jelas (0) atau tiadak jelas (1)). Pada bidang bioinformasi

oleh Akutsu, Miyano and Kuhara (2000) menggunakan penarikan kesimpulan

menurut kwalitas relasi pada network genetik dan pergantian zat pada setiap barisan,

ditujukan banyak network Boolean bersama dengan identifikasi algorithm.(Ching dan

Network Boolean adalah bagian dari pembuatan network genetik pada

dasarnya, maka n sebagai nomor pada pertimbangan gene bawah, yang mana verteks

i

v mewakili gene i, dan v_i(t) mewakili ungkapan tingkat gene i pada waktu t, ambil

salah satu 0 atau 1. ungkapan tingkat gen yang lain adalah hubungan fungsional untuk

itu pada gene-gene lain. Perhitungan model-model itu menyatakan hubungan yang

logis pada gagasan Bodnar (1997) menggunakan pemograman drosophila embryo.

Pada jurnal Biologi, Mendoza, Thieffry dan Alvarez (1999) menggunakan genetik

control dari bunga morphogenesis pada Arabidopsis Thaliana, dan oleh Huang dan

Ingber (2000) menggunakan model–bergantung (dependent) mengkontrol

pertumbuhan sel, differensial, dan apoptosis: perpindahan antara atractors pada sel

network regulatori, percobaan pada penelitian sel.(Ching dan Ng (2006)).

1.6Metode Penelitian

Uraian yang digunakan dalam penelitian secara rinci meliputi:

1. Mengestimasi jk

P dan jk ;

2. Menghitung frekuensi transisi dari keadan deret k sampai keadaan deret j, dari

sini dapat disusun matriks frekuensi pada deret data;

3. Setelah dinormalisasi, diperoleh estimasi pada matriks transisi probability;

4. Menghitung pada setiap kejadian masing-masing gene;

5. Menghitung tingkat pengaruh dari gene j ke gene i.

1.7Sistematika Penulisan

Adapun sistematika penulisan Tugas Akhir secara garis besar dibagi dalam 4 bab

masing-masing bab dibagi atas beberapa sub-sub bab yaitu:

Bab ini menjelaskan latar belakang, perumusan masalah, tujuan

penelitian, kontribusi penelitian, tinjauan pustaka, metode penelitian,

dan sistematika penulisan tugas akhir.

BAB 2 : TINJAUAN TEORITIS

Bab ini menguraiakan tentang teori-teori dan tinjauan tentang segala

sesuatu yang menyangkut terhadap penyelesaian masalah yang

dihadapi, sesuai judul yang diutarakan.

BAB 3 : PEMODELAN RANTAI MARKOV UNTUK NETWORK GENETIK

Bab ini menguraikan persoalan menggunakan pemodelan rantai

markov multivariat pada network genetik.

BAB 4 : KESIMPULAN DAN SARAN

Bab ini berisikan kesimpulan dari pembahasan didalam penyelesaian

skripsi serta saran-saran yang diberikan peneliti berdasarkan

BAB 2

LANDASAN TEORI

2.1 Rantai Markov

Rantai markov (Markov Chain) adalah suatu model teoritis yang menjelaskan keadaan

sebuah sistem pada suatu tahap tertentu. Model ini dapat memperkirakan

perubahan-perubahan pada waktu yang akan datang dalam variabel-variabel dinamis pada waktu

yang lalu. Teknik ini dapat juga digunakan untuk menganalisis kejadian-kejadian pada

waktu mendatang secara sistematis.

Penerapan rantai markov mula-mula digunakan untuk menganalisis dan

memperkirakan perilaku partikel-partikel gas dalam suatu wadah tertutup serta

meramalkan keadan cuaca. Sebagai suatu peralatan riset operasi dalam pengambilan

keputusan manajerial. Proses markov telah banyak diterapkan untuk menganalisa

tentang perpindahan merek (brands witching) dalam pemasaran, perhitungan rekening,

jasa persewaan mobil, perencanaan penjualan, masalah-masalah persediaan,

pemeliharaan mesin, antrian, perubahan harga pasar saham, dan administrasi rumah

sakit.

Rantai markov ini dikenalkan oleh Andrei A. Markov, ahli matematika dari

Rusia yang lahir tahun 1856 (Ching dan Ng, 2006). Analisis markov menghasilkan

suatu informasi probabilistik yang dapat digunakan untuk membantu pembuatan

keputusan, jadi analisis ini bukan suatu teknik optimisasi melainkan suatu teknik

deskriptif. Analisis markov merupakan suatu bentuk khusus dari model probabilistik

yang lebih umum dinamakan dengan Stochastic process, yaitu proses perubahan

Untuk dapat menerapkan analisis rantai markov kedalam suatu kasus, ada

beberapa syarat yang harus dipenuhi :

1. jumlah probabilitas transisi untuk suatu keadaan awal dari sistem sama dengan

1(satu),

2. Probabilitas-probabilitas tersebut berlaku untuk semua partisipan dalam

sistem,

3. Probabilitas transisi konstan sepanjang waktu,

4. kondisi merupakan kondisi yang independent sepanjang waktu.

Dalam realita, penerapan analisis markov biasa terbilang cukup terbatas karena

sulit menemukan masalah yang memenuhi semua sifat yang diperlukan untuk analisis

markov, terutama persyaratan bahwa probabilitas transisi harus konstan sepanjang

waktu (probabilitas transisi adalah probabilitas yang terjadi dalam pergerakan

perpindahan kondisi dalam sistem).

2.2 Model Rantai Markov Multivariat

Pada bagian ini, dibahas model rantai markov mutivariat menggambarkan deret

multiple kategorik dengan hasil yang sama. Diasumsikan s deret kategorik dan yang

lain m kemungkinan keadan dalam himpunan M = {1,2,…,m}.

Misalnya j

n

X keadan vektor deret j pada waktu n. jika deret j dalam keadaan

l pada waktu n maka dapat ditulis

t

j masukkan l

j

n e 0,,0,_1_ ,0,0

X

Pada persaman model rantai markov multivariat , diasumsikan sebagai berikut:

s j

untuk P

s

k

k n jk jk j

n , 1,2,..., 1

1 X

X (1)

Dengan _jk 0, 1 j,k s (2)

Dan

s

k

jk untuk j s 1

. ,..., 2 , 1 ,

Pada keadaan probability distribusi deret k pada waktu t (n+ 1) bergantung pada

rata-waktu n. Bentuk matriks dapat ditulis

.

Walaupun jumlah kolom Q tidak sama dengan satu (jumlah kolom jk

P sama dengan

satu), sebagaimana menurut dalil :

Dalil 1. jika parameter _jk 0, untuk 1 j,k s, maka matriks Q mempunyai nilai eigen sama dengan satu dan nilai eigen pada Q memiliki aturan lebih kecil dari atau

sama dengan satu.

terjabarkan. Theorema Perron-Frobenius, dimana ada sebuah vektor

T

harus satu nilai eigen pada Q.

Untuk menunjukkan semua nilai eigen pada Q kurang dari atau sama dengan

satu. Misalnya defenisi pada vektor-norm

adalah vektor-norm pada ms

R . Dapat didefenisikan menurut matriks norm

. 1 :

sup Q v v Q

M z z Sejak

ij

P matriks transisi, yang mana anggotanya

ij

P adalah kurang dari atau sama dengan satu.

Dengan 1 1, 1 , .

1 i j s

P ij z_j z_j Disini

1

. adalah 1-norm untuk sebuah

vektor.

s

j ij s

is is i

i i

i P P P v i s

1 1

2 2 2 1 1

1 z z ... z z . 1,1 dan dari sini

. 1

M

Q Sejak spectral radius pada Q selalu kurang dari atau sama setiap matriks

norm pada Q, dengan hasil sebagai berikut.

Dalil 2. menduga matriks jk

P (1≤ i, j ≤ s) adalah tak terjabarkan (irreducible) dan

. , 1 ,

0 untuk j k s

jk Maka disana adalah sebuah vektor tunggal

T s

x x

x

x 1, 2 ,, dengan demikian x Qx dan 1,1 .

1

s j

m

i

i j

x

Bukti. Dalil 1, di atas adalah tepat suatu nilai eigen pada Q sama dengan satu. Ini

tercantum n T

n

Q vu

lim setiap barisan matriks positif seperti Q adalah tak

terjabarkan (irreducible). Karena itu lim x ₁ lim x lim nx₀ vuTx₀ v.

n n n

n n

Q Q

Disini adalah positif sejak x 0 dan tidak negative. Pada xn cenderung menuju

pada sebuah vektor stasionary seperti n menuju tak hingga. Akhirnya, dinotasikan jika

0

x adalah vektor dengan demikian 1,1 ,

1

0 j s

m

i

i j

x maka Qx dan x juga

memiliki vektor-vektor.

Sekarang andaikan bahwa ada y dengan demikian y x dan lim n.

n x

y

Maka didapat x y x Qx 0. Ini adalah suatu penyangkalan dan karena itu

vektor x harus tunggal. Kemudian didapatkan hasilnya.

Dinotasikan x bukan vektor distribusi probability, tetapi j

x vektor distribusi

mengestimasi model parameter _ij. Andaikan untuk mendapatkan _ij yang mana

minimisasi Qxˆ xˆ tentu dibawah vektor norm . .

2.3 Estimasi Pada Model Parameter

Pada bagian ini, dibahas metode untuk estimasi jk _jk

dan

P . Mengestimasi matriks

transisi probability jk

P dengan mengikuti metode. Pertama menghitung frekuensi

transisi pada keadan deret k. Setelah menormalisasikan, diperoleh estimasi pada

matriks probability transisi. Mengestimasi n demikian m dengan m matriks transisi

probability untuk mendapat estimasi pada jk

P seperti dibawah ini:

jk

F dapat mengestimasi untuk jk

P seperti dibawah ini:

dapat mengestimasi dari deretan gene ekspresi dengan menghitung proporsi pada

kejadian masing-masing gene dan dinotasikan dengan:

T

Karena itu diharapkan bahwa

x

Dari persaman (4) mengangap satu kemungkinan untuk estimasi parameter

jk . Dalam fakta, dengan . seperti vektor norm untuk mengukur

perbedaan pada persamaan (4), dapat diselesaikan dengan cara minimisasi;

.

Persamaan (5) dapat dirumuskan seperti s masalah linier programming sebagai

berikut, dapat dilihat (Chvatal V (1983)). Untuk j lain:

Dengan

s js j

j

P P

P

B ˆ 1 xˆ 1 ˆ 2 xˆ 2  ˆ xˆ .

Dengan

( jk)

F = matriks frekuensi pada keaadan deret k ke keadaan deret j

jk

Pˆ = matriks transisi probability pada keadaan deret k ke keadaan deret j

_jk = parameter

2.4 Aplikasi Rantai Markov Multivariat Pada Network Genetik

Pada bagian ini, model rantai markov multivariat yaitu memodelkan network genetik.

Network Boolean merupakan faktor yang menentukan, keadaan tak pasti. Pada

umumnya network Boolean G V,F terdiri dari himpunan V v1,v2,,vn dan

t

v_i menggambarkan keadaan (0 atau 1) v_i pada waktu t. Fungsi Boolean

n

f f

f

F 1 , 2 ,, menggambarkan aturan regulatori interaksi antara simpul:

n i

t f t

v_i 1 i v , 1,2,, , dengan v t v₁ t ,v₂ t ,,v_n t . Pada

umumnya, sebagian simpul tak perlu pada fungsi Boolean. Untuk fungsi Boolean

j

f , variabel v_i t disebut tak benar jika

t v v

t v t v f t v t v t v t v

f j ₁ ,, _{i 1} ,0, _{i 1} ,, _n j ₁ ,, _{i 1} ,1, _{i 1},, _n untuk

semua nilai kemungkinan pada v₁ t ,,v_{i 1} t ,v_{i 1} t ,,v_n t . Dengan menganggap

bahwa ketika network boolean digunakan dalam penyusunan pada network genetik

utama, maka n melambangkan jumlah dari gene-gene berdasarkan pertimbangan,

setiap verteks vi mewakili gene i, dan vi(t) melambangkan tingkat ekspresi gene i

pada waktu t, salah satunya 0 atau 1. Tingkat ekspresi pada setiap gene adalah relasi

fungsional untuk gene lainnya.

Model network genetik regulatori dapat ditulis seperti:

, , , 1 li j i j

i f

F



dimana setiap prediktor i

j

dan l i jumlah kemungkinan prediktor untuk gene vi. Ini jelas bahwa i n

i F

F  ₁ .

Misalnya i

j mencapai kesalahan optimal dengan

i j

f dan _i adalah kesalahan pada

estimasi terbaik dari gene i dalam ketidakadaan suatu kondisi variabel, maka didapat

i

j semua positif, dapat diperoleh

i

v dapat diperoleh sebagai berikut:

n

Pada tingkat pengaruh dari gene j ke gene i dapat ditaksir dengan

i

pertama dibutuhkan untuk memperoleh semua prediktor i

n i 1 F

 Dianggap bahwa

untuk setiap himpunan dari F_i dengan 1 i n, jumlah maksimum dari prediktor

adalah sama pada 22n seperti 1 l i 22n , ini adalah benar untuk penyesuaian

probabilitas i

i l i

c c₁ ,, .

Probabiliti Network Boolean (PBN) yaitu proses pada waktu diskrit, distibusi

probability pada gene ekspresi diwaktu t+ 1 dari gene i dapat diestimasi dengan gene

ekspresi pada gene n yang lain diwaktu t-1 matriks transisi. Ini adalah proses markov

framework. Diingat bahwa model rantai markov multivariat untuk menduga network

genetik dari gene n. Pada network ini, tidak ada informasi sebelumnya pada hubungan

gene-gene n diterima, model yang ditunjukkan tersebut digunakan untuk menemukan

variasi hubungan gene yang utama, termasuk gene dan hubungan gene cyclic atau

acyclic. Ini dapat mengestimasi kondisi distribusi probability d

i

i n

X _,...,

ekspresi pada dasar t+ 1 yang diberikan dengan suatu himpunan pada gene input

ekspresi pada dasar t,

n

vektor probability d

i

i n

X _,...,

1 yaitu unit vektor dan untuk setiap d, disana

n

jumlah pada estimasi vektor probability dapat direduksi separuh. Setelah semuanya

penting d

dengan

1

tidak ada dan bentuknya tereliminasi. Ini menarik untuk membenarkan bagaimana

ekspresi dari gene i dipengaruhi oleh ekspresi gene j, oleh karena itu, tingkat

sensitivitas dari gene j ke gene i dapat diestimasi dengan persamaan (6) yang

disinggung pada bagian sebelumnya. Perhatikan dua kondisi I_j v_i 0,

1. Jika dk =0, maka gene j tidak memberikan suatu pengaruh pada gene i.

2. Pertama kedua kolom pada matriks jk

P adalah sama, artinya ekspresi pada

gene j tidak begitu penting, hasil pada vektor probability adalah tidak

berpengaruh.

Dengan:

i

j v

I = penghitungan keadaan (state) transisi probability tingkat pengaruh gene i

i k

f = prediktor gene i jika i k

c positif

i k

c = estimasi dari training data

n

v = nilai variabel ke n

d i

i _n

X _{, ,}

1 =estimasi kondisi probability untuk d output ekspresi pada t+ 1 dengan

himpunan gene input ekspresi t

d t

V ₁ = distribusi probability pada gene d pada waktu t+ 1

k t

V = tingkat pada gene k pada waktu t

dk = parameter

d g

c = estimasi probability pada prediktor d

g

f

d g

f = prediktor gene d tidak ada dan bentuknya tereliminasi jika d

g

BAB 3

PEMODELAN RANTAI MARKOV UNTUK NETWORK GENETIK

Pada bab ini akan dibahas pemodelan rantai markov untuk network genetik. Metode

pengambilan keputusan markov merupakan suatu metode yang telah dikenal luas

untuk pengambilan keputusan dalam model-model stokastik. Dalam bab ini dibahas

penggunaan salah satu metode pengambilan keputusan markov, yaitu aplikasi network

genetik, untuk menyelesaiakan ada tidaknya hubungan antara baris pertama dengan

baris kedua pada waktu t dalam pengambilan keputusan.

Andaikan suatu persoalan penentuan model parameter yaitu menggunakan dua

deret binary, yang mana anggotanya 0 dan 1.(Ching dan Ng, 2006). Dalam hal ini

dipertimbangkan terdapat 12 gene yang masing-masing baris diasumsikan 0 dan 1

(state-statenya). Pada waktu pertama, gene-1 bernilai 0, gene-2 bernilai 0, gene-3

bernilai 1, gene-4 bernilai 0, gene-5 bernilai 0, gene-6 bernilai 0, gene-7 bernilai 0,

gene-8 bernilai 0, gene-9 bernilai 1, gene10 bernilai 1, gene11 bernilai 0, dan gene-12

bernilai 0. Pada waktu kedua gene-1 bernilai 1, gene-2 bernilai 1, gene-3 bernilai 0,

gene-4 bernilai 0, gene-5 bernilai 1, gene-6 bernilai 0, gene-7 bernilai 0, gene-8

bernilai 0, gene-9 bernilai 0, gene10 bernilai 1, gene11 bernilai 0, dan gene-12 bernilai

1. Berdasarkan hal diatas gene-gene tersebut diformulasikan sebagai berikut:

1 , 0 , 1 , 0 , 0 , 0 , 0 , 1 , 0 , 0 , 1 , 1

0 , 0 , 1 , 1 , 0 , 0 , 0 , 0 , 0 , 1 , 0 , 0

2 1

s dan s

Karena anggotanya hanya 0 dan 1 maka gambar network hanya mengunakan

tanda panah saja.

Dengan menghitung frekuensi transisi sebagai berikut:

1 0 1 0 0 0 0 1 0 0 1 1 :

0 0 1 1 0 0 0 0 0 1 0 0 :

2 1

:

Diperoleh matriks frekuensi sebagai berikut:

1

Setelah menormalisasi diperoleh matriks transisi probability:

.

Dan diperoleh

T

Setelah menyelesaikan persoalan diatas, model Markov multivariate pada dua deret

binary adalah dengan membuat

Kondisi distribusi probability vektor 1 0 , 0

X dapat menaksir seperti:

56

Dengan cara yang sama diperoleh:

3 1 3 2

4 1 4 3

0 . 0

3 1 3 2

0 . 1

1 0

4 1

7 3

4 3

7 4

0 . 0 1 0

3 1

8 3

3 2

8 5

0 . 1

1 , 0

ˆ

0 . 0 1 , 0

ˆ

0 .

1 21 22

2 1 , 1

T T

P P

X

Dari bagian sebelumnya, probability i

j

c dapat memperoleh suatu hasil di dalam Tabel

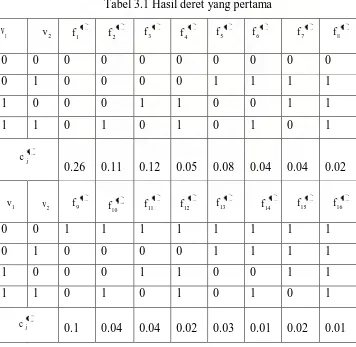
Tabel 3.1 Hasil deret yang pertama

0 0 0 0 0 0 0 0 0 0

0 1 0 0 0 0 1 1 1 1

1 0 0 0 1 1 0 0 1 1

1 1 0 1 0 1 0 1 0 1

0.26 0.11 0.12 0.05 0.08 0.04 0.04 0.02

1 10

f

0 0 1 1 1 1 1 1 1 1

0 1 0 0 0 0 1 1 1 1

1 0 0 0 1 1 0 0 1 1

1 1 0 1 0 1 0 1 0 1

0.1 0.04 0.04 0.02 0.03 0.01 0.02 0.01

1

v v₂

2

v

1 1

f f₂1 f₃1 f₄1 f₅1 f₆1 f₇1 f₈1

1 9

f f₁₁1 f₁₂1 f₁₃1 f₁₄1 f₁₅1 f₁₆1

1 j

c

1 j

c

1

Untuk mendapatkan hasil deret pertama berdasarkan table diatas dapat diuraikan

sebagai berikut:

01

Dengan cara yang sama, diperoleh:

03

Karena pada 22 0, tentu pada prediktor untuk deret yang kedua dapat memperkecil

signifikan.

Dari tabel 3.1 dan 3.2 tingkatan kesensitifan I_j v_i dapat memperoleh dengan

menunjukkan perhitungan.

Tabel 3.2 Hasil deret yang kedua

2

Dengan pembahasan diatas diperoleh hasil:

Dan

Dengan cara yang sama, diperoleh:

0

menentukan deret yang kedua. Tetapi, kejadian-kejadian ini telah diilustrasikan

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Berdasarkan hasil dari perhitungan dan pembahasan yang telah dikemukakan pada

bab-bab sebelumnya, maka dapat diambil kesimpulan sebagai berikut:

1. Pada tingkat sensitifitas I₁(v₁) 0.4 yang artinya ekspresi dari gene 1

dipengaruhi oleh ekspresi gene 1 sebesar 0.4,

2. Pada tingkat sensitifitas I₁(v₂) 0.45 yang artinya ekspresi dari gene 1

dipengaruhi oleh ekspresi gene 2 sebesar 0.45,

3. Pada tingkat sensitifitas I₂(v₁) 0.4 yang artinya ekspresi dari gene 2

dipengaruhi oleh ekspresi gene 1 sebesar 0.4,

4. Pada tingkat sensitifitas I₂(v₂) 0 yang artinya gene 2 tidak memberikan

suatu pengaruh pada gene 2,

5. Mengestimasi matriks frekuensi dapat menormalisasikan suatu keadan matriks

transisi probabiliti.

4.2 Saran

Ada baiknya jika ingin melanjutkan skripsi ini dengan menggunakan Model Markov

Tersembunyi atau lebih dikenal dengan Hidden Markov Model (HMM) adalah sebuah

model statistik dari sebuah sistem yang diasumsikan sebuah Markov Proses dengan

parameter yang tidak diketahui, dan tantangannya adalah menentukan

parameter-parameter tersembunyi (hidden) dari parameter-parameter-parameter-parameter yang dapat diamati.

Parameter-parameter yang ditentukan kemudian dapat digunakan untuk analisis yang

lebih jauh, misalnya untuk aplikasi Pattern Recoginition. Sebuah HMM dapat

DAFTAR PUSTAKA

Akutsu, T., Miyano, S., dan Kuhara, S. 2000. Inferring Qualitative Relation in

Genetic Networks and Metabolic Arrays. Bioinformatic.

Artzner, P., dan Delbaen, F. 1997. Default Risk Premium and Incomplkete

Markets. Mathematical Finance.

Bharucha-Reid, A.T. 1983. Probabilistic Analysis and Related Topics. New York

London: Academic Press.

Bodnar, J. 1997. Programming the Drosophila Embryo. Journal of Theoretical

Biology.

Bower, J. 2001. Computational Modeling of Genetik and Biochemical Networks.

MIT Press, Cambridge, M.A.

Ching, W., Fung, E., dan Ng, M. 2004. Building Genetic Networks in Gene

Expression Pattern. IDEAL2004. Lecture Notes in Computer Science. (Yang,

Z., Everson, R., dan Yin H(Eds.)). Springer.

Ching, W., dan Ng, M. 2006. Markov Chain: Models, Algorithms and

Application. New York: Springer Science + Business Media, Inc.

Clarke, A., Bruce, dan Disney Ralph, L. 1970. Probability and Random

Processes. New York: Jhon Wiley & Sons,Inc.

Chvatal, V. 1983. Linier Programming. Freeman. New York.

De Jong, H. 2002. Modeling and Simulation of Genetic Regulatory System:A

Literature Review. Journal Computational. Biology.

Hines William, W., dan Montgomery Douglas, C. 1990. Probabilita dan Statistik

Dalam Ilmu Rekayasa dan Manajemen. Jakarta: UI-Press.

Huang, S., dan Ingber, D. 2000. Shape-dependent Control of Cell Growt

Differentiation, and Apoptosis: Switching Between Atractors in Cell

Regulatory Networks. Experimental Cell Research.

Mendoza, L., Thieffry, D., dan Alfarez-Buylla, E. 1999. Genetic Control of

Flower Morphogenesis in Arabidopsis Thaliana: A Logical Analisys,

Bioinformatics.

Preston Gordon, dan Watterson Geoffrey. 1972. Probability and Statistics.

Smolen, P., Baxter, D., dan Byrne, J. 2000. Mathematical Modeling of Gene

Network, Neuron.